Ellipse
The orbit of planet Earth around the Sun is an ellipse.
Definitions
- $a$: the half-length of the ellipse along the $x$ axis, also known as the semi-major axis.
- $b$: the half-length of the ellipse along the $y$ axis.
- $F_1,F_2$: the two focal points of the ellipse.
- $\epsilon$: the eccentricity of the ellipse.
- $(x,y)$: a point on the ellipse.
- $r_1$: the distance from the point $(x,y)$ on the ellipse to $F_1$.
- $r_2$: the distance from the point $(x,y)$ on the ellipse to $F_2$.
Formulas
An ellipse is the curve you get if you trace out all the points such that the sum of the distances to the focal points is a constant length: \[ r_1 + r_2 = \text{const}. \]
There is a really neat way to draw a perfect ellipse using a piece of string and two tacks (pins). Take a piece of string and tack it to a picnic table at two points such that it is loose in the middle. Now take a pencil and without touching the table move the string until both sides are tout. Make a mark at that point. Since the two parts of the string are completely straight, their sum length, $r_1+r_2$ is the length of the whole piece, which plays the role of the constant in the above equation. When you make a mark at every point possible where the two “legs” of string are kept tout you get the following curve:
The mathematical formula for the ellipse is: \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \] where in the above drawing we have $a>b$ so the ellipse is elongated on the $x$ axis.
The coordinates of the focal points are: \[ F_1 = (-e,0), \qquad F_2 = (e,0), \] where $e=\sqrt{a^2 - b^2}$. The focal points correspond to the locations of the two tacks where the string is held fixed.
An important related quantity is the eccentricity: \[ \epsilon \equiv \sqrt{1- \frac{b^2}{a^2} }=\frac{e}{a} , \] which describes the shape of the ellipse in a scale-less fashion. The bigger $\epsilon$ the bigger the difference in the length of the major-axis and the minor-axis. In the special case when $\epsilon=0$, the equation of the ellipse becomes a circle of radius $a$.
Polar coordinates
Polar functions $r(\theta)$ describe the distance of some point from the centre as a function of the angle $\theta$ the point makes with the $x$-axis. Thus in the coordinate system $(r,\theta)$, the independent variable is $\theta$ and the dependent variable is $r$.
If we setup a polar coordinate system with centre at the origin $C=(0,0)$, the equation of the ellipse will be: \[ r(\theta) = \frac{ab}{b^2\cos^2(\theta) + a^2\sin^2(\theta)}. \]
For many applications, it is more convenient to put the centre of the polar coordinates system at $F_1$, the left focal point. Suppose that $(r_1,\phi)$ is a polar coordinate system with centre $C=F_1=(-e,0)$, then the equation of the ellipse is \[ r_1(\phi) = \frac{a(1-\epsilon^2)}{1 - \epsilon\cos(\phi)}, \] where the angle $\phi$ is with respect to the positive $x$-axis.
Applications
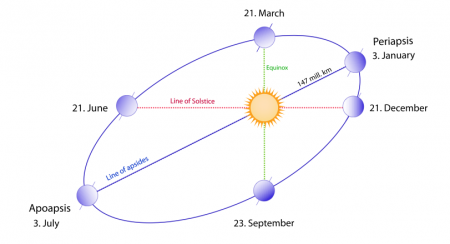
Orbit of the Earth around the Sun
To a very good approximation, the motion of the earth around the sun is described by an ellipse with the sun at one focus. The distance of the earth from the sun (positioned at $F_1$, so we are talking about $r_1$) as a function of the angle $\phi$ is given by: \[ r_1(\phi) = \frac{a(1-\epsilon^2)}{1 - \epsilon\cos(\phi)}. \]
The eccentricity of the earth's orbit around the sun is $\epsilon = 0.01671123 $ and the half-length of the major axis is $a=149\:598\:261$[km]. So the distance sun-earth $r_1$ is given by the equation: \[ r_{1}(\phi) = \frac{149556484.56}{1 - 0.01671123\cos(\phi)} \text{[km]}. \]
The moment where the earth is most distant from the sun is called aphelion and occurs around January 3rd. The closet point is called perihelion and it usually occurs around July 4th. The aphelion distance of the earth happens when $\phi=0$ so we have \[ r_{1,aphe}=r_1(0) = \frac{149556483}{1 - 0.01671123\cos(0)} = 152098232 \text{[km]}, \] and the closes pass of the earth near the sun is when $\phi=\pi$ at \[ r_{1,peri} = r_1(\pi) = \frac{149556483}{1 - 0.01671123\cos(\pi)} = 147098290 \text{[km]}. \] If you don't trust me, look up the numbers on wikipedia and compare them with the above predictions.
The angle $\phi$ of the earth relative to the sun, is a function of time. If we measure $t$ in days we have the following lookup table:
| t (day) | 1 | 2 | . | 182 | . | 365 | 365.242199 |
|---|---|---|---|---|---|---|---|
| t (date) | July 3 | July 4 | . | Jan 3 | . | July 2 | ? |
| phi (deg) | 0 | . | 180 | . | 359.761356 | 360 | |
| phi (rad) | 0 | . | pi | . | 6.27902 | 2 pi |
Note the extra amount of “day” that is roughly equal to $\frac{1}{4}=0.25$. Ever wonder why one of every four years is a leap year? That is why.
The exact formula of the function $\phi(t)$ that describes the angle as a function of time is complicated, but computable.
Note that the varying distance of the earth from the sun is not the cause of seasons. Seasons are predominantly caused by the tilt of the earth relative to the plane of its orbit around the sun. The day the tilt of the earth spin axis aligns with sun is either the longest day or the shortest day of the year, depending on which hemisphere you are in (the North or the South). We call those days solstices.
Newton's insight
Contrary to what is commonly believed, Newton did not come up with his theory of gravitation while sitting under a tree because an apple fell on his head. What actually happened is that he started from Kepler's laws of motion which describes the exact elliptical orbit of the Earth as a function of time. Newton asked “what kind of force would cause two bodies to spin around each other in an elliptical orbit” and he deducted that the gravitational force between the sun of mass $M$ and the earth of mass $m$ must be of the form $F_g=\frac{GMm}{r^2}$. We have to give props to the man, for connecting the dots, and we have to give props to Johannes Kepler studying the orbital periods and Tycho Brahe for doing all the astronomical measurements. Above all, we have to give props to the ellipse for being such an awesome shape.