Electrostatics is the study of charge and the electric forces that exist between charges. The same way that the force of gravity exists between any two objects with mass, the electric force (Coulomb force) exists between any two charged objects. We will see, however, that unlike gravity which is always attractive (tends to bring masses closer together), the electrostatic force can sometimes be repulsive (tends to push charges apart).

Electrostatics is a big deal. You are alive right now, because of the electric forces that exist between the amino acid chains (proteins) in your body. The attractive electric force that exists between protons and electrons helps to make atoms stable. The electric force is also an important factor in many chemical reactions.

The study of charged atoms and their chemistry can be kind of complicated. Each atom contains many charged particles: the positively charged protons in the negatively charged electrons. For example, a single iron atom has 26 positively charged particles (protons) in the nucleus and 26 negatively charged electrons in various energy shells surrounding the nucleus. To keep things simple, in this course we will study the electric force and potential energy of only a few charges at a time.

When I was growing up, television sets and computer monitors were bulky objects in which electrons were accelerated and crashed onto a phosphorescent surface to produce the image on the screen. A cathode ray tube (CRT) is a vacuum tube containing an electron gun (a source of electrons). What is the speed of the electrons which produce the image on an old-school TV?

Suppose the Voltage used to drive the electron gun is $4000$[V]. Since voltage is energy per unit charge, this means that each electron that goes through the electron gun will lose the following amount of potential energy \[ U_e = q_e V = 1.602\times10^{-19} \ \times \ 4000 \qquad \text{[J]}. \] In fact the potential energy is not lost but converted to kinetic energy \[ U_e \to K_e = \frac{1}{2}m_e v^2 = \frac{1}{2}(9.109\times10^{-31})v^2, \] where we have used the formula for the kinetic energy of an object with mass $m_e = 9.109\times10^{-31}$ [Kg]. Numerically we get: \[ 1.602\times10^{-19} \ \times \ 4000 = \frac{1}{2}(9.109\times10^{-31})v^2 \qquad \text{[J]}, \] where $v$, the velocity of the electrons, is the only unknown in the equation. Solving for $v$ we find that the elections inside the TV are flying at \[ v = \sqrt{\frac{2 q_e V}{m_e}} = \sqrt{\frac{2 \times 1.602\times10^{-19} \times 4000 }{9.109\times10^{-31}}} = 3.751\times 10^{7} \text{[m/s]}. \] This is pretty fast.

• $q$: Electric charge of some particle or object. It is measured in Coulombs $[C]$. If there are multiple charges in the proble we can call them $q,Q$ or $q_1, q_2, q_3$ to distinguish them.
• $\vec{r}$: The vector-distance between two charges.
• $r \equiv |\vec{r}|$: Distance between two charges, measured in meters $[m]$
• $\hat{r} \equiv \frac{ \vec{r} }{ |\vec{r}|}$: A direction vector (unit length vector) in the $\vec{r}$ direction.
• $\vec{F}_e$: Electic force strength and direction, measured in Newtons $[N]$
• $U_e$: The electric potential energy, measured in Joules $[J]=[N*m]$
• $\varepsilon_0=8.8542\ldots\times 10^{-12}$ $\left[\frac{\mathrm{F}}{\mathrm{m}}\right]$: The permittivity of free space, which is one of the fundamental constants of Nature.
• $k_e=8.987551\times 10^9$ $\left[\frac{\mathrm{Nm^2}}{\mathrm{C}^{2}}\right]$: The electric constant. It is related to the permittivity of free space by $k_e=\frac{1}{4 \pi \varepsilon_0}$.

One of the fundamental properties of matter is charge, which is measured in Coulombs [C]. An electron has the charge $q_e=-1.602\times10^{-19}$ [C]. The electric charge of the nucleus of a Helium atom is $q_{He}=2\times1.602\times10^{-19}$, because it contains two protons and each proton has a charge of $1.602\times10^{-19}$ [C].

Unlike mass, of which there is only one kind, there are two kinds of charge: positive and negative. Using the sign (positive vs. negative) to denote the “type” of charge is nothing more than a convenient mathematical trick. We could have instead called the two types of charges “hot” and “cold”. The important thing is that there are two kinds with “opposite” properties in some sense. In what sense opposite? In the sense of their behaviour in physical experiments. If the two charges are of the same kind, then they try to push each other away, but if the two charges are of different kinds then they will attract each other.

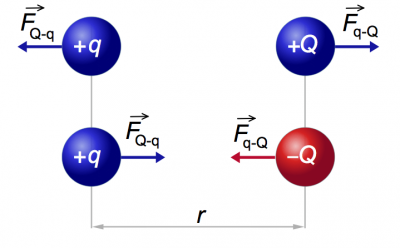Two point charges $Q$ and $q$ placed at a distance $r$ meters apart will interact via the electric force. The magnitude of the electric force is given by the following formula \[ |\vec{F}_e({r})| = \frac{k_eQq}{r^2} \qquad \text{[N]}, \] which is known as Coulomb's law.

If the charges are different (one positive and one negative) then the force will be attractive – it will tend to draw the two charges together. If the two charges are of the same sign then the force will be repulsive.

Every time you have a force, you can calculate the potential energy associated with that force, which represents the total effect (the integral) of the force over some distance. We now define the electric potential energy $U_e$, i.e., how much potential energy is stored in the configuration of two charges $Q$ and $q$ separated by a distance of $r$. The formula is \[ U({r}) = \frac{kQq}{r} \qquad \text{[J]}, \] which is very similar to the formulate for $|\vec{F}_e(Q,q,r)|$ above, but with a one-over-r relationship instead of a one-over-r-squared.

We learned in mechanics, that often times the most elegant way to solve problems in physics is not to calculate the forces involved directly, but to use the principle of conservation of energy. By simple accounting of the different types of energy: kinetic (K), potential (U) and the work done (W), we can often arrive at the answer.

In mechanics we studied the gravitational potential energy $U_g=mgh$ and the spring potential energy $U_s=\frac{1}{2}kx^2$ associated with the gravitational force and spring force respectively. Now you have a new kind of potential energy to account for: $U_e=\frac{kQq}{r}$.

A charge $Q=20$[$\mu$C] is placed 2.2 [m] away from a second charge $q=3$[$\mu$C]. What will be the magnitude of the force between them? Is the force attractive or repulsive?

A charge $Q=6$[$\mu$C] is placed at the origin $(0,0)$ and a second charge $q=-5$[$\mu$C] is placed at $(3,0)$ [m]. What will be the force on $q$. Express your answer as a vector.

If the charge $q$ was placed instead at $(0,3)$[m], what would be the resulting electric vector?

What if the charge $q$ is placed at $(2,4)$[m]. What will be the electric force on $q$ then? Express your answer both in terms of magnitude-and-direction and in component notation.

A fixed charge of $Q=3$[$\mu$C] and a movable charge $q=2$ [$\mu$C] are placed at a distance of 30 [cm] apart. If the charge $q$ is released it will fly off into the distance. How fast will it be going when it is $4$[m] away from $Q$?

The electric force is a vector quantity so the real formula for the electric force must be written as a vector.

Let $\vec{r}$ be the vector distance from $Q$ to $q$. The electric force on the charge $q$ is \[ \vec{F}_e({r}) = \frac{k_eQq}{r^2}\hat{r} \qquad \text{[N]}, \] where $\hat{r}$ is a direction vector pointing away from $Q$. This formula will automatically take care of the direction of the vector in both the attractive and repulsive cases. If $Q$ and $q$ are of the same charge the force will be in the positive $\hat{r}$ direction (repulsive force), but if the charges have opposite sign, the force will be in the negative $\hat{r}$ direction.

In general, it is easier to think of the magnitude of the electric force, and then add the vector part manually by thinking in terms of attractive/repulsive rather than to depend on the sign in the vector equation to figure out the direction for you.

The potential energy of a configuration of charges is defined as the negative of the amount of work which would be necessary in order to bring the charges into this configuration: $U_e = - W_{done}$.

To derive the potential energy formula for charges $Q$ and $q$ separated by a distance $R$ in meters, we can imagine that $Q$ is at the origin and the charge $q$ starts off infinitely far away on the $x$-axis and is brought to a distance of $R$ from the origin slowly. The electric potential energy is given by the following integral: \[ \Delta U_e = - W_{done} = - \int_{r=\infty}^{r=R} \vec{F}_{ext}({r}) \cdot d\vec{s}. \] By bringing the charge $q$ from infinitely far away we make sure that the initial potential energy is going to be zero. Just like with all potentials, we need to specify a reference point with respect to which we will measure it. We define the potential at infinity to be zero, so that $\Delta U_e = U_e({R})-U_e(\infty) = U_e({R})-0= U_e({R})$.

OK, so the charge $q$ starts at $(\infty,0)$ and we sum-up all the work that will be necessary to bring it to the coordinate $(R,0)$. Note that we need an integral an integral to calculate the work, because the strength of the force changes during the process.

Before we do the integral, we have to think about the direction of the force and the direction of the integration steps. If we want to obtain the correct sign, we better be clear about all the negative signs in the expression:

• The negative sign in the front of the integral comes from the definition $U_e \equiv - W_{done}$.
• The electric force on the charge $q$ when it is a distance $x$ away

will be $\vec{F}_e({x}) = \frac{k_eQq}{x^2}\hat{x}$.

  Therefore if we want to move the charge $q$ towards $Q$ we have
  to apply an external force $\vec{F}_{ext}$ on the charge in the opposite direction.
  The magnitude of the external force needed
  to hold the charge in place (or to move it towards the origin at a constant speed)
  is given by $\vec{F}_{ext}({x}) = -\frac{k_eQq}{x^2}\hat{x}$.
* The displacement vector $d\vec{s}$ always points in the 
  negative direction, since we start from $+\infty$ and move back to the origin.
  Therefore, in terms of the positive $x$-direction the displacements
  are small negative steps $d\vec{s} = - dx\; \hat{x}$.

The negative of the $W_{done}$ from $\infty$ to $R$ is given by the following integral: \[ \begin{align} \Delta U_e & = - W_{done} = - \int_{r=\infty}^{r=R} \vec{F}_{ext}({r}) \cdot d\vec{s} \nl & = -\int_{x=\infty}^{x=R} \left( - \frac{k_eQq}{x^2}\hat{x}\right) \cdot \left( -\hat{x}dx\right) \nl & = - \int_{\infty}^{R} \frac{k_eQq}{x^2} \ (\hat{x}\cdot\hat{x}) \ dx \nl & = - k_eQq \int_{\infty}^{R} \frac{1}{x^2} \ 1 \ dx \nl & = - k_eQq \left[ \frac{-1}{x} \right]_{\infty}^{R} \nl & = k_eQq \left[ \frac{1}{R} - \frac{1}{\infty} \right] \nl & = \frac{k_eQq}{R}. \end{align} \]

So we have that we have \[ \Delta U_e \equiv U_{ef} - U_{ei} = U_e({R}) - U_e(\infty), \] and since $U_e(\infty)=0$ we have derived that \[ U_e({R}) = \frac{k_eQq}{R}. \]

We say that the work done to bring the two charges together is stored in the electric potential energy $U_e({r})$ because if we were to let go of these charges they would fly away from each other, and give back all that energy as kinetic energy.

We can also use the relationship between force and potential energy in the other direction. If I were to tell you that the potential energy of two charges is \[ U({r}) = \frac{k_eQq}{r}, \] then, by definition, the force associated with that potential is given by \[ \vec{F}({r}) \equiv - \frac{dU({r}) }{dr} = \frac{k_eQq}{r^2} \hat{r}. \]

Opposite charges cancel out. If you have a sphere with $5$[$\mu$C] of charge on it, and you add some negative charge to it, say $-1$[$\mu$C], then the resulting charge on the sphere will be $4$[$\mu$C].

Charged particles will redistribute themselves between different objects brought into contact so as to minimize the repulsive force between them. This means that charge is always maximally spread out over the entire surface of the object. For example, if charge is placed on a metal ball made of conducting material the charge will all go to the surface of the body and will not penetrate into the interior.

As another example, consider two metal spheres that are connected by a conducting wire with a total charge $Q$ placed on the system. Because charge is free to move along the wire, it will end up distributed uniformly over the total area $A =A_1 +A_2$, where $A_1$ and $A_2$ are the surface areas of the two spheres. The surface charge density will be $\sigma = Q/A$ [C/m$^2$]. The charge on each sphere will be proportional to the surface area of the object: \[ Q_1 = \sigma A_1 = \frac{A_1}{A_1+A_2} Q, \qquad Q_2 = \sigma A_2 = \frac{A_2}{A_1+A_2} Q. \qquad \textrm{[C]} \] Note that the $Q_1 + Q_2=Q$ as expected.