More circuits
More complicated circuits cannot be solved by simple finding the equivalent resistance and simplyfing in each step. In general, we have to use the Kirchoff's loop law (the sum of thr voltages gained or lost around any loop in the circuit must add up to zero) and the Kirchoff junction law (the sum of the currents entering a junction is equal to the sum of the currents leaving the junction). The general procedure is to label all the unknown voltages and currents and then simultaneously solve the equations to find the unknowns.
Concepts
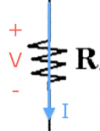
$I$: the electric current. It flows through all circuit components. We measure current in Amperes $[A]$.
We use wires to guide the flow of currents: to make them go where we want.
* {{ :electricity:circuit-element-voltage.png|}}
$V$: the electric potential difference between two points. We say //voltage// for short instead of "electric potential difference". There is no notion of "absolute" voltage, we only measure potential difference between //two// points. Thus if you should always label a (+) side and a (-) side when reporting a voltage. Conveniently, the unit of Voltage is the Volt [V], after Volta.
* $P$: power consumed or produced by some component. Measured in Watts [W].
* $R$: For resistors, the voltage across the leads is linearly related to current flowing in the resistor. We call //resistance// the ratio between the voltage and the current:
\[
R=\frac{V}{I}.
\]
We measure resistance in Ohms [$\Omega$].
Circuit components
Recall the basic building blocks for circuits are:
- wires
- batteris
- current sources
- resistors = light bulbs
- switches
General principles
Ohm's law
Electric power
The power consumed by an electric component is given by \[ P = V I, \] where $I$ is the current going into the (+) terminal of the device.
Kirchhoff's loop law
Kirchhoff's law says that the sum of the voltage gains and drops along any loop must add up to zero: \[ \sum_{\text{loop}} V_i = 0. \]
Kirchhoff current law
This is implied by conservation of charge: charge can't be created or destroyed so the sum of the currents coming into a junction, must equal the sum of the currents leaving the junction: \[ \sum I_{\text{in}} = \sum I_{\text{out}}. \]