Cette loi dit que les causes de l'acceleration c'est les forces sur un objet.

• $A$: Amplitude du mouvement
• $t$: temps
• $x(t)$: position de l'objet
• $\omega$: fréquence angulaire,
• $\phi$: constante phase
• $(\omega t + \phi)=\theta$: phase, l'argument de la fonction $\sin$
• $T$: période (combien de temps avant que le mouvement se répète) [s]
• $f$: fréquence $f=1/T=\frac{\omega}{2\pi}$ [Hz] = [1/s]

il faut aussi essayer de vous rappeler le concept de derivee d'une fonction

Le mouvement d'un objet en “mouvement harmonique” a la forme de
$x(t)=A\sin(\omega t + \phi)$

La commencencez pas a voir peur la. C'est vraiment simple. On va étudier la fonction $\sin$ un peu, apres ca on va utiliser $x(t)$ et sa dérivée $\frac{dx(t)}{dt}=v(t)$ la vitesse

$f(x)=sin(x)$ et $f(x)=cos(x)$ sont deux fonctions c'est a dire prennent un argument qui dans ce case est un angle $\theta$ Apartir de maintenant on va parler de $\theta$ comme ca on sait que c'est un angle pas une longeur

$\theta=0$ correspond a l'axe des $x$
$\theta=\pi$ correspond a la direction $-x$
$\theta=C$ est une direction perpendiculaire a l'axe des $x$ (aussi dite orthogonale). Pensez a votre coin de chambre. $\theta=\pi/2$ c'est $\theta=90^{\circ}$. Angle droit.

$\theta=\frac{\pi}{4}$: c'est quelque part au milieu entre $0$ et $\frac{\pi}{2}$, et ca correspond a l'angle $45^\circ$ en degrés.

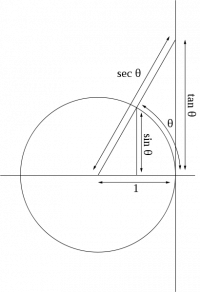
sin et cos ont rapport avec un triangle et un cercle
ces fonctions sont pour convertir du cercle au triangle

$\sin(0)=0$
$\sin(\pi/2)=1$

en fait cos c'est tres similaire mais completement oppose

mais commencons par le debut

$F=ma$

$F_{x_{ressort}} = -kx$

$a=\frac{dv}{dt}$ plus precisememt $a(t)=\frac{dv(t)}{dt}$

$F=ma$

$-kx = ma$ $-kx(t) = m\frac{d^2x(t)}{dt^2}$

$m\frac{d^2x}{dt^2}+ kx(t)= 0$

$\frac{d^2x}{dt^2}+ \frac{k}{m}x(t)= 0$

$x(t)=A \sin( \sqrt{ \frac{k}{m}}t + \phi )$

$\omega = \sqrt{ \frac{k}{m} }$

$T= \frac{2\pi}{\omega}$

$x(t)=A\sin(\omega t + \phi)$

$v(t)=A\omega \cos(\omega t + \phi)$

$a(t)=-A\omega^2\sin(\omega t + \phi)$

Potential energy is :
$U= \frac{1}{2} kx^2 =\frac{1}{2}kA^2\sin^2(\omega t +\phi)$

Cinematic energy is :
$K= \frac{1}{2} mv^2 = \frac {1}{2}m\omega^2A^2\cos^2(\omega t +\phi)$

Total energy:
$E_{total}= U_{max}=\frac{1}{2}kA^2 = K_{max} = \frac{1}{2}mv^2$

Total energy: $E_T = U+ K$

Conservation of energy says:
$E_i = E_f $
so in this case
$U_i + K_i = U_f + K_f$

voici un exemple.

voici un autre !

Des fois quand il n'y a pas d'acceleration $a_x=0$ ca peut nous permettre…