Techniques of integration
The operation of “taking the integral” of some function is usually much more complicated than that of taking the derivative. In fact, you can take the derivative of any function – no matter how complex – simply by using the product rule, the chain rule and the derivative formulas. The same is not true for integrals.
There are plenty of integrals for which there is no closed form solution, which means that the function doesn't have an anti-derivative. There simply doesn't exist a simple procedure to follow, such that you input a function and you “turn the crank” until the integral comes out. Integration is a bit of an art.
What can we integrate then and how? Back in the day, scientists used to collect big tables with integral formulas for various complicated functions. That is what you can lookup-integrate.
There are also some integration techniques which can help you make complicated integrals simpler. Think of the techniques below, as adapters you need to use for cases when the function you are trying to integrate doesn't appear in your table of integrals, but a similar one is in the table.
The intended audience for this chapter are Calculus II students. This is exactly the kind of skills which you will be asked to show on the final. Instead of using the table of integrals to lookup some complicated integral, you have know how to make your own table.
For people interested in learning physics, I will honestly tell
you that if you skip this section you won't miss much.
You should just read the section on substitution which is the important one,
but don't bother reading the details of all the recipes for
integrating things.
For most intents and purposes, once you understand
what an integral is, you can use a computer to calculate it.
A good tool for this is the computer algebra system at live.sympy.org.
>>> integrate( sin(x) )
-cos(x)
>>> integrate( x**2*exp(x) )
x**2*exp(x) - 2*x*exp(x) + 2*exp(x)
You can use sympy for all your integration needs.
For those of you reading this book for general culture and who want to understand what calculus is without having to write a final exam on it, consider the next couple of pages as an ethnographic survol of the academic realities in which bright first year students are forced to integrate things they don't want to integrate and this for many long hours. Just picture some unlucky science student locked up in her room doing calculus and hundreds of dangling integrals grabbing at her with their hooks, keeping her away from her friends.
Actually, it is not that bad. There are, like, four tricks to learn and if you practice you can learn all of them in a week or so. Mastering these four tricks is essentially the entire Calculus II class. If you understand the material in this section, you will be done with integral calculus and you will have two months to chill.
Substitution
Say you are integrating some complicated function which contains a square root $\sqrt{x}$. You are wondering how to go about computing this integral: \[ \int \frac{1}{x - \sqrt{x}} \; dx \ = \ ? \]
Sometimes you can simplify the integral by substituting a new variable in the expression. Let $u=\sqrt{x}$. Substitution is like search-and-replace in a word processor. Every time you see the expression $\sqrt{x}$, you have to replace it with $u$: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{1}{u^2 - u} \; dx. \] Note that we also replaced $x=(\sqrt{x})^2$ with $u^2$.
We are not done yet. When you change from the $x$ variable to the $u$ variable, you have to be thorough. You have to change the $dx$ to a $du$ also. Can we just replace $dx$ with $du$? Unfortunately no, otherwise it would be like saying that the “short step” $du$ is equal in length to the “short step” $dx$, which is only true for the trivial substitution $u=x$.
To find the relation between the infinitesimals we take the derivative: \[ u(x) = \sqrt{x} \quad \Rightarrow \quad u'(x) = \frac{du}{dx} = \frac{1}{2\sqrt{x}}. \] For the next step, I need you to stop thinking about the expression $\frac{du}{dx}$ as a whole, but think about it as a rise-over-run fraction which can be split. Lets take the run $dx$ to the other side of the equation: \[ du = \frac{1}{2\sqrt{x}} \; dx, \] and to isolate $dx$, we multiply both sides by $2\sqrt{x}$: \[ dx = 2\sqrt{x} \; du = 2u \; du, \] where in the last step we used the fact that $u=\sqrt{x}$ again.
Now we have an expression for $dx$ entirely in terms of $u$'s. Let's see what that gives: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{1}{u^2 - u} 2u \; du = \int \frac{2}{u - 1} \; du. \]
We can now recognize the general form $\frac{1}{x}$ which has integral $\ln(x)$, but we have to account for the $-1$ shift inside the function. The integral therefore is: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{2}{u - 1} \; du = 2\ln(u-1) = 2\ln(\sqrt{x}-1). \] Note that in the last step we changed back to the $x$ variable, to give the final answer. The variable $u$ exists only in our calculation. We invented it out of thin air, when we said “Let $u=\sqrt{x}$” in the beginning. It is only natural to convert back to the original variable $x$ in the last step.
Notice what happened thanks to the substitution? The integral got simpler since we got rid of the square roots. On the outside we had just an extra $u$ appearing, which ends up cancelling with the $u$ in the denominator making things even simpler. In practice, substituting inside $f$ is the easy part. The hard part is making sure that our choice of substitution leads to a replacement for $dx$ which helps to make the integral simpler.
For definite integrals, i.e., integrals that have explicit limits, there is an extra step that we need to take when changing variables: we have to change the $x$ limits of integration to $u$ limits. In our expression, when changing to the $u$ variable, we would have to write: \[ \int_a^b \frac{1}{x - \sqrt{x}} \; dx = \int_{u(a)}^{u(b)} \frac{2}{u - 1} \; du. \] If the integral had asked for the integral between $x_i=4$ and $x_f=9$, then the new limits will be $u_i=\sqrt{4}=2$ and $u_f=\sqrt{9}=3$, so we will have: \[ \int_4^9 \frac{1}{x - \sqrt{x}} \; dx = \int_{2}^{3} \frac{2}{u - 1} \; du = 2\ln(u-1)\bigg|_2^3 = 2(\ln(2) - \ln(1)) = 2\ln(2). \]
OK, so let's recap. Substitution involves three steps:
- Replace all occurrences of $u(x)$ with $u$.
- Replace $dx$ with $\frac{1}{u'(x)}du$.
- If there are limits, replace the $x$ limits with $u$ limits.
If the resulting integral is simpler to solve then good for you!
Example
We are asked to find $\int \tan(x)\; dx$. We know that $\tan(x)=\frac{\sin(x)}{\cos(x)}$, so we can use the substitution $u=\cos(x)$, $du=-\sin(x)dx$ as follows: \[ \begin{eqnarray} \int \tan(x)dx &=& \int \frac{\sin(x)}{\cos(x)} dx \nl &=& \int \frac{-1}{u} du \nl &=& -\ln |u| + C \nl &=& -\ln |\cos(x) | + C. \end{eqnarray} \]
Integrals of trig functions
Because $\sin$, $\cos$, $\tan$ and the other trig functions are related, we can often express one function in terms of another in order to simplify integrals.
Recall the trigonometric identity: \[ \cos^2(x) + \sin^2(x) = 1, \] which is the statement of Pythagoras theorem.
If we choose to make the substitution $u=\sin(x)$, then we can replace all kinds of trigonometric terms with the new variable $u$: \[ \begin{align*} \sin^2(x) &= u^2, \nl \cos^2(x) &= 1 - \sin^2(x) = 1 - u^2, \nl \tan^2(x) &= \frac{\sin^2(x)}{\cos^2(x)} = \frac{u^2}{1-u^2}. \end{align*} \]
Of course the change of variable $u=\sin(x)$ means that you have to change the $du=u'(x) dx= \cos(x) dx$ so there better be something to cancel this $\cos(x)$ term in the integral.
Let me show you one example when things work out perfectly. Suppose $m$ is some arbitrary number, and you have to integrate: \[ \int \left(\sin(x)\right)^{m}\cos^{3}(x) \; dx \equiv \int \sin^{m}(x)\cos^{3}(x) \; dx. \] This integral contains $m$ powers of the $\sin$ function and a three powers of the $\cos$ function. Let us split the $\cos$ term into two parts: \[ \int \sin^{m}(x)\cos^{3}(x) \; dx = \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx. \]
Making the change of variable $u=\sin(x)$, $du=\cos(x)dx$ means that we can replace $\sin^m(x)$ by $u^m$, and $\cos^2(x)=1-u^2$ in the above expression to get: \[ \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx = \int u^{m} \left(1-u^2\right) \cos(x) \; dx. \]
Conveniently we happen to have $du= \cos(x)dx$ so the complete change of variable step is: \[ \begin{align*} \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx & = \int u^{m} \left(1-u^2\right) \; du. \end{align*} \] This is what I was talking about earlier about “having an extra $\cos(x)$” to cancel the one that will appear from the $dx \to du$ change.
What is the answer then? It is a simple integral of a polynomial: \[ \begin{align*} \int u^{m} \left(1-u^2\right) \; du & = \int \left( u^{m} - u^{m+2} \right) \; du \nl & = \frac{1}{m+1}u^{m+1} - \frac{1}{m+3}u^{m+3} \nl & = \frac{1}{m+1}\sin^{m+1}(x) - \frac{1}{m+3}\sin^{m+3}(x). \end{align*} \]
You might be wondering how useful this substitution technique really is. I mean, how often do you have to integrate such a particular combinations of $\sin$ and $\cos$ powers so that the substitution works out perfectly. You would surprised! Sins and cos functions are used a lot in this thing called the Fourier transform, which is a way of expressing a sound wave $f(t)$ in terms of the frequencies it contains. Also on exams, they love to test this kinds of things. Teachers often want to check if you can do integrals and substitutions and they check if you remember all the trigonometric identities, which you are supposed to have learned in high school.
What other trigonometric functions should you know how to integrate? On an exam you should try any possible substitution you can think of, combined with any trigonometric identity that seems to simplify things. Some common ones are described below.
Cos
Just as we can substitute $\sin$, we can also substitute $u=\cos(x)$ and use $\sin^2(x)=1-u^2$. Again, this substitution only makes sense if you have a $\sin$ left over somewhere in the integral to cancel with the $du = -\sin(x)dx$.
Tan and sec
We can get some more mileage out of $\cos^2(x) + \sin^2(x) = 1$. If we divide both sides by $\cos^2(x)$ we get: \[ 1 + \tan^2(x) = \sec^2(x) \equiv \frac{1}{\cos^2(x)}, \] which is useful because $u=\tan(x)$ gives $du=\sec^2(x)dx$ so you can often “kill off” even powers of $\sec^2(x)$ in integrals of the form \[ \int\tan^m(x)\sec^n(x)\,dx. \]
Even powers of sin and cos
There are other trigonometric identities called half-angle and double-angle formulas which give you formulas like: \[ \sin^2(x)=\frac{1}{2}(1-\cos(2x)), \qquad \cos^2(x)=\frac{1}{2}(1+\cos(2x)). \]
These are useful if you have to integrate even powers of $\sin$ and $\cos$.
Example
Let's see how we would find $I=\int\sin^2(x)\cos^4(x)\,dx$: \[ \begin{eqnarray} I &=& \int\sin^2(x)\cos^4(x)\;dx \nl &=& \int \left( {1 \over 2}(1 - \cos(2x)) \right) \left( {1 \over 2}(1 + \cos(2x)) \right)^2 \;dx, \nl &=& \frac{1}{8} \int \left( 1 - \cos^2(2x) + \cos(2x)- \cos^3(2x) \right) \;dx. \nl & = & \frac{1}{8} \int \left( 1 - \cos^2(2x) + \cos(2x) -\cos^2(2x) \cos(2x) \right)\; dx \nl & = & \frac{1}{8} \int \left( 1 - \frac{1}{2} (1 + \cos(4x)) + \underline{\cos(2x)} - (\underline{1}-\sin^2(2x))\underline{\cos(2x)} \right) \; dx \nl & = & \frac{1}{8} \int \left( \frac{1}{2} - \frac{1}{2} \cos(4x) + \underbrace{\sin^2(2x)}_{u^2}\cos(2x) \right) \;dx \nl & = & \frac{1}{8} \left( \frac{x}{2} - \frac{\sin(4x)}{8} + \frac{\sin^3(2x)}{6} \right) \nl &=& \frac{x}{16}-\frac{\sin(4x)}{64} + \frac{\sin^3(2x)}{48}+C. \end{eqnarray} \]
There is no limit to the number of combinations of simplification steps you can try. On a homework question or an exam, the teacher will ask for something simple. You just have to find the right substitution.
Sneaky example
Sometime, the substitution is not obvious at all, as in the case of $\int \sec(x)dx$. To find the integral you need to know the following trick: multiply and divide by $\tan(x) +\sec(x) $.
What we get is \[ \begin{eqnarray} \int \sec(x) \, dx &=& \int \sec(x)\ 1 \, dx \nl &=& \int \sec(x)\frac{\tan(x) +\sec(x)}{\tan(x) +\sec(x)} \; dx \nl &=& \int \frac{\sec^2(x) + \sec(x) \tan(x)}{\tan(x) +\sec(x)} \; dx\nl &=& \int \frac{1}{u} du \nl &=& \ln |u| + C \nl &=& \ln |\tan(x) + \sec(x) | + C, \end{eqnarray} \] where in the fourth line we used the substitution $u=\tan(x)+\sec(x)$ and $du = (\sec^2(x) + \tan(x)\sec(x))dx$.
I highly recommend you view and practice all the examples you can get your hands on. Don't bother memorizing any recipes though, you will do just as well with trial and error.
Trig substitution
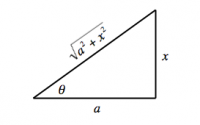
Often times when doing integrals for physics we get terms of the form $\sqrt{a^2-x^2}$, $\sqrt{a^2+x^2}$ or $\sqrt{x^2-a^2}$ which are not easy to handle. In each of the above three cases, we can do a trig substitution, in which we substitute $x$ with one of the trigonometric functions $a\sin(\theta)$, $a\tan(\theta)$ or $a\sec(\theta)$, and the resulting integral becomes much simpler.
Sine substitution
Consider an integral which contains an expression of the form $\sqrt{a^2-x^2}$. If we use the substitution $x=a\sin \theta$, the complicated square-root expression will get simpler: \[ \sqrt{a^2-x^2} = \sqrt{a^2-a^2\sin^2\theta} = a\sqrt{1-\sin^2\theta} = a\cos\theta, \] because we have $\cos^2\theta = 1 - \sin^2\theta$. The transformed integral now involves a trigonometric function which we know how to integrate.
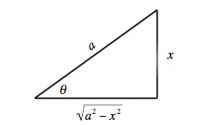 Once we find the integral in terms of $\theta$, we have to convert
the various $\theta$ expressions in the answer back
to the original variables $x$ and $a$:
\[
\sin\theta = \frac{x}{a}, \ \
\cos\theta = \frac{\sqrt{a^2-x^2}}{a}, \ \
\tan\theta = \frac{x}{\sqrt{a^2-x^2}}, \ \
\]
\[
\csc\theta = \frac{a}{x}, \ \
\sec\theta = \frac{a}{\sqrt{a^2-x^2}}, \ \
\cot\theta = \frac{\sqrt{a^2-x^2}}{x}. \ \
\]
Once we find the integral in terms of $\theta$, we have to convert
the various $\theta$ expressions in the answer back
to the original variables $x$ and $a$:
\[
\sin\theta = \frac{x}{a}, \ \
\cos\theta = \frac{\sqrt{a^2-x^2}}{a}, \ \
\tan\theta = \frac{x}{\sqrt{a^2-x^2}}, \ \
\]
\[
\csc\theta = \frac{a}{x}, \ \
\sec\theta = \frac{a}{\sqrt{a^2-x^2}}, \ \
\cot\theta = \frac{\sqrt{a^2-x^2}}{x}. \ \
\]
Example 1
Suppose you are asked to calculate $\int \sqrt{1-x^2}\; dx$.
We will approach the problem by making the substitution \[ x=\sin \theta, \qquad dx=\cos \theta \; d\theta, \] which is the simplest case of the sine substitution with $a=1$.
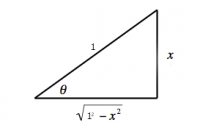 We proceed as follows:
\[
\begin{eqnarray}
\int \sqrt{1-x^2} \; dx
& = & \int \sqrt{1-\sin^2 \theta} \cos \theta \; d\theta \nl
& = & \int \cos^2 \theta \; d\theta \nl
& = & \frac{1}{2} \int \left[ 1+ \cos 2\theta \right] \; d\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{4}\sin2\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{2}\sin\theta\cos\theta \nl
& = & \frac{1}{2}\sin^{-1}\!\left(x \right)
+\frac{1}{2}\frac{x}{1}\frac{\sqrt{1-x^2}}{1}.
\end{eqnarray}
\]
We proceed as follows:
\[
\begin{eqnarray}
\int \sqrt{1-x^2} \; dx
& = & \int \sqrt{1-\sin^2 \theta} \cos \theta \; d\theta \nl
& = & \int \cos^2 \theta \; d\theta \nl
& = & \frac{1}{2} \int \left[ 1+ \cos 2\theta \right] \; d\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{4}\sin2\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{2}\sin\theta\cos\theta \nl
& = & \frac{1}{2}\sin^{-1}\!\left(x \right)
+\frac{1}{2}\frac{x}{1}\frac{\sqrt{1-x^2}}{1}.
\end{eqnarray}
\]
Note how in the last step we used the triangle diagram to “read off” the values of $\theta$, $\sin\theta$ and $\cos\theta$ from the triangle. The substitution $x = \sin\theta$ means the hypotenuse in the diagram should be of length 1, and the opposite side is of length $x$.
Example 2
We want to compute $\int \sqrt{ \frac{a+x}{a-x}} \; dx$. We can rewrite this fraction as follows: \[ \sqrt{\frac{a+x}{a-x}} = \sqrt{\frac{a+x}{a-x} \frac{1}{1}} = \sqrt{\frac{a+x}{a-x} \frac{a+x}{a+x}} =\frac{a+x}{\sqrt{a^2-x^2}}. \]
Next we can make the substitution \[ x=a \sin \theta, \qquad dx=a\cos \theta d\theta, \]
 \[
\begin{eqnarray}
\int \frac{a+x}{\sqrt{a^2-x^2}} dx
& = & \int \frac{a+a\sin \theta}{a\cos \theta} a \cos \theta \, d\theta \nl
& = & a \int \left[ 1+ \sin \theta \right] d\theta \nl
& = & a \left[ \theta - \cos \theta \right] \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - a\frac{\sqrt{a^2-x^2}}{a} \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - \sqrt{a^2-x^2}.
\end{eqnarray}
\]
\[
\begin{eqnarray}
\int \frac{a+x}{\sqrt{a^2-x^2}} dx
& = & \int \frac{a+a\sin \theta}{a\cos \theta} a \cos \theta \, d\theta \nl
& = & a \int \left[ 1+ \sin \theta \right] d\theta \nl
& = & a \left[ \theta - \cos \theta \right] \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - a\frac{\sqrt{a^2-x^2}}{a} \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - \sqrt{a^2-x^2}.
\end{eqnarray}
\]
Tan substitution
When an integral contains $\sqrt{a^2+x^2}$, we use the substitution: \[ x = a \tan \theta, \qquad dx = a \sec^2 \theta d\theta. \]
Because of the identity $1+\tan^2\theta=\sec^2\theta$, the square root expression will simplify drastically: \[ \sqrt{a^2+x^2} = \sqrt{a^2+a^2 \tan^2 \theta} = a\sqrt{1+\tan^2 \theta} = a \sec \theta. \] Simplification is a good thing. You are much more likely to be able to find the integral in terms of $\theta$, using trig identities, than in terms of $\sqrt{a^2+x^2}$.
Once you calculate the integral in terms of $\theta$, you will want to convert the answer back into $x$ coordinates. To do this, you need to use a triangle labeled according to our substitution: \[ \tan\theta = \frac{x}{a} = \frac{\text{opp}}{\text{adj}}. \] The equivalent of $\sin\theta$ in terms of $x$ is going to be $\sin\theta \equiv \frac{\text{opp}}{\text{hyp}} = \frac{x}{\sqrt{a^2+x^2}}$. Similarly, the other trigonometric functions are defined as various ratios of $a$, $x$ and $\sqrt{a^2+x^2}$.
Example
Calculate $\int\frac{1}{x^2+1}\,dx$.
The denominator of this function is equal to $\left(\sqrt{1+x^2}\right)^2$. This suggests that we try to substitute $\displaystyle x=\tan \theta\,$ and use the identity $\displaystyle 1 + \tan^2 \theta =\sec^2 \theta\,$. With this substitution, we obtain that $\displaystyle dx= \sec^2 \theta\, d\theta$ and thus: \[ \begin{align} \int\frac{1}{x^2+1}\,dx & =\int\frac{1}{\tan^2 \theta+1} \sec^2 \theta\,d\theta \nl & =\int\frac{1}{\sec^2 \theta} \sec^2 \theta\,d\theta \nl & =\int 1\;d\theta \nl &=\theta \nl &=\tan^{-1}(x) + C. \end{align} \]
Obfuscated example
What if we don't have $x^2 + 1$ in the denominator (a second degree polynomial with a missing linear term), but a full second degree polynomial like: \[ \frac{1}{y^2 - 6y + 10}. \] How would you integrate something like this? If there were no $-2y$, you would be able to use the tan substitution as above – or perhaps you can lookup the formula $\int \frac{1}{x^2+1}dx = \tan^{-1}(x)$ in the table of integrals. But there is no formula for \[ \int \frac{1}{y^2 - 6y + 10} \; dy, \] in the table so how should you proceed.
We will use the good old substitution technique $u=\ldots$ and a high-school algebra trick called “completing the square” in order to rewrite the fraction inside the integral so that it looks like $(y-h)^2 + k$, i.e., with no middle term.
The first step is to find “by inspection” the values of $h$ and $k$: \[ \frac{1}{y^2 - 6y + 10} = \frac{1}{(y-h)^2+k} = \frac{1}{(y-3)^2+1}. \] The “square completed” quadratic expression has no linear term, which is what we wanted. We can now use the substitution $x=y-3$ and $dx=dy$ to obtain an integral which we know how to solve: \[ \!\int \!\! \frac{1}{y^2 - 6y + 10}\; dy \!= \!\int \!\! \frac{1}{(y-3)^2+1}\; dy \!= \!\int \!\!\frac{1}{x^2+1}\; dx = \tan^{-1}(x) = \tan^{-1}(y-3). \]
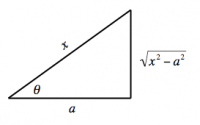
Sec substitution
In the last two sections we learned how to deal with $\sqrt{a^2-x^2}$, $\sqrt{x^2+a^2}$ and so only the last option remains: $\sqrt{x^2-a^2}$.
Recall the trigonometric identity $1+\tan^2\theta=\sec^2\theta$, or rewritten differently we get \[ \sec^2\theta - 1 = \tan^2\theta. \]
The appropriate substitution for terms like $\sqrt{x^2-a^2}$, is the following: \[ x = a \sec \theta, \qquad dx = a \tan \theta \sec \theta \; d\theta. \]
The substitution method and procedure is the same as in both previous cases, so we will not get into the details. We label the sides of the triangle in the appropriate fashion, namely: \[ \sec\theta = \frac{x}{a} = \frac{\text{hyp}}{\text{opp}}, \] and use this triangle when we are converting back from $\theta$ to $x$ in the final steps.
Interlude
By now, things are starting to get pretty tight for your Calculus teacher. You are starting to know how to “handle” any kind of integral he can throw at you: polynomials, fractions with $x^2$ plus or minus $a^2$ and square roots. He can't even use the dirty old trigonometric tricks, with the $\sin$, the $\cos$ and the $\tan$ since you know that too. What options are there left for him to come up with an integral that you wouldn't know how to solve?
OK, I am exaggerating, but you should at least feel, by now, that you know how to do some integrals that you didn't know before. Just remember to come back to this section when you are hit with some complicated integral. When this happens, check to see which of the examples in this section looks the most similar and use the same approach. Don't bother memorizing the steps in each problem. The substitution $u=\ldots$ may be different from any problem that you have seen so far. You should think of “integration techniques” like general recipe ideas which you must adapt depending on the ingredients that you have to work with.
The most important integration techniques is substation. Recall the steps involved: (1) the change of variable $u=\ldots$, (2) the associated $dx$ to $du$ change and (3) the change in the limits of integration required for definite integrals. With medium to advanced substitution skills you will get at least an 80% on your Calculus II final.
Where is the remaining 20% of the exam going to come from? There are two more recipes to go. I know all these tricks that I have been throwing at you during the last ten pages may seem arduous and difficult to understand, but this is what you got yourself into when you signed-up for the course “Integral Calculus”: there are integrals and you calculate them.
The good news is that we are almost done. There is just one more “trick” to go, and finally I will tell you about “integration by parts”, which is kind of the analogue of the product rule for derivatives $(fg)'=f'g + fg'$.
Partial fractions
Suppose you have to integrate a rational function $\frac{P(x)}{Q(x)}$, where $P$ and $Q$ are polynomials.
For example, you could be asked to integrate \[ \frac{P(x)}{Q(x)} = \frac{Dx+E}{Fx^2 + G x + H}, \] where $D$, $E$, $F$, $G$ and $H$ are arbitrary constants. To get even more specific, let's say you are asked to calculate: \[ \int {3x+ 1 \over x^2+x} \; dx. \]
By magical powers, I can transform the function in this integral into two partial fractions as follows: \[ \int {3x+ 1 \over x^2+x} \; dx = \int \left( \frac{1}{x} + \frac{2}{x+1} \right) \; dx = \int \frac{1}{x} \; dx \ + \ \int \frac{2}{x+1} \; dx, \] in which both terms will give something $\ln$-like when integrated (since $\frac{d}{dx}\ln(x)=\frac{1}{x}$). The final answer is: \[ \int {3x+ 1 \over x^2+x} \; dx = \ln \left| x \right| + 2 \ln \left| x+1 \right| + C. \]
How did I split the problem into partial fractions? Is it really magic or is there a method? There is a little bit of both. The method part is that I assumed that there exist constants $A$ and $B$ such that \[ {3x+ 1 \over x^2+x}={3x+ 1 \over x(x+1)}= {A \over x}+ {B \over x+1}, \] and then I solved the above equation for $A$ and $B$, by computing the sum of the two fractions: \[ {3x+1 \over x(x+1)} = {{A(x+1) + Bx} \over {x(x+1)}}. \]
The magic part is the fact that you can solve for two unknowns in one equation. The relevant part of the equation is just the numerator because both sides have the same denominator. To find $A$ and $B$ we have to solve \[ 3x+1 = (3)x + (1)1 = A(x+1)+Bx = (A+B)x + (A)1. \] To solve this you just have to group the unknown constants into bunches and then read off their value from the equation. The bunch of numbers in front of the constant 1 on the left-hand side is (1) and the coefficient of 1 on the right-hand side is $A$, so $A=1$. Similarly you can deduce that $B=2$ from $A+B=3$ having found that $A=1$ in the first step.
Another way of looking at this, is that the equation \[ 3x+1 = A(x+1)+Bx \] must hold for all values of the variable $x$. If we put in $x=0$ we get $1 = A$ and putting $x=-1$ gives $-2=-B$ so $B=2$.
The above problem highlights the power of the partial fractions method for attacking integrals of polynomial fractions $\frac{P(x)}{Q(x)}$. Most of the work goes into some high-school math (factoring and finding unknowns) and then you do some simple calculus steps once you have split the problem into partial fractions. Some people call this method separation of quotients, but whatever you call it, it is clear that having a way to split a fraction into multiple parts is a good thing: \[ \frac{3x+ 1}{x^2+x} = \frac{A}{x} + \frac{B}{x+1}. \]
How many parts are there going to be for a fraction $\frac{P(x)}{Q(x)}$? What will each part look like? The answer is that there will be as many as the degree of the polynomial $Q(x)$, which is in the denominator of the fraction. Each part will consist of one of the factors of $Q(x)$.
Here is the general procedure:
- Split the denominator $Q(x)$ into the product of parts (factorize),
and for each part assume an appropriate partial fraction term
on the right.
You will get three types of fractions:
* Simple factors like $(x-\alpha)^1$. For each of these
you should //assume// a partial fraction of the form:
\[
\frac{A}{x-\alpha},
\]
as in the above example.
* Repeated factors like $(x-\beta)^n$ for which we have to
assume $n$ different terms on the right-hand side:
\[
\frac{B}{x-\beta} + \frac{C}{(x-\beta)^2} + \cdots + \frac{F}{(x-\beta)^n}.
\]
* If the denominator contains a portion $ax^2+bx+c$ that cannot be factored, like
$x^2+1$ for example, we have to keep it as whole
and assume that a term of the form:
\[
\frac{Gx + H}{ax^2+bx+c}
\]
exists on the right-hand side. A polynomial $ax^2+bx+c$ cannot be factored
if $b^2 < 4ac$, which means it has no real roots $r_1$, $r_2$
such that $ax^2+bx+c=(x-r_1)(x-r_2)$.
- Add together all the parts on the right-hand side by first
cross multiplying them to set all the fractions to a
common denominator. If you followed the steps
correctly in Part 1, the //least common denominator// (LCD) will turn
out to be $Q(x)$,
so both sides will have the same denominator.
Solve for the unknown coefficients $A, B, C, \ldots$
in the numerators. Find the coefficients
of each power of $x$ on the right-hand side and set them
equal to the corresponding coefficient in the numerator $P(x)$ of the left-hand side.
- Use the appropriate integral formula for each kind of term:
* For simple factors we have
\[
\int \frac{1}{x-\alpha} \; dx= A \ln|x-\alpha| + C.
\]
* For higher powers in the denominator we have
\[
\int \frac{1}{(x-\beta)^m} \; dx= \frac{1-m}{(x-\beta)^{m-1}} + C.
\]
* For the quadratic denominator terms with "matching" numerator
terms we can obtain:
\[
\int \frac{2ax+b}{ax^2+bx+c} \; dx= \ln|ax^2+bx+c| + C.
\]
For quadratic terms with just a constant on top we use
a two step substitution process.
First we change to a complete-the-square variable $y=x-h$:
\[
\int \frac{1}{ax^2+bx+c} \; dx
=
\int \frac{1/a}{(x-h)^2+k} \; dx
=
\frac{1}{a}\int \frac{1}{y^2+k} \; dy,
\]
and then we use a trig substitution $y = \sqrt{k}\tan\theta$ to get
\[
\frac{1}{a} \int \frac{1}{y^2+k} \; dy =
\frac{\sqrt{k}}{a}\tan^{-1}\!\!\left(\frac{y}{\sqrt{k}} \right) =
\frac{\sqrt{k}}{a}\tan^{-1}\!\!\left(\frac{x-h}{\sqrt{k}} \right).
\]
Example
Find $\int {1 \over (x+1)(x+2)^2}dx$?
Here $P(x)=1$ and $Q(x)=(x+1)(x+2)^2$. If I wanted to be sneaky, I could have asked for $\int {1 \over x^3+5x^2+8x+4}dx$, instead – which is actually the same question, but you have to do the factoring yourself.
According to the recipe outlined above, we have to look for a split fraction of the form: \[ \frac{1}{(x+1)(x+2)^2}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}. \] To make the equation more explicit, let us add the fractions on the right. We set all of them to a the least common denominator and add up: \[ \begin{align} \frac{1}{(x+1)(x+2)^2} & =\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2} \nl &= \frac{A(x+2)^2}{(x+1)(x+2)^2}+\frac{B(x+1)(x+2)}{(x+1)(x+2)^2}+\frac{C(x+1)}{(x+1)(x+2)^2} \nl & = \frac{A(x+2)^2+B(x+1)(x+2)+C(x+1)}{(x+1)(x+2)^2}. \end{align} \]
The denominators are the same on both sides in the above equation, so we can focus our attention on the numerator: \[ A(x+2)^2+B(x+1)(x+2)+C(x+1) = 1. \] We choose three different values of $x$ in order to find the values of $A$, $B$ and $C$: \[ \begin{matrix} x=0 & 1= 2^2A +2B+C \nl x=-1 & 1=A \nl x=-2 & 1= -C \end{matrix} \] so $A=1$, $B=-1$, $C=-1$, and thus \[ \frac{1}{(x+1)(x+2)^2}=\frac{1}{x+1}-\frac{1}{x+2}-\frac{1}{(x+2)^2}. \]
We can now calculate the integral by integrating each of the terms: \[ \int \frac{1}{(x+1)(x+2)^2} dx= \ln(x+1) - \ln({x+2}) + \frac{1}{x+2} +C. \]
Integration by parts
Suppose you have to integrate the product of two functions. If one of the functions happens to look like the derivative of a function that you recognize, then you can do the following trick: \[ \int f(x) g'(x) \; dx \ \ = \ \ f(x) g(x) \ \ \ \ - \int f'(x)g(x) \; dx. \]
This means that you can shift the work to evaluating a different integral where one function is replaced by its derivative and another is replaced by its integral.
Derivatives tend to simplify functions whereas integrals make functions more complicated, so such shifting of work can be quite beneficial: you will save yourself some work on integrating the $f$ part, but you will do more work on the $g$ part.
It is easier to remember the integration by parts formula in the shorthand notation: \[ \int u\; dv = uv - \int v\; du. \] In fact, you can think of integration by parts as a form of “double substitution”, where you replace $u$ and $dv$ at the same time. To be sure of what is going on, I recommend you always make a little table like this: \[ \begin{align} u &= & \qquad dv &= \nl du &= & \qquad v &= \end{align} \] and fill in the blanks. The first row consists of the two parts that you see in your original problem. Then you differentiate in the left column, and integrate in the right column. If you do this, using the integration by parts formula will be really easy since you have all your expressions ready.
For definite integrals the integration by parts rule needs to take into account the evaluation at the limits: \[ \int_a^b u\; dv = \left(uv\right)\Big|_a^b \ \ - \ \ \int_a^b v \; du, \] which tells us to evaluate the difference of the value of $uv$ at the two endpoints and then subtract the switched integral with the same endpoints.
Example 1
Find $\int x e^x \, dx$. We identify the good candidates for $u$ and $dv$ in the original expression, and perform all the work necessary for the substitution: \[ \begin{align} u &=x & \qquad dv &= e^x \; dx, \nl du &=dx & \qquad v &= e^x. \end{align} \] Next we apply the integration by parts formula \[ \int u\; dv = uv - \int v\; du, \] to get the following: \[ \begin{align} \int xe^x \, dx &= x e^x - \int e^x \; dx \nl &= x e^x - e^x + C. \end{align} \]
Example 2
Find $\int x \sin x \; dx$. We choose $u=x$ and $dv=\sin x dx$. With these choices, we have $du=dx$ and $v=-\cos x$, and integrating by parts we get: \[ \begin{align} \int x \sin x \, dx &= -x \cos x - \int \left(-\cos x\right) \; dx \nl &= -x \cos x + \int \cos x \; dx \nl &= -x \cos x + \sin x + C. \end{align} \]
Example 3
Often times, you have to integrate by parts multiple times. To calculate $\int x^2 e^x \, dx$, we start by choosing: \[ \begin{align} u &=x^2 & \qquad dv &= e^x \; dx \nl du &= 2x \; dx & \qquad v &= e^x, \end{align} \] which gives the following after integration by parts: \[ \int x^2 e^x \; dx = x^2 e^x \ - \ 2 \int x e^x \; dx. \] We apply integration by parts again on the remaining integral this time using $u=x$ and $dv=e^x\; dx$, which gives $du = dx$ and $v=e^x$.
\[ \begin{align} \int x^2 e^x \; dx &= x^2 e^x - 2 \int x e^x \; dx \nl &= x^2 e^x - 2\left(x e^x - \int e^x \; dx \right) \nl &= x^2 e^x - 2x e^x + 2e^x + C. \end{align} \]
By now I hope you are starting to see that this integration by parts thing is good. If you always write down the substitutions clearly (who is who in $\int u dv$), and use the formula correctly ($=uv-\int v du$) you can do damage to any integral. Sometimes the choice of $u$ and $dv$ you make might not be good: if the integral $\int v du$ is not simpler than the original $\int u dv$ then what is the point of integrating by parts?
Sometimes, however, you can get into a weird self-referential loop when doing integration by parts. After a couple of integration-by-parts steps you might end up back with an integral you started with! The way out of this loop is best shown by example.
Example 4
Evaluate the integral $ \int \sin(x) e^x\; dx$. First we let $u = \sin(x) $ and $dv=e^x \; dx$, which gives $dv=\cos(x)dx$ and $v=e^x$. Using integration by parts gives \[ \int \sin(x) e^x\, dx = e^x\sin(x)- \int \cos(x)e^x\, dx. \]
We integrate by parts again. This time we set $u = \cos(x)$, $dv=e^x dx$ and $du=-\sin(x)dx$, $v=e^x$. We obtain \[ \underbrace{ \int \sin(x) e^x\, dx}_I \ = \ e^x\sin(x) - e^x\cos(x)\ \ -\ \ \underbrace{\int e^x \sin(x)\, dx}_I. \] Do you see the Ouroboros? We could continue integrating by parts indefinitely like that.
Let us define clearly what we are doing here. The question asked us to find $I$ where \[ I = \int \sin(x) e^x\, dx, \] and after doing two integration by parts steps we obtain the following equation: \[ I = e^x\sin(x) - e^x\cos(x) - I. \] OK, good. Now just move all the I's to one side: \[ 2I = e^x\sin(x) - e^x\cos(x), \] or finally \[ \int \sin(x) e^x\, dx = I = \frac{1}{2} e^x\left(\sin(x) - \cos(x) \right) +C. \]
Derivation of the Integration by parts formula
Remember the product rule for derivatives? \[ \frac{d}{dx}(f(x)g(x)) = \frac{df}{dx}g(x) + f(x)\frac{dg}{dx}. \] We can rewrite this as: \[ f(x)\frac{dg}{dx} = \frac{d}{dx}(f(x)g(x)) \ -\ \frac{df}{dx}g(x) . \] Now we take the integral on both sides \[ \int f(x)\frac{dg}{dx} \ dx \ = \ \int \left[ \frac{d}{dx}(f(x)g(x)) \; dx - \frac{df}{dx}g(x) \; dx \right]. \]
At this point, you need to recall the Fundamental Theorem of Calculus, which says that taking the derivative and taking an integral are inverse operations \[ \int \frac{d}{dx} h(x) \; dx = h(x). \] We use this to simplify the product rule equation as follows: \[ \int f(x)\frac{dg}{dx} \; dx \ = \ f(x)g(x) \ \ - \ \ \int \frac{df}{dx}g(x) \; dx. \]
Outro
We are done. Now you know all the integration techniques. I know it took a while, but we had to go through a lot of tricks. In any case, I must say I am glad to be done writing this section. My job of teaching you is done. Now your job begins. Do all the examples you can find. Do all the exercises. Practice the tricks.
Here is a suggestion for you. Make your own formula-sheet-slash-trophy-case where you record any complex integral that you have personally calculated from first principles in homework assignments. If by the end of the class you trophy case has 50 integrals which you calculated yourself, then you will get $100\%$ on your final. Another thing to try is to go over the integral formulas in the back of the book and see how many of them you can derive.
Links
[ More examples of integration techniques ]
http://en.wikibooks.org/wiki/Calculus/Integration_techniques/
From here on you can consult the index and see which other topics might interest you.