Circle
The circle is a set of points that are a constant distance from the centre. It is a very simple geometrical shape which comes up in many situations.
Definitions
- $r$: the radius of the circle
- $A$: the area of the circle
- $C$: the circumference of the circle
- $(x,y)$: is a point on the circle
- $\theta$: the angle (measured from the $x$-axis) of some point on the circle.
Formulas
The circle of radius $r$ centred at the origin is described by the following equation: \[ x^2 + y^2 = r^2. \] All points $(x,y)$ which satisfy this equation are part of the circle.
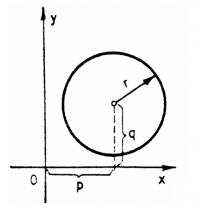 Instead of being centred at the origin, the
centre of the circle could be at any point in the plane $(p,q)$:
\[
(x-p)^2 + (y-q)^2 = r^2.
\]
Instead of being centred at the origin, the
centre of the circle could be at any point in the plane $(p,q)$:
\[
(x-p)^2 + (y-q)^2 = r^2.
\]
Explicit function
The equation of a circle is a relation or an implicit function involving $x$ and $y$. If we want an explicit function $f(x)$ for the circle, we can solve for $y$ to obtain: \[ y = \sqrt{ r^2 - x^2}, \quad -r \leq x \leq r, \] and \[ y = -\sqrt{ r^2 - x^2}, \quad -r \leq x \leq r. \] There are two functions, because a vertical line crosses that circle in two places. The first function corresponds to the top half of the circle and the second function corresponds to the bottom half.
Polar coordinates
Circles are such a common shape in mathematics that mathematicians developed a special “circular coordinate system” in order to describe them more easily.
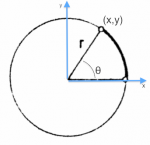 It is possible to specify the coordinates $(x,y)$ of any point on the circle
in terms of the polar coordinates $r\angle\theta$, where $r$ measures the distance of
the point from the origin and $\theta$ is the angle measured from the $x$ axis.
It is possible to specify the coordinates $(x,y)$ of any point on the circle
in terms of the polar coordinates $r\angle\theta$, where $r$ measures the distance of
the point from the origin and $\theta$ is the angle measured from the $x$ axis.
To convert from the polar coordinates $r\angle\theta$ to the $(x,y)$ coordinates we use the trigonometric functions: \[ x = r\cos \theta, \qquad y = r\sin \theta. \]
Parametric equation
We can describe all the points on the circle in we specify a fixed radius $r$ and vary the angle $\theta$ over all angles: $\theta \in [0, 360^\circ)$. A parametric equation specifies the coordinates $(x(\theta), y(\theta))$ for the points on a curve for all values of the paramter $\theta$. The parametric equation for a circle of radius $r$ is given by: \[ \{ (x,y)\in\mathbb{R}^2 \ | \ x=r \cos\theta, y = r\sin\theta, \ \theta \in [0, 360^\circ) \}. \] You should try to visualize the curve traced by the point $(x(\theta),y(\theta))=(r\cos\theta,r\sin\theta)$ as $\theta$ varies from $0$ to $360^\circ$ and convince yourself that it traces out a circle of radius $r$.
If we let the parameter $\theta$ vary over a smaller interval, we will obtain subsets of the circle. For example, the parametric equation for the top half of the circle is: \[ \{ (x,y)\in\mathbb{R}^2 \ | \ x=r \cos\theta, y = r\sin\theta, \ \theta \in [0, 180^\circ] \}. \] The top half of the circle is also described by $\{ (x,y) \in\mathbb{R}^2 \ | \ y = \sqrt{ r^2 - x^2},\ x \in [-r,r] \}$, where the parameter used is the $x$ coordinate.
Area
The area of a circle of radius $r$ is given by \[ A = \pi r^2. \]
Circumference and arc length
The circumference of a circle is \[ C = 2 \pi r. \] This is the total length you would measure out if you were to follow the line of the circle.
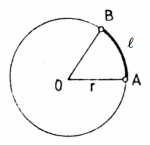 What is the length of a part of the circle?
Say you have a piece of the circle, that corresponds
to the angle $\theta=30^\circ$. What is its length?
If the total length is $C=2 \pi r$ corresponds to
doing a full turn around the circle $360^\circ$, then
the arc length $\ell$ for a portion which corresponds to the angle $\theta$ is
\[
\ell = 2 \pi r \frac{\theta}{360}.
\]
We say that $\ell$ is the act length subtended by the angle $\theta$.
What is the length of a part of the circle?
Say you have a piece of the circle, that corresponds
to the angle $\theta=30^\circ$. What is its length?
If the total length is $C=2 \pi r$ corresponds to
doing a full turn around the circle $360^\circ$, then
the arc length $\ell$ for a portion which corresponds to the angle $\theta$ is
\[
\ell = 2 \pi r \frac{\theta}{360}.
\]
We say that $\ell$ is the act length subtended by the angle $\theta$.
Radians
Though degrees are a commonly used unit for angles, it is much better to measure angles in radians, which is the natural angle parameter. The conversion ratio is: \[ 2\pi \ \text{[radians]} = 360 \ \text{[degrees]}. \] For a circle of radius $r=1$, the arc length is equal to the angle in radians: \[ \ell = \theta_{radians}. \] Measuring radians is equivalent to measuring arc length on a circle of radius one.