When the input variable for the function is the time, $t$, we usually write the sin function as follows: \[ g(t) = A \sin(\omega t - \phi), \] where instead of $k$ we have $\omega$, which is called the angular frequency and $f=\frac{\omega}{2\pi}$ is called the frequency. Instead of $\lambda$, we have $T=\frac{2\pi}{\omega}=\frac{1}{f}$, which is called the period.
My high school teacher used to repeat this to us all the time “a binomial times a binomial gives a trinomial” trying to make us remember this key fact.
The only exception to this binomial-times-binomial-gives-a-trinomial rule is when we have $(x+a)(x-a)=x^2-a^2$ which is known as the difference of two squares. The middle term is zero because $ax-xa=0$.
Recall curve
The recall curve is described by the function $R(t) = e^{-t/S}$, where $R$ is the probability that you remember some memory and $S$ is the strength of the memory. A student who is cramming for an exam has a
http://en.wikipedia.org/wiki/Forgetting_curve
“And Pythagoras theorem?”
“I know $c^2=a^2 + b^2$ in a triangle of sides $a$ and $b$ and hypotenuse $c$. Right?”
“Right. So what he has been trying to tell you is that
if $c=1$, then I am $b$ and cos is $a$ in that equation.”
“Ok what is with the whole circle thing then?”
Applications
The hull speed is the maximum speed that a sailboat can reach. It can be calculated using the empirical formula: \[ v_{hull} \approx 1.34 \times \sqrt{LWL}, \] where $LWL$ is the length of the waterline in feet and $v_{hull}$ is the hull speed of the vessel in knots. For a 20 foot boat, the hull speed is about 6 knots. For a 30 foot boat, the hull speed is about 7.3 knots.
Two parts
Now let us try to solve $1 < (x-3)^2 < 4$. We are looking for the values of $x$ for which the function $(x-3)^2$ has outputs between $1$ and $4$. The steps are similar to the above example, but when we compute the inverse of the quadratic function we will get two separate intervals: \[ \begin{align*} -2 < & (x-3) < -1 \qquad \qquad &1 < (x-3) < 2 \nl 1 < & \ \ \ x \ \ \ < 2, \qquad \qquad &4 < \ \ \ x \ \ \ < 5. \end{align*} \] We can write the answer as $(1,2)\cup (4,5)$.
At the time I wondered why he is putting so much emphasis on this subject, since it involved simply the application of the distributive property of numbers. A lot of people $(x+3)(x+2)$ is the first step into the world of algebra. Most people don't like it.
Add the fractions $1\frac{3}{4} + 1\frac{31}{32}$. Ans: $3\frac{23}{32}$ Ans: 7/4 = 14/8 = 28/16 = 56 / 32 1 31/32 = 63/32 56/32 + 63/32 = 119 / 32 3 23/32
Gas prices
3.10 / 3.78
0.82010582010582023
3.45 / 3.78
0.91269841269841279
30/120
0
30.0/120
0.25
(3.45-3.15)/3.15
0.09523809523809533
This is a subject for another lesson, but I wanted also to mention that $e^x$ is actually related to $\sin(x)$ and $\cos(x)$.
The material on this page will give you the ability to transfer the “complexity” of the problem from the left side of the equation to the right side. First we will do: Focus your eyes on the left-hand side. Magic stuff is about to go down! The $f^{-1}$ will cancel the $f$ and we get the simpler version: \[ g(x) = f^{-1}(5), \] and then to solve for $x$ we will have to undo the $g$ function as well: \[ x = g^{-1}\!\!\left( \ f^{-1}(5) \ \right). \]
Indeed, on computers systems which don't have a hardware multiplication circuit, every time you write $ab$ the computer will repeatedly add the number $a$ for a total of $b$ iterations.
Before Newton, people used called the the word number referred only to the natural numbers $\mathbb{N}$, which are sufficient if everything
In math you have to be precise, otherwise you are bullshitting. And trust me you don't want to bullshit with abstract things. At the beginning of all matters we have to define the players in the world of math. Numbers are the basic objects which you can type into a calculator. If you choose to bullshit at any point in your mathematical dealings, you will get slapped pretty hard. This is because math is abstract so if you are not clear about what you are talking about, things can go wrong very quickly. Let's start from the basics.
This is a subject for another lesson, but I wanted also to mention that $e^x$ is related to $\sin(x)$ and $\cos(x)$ through Euler's formula: $e^{ix} = \cos(x) + i\sin(x)$. We will learn more about that in the section on complex numbers $\mathbb{C}$.
We say that The sets are related to the fundamental operations of addition, subtraction, division
\[ \textrm{if } x,y \in \mathbb{N}, \textrm{ then } (x+y) \in \mathbb{N}. \]
\[ \textrm{if } x,y \in \mathbb{Z}, \textrm{ then } (x+y) \in \mathbb{Z} \textrm{ and } (x-y) \in \mathbb{Z}. \]
\[ \mathbb{Q} = \{ \text{ all } z \text{ such that } z=\frac{x}{y}, x \in \mathbb{Z}, y \in \mathbb{N} \}. \]
Explanations
Focal points
To derive the relation between $e$ and the parameters $a$ and $b$ we consider the point $A$ in the diagram on the previous page where \[ r_1 + r_2 = (e+a) + (a-e) = 2a. \] We will also consider the point $B$ where the two lengths $r_1,r_2$, are form the hypotenuse side of a triangle with sides $e$ and $b$ so we have \[ r_1 + r_2 = \sqrt{b^2+e^2} + \sqrt{b^2+e^2}. \] If we equate the two we get \[ 2a = 2\sqrt{b^2+e^2}, \] which, after dividing by 4 and squaring both sides, becomes \[ a^2= b^2+e^2. \] Thus $e=\sqrt{a^2 - b^2}$.
Double the speakers
The human ear's sensitivity to sound varies on a logarithmic scale. I.e., the stereo volume on notches 1, 2 and 3 has leads to “sound power” 2^1=2mW, 2^2=4mW, 2^3=8mW… (assuming a powers-of-two amplifier setup…) What age are your students? Maybe the above is not the best example….. Oh… and maybe you can ask “If I put two speakers on 2nd notch next to each other, do I get the equivalent of sound of having the speaker at notch 3 or notch 4? notch 2 = log_2(4mW) but you don't add notches, you should add the power right? So 4mW + 4mW = 8mW, which is equiv to notch 3.
Decidbels
0.5 = -3.01 dB
1 = 0dB
2 = 3.01
10 = 10dB
20 = 13.01
Using the properties of
Discussion
Applications of logarithms
In many sciences people often interchange multiplication and addition by using a logarithm transform \[ \log_3(f(x)) + \log_3(g(x)) = z, \] which by the properties of logarithms (see definition) can be written as \[ \log_3(f(x)g(x)) = z, \] which in turn means $f(x)g(x)=3^z$.
This is useful in probability theory since if you have some probability distribution $p_{XY}(x,y)$ that is independent then $p_{XY}(x,y)=p_X(x)p_Y(y)$. If you take the logarithm of this expression (the concept of log likelihood is a big deal in machine learning) then you get \[ \log(p_X(x)p_Y(y)) = \log(p_X(x)) + \log(p_Y(y)), \] so a complicated product expression can be evaluated as a sum. Human and computers are much better at adding numbers than multiplying them, so we use this trick all the time. This is especially useful when the two numbers $p_X(x)$ and $p_Y(y)$ are very small, so that their product would almost vanish if computed on a computer.
Exercises
You know that $1 = 0dB$, $2 = 3.0102dB$ and $10 = 10dB$ Using the properties of logarithms and the above two values, find $20$ in dB. Find 20 in dB us ANS: $10\log_{10}(20) = 10( \log_{10}( 2 ) + \log_{10}(10) ) = 3.0102 + 10 = 13.0102dB$.
Variables vs parameters
Sometimes however, symbolic manipulations can get confusing. Say you are looking for the variable $T$ in the equation: \[ m g\sin\alpha - \mu_k m g \cos\alpha + T = m g\sin\beta - \mu_k m g\cos\beta - T. \] This is a lot of variables right? Actually, there is just one unknown variable in the above equation, $T$, whereas all the others $m, g, \mu_k, \alpha$ and $\beta$ are just parameters, i.e., constants that are specified by the problem. Focus your attention on the $T$ and move all the non-$T$ terms on the other side like this: \[ 2T = m g\sin\beta - \mu_k m g\cos\beta - m g\sin\alpha + \mu_k m g \cos\alpha. \] You can now solve for $T$ (the unknown) in terms of all the parameters: \[ \begin{align} T & = \frac{1}{2}\left( m g\sin\beta - \mu_k m g\cos\beta - m g\sin\alpha + \mu_k m g \cos\alpha\right) \nl & = \frac{mg}{2}\left( \sin\beta - \mu_k\cos\beta - \sin\alpha + \mu_k \cos\alpha\right). \end{align} \] Though the expression on the right-hand side might still look complicated, in reality it is just some number. If I were to tell you that $m=140$[kg], $\mu_k=0.3$, $g=9.81$ and the values of the angles $\alpha=30^\circ$ and $\beta=20^\circ$, then you would be able to plug those in to get: \[ T = \frac{140(9.8)}{2}\left( \sin(20^\circ) - 0.3\cos(20^\circ) - \sin(30^\circ) + 0.3\cos(30^\circ)\right). \] Using your calculator to compute the right-hand side, you would be able to find the numeric value of $T$.
This variable-parameter distinction also applies for functions. For example, the formula that describes the position $x$ of a particle at time $t$ in mechanics is: \[ x(t)\ = \ x_i + v_i t + \frac{1}{2}at^2 \ =\ x(t\ ; \ x_i, v_i, a), \] where the semicolon notation indicates explicitly that $t$ is the variable whereas $x_i$, $v_i$ and $a$ are parameters.
Parameters
* You can also scale, and shift the absolute function to obtain
\[
f(x) = A|x-h| + k,
\]
which will have slope $A$, horizontal displacement $h$ and
vertical displacement $k$.
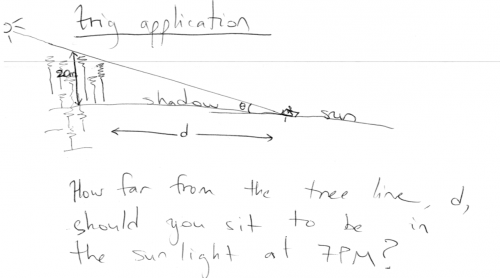
Tam tams in the sun
Rotations
The polar coordinate representation for cycles is
intimately related to the notion of rotations.
Suppose we wanted to rotate a point $(x,y)$ by $\theta$ degrees
around the origin in the clockwise direction. What will be the new
coordinates $(x',y')$ of the point?
$\quad x' = \cos\theta x - \sin\theta y$
$\quad y' = \sin\theta x + \cos\theta y$
You can verify these equations by thinking about the two points $(1,0)$ and $(0,1)$
and check that they are properly rotated.
Once For those of you who like to look at the unity and purity in your conceptual world, this is about to be a buzzed moment. You may, experience, as my Calculus professor from CEGEP says, a feeling that like the one when you smoke that funny stuff.
Consider the following three functions: \[ \{ e^x \equiv \text{exp}(x), \sin(x), \cos(x) \}, \] which are the exponential and the two trigonometric functions.