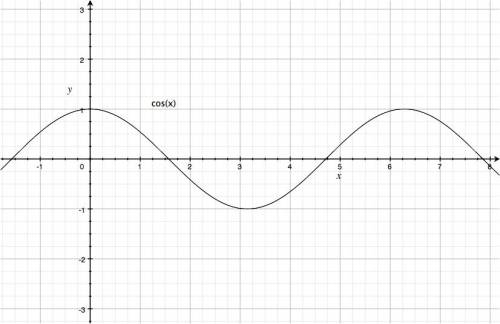
Cosine
Definition
\[ f(x)=\cos(x). \]
Graph
Cos starts off from $\cos(0)=1$ and then drops down to cross the $x$ axis at $x=\frac{\pi}{2}$. Cos then continues until it reaches its minimum value at $x=\pi$. The function then comes back up, crosses the $x$ axis again at $x=\frac{3\pi}{2}$, and goes back up to its maximum value at $x=2\pi$.
Properties
- The $\cos$ function is even, which means it doesn't care
about the sign of the input:
\[
\cos(-x) = \cos(x).
\]
* The cosine function is a shifted version of the sine function
\[
\cos(x) = \sin(x+\frac{\pi}{2}).
\]