$$f(x)=Ae^{\gamma x}.$$

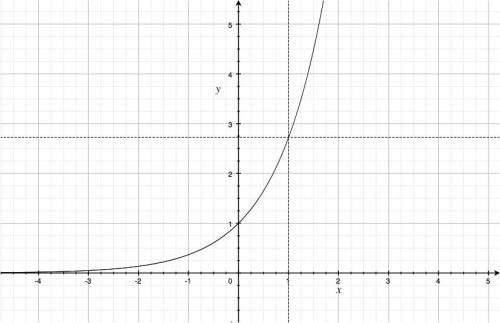
The exponential function graph:

• $A$: the initial value, $A=f(0)$. The graph shows the case $A=1$.
• $\gamma$: the rate of the exponential.

For $\gamma > 0$ the function is increasing.

  for $\gamma < 0$ the function is decreasing
  and tends to zero for large values of $x$.
  The case $\gamma=0$ is special since $e^{0}=1$,
  and so the exponential becomes the constant function $f(x)=A$.
  The graph shows the case $\gamma=1$.

• The number $e$ is related to the following limit argument

$$e = \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n,$$

  which can be interpreted as a formula for compounding interest.
  The limit as $n$ goes to infinity refers to a scenario when
  the compounding is performed infinitely often.
* The derivative (slope) of the exponential function is
  equal to the exponential function:
  \[
    f(x) = e^x  \ \ \Rightarrow \ \ f'(x)=e^x.
  \]
  In function $e^x$ is equal to its derivative: $f(x)=f'(x)$.

[ the exponential function $2^x$ for the naturals $x \in \mathbb{N}$ can easily be evaluated by drawing ]
http://www.youtube.com/watch?v=e4MSN6IImpI