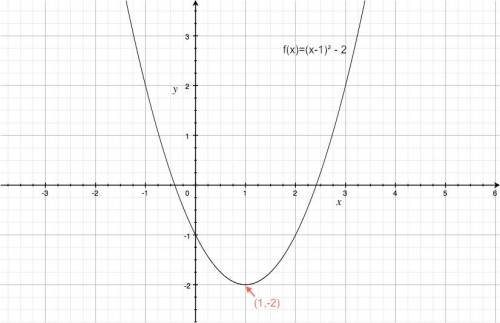
The general quadratic function has the following form: $$f(x) = A(x-h)^2 + k,$$ where $x$ is the input and $A,h$ and $k$ are the parameters.

• $A$: slope multiplier.
  • The larger the value of $A$ the steeper the slope.
  • If $A<0$ (negative), then the function opens downwards.
• $h$: horizontal displacement of the function centre. Notice that subtracting a

number inside the bracket $(\ )^2$ (i.e. positive $h$) makes the function go to the right.

• $k$: vertical displacement of the function.

If a quadratic crosses the $x$-axis, then it can be written in factored form $$f(x) = (x-a)(x-b),$$ where $a$ and $b$ are the two roots.

Another very common way of writing a quadratic function is $$f(x) = Ax^2 + Bx + C.$$

• There is a unique parabola that passes through any three points $(x_1,y_1),$ $(x_2,y_2)$ and $(x_3,y_3)$ if

the points have different $x$ coordinates $x_1 \neq x_2$, $x_2 \neq x_3$ and $x_1 \neq x_3$.

• The derivative of $f(x)=Ax^2 + Bx + C$ is $f'(x)=2Ax + B$.

When $h=1$ (one unit shifted to the right) and $k=-2$ (two units shifted downwards), we get the following graph: