Hyperbolic cos and sin
If we follow the $x$ and $y$ coordinates of a point $P$ that is on the unit circle, we will see that the $x=\cos(\theta)$ and $y=\sin(\theta)$, where $\theta$ is the angle of the point. This is called circular trigonometry.
We can also have hyperbolic trigonometry, if we replace the circle with a hyperbola. The $x$-coordinate of a point $Q$ that traces out the shape of a hyperbola will have the formula $\cosh$ and its $y$ coordinate will be $\sinh$.
Definition
We can define the hyperbolic functions in terms of the exponential function: \[ \cosh x = \frac{e^{x} + e^{-x}}{2}, \qquad \sinh x = \frac{e^{x} - e^{-x}}{2}. \]
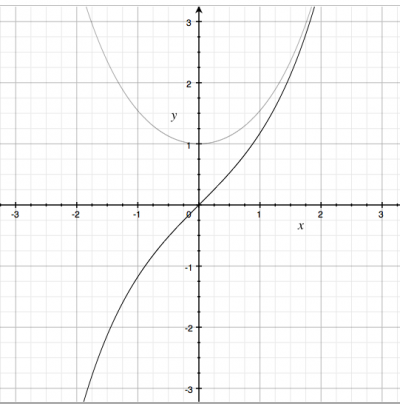
Graph
Parameters
Properties
- $\cosh$ is an even function, while $\sinh$ is odd.
In fact you can think of $\cosh x$ as the “even part of $e^x$,
and $\sinh x$ as the odd part of $e^x$ since \[ e^x = \cosh x + \sinh x. \]
The equivalent of the circular-trigonometric identity $\cos^2 \theta + \sin^2 \theta = 1$, is the following: \[ \cosh^2 x - \sinh^2 x = 1. \]
Applications
A long wire suspended between two lamp posts will sag in the middle producing a curved shape. The exact equation that describes the shape of the cable is the hyperbolic cosine function: $\cosh x$.