Sine
Contrary to what religious leaders might lead you to believe, there is nothing wrong with $\sin$. At least not with the mathematical $\sin$. The sinus, sine or $\sin$ function tells you the ratio of the lengths of two sides in a right angle triangle.
Definition
Let us not talk about triangles, angles and lengths of sides for now, but think of the $\sin$ function as a generic function of $x$: \[ f(x)=\sin(x). \]
Properties
- The $\sin$ function is odd, which the mathematical term for saying:
\[ f(-x) = -f(x). \]
- The function is periodic, with period $2\pi$, that is:
\[ f(x) = f(x+2\pi). \]
- Relation to $\cos$: $\sin^2 x + \cos^2 x = 1$.
- Relation to $\csc$: $\csc(x) \equiv \frac{1}{\sin x}$ ($\csc$ is read cosecant).
- The inverse function is $\sin^{-1}(x)=\arcsin(x)$, and is not
to be confused with $(\sin(x))^{-1}=\frac{1}{\sin(x)} \equiv \csc(x)$.
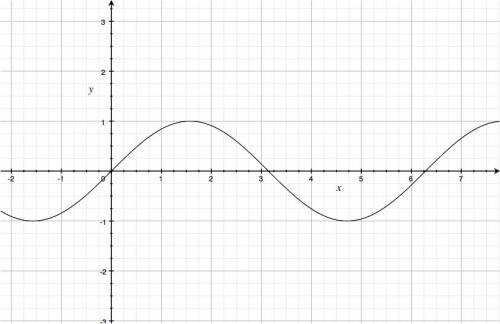
Graph
The function starts from zero $\sin(0)=0$, then goes up to take on the value $1$ at $x=\frac{\pi}{4}$, then falls down until it crosses the $x$ axis at $x=\pi$.
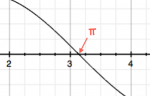
After $\pi$ the function drops below the $x$ axis and reaches its minimum value of $-1$ at $x=\frac{3\pi}{2}$ only to come up again and repeat the $2\pi$-long cycle starting from $x=2\pi$.
We have $0=\sin(0)=\sin(\pi)=\sin(2\pi)=\sin(3\pi)=\cdots$, in fact $\sin(x)$ has a root at each multiples of $\pi$.