Tangent
Definition
\[ f(x)=\tan(x)\equiv \frac{ \sin(x) } { \cos(x) }. \]
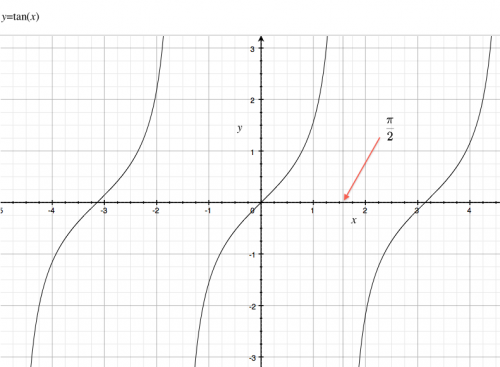
Graph
Properties
- The function $\tan$ is periodic with period $\pi$, not $2\pi$ like $\sin$ and $\cos$.
- The $\tan$ function has asymptotes at all values of $x$ for which the denominator ($\cos$) goes to zero.
- The locations of the asymptotes are $x=\frac{\pi}{2},\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\ldots$.
- At those values, $\tan$ approaches $\infty$ from the left, and $-\infty$ from the right.
- Value at $0$: $\tan(0)=\frac{0}{1}=0$ because $\sin(0)=0$.
- The angle $x=\frac{\pi}{4}$ is special since both $\sin$ and $\cos$ are equal
and we get:
\[
\tan\left(\frac{\pi}{4} \right)
= \frac{ \sin\left(\frac{\pi}{4}\right) }{ \cos\left(\frac{\pi}{4}\right) }
= \frac{ \frac{\sqrt{2}}{2} }{ \frac{\sqrt{2}}{2} }
= 1.
\]