Golden ratio
The golden ratio, usually denoted $\phi\approx 1.6180339887$ is very important proportion in geometry, art, aesthetics, biology and mysticism. If you have a stick of length $1$m and you wan to cut it into two pieces, say from $0$ (the left) to $x$ and from $x$ to $1$ (the right end). You have to pick the point $x$ closer to the right end, such that the ratio of the lengths of the short piece and the long piece is the same as the ratio of the long piece and the whole stick. Mathematically, this means this: \[ \frac{l_{\text{remaining short}}} {l_{\text{long}}} \equiv \frac{1-x}{x} = \frac{x}{1m} \equiv \frac{l_{\text{long}}}{l_{\text{whole}}}. \]
To see how the quadratic equation comes about, just multiply both sides by $x$ to get: \[ 1-x = x^2, \] which after moving all the terms to one side becomes \[ x^2 +x -1 = 0. \]
Using the quadratic formula we get the two solutions which are \[ x_1 = \frac{-1+\sqrt{5}}{2} = \frac{1}{\phi} \approx 0.618030, \qquad x_2 = \frac{-1-\sqrt{5}}{2} = -\phi \approx - 1.61803. \] The solution $x_2$ is some negative number, so it cannot be the $x$ we want – we wanted a ratio, i.e., $0 \leq x\leq 1$. The golden ration then is \[ \begin{align*} \phi &= \frac{1}{x_1} = \frac{2}{\sqrt{5}-1} \nl &= \frac{2}{\sqrt{5}-1}\frac{\sqrt{5}+1}{\sqrt{5}+1} = \frac{2(\sqrt{5}+1)}{5-1} = \frac{\sqrt{5}+1}{2}. \end{align*} \]
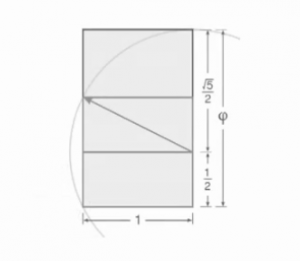
Geometry
Trigonometric functions
\[ \cos \left( \frac {\pi} {5} \right) = \cos 36^\circ={\sqrt{5}+1 \over 4} = \frac{\varphi }{2} \]
\[ \sin \left( \frac {\pi} {10} \right) = \sin 18^\circ = {\sqrt{5}-1 \over 4} = {\varphi - 1 \over 2} = {1 \over 2\varphi} \]
Fibonacci connection
The Fibonacci sequence, is defined by the recurrence relation: $F_n=F_{n-1}+F_{n-2}$ with $F_1=1$, and $F_2=1$.
Binet's formula
The $n$th term in the Fibonacci sequence has a closed formed expression \[ F_n=\frac{\phi^n-(1-\phi)^n}{\sqrt{5}}, \] where $\phi=\frac{1+\sqrt{5}}{2}$ is the golden ratio.
in the limit of large $n$, this term will dominate the rate of growth of the Fibonacci sequence. Consider the ratio between $F_n$ and $F_{n-1}$, i.e. at what rate is the sequence growing? \[ \frac{F_n}{F_{n-1}} = \frac{\phi^n-(1-\phi)^n}{\phi^{n-1} - (1- \phi)^{n-1} } \]
http://en.wikipedia.org/wiki/Fibonacci_number#Closed-form_expression
Five-pointed star
The golden ratio also appears in the ratios of two lengths in the pentagram, or five-pointed star. I am choosing not to discuss this here, because the five-pointed star is a symbol associated with satanism, freemasonry and communism, and I want nothing to do with any of these.
Electronic circuits
Links
[ The golden ratio in web design ]
http://www.pearsonified.com/2011/12/golden-ratio-typography.php