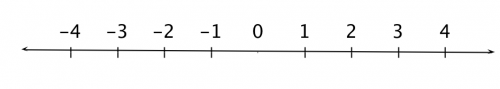The number line is a useful graphical representation for numbers. The integers $\mathbb{Z}$ correspond to the notches on the line while the rationals $\mathbb{Q}$ and the reals $\mathbb{R}$ cover (densely) the whole line:

You can clearly see the ordering of the numbers from the smallest on the left, to largest on the right. The line extends indefinitely on both sides: on the left it goes all the way to negative infinity $-\infty$ and on the right to positive infinity $\infty$.

We can represent subsets of the real numbers by setting in bold some section of the real line. For example, the set of numbers that lie strictly between $2$ and $4$, \[ \{ x \in \mathbb{R} | 2 < x < 4 \}, \] is represented graphically as follows.

Note that this subset is described by strict inequalities, which means that it does not contain its endpoints $2$ and $4$. It contains $2.000000001$ and $3.99999999$ but not the limits $2$ and $4$. We say call this kind of endpoints open and use an “empty dot” to denote them on the number line so that it is clear that the limit is not included in the set.

We denote intervals on the number lines which consist of disjoint sets by using the union ($\cup$) notation. For example, the set of numbers \[ \{ x \in \mathbb{R} | -3 \leq x \leq 0 \} \cup \{ x \in \mathbb{R} | 1 \leq x \leq 2 \}, \] can be represented graphically as:

This time we have less-than-or-equal limits so the intervals contain their endpoints. We call these endpoints closed and denote them with a dot that is filled-in on the number line.

[ Better number line diagrams and five great exercises on intervals ]
http://www.sosmath.com/algebra/inequalities/ineq02/ineq02.html