A set is mathematically precise way to talk about different groups of objects. To do simple math, you don't need to know about sets, but for more advanced topics you need to know what a set is and how we denote set membership and subset relations between sets.

• set: some collection of mathematical objects with a precise definition.
• $S,T$: usual variable names for sets.
• $\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}$: some important sets of numbers. These correspond to the naturals, the integers,

the rationals and the real numbers respectively.

• $\{ definition \}$: The curly brackets are used to surround the definition of a set and the expression inside is supposed

to completely describe what the set is.

NOINDENT Set operations:

• $S\cup T$: the union of two sets. The elements that are either in $S$ or $T$.
• $S \cap T$: the intersection of the two sets. The elements that are in both $S$ and $T$.
• $S \setminus T$: set minus. The elements of $S$ that are not in $T$.

NOINDENT Set relations:

• $\subset$: is a subset of.
• $\subseteq$: is subset or equal to.

NOINDENT Special mathematical shorthand and corresponding meaning in English:

• $\forall$: for all
• $\exists$: there exists
• $\nexists$: there doesn't exist
• $:$ or $|$: such that
• $\in$: is element of
• $\notin$: is not an element of

A lot of the power of math comes from abstraction: the ability to think meta thoughts and seeing the bigger picture about what math objects have in common. We can think of individual numbers like $3$, $5$ and $222$ or talk about the set of all numbers. You can think of functions like $f(x)=x$, and $f(x)=x^2$ or you can think of the set of all functions $f\colon \mathbb{R} \to \mathbb{R}$ that take real numbers as inputs and give real numbers as outputs.

Define $\mathbb{R}_+ \subset \mathbb{R}$ to be the set of non-negative real numbers: \[ \mathbb{R}_+ = \{ \text{all } x \text{ from } \mathbb{R} \text{ such that } x \geq 0 \}, \] or expressed more compactly: \[ \mathbb{R}_+ = \{ x \in \mathbb{R} \ | \ x \geq 0 \}. \]

Define the set of even integers as: \[ E = \{ n \in \mathbb{Z} \ | \ \frac{n}{2} \in \mathbb{Z} \} = \{ \ldots, -2, 0, 2, 4, 6, \ldots \}. \] and the set of odd integers as: \[ O = \{ n \in \mathbb{Z} \ | \ \frac{n+1}{2} \in \mathbb{Z} \} = \{ \ldots, -3, -1, 1, 3, 5, \ldots \}. \] In each case the mathematical notation $\{ \ldots \ | \ \ldots \}$ follows the same pattern where you first say what kind of objects we are talking about, followed by the “such that” sign $|$ followed by the conditions which must be satisfied by all elements of the set.

The natural numbers are the set of number you can get by starting from $0$ and adding $1$ arbitraryly many times: \[ \mathbb{N} \equiv \{ 0, 1, 2, 3, 4, \ldots \}. \] The integers are the number you get by adding or subtracting 1 arbitrary many times: \[ \mathbb{Z} \equiv \{ \ldots, -3, -2, -1, 0, 1, 2, 3, 4, \ldots \}. \] If you allow for divisions between integers, you get the rational numbers: \[ \mathbb{Q} = \{ -1.5, 1/3, 22/7, 0.125, \ldots \}. \] The more general class of real numbers includes also irrational numbers: \[ \mathbb{R} = \{\pi, e, -1.53929411..,\ 4.99401940129401.., \ \ldots \}. \] Finally we have the set of complex numbers: \[ \mathbb{C} = \{ 1, i, 1+i, 2+3i, \ldots \}= \{ a + bi \ | \ a,b \in \mathbb{R}, i^2=-1 \}. \]

Note the inclusion relationship which holds for these sets: \[ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}. \] Every natural number is also an integer. Every integer is a rational number. Every rational number is a real. Every real number is also a complex number.

Let's practice the new vocabulary by looking at a simple mathematical proof.

Claim: $\sqrt{2} \notin \mathbb{Q}$. This means that there are no integers $m \in \mathbb{Z}$ and $n \in \mathbb{N}$ such that $m/n = \sqrt{2}$. The same sentence in mathematical notation would read: \[ \nexists m \in \mathbb{Z}, n\in\mathbb{N} \ | \ m/n = \sqrt{2}. \]

Proof: Suppose for a contradiction that there existed $m$ and $n$ such that $m/n=\sqrt{2}$. We can further assume that integers $m$ and $n$ are such that they have no common factors: we can always make sure this is the case if we cancel the common factors. In particular this implies that $m$ and $n$ cannot both be even since we would be able to cancel at least one factor of two. We therefore have $\textrm{gcd}(m,n)=1$: the their greatest common divisor is $1$. We will now investigate a simple question which is whether $m$ is an even number $m\in E$ or $m$ is an odd number $m \in O$.

Before we begin, lemme point out the fact that the action of squaring an integers preserves its odd/even nature. Indeed, an even number times an even number gives and even number: if $e \in E$ then $e^2 \in E$. Also an odd number times an odd number also gives an odd number: if $o \in O$ then $o^2 \in O$.

The proof proceeds as follows. We assumed that $m/n = \sqrt{2}$, so if we take the square of this equation we have: \[ \frac{m^2}{n^2} = 2, \qquad m^2 = 2n^2. \] If $m$ is an odd number then $m^2$ is also going to be odd, which contradicts the above equation since we see that $m^2$ “contains” a factor $2$, so $m \notin O$. If $m$ is even then $m^2$ is also an even number, so it can be written as $m=2q$ for some other number $q\in \mathbb{Z}$. The equation would then become: \[ 2^2 q^2 = 2 n^2 \quad \Rightarrow \quad 2 q^2 = n^2. \] This implies that $n \in E$ which leads to a contradiction with the fact that we said $m$ and $n$ cannot both be even. Therefore $m \notin E$, and since $m \notin O$ either, this means that there is no such $m \in \mathbb{Z}$ and therefore $\sqrt{2}$ is irrational.

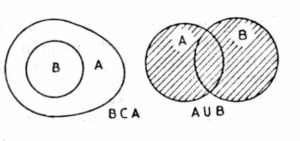
We say that $B \subset A$ if $\forall b \in B$ we also have $b \in A$, and $\exists a \in A$, such that $a \notin B$. We say “$B$ is strictly contained in $A$” which is illustrated graphically in the figure below. Also illustrated in the figure is the union of two sets $A \cup B$ which includes all the elements of $A$ and $B$. We have $e \in A \cup B$, if and only if $e \in A$ or $e \in B$.

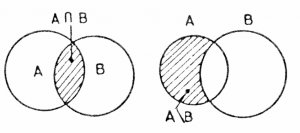
The set intersection is $A \cap B$ and set minus $A \setminus B$ are shown below.

The set of all functions of a real variable, that return a real variable is denoted: \[ f : \mathbb{R} \to \mathbb{R}. \]

The domain of a function is the set of all possible inputs. An input is not possible if the function is not defined for that input, like in the case of a “divide by zero” error.

The image set of a function is the set of all possible outputs of the function: \[ \textrm{Im}(f) = \{ y \in \mathbb{R} \ | \ \exists x\in\mathbb{R},\ y=f(x) \}. \]

Knowledge of the precise mathematical jargon introduced in this section is not crucial to the rest of this book, but I wanted to expose you to it because this is the language in which mathematicians think. Most advanced math textbooks will take it for granted that you understand this kind of notation.