A mass of one kilogram is attached

A heavy (not massless!) rope of mass M and length L is suspended vertically. You excite a wave at the bottom of the rope, and it propagates vertically upwards along the rope. Sketch the speed of the wave as a function of the position from the bottom of the rope, and explain your reasoning.

A8) This a waves question. The velcity of wave propagation in a rope is given by v = T/µ, where µ=m/L is the density of the rope and T is the tension in the rope. At the bottom of the rope there is not much tension since there is very little rope below …. so velocity at the bottom starts off small. Higher up along the rope, there will be a lot of rope pulling downwards so the tenstion in the rope will be larger leading to higher propagation v. Therefore a sinosoid shape with increasing frequency should be drawn.

Explain how you could measure both your mass and the position of your body’s centre of mass if all you had as experimental equipment was two spring balances (calibrated, of course), and a light, rigid plank, set up as shown in the figure.

A6) The mass of the person is the sum of the masses measured on the two balances. If we measure distance from the head balance the as x, and the distance to the feet balance is L, then the centre of mass will be at: x_cm = (R1*0 + R2*L)/(R1+R2) where R1 is the reading of balance one (head) and R2 is the reading of balance 2 (feet).

Q4) [4 pts] The figure below shows the trajectory (x vs y) of a particle moving on a plane. The particle moves at constant speed along the curve shown. At which of the points shown (A, B, or C) is the magnitude of the force on the particle the greatest? Explain your reasoning.

A4) This is a circular motion question. The centripetal acceleration equation is a_c = v²/R. The centripeal force required to produce this acceleration is F_c = ma_c. Combining these we see that for a constant motion with velcoticy v, the cetripetal force required to make an object turn in a right circle (like the middle point (B)) is the largest F_c = mv²/R – since (B) has the smallest radius of curvature, it is the place where particle will experience the most F_c.

A phase change may occur during reflection if the light is coming from a medium with a higher refractive index. It is useful to remember the following mnemonic for the amount of phase shift that occurs:

• From high ($n_1$) to low ($n_2$), no.
• From low to high, $\pi$!

This phase change is important in situations where you have to take into account the wave-like properties of light, like say, to when dealing with the phenomenon of interference.

TODO Power? different lenght-arms for leverage lifting something ⇒> force converter / amplifier same with pulleys ….

• $\vec{T}$: Tension in a rope. Tension is always pulling away from an object: you can't push a dog on a leash.

• $\vec{C}$: Contact force between two rigid objects. We generally brake-up contact forces into two

components: perpendicular and parallel to the contact surface.

• $\vec{N}\equiv\vec{C}_{\perp}$: Normal force: the force between two surfaces. Normal is a mathematically precise way to say “perpendicular to a surface”. Intuitively, you can think of $\vec{N}$ as the force that a surface exerts on an object to keep it where it is. The reason why my coffee mug does not fall to the floor, is that the table exerts a normal force on it keeping in place.
• $\vec{F}_f\equiv\vec{C}_{||}$: Force of friction between two surfaces. There are two kinds, both of which are proportional to the normal force between the surfaces:
  

Kinetic:

  \[
  F_{fk}=\mu_k|\vec{N}|.
  \]
  Static:
  \[
   F_{fs}=\mu_s|\vec{N}|.
  \]

• $\vec{F}_{fs}=\mu_s|\vec{N}|$: Static force of friction, for objects that are not moving.
• $\mu_s$: The static coefficient of friction. ex: 0.3.

It describes the maximum amount of friction that can exist between two objects. If a horizontal force exists greater than $F_{fs} = \mu_s N$, then the object will start to slip.

• $\vec{F}_{fk}=\mu_k|\vec{N}|$: Kinetic force of friction acts when two objects are sliding relative to each other. It always acts in a direction opposing the motion.
• $\mu_k$: Kinetic coefficient of friction. ex: $\mu_k=0.1$. Dimensionless. It is just the ratio that describes how much friction an object feels for a given amount of normal force.

Manifestations of the gravitational pull of the planet Earth on massive objects:

• $m$: mass of an object.
• $\vec{W}=\vec{F}_g$: The weight (the force on a object due to gravity).
• $G$: Gravitational constant $G=6.67x10^{-11}$ $\left[\frac{\textrm{N}\:\textrm{m}^2}{\textrm{kg}^2}\right]$.
• $F_g=\frac{GMm}{r^2}$: Force of gravity between two objects of mass $M$ and $m$ respectively. Measured in Newtons [N].
• $\vec{F}_g=-gm\hat{\jmath}$: The force of gravity on the surface of the earth.

The position of a particle is given by the equation $x(t)=-20+5t+5t^2$, where $x$ is measured in metres, and $t$ in seconds. Find the velocity and the acceleration at $t=2$[s].

To find the velocity function, we take the derivative of $x(t)$: \[ v(t) \equiv x'(t)=5 + 10t. \] To find the velocity at $t=2$ we plug this $t$-value into $v(t)$ to obtain \[ v(2) = 5 + 10(2) = 25 \text{ [m/s]}. \] To find the acceleration, we take the derivative of the velocity: \[ a(t) \equiv v'(t) = 10. \] Thus the acceleration is equal to $10$[$\frac{m}{s^2}$] at all times, including $t=2$[s].

Recall that $a(t)$ measures the instantaneous changes in $v(t)$: \[ a(t) \equiv \frac{d}{dt} v(t). \] It follows that if we sum up (integrate) all the acceleration over some time period we will obtain the total change in the velocity $v_f-v_i=\int_0^t a(t) \; dt$. Similarly, the integral of the velocity gives us the total change $x_f-x_i = \int_0^t v(t)\; dt$,

The velocity $v(t)$ is defined as the instantaneous change in the position: \[ v(t) \equiv \frac{d}{dt} x(t). \]

which means that starting from the position function $x(t)$, we can use the derivative operation to obtain the velocity $v(t)$ and the acceleration $a(t)$. Since $v(t)$ is the derivative of $x(t)$, and $a(t)$ is the derivative of $v(t)$, we say that $a(t)$ is the second derivative of $x(t)$: \[ a(t) \equiv \frac{d}{dt} v(t) = \frac{d}{dt}\left( \frac{d}{dt} x(t) \right) = \frac{d^2}{dt^2} x(t) = x''(t). \] It is the rate of change of the rate of change. Graphically, the rate of change of the rate of change corresponds to the curvature of the function $x(t)$. In regions with positive acceleration the graph of $x(t)$ curves up (convex). In regions with negative acceleration the graph of $x(t)$ curves down (concave).

There are also psychological benefits to learning physics, since you will boost your confidence in your analytical skills. therapy for bad experiences can solve problems – the real world is messy and complicated and there are rarely things that can be describes with mathematical precision

simple to predict == you can be good at it

cartesian

It is important to train your superpowers so the more exercises you solve the better off you will be.

TODO ZZZZZ

There will be math, yes, but nothing too complicated. You have to known how to solve quadratic equations, and how to calculate simple integrals, but these are things that you know how to do already. Mechanics is not about solving equations, but about developing a better understanding of the world around us in terms of concepts like forces, energies, velocities, accelerations, etc.

Some equations, like the formula for predicting the elongation of an aluminum rod as a function of temperature $T$[$^\circ$C] $\Delta \ell=\ell \alpha_{\textrm{Al}} (T - 20^\circ)$, are empirical, which means that they obtained by measuring the real world. Someone took an aluminum rod of length $\ell$, heated it up from $T=20$[$^\circ$C] to $T=50$[$^\circ$C] and measured the thermal expansion $\Delta \ell$ in order to measure the coefficient of thermal expansion for aluminum $\alpha_{\textrm{Al}}$[1/$^\circ$C]. Other equations, l $\alpha_{\textrm{Al}}=23.1\times 10^{-6}$[1/$^\circ$C].

this equation starting from first principles. This means that we will start from the equation of some law of nature (Newton's second law) and order to obtain the equation of motion. This kind of physics-laws-and-math-methods reasoning is the bread and butter of physicists.

The first subject we learn in physics is classical mechanics, since it is the part of physics that is most well understood.

So far we studied only motion in one dimension. What about motion in two dimensions? For this we will need to describe the position of the object as a vector $\vec{r}(t)=(x(t),y(t))$. Forces are vectors too. In fact Newton's second law is a vector equation: $\vec{F}=m\vec{a}$. It seems that it would be worthwhile to learn a thing or two about vectors now.

When solving some problem where we calculate the motion of an object that starts form an initial point an goes to a final point we will use the following terminology:

• $t_i=0$: initial time (the beginning of the motion).
• $t_f$: final time (when the motion stops).
• $x_i=x(0)$: initial position.
• $x_f=x(t_f)$: final position.
• $v_i=v(0)$: initial velocity of the object, e.g. when the object is thrown.
• $v_f=v(t_f)$: final velocity of the object, e.g. when the object hits the ground.

If you know the acceleration of an object $a(t)$ as a function of time and its initial velocity $v_i=v(0)$, you can find its velocity $v(t)$ function at all later times. This is because the acceleration function $a(t)$ describes the change in the velocity of the object. If you know that the object started with an initial velocity of $v_i \equiv v(0)$, the velocity at a later time $t=\tau$ is equal to $v_i$ plus the ``total velocity change” between $t=0$ and $t=\tau$. The mathematical way of saying this is $v(\tau)=v_i+\int_0^\tau a(t)\;dt$. The symbol $\int \cdot \;dt$ is called an integral and is fancy way of finding the total of some quantity over a given time period. To find the change in the velocity we calculate the total of $a(t)$ between $t=0$ and $t=\tau$.

To understand what is going on, it may be useful to draw an analogy with a scenario you are more familiar with. Consider the function $\textrm{ba}(t)$ which represents your bank account balance at time $t$, and the function $\textrm{tr}(t)$ which corresponds to the transactions (deposits and withdraws) on your account. The function $\textrm{tr}(t)$ describes the change in the function $\textrm{ba}(t)$, the same way the function $a(t)$ describes the change in $v(t)$. Knowing the balance of your account at the beginning of the month, you can calculate the balance at the end of the month as follows: $\textrm{ba}(30)=\textrm{ba}(0)+\int_0^{30} \textrm{tr}(t)\:dt$.

If you know the initial position $x_i$ and the velocity function $v(t)$ you can find the position function $x(t)$ by using integration again. We find the position at time $t=\tau$ by adding up all the velocity (changes in the position). The formula is $x(\tau) = x_i + \int_0^\tau v(t)\:dt$.

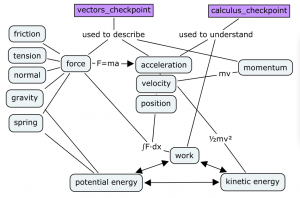
The causes and effects of the motion of bodies are represented in this diagram:

To understand any physics problem you must first check which kinds of forces are relevant, make a force diagram and add up all the forces to obtain $\vec{F}_{net}$, the net force on the object. Then you use $\vec{a}=\frac{\vec{F}_{net}}{m}$ and you have your acceleration. Problem solved, because once you have $a$ you just need to plug it into equations of motion: \[ \vec{a}(t) = \vec{a}, \] \[ \vec{v}(t) = \vec{a}t+\vec{v}_i, \] \[ \vec{r}(t) = \frac{1}{2}\vec{a}t^2+\vec{v}_it + \vec{r}_i. \] There you have it. All of undergraduate level mechanics boils down to your understanding and usage of the equation $F=ma$.

Disclaimer: Of course physics is more complicated than that, but what you are learning is an important and very useful subset. Namely, the above three equations make the assumption that the acceleration is constant, which in turn assumes that the balance of the forces acting on the object will always remain the same. We assume that during the entire time between $t_i$ and $t_f$ the force $\vec{F}_{net}$ stays constant. In a lot of situations this assumption is true.

In more complicated situations you could have $\vec{F}_{net}$ changing over time and thus $a(t)$ changing over time too. You would have to start from $a(t)$ and do the integration thing twice on $a(t)$ to get the $x(t)$ for the motion.

Sometimes the net force on the object $\vec{F}_{net}$ might be constant, but the mass of the object may change over time (like a multi-stage rocket losing its booster tanks) so you would still have $a(t)=\frac{F_{net}}{m(t)}$ changing with time because $m(t)$ would be changing. Again, for those situations you have to go back to calculus and integrate $a(t)$ twice to get the $x(t)$ function.

If you look carefully, you will see that the mass $m$ appears in two very different contexts.

1. The inertial mass appears in $\vec{F}_{net} = m \vec{a}$, and this notion of mass measures how much resistance the object offers to being moved.
2. The gravitational mass that gives the weight of an object $\vec{W}=m\vec{g}$. This mass measures the attraction of the object to the gravitational field of the earth.

The fact that these two masses are the same is a sign of a deeper relationship between acceleration and gravitation.

Simple harmonic motion is equally well described by the $\sin$ function or the $\cos$ function. The choice is up to you, but remember to add an appropriate phase shift $\phi$ (if necessary), so that the function you choose correctly describes the initial conditions.

It can be difficult to see what the motion is with two amplitudes. (one for stretched initial conditions, and one for centred initial conditions) and a sum of sin and cos:

$a\sin(x)+b\cos(x)$ can be expressed as $A\cos(x+\phi)$ or $A\sin(x-\psi)$ is not magic, but simple application of the trigonometric identities.

When $\theta$ is a small angle we can use the following approximations: \[ \sin(\theta)\ \approx \ \theta, \qquad \cos(x) \ \approx \ 1 - \frac{\theta^2}{2}, \qquad \text{ for } \theta \ll 1. \]

You will find that $A_1=A\cos(b)$, $A_2 =A\sin(b)$ and $A=\sqrt{A_1^2 + A_2^2}$.

If for some reason you are more comfortable with the function $\sin$, then you can use an equivalent set of equations of motion based on it: $x(t)=A\sin(\omega t + \psi)$, $v(t)=A\omega\cos(\omega t + \psi)$, $a(t)=-A\omega^2\sin(\omega t + \psi)$. Using this form for the equations of motion, the phase constant $\psi$ (psy) for the case where the initial position is zero $x_i=0, \Rightarro \psi=0$ and $x_i=A \Rightarrow \psi=+\pi/2$.

Simple harmonic motion is produced every time there is a restorative force acting on the object, which tends to always bring it to its equilibrium position. Recall that the force of a spring is given by $\vec{F}_s=-k\vec{x}$

This is as far as Newton's second law will be able to bring us. The formula $F=ma$ is not enough to tell us the exact function $x(t)$, like in the UVM and UAM kinematics motion in the kinematics chapter.

When it comes down to the question how much you can pull, and you want to answer it by looking at the specs of your truck, you have to look at (1) the max torque $\mathcal{T}$ and (2) the radius of your wheels $r$, and divide the numbers to get the maximum pulling force $F$.

People living in rural areas like to buy trucks because they have a lot of torque. Big engine, big torque. You can pull stuff. Wait isn't that force? But toque should be good too? What is the difference? I am confused.

Torque is force times distance, i.e., we have to take into account not only what force is exerted but also the leverage: how far from the centre of rotation you are exerting the force: \[ \mathcal{T} = F_{\!\perp}\: r. \] The bigger the leverage $r$, the bigger torque you will create with a fixed amount of force.

Though the equations in this chapter will be new, the reasoning used to understand rotations parallels exactly the reasoning we used to understand linear motion.

For example, if we attach a second rock half-way along length the rope

 multiple objects different parts of the stpoints on a rotating disk will have different tangential speeds $v_t$

depending on how far from the radius they are, so it is much better to describe the angular velocity and multiply by the radius as needed.

• $\vec{r}=(0, \ell(t))_{\hat{r}\hat{t}}$: The position of the object is described by

the length $\ell(t)$ travelled along the circle as a function of time.

To understand this whole $\hat{r}$ and $\hat{t}$ business, I want you to imagine for a second that you can freeze time. The $\hat{r}$ direction will be towards the centre of the circle and $\hat{t}$ is along a line touching the circle, i.e., though moving in a circle overall, instantaneously you are moving in the $\hat{t}$ direction. If you unfreeze time and one microsecond elapses the $\hat{r}$ and $\hat{t}$ directions will change, you will have moved a little along the circle and the $\hat{r}$ vector will have to rotate to keep pointing at the centre. Similarly, your instantaneous direction of motion $\hat{t}$ will have shifted a bit.

• $\hat{r},\hat{t}$: the radial and tangential directions of a circular coordinate system. No matter where you are on the circle, the radial direction always points towards the centre, while the tangential direction is always perpendicular.

Every time you have uniform circular motion ($v_{t}=const$), these variables will be related:

• $R$: Radius of the circle of motion.
• $v_t$: Speed of the circular motion in $[m/s]$. Sometimes referred to as tangential speed.
• $a_r$: Radial acceleration. The relation is $a_r=\frac{v_t^2}{R}$.

Actually, the exact time it takes the earth to do one rotation is 23 hours 56 minutes 4.09 seconds, so the Earth angular speed is $7.2921\times 10^{-5}$ [rad/s].

       === Period ===

From kinematics we know that motion with constant velocity (UVM) is described by the formula $x = vt$, where the speed is defined as ratio of distance travelled over time: $v=\frac{\Delta x}{\Delta t}$. In this case the distance travelled $\Delta x$ is not a straight line but a curve following the circumference of a circle: \[ C = 2\pi R. \] The period is defined as the time it takes for the object to complete one full turn: \[ T = \frac{\text{distance}}{\text{speed}} = \frac{2\pi R}{v_t}. \]

Tangential speed $v_t$ is measured in $[m/s]$, whereas $R$ is measured in $[m]$ so if you divide the two you get seconds $[s]$.

The proof of $a_r=\frac{v_t^2}{R}$ is somewhat complicated. You have to draw a diagram showing the motion of the object along the circle at three points and then do some vector Kung Fu to show that the relation holds.

Let us analyze the forces involved in the problem:

• $\vec{F}_{dp}$: The amount of force the door is exerting on the passenger.
• $\vec{F}_{pd}$: The amount of force the passenger is exerting on the door.

We know from Newton's third law, that these forces are equal in magnitude and act in opposite directions.

Viewed from the point of view of the passenger there is no confusion. The force $F_{dp}$ acting towards the centre of rotation is causing a $ma_r=m\frac{v_t^2}{R}$, and thus the circular motion of the passenger results.

Viewed from the point of view of the door, it feels a certain push towards the outside of the circle which corresponds to the counter-force to the force that the passenger feels. This comes from Newton's third law, which says that for each contact force $C_{12}$ exerted by Object 1 on Object 2, there exists a counter force $C_{21}$ exerted of equal magnitude and opposite direction, which is the force of Object 2 pushing back on Object 1.

The confusion people get into, and the whole false concept of centrifugal force, comes from thinking of a force diagram on yourself and falsely including the outwards force on the door. You have to be clear. Which force diagram are you doing? If you are thinking of yourself as the object, the force that you feel is a centripetal force.

An old grandma approaches you in the bus station while you are waiting for the bus. You strike up a conversation about this and that, and somehow you get to the question of physics and torque and she challenges you to a contest of force. You will go into opposite sides of the turning doors and force against each other. You will try to make the doors spin counterclockwise, while she attempts to spin the door clockwise. You accept, and not only that, but also bet 5 bucks against her, feeling confident that you will be able to push her off with no stress. The only condition she has is that you are only allowed to push on the inside of the door, close to the centre of rotation.

You lose – because she has more torque. Though she may have less force $F$, the fact that she is pushing at a longer distance from the centre of rotation $r$ makes her torque bigger. Don't bet against grandma physicists. They will own you.

This entire section is dedicated to that formula, which applies to all objects moving around in a circle.

of its this height, and every time the wheel makes a turn, the detector “feels” the magnet pass by. The more often the detector sees the magnet pass by (how many times per second) the faster the bike must be going. But how fast exactly? If I see the magnet pass by 10 times per second, and the radius of the wheel is $R=14$[in], how fast is the bike going?

Work: \[ W = \int \vec{F}(x) \cdot dx \] for constant force: \[ W = \int_0^d \vec{F} \cdot d\vec{x} = \int_0^d \vec{F} \cdot d\vec{x} = \vec{F}\cdot \vec{d} = \|F\|\|d\|\cos\theta. \]

The momentum of an object is the mass of the object times its velocity: \[ \vec{p} = m\vec{v}. \]

The conservation of momentum equation says that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out}. \] Plugging in the values we get \[ 0.4\times 10 \hat{\imath} - 2\times 30 \hat{\jmath} = 2.4\vec{v}_{out}, \] or solving for $\vec{v}_{out}$ we find: \[ \vec{v}_{out} = \ \frac{ 0.4\times 10 \hat{\imath} - 2\times 30 \hat{\jmath}} {2.4} = 1.666\hat{\imath} - 25.0\hat{\jmath}. \]

If you are moving at velocity $100$[m/s] and you accelerate at a rate of $10$[m/s^2] during 3 seconds, then your final velocity at the end of the three seconds will be \[ v(3) = \int_0^3 10\ dt + 100 = 10(3) + 100 = 130 [m/s]. \]

If you feel mystified by this integral sign, you are not alone. Just keep in mind that integration is accumulating some quantity to see what the total contribution is going to be.

The meaning of integration is actually a bit simpler to see with the relation: \[ x_f \equiv x(t_f) = \int_{t_i}^{t_f} v(t) \ dt + x_i, \] which says that if you start at position $x_i = x(t_i)$ and move at a velocity $v(t)$ between $t_i$ and $t_f$, then you final position will be $x_f$. You are probably most familiar with this kind of reasoning from the context of driving in your car. Indeed you know that if you start at Montreal $x_i=0$[km], and drive at $110$[km/h] for 2 hours, you can get to Quebec city which is at $x_f=220$[km]. Most people have an intuitive feel about this kind of calculation, but mathematicians invented a fancy notation to describe it: \[ \int_{t_i=0}^{t_f=2} 110 \ dt + 0 = 220. \] We accumulate a total of 220[km] displacement. During the first hour we move 110[km], and during the second hour another 110[km].

Note that the units of $g$ are also

What was its speed when it hit the ground? To find the velocity as it hits the ground, we use the velocity equation $v(t) = at + v_i$, with the initial value $v_i=0$ and the value of $a$ we just obtained: \[ v_f = v(3) = (-9.81)(3) + 0 = -29.43 \text{ [m/s]}. \] The velocity is negative, because the ball is moving in the opposite direction of our $y$-axis, which starts at the base of the building.

1. In the absence of external forces, object will maintain their velocity

and their direction of motion.

1. Force causes acceleration:

\[ \vec{F}=m\vec{a}(t), \]

           where the acceleration $\vec{a}(t)$ describes the change in velocity $\vec{v}(t)$,
           and velocity describes the change in position $\vec{r}(t)$.
           Using calculus notation we write:
           \[
             \vec{a}(t) \equiv \frac{d\vec{v}(t)}{dt}, \qquad
                            \vec{v}(t) \equiv \frac{d\vec{r}(t)}{dt}.
           \]

$x(t)$ right describe When you have $x(t)$, you have a description of the position for all times. The velocity is a function of time too; it describes the way $x(t)$ is changing at time $t$. The acceleration is important because it appears in Newton's second law $\vec{F}(t)=m\vec{a}(t)$, so we can easily calculate the acceleration of some object if we know its mass and the forces acting on it. The kind of problem where you find the force and divide by $m$ to find the acceleration are called dynamics and are the subject of another chapter.

In this chapter we will just observe the motion: where is starts $x_i$, where it ends $x_f$, when it starts $t_i$, and when it stops $t_f$. We will also often be given the initial value of the velocity $v_i \equiv v(0)$. For most problems you will need to solve, you can assume that the acceleration is a constant function $a(t)=a$. Do not confuse $x(t)$, the function, with particular values like the initial position $x_i \equiv x(0)$, where $t_i$ is the initial time or final position $x_f \equiv x(t_f)$, where $t_f$ is the final time.

What is the acceleration? Acceleration is the derivative of velocity, or you can say it the other way around: velocity is the integral of the acceleration.

Because we are doing this for real, where this is physics and for real means I will show you the real math and not some simplifications, you will also need to review vector products. The concept of work is defined as the dot product of the force and the displacement. The cross product is all over electromagnetism under the guise of various “right-hand rules”.

The simple triple rule is very useful when you want to convert quantities. If you are making a rhum-and-coke drink for yourself, you know that to make it drinkable (not too strong, not too weak) you have to mix one shot (50[ml]) of rhum with 150[ml] of coke to obtain a 200[ml] drink. Suppose, however, that you are going to the Jazz fest and you want to make a large quantity of this mix. Say you have a 1[L] coke bottle which you want to sneak into the Jazz fest. How much rhum should you mix in?

You want to keep the same ratio of rhum to coke, so mathematically speaking you want the following two fractions to be equal: \[ \frac{ 50 \text{ [ml] } }{ 200 \text{ [ml] } } = \frac{ ? \text{ [ml] } }{ 1000 \text{ [ml] } }. \]

The simple triple rule, a.k.a. cross-multiplying says that the unknown $?$ is obtained by multiplying together the two known quantities on the other diagonal and dividing by the quantity opposite to $?$: \[ ? = 50 \times 1000 / 200 = 250 \text{[ml]}. \] This is shaping up to be a serious drink, so you better share it with people.

There is a more general version of this multiplication procedure which allows you to convert from any units to any units, by multiplying with conversion fractions equal to one. If you make 9 dollars per hour, what is your annual salary? \[ \frac{ 9 \text{ [dollars] } }{ 1 \text{ [h] } } \cdot \frac{ 40 \text{ [h] } }{ 1 \text{ [week] } } \cdot \frac{ 52 \text{ [week] } }{ 1 \text{ [year] } } = \ \ \frac{ ? \text{ [dollars] } }{ 1 \text{ [year] } }. \] We multiply all the numbers and units on the top, and divide by all the numbers and units on the bottom: \[ \frac{ 9 \times 40 \times 52} { 1}\text{ [dollars / year]} = 18720 \text{ [dollars / year]}, \] where all the other units cancelled out, since they appear on the top and on the bottom.

And don't worry about the money: if you learn math, you will be like hot cakes on the job market and definitely won't be working for minimum wage. You can also choose to start your own business and change the world.

Example: One litre 1[L] is equal to 1000000[mm^3]? Calculate the length of the side of a cube with volume 1[L]$. State your answer in [cm]$. Let the side of the cube be $x$, then we have: \[ x^3 = 1000000[mm^3] = (100[mm])(100[mm])(100[mm]) = (10[cm])(10[cm])(10[cm]) \] So $x$ is either 100[mm] or 10[cm]. A cube of sides 10[cm] by 10[cm] by 10[cm] has volume 1[L].

Physics is a special kind of science. On the one hand there is a lot of math, since all the laws of physics are expressed in terms of mathematical equations, but on the other hand you need a lot of intuition to feel what is happening. In this section we outline the mathematical tools which you need to bring to the physics scene. You see physics is really quite simple once you beef-up your math skills. Be sure to review the relevant chapters of the book. This book is organized so that you will have everything you need in one place.

The remainder of this chapter will describe how can obtain the equation $y_c(t)=\frac{1}{2}(-9.8)t^2 + 12t+0$ from first principles. This chapter serves as a showcase of the power of calculus to manipulate function $f:\mathbb{R} \to \mathbb{R}$. In high school you learn about numbers instead of just

and the and the simplicity of physics.

If the predictions of the equations do not match with your measurements, it is probably due to air friction which we ignored in the above equation. In those cases you should repeat the experiment in vacuum, where there will be no air friction. If that is not an option and you really need to predict $y(t)$ accurately, you will need another model $x_a(t)$ which takes into account the effects of air friction. Things become very complicated there and this is why even the general public respect rocket scientists. Don't worry though. We won't be going there.

  \textrm{force} 	  	& [\textrm{N}] (\textrm{Newton})&			& \textrm{dynamometer}

Mathematicians want things to be exact, but in physics we just want to get the answer. Sometimes we are willing to bend the truth to make our equations simple.

When $x$ is a small number we can approximate: \[ \sin(x)\ \approx \ x, \qquad x \ll 1, \] which is useful since it allows us to replace the $\sin(x)$ function with a simpler function $x$. We also have \[ \cos(x) \ \approx \ 1, \qquad x \ll 1. \] These two are called small angle approximations. If you want to see where they come from, find a plot of the functions and zoom in many times around $x=0$. The above formulas come from the first degree Taylor series approximations $\sin$ and $\cos$.

Perhaps the most useful skill from your evolutionary toolset which you will be able to apply to physics is the pattern matching skill. Say you are at an exam, and you are asked to solve for the energy of something as it hits something else. Energy. Did you hear that? What equations do you know that involve energy? Which ones involve the variables that are given in the statement of the problem. Write everything down.

Of course, it is better to really understand what is going on, but pattern matching is nothing to be ashamed of when you are getting started. You will be surprised how far it will take you. Don't be fooled though, the success of pattern matching at homework problems and exams is only due to the fact that your teachers are really limited in the kind of questions they are allowed to ask you. The course syllabus protects you!

The beauty of physics are or natural law is deep stuff . Physics is the study of the phenomena in the world around us. Why do objects move? Can we predict their motion? What kinds of forces exist between objects?

Starting from very general principles like forces and energy, we can derive the equation of motion of objects.