Force diagrams
Welcome to Force-Accounting 101. In this section we will learn how to identify all the forces acting on an object and use Newton's 2nd law $\sum \vec{F}=\vec{F}_{net} = m\vec{a}$ to predict the resulting acceleration.
Concepts
Newton's second law describes a relationship between these three quantities:
- $m$: the mass of an object.
- $\vec{F}_{net}$: the net force on the object.
- $\vec{a}$: the acceleration of the object.
Forces and accelerations are vectors. To work with vectors, we work with their components:
- $F_x$: the component of $\vec{F}$ in the $x$ direction.
- $F_y$: the component of $\vec{F}$ in the $y$ direction.
Vectors are meaningless unless it is clear with respect to which coordinate system they are expressed.
- $x$ axis: Usually the $x$ axis is horizontal and to the right, however, for problems with inclines,
it will be more convenient to use an inclined $x$ axis that is parallel to the slope.
- $y$ axis: The $y$ axis is always perpendicular to the $x$ axis.
- $\hat{\imath},\hat{\jmath}$: Unit vectors in the $x$ and $y$ directions. Any vector can be written as $\vec{v}=v_x\hat{\imath}+v_y\hat{\jmath}$ or as $\vec{v}=(v_x,v_y)$.
Provided we have a coordinate system, we can write any force vector in three equivalent ways: \[ \vec{F} \equiv F_x\hat{\imath} + F_y\hat{\jmath} \equiv (F_x,F_y) \equiv \|\vec{F}\|\angle \theta. \]
What types of forces are there in force diagrams?
- $\vec{W}\equiv\vec{F}_{gravity}=m\vec{g}$: The weight. This is the force on a object due to its gravity. The gravitational pull $\vec{g}$ always points downwards – towards the centre of the earth. $g=9.81$[N/kg].
- $\vec{T}$: Tension in a rope. Tension is always pulling away from the object.
- $\vec{N}$: Normal force – the force between two surfaces.
- $\vec{F}_{fs}=\mu_s\|\vec{N}\|$: Static force of friction.
- $\vec{F}_{fk}=\mu_k\|\vec{N}\|$: Kinetic force of friction.
- $\vec{F}_{s}=-kx$: The force (pull or push) of a spring that is displaced (stretched or compressed) by $x$ metres.
Formulas
Newton's 2nd law
The sum of the forces acting on an object, divided by the mass, gives you the acceleration of the object: \[ \sum \vec{F} \equiv \vec{F}_{net}= m\vec{a}. \]
Vector components
If a vector $\vec{v}$ makes an angle $\theta$ with the $x$ axis then: \[ v_x = \|\vec{v}\|\cos\theta, \qquad \text{and} \qquad v_y = \|\vec{v}\|\sin\theta. \] The vector $v_x\hat{\imath}$ corresponds to the part of $\vec{v}$ that points in the $x$ direction.
In what follows, you will be asked a countless number of times to \[ \text{Find the component of } \vec{F} \text{ in the ? direction. } \] Which is another way of asking you to find the number $v_?$.
The answer is usually equal to the length $\|\vec{F}\|$ multiplied by either $\cos$ or $\sin$ and sometimes $-1$ all depending on way the coordinate system is chosen. So don't guess. Look at the coordinate system. If the vector points in the direction where $x$ increases, then $v_x$ should be a positive number. If $\vec{v}$ points in the opposite direction, then $v_x$ should be negative.
To add forces $\vec{F}_1$ and $\vec{F}_2$ you have to add their components: \[ \vec{F}_1 + \vec{F}_2 = (F_{1x},F_{1y}) + (F_{1x},F_{2y}) = (F_{1x}+F_{2x},F_{1y}+F_{2y}) = \vec{F}_{net}. \] Instead of dealing with vectors in the bracket notation as above, when solving force diagrams it is easier to simply write the $x$ equation on one line, and the $y$ equation on a separate line below it: \[ F_{netx} = F_{1x}+F_{2x}, \] \[ F_{nety} = F_{1y}+F_{2y}. \] It is a good idea to always write those two equations together as a block – so it remains clear that you are talking about the same problem, but the first row represents the $x$-dimension and the second row represents the $y$-dimension.
Force check
It is important to account for all the forces acting on an object. Any object with mass on the surface of the earth will feel a downwards gravitational pull of magnitude $F_{g}=W=m\vec{g}$. Then you have to think about which of the other forces might be present: $\vec{T}$, $\vec{N}$, $\vec{F}_{f}$, $\vec{F}_{s}$. Anytime you see a rope tugging on the object, you know there must be some tension $\vec{T}$, which is a force vector pulling on the block. Anytime you have an object sitting on a surface, the surface will push back with a normal force $\vec{N}$. If the object is sliding on the surface there will be a force of friction acting against the direction of the motion: \[ F_{fk}=\mu_k\|\vec{N}\|. \] If the object is not moving, then you have to use $\mu_s$ in the friction force equation, to get the maximum static friction force that the contact between the object and the ground can support before the object starts to slip: \[ \max\{ F_{fs} \}=\mu_s\|\vec{N}\|. \] If you see a spring that is either stretched or compressed by the object, then you must account for the spring force. The force of a spring is restorative: it always acts against the deformation you are making to the spring. If you stretch it by $x$[cm], then it will try to pull itself back to its normal length with a force of: \[ \vec{F}_s = -kx \hat{\imath}. \] The constant of proportionality $k$ is called the spring constant and is measured in [N/m].
Recipe for solving force diagrams
Below we list the steps of the general procedure to follow when solving problems in dynamics.
- Draw a force diagram focussed on the object and indicate all the forces acting on it.
- Choose a coordinate system, and indicate clearly in the diagram what you will call the positive $x$ direction, and what you will call the positive $y$ direction. All quantities in the subsequent equations will be expressed with respect to this coordinate system.
- Write down the following “template”:
\[ \sum F_x = \qquad \qquad \qquad = ma_x, \] \[ \sum F_y = \qquad \qquad \qquad = ma_y. \]
- Fill in the template by calculating the $x$ and $y$ components
of each force acting on the object:
$\vec{W}$, $\vec{N}$, $\vec{T}$, $\vec{F}_{fs}$, $\vec{F}_{fk}$,
$\vec{F}_{s}$ as applicable.
- Solve the equations for the unknown quantities.
I highly recommend that you perform some consistency checks after Step 4. You should check the signs: if the force in the diagram is acting in the $x$ direction, then its component must be positive. If the force is acting in the direction opposite to the $x$ axis, then its component should be negative. You should also check that whenever $F_x \propto \cos\theta$, then $F_y \propto \sin\theta$. If instead we use the angle $\phi$ defined with respect to the $y$ axis, we would have $F_x \propto \sin\phi$, and $F_y \propto \cos\phi$.
We will now illustrate how to use this recipe through a series of examples.
Examples
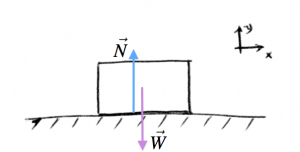
Block on a table
You place a block of mass $m$ on the table. If it has mass $m$ then it feels its weight $\vec{W}$ pulling down on it, but the table is not letting it drop to the floor. The table pushes back on the block with a normal force $\vec{N}$.
Steps 1,2: We draw the force diagram and choose a coordinate system:
Step 3: Next, we write down the empty equations template: \[ \begin{align*} \sum F_x &= \qquad \qquad = ma_x, \nl \sum F_y &= \qquad \qquad = ma_y. \end{align*} \]
Step 4: There is nothing much going on in the $x$ direction: no forces acting in the $x$ direction and the block is not moving so $a_x=0$. In the $y$ direction we have the force of gravity and the normal force exerted by the table: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \] We set $a_y=0$, because we see that the block is just sitting there on the table without moving. The technical term for situations where $a_x=0, a_y=0$ is called static equilibrium. Force diagrams with static equilibrium are easy to solve, because the entire right-hand side is equal to zero, which means that the forces on the object must be counter-balancing each other.
Step 5: Suppose the teacher was asking you “What is the magnitude of the normal force?”. You can easily answer this by looking at the second equation: “$N=mg$ bro!”
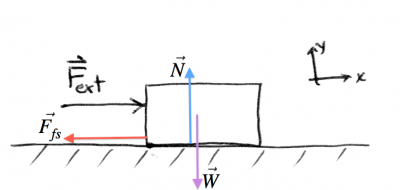
Moving the fridge
You are trying to push your fridge across the kitchen floor. Because it weights quite a lot, it is “gripping” the floor quite a bit. If the static coefficient of friction between the metal “feet” of your fridge and the tiles of the floor is $\mu_s$, how much force $\vec{F}_{ext}$ would it take to get the fridge to start moving?
\[ \begin{align*} \sum F_x &= F_{ext} - F_{fs} = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
If you push with force $F_{ext}=30$[N], the fridge will push back (via its connection to the floor) with a force $F_{fs}=30$[N]. If you push harder, the fridge will push back harder and it will still not move. Only when you reach the slipping threshold will it move. This means you have to push with force equal to the maximum static friction force $F_{fs}=\mu_s N$, so we have: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_s N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
To solve for $F_{ext}$ you first isolate $N=mg$ in the bottom line, and then substitute the value of $N$ in the top line to get $F_{ext} = \mu_s m g$.
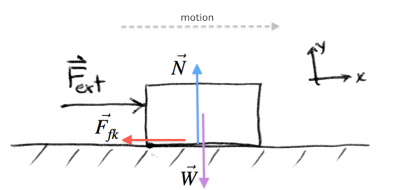
Friction slowing you down
OK, so you have the fridge moving now and you are moving at a steady pace across the room:
Your equation of motion is going to be: \[ \begin{align*} \sum F_x &= F_{ext} - \vec{F}_{fk} = ma_x, \nl \sum F_y &= N - mg = 0. \end{align*} \]
In particular if you want to keep a steady speed ($v=const$) as you move across the room, you will push with such a force just to balance the friction force and keep $a_x=0$.
To find the value of $F_{ext}$ to keep a constant speed we solve: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_k N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
We get a similar expression as above, but with $\mu_k$ instead of $\mu_s$: $F_{ext} = \mu_k m g$. Generally, $\mu_k < \mu_s$ so it takes less force to keep the fridge moving than it took to get it to start moving.
Let us now take a different slant on this whole friction thing.
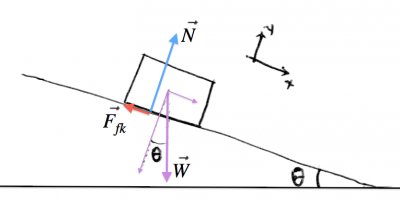
Incline
At this point, my dear readers, we are getting into the main kind of question that will be, without a doubt, asked in your homework or at the final exam. A block sliding down an incline. What is its acceleration?
Step 1: We draw a diagram which includes the weight $\vec{W}$, the normal force $\vec{N}$ and the friction force $\vec{F}_{fk}$.
Step 2: We pick the coordinate system to be tilted along the incline. This is important because this way the motion is purely in the $x$ direction, while the $y$ direction will be static.
Step 3,4: Let's copy the empty template, and fill in the equations: \[ \begin{align*} \sum F_x &= \|\vec{W}\|\sin\theta - F_{fk} = ma_x, \nl \sum F_y &= N - \|\vec{W}\|\cos\theta \ \ = 0, \end{align*} \] or substituting the values that we know: \[ \begin{align*} \sum F_x &= mg\sin\theta - \mu_kN = ma_x, \nl \sum F_y &= N - mg\cos\theta \ \ \ = 0. \end{align*} \]
Step 5: From the $y$ equation, we obtain $N=mg\cos\theta$ and substituting this into the $x$ equation we get: \[ a_x = \frac{1}{m}\left( mg\sin\theta - \mu_k mg\cos\theta \right) = g\sin\theta - \mu_k g\cos\theta. \]
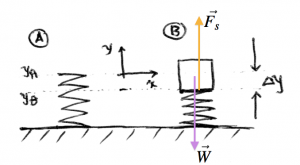
Bathroom scale
You have a spring with spring constant $k$ on which you put a block of mass $m$. By what length $\Delta y$ will the spring be compressed?
Step 1,2: We draw a before and after picture, with the $y$ axis placed at the natural length of the spring.
Step 3,4: Filling in the template we get: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= F_s - mg = 0. \end{align*} \]
Step 5: We know that the force exerted by a spring is proportional to its displacement according to \[ F_s = -k y_B, \] so we can find $y_B = -\frac{mg}{k}$. The length of compression is therefore: \[ |\Delta y| = \frac{mg}{k}. \]
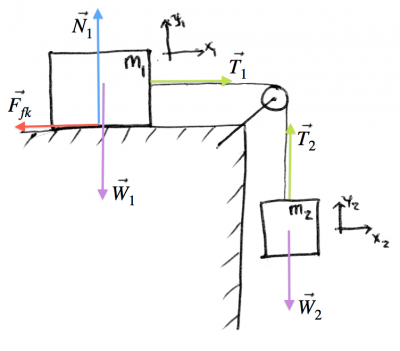
Two blocks
Now for a more involved example with two blocks. One block is sitting on the surface, and another one is falling straight down. The two are connected by a stiff rope. What is the acceleration of the system as a whole?
Steps 1,2: We have two objects, so we have to draw two force diagrams.
Step 3: We also have two sets of equations. One set of equations for the left block, and one for the right block: \[ \begin{align*} & \sum F_{1x} = \qquad\qquad = m_1a_{x_1} & \qquad & \sum F_{2x} = \qquad\quad = m_2a_{x_2} \nl & \sum F_{1y} = \qquad\qquad = m_1a_{y_1} & \qquad & \sum F_{2y} = \qquad\quad = m_2a_{y_2} \end{align*} \]
Steps 4: We fill them in with all the forces drawn in the diagram: \[ \begin{align*} & \sum F_{1x} = -F_{fk} + T_1 = m_1a_{x_1} & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - W_1 = 0 & \qquad & \sum F_{2y} = -W_2 + T_2 = m_2a_{y_2} \end{align*} \]
Step 5: What are the connections between the two blocks? Since it is the same rope that connects the two blocks, this means that the tension in the rope is the same on both ends so $T_1=T_2=T$. Also since the rope is of fixed length we have that the $x_1$ and $y_2$ coordinates are related by a constant (though they point in different directions), so it must be that $a_{x_1}= -a_{y_2} = a$.
Rewriting in terms of the new common variables $T$ and $a$ we have: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - m_1g = 0 & \qquad & \sum F_{2y} = -m_2g + T = - m_2a \end{align*} \]
We isolate $N_1$ on the bottom left, and isolate $T$ on the bottom right: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & N_1 = m_1g & \qquad & T = - m_2a + m_2g \end{align*} \]
Now substitute the values into the top left equation to get \[ \sum F_{1x} = -\mu_k(m_1g) + (- m_2a + m_2g) = m_1 a, \] or moving all the $a$ terms to one side we have \[ -\mu_km_1g + m_2g = m_1 a + m_2 a = (m_1 + m_2) a, \] which makes sense since the “two blocks attached with a rope” is in some sense an object of collective mass $(m_1 + m_2)$ with two external forces on it. From this point of view, the tension $T$ is an internal force of the object and doesn't appear in the external force equation.
The acceleration of the whole two-block system going to be: \[ a = \frac{m_2g - \mu_km_1g}{m_1+m_2}. \]
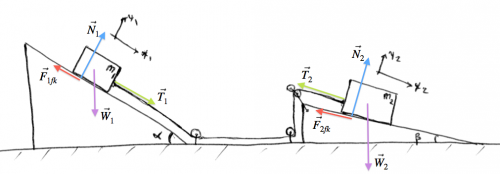
Two inclines
OK, let's just go crazy now! Let's have two inclines, two blocks, a rope, and friction everywhere. We want to find the acceleration as usual.
Steps 1,2: We draw a force diagram with two different coordinate systems each adapted for the angle of the incline:
Steps 3,4: Fill in all force components, and set $a_{y_1}=0,a_{y_2}=0$: \[ \begin{align*} & \sum F_{1x} = W_1\sin\alpha - F_{1fk} + T_1 = m_1a_{x_1}, \nl & \sum F_{1y} = -W_1\cos\alpha + N_1 \quad \ \ \ = 0, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = W_2\sin\beta - F_{2fk} - T_2 = m_2a_{x_2}, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2y} = -W_2\cos\beta + N_2 \quad \ \ \ =0. \end{align*} \]
Step 5: The links between the two worlds are two: the tension in the rope is the same $T=T_1=T_2$ and also the acceleration since the blocks are moving together $a=a_{x_1}=a_{x_2}$. Rewriting and expanding we have: \[ \begin{align*} & \sum F_{1x} = m_1g\sin\alpha - \mu_k N_1 + T = m_1a, \nl & N_1 = m_1g\cos\alpha, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k N_2 - T = m_2a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad N_2 = m_2g\cos\beta. \end{align*} \]
Let's substitute the values of $N_1$ and $N_2$ into the $x$ equations: \[ \begin{align} & \sum F_{1x} = m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k m_2g\cos\beta - T = m_2a. \end{align} \]
There are many ways to solve for the two unknowns in this pair of equations. Either (A) we isolate $T$ in one of the equations and substitute the value of $T$ into the second or (B) we isolate $a$ in both equations and set them equal to each other.
We will use approach (A) and isolate $T$ in the bottom equation to get: \[ \begin{align} & m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a = T. \end{align} \] and finally substitute the expression for $T$ into the top equation to obtain \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + ( m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a) = m_1a, \] which can be rewritten as \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + m_2g\sin\beta - \mu_k m_2g\cos\beta = (m_1 + m_2)a. \] Since we know the values of $m_1$, $m_2$, $\mu_k$, $\alpha$ and $\beta$, we can calculate all the quantities on the left-hand side and solve for $a$.
Other types of problems
All the examples shown asked you to find the acceleration, but sometimes you might be told the acceleration and asked to solve for some other unknown in the equations. Regardless of what you have to solve for, you should always start with the diagram and the sum-of-the-forces template. Once you have these equations in front of you, you will be able to reason about the problem more easily.
Experiment
Suspend an object of known mass (say a 100g chocolate bar) on the spring taken out from a retractable pen. Use a ruler to measure by how much the spring stretches in the process. What is the spring constant $k$?
Discussion
In previous sections we discussed the kinematics problem of finding the position of an object $x(t)$ given the knowledge of its acceleration function $a(t)$ and the initial conditions $x_i$ and $v_i$. In this section we studied the dynamics problem, which involved drawing force diagrams and calculating the net force on the object. Understanding these topics means that you fully understand Newton's equation $F=ma$ which is perhaps the most important equation in this book.
We can summarize the entire procedure for predicting the position of an object $x(t)$ from first principles in the following equation: \[ \frac{1}{m} \underbrace{ \left( \sum \vec{F} = \vec{F}_{net} \right) }_{\text{dynamics}} = \underbrace{ a(t) \ \overset{v_i+ \int\!dt }{\longrightarrow} \ v(t) \ \overset{x_i+ \int\!dt }{\longrightarrow} \ x(t) }_{\text{kinematics}}. \] The left-hand side calculates the net force, which is the cause of acceleration. The right-hand side indicates how we can calculate the equation of motion $x(t)$ from the knowledge of the acceleration and the initial conditions. This means that if you know the forces acting on any object (rocks, projectiles, cars, stars, planets, etc.) then we can predict its motion, which is kind of cool.