<texit info> author=Ivan Savov title=MATH minireference backgroundtext=off </texit>
Math fundamentals
As soon as the keyword “math” comes-up during a conversation, people start to feel uneasy. There are a number of common strategies that people use to escape this subject of conversation. The most common approach is to say something like “I always hated math”, or “I am terrible at math”, which is a clear social cue that a change of subject is requested. Another approach is to generally be sympathetic to the idea of mathematics, so long as it appears in the third person: “she solved the equation” is fine but “I solved the equation” is not thinkable. The usual motivation for this mathematics pour les autres approach is that it is highly specialized knowledge that does not contain any true value for the general audience. A variant of the above is to believe that a special kind of brain is required in order to do math.
Mathematical knowledge is actually really cool. Knowing math is like having analytic superpowers. You can use the power of abstraction to see the math behind any real world situation. And once in the math world you can jot down some numbers and functions on a piece of paper and you can calculate the answer. Unfortunately, this is not the image that most people have of mathematics. Math is taught usually taught with a lot of focus placed on the mechanical steps. Mindlessly number crunching and following steps without understanding what they are doing is not cool. If this is how you learned about the basic ideas of math, I can't blame you if you hate it, as it is kind of boring.
Often times, my students ask me to review some basic notion from high school math which is needed for a more advanced topic. This chapter is a collection of short review articles that cover a lot of useful topics from high school math.
Topics math
This chapter should help you learn most of the useful concepts from the high school math curriculum, and in particular all the prerequisite topics for University-level math and physics courses.
Solving equations
Most math skills boil down to being able to manipulate and solve equations. To solve an equation means to find the value of the unknown in the equation.
Check this shit out: \[ x^2-4=45. \]
To solve the above equation is to answer the question “What is $x$?” More precisely, we want to find the number which can take the place of $x$ in the equation so that the equality holds. In other words, we are asking \[ \text{"Which number times itself minus four gives 45?"} \]
That is quite a mouthful don't you think? To remedy this verbosity, mathematicians often use specialized mathematical symbols. The problem is that the specialized symbols used by mathematicians are confuse people. Sometimes even the simplest concepts are inaccessible if you don't know what the symbols mean.
What are your feelings about math, dear reader? Are you afraid of it? Do you have anxiety attacks because you think it will be too difficult for you? Chill! Relax my brothers and sisters. There is nothing to it. Nobody can magically guess what the solution is immediately. You have to break the problem down into simpler steps.
To find $x$, we can manipulate the original equation until we transform it to a different equation (as true as the first) that looks like this: \[ x= just \ some \ numbers. \]
That's what it means to solve. The equation is solved because you could type the numbers on the right hand side of the equation into a calculator and get the exact value of $x$.
To get $x$, all you have to do is make the right manipulations on the original equation to get it to the final form. The only requirement is that the manipulations you make transform one true equation into another true equation.
Before we continue our discussion, let us take the time to clarify what the equality symbol $=$ means. It means that all that is to the left of $=$ is equal to all that is to the right of $=$. To keep this equality statement true, you have to do everything that you want to do to the left side also to the right side.
In our example from earlier, the first simplifying step will be to add the number four to both sides of the equation: \[ x^2-4 +4 =45 +4, \] which simplifies to \[ x^2 =49. \] You must agree that the expression looks simpler now. How did I know to do this operation? I was trying to “undo” the effects of the operation $-4$. We undo an operation by applying its inverse. In the case where the operation is subtraction of some amount, the inverse operation is the addition of the same amount.
Now we are getting closer to our goal, namely to isolate $x$ on one side of the equation and have just numbers on the other side. What is the next step? Well if you know about functions and their inverses, then you would know that the inverse of $x^2$ ($x$ squared) is to take the square root $\sqrt{ }$ like this: \[ \sqrt{x^2} = \sqrt{49}. \] Notice that I applied the inverse operation on both sides of the equation. If we don't do the same thing on both sides we would be breaking the equality!
We are done now, since we have isolated $x$ with just numbers on the other side: \[ x = \pm 7. \]
What is up with the $\pm$ symbol? It means that both $x=7$ and $x=-7$ satisfy the above equation. Seven squared is 49, and so is $(-7)^2 = 49$ because two negatives cancel out.
If you feel comfortable with the notions of high school math and you could have solved the equation $x^2-4=25$ on your own, then you should consider skipping ahead to Chapter 2. If on the other hand you are wondering how the squiggle killed the power two, then this chapter is for you! In the next sections we will review all the essential concepts from high school math which you will need for the rest of the book. First let me tell you about the different kinds of numbers.
Numbers
We will start the exposition like a philosophy paper and define precisely what we are going to be talking about. At the beginning of all matters we have to define the players in the world of math: numbers.
Definitions
Numbers are the basic objects which you can type into a calculator and which you use to calculate things. Mathematicians like to classify the different kinds of number-like objects into sets:
- The Naturals: $\mathbb{N} = \{0,1,2,3,4,5,6,7, \ldots \}$,
- The Integers: $\mathbb{Z} = \{\ldots, -3,-2,-1,0,1,2,3 , \ldots \}$,
- The Rationals: $\mathbb{Q} = \{-1,0,0.125,1,1.5, \frac{5}{3}, \frac{22}{7}, \ldots \} $,
- The Reals: $\mathbb{R} = \{-1,0,1,e,\pi, -1.539..,\ 4.94.., \ \ldots \}$,
- The Complex numbers: $\mathbb{C} = \{ -1, 0, 1, i, 1+i, 2+3i, \ldots \}$.
These categories of numbers should be somewhat familiar to you. Think of them as neat classification labels for everything that you would normally call a number. Each item in the above list is a set. A set is a collection of items of the same kind. Each collection has a name and a precise definition. We don't need to go into the details of sets and set notation for our purposes, but you have to be aware of the different categories. Note also that each of the sets in the above list contains all the sets above it.
Why do you need so many different sets of numbers? The answer is partly historical and partly mathematical. Each of the set of numbers is associated with more and more advanced mathematical problems.
The simplest kind of numbers are the natural numbers $\mathbb{N}$, which are sufficient for all your math needs if all you are going to do is count things. How many goats? Five goats here and six goats there so the total is 11. The sum of any two natural numbers is also a natural number.
However, as soon as you start to use subtraction (the inverse operation of addition), you start to run into negative numbers, which are numbers outside of the set of natural numbers. If the only mathematical operations you will ever use are addition and subtraction then the set of integers $\mathbb{Z} = \{ \ldots, -2, -1, 0, 1, 2, \ldots \}$ would be sufficient. Think about it. Any integer plus or minus any other integer is still an integer.
You can do a lot of interesting math with integers. There is an entire field in math called number theory which deals with integers. However, if you restrict yourself to integers you would be limiting yourself somewhat. You can't use the notion of 2.5 goats for example. You would get totally confused by the menu at Rotisserie Romados which offers $\frac{1}{4}$ of a chicken.
If you want to use division in your mathematical calculations then you will need the rationals $\mathbb{Q}$. The rationals are the set of quotients of two integers: \[ \mathbb{Q} = \{ \text{ all } z \text{ such that } z=\frac{x}{y}, x \text{ is in } \mathbb{Z}, y \text{ is in } \mathbb{N}, y \neq 0 \}. \] You can add, subtract, multiply and divide rational numbers and the result will always be a rational number. However even rationals are not enough for all of math!
In geometry, we can obtain quantities like $\sqrt{2}$ (the diagonal of a square with side 1) and $\pi$ (the ratio between a circle's circumference and its diameter) which are irrational. There are no integers $x$ and $y$ such that $\sqrt{2}=\frac{x}{y}$, therefore, $\sqrt{2}$ is not part of $\mathbb{Q}$. We say that $\sqrt{2}$ is irrational. An irrational number has an infinitely long decimal expansion. For example, $\pi = 3.1415926535897931..$ where the dots indicate that the decimal expansion of $\pi$ continues all the way to infinity.
If you add the irrational numbers to the rationals you get all the useful numbers, which we call the set of real numbers $\mathbb{R}$. The set $\mathbb{R}$ contains the integers, the fractions $\mathbb{Q}$, as well as irrational numbers like $\sqrt{2}=1.4142135..$. You will see that using the reals you can compute pretty much anything you want. From here on in the text, if I say number I will mean an element of the set of real numbers $\mathbb{R}$.
The only thing you can't do with the reals is take the square root of a negative number—you need the complex numbers for that. We defer the discussion on $\mathbb{C}$ until Chapter 3.
Operations on numbers
Addition
You can add and subtract numbers. I will assume you are familiar with this kind of stuff. \[ 2+5=7,\ 45+56=101,\ 65-66=-1,\ 9999 + 1 = 10000,\ \ldots \]
The visual way to think of addition is the number line. Adding numbers is like adding sticks together: the resulting stick has length equal to the sum of the two constituent sticks.
Addition is commutative, which means that $a+b=b+a$. It is also associative, which means that if you have a long summation like $a+b+c$ you can compute it in any order $(a+b)+c$ or $a+(b+c)$ and you will get the same answer.
Subtraction is the inverse operation of addition.
Multiplication
You can also multiply numbers together. \[ ab = \underbrace{a+a+\cdots+a}_{b \ times}=\underbrace{b+b+\cdots+b}_{a \ times}. \] Note that multiplication can be defined in terms of repeated addition.
The visual way to think about multiplication is through the concept of area. The area of a rectangle of base $a$ and height $b$ is equal to $ab$. A rectangle which has height equal to its base is a square, so this why we call $aa=a^2$ “$a$ squared.”
Multiplication of numbers is also commutative $ab=ba$, and associative $abc=(ab)c=a(bc)$. In modern notation, no special symbol is used to denote multiplication; we simply put the two factors next to each other and say that the multiplication is implicit. Some other ways to denote multiplication are $a\cdot b$, $a\times b$ and, on computer systems, $a*b$.
Division
Division is the inverse of multiplication. \[ a/b = \frac{a}{b} = \text{ one } b^{th} \text{ of } a. \] Whatever $a$ is, you need to divide it into $b$ equal pieces and take one such piece. Some texts denote division by $a\div b$.
Note that you cannot divide by $0$. Try it on your
calculator or computer. It will say error divide by zero,
because it simply doesn't make sense.
What would it mean to divide something into zero equal pieces?
Exponentiation
Very often you have to multiply things together many times. We call that exponentiation and denote that with a superscript: \[ a^b = \underbrace{aaa\cdots a}_{b\ times}. \]
We can also have negative exponents. The negative in the exponent does not mean “subtract”, but rather “divide by”: \[ a^{-b}=\frac{1}{a^b}=\frac{1}{\underbrace{aaa\cdots a}_{b\ times}}. \]
An exponent which is a fraction means that it is some sort of square-root-like operation: \[ a^{\frac{1}{2}} \equiv \sqrt{a} \equiv \sqrt[2]{a}, \qquad a^{\frac{1}{3}} \equiv \sqrt[3]{a}, \qquad a^{\frac{1}{4}} \equiv \sqrt[4]{a} = a^{\frac{1}{2}\frac{1}{2}}=\left(a^{\frac{1}{2}}\right)^{\frac{1}{2}} = \sqrt{\sqrt{a}}. \] Square root $\sqrt{x}$ is the inverse operation of $x^2$. Similarly, for any $n$ we define the function $\sqrt[n]{x}$ (the $n$th root of $x$) to be the inverse function of $x^n$.
It is worth clarifying what “taking the $n$th root” means and what this operation can be used for. The $n$th root of $a$ is a number which, when multiplied together $n$ times, will give $a$. So for example a cube root satisfies \[ \sqrt[3]{a} \sqrt[3]{a} \sqrt[3]{a} = \left( \sqrt[3]{a} \right)^3 = a = \sqrt[3]{a^3}. \] Do you see now why $\sqrt[3]{x}$ and $x^3$ are inverse operations?
The fractional exponent notation makes the meaning of roots much more explicit: \[ \sqrt[n]{a} \equiv a^{\frac{1}{n}}, \] which means that $n$th root is equal to one $n$th of a number with respect to multiplication. Thus, if we want the whole number, we have to multiply the number $a^{\frac{1}{n}}$ times itself $n$ times: \[ \underbrace{a^{\frac{1}{n}}a^{\frac{1}{n}}a^{\frac{1}{n}}a^{\frac{1}{n}} \cdots a^{\frac{1}{n}}a^{\frac{1}{n}}}_{n\ times} = \left(a^{\frac{1}{n}}\right)^n = a^{\frac{n}{n}} = a^1 = a. \] The $n$-fold product of $\frac{1}{n}$ fractional exponents of any number products the number with exponent one, therefore the inverse operation of $\sqrt[n]{x}$ is $x^n$.
The commutative law of multiplication $ab=ba$ implies that we can see any fraction $\frac{a}{b}$ in two different ways $\frac{a}{b}=a\frac{1}{b}=\frac{1}{b}a$. First we multiply by $a$ and then divide the result by $b$, or first we divide by $b$ and then we multiply the result by $a$. This means that when we have a fraction in the exponent, we can write the answer in two equivalent ways: \[ a^{\frac{2}{3} }=\sqrt[3]{a^2} = (\sqrt[3]{a})^2, \qquad a^{-\frac{1}{2}}=\frac{1}{a^{\frac{1}{2}}} = \frac{1}{\sqrt{a}}, \qquad a^{\frac{m}{n}} = \left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}. \]
Make sure the above notation makes sense to you. As an exercises try to compute $5^{\frac{4}{3}}$ on your calculator, and check that you get around 8.54987973.. as an answer.
Operator precedence
There is a standard convention for the order in which mathematical operations have to be performed. The three basic operations have the following precedence:
- Exponents and roots.
- Products and divisions.
- Additions and subtractions.
This means that the expression $5\times3^2+13$ is interpreted as “first take the square of $3$, then multiply by $5$ and then add $13$.” If you want the operations to be carried out in a different order, say you wanted to multiply $5$ times $3$ first and then take the square you should use parentheses: $(5\times 3)^2 + 13$, which now shows that the square acts on $(5 \times 3)$ as a whole and not on $3$ alone.
Other operations
We can define all kinds of operations on numbers. The above three are special since they have a very simple intuitive feel to them, but we can define arbitrary transformations on numbers. We call those functions. Before we learn about functions, let us talk about variables first.
Variables
In math we use a lot of variables, which are placeholder names for any number or unknown.
Example
Your friend has some weirdly shaped shooter glasses and you can't quite tell if it is 25[ml] of vodka in there or 50[ml] or somewhere in between. Since you can't say how much booze there is in each shot glass we will say there was $x$[ml] in there. So how much alcohol did you drink over the whole evening? Say you had three shots then you drank $3x$[ml] of vodka. If you want to take it one step further, you can say that you drank $n$ shots then the total amount of alcohol you drank is $nx$[ml].
As you see, variables allow us to talk about quantities without knowing the details. This is abstraction and is very powerful stuff: it allows you to get drunk without knowing how drunk exactly!
Variable names
There are common naming patterns for variables:
- $x$: general name for the unknown in equations. Also used to denote the input to a function
and the position in physics problems.
- $v$: velocity.
- $\theta,\varphi$: the Greek letters “theta” and “phi” are often used to denote angles.
- $x_i,x_f$: Denote initial and final position in physics problems.
- $X$: A random variable in probability theory.
- $C$: Costs in business along with $P$ profit, and $R$ revenues.
Variable substitution
We often need to “change variables” and replace some unknown variable with another. For example, say you don't feel comfortable with square roots. Every time you see a square root, you freak out and you find yourself on an exam trying to solve for $x$ in the following: \[ \frac{6}{5 - \sqrt{x}} = \sqrt{x}. \] Needless to say that you are freaking out big time! Substitution can help with your root phobia. You just write down “Let $u=\sqrt{x}$” and then you are allowed to rewrite the equation in terms of $u$: \[ \frac{6}{5 - u} = u, \] which contains no square roots.
The next step when trying to solve for $u$ is to undo the fraction by multiplying both sides of the equation by $(5-u)$ to obtain: \[ 6 = u(5-u) = 5u - u^2. \] This can be rewritten as a quadratic equation $u^2-5u+6=(u-2)(u-3)=0$ for which $u_1=2$ and $u_2=3$ are the solutions. The last step is to convert our $u$-answers into $x$-answers by using $u=\sqrt{x}$, which is equivalent to $x = u^2$. The final answers are $x=2^2=4$ and $x=3^2=9$. You should try plugging these values of $x$ into the original equation with the square root to verify that they satisfy the equation.
Compact notation
Symbolic manipulation is very powerful, because it allows you to manage complexity. Say you are solving a physics problem in which you are told the mass of an object is $m=140$[kg]. If there are many steps in the calculation, would you rather use the number $140$[kg] in each step, or the shorter variable $m$? It is much better to use the variable $m$ throughout your calculation, and only substitute the value $140$[kg] in the last step when you are computing the final answer.
Basic rules of algebra
It's important for you to know the general rules for manipulating numbers and variables (algebra) so we will do a little refresher on these concepts to make sure you feel comfortable on that front. We will also review some important algebra tricks like factoring and completing the square which are useful when solving equations.
When an expression contains multiple things added together, we call those things terms. Furthermore, terms are usually composed of many things multiplied together. If we can write a number $x$ as $x=abc$, we say that $x$ factors into $a$, $b$ and $c$. We call $a$, $b$ and $c$ the factors of $x$.
Given any four numbers $a,b,c$ and $d$, we can use the following algebra properties:
- Associative property: $a+b+c=(a+b)+c=a+(b+c)$ and $abc=(ab)c=a(bc)$.
- Commutative property: $a+b=b+a$ and $ab=ba$.
- Distributive property: $a(b+c)=ab+ac$.
We use the distributive property every time we expand a bracket. For example $a(b+c+d)=ab + ac + ad$. The opposite operation of expanding is called factoring and consists of taking out the common parts of an expression to the front of a bracket: $ac+ac = a(b+c)$. We will discuss both of these operations in this section and illustrate what they are used for.
Expanding brackets
The distributive property is useful when you are dealing with polynomials: \[ (x+3)(x+2)=x(x+2) + 3(x+2)= x^2 +x2 +3x + 6. \] We can now use the commutative property on the second term $x2=2x$, and then combine the two $x$ terms into a single one to obtain \[ (x+3)(x+2)= x^2 + 5x + 6. \]
This calculation shown above happens so often that it is good idea to see it in more abstract form: \[ (x+a)(x+b) = x(x+b) + a(x+b) = x^2 + (a+b)x + ab. \] The product of two linear terms (expressions of the form $x+?$) is equal to a quadratic expression. Furthermore, observe that the middle term on the right-hand side contains the sum of the two constants on the left-hand side while the third term contains the their product.
It is a very common for people to get this wrong and write down false equations like $(x+a)(x+b)=x^2+ab$ or $(x+a)(x+b)=x^2+a+b$ or some variation of the above. You will never make such a mistake if you keep in mind the distributive property and expand the expression using a step-by-step approach. As a second example, consider the slightly more complicated algebraic expression and its expansion: \[ \begin{align*} (x+a)(bx^2+cx+d) &= x(bx^2+cx+d) + a(bx^2+cx+d) \nl &= bx^3+cx^2+dx + abx^2 +acx +ad \nl &= bx^3+ (c+ab)x^2+(d+ac)x +ad. \end{align*} \] Note how we grouped together all the terms which contain $x^2$ in one term and all the terms which contain $x$ in a second term. This is a common pattern when dealing with expressions which contain different powers of $x$.
Example
Suppose we are asked to solve for $t$ in the following equation \[ 7(3 + 4t) = 11(6t - 4). \] The unknown $t$ appears on both sides of the equation so it is not immediately obvious how to proceed.
To solve for $t$ in the above equation, we have to bring all the $t$ terms to one side and all the constant terms to the other side. The first step towards this goal is to expand the two brackets to obtain \[ 21 + 28t = 66t - 44. \] Now we move things around to get all the $t$s on the right-hand side and all the constants on the left-hand side \[ 21 + 44 = 66t - 28t. \] We see that $t$ is contained in both terms on the right-hand side so we can rewrite the equation as \[ 21 + 44 = (66 - 28)t. \] The answer is now obvious $t = \frac{21 + 44}{66 - 28} = \frac{65}{38}$.
Factoring
Factoring means to take out some common part in a complicated expression so as to make it more compact. Suppose you are given the expression $6x^2y + 15x$ and you are asked to simplify it by “taking out” common factors. The expression has two terms and when we split each terms into it constituent factors we obtain: \[ 6x^2y + 15x = (3)(2)(x)(x)y + (5)(3)x. \] We see that the factors $x$ and $3$ appear in both terms. This means we can factor them out to the front like this: \[ 6x^2y + 15x = 3x(2xy+5). \] The expression on the right is easier to read than the expression on the right since it shows that the $3x$ part is common to both terms.
Here is another example of where factoring can help us simplify an expression: \[ 2x^2y + 2x + 4x = 2x(xy+1+2) = 2x(xy+3). \]
Quadratic factoring
When dealing with a quadratic function, it is often useful to rewrite it as a product of two factors. Suppose you are given the quadratic function $f(x)=x^2-5x+6$ and asked to describe its properties. What are the roots of this function, i.e., for what values of $x$ is this function equal to zero? For which values of $x$ is the function positive and for which values is it negative?
When looking at the expression $f(x)=x^2-5x+6$, the properties of the function are not immediately apparent. However, if we factor the expression $x^2+5x+6$, we will be able to see its properties more clearly. To factor a quadratic expression is to express it as product of two factors: \[ f(x) = x^2-5x+6 = (x-2)(x-3). \] We can now see immediately that its solutions (roots) are at $x_1=2$ and $x_2=3$. You can also see that, for $x>3$, the function is positive since both factors will be positive. For $x<2$ both factors will be negative, but a negative times a negative gives positive, so the function will be positive overall. For values of $x$ such that $2<x<3$, the first factor will be positive, and the second negative so the overall function will be negative.
For some simple quadratics like the above one you can simply guess what the factors will be. For more complicated quadratic expressions, you need to use the quadratic formula. This will be the subject of the next section. For now let us continue with more algebra tricks.
Completing the square
Any quadratic expression $Ax^2+Bx+C$ can be written in the form $A(x-h)^2+k$. This is because all quadratic functions with the same quadratic coefficient are essentially shifted versions of each other. By completing the square we are making these shifts explicit. The value of $h$ is how much the function is shifted to the right and the value $k$ is the vertical shift.
Let's try to find the values $A,k,h$ for the quadratic expression discussed in the previous section: \[ x^2+5x+6 = A(x-h)^2+k = A(x^2-2hx + h^2) + k = Ax^2 - 2Ahx + Ah^2 + k. \]
By focussing on the quadratic terms on both sides of the equation we see that $A=1$, so we have \[ x^2+\underline{5x}+6 = x^2 \underline{-2hx} + h^2 + k. \] Next we look at the terms multiplying $x$ (underlined), and we see that $h=-2.5$, so we obtain \[ x^2+5x+\underline{6} = x^2 - 2(-2.5)x + \underline{(-2.5)^2 + k}. \] Finally, we pick a value of $k$ which would make the constant terms (underlined again) match \[ k = 6 - (-2.5)^2 = 6 - (2.5)^2 = 6 - \left(\frac{5}{2}\right)^2 = 6\times\frac{4}{4} - \frac{25}{4} = \frac{24 - 25}{4} = \frac{-1}{4}. \] This is how we complete the square, to obtain: \[ x^2+5x+6 = (x+2.5)^2 - \frac{1}{4}. \] The right-hand side in the above expression tells us that our function is equivalent to the basic function $x^2$, shifted $2.5$ units to the left, and $\frac{1}{4}$ units downwards. This would be really useful information if you ever had to draw this function, since it is easy to plot the basic graph of $x^2$ and then shift it appropriately.
It is important that you become comfortable with the procedure for completing the square outlined above. It is not very difficult, but it requires you to think carefully about the unknowns $h$ and $k$ and to choose their values appropriately. There is a simple rule you can remember for completing the square in an expression of the form $x^2+bx+c=(x-h)^2+k$: you have to use half of the coefficient of the $x$ term inside the bracket, i.e., $h=-\frac{b}{2}$. You can then work out both sides of the equation and choose $k$ so that the constant terms match. Take out a pen and a piece of paper now and verify that you can correctly complete the square in the following expressions $x^{2} - 6 x + 13=(x-3)^2 + 4$ and $x^{2} + 4 x + 1=(x + 2)^2 -3$.
Functions
Your function vocabulary determines how well you will be able to express yourself mathematically in the same way that your English vocabulary determines how well you can express yourself in English.
The purpose of the following pages is to embiggen your vocabulary a bit so you won't be caught with your pants down when the teacher tries to pull some trick on you at the final. I give you the minimum necessary, but I recommend you explore these functions on your own via wikipedia and by plotting their graphs on Wolfram alpha.
To “know” a function you have to understand and connect several different aspects of the function. First you have to know its mathematical properties (what does it do, what is its inverse) and at the same time have a good idea of its graph, i.e., what it looks like if you plot $x$ versus $f(x)$ in the Cartesian plane. It is also really good idea if you can remember the function values for some important inputs.
Definition
A function is a mathematical object that takes inputs and gives outputs. We use the notation \[ f \colon X \to Y, \] to denote a functions from the set $X$ to the set $Y$. In this book, we will study mostly functions which take real numbers as inputs and give real numbers as outputs: $f\colon\mathbb{R} \to \mathbb{R}$.
We now define some technical terms used to describe the input and output sets.
- The domain of a function is the set of allowed input values.
- The image or range of the function $f$ is the set of all possible
output values of the function.
- The codomain of a function is the type of outputs that the functions has.
To illustrate the subtle difference between the image of a function and its codomain, let us consider the function $f(x)=x^2$. The quadratic function is of the form $f\colon\mathbb{R} \to \mathbb{R}$. The domain is $\mathbb{R}$ (it takes real numbers as inputs) and the codomain is $\mathbb{R}$ (the outputs are real numbers too), however, not all outputs are possible. Indeed, the image the function $f$ consists only of the positive numbers $\mathbb{R}_+$. Note that the word “range” is also sometimes used refer to the function codomain.
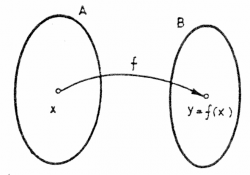
A function is not a number, it is a mapping from numbers to numbers. If you specify a given $x$ as input, we denote as $f(x)$ is the output value of $f$ for that input. Here is a graphical representation of a function with domain $A$ and codomain $B$.
The function corresponds to the arrow in the above picture.
We say that “$f$ maps $x$ to $y=f(x)$” and use the following terminology to classify the type of mapping that a function performs:
- A function is one-to-one or injective if it maps different inputs to different outputs.
- A function is onto or surjective if it covers the entire output set,
i.e., if the image of the function is equal to the function codomain.
- A function is bijective if it is both injective and surjective.
In this case $f$ is a one-to-one correspondence between the input
set and the output set: for each input of the possible outputs $y \in Y$ there exists (surjective part) exactly one input $x \in X$, such that $f(x)=y$ (injective part).
The term injective is a 1940s allusion inviting us to think of injective functions as some form of fluid flow. Since fluids cannot be compressed, the output space must be at least as large as the input space. A modern synonym for injective functions is to say that they are two-to-two. If you imagine two specks of paint inserted somewhere in the “input fluid”, then an injective function will lead to two distinct specks of paint in the “output fluid.” In contrast, functions which are not injective could map several different inputs to the same output. For example $f(x)=x^2$ is not injective since the inputs $2$ and $-2$ both get mapped to output value $4$.
Function names
Mathematicians have defined symbols $+$, $-$, $\times$ (usually omitted) and $\div$ (usually denoted as a fraction) for most important functions used in everyday life. We also use the weird surd notation to denote $n$th root $\sqrt[n]{\ }$ and the superscript notation to denote exponents. All other functions are identified and used by their name. If I want to compute the cosine of the angle $60^\circ$ (a function which describes the ratio between the length of one side of a right-angle triangle and the hypotenuse), then I would write $\cos(60^\circ)$, which means that we want the value of the $\cos$ function for the input $60^\circ$.
Incidentally, for that specific angle the function $\cos$ has a nice value: $\cos(60^\circ)=\frac{1}{2}$. This means that seeing $\cos(60^\circ)$ somewhere in an equation is the same as seeing $0.5$ there. For other values of the function like say $\cos(33.13^\circ)$, you will need to use a calculator. A scientific calculator will have a $\cos$ button on it for that purpose.
Handles on functions
When you learn about functions you learn about different “handles” onto these mathematical objects. Most often you will have the function equation, which is a precise way to calculate the output when you know the input. This is an important handle, especially when you will be doing arithmetic, but it is much more important to “feel” the function.
How do you get a feel for some function?
One way is to look at list of input-output pairs $\{ \{ \text{input}=x_1, \text{output}=f(x_1) \},$ $\{ \text{input}=x_2,$ $\text{output}=f(x_2) \},$ $\{ \text{input}=x_3, \text{output}=f(x_3) \}, \ldots \}$. A more compact notation for the input-output pairs $\{ (x_1,f(x_1)),$ $(x_2,f(x_2)),$ $(x_3,f(x_3)), \ldots \}$. You can make a little table of values for yourself, pick some random inputs and record the output of the function in the second column: \[ \begin{align*} \textrm{input}=x \qquad &\rightarrow \qquad f(x)=\textrm{output} \nl 0 \qquad &\rightarrow \qquad f(0) \nl 1 \qquad &\rightarrow \qquad f(1) \nl 55 \qquad &\rightarrow \qquad f(55) \nl x_4 \qquad &\rightarrow \qquad f(x_4) \end{align*} \]
Apart from random numbers it is also generally a good idea to check the value of the function at $x=0$, $x=1$, $x=100$, $x=-1$ and any other important looking $x$ value.
One of the best ways to feel a function is to look at its graph.
A graph is a line on a piece of paper that passes through all input-output
pairs of the function.
What? What line? What points?
Ok let's backtrack a little.
Imagine that you have a piece of paper you have drawn
a coordinate system on the paper.
The horizontal axis will be used to measure $x$, this is also called the abscissa. The vertical axis will be used to measure $f(x)$, but because writing out $f(x)$ all the time is long and tedious, we will invent a short single-letter alias to denote the output value of $f$ as follows: \[ y \equiv f(x) = \text{output}. \]
Now you can take each of the input-output pairs for the function $f$ and think of them as points $(x,y)$ in the coordinate system. Thus the graph of a function is a graphical representation of everything the function does. If you understand the simple “drawing” on this page, you will basically understand everything there is to know about the function.
Another way to feel functions is through the properties of the function: either the way it is defined, or its relation to other functions. This boils down to memorizing facts about the function and its relations to other functions. An example of a mathematical fact is $\sin(30^\circ)=\frac{1}{2}$. An example of a mathematical relation is the equation $\sin^2 x + \cos^2 x =1$, which is a link between the $\sin$ and the $\cos$ functions.
The last part may sound contrary to my initial promise about the book saying that I will not make you memorize stuff for nothing. Well, this is not for nothing. The more you know about any function, the more “paths” you have in your brain that connect to that function. Real math knowledge is not memorization but an establishment of a graph of associations between different areas of knowledge in your brain. Each concept is a node in this graph, and each fact you know about this concept is an edge in the graph. Analytical thought is the usage of this graph to produce calculations and mathematical arguments (proofs). For example, knowing the fact $\sin(30^\circ)=\frac{1}{2}$ about $\sin$ and the relationship $\sin^2 x + \cos^2 x = 1$ between $\sin$ and $\cos$, you could show that $\cos(30^\circ)=\frac{\sqrt{3}}{2}$. Note that the notation $\sin^2(x)$ means $(\sin(x))^2$.
To develop mathematical skills, it is therefore important to practice this path-building between related concepts by solving exercises and reading and writing mathematical proofs. My textbook can only show you the paths between the concepts, it is up to you to practice the exercises in the back of each chapter to develop the actual skills.
Example: Quadratic function
Consider the function from the real numbers ($\mathbb{R}$) to the real numbers ($\mathbb{R}$) \[ f \colon \mathbb{R} \to \mathbb{R} \] given by \[ f(x)=x^2+2x+3. \] The value of $f$ when $x=1$ is $f(1)=1^2+2(1)+3=1+2+3=6$. When $x=2$, we have $f(2)=2^2+2(2)+3=4+4+3=11$. What is the value of $f$ when $x=0$?
Example: Exponential function
Consider the exponential function with base two: \[ f(x) = 2^x. \] This function is of crucial importance in computer systems. When $x=1$, $f(1)=2^1=2$. When $x$ is 2 we have $f(2)=2^2=4$. The function is therefore described by the following input-output pairs: $(0,1)$, $(1,2)$, $(2,4)$, $(3,8)$, $(4,16)$, $(5,32)$, $(6,64)$, $(7,128)$, $(8,256)$, $(9,512)$, $(10,1024)$, $(11, 2048)$, $(12,4096)$, etc. (RAM memory chips come in powers of two because the memory space is exponential in the number of “address lines” on the chip.) Some important input-output pairs for the exponential function are $(0,1)$, because by definition any number to the power 0 is equal to 1, and $(-1,\frac{1}{2^1}=\frac{1}{2}), (-2,\frac{1}{2^2}=\frac{1}{4}$), because negative exponents tells you that you should dividing by that number this many times instead of multiplying.
Function inverse
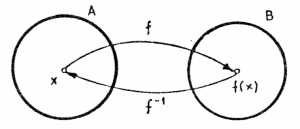 Recall that a bijective function is a one-to-one correspondence between
the set of inputs and the set of output values.
If $f$ is a bijective function, then there exists an inverse function $f^{-1}$,
which performs the inverse mapping of $f$.
Thus, if you start from some $x$, apply $f$ and then apply $f^{-1}$,
you will get back to the original input $x$:
\[
x = f^{-1}\!\left( \; f(x) \; \right).
\]
This is represented graphically in the diagram on the right.
Recall that a bijective function is a one-to-one correspondence between
the set of inputs and the set of output values.
If $f$ is a bijective function, then there exists an inverse function $f^{-1}$,
which performs the inverse mapping of $f$.
Thus, if you start from some $x$, apply $f$ and then apply $f^{-1}$,
you will get back to the original input $x$:
\[
x = f^{-1}\!\left( \; f(x) \; \right).
\]
This is represented graphically in the diagram on the right.
Function composition
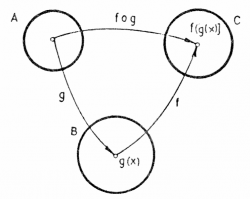 We can combine two simple functions to build a more complicated function
by chaining them together.
The resulting function is denoted
\[
z = f\!\circ\!g \, (x) \equiv z = f\!\left( \: g(x) \: \right).
\]
We can combine two simple functions to build a more complicated function
by chaining them together.
The resulting function is denoted
\[
z = f\!\circ\!g \, (x) \equiv z = f\!\left( \: g(x) \: \right).
\]
The diagram on the left shows a function $g:A\to B$ acting on some input $x$ to produce an intermediary value $y \in B$, which is then input to the function $f:B \to C$ to produce the final output value $z = f(y) = f(g(x))$.
The composition of applying $g$ first followed by $f$ is a function of the form: $f\circ g: A \to C$ defined through the equation $f\circ g(x) = f(g(x))$. Note that “first” in the context of function composition means the first to first to touch the input.
Discussion
In the next sections, we will look into the different functions that you will be dealing with. What we present here is far from and exhaustive list, but if you get a hold of these ones, you will be able to solve any problem a teacher can throw at you.
Links
[ Tank game where you specify the function of the projectile trajectory ]
http://www.graphwar.com/play.html
NOINDENT
[ Gallery of function graphs ]
http://mpmath.googlecode.com/svn/gallery/gallery.html
Functions and their inverses
As we saw in the section on solving equations, the ability to “undo” functions is a key skill to have when solving equations.
Example
Suppose you have to solve for $x$ in the equation \[ f(x) = c. \] where $f$ is some function and $c$ is some constant. Our goal is to isolate $x$ on one side of the equation but there is the function $f$ standing in our way.
The way to get rid of $f$ is to apply the inverse function (denoted $f^{-1}$) which will “undo” the effects of $f$. We find that: \[ f^{-1}\!\left( f(x) \right) = x = f^{-1}\left( c \right). \] By definition the inverse function $f^{-1}$ does the opposite of what the function $f$ does so together they cancel each other out. We have $f^{-1}(f(x))=x$ for any number $x$.
Provided everything is kosher (the function $f^{-1}$ must be defined for the input $c$), the manipulation we made above was valid and we have obtained the answer $x=f^{-1}( c)$.
\[ \ \]
Note the new notation for denoting the function inverse $f^{-1}$ that we introduced in the above example. This notation is borrowed from the notion of “inverse number”. Multiplication by the number $d^{-1}$ is the inverse operation of multiplication by the number $d$: $d^{-1}dx=1x=x$. In the case of functions, however, the negative one exponent does not mean the inverse number $\frac{1}{f(x)}=(f(x))^{-1}$ but functions inverse, i.e., the number $f^{-1}(y)$ is equal to the number $x$ such that $f(x)=y$.
You have to be careful because sometimes the applying the inverse leads to multiple solutions. For example, the function $f(x)=x^2$ maps two input values ($x$ and $-x$) to the same output value $x^2=f(x)=f(-x)$. The inverse function of $f(x)=x^2$ is $f^{-1}(x)=\sqrt{x}$, but both $x=+\sqrt{c}$ and $x=-\sqrt{c}$ would be solutions to the equation $x^2=c$. A shorthand notation to indicate the solutions for this equation is $x=\pm c$.
Formulas
Here is a list of common functions and their inverses:
\[ \begin{align*} \textrm{function } f(x) & \ \Leftrightarrow \ \ \textrm{inverse } f^{-1}(x) \nl x+2 & \ \Leftrightarrow \ \ x-2 \nl 2x & \ \Leftrightarrow \ \ \frac{1}{2}x \nl -x & \ \Leftrightarrow \ \ -x \nl x^2 & \ \Leftrightarrow \ \ \pm\sqrt{x} \nl 2^x & \ \Leftrightarrow \ \ \log_{2}(x) \nl 3x+5 & \ \Leftrightarrow \ \ \frac{1}{3}(x-5) \nl a^x & \ \Leftrightarrow \ \ \log_a(x) \nl \exp(x)=e^x & \ \Leftrightarrow \ \ \ln(x)=\log_e(x) \nl \sin(x) & \ \Leftrightarrow \ \ \arcsin(x)=\sin^{-1}(x) \nl \cos(x) & \ \Leftrightarrow \ \ \arccos(x)=\cos^{-1}(x) \end{align*} \]
The function-inverse relationship is reflexive. This means that if you see a function on one side of the above table (no matter which), then its inverse is on the opposite side.
Example
Let's say your teacher doesn't like you and right away on the first day of classes, he gives you a serious equation and wants you to find $x$: \[ \log_5\left(3 + \sqrt{6\sqrt{x}-7} \right) = 34+\sin(5.5)-\Psi(1). \] Do you see now what I meant when I said that the teacher doesn't like you?
First note that it doesn't matter what $\Psi$ is, since $x$ is on the other side of the equation. We can just keep copying $\Psi(1)$ from line to line and throw the ball back to the teacher in the end: “My answer is in terms of your variables dude. You have to figure out what the hell $\Psi$ is since you brought it up in the first place.” The same goes with $\sin(5.5)$. If you don't have a calculator, don't worry about it. We will just keep the expression $\sin(5.5)$ instead of trying to find its numerical value. In general, you should try to work with variables as much as possible and leave the numerical computations for the last step.
OK, enough beating about the bush. Let's just find $x$ and get it over with! On the right side of the equation, we have the sum of a bunch of terms and no $x$ in them so we will just leave them as they are. On the left-hand side, the outer most function is a logarithm base $5$. Cool. No problem. Looking in the table of inverse functions we find that the exponential function is the inverse of the logarithm: $a^x \Leftrightarrow \log_a(x)$. To get rid of the $\log_5$ we must apply the exponential function base five to both sides: \[ 5^{ \log_5\left(3 + \sqrt{6\sqrt{x}-7} \right) } = 5^{ 34+\sin(5.5)-\Psi(1) }, \] which simplifies to: \[ 3 + \sqrt{6\sqrt{x}-7} = 5^{ 34+\sin(5.5)-\Psi(1) }, \] since $5^x$ canceled the $\log_5 x$.
From here on it is going to be like if Bruce Lee walked into a place with lots of bad guys. Addition of $3$ is undone by subtracting $3$ on both sides: \[ \sqrt{6\sqrt{x}-7} = 5^{ 34+\sin(5.5)-\Psi(1) } - 3. \] To undo a square root you take the square \[ 6\sqrt{x}-7 = \left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2. \] Add $7$ to both sides \[ 6\sqrt{x} = \left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2+7. \] Divide by $6$: \[ \sqrt{x} = \frac{1}{6}\left(\left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2+7\right), \] and then we square again to get the final answer: \[ \begin{align*} x &= \left[\frac{1}{6}\left(\left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2+7\right) \right]^2. \end{align*} \]
Did you see what I was doing in each step? Next time a function stands in your way, hit it with its inverse, so that it knows not to ever challenge you again.
Discussion
The recipe I have outlined above is not universal. Sometimes $x$ isn't alone on one side. Sometimes $x$ appears in several places in the same equation so can't just work your way towards $x$ as shown above. You need other techniques for solving equations like that.
The bad news is that there is no general formula for solving complicated equations. The good news is that the above technique of “digging towards $x$” is sufficient for 80% of what you are going to be doing. You can get another 15% if you learn how to solve the quadratic equation: \[ ax^2 +bx + c = 0. \]
Solving third order equations $ax^3+bx^2+cx+d=0$ with pen and paper is also possible, but at this point you really might as well start using a computer to solve for the unknown(s).
There are all kinds of other equations which you can learn how to solve: equations with multiple variables, equations with logarithms, equations with exponentials, and equations with trigonometric functions. The principle of digging towards the unknown and applying the function inverse is very important so be sure to practice it.
Solving quadratic equations
What would you do if you were asked to find $x$ in the equation $x^2 = 45x + 23$? This is called a quadratic equation since it contains the unknown variable $x$ squared. The name name comes from the Latin quadratus, which means square. Quadratic equations come up very often so mathematicians came up with a general formula for solving these equations. We will learn about this formula in this section.
Before we can apply the formula, we need to rewrite the equation in the form \[ ax^2 + bx + c = 0, \] where we moved all the numbers and $x$s to one side and left only $0$ on the other side. This is the called the standard form of the quadratic equation. For example, to get the expression $x^2 = 45x + 23$ into the standard form, we can subtract $45x+23$ from both sides of the equation to obtain $x^2 - 45x - 23 = 0$. What are the values of $x$ that satisfy this formula?
Claim
The solutions to the equation \[ ax^2 + bx + c = 0, \] are \[ x_1 = \frac{-b + \sqrt{b^2-4ac} }{2a} \ \ \text{ and } \ \ x_2 = \frac{-b - \sqrt{b^2-4ac} }{2a}. \]
Let us now see how this formula is used to solve the equation $x^2 - 45x - 23 = 0$. Finding the two solutions is a simple mechanical task of identifying $a$, $b$ and $c$ and plugging these numbers into the formula: \[ x_1 = \frac{45 + \sqrt{45^2-4(1)(-23)} }{2} = 45.5054\ldots, \] \[ x_2 = \frac{45 - \sqrt{45^2-4(1)(-23)} }{2} = -0.5054\ldots. \]
Proof of claim
This is an important proof. You should know how to derive the quadratic formula in case your younger brother asks you one day to derive the formula from first principles. To derive this formula, we will use the completing-the-square technique which we saw in the previous section. Don't bail out on me now, the proof is only two pages.
Starting from the equation $ax^2 + bx + c = 0$, our first step will be to move $c$ to the other side of the equation \[ ax^2 + bx = -c, \] and then to divide by $a$ on both sides \[ x^2 + \frac{b}{a}x = -\frac{c}{a}. \]
Now we must complete the square on the left-hand side, which is to say we ask the question: what are the values of $h$ and $k$ for this equation to hold \[ (x-h)^2 + k = x^2 + \frac{b}{a}x = -\frac{c}{a}? \] To find the values for $h$ and $k$, we will expand the left-hand side to obtain $(x-h)^2 + k= x^2 -2hx +h^2+k$. We can now identify $h$ by looking at the coefficients in front of $x$ on both sides of the equation. We have $-2h=\frac{b}{a}$ and hence $h=-\frac{b}{2a}$.
So what do we have so far: \[ \left(x + \frac{b}{2a} \right)^2 = \left(x + \frac{b}{2a} \right)\!\!\left(x + \frac{b}{2a} \right) = x^2 + \frac{b}{2a}x + x\frac{b}{2a} + \frac{b^2}{4a^2} = x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}. \] If we want to figure out what $k$ is, we just have to move that last term to the other side: \[ \left(x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a^2} = x^2 + \frac{b}{a}x. \]
We can now continue with the proof where we left off \[ x^2 + \frac{b}{a}x = -\frac{c}{a}. \] We replace the left-hand side by the complete-the-square expression and obtain \[ \left(x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a^2} = -\frac{c}{a}. \] From here on, we can use the standard procedure for solving equations. We put all the constants on the right-hand side \[ \left(x + \frac{b}{2a} \right)^2 = -\frac{c}{a} + \frac{b^2}{4a^2}. \] Next we take the square root of both sides. Since the square function maps both positive and negative numbers to the same value, this step will give us two solutions: \[ x + \frac{b}{2a} = \pm \sqrt{ -\frac{c}{a} + \frac{b^2}{4a^2} }. \] Let's take a moment to cleanup the mess on the right-hand side a bit: \[ \sqrt{ -\frac{c}{a} + \frac{b^2}{4a^2} } = \sqrt{ -\frac{(4a)c}{(4a)a} + \frac{b^2}{4a^2} } = \sqrt{ \frac{- 4ac + b^2}{4a^2} } = \frac{\sqrt{b^2 -4ac} }{ 2a }. \]
Thus we have: \[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 -4ac} }{ 2a }, \] which is just one step away from the final answer \[ x = \frac{-b}{2a} \pm \frac{\sqrt{b^2 -4ac} }{ 2a } = \frac{-b \pm \sqrt{b^2 -4ac} }{ 2a }. \] This completes the proof.
Alternative proof of claim
To have a proof we don't necessarily need to show the derivation of the formula as we did. The claim was that $x_1$ and $x_2$ are solutions. To prove the claim we could have simply plugged $x_1$ and $x_2$ into the quadratic equation and verified that we get zero. Verify on your own.
Applications
The Golden Ratio
The golden ratio, usually denoted $\varphi=\frac{1+\sqrt{5}}{2}=1.6180339\ldots$ is a very important proportion in geometry, art, aesthetics, biology and mysticism. It comes about from the solution to the quadratic equation \[ x^2 -x -1 = 0. \]
Using the quadratic formula we get the two solutions: \[ x_1 = \frac{1+\sqrt{5}}{2} = \varphi, \qquad x_2 = \frac{1-\sqrt{5}}{2} = - \frac{1}{\varphi}. \]
You can learn more about the various contexts in which the golden ratio appears from the excellent wikipedia article on the subject. We will also see the golden ratio come up again several times in the remainder of the book.
Explanations
Multiple solutions
Often times, we are interested in only one of the two solutions to the quadratic equation. It will usually be obvious from the context of the problem which of the two solutions should be kept and which should be discarded. For example, the time of flight of a ball thrown in the air from a height of $3$ meters with an initial velocity of $12$ meters per second is obtained by solving a quadratic equation $0=(-4.9)t^2+12t+3$. The two solutions of the quadratic equation are $t_1=-0.229$ and $t_2=2.678$. The first answer $t_1$ corresponds to a time in the past so must be rejected as invalid. The correct answer is $t_2$. The ball will hit the ground after $t=2.678$ seconds.
Relation to factoring
In the previous section we discussed the quadratic factoring operation by which we could rewrite a quadratic function as the product of two terms $f(x)=ax^2+bx+c=(x-x_1)(x-x_2)$. The two numbers $x_1$ and $x_2$ are called the roots of the function: this is where the function $f(x)$ touches the $x$ axis.
Using the quadratic equation you now have the ability to factor any quadratic equation. Just use the quadratic formula to find the two solutions $x_1$ and $x_2$ and then you can rewrite the expression as $(x-x_1)(x-x_2)$.
Some quadratic expression cannot be factored, however. These correspond to quadratic functions whose graphs do not touch the $x$ axis. They have no solutions (no roots). There is a quick test you can use to check if a quadratic function $f(x)=ax^2+bx+c$ has roots (touches or crosses the $x$ axis) or doesn't have roots (never touches the $x$ axis). If $b^2-4ac>0$ then the function $f$ has two roots. If $b^2-4ac=0$, the function has only one root. This corresponds to the special case when the function touches the $x$ axis only at one point. If $b^2-4ac<0$, the function has no real roots. If you try to use the formula for finding the solutions, you will fail because taking the square root of a negative number is not allowed. Think about it—how could you square a number and obtain a negative number?
Polynomials
The polynomials are a very simple and useful family of functions. For example quadratic polynomials of the form $f(x) = ax^2 + bx +c$ often arise in the description of physics phenomena.
Definitions
- $x$: the variable
- $f(x)$: the polynomial. We sometimes sometimes denote polynomials $P(x)$ to
distinguish them from generic function $f(x)$.
- degree of $f(x)$: the largest power of $x$ that appears in the polynomial
- roots of $f(x)$: the values of $x$ for which $f(x)=0$
Polynomials
The most general polynomial of the first degree is a line $f(x) = mx + b$, where $m$ and $b$ are arbitrary constants.
The most general polynomial of second degree is $f(x) = a_2 x^2 + a_1 x + a_0$, where again $a_0$, $a_1$ and $a_2$ are arbitrary constants. We call $a_k$ the coefficient of $x^k$ since this is the number that appears in front of it.
By now you should be able to guess that a third degree polynomial will look like $f(x) = a_3 x^3 + a_2 x^2 + a_1 x + a_0$.
In general, a polynomial of degree $n$ has equation: \[ f(x) = a_n x^n + a_{n-1}x^{n-1} + \cdots + a_2 x^2 + a_1 x + a_0. \] or if you want to use the sum notation we can write it as: \[ f(x) = \sum_{k=0}^n a_kx^k, \] where $\Sigma$ (the capital Greek letter sigma) stands for summation.
Solving polynomial equations
Very often you will have to solve a polynomial equations of the form: \[ A(x) = B(x), \] where $A(x)$ and $B(x)$ are both polynomials. Remember that solving means to find the value of $x$ which makes the equality true.
For example, say the revenue of your company, as function of the number of products sold $x$ is given by $R(x)=2x^2 + 2x$ and the costs you incur to produce $x$ objects is $C(x)=x^2+5x+10$. A very natural question to ask is the amount of product you need to produce to break even, i.e., to make your revenue equal your costs $R(x)=C(x)$. To find the break-even $x$, you will have to solve the following equation: \[ 2x^2 + 2x = x^2+5x+10. \]
This may seem complicated since there are $x$s all over the place and it is not clear how to find the value of $x$ that makes this equation true. No worries though, we can turn this equation into the “standard form” and then use the quadratic equation. To do this, we will move all the terms to one side until we have just zero on the other side: \[ \begin{align} 2x^2 + 2x \ \ \ -x^2 &= x^2+5x+10 \ \ \ -x^2 \nl x^2 + 2x \ \ \ -5x &= 5x+10 \ \ \ -5x \nl x^2 - 3x \ \ \ -10 &= 10 \ \ \ -10 \nl x^2 - 3x -10 &= 0. \end{align} \]
Remember that if we do the same thing on both sides of the equation, it remains true. Therefore, the values of $x$ that satisfy \[ x^2 - 3x -10 = 0, \] namely $x=-2$ and $x=5$, will also satisfy \[ 2x^2 + 2x = x^2+5x+10, \] which was the original problem that we were trying to solve.
This “shuffling of terms” approach will work for any polynomial equation $A(x)=B(x)$. We can always rewrite it as some $C(x)=0$, where $C(x)$ is a new polynomial that has as coefficients the difference of the coefficients of $A$ and $B$. Don't worry about which side you move all the coefficients to because $C(x)=0$ and $0=-C(x)$ have exactly the same solutions. Furthermore, the degree of the polynomial $C$ can be no greater than that of $A$ or $B$.
The form $C(x)=0$ is the standard form of a polynomial and, as you will see shortly, there are formulas which you can use to find the solution(s).
Formulas
The formula for solving the polynomial equation $P(x)=0$ depend on the degree of the polynomial in question.
First
For first degree: \[ P_1(x) = mx + b = 0, \] the solution is $x=b/m$. Just move $b$ to the other side and divide by $m$.
Second
For second degree: \[ P_2(x) = ax^2 + bx + c = 0, \] the solutions are $x_1=\frac{-b + \sqrt{ b^2 -4ac}}{2a}$ and $x_2=\frac{-b - \sqrt{b^2-4ac}}{2a}$.
Note that if $b^2-4ac < 0$, the solutions involve taking the square root of a negative number. In those cases, we say that no real solutions exist.
Third
The solutions to the cubic polynomial equation \[ P_3(x) = x^3 + ax^2 + bx + c = 0, \] are given by \[ x_1 = \sqrt[3]{ q + \sqrt{p} } \ \ + \ \sqrt[3]{ q - \sqrt{p} } \ -\ \frac{a}{3}, \] and \[ x_{2,3} = \left( \frac{ -1 \pm \sqrt{3}i }{2} \right)\sqrt[3]{ q + \sqrt{p} } \ \ + \ \left( \frac{ -1 \pm \sqrt{3}i }{2} \right) \sqrt[3]{ q - \sqrt{p} } \ - \ \frac{a}{3}, \] where $q \equiv \frac{-a^3}{27}+ \frac{ab}{6} - \frac{c}{2}$ and $p \equiv q^2 + \left(\frac{b}{3}-\frac{a^2}{9}\right)^3$.
Note that, in my entire career as an engineer, physicist and computer scientist, I have never used the cubic equation to solve a problem by hand. In math homework problems and exams you will not be asked to solve equations of higher than second degree, so don't bother memorizing the solutions of the cubic equation. I included the formula here just for completeness.
Higher degrees
There is also a formula for polynomials of degree $4$, but it is complicated. For polynomials with order $\geq 5$, there does not exist a general analytical solution.
Using a computer
When solving real world problems,
you will often run into much more complicated equations.
For anything more complicated than the quadratic equation,
I recommend that you use a computer algebra system like
sympy to find the solutions.
Go to http://live.sympy.org and type in:
>>> solve( x**2 - 3*x +2, x) [ shift + Enter ] [1, 2]
Indeed $x^2-3x+2=(x-1)(x-2)$ so $x=1$ and $x=2$ are the two solutions.
Substitution trick
Sometimes you can solve polynomials of fourth degree by using the quadratic formula. Say you are asked to solve for $x$ in \[ g(x) = x^4 - 3x^2 -10 = 0. \] Imagine this comes up on your exam. Clearly you can't just type it into a computer, since you are not allowed the use of a computer, yet the teacher expects you to solve this. The trick is to substitute $y=x^2$ and rewrite the same equation as: \[ g(y) = y^2 - 3y -10 = 0, \] which you can now solve by the quadratic formula. If you obtain the solutions $y=\alpha$ and $y=\beta$, then the solutions to the original fourth degree polynomial are $x=\sqrt{\alpha}$ and $x=\sqrt{\beta}$ since $y=x^2$.
Of course, I am not on an exam, so I am allowed to use a computer:
>>> solve(y**2 - 3*y -10, y) [-2, 5] >>> solve(x**4 - 3*x**2 -10 , x) [sqrt(2)i, -sqrt(2)i, -sqrt(5) , sqrt(5) ]
Note how a 2nd degree polynomial has two roots and a fourth degree polynomial has four roots, two of which are imaginary, since we had to take the square root of a negative number to obtain them. We write $i=\sqrt{-1}$. If this was asked on an exam though, you should probably just report the two real solutions: $\sqrt{5}$ and $-\sqrt{5}$ and not talk about the imaginary solutions since you are not supposed to know about them yet. If you feel impatient though, and you want to know about the complex numbers right now you can skip ahead to the section on complex numbers.
Cartesian plane
The Cartesian plane, named after René Descartes, the famous philosopher and mathematician, is the graphical representation of the space of pairs of real numbers.
We generally call the horizontal axis “the $x$ axis” and the vertical axis “the $y$ axis.” We put notches at regular intervals on each axis so that we can measure distances. The figure below is an example of an empty Cartesian coordinate system. Think of the coordinate system as an empty canvas. What can you draw on this canvas?
Vectors and points
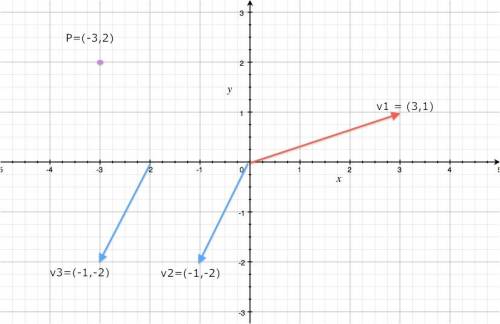
A point $P$ in the Cartesian plane has an $x$-coordinate and a $y$-coordinate. We say $P=(P_x,P_y)$. To find this point, we start from the origin (the point (0,0)) and move a distance $P_x$ on the $x$ axis, then move a distance $P_y$ on the $y$ axis.
Similar to points, a vector $\vec{v}=(v_x,v_y)$ is a pair of displacements, but unlike points, we don't have to necessarily start from the origin. We draw vectors as arrows – so we see explicitly where the vector starts and where it ends.
Here are some examples:
Note that the vectors $\vec{v}_2$ and $\vec{v}_3$ are actually the same vector – the “displace downwards by 2 and leftwards by one” vector. It doesn't matter where you draw this vector, it will always be the same.
Graphs of functions
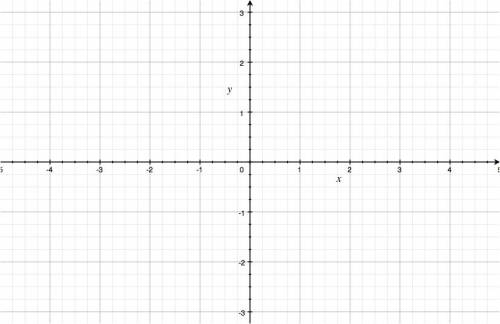
The Cartesian plane is also a good way to visualize functions \[ f: \mathbb{R} \to \mathbb{R}. \] Indeed, you can think of a function as a set of input-output pairs $(x,f(x))$, and if we identify the output values of the function with the $y$-coordinate we can trace the set of points \[ (x,y) = (x,f(x)). \]
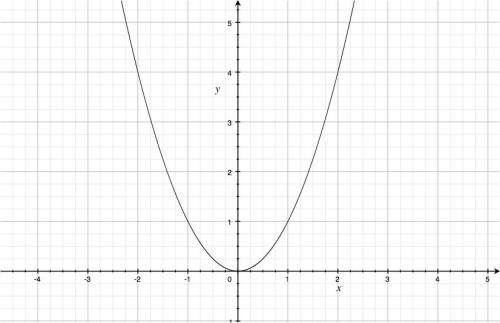
For example, if we have the function $f(x)=x^2$, we can pass a line through the set of points \[ (x,y) = (x, x^2), \] to obtain:
When plotting functions by setting $y=f(x)$, we use a special terminology for the two axes. The $x$ axis is the independent variable (the one that varies freely), whereas the $y$ is the dependent variable since $y=f(x)$ depends on $x$.
Dimensions
Note that a Cartesian plot has two dimensions: the $x$ dimension and the $y$ dimension. If we only had one dimension, then we would use a number line. If we wanted to plot in 3D we can build a three-dimensional coordinate system with $x$, $y$ and $z$ axes.
Exponents
We often have to multiply together the same number many times in math so we use the notation \[ b^n = \underbrace{bbb \cdots bb}_{n \text{ times} } \] to denote some number $b$ multiplied by itself $n$ times. In this section we will review the basic terminology associated with exponents and discuss their properties.
Definitions
The fundamental ideas of exponents are:
- $b^n$: the number $b$ raised to the power $n$
- $b$: the base
- $n$: the exponent or power of $b$ in the expression $b^n$
By definitions, the zeroth power of any number is equal to one $b^0=1$.
We can also discuss exponential functions of the form $f:\mathbb{R} \to \mathbb{R}$ Define following functions:
- $b^x$: the exponential function base $b$
- $10^x$: the exponential function base $10$
- $\exp(x)=e^x$: the exponential function base $e$. The number $e$ is called Euler's number.
- $2^x$: the exponential function base $2$. This function is very important in computer science.
The number $e=2.7182818\ldots$ is a special base that has lots of applications. We call $e$ the natural base.
Another special base is $10$ because we use the decimal system for our numbers. We can write down very large numbers and very small numbers as powers of $10$. For example, one thousand can be written as $1\:000=10^3$, one million is $1\:000\:000=10^6$ and one billion is $1\:000\:000\:000=10^9$.
Formulas
The following properties follow from the definition of exponentiation as repeated multiplication.
Property 1
Multiplying together two exponential expressions with the same base is the same as adding the exponents: \[ b^m b^n = \underbrace{bbb \cdots bb}_{m \text{ times} } \underbrace{bbb \cdots bb}_{n \text{ times} } = \underbrace{bbbbbbb \cdots bb}_{m + n \text{ times} } = b^{m+n}. \]
Property 2
Division by a number can be expressed as an exponent of minus one: \[ b^{-1} \equiv \frac{1}{b}. \] More generally any negative exponent corresponds to a division: \[ b^{-n} = \frac{1}{b^n}. \]
Property 3
By combining Property 1 and Property 2 we obtain the following rule: \[ \frac{b^m}{b^n} = b^{m-n}. \]
In particular we have $b^{n}b^{-n}=b^{n-n}=b^0=1$. Multiplication by the number $b^{n}$ is the inverse operation of division by the number $b^{n}$. The net effect of the combination of both operations is the same as multiplying by one, i.e., the identity operation.
Property 4
When an exponential expression is exponentiated, the inner exponent and the outer exponent multiply: \[ ({b^m})^n = \underbrace{(\underbrace{bbb \cdots bb}_{m \text{ times} }) (\underbrace{bbb \cdots bb}_{m \text{ times} }) \cdots (\underbrace{bbb \cdots bb}_{m \text{ times} })}_{n \text{ times} } = b^{mn}. \]
Property 5.1
\[ (ab)^n =\underbrace{(ab)(ab)(ab) \cdots (ab)(ab)}_{n \text{ times} } = \underbrace{aaa \cdots aa}_{n \text{ times} } \underbrace{bbb \cdots bb}_{n \text{ times} } = a^n b^n. \]
Property 5.2
\[ \left(\frac{a}{b}\right)^n = \underbrace{\left(\frac{a}{b}\right)\left(\frac{a}{b}\right)\left(\frac{a}{b}\right) \cdots \left(\frac{a}{b}\right)\left(\frac{a}{b}\right)}_{n \text{ times} } = \frac{ \overbrace{aaa \cdots aa}^{n \text{ times} } }{\underbrace{bbb \cdots bb}_{n \text{ times} } } = \frac{a^n}{b^n}. \]
Property 6
Raising a number to the power $\frac{1}{n}$ is equivalent to finding the $n$th root of the number: \[ b^{\frac{1}{n}} = \sqrt[n]{b}. \] In particular, the square root corresponds to the exponent of one half $\sqrt{b}=b^{\frac{1}{2}}$. The cube root (the inverse of $x^3$) corresponds to $\sqrt[3]{b}\equiv b^{\frac{1}{3}}$. We can verify the inverse relationship between $\sqrt[3]{x}$ and $x^3$ using either Property 1: $(\sqrt[3]{x})^3=(x^{\frac{1}{3}})(x^{\frac{1}{3}})(x^{\frac{1}{3}})=x^{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}}=x^1=x$ or using Property 4: $(\sqrt[3]{x})^3=(x^{\frac{1}{3}})^3=x^{\frac{3}{3}}=x^1=x$.
Properties 5.1 and 5.2 also apply for fractional exponents: \[ \sqrt[n]{ab} = \sqrt[n]{a}\sqrt[n]{b}, \] \[ \sqrt[n]{\left(\frac{a}{b}\right)} = \frac{\sqrt[n]{a} }{ \sqrt[n]{b} }. \]
Discussion
Even and odd exponents
The function $f(x)=x^{n}$ behaves differently when the exponent $n$ is an even or odd. If $n$ is odd we have \[ \left( \sqrt[n]{b} \right)^n = \sqrt[n]{ b^n } = b. \]
However if $n$ is even the function $x^n$ destroys the sign of the number (e.g. $x^2$ which maps both $-x$ and $x$ to $x^2$). Thus the successive application of exponentiation by $n$ and the $n$th root has the same effect as the absolute value function: \[ \sqrt[n]{ b^n } = |b|. \] Recall that the absolute value function $|x|$ simply discards the information about the sign of $x$.
The expression $\left( \sqrt[n]{b} \right)^n$ cannot be computed whenever $b$ is a negative number. The reason is that we can't evaluate $\sqrt[n]{b}$ for $b<0$ in terms of real numbers (there is no real number which multiplied times itself an even number of times gives a negative number).
Scientific notation
In science we often have to deal with very large numbers like the speed of light ($c=299\:792\:458$[m/s]), and very small numbers like the permeability of free space ($\mu_0=0.000001256637\ldots$[N/A$^2$]). It can be difficult to judge the magnitude of such numbers and to carry out calculations on them using the usual decimal notation.
Dealing with such numbers is much easier if we use scientific notation. For example the speed of light can be written as $c=2.99792458\times 10^{8}$[m/s] and the the permeability of free space is $\mu_0=1.256637\times 10^{-6}$[N/A$^2$]. In both cases we express the number as a decimal number between $1.0$ and $9.9999\ldots$ followed by the number $10$ raised to some power. The effect of multiplication by $10^8$ is to move the decimal point eight steps to the right thus making the number bigger. The effects of multiplying by $10^{-6}$ has the opposite effect of moving the decimal to the left thus making the number smaller. Scientific notation is very useful because it allows us to see clearly the size of numbers: $1.23\times 10^{6}$ is $1\:230\:000$ whereas $1.23\times 10^{-10}$ is $0.000\:000\:000\:123$. With scientific notation you don't have to count the zeros. Cool no?
The number of decimal places we use when specifying a certain physical quantity is usually an indicator of the precision with which we were able to measure this quantity. Taking into account the precision of the measurements we make is an important aspect of all quantitative research, but going into that right now would be a digression. If you want to read more about this, search for significant digits on the wikipedia page for scientific notation linked to below.
On computer systems, the floating point numbers are represented exactly like in scientific notation—a decimal part and an exponent. To separate the decimal part from exponent when entering a floating point number on the computer we use the character e,
which stands for $\times 10^{?}$. For example to enter the permeability of free space into your calculator you should type 1.256637e-6.
Links
Logarithms
The word “logarithm” makes most people think about some mythical mathematical beast. Surely logarithms are many headed, breathe fire and are extremely difficult to understand. Nonsense! Logarithms are simple. It will take you at most a couple of pages to get used to manipulating them, and that is a good thing because logarithms are used all over the place.
For example, the strength of your sound system is measured in logarithmic units called decibels $[\textrm{dB}]$. This is because your ear is sensitive only to exponential differences in sound intensity. Logarithms allow us to compare very large numbers and very small numbers on the same scale. If we were measuring sound in linear units instead of logarithmic units then your sound system volume control would have to go from $1$ to $1048576$. That would be weird no? This is why we use the logarithmic scale for the volume notches. Using a logarithmic scale, we can go from sound intensity level $1$ to sound intensity level $1048576$ in 20 “progressive” steps. Assume each notch doubles the sound intensity instead of increasing it by a fixed amount, the first notch corresponds to $2$, the second notch is $4$ (still probably inaudible) but by the time you get to sixth notch you are at $2^6=64$ sound intensity (audible music). The tenth notch corresponds to sound intensity $2^{10}=1024$ (medium strength sound) and the finally the twentieth notch will be max power $2^{20}=1048576$ (at this point the neighbours will come knocking to complain).
Definitions
You are probably familiar with these concepts already:
- $b^x$: the exponential function base $b$
- $\exp(x)=e^x$: the exponential function base $e$, Euler's number
- $2^x$: exponential function base $2$
- $f(x)$: the notion of a function $f:\mathbb{R}\to\mathbb{R}$
- $f^{-1}(x)$: the inverse function of $f(x)$. It is defined in terms of
$f(x)$ such that the following holds $f^{-1}(f(x))=x$, i.e.,
if you apply $f$ to some number and get the output $y$,
and then you pass $y$ through $f^{-1}$ the output will be $x$ again.
The inverse function $f^{-1}$ undoes the effects of the function $f$.
NOINDENT In this section we will play with the following new concepts:
- $\log_b(x)$: logarithm of $x$ base $b$. This is the inverse function of $b^x$
- $\ln(x)$; the “natural” logarithm base $e$. This is the inverse of $e^x$
- $\log_2(x)$: the logarithm base $2$ is is the inverse of $2^x$
I say play, because there is nothing much new to learn here: logarithms are just a clever way to talk about the size of number – i.e., how many digits the number has.
Formulas
The main thing to realize is that $\log$s don't really exist on their own. They are defined as the inverses of the corresponding exponential function. The following statements are equivalent: \[ \log_b(x)=m \ \ \ \ \ \Leftrightarrow \ \ \ \ \ b^m=x. \]
For logarithms with base $e$ one writes $\ln(x)$ for “logarithme naturel” because $e$ is the “natural” base. Another special base is $10$ because we use the decimal system for our numbers. $\log_{10}(x)$ tells you roughly the size of the number $x$—how many digits the number has.
Example
When someone working for the system (say someone with a high paying job in the financial sector) boasts about his or her “six-figure” salary, they are really talking about the $\log$ of how much money they make. The “number of figures” $N_S$ in you salary is calculated as one plus the logarithm base ten of your salary $S$. The formula is \[ N_S = 1 + \log_{10}(S). \] So a salary of $S=100\:000$ corresponds to $N_S=1+\log_{10}(100\:000)=1+5=6$ figures. What will be the smallest “seven figure” salary? We have to solve for $S$ given $N_S=7$ in the formula. We get $7 = 1+\log_{10}(S)$ which means that $6=\log_{10}(S)$ and using the inverse relationship between logarithm base ten and exponentiation base ten we find that $S=10^6 = 1\:000\:000$. One million per year. Yes, for this kind of money I see how someone might want to work for the system. But I don't think most system pawns ever make it to the seven figure level. Even at the higher ranks, the salaries are more in the $1+\log_{10}(250\:000) = 1+5.397=6.397$ digits range. There you have it. Some of the smartest people out there selling their brains out to the finance sector for some lousy $0.397$ extra digits. What wankers! And who said you need to have a six digit salary in the first place? Why not make $1+\log_{10}(44\:000)=5.64$ digits as a teacher and do something with your life that actually matters?
Properties
Let us now discuss two important properties that you will need to use when dealing with logarithms. Pay attention because the arithmetic rules for logarithms are very different from the usual rules for numbers. Intuitively, you can think of logarithms as a convenient of referring to the exponents of numbers. The following properties are the logarithmic analogues of the properties of exponents
Property 1
The first property states that the sum of two logarithms is equal to the logarithm of the product of the arguments: \[ \log(x)+\log(y)=\log(xy). \] From this property, we can derive two other useful ones: \[ \log(x^k)=k\log(x), \] and \[ \log(x)-\log(y)=\log\left(\frac{x}{y}\right). \]
Proof: For all three equations above we have to show that the expression on the left is equal to the expression on the right. We have only been acquainted with logarithms for a very short time, so we don't know each other that well. In fact, the only thing we know about $\log$s is the inverse relationship with the exponential function. So the only way to prove this property is to use this relationship.
The following statement is true for any base $b$: \[ b^m b^n = b^{m+n}, \] which follows from first principles. Exponentiation means multiplying together the base many times. If you count the total number of $b$s on the left side you will see that there is a total of $m+n$ of them, which is what we have on the right.
If you define some new variables $x$ and $y$ such that $b^m=x$ and $b^n=y$ then the above equation will read \[ xy = b^{m+n}, \] if you take the logarithm of both sides you get \[ \log_b(xy) = \log_b\left( b^{m+n} \right) = m + n = \log_b(x) + \log_b(y). \] In the last step we used the definition of the $\log$ function again which states that $b^m=x \ \ \Leftrightarrow \ \ m=\log_b(x)$ and $b^n=y \ \ \Leftrightarrow \ \ n=\log_b(y)$.
Property 2
We will now discuss the rule for changing from one base to another. Is a relation between $\log_{10}(S)$ and $\log_2(S)$?
There is. We can express the logarithm in any base $B$ in terms of a ratio of logarithms in another base $b$. The general formula is: \[ \log_{B}(x) = \frac{\log_b(x)}{\log_b(B)}. \]
This means that: \[ \log_{10}(S) =\frac{\log_{10}(S)}{1} =\frac{\log_{10}(S)}{\log_{10}(10)} = \frac{\log_{2}(S)}{\log_{2}(10)}=\frac{\ln(S)}{\ln(10)}. \]
This property is very useful in case when you want to compute $\log_{7}$, but your calculator only gives you $\log_{10}$. You can simulate $\log_7(x)$ by computing $\log_{10}(x)$ and dividing by $\log_{10}(7)$.
Geometry
Triangles
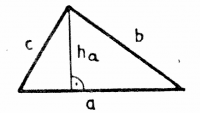 The area of a triangle is equal to $\frac{1}{2}$
times the length of the base times the height:
\[
A = \frac{1}{2} a h_a.
\]
Note that $h_a$ is the height of the triangle relative to the side $a$.
The area of a triangle is equal to $\frac{1}{2}$
times the length of the base times the height:
\[
A = \frac{1}{2} a h_a.
\]
Note that $h_a$ is the height of the triangle relative to the side $a$.
The perimeter of the triangle is: \[ P = a + b + c. \]
Consider now a triangle with internal angles $\alpha$, $\beta$ and $\gamma$. The sum of the inner angles in any triangle is equal to two right angles: $\alpha+\beta+\gamma=180^\circ$.
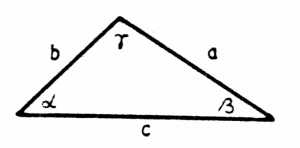 The sine law is:
\[
\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)},
\]
where $\alpha$ is the angle opposite to $a$, $\beta$ is the angle opposite to $b$ and $\gamma$ is the angle opposite to $c$.
The sine law is:
\[
\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)},
\]
where $\alpha$ is the angle opposite to $a$, $\beta$ is the angle opposite to $b$ and $\gamma$ is the angle opposite to $c$.
The cosine rules are: \[ \begin{align} a^2 & =b^2+c^2-2bc\cos(\alpha), \nl b^2 & =a^2+c^2-2ac\cos(\beta), \nl c^2 & =a^2+b^2-2ab\cos(\gamma). \end{align} \]
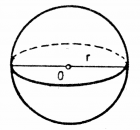
Sphere
A sphere is described by the equation \[ x^2 + y^2 + z^2 = r^2. \]
Surface area: \[ A = 4\pi r^2. \]
Volume: \[ V = \frac{4}{3}\pi r^3. \]
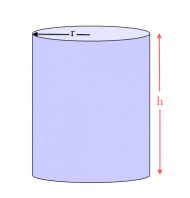
Cylinder
The surface area of a cylinder consists of the top and bottom circular surfaces plus the area of the side of the cylinder: \[ A = 2 \left( \pi r^2 \right) + (2\pi r) h. \]
The volume is given by product of the area of the base times the height of the cylinder: \[ V = \left(\pi r^2 \right)h. \]
Example
You open the hood of your car and see 2.0L written on top of the engine. The 2[L] refers to the total volume of the four pistons, which are cylindrical in shape. You look in the owner's manual and find out that the diameter of each piston (bore) is 87.5[mm] and the height of each piston (stroke) is 83.1[mm]. Verify that the total volume of the cylinder displacement of your engine is indeed 1998789[mm$^3$] $\approx 2$[L].
Links
[ A formula for calculating the distance between two points on a sphere ]
http://www.movable-type.co.uk/scripts/latlong.html
Inequalities
To solve an equation we have to find the one (or many) values of $x$ which satisfy the equation. The solution set for an equation consists of a discrete set of values. For example, the solutions to $(x-3)^2=4$ are $x=1$ and $x=5$.
In this section, we will learn how to solve equations which involve inequalities. The solution to an inequality is usually an entire range of numbers. For example the inequality $(x-3)^2 \leq 4$ is equivalent to asking the question “for which values of $x$ is $(x-3)^2$ less than or equal to $4$.” The answer is the interval $[1,5] \equiv \{ x\in \mathbb{R}\ | \ 1 \leq x \leq 5 \}$.
The techniques used to deal with inequalities are roughly the same as the techniques which we learned for dealing with equations: we have to perform simplifying steps to both sides of the inequality until we obtain the answer.
Definitions
The different type of inequality conditions are:
- $f(x) < g(x)$: a strict inequality. The function $f$ is always strictly less than $g$.
- $f(x) \leq g(x)$: the function $f$ is less than or equal to the function $g$.
- $f(x) > g(x)$: $f$ is strictly greater than $g$.
- $f(x) \geq g(x)$: $f$ is greater than or equal to $g$.
The solutions to an inequality correspond to subsets of the real line. Depending on the type of inequality we are dealing with, the answer will be either a closed or open interval:
- $[a,b]$: the closed interval from $a$ to $b$. This corresponds to the set of numbers between $a$ and $b$ on the real line, including the endpoints $a$ and $b$. $[a,b] = \{ x\in \mathbb{R}\ | \ a \leq x \leq b \}$.
- $(a,b)$: the open interval from $a$ to $b$. This corresponds to the set of numbers between $a$ and $b$ on the real line, not including the $a$ and $b$. $(a,b) = \{ x\in \mathbb{R}\ | \ a < x < b \}$.
- $[a,b)$: the mixed interval which includes the left endpoint $a$, but not the right endpoint $b$.
Sometimes the we will have to deal with intervals which consists of two disjoint parts:
- $[a,b] \cup [c,d]$: The set of all numbers that are either between $a$ and $b$ (inclusive) or between $c$ and $d$ (inclusive).
Formulas
The main idea for solving inequalities is the same as solving equations except for one small special step. When multiplying by a negative number on both sides, the direction of the inequality must be flipped: \[ f(x) \leq g(x) \qquad \Rightarrow \qquad -f(x) \geq -g(x). \]
Example
To solve $(x-3)^2\leq 4$ we must dig towards the $x$ and undo all the operations that stand in our way: \[ \begin{align*} & \ (x-3)^2 \leq 4, \nl -2 \leq & \ (x-3) \leq 2, \nl 1 \leq & \ \ \ \ \ x \ \ \ \ \leq 5. \end{align*} \] where in the first step we took the square root operation (the inverse of the quadratic function) and then we added $3$ to both sides. The final answer is $x\in[1,5]$.
Discussion
As you can see, solving inequalities is not more complicated than solving equations. Indeed, the best way to think about an inequality is in terms of the end points – which correspond to the equality condition.
Base representation
other topics:
working in base 2 and base 16 discrete exponentiation Hamming distance (& friends)
modular arithmetic primality testing basic stats (standard deviation & variance)
Number systems
Decimal system
Binary system
Hexadecimal system
Formulas
Discussion
Series
Can you compute $\ln(2)$ using only a basic
calculator with four operations: [+], [-], [$\times$], [$\div$]?
I can tell you one way. Simply compute the following sum:
\[
1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} + \ldots.
\]
We can compute the above sum for large values of $n$ using live.sympy.org:
>>> def axn_ln2(n): return 1.0*(-1)**(n+1)/n
>>> sum([ axn_ln2(n) for n in range(1,100) ])
0.69(817217931)
>>> sum([ axn_ln2(n) for n in range(1,1000) ])
0.693(64743056)
>>> sum([ axn_ln2(n) for n in range(1,1000000) ])
0.693147(68056)
>>> ln(2).evalf()
0.693147180559945
As you can see, the more terms you add in this series, the more accurate the series approximation of $\ln(2)$ becomes. A lot of practical mathematical computations are done in this iterative fashion. The notion of series is a powerful way to calculate quantities to arbitrary precision by summing together more and more terms.
Definitions
- $\mathbb{N}$: $ = \{0, 1, 2, 3, 4, 5, 6, \ldots \}$.
- $\mathbb{N}^*=\mathbb{N} \setminus \{0\}$: = $\{1, 2, 3, 4, 5, 6, \ldots \}$.
- $a_n$: sequence of numbers $a_0, a_1, a_2, a_3, a_4, \ldots$.
- $\sum$: sum. Means to take the sum of several objects
put together. The summation sign is the short way to express
certain long expressions:
\[
a_3 + a_4 + a_5 + a_6 + a_7 = \sum_{3 \leq i \leq 7} a_i = \sum_{i=3}^7 a_i.
\]
* $\sum a_i$: series. The running total of a sequence until $n$:
\[
S_n = \sum_{i=1}^n a_i = a_1 + a_2 + \ldots + a_{n-1} + a_n.
\]
Most often, we take the sum of all the terms in the sequence:
\[
S_\infty = \sum_{i=1}^\infty = a_1 + a_2 + a_{3} + a_4 + \ldots.
\]
* $n!$: the //factorial// function: $n!=n(n-1)(n-2)\cdots 3\cdot2\cdot1$.
* $f(x)=\sum_{n=0}^\infty a_n x^n$: //Taylor series// approximation
of the function $f(x)$. It has the form of an infinitely long polynomial
$a_0 + a_1x + a_2x^2 + a_3x^3 + \ldots$ where the coefficients $a_n$ are
chosen so as to encode the properties of the function $f(x)$.
Exact sums
There exist formulas for calculating the exact sum of certain series. Sometimes even infinite series can be calculated exactly.
The sum of the geometric series of length $n$ is: \[ \sum_{k=0}^n r^k = 1 + r + r^2 + \cdots + r^n =\frac{1-r^{n+1}}{1-r}. \]
If $|r|<1$, we can take the limit as $n\to \infty$ in the above expression to obtain: \[ \sum_{k=0}^\infty r^k=\frac{1}{1-r}. \]
Example
Consider the geometric series with $r=\frac{1}{2}$. If we apply the above formula formula we obtain \[ \sum_{k=0}^\infty \left(\frac{1}{2}\right)^k=\frac{1}{1-\frac{1}{2}} = 2. \]
You can also visualize this infinite summation graphically. Imagine you start with a piece of paper of size one-by-one and then you add next to it a second piece of paper with half the size of the first, and a third piece with half the size of the second, etc. The total area that this sequence of pieces of papers will occupy is:
\[ \ \]
The sum of the first $N+1$ terms in arithmetic progression is given by: \[ \sum_{n=0}^N (a_0+nd)= a_0(N+1)+\frac{N(N+1)}{2}d. \]
We have the following closed form expression involving the first $N$ integers: \[ \sum_{k=1}^N k = \frac{N(N+1)}{2}, \qquad \quad \sum_{k=1}^N k^2=\frac{N(N+1)(2N+1)}{6}. \]
Other series which have exact formulas for their sum are the $p$-series with even values of $p$: \[ \sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}, \quad \sum_{n=1}^\infty\frac{1}{n^4}=\frac{\pi^4}{90}, \quad \sum_{n=1}^\infty\frac{1}{n^6}=\frac{\pi^6}{945}. \] These series are computed by Euler's method.
Other closed form sums: \[ \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^2}=\frac{\pi^2}{12}, \qquad \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n}=\ln(2), \] \[ \sum_{n=1}^\infty\frac{1}{4n^2-1}=\frac{1}{2}, \] \[ \sum_{n=1}^\infty\frac{1}{(2n-1)^2}=\frac{\pi^2}{8}, \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{(2n-1)^3}=\frac{\pi^3}{32}, \quad \sum_{n=1}^\infty\frac{1}{(2n-1)^4}=\frac{\pi^4}{96}. \]
Convergence and divergence of series
Even when we cannot compute an exact expression for the sum of a series it is very important to distinguish series that converge from series that do not converge. A great deal of what you need to know about series is different tests you can perform on a series in order to check whether it converges or diverges.
Note that convergence of a series is not the same as convergence of the underlying sequence $a_i$. Consider the sequence of partial sums $S_n = \sum_{i=0}^n a_i$: \[ S_0, S_1, S_2, S_3, \ldots , \] where each of these corresponds to \[ a_0, \ \ a_0 + a_1, \ \ a_0 + a_1 + a_2, \ \ a_0 + a_1 + a_2 + a_3, \ldots. \]
We say that the series $\sum a_i$ converges if the sequence of partial sums $S_n$ converges to some limit $L$: \[ \lim_{n \to \infty} S_n = L. \]
As with all limits, the above statement means that for any precision $\epsilon>0$, there exists an appropriate number of terms to take in the series $N_\epsilon$, such that \[ |S_n - L | < \epsilon,\qquad \text{ for all } n \geq N_\epsilon. \]
Sequence convergence test
The only way the partial sums will converge is if the entries in the sequences $a_n$ tend to zero for large $n$. This observation gives us a simple series divergence test. If $\lim\limits_{n\rightarrow\infty}a_n\neq0$ then $\sum\limits_n a_n$ diverges. How could an infinite sum of non-zero quantities add up to a finite number?
Absolute convergence
If $\sum\limits_n|a_n|$ converges, $\sum\limits_n a_n$ also converges. The opposite is not necessarily true, since the convergence of $a_n$ might be due to some negative terms cancelling with the positive ones.
A sequence $a_n$ for which $\sum_n |a_n|$ converges is called absolutely convergent. A sequence $b_n$ for which $\sum_n b_n$ converges, but $\sum_n |b_n|$ diverges is called conditionally convergent.
Decreasing alternating sequences
An alternating series of which the absolute values of the terms are decreasing and go to zero converges.
p-series
The series $\displaystyle\sum_{n=1}^\infty \frac{1}{n^p}$ converges if $p>1$ and diverges if $p\leq1$.
Limit comparison test
Suppose $\displaystyle\lim_{n\rightarrow\infty}\frac{a_n}{b_n}=p$, then the following is true:
- if $p>0$ then $\sum\limits_{n}a_n$ and $\sum\limits_{n}b_n$ either both converge or both diverge.
- if $p=0$ holds: if $\sum\limits_{n}b_n$ converges, then $\sum\limits_{n}a_n$ also converges.
n-th root test
If $L$ is defined by $\displaystyle L=\lim_{n\rightarrow\infty}\sqrt[n]{|a_n|}$ then $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Ratio test
$\displaystyle L=\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|$, then is $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Radius of convergence for power series
In a power series $a_n=c_nx^n$, the $n$th term is multiplied by the $n$th power of $x$. For such series, the convergence or divergence of the series depends on the choice of the variable $x$.
The radius of convergence $\rho$ of $\sum\limits_n c_n$ is given by: $\displaystyle\frac{1}{\rho}=\lim_{n\rightarrow\infty}\sqrt[n]{|c_n|}= \lim_{n\rightarrow\infty}\left|\frac{c_{n+1}}{c_n}\right|$. For all $-\rho < x < \rho$ the series $a_n$ converges.
Integral test
If $\int_a^{\infty}f(x)dx<\infty$, then $\sum\limits_n f(n)$ converges.
Taylor series
The Taylor series approximation to the function $\sin(x)$ to the 9th power of $x$ is given by \[ \sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!}. \] If we want to get rid of the approximate sign, we have to take infinitely many terms in the series: \[ \sin(x) = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \frac{x^{11}}{11!} + \ldots . \]
This kind of formula is known as a Taylor series approximation. The Taylor series of a function $f(x)$ around the point $a$ is given by: \[ \begin{align*} f(x) & =f(a)+f'(a)(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3+\cdots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n. \end{align*} \]
The McLaurin series of $f(x)$ is the Taylor series expanded at $a=0$: \[ \begin{align*} f(x) & =f(0)+f'(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3 + \ldots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n . \end{align*} \]
Taylor series of some common functions: \[ \begin{align*} \cos(x) &= 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} + \ldots \nl e^x &= 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots \nl \ln(x+1) &= x - \frac{x^2}2 + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} - \frac{x^6}{6} + \ldots \nl \cosh(x) &= 1 + \frac{x^2}{2} + \frac{x^4}{4!} + \frac{x^6}{6!} + \frac{x^8}{8!} + \frac{x^{10} }{10!} + \ldots \nl \sinh(x) &= x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!} + \frac{x^9}{9!} + \frac{x^{11} }{11!} + \ldots \end{align*} \] Note the similarity in the Taylor series of $\sin$, $\cos$ and $\sinh$ and $\cosh$. The formulas are the same, but the hyperbolic version do not alternate.
Explanations
Taylor series
The names Taylor series and McLaurin series are used interchangeably. Another synonym for the same concept is a power series. Indeed, we are talking about a polynomial approximation with coefficients $a_n=\frac{f^{(n)}(0)}{n!}$ in front of different powers of $x$.
If you remember your derivative rules correctly, you can calculate the McLaurin series of any function simply by writing down a power series $a_0 + a_1x + a_2x^2 + \ldots$ taking as the coefficients $a_n$ the value of the n'th derivative divided by the appropriate factorial. The more terms in the series you compute, the more accurate your approximation is going to get.
The zeroth order approximation to a function is \[ f(x) \approx f(0). \] It is not very accurate in general, but at least it is correct at $x=0$.
The best linear approximation to $f(x)$ is its tangent $T(x)$, which is a line that passes through the point $(0, f(0))$ and has slope equal to $f'(0)$. Indeed, this is exactly what the first order Taylor series formula tells us to compute. The coefficient in front of $x$ in the Taylor series is obtained by first calculating $f'(x)$ and then evaluating it at $x=0$: \[ f(x) \approx f(0) + f'(0)x = T(x). \]
To find the best quadratic approximation to $f(x)$, we find the second derivative $f^{\prime\prime}(x)$. The coefficient in front of the $x^2$ term will be $f^{\prime\prime}(0)$ divided by $2!=2$: \[ f(x) \approx f(0) + f'(0)x + \frac{f^{\prime\prime}(0)}{2!}x^2. \]
If we continue like this we will get the whole Taylor series of the function $f(x)$. At step $n$, the coefficient will be proportional to the $n$th derivative of $f(x)$ and the resulting $n$th degree approximation is going to imitate the function in its behaviour up the $n$th derivative.
Proof of the sum of the geometric series
We are looking for the sum $S$ given by: \[ S = \sum_{k=0}^n r^k = 1 + r + r^2 + r^3 + \cdots + r^n. \] Observe that there is a self similar pattern in the expanded summation $S$ where each term to the right has an additional power of $r$. The effects of multiplying by $r$ will therefore to “shift” all the terms of the series: \[ rS = r\sum_{k=0}^n r^k = r + r^2 + r^3 + \cdots + r^n + r^{n+1}, \] we can further add one to both sides to obtain \[ 1 + rS = \underbrace{1 + r + r^2 + r^3 + \cdots + r^n}_S + r^{n+1} = S + r^{n+1}. \] Note how the sum $S$ appears as the first part of the expression on the right-hand side. The resulting equation is quite simple: $1 + rS = S + r^{n+1}$. Since we wanted to find $S$, we just isolate all the $S$ terms to one side: \[ 1 - r^{n+1} = S - rS = S(1-r), \] and then solve for $S$ to obtain $S=\frac{1-r^{n+1}}{1-r}$. Neat no? This is what math is all about, when you see some structure you can exploit to solve complicated things in just a few lines.
Examples
An infinite series
Compute the sum of the infinite series \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n. \] This may appear complicated, but only until you recognize that this is a type of geometric series $\sum ar^n$, where $a=\frac{1}{N+1}$ and $r=\frac{N}{N+1}$: \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n = \sum_{n=0}^\infty a r^n = \frac{a}{1-r} = \frac{1}{N+1}\frac{1}{1-\frac{N}{N+1}} = 1. \]
Calculator
How does a calculator compute $\sin(40^\circ)=0.6427876097$ to ten decimal places? Clearly it must be something simple with addition and multiplication, since even the cheapest scientific calculators can calculate that number for you.
The trick is to use the Taylor series approximation of $\sin(x)$: \[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} + \ldots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}. \]
To calculate sin of 40 degrees we just compute the sum of the series on the right with $x$ replaced by 40 degrees (expressed in radians). In theory, we need to sum infinitely many terms to satisfy the equality, but in practice you calculator will only have to sum the first seven terms in the series in order to get an accuracy of 10 digits after the decimal. In other words, the series converges very quickly.
Let me show you how this is done in Python.
First we define the function for the $n^{\text{th}}$ term:
\[
a_n(x) = \frac{(-1)^nx^{2n+1}}{(2n+1)!}
\]
>>> def axn_sin(x,n): return (-1.0)**n * x**(2*n+1) / factorial(2*n+1)
Next we convert $40^\circ$ to radians:
>>> forti = (40*pi/180).evalf()
0.698131700797732 # 40 degrees in radians
NOINDENT These are the first 10 coefficients in the series:
>>> [ axn_sin( forti ,n) for n in range(0,10) ] [(0, 0.69813170079773179), # the values of a_n for Taylor(sin(40)) (1, -0.056710153964883062), (2, 0.0013819920621191727), (3, -1.6037289757274478e-05), (4, 1.0856084058295026e-07), (5, -4.8101124579279279e-10), (6, 1.5028144059670851e-12), (7, -3.4878738801065803e-15), (8, 6.2498067170560129e-18), (9, -8.9066666494280343e-21)]
NOINDENT To compute $\sin(40^\circ)$ we sum together all the terms:
>>> sum( [ axn_sin( forti ,n) for n in range(0,10) ] )
0.642787609686539 # the Taylor approximation value
>>> sin(forti).evalf()
0.642787609686539 # the true value of sin(40)
Discussion
You can think of the Taylor series as “similarity coefficients” between $f(x)$ and the different powers of $x$. By choosing the coefficients as we have $a_n = \frac{f^{(n)}(?)}{n!}$, we guarantee that Taylor series approximation and the real function $f(x)$ will have identical derivatives. For a McLaurin series the similarity between $f(x)$ and its power series representation is measured at the origin where $x=0$, so the coefficients are chosen as $a_n = \frac{f^{(n)}(0)}{n!}$. The more general Taylor series allow us to build an approximation to $f(x)$ around any point $x_o$, so the similarity coefficients are calcualted to match the derivatives at that point: $a_n = \frac{f^{(n)}(x_o)}{n!}$.
Another way of looking at the Taylor series is to imagine that it is a kind of X-ray picture for each function $f(x)$. The zeroth coefficient $a_0$ in the power series tells you how much of the constant function there is in $f(x)$. The first coefficient, $a_1$, tells you how much of the linear function $x$ there is in $f$, the coefficient $a_2$ tells you about the $x^2$ contents of $f$, and so on and so forth.
Now get ready for some crazy shit. Using your new found X-ray vision for functions, I want you to go and take a careful look at the power series for $\sin(x)$, $\cos(x)$ and $e^x$. As you will observe, it is as if $e^x$ contains both $\sin(x)$ and $\cos(x)$, except for the alternating negative signs. How about that? This is a sign that these three functions are somehow related in a deeper mathematical sense: recall Euler's formula.
Exercises
Derivative of a series
Show that \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n n = N. \] Hint: take the derivative with respect to $r$ on both sides of the formula for the geometric series.
Limits
To understand the ideas behind derivatives and integrals, you need to understand what a limit is and how to deal with the infinitely small, infinitely large and the infinitely many. In practice, using calculus doesn't actually involve taking limits since we will learn direct formulas and algebraic rules that are more convenient than doing limits. Do not skip this section though just because it is “not on the exam”. If you do so, you will not know what I mean when I write things like $0,\infty$ and $\lim$ in later sections.
Introduction in three acts
Zeno's paradox
The ancient greek philosopher Zeno once came up with the following argument. Suppose an archer shoots an arrow and sends it flying towards a target. After some time it will have travelled half the distance, and then at some later time it will have travelled the half of the remaining distance and so on always getting closer to the target. Zeno observed that no matter how little distance remains to the target, there will always be some later instant when the arrow will have travelled half of that distance. Thus, he reasoned, the arrow must keep getting closer and closer to the target, but never reaches it.
Zeno, my brothers and sisters, was making some sort of limit argument, but he didn't do it right. We have to commend him for thinking about such things centuries before calculus was invented (17th century), but shouldn't repeat his mistake. We better learn how to take limits, because limits are important. I mean a wrong argument about limits could get you killed for God's sake! Imagine if Zeno tried to verify experimentally his theory about the arrow by placing himself in front of one such arrow!
Two monks
Two young monks were sitting in silence in a Zen garden one autumn afternoon.
“Can something be so small as to become nothing?” asked one of the monks, braking the silence.
“No,” replied the second monk, “if it is something then it is not nothing.”
“Yes, but what if no matter how close you look you cannot see it, yet you know it is not nothing?”, asked the first monk, desiring to see his reasoning to the end.
The second monk didn't know what to say, but then he found a counterargument. “What if, though I cannot see it with my naked eye,
I could see it using a magnifying glass?”.
The first monk was happy to hear this question, because he had already prepared a response for it. “If I know that you will be looking with a magnifying glass, then I will make it so small that you cannot see with you magnifying glass.”
“What if I use a microscope then?”
“I can make the thing so small that even with a microscope you cannot see it.”
“What about an electron microscope?”
“Even then, I can make it smaller, yet still not zero.” said the first monk victoriously and then proceeded to add “In fact, for any magnifying device you can come up with, you just tell me the resolution and I can make the thing smaller than can be seen”.
They went back to concentrating on their breathing.
Epsilon and delta
The monks have the right reasoning but didn't have the right language to express what they mean. Zeno has the right language, the wonderful Greek language with letters like $\epsilon$ and $\delta$, but he didn't have the right reasoning. We need to combine aspects of both of the above stories to understand limits.
Let's analyze first Zeno's paradox. The poor brother didn't know about physics and the uniform velocity equation of motion. If an object is moving with constant speed $v$ (we ignore the effects of air friction on the arrow), then its position $x$ as a function of time is given by \[ x(t) = vt+x_i, \] where $x_i$ is the initial location where the object starts from at $t=0$. Suppose that the archer who fired the arrow was at the origin $x_i=0$ and that the target is at $x=L$ metres. The arrow will hit the target exactly at $t=L/v$ seconds. Shlook!
It is true that there are times when the arrow will be $\frac{1}{2}$, $\frac{1}{4}$, $\frac{1}{8}$th, $\frac{1}{16}$th, and so forth distance from the target. In fact there infinitely many of those fractional time instants before the arrow hits, but that is beside the point. Zeno's misconception is that he thought that these infinitely many timestamps couldn't all fit in the timeline since it is finite. No such problem exists though. Any non-zero interval on the number line contains infinitely many numbers ($\mathbb{Q}$ or $\mathbb{R}$).
Now let's get to the monks conversation. The first monk was talking about the function $f(x)=\frac{1}{x}$. This function becomes smaller and smaller but it never actually becomes zero: \[ \frac{1}{x} \neq 0, \textrm{ even for very large values of } x, \] which is what the monk told us.
Remember that the monk also claimed that the function $f(x)$ can be made arbitrarily small. He wants to show that, in the limit of large values of $x$, the function $f(x)$ goes to zero. Written in math this becomes \[ \lim_{x\to \infty}\frac{1}{x}=0. \]
To convince the second monk that he can really make $f(x)$ arbitrarily small, he invents the following game. The second monk announces a precision $\epsilon$ at which he will be convinced. The first monk then has to choose an $S_\epsilon$ such that for all $x > S_\epsilon$ we will have \[ \left| \frac{1}{x} - 0 \right| < \epsilon. \] The above expression indicates that $\frac{1}{x}\approx 0$ at least up to a precision of $\epsilon$.
The second monk will have no choice but to agree that indeed $\frac{1}{x}$ goes to 0 since the argument can be repeated for any required precision $\epsilon >0$. By showing that the function $f(x)$ approaches $0$ arbitrary closely for large values of $x$, we have proven that $\lim_{x\to \infty}f(x)=0$.
 More generally, the function $f(x)$ can converge to any number $L$
for as $x$ takes on larger and larger values:
\[
\lim_{x \to \infty} f(x) = L.
\]
The above expressions means that, for any precision $\epsilon>0$,
there exists a starting point $S_\epsilon$,
after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision:
\[
\left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon.
\]
More generally, the function $f(x)$ can converge to any number $L$
for as $x$ takes on larger and larger values:
\[
\lim_{x \to \infty} f(x) = L.
\]
The above expressions means that, for any precision $\epsilon>0$,
there exists a starting point $S_\epsilon$,
after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision:
\[
\left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon.
\]
Example
You are asked to calculate $\lim_{x\to \infty} \frac{2x+1}{x}$, that is you are given the function $f(x)=\frac{2x+1}{x}$ and you have to figure out what the function looks like for very large values of $x$. Note that we can rewrite the function as $\frac{2x+1}{x}=2+\frac{1}{x}$ which will make it easier to see what is going on: \[ \lim_{x\to \infty} \frac{2x+1}{x} = \lim_{x\to \infty}\left( 2 + \frac{1}{x} \right) = 2 + \lim_{x\to \infty}\left( \frac{1}{x} \right) = 2 + 0, \] since $\frac{1}{x}$ tends to zero for large values of $x$.
In a first calculus course you are not required to prove statements like $\lim_{x\to \infty}\frac{1}{x}=0$, you can just assume that the result is obvious. As the denominator $x$ becomes larger and larger, the fraction $\frac{1}{x}$ becomes smaller and smaller.
Types of limits
Limits to infinity
\[ \lim_{x\to \infty} f(x) \] what happens to $f(x)$ for very large values of $x$.
Limits to a number
The limit of $f(x)$ approaching $x=a$ from above (from the right) is denoted: \[ \lim_{x\to a^+} f(x) \] Similarly, the expression \[ \lim_{x\to a^-} f(x) \] describes what happens to $f(x)$ as $x$ approaches $a$ from below (from the left), i.e., with values like $x=a-\delta$, with $\delta>0, \delta \to 0$. If both limits from the left and from the right of some number are equal, then we can talk about the limit as $x\to a$ without specifying the direction: \[ \lim_{x\to a} f(x) = \lim_{x\to a^+} f(x) = \lim_{x\to a^-} f(x). \]
Example 2
You now asked to calculate $\lim_{x\to 5} \frac{2x+1}{x}$. \[ \lim_{x\to 5} \frac{2x+1}{x} = \frac{2(5)+1}{5} = \frac{11}{5}. \]
Example 3
Find $\lim_{x\to 0} \frac{2x+1}{x}$. If we just plug $x=0$ into the fraction we get an error divide by zero $\frac{2(0)+1}{0}$ so a more careful treatment will be required.
Consider first the limit from the right $\lim_{x\to 0+} \frac{2x+1}{x}$. We want to approach the value $x=0$ with small positive numbers. The best way to carry out the calculation is to define some small positive number $\delta>0$, to choose $x=\delta$, and to compute the limit: \[ \lim_{\delta\to 0} \frac{2(\delta)+1}{\delta} = 2 + \lim_{\delta\to 0} \frac{1}{\delta} = 2 + \infty = \infty. \] We took it for granted that $\lim_{\delta\to 0} \frac{1}{\delta}=\infty$. Intuitively, we can imagine how we get closer and closer to $x=0$ in the limit. When $\delta=10^{-3}$ the function value will be $\frac{1}{\delta}=10^3$. When $\delta=10^{-6}$, $\frac{1}{\delta}=10^6$. As $\delta \to 0$ the function will blow up—$f(x)$ will go up all the way to infinity.
If we take the limit from the left (small negative values of $x$) we get \[ \lim_{\delta\to 0} f(-\delta) =\frac{2(-\delta)+1}{-\delta}= -\infty. \] Therefore, since $\lim_{x\to 0^+}f(x)$ does not equal $\lim_{x\to 0^-} f(x)$, we say that $\lim_{x\to 0} f(x)$ does not exist.
Continuity
A function $f(x)$ is continuous at $a$ if the limit of $f$ as $x\to a$ converges to $f(a)$: \[ \lim_{x \to a} f(x) = f(a). \]
Most functions we will study in calculus are continuous, but not all functions are. For example, functions which make sudden jumps are not continuous. Another examples is the function $f(x)=\frac{2x+1}{x}$ which is discontinuous at $x=0$ (because the limit $\lim_{x \to 0} f(x)$ doesn't exist and $f(0)$ is not defined). Note that $f(x)$ is continuous everywhere else on the real line.
Formulas
We now switch gears into reference mode, as I will state a whole bunch known formulas for limits of various kinds of functions. You are not meant to know why these limit formulas are true, but simply understand what they mean.
The following statements tell you about the relative sizes of functions. If the limit of the ratio of two functions is equal to $1$, then these functions must behave similarly in the limit. If the limit of the ratio goes to zero, then one function must be much larger than the other in the limit.
Limits of trigonometric functions: \[ \lim_{x\rightarrow0}\frac{\sin(x)}{x}=1,\quad \lim_{x\rightarrow0} \cos(x)=1,\quad \lim_{x\rightarrow 0}\frac{1-\cos x }{x}=0, \quad \lim_{x\rightarrow0}\frac{\tan(x)}{x}=1. \]
The number $e$ is defined as one of the following limits: \[ e \equiv \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n = \lim_{\epsilon\to 0 }(1+\epsilon)^{1/\epsilon}. \] The first limit corresponds to a compound interest calculation, with annual interest rate of $100\%$ and compounding performed infinitely often.
For future reference, we state some other limits involving the exponential function: \[ \lim_{x\rightarrow0}\frac{{\rm e}^x-1}{x}=1,\qquad \quad \lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n={\rm e}^x. \]
These are some limits involving logarithms: \[ \lim_{x\rightarrow 0^+}x^a\ln(x)=0,\qquad \lim_{x\rightarrow\infty}\frac{\ln^p(x)}{x^a}=0, \ \forall p < \infty \] \[ \lim_{x\rightarrow0}\frac{\ln(x+a)}{x}=a,\qquad \lim_{x\rightarrow0}\left(a^{1/x}-1\right)=\ln(a). \]
A polynomial of degree $p$ and the exponential function base $a$ with $a > 1$ both go to infinity as $x$ goes to infinity: \[ \lim_{x\rightarrow\infty} x^p= \infty, \qquad \qquad \lim_{x\rightarrow\infty} a^x= \infty. \] Though both functions go to infinity, the exponential function does so much faster, so their relative ratio goes to zero: \[ \lim_{x\rightarrow\infty}\frac{x^p}{a^x}=0, \qquad \mbox{for all } p \in \mathbb{R}, |a|>1. \] In computer science, people make a big deal of this distinction when comparing the running time of algorithms. We say that a function is computable if the number of steps it takes to compute that function is polynomial in the size of the input. If the algorithm takes an exponential number of steps, then for all intents and purposes it is useless, because if you give it a large enough input the function will take longer than the age of the universe to finish.
Other limits: \[ \lim_{x\rightarrow0}\frac{\arcsin(x)}{x}=1,\qquad \lim_{x\rightarrow\infty}\sqrt[x]{x}=1. \]
Limit rules
If you are taking the limit of a fraction $\frac{f(x)}{g(x)}$, and you have $\lim_{x\to\infty}f(x)=0$ and $\lim_{x\to\infty}g(x)=\infty$, then we can informally write: \[ \lim_{x\to \infty} \frac{f(x)}{g(x)} = \frac{\lim_{x\to \infty} f(x)}{ \lim_{x\to \infty} g(x)} = \frac{0}{\infty} = 0, \] since both functions are helping to drive the fraction to zero.
Alternately if you ever get a fraction of the form $\frac{\infty}{0}$ as a limit, then both functions are helping to make the fraction grow to infinity so we have $\frac{\infty}{0} = \infty$.
L'Hopital's rule
Sometimes when evaluating limits of fractions $\frac{f(x)}{g(x)}$, you might end up with a fraction like \[ \frac{0}{0}, \qquad \text{or} \qquad \frac{\infty}{\infty}. \] These are undecidable conditions. Is the effect of the numerator stronger or the effect of the denominator stronger?
One way to find out, is to compare the ratio of their derivatives. This is called L'Hopital's rule: \[ \lim_{x\rightarrow a}\frac{f(x)}{g(x)} \ \ \ \overset{\textrm{H.R.}}{=} \ \ \ \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}. \]
Eigenvalues and eigenvectors
The set of eigenvectors of a matrix is a special set of input vectors for which the action of the matrix is described as a scaling. Decomposing a matrix in terms of its eigenvalues and its eigenvectors gives valuable insights into the properties of the matrix.
Certain matrix calculations like computing the power of the matrix become much easier when we use the eigendecomposition of the matrix. For example, suppose you are given a square matrix $A$ and you want to compute $A^5$. To make this example more concrete, let's use the matrix \[ A = \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix}. \]
We want to compute \[ A^5 = \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix}. \] That is a lot of matrix multiplications. You'll have to multiply and add entries for a while! Imagine how many times you would have to multiply the matrix if I had asked for $A^{55}$ instead?
Let's be smart about this. Every matrix corresponds to some linear operation. This means that it is a legitimate question to ask “what does the matrix $A$ do?” and once we figure out what it does, we can compute $A^{55}$ by simply doing what $A$ does $55$ times.
The best way to see what a matrix does is to look inside of it and see what it is made of. What is its natural basis (own basis) and what are its values (own values).
Deep down inside, the matrix $A$ is really a product of three matrices: \[ \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} = \underbrace{\begin{bmatrix} 0.850.. & -0.525.. \nl 0.525.. & 0.850.. \end{bmatrix} }_Q \ \underbrace{\! \begin{bmatrix} 1.618.. & 0 \nl 0 &-0.618.. \end{bmatrix} }_{\Lambda} \underbrace{ \begin{bmatrix} 0.850.. & 0.525.. \nl -0.525.. & 0.850.. \end{bmatrix} }_{Q^{-1}}. \] \[ A = Q\Lambda Q^{-1} \] I am serious. You can multiply these three matrices together and you will get $A$. Notice that the “middle matrix” $\Lambda$ (the capital Greek letter lambda) has entries only on the diagonal, the matrix $\Lambda$ is sandwiched between between the matrix $Q$ on the left and $Q^{-1}$ (the inverse of $Q$) on the right. This way of writing $A$ will allow us to compute $A^5$ in a civilized manner: \[ \begin{eqnarray} A^5 & = & A A A A A \nl & = & Q\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda Q^{-1} \nl & = & Q\Lambda I \Lambda I \Lambda I \Lambda I \Lambda Q^{-1} \nl & = & Q\Lambda \Lambda \Lambda \Lambda \Lambda Q^{-1} \nl & = & Q\Lambda^5 Q^{-1}. \end{eqnarray} \]
Since the matrix $\Lambda$ is diagonal, it is really easy to compute its fifth power $\Lambda^5$: \[ \begin{bmatrix} 1.618.. & 0 \nl 0 &-0.618.. \end{bmatrix}^5 = \begin{bmatrix} (1.618..)^5 & 0 \nl 0 &(-0.618..)^5 \end{bmatrix} = \begin{bmatrix} 11.090.. & 0 \nl 0 &-0.090.. \end{bmatrix}\!. \]
Thus we have \[ \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix}^5 \! = \underbrace{\begin{bmatrix} 0.850..\! & -0.525.. \nl 0.525..\! & 0.850.. \end{bmatrix} }_Q \! \begin{bmatrix} 11.090.. \! & 0 \nl 0 \! &-0.090.. \end{bmatrix} \! \underbrace{ \begin{bmatrix} 0.850.. & 0.525.. \nl -0.525.. & 0.850.. \end{bmatrix} }_{Q^{-1}}\!. \] We still have to multiply these three matrices together, but we have brought down the work from $4$ matrix multiplications down to just two.
The answer is \[ A^5 = Q\Lambda^5 Q^{-1} = \begin{bmatrix} 8 & 5 \nl 5 & 3 \end{bmatrix}. \]
Using the same technique, we can just as easily compute $A^{55}$: \[ A^{55} = Q\Lambda^{55} Q^{-1} = \begin{bmatrix} 225851433717 & 139583862445 \nl 139583862445 & 86267571272 \end{bmatrix}. \]
We could even compute $A^{5555}$ if we wanted to, but you get the point. If you look at $A$ in the right basis, repeated multiplication only involves computing the powers of its eigenvalues.
Definitions
- $A$: an $n\times n$ square matrix.
When necessary, we will denote the individual entries of $A$ as $a_{ij}$.
- $\textrm{eig}(A)\equiv(\lambda_1, \lambda_2, \ldots, \lambda_n )$:
the list of eigenvalues of $A$. Usually denoted with the greek letter lambda.
Note that some eigenvalues could be repeated.
* $p(\lambda)=\det(A - \lambda I)$:
the //characteristic polynomial// for the matrix $A$. The eigenvalues are the roots of this polynomial.
* $\{ \vec{e}_{\lambda_1}, \vec{e}_{\lambda_2}, \ldots, \vec{e}_{\lambda_n} \}$:
the set of //eigenvectors// of $A$. Each eigenvector is associated with a corresponding eigenvalue.
* $\Lambda \equiv {\rm diag}(\lambda_1, \lambda_2, \ldots, \lambda_n)$:
the diagonal version of $A$. The matrix $\Lambda$ contains the eigenvalues of $A$ on the diagonal:
\[
\Lambda =
\begin{bmatrix}
\lambda_1 & \cdots & 0 \nl
\vdots & \ddots & 0 \nl
0 & 0 & \lambda_n
\end{bmatrix}.
\]
The matrix $\Lambda$ corresponds to the matrix representation of $A$ with respect to its eigenbasis.
* $Q$: a matrix whose columns are the eigenvectors of $A$:
\[
Q
\equiv
\begin{bmatrix}
| & & | \nl
\vec{e}_{\lambda_1} & \cdots & \vec{e}_{\lambda_n} \nl
| & & |
\end{bmatrix}
= \
_{B_s}\![I]_{B_\lambda}.
\]
The matrix $Q$ corresponds to the //change of basis matrix//
from the eigenbasis $B_\lambda = \{ \vec{e}_{\lambda_1}, \vec{e}_{\lambda_2}, \vec{e}_{\lambda_3}, \ldots \}$
to the standard basis $B_s = \{\hat{\imath}, \hat{\jmath}, \hat{k}, \ldots \}$.
* $A=Q\Lambda Q^{-1}$: the //eigendecomposition// of the matrix $A$.
* $\Lambda = Q^{-1}AQ$: the //diagonalization// of the matrix $A$.
TODO: fix/tensorify indices above and use \ mathbbm{1} instead of I
Eigenvalues
The eigenvalue equation is \[ A\vec{e}_\lambda =\lambda\vec{e}_\lambda, \] where $\lambda$ is an eigenvalue and $\vec{e}_\lambda$ is an eigenvector of the matrix $A$. If we multiply $A$ by an eigenvector $\vec{e}_\lambda$, we get back the same vector scaled by the constant $\lambda$.
To find the eigenvalue of a matrix we start from the eigenvalue equation $A\vec{e}_\lambda =\lambda\vec{e}_\lambda$, insert the identity ${11}$, and rewrite it as a null-space problem: \[ A\vec{e}_\lambda =\lambda{11}\vec{e}_\lambda \qquad \Rightarrow \qquad \left(A - \lambda{11}\right)\vec{e}_\lambda = \vec{0}. \] This equation will have a solution whenever $|A - \lambda{11}|=0$. The eigenvalues of $A \in \mathbb{R}^{n \times n}$, denoted $(\lambda_1, \lambda_2, \ldots, \lambda_n )$, are the roots of the characteristic polynomial: \[ p(\lambda)=\det(A - \lambda I) \equiv |A-\lambda I|=0. \] When we calculate this determinant, we'll obtain an expression involving the coefficients $a_{ij}$ and the variable $\lambda$. If $A$ is an $n \times n $ matrix, the characteristic polynomial is of degree $n$ in the variable $\lambda$.
We denote the list of eigenvalues as $\textrm{eig}(A)=( \lambda_1, \lambda_2, \ldots, \lambda_n )$. If a $\lambda_i$ is a repeated root of the characteristic polynomial $p(\lambda)$, we say that it is a degenerate eigenvalue. For example the identity matrix $I \in \mathbb{R}^{2\times 2}$ has the characteristic polynomial $p_I(\lambda)=(\lambda-1)^2$ which has a repeated root at $\lambda=1$. We say the eigenvalue $\lambda=1$ has algebraic multiplicity $2$. It is important to keep track of degenerate eigenvalues, so we'll specify the multiplicity of an eigenvalue by repeatedly including it in the list of eigenvalues $\textrm{eig}(I)=(\lambda_1, \lambda_2) = (1,1)$.
Eigenvectors
The eigenvectors associated with eigenvalue $\lambda_i$ of matrix $A$ are the vectors in the null space of the matrix $(A-\lambda_i I )$.
To find the eigenvectors associated with the eigenvalue $\lambda_i$, you have to solve for the components $e_{\lambda,x}$ and $e_{\lambda,y}$ of the vector $\vec{e}_\lambda=(e_{\lambda,x},e_{\lambda,y})$ that satisfies the equation: \[ A\vec{e}_\lambda =\lambda\vec{e}_\lambda, \] or equivalently \[ (A-\lambda I ) \vec{e}_\lambda = 0\qquad \Rightarrow \qquad \begin{bmatrix} a_{11}-\lambda & a_{12} \nl a_{21} & a_{22}-\lambda \end{bmatrix} \begin{bmatrix} e_{\lambda,x} \nl e_{\lambda,y} \end{bmatrix} = \begin{bmatrix} 0 \nl 0 \end{bmatrix}. \]
If $\lambda_i$ is a repeated root (degenerate eigenvalue), the null space $(A-\lambda_i I )$ could contain multiple eigenvectors. The dimension of the null space of $(A-\lambda_i I )$ is called the geometric multiplicity of the eigenvalue $\lambda_i$.
Eigendecomposition
If an $n \times n$ matrix $A$ is diagonalizable, this means that we can find $n$ eigenvectors for that matrix. The eigenvectors that come from different eigenspaces are guaranteed to be linearly independent (see exercises). We can also pick a set of linearly independent vectors within each of the degenerate eigenspaces. Combining the eigenvectors from all the eigenspaces we get a set of $n$ linearly independent eigenvectors, which form a basis for $\mathbb{R}^n$. We call this the eigenbasis.
Let's put the $n$ eigenvectors next to each other as the columns of a matrix: \[ Q = \begin{bmatrix} | & & | \nl \vec{e}_{\lambda_1} & \cdots & \vec{e}_{\lambda_n} \nl | & & | \end{bmatrix}. \]
We can decompose $A$ into its eigenvalues and its eigenvectors: \[ A = Q \Lambda Q^{-1} = \begin{bmatrix} | & & | \nl \vec{e}_{\lambda_1} & \cdots & \vec{e}_{\lambda_n} \nl | & & | \end{bmatrix} \begin{bmatrix} \lambda_1 & \cdots & 0 \nl \vdots & \ddots & 0 \nl 0 & 0 & \lambda_n \end{bmatrix} \begin{bmatrix} \ \nl \ \ \ \ \ \ Q^{-1} \ \ \ \ \ \ \nl \ \end{bmatrix}. \] The matrix $\Lambda$ is a diagonal matrix of eigenvalues and the matrix $Q$ is the “change of basis” matrix which contains the corresponding eigenvectors as columns.
Note that only the direction of each eigenvector is important and not the length. Indeed if $\vec{e}_\lambda$ is an eigenvector (with value $\lambda$), then so is any $\alpha \vec{e}_\lambda$ for all $\alpha \in \mathbb{R}$. Thus we are free to use any multiple of the vectors $\vec{e}_{\lambda_i}$ as the columns of the matrix $Q$.
Example
Find the eigenvalues, the eigenvectors and the diagonalization of the matrix: \[ A=\begin{bmatrix} 1 & 2 & 0 \nl 0 & 3 & 0 \nl 2 & -4 & 2 \end{bmatrix}. \]
The eigenvalues of the matrix are (in decreasing order) \[ \lambda_1 = 3, \quad \lambda_2 = 2, \quad \lambda_3= 1. \] When an $n \times n$ matrix has $n$ distinct eigenvalues, it is diagonalizable since it will have $n$ linearly independent eigenvectors. Since the matrix $A$ has has $3$ different eigenvalues it is diagonalizable.
The eigenvalues of $A$ are the values that will appear in the diagonal of $\Lambda$, so by finding the eigenvalues of $A$ we already know its diagonalization. We could stop here, but instead, let's continue and find the eigenvectors of $A$.
The eigenvectors of $A$ are found by solving for the null space of the matrices $(A-3I)$, $(A-2I)$, and $(A-I)$ respectively: \[ \vec{e}_{\lambda_1} = \begin{bmatrix} -1 \nl -1 \nl 2 \end{bmatrix}, \quad \vec{e}_{\lambda_2} = \begin{bmatrix} 0 \nl 0 \nl 1 \end{bmatrix}, \quad \vec{e}_{\lambda_3} = \begin{bmatrix} -1 \nl 0 \nl 2 \end{bmatrix}. \] Check that $A \vec{e}_{\lambda_k} = \lambda_k \vec{e}_{\lambda_k}$ for each of the above vectors. Let $Q$ be the matrix with these eigenvectors as its columns: \[ Q= \begin{bmatrix} -1 & 0 & -1 \nl -1 & 0 & 0 \nl 2 & 1 & 2 \end{bmatrix}, \qquad \textrm{and} \qquad Q^{-1} = \begin{bmatrix} 0 & -1 & 0 \nl 2 & 0 & 1 \nl -1 & 1 & 0 \end{bmatrix}. \] These matrices form the eigendecomposition of the matrix $A$: \[ A = Q\Lambda Q^{-1} = \begin{bmatrix} 1 & 2 & 0 \nl 0 & 3 & 0 \nl 2 & -4 & 2 \end{bmatrix} = \begin{bmatrix} -1 & 0 & -1 \nl -1 & 0 & 0 \nl 2 & 1 & 2 \end{bmatrix} \!\! \begin{bmatrix} 3 & 0 & 0 \nl 0 & 2 & 0 \nl 0 & 0 & 1\end{bmatrix} \!\! \begin{bmatrix} 0 & -1 & 0 \nl 2 & 0 & 1 \nl -1 & 1 & 0 \end{bmatrix}\!. \]
To find the diagonalization of $A$, we must move $Q$ and $Q^{-1}$ to the other side of the equation. More specifically, we multiply the equation $A=Q\Lambda Q^{-1}$ by $Q^{-1}$ on the left and by $Q$ on the right to obtain the diagonal matrix: \[ \Lambda = Q^{-1}AQ = \begin{bmatrix} 0 & -1 & 0 \nl 2 & 0 & 1 \nl -1 & 1 & 0 \end{bmatrix} \!\! \begin{bmatrix} 1 & 2 & 0 \nl 0 & 3 & 0 \nl 2 & -4 & 2 \end{bmatrix} \!\! \begin{bmatrix} -1 & 0 & -1 \nl -1 & 0 & 0 \nl 2 & 1 & 2 \end{bmatrix} = \begin{bmatrix} 3 & 0 & 0 \nl 0 & 2 & 0 \nl 0 & 0 & 1\end{bmatrix}\!. \]
Explanations
Eigenspaces
Recall the definition of the null space of a matrix $M$: \[ \mathcal{N}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \ | \ M\vec{v} = 0 \}. \] The dimension of the null space is the number of linearly independent vectors you can find in the null space. If $M$ sends exactly two linearly independent vectors $\vec{v}$ and $\vec{w}$ to the zero vector: \[ M\vec{v} = 0, \qquad M\vec{w} = 0, \] then the null space is two-dimensional. We can always choose the vectors $\vec{v}$ and $\vec{w}$ to be orthogonal $\vec{v}\cdot\vec{w}=0$ and thus obtain an orthogonal basis for the null space.
Each eigenvalue $\lambda_i$ has an eigenspace associated with it. The eigenspace is the null space of the matrix $(A-\lambda_i I)$: \[ E_{\lambda_i} \equiv \mathcal{N}\left( A-\lambda_i I \right) = \{ \vec{v} \in \mathbb{R}^n \ | \ \left( A-\lambda_i I \right)\vec{v} = 0 \}. \] For degenerate eigenvalues (repeated roots of the characteristic polynomial) the null space of $\left( A-\lambda_i I \right)$ could contain multiple eigenvectors.
Change of basis
The matrix $Q$ can be interpreted as a change of basis matrix. Given a vector written in terms of the eigenbasis $[\vec{v}]_{B_{\lambda}}=(v^\prime_1,v^\prime_2,v^\prime_3)_{B_{\lambda}} = v^\prime_1\vec{e}_{\lambda_1}+ v^\prime_2\vec{e}_{\lambda_3}+v^\prime_3\vec{e}_{\lambda_3}$, we can use the matrix $Q$ to convert it to the standard basis $[\vec{v}]_{B_{s}} = (v_1, v_2,v_3) = v_1\hat{\imath} + v_2\hat{\jmath}+v_3\hat{k}$ as follows: \[ [\vec{v}]_{B_{s}} = \ Q [\vec{v}]_{B_{\lambda}} = \ _{B_{s}\!}[{11}]_{B_{\lambda}} [\vec{v}]_{B_{\lambda}}. \]
The change of basis in the other direction is given by the inverse matrix: \[ [\vec{v}]_{B_{\lambda}} = \ Q^{-1} [\vec{v}]_{B_{s}} = _{B_{\lambda}\!}\left[{11}\right]_{B_{s}} [\vec{v}]_{B_{s}}. \]
Interpretations
The eigendecomposition $A = Q \Lambda Q^{-1}$ allows us to interpret the action of $A$ on an arbitrary input vector $\vec{v}$ as the following three steps: \[ [\vec{w}]_{B_{s}} = \ _{B_{s}\!}[A]_{B_{s}} [\vec{v}]_{B_{s}} = Q\Lambda Q^{-1} [\vec{v}]_{B_{s}} = \ \underbrace{\!\!\ _{B_{s}\!}[{11}]_{B_{\lambda}} \ \underbrace{\!\!\ _{B_{\lambda}\!}[\Lambda]_{B_{\lambda}} \underbrace{\ _{B_{\lambda}\!}[{11}]_{B_{s}} [\vec{v}]_{B_{s}} }_1 }_2 }_3. \]
- In the first step we convert the vector $\vec{v}$ from the standard basis
to the eigenabasis.
- In the second step the action of $A$ on vectors expressed with respect to its eigenbasis
corresponds to a multiplication by the diagonal matrix $\Lambda$.
- In the third step we convert the output $\vec{w}$ from the eigenbasis
back to the standard basis.
Another way of interpreting the above steps is to say that, deep down inside, the matrix $A$ is actually the diagonal matrix $\Lambda$. To see the diagonal form of the matrix, we have to express the input vectors with respect to the eigenabasis: \[ [\vec{w}]_{B_{\lambda}} = \ _{B_{\lambda}\!}[\Lambda]_{B_{\lambda}} [\vec{v}]_{B_{\lambda}}. \]
It is extremely important that you understand the the equation $A=Q\Lambda Q^{-1}$ intuitively in terms of the three step procedure. To help you understand, we'll analyze in detail what happens when we multiply $A$ by one of its eigenvectors. Let's pick $\vec{e}_{\lambda_1}$ and verify the equation $A\vec{e}_{\lambda_1} = Q\Lambda Q^{-1}\vec{e}_{\lambda_1} \lambda_1\vec{e}_{\lambda_1}$ by follow the vector through the three steps: \[ \ _{B_{s}\!}[A]_{B_{s}} [\vec{e}_{\lambda_1}]_{B_{s}} = Q\Lambda Q^{-1} [\vec{e}_{\lambda_1}]_{B_{s}} = \ \underbrace{\!\!\ _{B_{s}\!}[{11}]_{B_{\lambda}} \ \underbrace{\!\!\ _{B_{\lambda}\!}[\Lambda]_{B_{\lambda}} \underbrace{\ _{B_{\lambda}\!}[{11}]_{B_{s}} [\vec{e}_{\lambda_1}]_{B_{s}} }_{ (1,0,\ldots)^T_{B_\lambda} } }_{ (\lambda_1,0,\ldots)^T_{B_\lambda} } }_{ \lambda_1 [\vec{e}_{\lambda_1}]_{B_{s}} } = \lambda_1 [\vec{e}_{\lambda_1}]_{B_{s}} \] In the first step, we convert the vector $[\vec{e}_{\lambda_1}]_{B_{s}}$ to the eigenbasis and obtain $(1,0,\ldots,0)^T_{B_\lambda}$. The result of the second step is $(\lambda_1,0,\ldots,0)^T_{B_\lambda}$ because multiplying $\Lambda$ by the vector $(1,0,\ldots,0)^T_{B_\lambda}$ “selects only the first column of $\Lambda$. In the third step we convert $(\lambda_1,0,\ldots,0)^T_{B_\lambda}=\lambda_1(1,0,\ldots,0)^T_{B_\lambda}$ back to the standard basis to obtain $\lambda_1[\vec{e}_{\lambda_1}]_{B_{s}}$.
Invariant properties of matrices
The determinant and the trace of a matrix are strictly functions of the eigenvalues. The determinant of $A$ is the product of its eigenvalues: \[ \det(A) \equiv |A| =\prod_i \lambda_i = \lambda_1\lambda_2\cdots\lambda_n, \] and the trace is their sum: \[ {\rm Tr}(A)=\sum_i a_{ii}=\sum_i \lambda_i = \lambda_1 + \lambda_2 + \cdots \lambda_n. \]
Here are the steps we followed to obtain these equations: \[ |A|=|Q\Lambda Q^{-1}| =|Q||\Lambda| |Q^{-1}| =|Q||Q^{-1}||\Lambda| =|Q| \frac{1}{|Q|}|\Lambda| =|\Lambda| =\prod_i \lambda_i, \] \[ {\rm Tr}(A)={\rm Tr}(Q\Lambda Q^{-1}) ={\rm Tr}(\Lambda Q^{-1}Q) ={\rm Tr}(\Lambda)=\sum_i \lambda_i. \]
In fact the above calculations remain valid when the matrix undergoes any similarity transformation. A similarity transformation is essentially a “change of basis”-type of calculation: the matrix $A$ gets multiplied by an invertible matrix $P$ from the left and by the inverse of $P$ on the right: $A \to PA P^{-1}$. Therefore, the determinant and the trace of a matrix are two properties that do not depend on the choice of basis used to represent the matrix! We say the determinant and the trace are invariant properties of the matrix.
Relation to invertibility
Let us briefly revisit three of the equivalent conditions we stated in the invertible matrix theorem. For a matrix $A \in \mathbb{R}^{n \times n}$, the following statements are equivalent:
- $A$ is invertible
- $|A|\neq 0$
- The null space contains only the zero vector $\mathcal{N}(A)=\vec{0}$
Using the formula $|A|=\prod_{i=1}^n \lambda_i$, it is easy to see why the last two statements are equivalent. If $|A|\neq 0$ then none of the $\lambda_i$s is zero, otherwise the product of the eigenvalues would be zero. We know that $\lambda=0$ is not and eigenvalues of $A$ which means that there is no vector $\vec{v}$ such that $A\vec{v} = 0\vec{v}=\vec{0}$. Therefore there are no vectors in the null space: $\mathcal{N}(A)=\{ \vec{0} \}$.
We can also follow the reasoning in the other direction. If the null space of $A$ is empty, then there is no non-zero vector $\vec{v}$ such that $A\vec{v} = \vec{0}$, which means $\lambda=0$ is not an eigenvalue of $A$, and hence the product $\lambda_1\lambda_2\cdots \lambda_n \neq 0$.
However, if there exists a non-zero vector $\vec{v}$ such that $A\vec{v} = \vec{0}$, then $A$ has a non-empty null space and $\lambda=0$ is an eigenvalue of $A$ and thus $|A|=0$.
Normal matrices
A matrix $A$ is normal if it satisfies the equation $A^TA = A A^T$. All normal matrices are diagonalizable and furthermore the diagonalization matrix $Q$ can be chosen to be an orthogonal matrix $O$.
The eigenvectors corresponding to different eigenvalues of a normal matrix are orthogonal. Furthermore we can always choose the eigenvectors within the same eigenspace to be orthogonal. By collecting the eigenvectors from all of the eigenspaces of the matrix $A \in \mathbb{R}^{n \times n}$, it is possible to obtain a complete basis $\{\vec{e}_1,\vec{e}_2,\ldots, \vec{e}_n\}$ of orthogonal eigenvectors: \[ \vec{e}_{i} \cdot \vec{e}_{j} = \left\{ \begin{array}{ll} \|\vec{e}_i\|^2 & \text{ if } i =j, \nl 0 & \text{ if } i \neq j. \end{array}\right. \] By normalizing each of these vectors we can find a set of eigenvectors $\{\hat{e}_1,\hat{e}_2,\ldots, \hat{e}_n \}$ which is an orthonormal basis for the space $\mathbb{R}^n$: \[ \hat{e}_{i} \cdot \hat{e}_{j} = \left\{ \begin{array}{ll} 1 & \text{ if } i =j, \nl 0 & \text{ if } i \neq j. \end{array}\right. \]
Consider now the matrix $O$ constructed by using these orthonormal vectors as the columns: \[ O= \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix}. \]
The matrix $O$ is an orthogonal matrix, which means that it satisfies $OO^T=I=O^TO$. In other words, the inverse of $O$ is obtained by taking the transpose $O^T$. To see that this is true consider the following product: \[ O^T O = \begin{bmatrix} - & \hat{e}_{1} & - \nl & \vdots & \nl - & \hat{e}_{n} & - \end{bmatrix} \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \nl 0 & \ddots & 0 \nl 0 & 0 & 1 \end{bmatrix} ={11}. \] Each of the ones on the diagonal arises from the dot product of a unit-length eigenvector with itself. The off-diagonal entries are zero because the vectors are orthogonal. By definition, the inverse $O^{-1}$ is the matrix which when multiplied by $O$ gives $I$, so we have $O^{-1} = O^T$.
Using the orthogonal matrix $O$ and its inverse $O^T$, we can write the eigendecomposition of a matrix $A$ as follows: \[ A = O \Lambda O^{-1} = O \Lambda O^T = \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix} \begin{bmatrix} \lambda_1 & \cdots & 0 \nl \vdots & \ddots & 0 \nl 0 & 0 & \lambda_n \end{bmatrix} \begin{bmatrix} - & \hat{e}_{1} & - \nl & \vdots & \nl - & \hat{e}_{n} & - \end{bmatrix}\!. \]
The key advantage of using a diagonalization procedure with an orthogonal matrix $O$ is that computing the inverse is simplified significantly since $O^{-1}=O^T$.
Discussion
Non-diagonalizable matrices
Not all matrices are diagonalizable. For example, the matrix \[ B= \begin{bmatrix} 3 & 1 \nl 0 & 3 \end{bmatrix}, \] has $\lambda = 3$ as a repeated eigenvalue, but the null space of $(B-3{11})$ contains only one vector $(1,0)^T$. The matrix $B$ has a single eigenvector in the eigenspace $\lambda=3$. We're one eigenvector short, and it is not possible to obtain a complete basis of eigenvectors. Therefore we cannot build the diagonalizing change of basis matrix $Q$. We say $B$ is not diagonalizable.
Matrix power series
One of the most useful concepts of calculus is the idea that functions can be represented as Taylor series. The Taylor series of the exponential function $f(x) =e^x$ is \[ e^x = \sum_{k=0}^\infty \frac{x^k}{n!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots. \] Nothing stops us from using the same Taylor series expression to define the exponential function of a matrix: \[ e^A = \sum_{k=0}^\infty \frac{A^k}{n!} = 1 + A + \frac{A^2}{2} + \frac{A^3}{3!} + \frac{A^4}{4!} + \frac{A^5}{5!} + \ldots . \] Okay, there is one thing stopping us, and that is having to compute an infinite sum of progressively longer matrix products! But wait, remember how we used the diagonalization of $A=Q\Lambda Q^{-1}$ to easily compute $A^{55}=Q\Lambda^{55} Q^{-1}$? We can use that trick here too and obtain the exponential of a matrix in a much simpler form: \[ \begin{align*} e^A & = \sum_{k=0}^\infty \frac{A^k}{n!} = \sum_{k=0}^\infty \frac{(Q\Lambda Q^{-1})^k}{n!} \nl & = \sum_{k=0}^\infty \frac{Q\:\Lambda^k\:Q^{-1} }{n!} \nl & = Q\left[ \sum_{k=0}^\infty \frac{ \Lambda^k }{n!}\right]Q^{-1} \nl & = Q\left( 1 + \Lambda + \frac{\Lambda^2}{2} + \frac{\Lambda^3}{3!} + \frac{\Lambda^4}{4!} + \ldots \right)Q^{-1} \nl & = Qe^\Lambda Q^{-1} = \begin{bmatrix} \ \nl \ \ \ \ \ \ Q \ \ \ \ \ \ \ \nl \ \end{bmatrix} \begin{bmatrix} e^{\lambda_1} & \cdots & 0 \nl \vdots & \ddots & 0 \nl 0 & 0 & e^{\lambda_n} \end{bmatrix} \begin{bmatrix} \ \nl \ \ \ \ \ \ Q^{-1} \ \ \ \ \ \ \nl \ \end{bmatrix}\!. \end{align*} \]
We can use this approach to talk about “matrix functions” of the form: \[ F: \mathbb{M}(n,n) \to \mathbb{M}(n,n), \] simply by defining them as Taylor series of matrices. Computing the matrix function $F(M)$ on an input matrix $M=Q\Lambda Q^{-1}$ is equivalent to computing the function $f$ to the eigenvalues of $M$ as follows: $F(M)=Q\:f(\Lambda)\:Q^{-1}$.
Review
In this section we learned how to decompose matrices in terms of their eigenvalues and eigenvectors. Let's briefly review everything that we discussed. The fundamental equation is $A\vec{e}_{\lambda_i} = \lambda_i\vec{e}_{\lambda_i}$, where the vector $\vec{e}_{\lambda_i}$ is an eigenvector of the matrix $A$ and the number $\lambda_i$ is an eigenvalue of $A$. The word eigen is the German word for self.
The characteristic polynomial comes about from a simple manipulations of the eigenvalue equation: \[ \begin{eqnarray} A\vec{e}_{\lambda_i} & = &\lambda_i\vec{e}_{\lambda_i} \nl A\vec{e}_{\lambda_i} - \lambda \vec{e}_{\lambda_i} & = & 0 \nl (A-{\lambda_i} I)\vec{e}_{\lambda_i} & = & 0. \end{eqnarray} \]
There are two ways we can get a zero, either the vector $\vec{e}_\lambda$ is the zero vector or it lies in the null space of $(A-\lambda I)$. The problem of finding the eigenvalues therefore reduces to finding the values of $\lambda$ for which the matrix $(A-\lambda I)$ is not invertible, i.e., it has a null space. The easiest way to check if a matrix is invertible is to compute the determinant: $|A-\lambda I| = 0$.
There will be multiple eigenvalues and eigenvector that satisfy this equation, so we keep a whole list of eigenvalues $(\lambda_1, \lambda_2, \ldots, \lambda_n )$, and corresponding eigenvectors $\{ \vec{e}_{\lambda_1}, \vec{e}_{\lambda_2}, \ldots \}$.
Applications
Many scientific applications use the eigen-decomposition of a matrix as a building block.
We'll mention a few of these applications without going into too much detail.
- Principal component analysis
- PageRank
- quantum mechanics energy, and info-theory
TODO, finish the above points
Analyzing a matrix in terms of its eigenvalues and its eigenvectors is a very powerful way to “see inside the matrix” and understand what the matrix does. In the next section we'll analyze several different types of matrices and discuss their properties in terms of their eigenvalues.
Links
[ Good visual examples from wikipedia ]
http://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors
Exercises
Q1
Prove that a collection of nonzero eigenvectors corresponding to distinct eigenvalues is linearly independent.
Hint: Proof by contradiction. Assume that we have $n$ distinct eigenvalues $\lambda_i$ and eigenvectors $\{ \vec{e}_i \}$ which are linearly dependent: $\sum_{i=1}^n \alpha_i \vec{e}_i = \vec{0}$ with some $\alpha_i \neq 0$. If a non-zero combination of $\alpha_i$ really could give the zero vector as a linear combination then this equation would be true: $(A-\lambda_n I )\left(\sum \alpha_i\vec{e}_i\right) = (A-\lambda_n I )\vec{0}=\vec{0}$, but if you expand the expression on the left you will see that it is not equal to zero.
Q2
Show that an $n \times n$ matrix has at most $n$ distinct eigenvalues.
Q3
Check out Problems 1 through 5 in the following book
http://en.wikibooks.org/wiki/Linear_Algebra/Eigenvalues_and_Eigenvectors
http://en.wikibooks.org/wiki/Linear_Algebra/Eigenvalues_and_Eigenvectors/Solutions
Linear algebra
Topics linear_algebra
Basis
One of the most important concepts in the study of vectors is the concept of a basis. In the English language, the word basis carries the meaning of criterion. Thus, in the sentence “The students were selected on the basis of their results in the MEQ exams” means that the numerical results of some stupid test were used in order to classify the worth of the candidates. Sadly, this type of thing happens a lot and people often disregard the complex characteristics of a person and focus on a single criterion. The meaning of basis in mathematics is more holistic. A basis is a set of criteria that collectively capture all the information about an object.
Let's start with a simple example. If one looks at the HTML code behind the average
web-page there will certainly be at least one mention of a colour like
background-color:#336699; which should be read as a triplet of values $(33,66,99)$,
each one describing how much red, green and blue is needed to create the given colour.
The triple $(33,66,99)$ describes the colour “hotmail blue.”
This convention for colour representation is called
the RGB scale or something I would like to call this the RGB basis. A basis is a
set of elements which can be used together to express something more
complicated. In our case we have the R, G and B elements which are pure colours
and when mixed appropriately they can create any colour. Schematically we can
write this as:
\[
{\rm RGB\_color}(33,66,99)=33{\mathbf R}+66{\mathbf G}+99{\mathbf B},
\]
where we are using the coefficients to determine the strength of each
colour component.
To create the colour, we combine its components and
the $+$ operation symbolizes the mixing of the colours.
The reason why we are going into such detail is to illustrate that the
coefficients by themselves do not mean much. In fact they do not mean
anything unless we know the basis that is being used.
Another colour scheme that is commonly used is the cyan, magenta and yellow (CMY) colour basis. We would get a completely different colour if we were to interpret the same triplet of coordinates $(33,66,99)$ with respect to the CMY basis. To express the “hotmail blue” colour in the CMY basis you would need the following coefficients: \[ {\rm Hotmail Blue} = (33,66,99)_{RGB} = (222,189,156)_{CMY}. \]
A basis is a mapping which converts mathematical objects like the triple $(a,b,c)$ into real world ideas like colours. If there is ever an ambiguity about which basis is being used for a given vector, we can indicate the basis as a subscript after the bracket as we did above.
The ijk Basis
Look at the bottom left corner of the room you are in. Let's call “the $x$ axis” the edge between the wall that is to your left and the floor. The right wall and the floor meet at the $y$ axis. Finally, the vertical line where the two walls meet will be called the $z$ axis. This is a right-handed $xyz$ coordinate system. It is used by everyone in math and physics. It has three very nice axes. They are nice because they are orthogonal (perpendicular, i.e., at 90$^\circ$ with each other) and orthoginal is good for your life. We will see why that is shortly.
Now take an object of fixed definite length, say the size of your foot. We will call this the unit length. Measure a unit length along the $x$ axis. This is the $\hat{\imath}$ vector. Repeat the same procedure with the $y$ axis and you will have the $\hat{\jmath}$ vector. Using these two vectors and the property of addition, we can build new vectors. For example, I can describe a vector pointing at 45$^\circ$ with both the $x$ axis and the $y$ axis by the following expression: \[ \vec{v}=1\:\hat{\imath}+ 1\:\hat{\jmath}, \] which means measure one step out on the $x$ axis, one step out on the $y$ axis. Using our two basis vectors we can express any vector in the plane of the floor by a linear combination like \[ \vec{v}_{\mathrm{spoint\ on\ the\ floor}}=a\:\hat{\imath}+b\:\hat{\jmath}. \] The precise mathematical statement that describtes this situation is that the basis formed by the pair $\hat{\imath}$,$\hat{\jmath}$ span the two dimensional space of the floor. We can extend this idea to three dimensions by specifying the coordinates of any point in room as a weighted sum of the three basis vectors: \[ \vec{v}_{\mathrm{point\ in\ the\ room}}=a\:\hat{\imath}+b\:\hat{\jmath}+c\:\hat{k}, \] where $\hat{k}$ is the unit length vector along the $z$ axis.
Choice of basis
In the case where it is clear which coordinate system we are using in a particular situation, we can take the liberty to omit the explicit mention of the basis vectors and simply write $(a,b,c)$ as an ordered triplet which contains only the coefficients. When there is more than one basis in some context (like in problems where you have to change basis, then for every tuple of numbers we should be explicit about which basis it refers to. We can do this by putting a subscript after the tuple. For example, the vector $\vec{v}=a\:\hat{\imath} + b\:\hat{\jmath}+c\:\hat{k}$ in the standard basis is referred to as $(a,b,c)_{\hat{\imath}\hat{\jmath}\hat{k}}$.
Discussion
It is hard to over-emphasize the importance of the notion of a basis. Every time you solve a problem with vectors, you need to be consistent in your choice of basis, because all the numbers and variables in your equations will depend on it. The basis is the bridge between real world vector quantities and their mathematical representation in terms of components.
Vectors
Vectors are mathematical objects that have multiple components. The vector $\vec{v}$ is equivalent to a pair of numbers \[ \vec{v} \equiv (v_x, v_y), \] where $v_x$ is the $x$ component of $\vec{v}$ and $v_y$ is the $y$ component.
Just like numbers, you can add vectors \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y), \] subtract them \[ \vec{v}-\vec{w} = (v_x, v_y) - (w_x, w_y) = (v_x-w_x, v_y-w_y), \] and solve all kinds of equations where the unknown variable is a vector.
This might sound like a formidably complicated new development in mathematics, but it is not. Doing arithmetic calculations on vectors is simply doing arithmetic operations on their components.
Thus, if I told you that $\vec{v}=(4,2)$ and $\vec{w}=(3,7)$, then \[ \vec{v}-\vec{w} = (4, 2) - (3, 7) = (1, -5). \]
Vectors are extremely useful in all areas of life. In physics, for example, to describe phenomena in the three-dimensional world we use vectors with three components: $x,y$ and $z$. It is of no use to say that we have a force of 20[N] pushing on a block unless we specify in which direction the force acts. Indeed, both of these vectors have length 20 \[ \vec{F}_1 = (20,0,0), \qquad \vec{F}_2=(0,20,0), \] but one points along the $x$ axis, and the other along the $y$ axis, so they are completely different vectors.
Definitions
- $\hat{x},\hat{y},\hat{z}$: the usual coordinate system. Every vector is implicitly defined in terms of this coordinate system. When you and I talk about the point $P=(3,4,2)$,
we are really saying “start from the origin, $(0,0,0)$, move 3 units in the $x$ direction, then move 4 units in the $y$ direction, and finally move 2 units in the $z$ direction.” Obviously it is simpler to just say $(3,4,2)$, but keep in mind that these numbers are relative to the coordinate system $\hat{x}\hat{y}\hat{z}$.
- $\hat{\imath},\hat{\jmath},\hat{k}$: is an alternate way of describing the $xyz$-coordinate system
in terms of three unit length vectors:
\[\hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1).\]
Any number multiplied by $\hat{\imath}$ corresponds to a vector
with that number in the first coordinate. For example, $\vec{v}=3\hat{\imath}\equiv(3,0,0)$.
* $\vec{v}=(v_x,v_y,v_z)=v_x\hat{\imath} + v_y \hat{\jmath}+v_z\hat{k}$:
A //vector// expressed in terms of components and in terms of $\hat{\imath}$, $\hat{\jmath}$ and $\hat{k}$.
In two dimensions there are two equivalent ways to denote vectors:
- In component notation $\vec{v} =(v_x, v_y)$,
which describes the vector as seen from the $x$ axis and the $y$ axis.
- As a length and direction $\vec{v}=\|\vec{v}\|\angle \theta$, where $\|\vec{v}\|$
is the length of the vector and $\theta$ is the angle that the vector
makes with the $x$ axis.
Vector dimension
The most common types of vectors are $2$-dimensional vectors (like the ones in the Cartesian plane), and $3$-dimensional vectors (directions in 3D space). These kinds of vectors are easier to work with since we can visualize them and draw them in diagrams. Vectors in general can exist in any number of dimensions. An example of a $n$-dimensional vector is \[ \vec{v} = (v_1, v_2, \ldots, v_n) \in \mathbb{R}^n. \]
Vector arithmetic
Addition of vectors is done component wise \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y). \] Vector subtraction works the same way: component by component.
The length of a vector is obtained from Pythagoras theorem. Imagine a triangle with one side of length $v_x$ and the other side of length $v_y$. The length of the vector is equal to the length of the hypotenuse: \[ \|\vec{v}\| = \sqrt{ v_x^2 + v_y^2 }. \]
We can also scale a vector by any number $\alpha \in \mathbb{R}$: \[ \alpha \vec{v} = (\alpha v_x, \alpha v_y), \] where we see that each component gets multiplied by the scaling factor $\alpha$. If $\alpha>1$ the vector will get longer, if $0\leq \alpha <1 $ then the vector will shrink. If $\alpha$ is a negative number, then the resulting vector will point in the opposite direction.
A particularly useful scaling is to divide a vector $\vec{v}$ by its length $\|\vec{v}\|$ to obtain a unit length vector that points in the same direction as $\vec{v}$: \[ \hat{v} = \frac{\vec{v}}{ \|\vec{v}\| }. \] Unit-length vectors (denoted with a hat instead of an arrow) are useful when you want to describe a direction in space.
Vector geometry
 You can think of a vectors as arrows, and addition
as putting together of vectors head-to-tail
as shown in the diagram.
You can think of a vectors as arrows, and addition
as putting together of vectors head-to-tail
as shown in the diagram.
The negative of a vector—a vector multiplied by $\alpha=-1$—is a vector of same length but in the opposite direction. So the graphical subtraction of vectors is also possible.
Length and direction of vectors
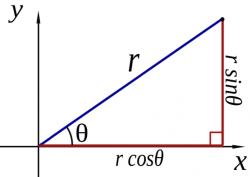 We have seen so far how to represent vectors as coefficients.
There is also another way of expressing vectors: we can
specify their length $||\vec{v}||$ and their orientation—the angle they
make with the $x$ axis.
For example,
the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$.
It is useful to represent vectors in the
magnitude and direction notation because their physical
size becomes easier to see.
We have seen so far how to represent vectors as coefficients.
There is also another way of expressing vectors: we can
specify their length $||\vec{v}||$ and their orientation—the angle they
make with the $x$ axis.
For example,
the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$.
It is useful to represent vectors in the
magnitude and direction notation because their physical
size becomes easier to see.
There are formulas for converting between the two notations. To convert the length-and-direction vector $\|\vec{r}\|\angle\theta$ to components $(r_x,r_y)$ use: \[ r_x=\|\vec{r}\|\cos\theta, \qquad\qquad r_y=\|\vec{r}\|\sin\theta. \] To convert from component notation $(r_x,r_y)$ to length-and-direction $\|\vec{r}\|\angle\theta$ use \[ r=\|\vec{r}\|=\sqrt{r_x^2+r_y^2}, \qquad\quad \theta=\tan^{-1}\!\left(\frac{r_y}{r_x}\right). \]
Note that the second part of the equation involves the arctangent (or inverse tan) function which by convention returns values between $\pi/2$ and $\mbox{-}\pi/2$ and must be used carefully for vectors that have direction outside of this range.
Alternate notation
A vector $\vec{v}=(v_x, v_y, v_z)$ is really a prescription to “go a distance $v_x$ in the $x$-direction, then a distance $v_y$ in the $y$-direction and $v_z$ in the $z$-direction.”
A more explicit notation for denoting vectors is as multiples of the basis vectors $\hat{\imath}, \hat{\jmath}$ and $\hat{k}$, which are unit length vectors pointing in the $x$, $y$ and $z$ direction respectively: \[ \hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1). \]
People who do a lot of numerical calculations with vectors often prefer to use the following alternate notation: \[ v_x \hat{\imath} + v_y\hat{\jmath} + v_z \hat{k} \qquad \Leftrightarrow \qquad \vec{v} \qquad \Leftrightarrow \qquad (v_x, v_y, v_z) . \]
The addition rule looks as follows in the new notation: \[ \underbrace{2\hat{\imath}+ 3\hat{\jmath}}_{\vec{v}} \ \ + \ \ \underbrace{ 5\hat{\imath} - 2\hat{\jmath}}_{\vec{w}} \ = \ \underbrace{ 7\hat{\imath} + 1\hat{\jmath} }_{\vec{v}+\vec{w}}. \] It is the same story repeating: adding $\hat{\imath}$s with $\hat{\imath}$s and $\hat{\jmath}$s with $\hat{\jmath}$s.
Examples
Vector addition example
You are heading to your physics class after a safety meeting with a friend and looking forward to two hours of amazement and absolute awe of the laws of Mother nature. As it turns out, there is no enlightenment to be had that day because there is going to be an in-class midterm. The first question you have to solve involves a block sliding down an incline. You look at it, draw a little diagram and then wonder how the hell you are going to find the net force acting on the block (this is what they are asking you to find). The three forces acting on the block are $\vec{W} = 30 \angle -90^{\circ} $, $\vec{N} = 200 \angle -290^{\circ} $ and $\vec{F}_f = 50 \angle 60^{\circ} $.
You happen to remember the formula: \[ \sum \vec{F} = \vec{F}_{net} = m\vec{a}. \qquad \text{[ Newton's \ 2nd law ]} \]
You get the feeling that this is the answer to all your troublems. You know that because the keyword “net force” that appeared in the question appears in this equation also.
The net force is simply the sum of all the forces acting on the block: \[ \vec{F}_{net} = \sum \vec{F} = \vec{W} + \vec{N} + \vec{F}_f. \]
All that separates you from the answer is the addition of these vectors. Vectors right. Vectors have components, and there is the whole sin cos thing for decomposing length and direction vectors in terms of their components. But can't you just add them together as arrows too? It is just a sum, of things right, should be simple.
OK, chill. Let's do this one step at a time. The net force must have and $x$-component which, according to the equation, must be equal to the sum of the $x$ components of all the forces: \[ \begin{align*} F_{net,x} & = W_x + N_x + F_{f,x} \nl & = 30\cos(-90^{\circ}) + 200\cos(-290^{\circ})+ 50\cos(60^{\circ}) \nl & = 93.4[\textrm{N}]. \end{align*} \] You find the $y$ component of the net force using the $\sin$ of the angles: \[ \begin{align*} F_{net,y} & = W_y + N_y + F_{f,y} \nl & = 30\sin(-90) + 200\sin(-290)+ 50\sin(60) \nl & = 201.2[\textrm{N}]. \end{align*} \]
Combining the two components of the victor, we get the final answer: \[ \vec{F}_{net} = (F_{net,x},F_{net,y}) =(93.4,201.2) =93.4 \hat{\imath} + 201.2 \hat{\jmath}. \] Bam! Just like that you are done because you overstand them mathematics. Nuh problem. What-a-di next question fi me?
Relative motion example
A boat can reach a top speed of 12 knots in calm seas. Instead of being in a calm sea, however, it is trying to sail up the St-Laurence river. The speed of the current is 5 knots.
If the boat goes directly upstream at full throttle 12$\vec{\imath}$, then the speed of the boat relative to the shore will be \[ 12\hat{\imath} - 5 \hat{\imath} = 7\hat{\imath}, \] since we have to “deduct” the speed of the current from the speed of the boat relative to the water.
 If the boat wants to cross the river perpendicular to
the current flow, then it can use some
of its thrust to counterbalance the current, and the other
part to push across.
What direction should the boat sail in so that it moves
in the across-the-river direction?
We are looking for the direction of $\vec{v}$ the boat
should take such that, after adding the current
component, the boat moves in a straight line
between the two banks (the $\hat{\jmath}$ direction).
If the boat wants to cross the river perpendicular to
the current flow, then it can use some
of its thrust to counterbalance the current, and the other
part to push across.
What direction should the boat sail in so that it moves
in the across-the-river direction?
We are looking for the direction of $\vec{v}$ the boat
should take such that, after adding the current
component, the boat moves in a straight line
between the two banks (the $\hat{\jmath}$ direction).
The geometrical picture is necessary so draw a river and a triangle in the river with the long side perpendicular to the current flow. Make the short side of length $5$ and the hypotenuse of length $12$. We will take the up-the-river component of the speed $\vec{v}$ to be equal to $5\hat{\imath}$ so that it cancels exactly the $-5\hat{\imath}$ flow of the river. We have also labeled the hypotenuse as 12 since this is the ultimate speed that the boat can have relative to the water.
From all of this we can answer the questions like professionals. You want the angle? OK, well we have that $12\sin(\theta)=5$, where $\theta$ is the angle of the boat's course relative to the straight line between the two banks. We can use the inverse-sin function to solve for the angle: \[ \theta = \sin^{-1}\!\left(\frac{5}{12} \right) = 24.62^\circ. \] The accross-the-river component speed can be calculated from $v_y = 12\cos(\theta)$, or from Pythagoras Theorem if you prefer $v_y = \sqrt{ \|\vec{v}\|^2 - v_x^2 } = \sqrt{ 12^2 - 5^2 }=10.91$.
Throughout this section we have used the $x$, $y$ and $z$ axes and described vectors as components along each of these directions. It is very convenient to have perpendicular axes like this, and a set of unit vectors pointing in each of the three directions like the vectors $\{\hat{\imath},\hat{\jmath},\hat{k}\}$.
More generally, we can express vectors in terms of any basis $\{ \hat{e}_1, \hat{e}_2, \hat{e}_3 \}$ for the space of three-dimensional vectors $\mathbb{R}^3$. What is a basis you ask? I am glad you asked, because it is a very important concept.
Set notation
A set is mathematically precise way to talk about different groups of objects. To do simple math, you don't need to know about sets, but for more advanced topics you need to know what a set is and how we denote set membership and subset relations between sets.
Definitions
- set: some collection of mathematical objects with a precise definition.
- $S,T$: usual variable names for sets.
- $\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}$: some important sets of numbers. These correspond to the naturals, the integers,
the rationals and the real numbers respectively.
- $\{ definition \}$: The curly brackets are used to surround the definition of a set and the expression inside is supposed
to completely describe what the set is.
NOINDENT Set operations:
- $S\cup T$: the union of two sets. The elements that are either in $S$ or $T$.
- $S \cap T$: the intersection of the two sets. The elements that are in both $S$ and $T$.
- $S \setminus T$: set minus. The elements of $S$ that are not in $T$.
NOINDENT Set relations:
- $\subset$: is a subset of.
- $\subseteq$: is subset or equal to.
NOINDENT Special mathematical shorthand and corresponding meaning in English:
- $\forall$: for all
- $\exists$: there exists
- $\nexists$: there doesn't exist
- $:$ or $|$: such that
- $\in$: is element of
- $\notin$: is not an element of
Sets
A lot of the power of math comes from abstraction: the ability to think meta thoughts and seeing the bigger picture about what math objects have in common. We can think of individual numbers like $3$, $5$ and $222$ or talk about the set of all numbers. You can think of functions like $f(x)=x$, and $f(x)=x^2$ or you can think of the set of all functions $f\colon \mathbb{R} \to \mathbb{R}$ that take real numbers as inputs and give real numbers as outputs.
Example 1: Non-negative numbers
Define $\mathbb{R}_+ \subset \mathbb{R}$ to be the set of non-negative real numbers: \[ \mathbb{R}_+ = \{ \text{all } x \text{ from } \mathbb{R} \text{ such that } x \geq 0 \}, \] or expressed more compactly: \[ \mathbb{R}_+ = \{ x \in \mathbb{R} \ | \ x \geq 0 \}. \]
Example 2: Odd and even
Define the set of even integers as: \[ E = \{ n \in \mathbb{Z} \ | \ \frac{n}{2} \in \mathbb{Z} \} = \{ \ldots, -2, 0, 2, 4, 6, \ldots \}. \] and the set of odd integers as: \[ O = \{ n \in \mathbb{Z} \ | \ \frac{n+1}{2} \in \mathbb{Z} \} = \{ \ldots, -3, -1, 1, 3, 5, \ldots \}. \] In each case the mathematical notation $\{ \ldots \ | \ \ldots \}$ follows the same pattern where you first say what kind of objects we are talking about, followed by the “such that” sign $|$ followed by the conditions which must be satisfied by all elements of the set.
Important sets
The natural numbers are the set of number you can get by starting from $0$ and adding $1$ arbitraryly many times: \[ \mathbb{N} \equiv \{ 0, 1, 2, 3, 4, \ldots \}. \] The integers are the number you get by adding or subtracting 1 arbitrary many times: \[ \mathbb{Z} \equiv \{ \ldots, -3, -2, -1, 0, 1, 2, 3, 4, \ldots \}. \] If you allow for divisions between integers, you get the rational numbers: \[ \mathbb{Q} = \{ -1.5, 1/3, 22/7, 0.125, \ldots \}. \] The more general class of real numbers includes also irrational numbers: \[ \mathbb{R} = \{\pi, e, -1.53929411..,\ 4.99401940129401.., \ \ldots \}. \] Finally we have the set of complex numbers: \[ \mathbb{C} = \{ 1, i, 1+i, 2+3i, \ldots \}= \{ a + bi \ | \ a,b \in \mathbb{R}, i^2=-1 \}. \]
Note the inclusion relationship which holds for these sets: \[ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}. \] Every natural number is also an integer. Every integer is a rational number. Every rational number is a real. Every real number is also a complex number.
New vocabulary
Let's practice the new vocabulary by looking at a simple mathematical proof.
Square-root of two is irrational
Claim: $\sqrt{2} \notin \mathbb{Q}$. This means that there are no integers $m \in \mathbb{Z}$ and $n \in \mathbb{N}$ such that $m/n = \sqrt{2}$. The same sentence in mathematical notation would read: \[ \nexists m \in \mathbb{Z}, n\in\mathbb{N} \ | \ m/n = \sqrt{2}. \]
Proof: Suppose for a contradiction that there existed $m$ and $n$ such that $m/n=\sqrt{2}$. We can further assume that integers $m$ and $n$ are such that they have no common factors: we can always make sure this is the case if we cancel the common factors. In particular this implies that $m$ and $n$ cannot both be even since we would be able to cancel at least one factor of two. We therefore have $\textrm{gcd}(m,n)=1$: the their greatest common divisor is $1$. We will now investigate a simple question which is whether $m$ is an even number $m\in E$ or $m$ is an odd number $m \in O$.
Before we begin, lemme point out the fact that the action of squaring an integers preserves its odd/even nature. Indeed, an even number times an even number gives and even number: if $e \in E$ then $e^2 \in E$. Also an odd number times an odd number also gives an odd number: if $o \in O$ then $o^2 \in O$.
The proof proceeds as follows. We assumed that $m/n = \sqrt{2}$, so if we take the square of this equation we have: \[ \frac{m^2}{n^2} = 2, \qquad m^2 = 2n^2. \] If $m$ is an odd number then $m^2$ is also going to be odd, which contradicts the above equation since we see that $m^2$ “contains” a factor $2$, so $m \notin O$. If $m$ is even then $m^2$ is also an even number, so it can be written as $m=2q$ for some other number $q\in \mathbb{Z}$. The equation would then become: \[ 2^2 q^2 = 2 n^2 \quad \Rightarrow \quad 2 q^2 = n^2. \] This implies that $n \in E$ which leads to a contradiction with the fact that we said $m$ and $n$ cannot both be even. Therefore $m \notin E$, and since $m \notin O$ either, this means that there is no such $m \in \mathbb{Z}$ and therefore $\sqrt{2}$ is irrational.
Set relations and operations
We say that $B \subset A$ if $\forall b \in B$ we also have $b \in A$, and $\exists a \in A$, such that $a \notin B$. We say “$B$ is strictly contained in $A$” which is illustrated graphically in the figure below. Also illustrated in the figure is the union of two sets $A \cup B$ which includes all the elements of $A$ and $B$. We have $e \in A \cup B$, if and only if $e \in A$ or $e \in B$.
The set intersection is $A \cap B$ and set minus $A \setminus B$ are shown below.
Sets related to functions
The set of all functions of a real variable, that return a real variable is denoted: \[ f : \mathbb{R} \to \mathbb{R}. \]
The domain of a function is the set of all possible inputs. An input is not possible if the function is not defined for that input, like in the case of a “divide by zero” error.
The image set of a function is the set of all possible outputs of the function: \[ \textrm{Im}(f) = \{ y \in \mathbb{R} \ | \ \exists x\in\mathbb{R},\ y=f(x) \}. \]
Discussion
Knowledge of the precise mathematical jargon introduced in this section is not crucial to the rest of this book, but I wanted to expose you to it because this is the language in which mathematicians think. Most advanced math textbooks will take it for granted that you understand this kind of notation.
Vector spaces
We will now discuss no vector in particular, but rather the set of all possible vectors. In three dimensions this is the space $(\mathbb{R},\mathbb{R},\mathbb{R}) \equiv \mathbb{R}^3$. We will also discuss vector subspaces of $\mathbb{R}^3$ like lines and planes thought the origin.
In this section we develop the vocabulary needed to talk about vector spaces. Using this language will allow us to say some interesting things about matrices. We will formally define the fundamental subspaces for a matrix $A$: the column space $\mathcal{C}(A)$, the row space $\mathcal{R}(A)$, and the null space $\mathcal{N}(A)$.
Definitions
Vector space
A vector space $V \subseteq \mathbb{R}^n$ consists of a set of vectors and all possible linear combinations of these vectors. The notion of all possible linear combinations is very powerful. In particular it has the following two useful properties. We say that vector spaces are closed under addition, which means the sum of any two vectors taken from the vector space is a vector in the vector space. Mathematically, we write: \[ \vec{v}_1+\vec{v}_2 \in V, \qquad \forall \vec{v}_1, \vec{v}_2 \in V. \] A vector space is also closed under scalar multiplication: \[ \alpha \vec{v} \in V, \qquad \forall \alpha \in \mathbb{R},\ \vec{v} \in V. \]
Span
Given a vector $\vec{v}_1$, we can define the following vector space: \[ V_1 = \textrm{span}\{ \vec{v}_1 \} \equiv \{ \vec{v} \in V \ | \vec{v} = \alpha \vec{v}_1 \textrm{ for some } \alpha \in \mathbb{R} \}. \] We say $V_1$ is the space spanned by $\vec{v}_1$ which means that it is the set of all possible multiples of $\vec{v}_1$. The shape of $V_1$ is an infinite line.
Given two vectors $\vec{v}_1$ and $\vec{v}_2$ we can define a vector space: \[ V_{12} = \textrm{span}\{ \vec{v}_1, \vec{v}_2 \} \equiv \{ \vec{v} \in V \ | \vec{v} = \alpha \vec{v}_1 + \beta\vec{v}_2 \textrm{ for some } \alpha,\beta \in \mathbb{R} \}. \] The vector space $V_{12}$ contains all vectors that can be written as a linear combination of $\vec{v}_1$ and $\vec{v}_2$. This is a two-dimensional vector space which has the shape of an infinite plane.
Note that the same space $V_{12}$ can be obtained as the span of different vectors: $V_{12} = \textrm{span}\{ \vec{v}_1, \vec{v}_{2^\prime} \}$, where $\vec{v}_{2^\prime} = \vec{v}_2 + 30\vec{v}_1$. Indeed, $V_{12}$ can be written as the span of any two linearly independent vectors contained in $V_{12}$. This is precisely what is cool about vector spaces: you can talk about the space as a whole without necessarily having to talk about the vectors in it.
As a special case, consider the the situation when $\vec{v}_1 = \gamma\vec{v}_2$, for some $\gamma \in \mathbb{R}$. In this case, the vector space $V_{12} = \textrm{span}\{ \vec{v}_1, \vec{v}_2 \}=\textrm{span}\{ \vec{v}_1 \}$ is actually one-dimensional since $\vec{v}_2$ can be written as a multiple of $\vec{v}_1$.
Vector subspaces
A subset $W$ of the vector space $V$ is called a subspace if:
- It is closed under addition: $\vec{w}_1 + \vec{w}_2 \in W$, for all $\vec{w}_1,\vec{w}_2 \in W$.
- It is closed under scalar multiplication: $\alpha \vec{w} \in W$, for all $\vec{w} \in W$.
This means that if you take any linear combination of vectors in $W$, the result will also be a vector in $W$. We use the notation $W \subseteq V$ to indicate that $W$ is a subspace of $V$.
An important fact about subspaces is that they always contains the zero vector $\vec{0}$. This is implied by the second property, since any vector becomes the zero vector when multiplied by the scalar $\alpha=0$: $\alpha \vec{w} = \vec{0}$.
Constraints
One way to define a vector subspace $W$ is to start with a larger space $(x,y,z) \in V$ and describe the a set of constraints that must be satisfied by all points $(x,y,z)$ in the subspace $W$. For example, the $xy$-plane can be defined as the set points $(x,y,z) \in \mathbb{R}^3$ that satisfy \[ (0,0,1) \cdot (x,y,z) = 0. \] More formally, we define the $xy$-plane as follows: \[ P_{xy} = \{ (x,y,z) \in \mathbb{R}^3 \ | \ (0,0,1) \cdot (x,y,z) = 0 \}. \] The vector $\hat{k}\equiv(0,0,1)$ is perpendicular to all the vectors that lie in the $xy$-plane so another description for the $xy$-plane is “the set of all vectors perpendicular to the vector $\hat{k}$.” In this definition, the parent space is $V=\mathbb{R}^3$, and the subspace $P_{xy}$ is defined as the set of points that satisfy the constraint $(0,0,1) \cdot (x,y,z) = 0$.
Another way to represent the $xy$-plane would be to describe it as the span of two linearly independent vectors in the plane: \[ P_{xy} = \textrm{span}\{ (1,0,0), (1,1,0) \}, \] which is equivalent to saying: \[ P_{xy} = \{ \vec{v} \in \mathbb{R}^3 \ | \ \vec{v} = \alpha (1,0,0) + \beta(1,1,0), \forall \alpha,\beta \in \mathbb{R} \}. \] This last expression is called an explicit parametrization of the space $P_{xy}$ and $\alpha$ and $\beta$ are the two parameters. There corresponds a unique pair $(\alpha,\beta)$ for each point in the plane. The explicit parametrization of an $m$-dimensional vector space requires $m$ parameters.
Matrix subspaces
Consider the following subspaces which are associated with a matrix $M \in \mathbb{R}^{m\times n}$. These are sometiemes referred to as the fundamental subspaces of the matrix $M$.
- The row space $\mathcal{R}(M)$ is the span of the rows of the matrix.
Note that computing a given linear combination of the rows of a matrix can be
done by multiplying the matrix //on the left// with an $m$-vector:
\[
\mathcal{R}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \ | \ \vec{v} = \vec{w}^T M \textrm{ for some } \vec{w} \in \mathbb{R}^{m} \},
\]
where we used the transpose $T$ to make $\vec{w}$ into a row vector.
* The null space $\mathcal{N}(M)$ of a matrix $M \in \mathbb{R}^{m\times n}$
consists of all the vectors that the matrix $M$ sends to the zero vector:
\[
\mathcal{N}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \ | \ M\vec{v} = \vec{0} \}.
\]
The null space is also known as the //kernel// of the matrix.
* The column space $\mathcal{C}(M)$ is the span of the columns of the matrix.
The column space consist of all the possible output vectors that the matrix can produce
when multiplied by a vector on the right:
\[
\mathcal{C}(M) \equiv \{ \vec{w} \in \mathbb{R}^m
\ | \
\vec{w} = M\vec{v} \textrm{ for some } \vec{v} \in \mathbb{R}^{n} \}.
\]
* The left null space $\mathcal{N}(M^T)$ which is the null space of the matrix $M^T$.
We say //left// null space,
because this is the null space of vectors when multiplying the matrix by a vector on the left:
\[
\mathcal{N}(M^T) \equiv \{ \vec{w} \in \mathbb{R}^m \ | \ \vec{w}^T M = \vec{0}^T \}.
\]
The notation $\mathcal{N}(M^T)$ is suggestive of the fact that we can
rewrite the condition $\vec{w}^T M = \vec{0}^T$ as $M^T\vec{w} = \vec{0}^T$.
Hence the left null space of $A$ is equivalent to the null space of $A^T$.
The left null space consists of all the vectors $\vec{w} \in \mathbb{R}^m$
that are orthogonal to the columns of $A$.
The matrix-vector product $M \vec{x}$ can be thought of as the action of a vector function (a linear transformation $T_M:\mathbb{R}^n \to \mathbb{R}^m$) on an input vector $\vec{x}$. The columns space $\mathcal{C}(M)$ plays the role of the image of the linear transformation $T_M$, and the null space $\mathcal{N}(M)$ is the set of zeros (roots) of the function $T_M$. The row space $\mathcal{R}(M)$ is the pre-image of the column space $\mathcal{C}(M)$. To every point in $\mathcal{R}(M)$ (input vector) corresponds one point (output vector) in $\mathcal{C}(M)$. This means the column space and the rows space must have the same dimension. We call this dimension the rank of the matrix $M$: \[ \textrm{rank}(M) = \dim\left(\mathcal{R}(M) \right) = \dim\left(\mathcal{C}(M) \right). \] The rank is the number of linearly independent rows, which is also equal to the number of independent columns.
We can characterize the domain of $M$ (the space of $n$-vectors) as the orthogonal sum ($\oplus$) of the row space and the null space: \[ \mathbb{R}^n = \mathcal{R}(M) \oplus \mathcal{N}(M). \] Basically a vector either has non-zero product with at least one of the rows of $M$ or it has zero product with all of them. In the latter case, the output will be the zero vector – which means that the input vector was in the null space.
If we think of the dimensions involved in the above equation: \[ \dim(\mathbb{R}^n) = \dim(\mathcal{R}(M)) + \dim( \mathcal{N}(M)), \] we obtain an important fact: \[ n = \textrm{rank}(M) + \dim( \mathcal{N}(M)), \] where $\dim( \mathcal{N}(M))$ is called the nullity of $M$.
Linear independence
The set of vectors $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n \}$ is linear independent if the only solution to the equation \[ \sum\limits_i\lambda_i\vec{v}_i= \lambda_1\vec{v}_1 + \lambda_2\vec{v}_2 + \cdots + \lambda_n\vec{v}_n = \vec{0} \] is $\lambda_i=0$ for all $i$.
The above condition guarantees that none of the vectors can be written as a linear combination of the other vectors. To understand the importance of the “all zeros” solutions, let's consider an example where a non-zero solution exists. Suppose we have a set of three vectors $\{\vec{v}_1, \vec{v}_2, \vec{v}_3 \}$ which satisfy $\lambda_1\vec{v}_1 + \lambda_2\vec{v}_2 + \lambda_3\vec{v}_3 = 0$ with $\lambda_1=-1$, $\lambda_2=1$, and $\lambda_3=2$. This means that \[ \vec{v}_1 = 1\vec{v}_2 + 2\vec{v}_3, \] which shows that $\vec{v}_1$ can be written as a linear combination of $\vec{v}_2$ and $\vec{v}_3$, hence the vectors are not linearly independent.
Basis
In order to carry out calculations with vectors in a vector space $V$, we need to know a basis $B=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ for that space. A basis for an $n$-dimensional vector space $V$ is a set of $n$ linearly independent vectors in $V$. Intuitively, a basis is a set of vectors that can be used as a coordinate system for a vector space.
A basis $B=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ for the vector space $V$ has the following two properties:
- Spanning property.
Any vector $\vec{v} \in V$ can be expressed as a linear combination of the basis elements:
\[
\vec{v} = v_1\vec{e}_1 + v_2\vec{e}_2 + \cdots + v_n\vec{e}_n.
\]
This property guarantees that the vectors in the basis $B$ are //sufficient// to represent any vector in $V$.
* **Linear independence property**.
The vectors that form the basis $B = \{ \vec{e}_1,\vec{e}_2, \ldots, \vec{e}_n \}$ are linearly independent.
The linear independence of the vectors in the basis guarantees that none of the vectors $\vec{e}_i$ is redundant.
If a set of vectors $B=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ satisfies both properties, we say $B$ is a basis for $V$. In other words $B$ can serve as a coordinate system for $V$. Using the basis $B$, we can represent any vector $\vec{v} \in V$ as a unique tuple of coordinates \[ \vec{v} = v_1\vec{e}_1 + v_2\vec{e}_2 + \cdots + v_n\vec{e}_n \qquad \Leftrightarrow \qquad (v_1,v_2, \ldots, v_n)_B. \] The coordinates of $\vec{v}$ are calculated with respect to the basis $B$.
The dimension of a vector space is defined as the number of vectors in a basis for that vector space. A basis for an $n$-dimensional vector space contains exactly $n$ vectors. Any set of less than $n$ vectors would not satisfy the spanning property. Any set of with more than $n$ vectors from $V$ cannot be linearly independent. To form a basis for a vector space, the set of vectors must be “just right”: it must contain a sufficient number of vectors but not too many so that the coefficients of each vector will be uniquely determined.
Distilling a basis
A basis for an $n$-dimensional vector space $V$ consist of exactly $n$ vectors. Any set of vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ can serve as a basis as long as they are linearly independent and there is exactly $n$ of them.
Sometimes an $n$-dimensional vector space $V$ will be specified as the span of more than $n$ vectors: \[ V = \textrm{span}\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}, \quad m > n. \] Since there are $m>n$ of the $\vec{v}$-vectors, they are too many to form a basis. We say this set of vectors is over-complete. They cannot all be linearly independent since there can be at most $n$ linearly independent vectors in an $n$-dimensional vector space.
If we want to have a basis for the space $V$, we'll have to reject some of the vectors. Given the set of vectors $\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}$, our task is to distill a set of $n$ linearly indecent vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ from them.
We can use the Gauss–Jordan elimination procedure to distil a set of linearly independent vectors. Actually, you know how to do this already! You can write the set of $m$ vectors as the rows of a matrix and then do row operations on this matrix until you find the reduced row echelon form. Since row operations do not change the row space of the matrix, there will be $n$ non-zero rows of the final RREF of the matrix which form a basis for $V$. We will learn more about this procedure in the next section.
Examples
Example 1
Describe the set of vectors which are perpendicular to the vector $(0,0,1)$ in $\mathbb{R}^3$.
Sol: We need to find all the vectors $(x,y,z)$ such that $(x,y,z)\cdot (0,0,1) = 0$.
By inspection we see that whatever choice of $x$ and $y$ components we choose will
work so we say that the set of vectors perpendicular to
$(0,0,1)$ is $\textrm{span}\{ (1,0,0), (0,1,0) \}$.