The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Functions
Your function vocabulary determines how well you will be able to express yourself mathematically in the same way that your English vocabulary determines how well you can express yourself in English.
The purpose of the following pages is to embiggen your vocabulary a bit so you won't be caught with your pants down when the teacher tries to pull some trick on you at the final. I give you the minimum necessary, but I recommend you explore these functions on your own via wikipedia and by plotting their graphs on Wolfram alpha.
To “know” a function you have to understand and connect several different aspects of the function. First you have to know its mathematical properties (what does it do, what is its inverse) and at the same time have a good idea of its graph, i.e., what it looks like if you plot $x$ versus $f(x)$ in the Cartesian plane. It is also really good idea if you can remember the function values for some important inputs.
Definition
A function is a mathematical object that takes inputs and gives outputs. We use the notation \[ f \colon X \to Y, \] to denote a functions from the set $X$ to the set $Y$. In this book, we will study mostly functions which take real numbers as inputs and give real numbers as outputs: $f\colon\mathbb{R} \to \mathbb{R}$.
We now define some technical terms used to describe the input and output sets.
- The domain of a function is the set of allowed input values.
- The image or range of the function $f$ is the set of all possible
output values of the function.
- The codomain of a function is the type of outputs that the functions has.
To illustrate the subtle difference between the image of a function and its codomain, let us consider the function $f(x)=x^2$. The quadratic function is of the form $f\colon\mathbb{R} \to \mathbb{R}$. The domain is $\mathbb{R}$ (it takes real numbers as inputs) and the codomain is $\mathbb{R}$ (the outputs are real numbers too), however, not all outputs are possible. Indeed, the image the function $f$ consists only of the positive numbers $\mathbb{R}_+$. Note that the word “range” is also sometimes used refer to the function codomain.
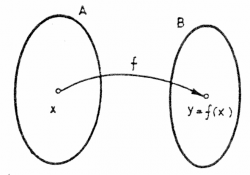
A function is not a number, it is a mapping from numbers to numbers. If you specify a given $x$ as input, we denote as $f(x)$ is the output value of $f$ for that input. Here is a graphical representation of a function with domain $A$ and codomain $B$.
The function corresponds to the arrow in the above picture.
We say that “$f$ maps $x$ to $y=f(x)$” and use the following terminology to classify the type of mapping that a function performs:
- A function is one-to-one or injective if it maps different inputs to different outputs.
- A function is onto or surjective if it covers the entire output set,
i.e., if the image of the function is equal to the function codomain.
- A function is bijective if it is both injective and surjective.
In this case $f$ is a one-to-one correspondence between the input
set and the output set: for each input of the possible outputs $y \in Y$ there exists (surjective part) exactly one input $x \in X$, such that $f(x)=y$ (injective part).
The term injective is a 1940s allusion inviting us to think of injective functions as some form of fluid flow. Since fluids cannot be compressed, the output space must be at least as large as the input space. A modern synonym for injective functions is to say that they are two-to-two. If you imagine two specks of paint inserted somewhere in the “input fluid”, then an injective function will lead to two distinct specks of paint in the “output fluid.” In contrast, functions which are not injective could map several different inputs to the same output. For example $f(x)=x^2$ is not injective since the inputs $2$ and $-2$ both get mapped to output value $4$.
Function names
Mathematicians have defined symbols $+$, $-$, $\times$ (usually omitted) and $\div$ (usually denoted as a fraction) for most important functions used in everyday life. We also use the weird surd notation to denote $n$th root $\sqrt[n]{\ }$ and the superscript notation to denote exponents. All other functions are identified and used by their name. If I want to compute the cosine of the angle $60^\circ$ (a function which describes the ratio between the length of one side of a right-angle triangle and the hypotenuse), then I would write $\cos(60^\circ)$, which means that we want the value of the $\cos$ function for the input $60^\circ$.
Incidentally, for that specific angle the function $\cos$ has a nice value: $\cos(60^\circ)=\frac{1}{2}$. This means that seeing $\cos(60^\circ)$ somewhere in an equation is the same as seeing $0.5$ there. For other values of the function like say $\cos(33.13^\circ)$, you will need to use a calculator. A scientific calculator will have a $\cos$ button on it for that purpose.
Handles on functions
When you learn about functions you learn about different “handles” onto these mathematical objects. Most often you will have the function equation, which is a precise way to calculate the output when you know the input. This is an important handle, especially when you will be doing arithmetic, but it is much more important to “feel” the function.
How do you get a feel for some function?
One way is to look at list of input-output pairs $\{ \{ \text{input}=x_1, \text{output}=f(x_1) \},$ $\{ \text{input}=x_2,$ $\text{output}=f(x_2) \},$ $\{ \text{input}=x_3, \text{output}=f(x_3) \}, \ldots \}$. A more compact notation for the input-output pairs $\{ (x_1,f(x_1)),$ $(x_2,f(x_2)),$ $(x_3,f(x_3)), \ldots \}$. You can make a little table of values for yourself, pick some random inputs and record the output of the function in the second column: \[ \begin{align*} \textrm{input}=x \qquad &\rightarrow \qquad f(x)=\textrm{output} \nl 0 \qquad &\rightarrow \qquad f(0) \nl 1 \qquad &\rightarrow \qquad f(1) \nl 55 \qquad &\rightarrow \qquad f(55) \nl x_4 \qquad &\rightarrow \qquad f(x_4) \end{align*} \]
Apart from random numbers it is also generally a good idea to check the value of the function at $x=0$, $x=1$, $x=100$, $x=-1$ and any other important looking $x$ value.
One of the best ways to feel a function is to look at its graph.
A graph is a line on a piece of paper that passes through all input-output
pairs of the function.
What? What line? What points?
Ok let's backtrack a little.
Imagine that you have a piece of paper you have drawn
a coordinate system on the paper.
The horizontal axis will be used to measure $x$, this is also called the abscissa. The vertical axis will be used to measure $f(x)$, but because writing out $f(x)$ all the time is long and tedious, we will invent a short single-letter alias to denote the output value of $f$ as follows: \[ y \equiv f(x) = \text{output}. \]
Now you can take each of the input-output pairs for the function $f$ and think of them as points $(x,y)$ in the coordinate system. Thus the graph of a function is a graphical representation of everything the function does. If you understand the simple “drawing” on this page, you will basically understand everything there is to know about the function.
Another way to feel functions is through the properties of the function: either the way it is defined, or its relation to other functions. This boils down to memorizing facts about the function and its relations to other functions. An example of a mathematical fact is $\sin(30^\circ)=\frac{1}{2}$. An example of a mathematical relation is the equation $\sin^2 x + \cos^2 x =1$, which is a link between the $\sin$ and the $\cos$ functions.
The last part may sound contrary to my initial promise about the book saying that I will not make you memorize stuff for nothing. Well, this is not for nothing. The more you know about any function, the more “paths” you have in your brain that connect to that function. Real math knowledge is not memorization but an establishment of a graph of associations between different areas of knowledge in your brain. Each concept is a node in this graph, and each fact you know about this concept is an edge in the graph. Analytical thought is the usage of this graph to produce calculations and mathematical arguments (proofs). For example, knowing the fact $\sin(30^\circ)=\frac{1}{2}$ about $\sin$ and the relationship $\sin^2 x + \cos^2 x = 1$ between $\sin$ and $\cos$, you could show that $\cos(30^\circ)=\frac{\sqrt{3}}{2}$. Note that the notation $\sin^2(x)$ means $(\sin(x))^2$.
To develop mathematical skills, it is therefore important to practice this path-building between related concepts by solving exercises and reading and writing mathematical proofs. My textbook can only show you the paths between the concepts, it is up to you to practice the exercises in the back of each chapter to develop the actual skills.
Example: Quadratic function
Consider the function from the real numbers ($\mathbb{R}$) to the real numbers ($\mathbb{R}$) \[ f \colon \mathbb{R} \to \mathbb{R} \] given by \[ f(x)=x^2+2x+3. \] The value of $f$ when $x=1$ is $f(1)=1^2+2(1)+3=1+2+3=6$. When $x=2$, we have $f(2)=2^2+2(2)+3=4+4+3=11$. What is the value of $f$ when $x=0$?
Example: Exponential function
Consider the exponential function with base two: \[ f(x) = 2^x. \] This function is of crucial importance in computer systems. When $x=1$, $f(1)=2^1=2$. When $x$ is 2 we have $f(2)=2^2=4$. The function is therefore described by the following input-output pairs: $(0,1)$, $(1,2)$, $(2,4)$, $(3,8)$, $(4,16)$, $(5,32)$, $(6,64)$, $(7,128)$, $(8,256)$, $(9,512)$, $(10,1024)$, $(11, 2048)$, $(12,4096)$, etc. (RAM memory chips come in powers of two because the memory space is exponential in the number of “address lines” on the chip.) Some important input-output pairs for the exponential function are $(0,1)$, because by definition any number to the power 0 is equal to 1, and $(-1,\frac{1}{2^1}=\frac{1}{2}), (-2,\frac{1}{2^2}=\frac{1}{4}$), because negative exponents tells you that you should dividing by that number this many times instead of multiplying.
Function inverse
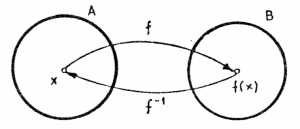 Recall that a bijective function is a one-to-one correspondence between
the set of inputs and the set of output values.
If $f$ is a bijective function, then there exists an inverse function $f^{-1}$,
which performs the inverse mapping of $f$.
Thus, if you start from some $x$, apply $f$ and then apply $f^{-1}$,
you will get back to the original input $x$:
\[
x = f^{-1}\!\left( \; f(x) \; \right).
\]
This is represented graphically in the diagram on the right.
Recall that a bijective function is a one-to-one correspondence between
the set of inputs and the set of output values.
If $f$ is a bijective function, then there exists an inverse function $f^{-1}$,
which performs the inverse mapping of $f$.
Thus, if you start from some $x$, apply $f$ and then apply $f^{-1}$,
you will get back to the original input $x$:
\[
x = f^{-1}\!\left( \; f(x) \; \right).
\]
This is represented graphically in the diagram on the right.
Function composition
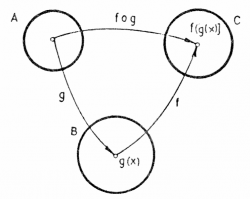 We can combine two simple functions to build a more complicated function
by chaining them together.
The resulting function is denoted
\[
z = f\!\circ\!g \, (x) \equiv z = f\!\left( \: g(x) \: \right).
\]
We can combine two simple functions to build a more complicated function
by chaining them together.
The resulting function is denoted
\[
z = f\!\circ\!g \, (x) \equiv z = f\!\left( \: g(x) \: \right).
\]
The diagram on the left shows a function $g:A\to B$ acting on some input $x$ to produce an intermediary value $y \in B$, which is then input to the function $f:B \to C$ to produce the final output value $z = f(y) = f(g(x))$.
The composition of applying $g$ first followed by $f$ is a function of the form: $f\circ g: A \to C$ defined through the equation $f\circ g(x) = f(g(x))$. Note that “first” in the context of function composition means the first to first to touch the input.
Discussion
In the next sections, we will look into the different functions that you will be dealing with. What we present here is far from and exhaustive list, but if you get a hold of these ones, you will be able to solve any problem a teacher can throw at you.
Links
[ Tank game where you specify the function of the projectile trajectory ]
http://www.graphwar.com/play.html
NOINDENT
[ Gallery of function graphs ]
http://mpmath.googlecode.com/svn/gallery/gallery.html