We now begin our discussion of integrals, which is the second topic in calculus. Integrals are a fancy way to add up the value of a function to get “the whole” or the sum of its values over some interval. Normally integral calculus is taught as a separate course after differential calculus, but this separation is not necessary and can be even counter-productive.

The derivative $f'(x)$ measures the change in $f(x)$, i.e., the derivative measures the differences in $f$ for an $\epsilon$-small change in the input variable $x$: \[ \text{derivative } \ \propto \ \ f(x+\epsilon)-f(x). \] Integrals, on the other hand, measure the sum of the values of $f$, between $a$ and $b$ at regular intervals of $\epsilon$: \[ \text{integral } \propto \ \ \ f(a) + f(a+\epsilon) + f(a+2\epsilon) + \ldots + f(b-2\epsilon) + f(b-\epsilon). \] The best way to understand integration is to think of it as the opposite operation of differentiation: adding up all the changes in function gives you the function value.

In Calculus I we learned how to take a function $f(x)$ and find its derivative $f'(x)$. In integral calculus, we will be given a function $f(x)$ and we will be asked to find its integral on various intervals.

These are some concepts that you should already be familiar with:

• $\mathbb{R}$: The set of real numbers.
• $f(x)$: A function:

\[ f: \mathbb{R} \to \mathbb{R}, \]

  which means that $f$ takes as input some number (usually we call that number $x$)
  and it produces as an output another number $f(x)$ (sometimes we also give an alias for the output $y=f(x)$).
* $\lim_{\epsilon \to 0}$: limits are the mathematically rigorous
  way of speaking about very small numbers.
* $f'(x)$: the derivative of $f(x)$ is the rate of change of $f$ at $x$:
  \[
f'(x) = \lim_{\epsilon \to 0} \frac{f(x+\epsilon)\ - \ f(x)}{\epsilon}.
  \]
  The derivative is also a function of the form
  \[
     f': \mathbb{R} \to \mathbb{R}.
  \]
  The function $f'(x)$ represents the //slope// of
  the function $f(x)$ at the point $(x,f(x))$.

NOINDENT These are the new concepts:

• $x_i=a$: where the integral starts, i.e., some given point on the $x$ axis.
• $x_f=b$: where the integral stops.
• $A(x_i,x_f)$: The value of the area under the curve $f(x)$ from $x=x_i$ to $x=x_f$.
• $\int f(x)\; dx$: the integral of $f(x)$.

More precisely we can define the antiderivative of $f(x)$ as follows:

  \[
     F(b) = \int_0^b f(x) dx \ \ + \ \ F(0).
  \]
  The area $A$ of the region under $f(x)$ from $x=a$ to $x=b$ is given by:
  \[
      \int_a^b f(x) dx = F(b) - F(a) = A(a,b).
  \]
  The $\int$ sign is a mnemonic for //sum//.
  Indeed the integral is nothing more than the "sum" of $f(x)$ for all values of $x$ between $a$ and $b$:
  \[ 
   A(a,b) = \lim_{\epsilon \to 0}\left[ \epsilon f(a) + \epsilon f(a+\epsilon) + \ldots + \epsilon f(b-2\epsilon) + \epsilon f(b-\epsilon) \right],
  \]
  where we imagine the total area broken-up into thin rectangular 
  strips of width $\epsilon$ and height $f(x)$. 
* The name antiderivative comes from the fact that
  \[
     F'(x) = f(x),
  \]
  so we have:
  \[
   F(x) \!= \text{int}\!\left( \text{diff}( F(x) ) \right)= \int_0^x \left( \frac{d}{dt} F(t) \right) \ dt = \int_0^x \! f'(t) \ dt = F(x).
  \]
  Indeed, the //fundamental theorem of calculus//,
  tells us that the derivative and integral are //inverse operations//,
  so we also have:
  \[
   f(x) \!= \text{diff}\!\left(  \text{int}( f(x)  ) \right)
   = \frac{d}{dx}\left[\int_0^x f(t) dt\right]
   = \frac{d}{dx}\left[ F(x) - F(0) \right]
   = f(x).
  \]     

The Riemann sum is a good way to define the integral from first principles. We will brake up the area under the curve into many little strips of height varying according to $f(x)$. To obtain the total area, we sum-up all the areas of the rectangles. We will discuss Riemann sums in the next section, but first we look at the properties of integrals.

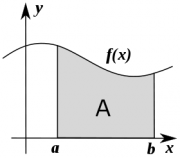The value of an integral corresponds to the area $A$, under the curve $f(x)$ between $x=a$ and $x=b$: \[ A(a,b) = \int_a^b f(x) \; dx. \]

For certain functions it is possible to find an anti-derivative function $F(\tau)$, which describes the “running total” of the area under the curve starting from some arbitrary left endpoint and going all the way until $t=\tau$. We can compute the area under $f(t)$ between $a$ and $b$ by looking at the change in $F(\tau)$ between $a$ and $b$. \[ A(a,b) = F(b) - F(a). \]

We can illustrate the reasoning behind the above formula graphically: 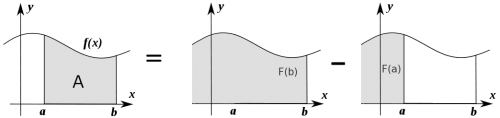The area $A(a,b)$ is equal to the “running total” until $x=b$ minus the running total until $x=a$.

The problem of finding the anti-derivative is also called integration. We say that we are finding an indefinite integral, because we haven't defined the limits $x_i$ and $x_f$.

So an integration problem is one in which you are given the $f(x)$, and you have to find the function $F(x)$. For example, if $f(x)=3x^2$, then $F(x)=x^3$. This is called “finding the integral of $f(x)$”.

A definite integral specifies the function to integrate as well as the limits of integration $x_i$ and $x_f$: \[ \int_{x_i=a}^{x_f=b} f(x) \; dx = \int_{a}^{b} f(x) \; dx. \]

To find the value of the definite integral first calculate the indefinite integral (the antiderivative): \[ F(x) = \int f(x)\; dx, \] and then use it to compute the area as the difference of $F(x)$ at the two endpoints: \[ A(a,b) = \int_{x=a}^{x=b} f(x) \; dx = F(b) - F(a) \equiv F(x)\bigg|_{x=a}^{x=b}. \]

Note the new “vertical bar” notation: $g(x)\big\vert_{\alpha}^\beta=g(\beta)-g(\alpha)$, which is shorthand notation to denote the expression to the left evaluated at the top limit minus the same expression evaluated at the bottom limit.

What is the value of the integral $\int_a^b x^2 \ dx$? We have \[ \int_a^b x^2 dx = \frac{1}{3}x^3\bigg|_{x=a}^{x=b} = \frac{1}{3}(b^3-a^3). \]

If $a < b$ and $f(x) > 0$, then the area \[ A(a,b) = \int_{a}^{b} f(x) \ dx, \] will be positive.

However if we swap the limits of integration, in other words we start at $x=b$ and integrate backwards all the way to $x=a$, then the area under the curve will be negative! This is because $dx$ will always consist of tiny negative steps. Thus we have that: \[ A(b,a) = \int_{b}^{a} f(x) \ dx = - \int_{a}^{b} f(x) \ dx = - A(a,b). \] In all expressions involving integrals, if you want to swap the limits of integration, you have to add a negative sign in front of the integral.

The area could also come out negative if we integrate a negative function from $a$ to $b$. In general, if $f(x)$ is above the $x$ axis in some places these will be positive contributions to the total area under the curve, and places where $f(x)$ is below the $x$ axis will count as negative contributions to the total area $A(a,b)$.

The integral from $a$ to $b$ plus the integral from $b$ to $c$ is equal to the integral from $a$ to $c$: \[ A(a,b) + A(b,c) = \int_a^b f(x) \; dx + \int_b^c f(x) \; dx = \int_a^c f(x) \; dx = A(a,c). \]

Integration is a linear operation: \[ \int [\alpha f(x) + \beta g(x)]\; dx = \alpha \int f(x)\; dx + \beta \int g(x)\; dx, \] for arbitrary constants $\alpha, \beta$.

Recall that this was true for differentiation: \[ [\alpha f(x) + \beta g(x)]' = \alpha f'(x) + \beta g'(x), \] so we can say that the operations of calculus as a whole are linear operations.

So far we have looked only at definite integrals where the limits of integration were constants $x_i=a$ and $x_f=b$, and so the integral was a number $A(a,b)$.

More generally, we can have one (or more) variable integration limits. For example we can have $x_i=a$ and $x_f=x$. Recall that area under the curve $f(x)$ is, by definition, computed as a difference of the anti-derivative function $F(x)$ evaluated at the limits: \[ A(x_i,x_f) = A(a,x) = F(x) - F(a). \]

The expression $A(a,x)$ is a bit misleading as a function name since it looks like both $a$ and $x$ are variable when in fact $a$ is a constant parameter, and only $x$ is the variable. Let's call it $A_a(x)$ instead. \[ A_a(x) = \int_a^x f(t) \; dt = F(x) - F(a). \]

Two observations. First, note that $A_a(x)$ and $F(x)$ differ only by a constant, so in fact the anti-derivative is the integral up to a constant which is usually not important. Second, note that because the variable $x$ appears in the upper limit of the expression, I had to use a dummy variable $t$ inside the integral. If we don't use a different variable, we could confuse the running variable inside the integral, with the limit of integration.

Let $f(x)$ be a continuous function, and let $F(x)$ be its antiderivative on the interval $[a,b]$: \[ F(x) = \int_a^x f(t) \; dt, \] then, the derivative of $F(x)$ is equal to $f(x)$: \[ F'(x) = f(x), \] for any $x \in (a,b)$.

We see that differentiation and integration are inverse operations: \[ F(x) \!= \text{int}\left( \text{diff}( F(x) ) \right)= \int_0^x \left( \frac{d}{dt} F(t) \right) \; dt = \int_0^x f(t) \; dt = F(x) + C, \] \[ f(x) \!= \text{diff}\left( \text{int}( f(x) ) \right) = \frac{d}{dx}\left[\int_0^x f(t) dt\right] = \frac{d}{dx}\left[ F(x) - F(0) \right] = f(x). \]

We can think of the inverse operators $\frac{d}{dt}$ and $\int\cdot dt$ symbolically on the same footing as the other mathematical operations that you know about. The usual equation solving techniques can then be applied to solve equations which involve derivatives. For example, suppose that you want to solve for $f(t)$ in the equation \[ \frac{d}{dt} \; f(t) = 100. \] To get to $f(t)$ we must undo the $\frac{d}{dt}$ operation. We apply the integration operation to both sides of the equation: \[ \int \left(\frac{d}{dt}\; f(t)\right) dt = f(t) = \int 100\;dt = 100t + C. \] The solution to the equation $f'(t)=100$ is $f(t)=100t+C$ where $C$ is called the integration constant.

OK, enough theory. Let's do some anti-derivatives. But how does one do anti-derivatives? It's in the name, really. Derivative and anti. Whatever the derivative does, the integral must do the opposite. If you have: \[ F(x)=x^4 \qquad \overset{\frac{d}{dx} }{\longrightarrow} \qquad F'(x)=4x^3 \equiv f(x), \] then it must be that: \[ f(x)=4x^3 \qquad \overset{\ \int\!dx }{\longrightarrow} \qquad F(x)=x^4 + C. \] Each time you integrate, you will always get the answer up to an arbitrary additive constant $C$, which will always appear in your answers.

Let us look at some more examples:

• The integral of $\cos\theta$ is:

\[ \int \cos\theta \ d\theta = \sin\theta + C, \]

  since $\frac{d}{d\theta}\sin\theta = \cos\theta$,
  and similarly the integral for $\sin\theta$ is:
  \[
   \int \sin\theta \ d\theta = - \cos\theta + C,
  \]
  since $\frac{d}{d\theta}\cos\theta = - \sin\theta$.
* The integral of $x^n$ for any number $n \neq -1$ is:
  \[
   \int x^n \ dx = \frac{1}{n+1}x^{n+1} + C,
  \]
  since $\frac{d}{d\theta}x^n = nx^{n-1}$.
* The integral of $x^{-1}=\frac{1}{x}$ is
  \[
   \int \frac{1}{x} \ dx = \ln x + C,
  \]
  since $\frac{d}{dx}\ln x = \frac{1}{x}$.

I could go on but I think you get the point: all the derivative formulas you learned can be used in the opposite direction as an integral formula.

What is the area under the curve $f(x)=\sin(x)$, between $x=0$ and $x=\pi$? First we take the anti derivative \[ F(x) = \int \sin(x) \ dx = - \cos(x) + C. \] Now we calculate the difference between $F(x)$ at the end-point minus $F(x)$ at the start-point: \[ \begin{align} A(0,\pi) & = \int_{x=0}^{x=\pi} \sin(x) \ dx \nl & = \underbrace{\left[ - \cos(x) + C \right]}_{F(x)} \bigg\vert_0^\pi \nl & = [- \cos\pi + C] - [- \cos(0) + C] \nl & = \cos(0) - \cos\pi \ \ = \ \ 1 - (-1) = 2. \end{align} \]

The constant $C$ does not appear in the answer, because it is in both the upper and the lower limits.

If integration is nothing more than backwards differentiation and you already know differentiation inside out from differential calculus, you might be wondering what you are going to do during an entire semester of integral calculus. For all intents and purposes, if you understood the conceptual material in this section, then you understand integral calculus. Give yourself a tap on the back—you are done.

The establishment, however, doesn't just want you to know the concepts of integral calculus, but also wants you to know how to apply them in the real world. Thus, you need not only understand, but also practice the techniques of integration. There are a bunch of techniques, which allow you to integrate complicated functions. For example, if I asked you to integrate $f(x)=\sin^2(x) = (\sin(x))^2$ from $0$ to $\pi$ and you look in the formula sheet you won't find a function $F(x)$ who's derivative equals $f(x)$. So how do we solve: \[ \int_0^\pi \sin^2(x) \ dx = ?. \] One way to approach this problem is to use the trigonometric identity which says that $\sin^2(x)=\frac{1-\cos(2x)}{2}$ so we will have \[ \int_0^\pi \! \sin^2(x) dx = \int_0^\pi \left[ \frac{1}{2} - \frac{1}{2}\cos(2x) \right] dx = \underbrace{ \frac{1}{2} \int_0^\pi 1 \ dx}_{T_1} - \underbrace{ \frac{1}{2} \int_0^\pi \cos(2x) \ dx }_{T_2}. \] The fact that we can split the integral into two parts, and factor out the constant $\frac{1}{2}$ comes from the fact that integration is linear.

Let's continue the calculation of our integral, where we left off: \[ \int_0^\pi \sin^2(x) \ dx = T_1 - T_2. \] The value of the integral in the first term is: \[ T_1 = \frac{1}{2} \int_0^\pi 1 \ dx = \frac{1}{2} x \bigg\vert_0^\pi = \frac{\pi-0}{2} =\frac{\pi}{2}. \] The value of the second term is \[ T_2 =\frac{1}{2} \int_0^\pi \cos(2x) \ dx = \frac{1}{4} \sin(2x) \bigg\vert_0^\pi = \frac{\sin(2\pi) - \sin(0) }{4} = \frac{0 - 0 }{4} = 0. \] Thus we find the final answer for the integral to be: \[ \int_0^\pi \sin^2(x) \ dx = T_1 - T_2 = \frac{\pi}{2} - 0 = \frac{\pi}{2}. \]

Do you see how integration can quickly get tricky? You need to learn all kinds of tricks to solve integrals. I will teach you all the necessary tricks, but to become proficient you can't just read: you have to practice the techniques. Promise me you will practice! As my student, I expect nothing less than a total ass kicking of the questions you will face on the final exam.