Kinematics (from the Greek word kinema for motion) is the study of trajectories of moving objects. The equations of kinematics can be used to calculate how long a ball thrown upwards will stay in the air, or to calculate the acceleration needed to go from 0 to 100 km/h in 5 seconds. To carry out these calculations we need to know which equation of motion to use and the initial conditions (the initial position $x_i$ and the initial velocity $v_{i}$). Plug in the knowns into the equations of motion and then you can solve for the desired unknown using one or two simple algebra steps. This entire section boils down to three equations. It is all about the plug-number-into-equation technique.

The purpose of this section is to make sure that you know how to use the equations of motion and understand concepts like velocity and accretion well. You will also learn how to easily recognize which equation is appropriate need to use to solve any given physics problem.

The key notions used to describe the motion of an objects are:

• $t$: the time, measured in seconds [s].
• $x(t)$: the position of an object as a function of time—also known as the equation of motion. The position of an object is measured in metres [m].
• $v(t)$: the velocity of the object as a function of time. Measured in [m/s].
• $a(t)$: the acceleration of the object as a function of time. Measured in [m/s$^2$].
• $x_i=x(0), v_i=v(0)$: the initial (at $t=0$) position and velocity of the object (initial conditions).

The motion of an object is characterized by three functions: the position function $x(t)$, the velocity function $v(t)$ and the acceleration function $a(t)$. The functions $x(t)$, $v(t)$ and $a(t)$ are connected—they all describe different aspects of the same motion.

You are already familiar with these notions from your experience driving a car. The equation of motion $x(t)$ describes the position of the car as a function of time. The velocity describes the change in the position of the car, or mathematically \[ v(t) \equiv \text{rate of change in } x(t). \] If we measure $x$ in metres [m] and time $t$ in seconds [s], then the units of $v(t)$ will be metres per second [m/s]. For example, an object moving at a constant speed of $30$[m/s] will have its position change by $30$[m] each second.

The rate of change of the velocity is called the acceleration: \[ a(t) \equiv \text{rate of change in } v(t). \] Acceleration is measured in metres per second squared [m/s$^2$]. A constant positive acceleration means the velocity of the motion is steadily increasing, like when you press the gas pedal. A constant negative acceleration means the velocity is steadily decreasing, like when you press the brake pedal.

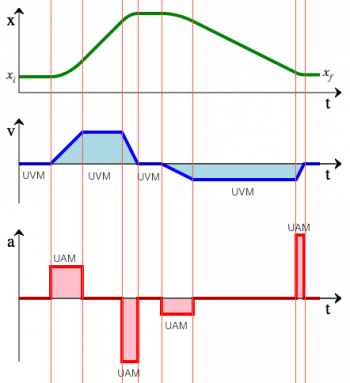The illustration on the right shows the simultaneous graph of the position, velocity and acceleration of a car during some time interval. In a couple of paragraphs, we will discuss the exact mathematical equations which describe $x(t)$, $v(t)$ and $a(t)$. But before we get to the math, let us visually analyze the motion illustrated on the right.

The car starts off with an initial position $x_i$ and just sits there for some time. The driver then floors the pedal to produce a maximum acceleration for some time, picks up speed and then releases the accelerator, but keeps it pressed enough to maintain a constant speed. Suddenly the driver sees a police vehicle in the distance and slams on the brakes (negative acceleration) and shortly afterwards brings the car to a stop. The driver waits for a few seconds to make sure the cops have passed. The car then accelerates backwards for a bit (reverse gear) and then maintains a constant backwards speed for an extended period of time. Note how “moving backwards” corresponds to negative velocity. In the end the driver slams on the brakes again to bring the car to a stop. The final position is $x_f$.

In the above example, we can observe two distinct types of motion. Motion at a constant velocity (uniform velocity motion, UVM) and motion with constant acceleration (uniform acceleration motion, UAM). Of course, there could be many other types of motion, but for the purpose of this section you are only responsible for these two.

• UVM: During times when there is no acceleration,

the car maintains a uniform velocity, that is,

  $v(t)$ will be a constant function.
  Constant velocity means that the position function
  will be a line with a constant slope because, by definition, $v(t)= \text{slope of } x(t)$.
* UAM: During times where the car experiences a constant acceleration $a(t)=a$,
  the velocity of the function will change at a constant rate.
  The rate of change of the velocity is constant $a=\text{slope of } v(t)$,
  so the velocity function must look like a line with slope $a$.
  The position function $x(t)$ has a curved shape (quadratic) during moments of 
  constant acceleration.

There are basically four equations that you need to know for this entire section. Together, these three equations fully describe all aspects of any motion with constant acceleration.

If the object undergoes a constant acceleration $a(t)=a$, like your car if you floor the accelerator, then its motion will be described by the following equations: \[ \begin{align*} x(t) &= \frac{1}{2}at^2 + v_i t + x_i, \nl v(t) &= at + v_i, \nl a(t) &= a, \end{align*} \] where $v_i$ is the initial velocity of the object and $x_i$ is its initial position.

There is also another useful equation to remember: \[ [v(t)]^2 = v_i^2 + 2a[x(t)- x_i], \] which is usually written \[ v_f^2 = v_i^2 + 2a\Delta x, \] where $v_f$ denotes the final velocity and $\Delta x$ denotes the change in the $x$ coordinate.

That is it. Memorize these equations, plug-in the right numbers, and you can solve any kinematics problem humanly imaginable. Chapter done.

The special case where there is zero acceleration ($a=0$), is called uniform velocity motion or UVM. The velocity stays uniform (constant) because there is no acceleration. The following three equations describe the motion of the object under uniform velocity: \[ \begin{align} x(t) &= v_it + x_i, \nl v(t) &= v_i, \nl a(t) &= 0. \end{align} \] As you can see, these are really the same equations as in the UAM case above, but because $a=0$, some terms are missing.

We say that an object is in free fall if the only force acting on it is the force of gravity. On the surface of the earth, the force of gravity produces a constant acceleration of $a=-9.81$[m/s$^2$]. The negative sign is there because the gravitational acceleration is directed downwards, and we assume that the $y$ axis points upwards. The motion of an object in free fall is described by the UAM equations.

We will now illustrate how the equations of kinematics are used to solve physics problems.

Suppose your friend wants to send you a ball wrapped in aluminum foil from his balcony, which is located at a height of $x_i=44.145$[m]. How long does it take for the ball to hit the ground?

We recognize that this is a problem with acceleration, so we start by writing out the general UAM equations: \[ \begin{align*} y(t) &= \frac{1}{2}at^2 + v_i t + y_i, \nl v(t) &= at + v_i. \end{align*} \] To find the answer, we substitute the known values $y(0)=y_i=44.145$[m], $a=-9.81$ and $v_i=0$[m/s] (since the ball was released from rest) and solve for $t_{fall}$ in the equation $y(t_{fall}) = 0$ since we are interested in the time when the ball will reach a heigh of zero. The equation is \[ y(t_{fall}) = 0 = \frac{1}{2}(-9.81)(t_{fall})^2+0(t_{fall}) + 44.145, \] which has solution $t_{fall} = \sqrt{\frac{44.145\times 2}{9.81}}= 3$[s].

Suppose you want to be able to go from $0$ to $100$[km/h] in $5$ seconds with your car. How much acceleration does your engine need to produce, assuming it produces a constant amount of acceleration.

We can calculate the necessary $a$ by plugging the required values into the velocity equation for UAM: \[ v(t) = at + v_i. \] Before we get to that, we need to convert the velocity in [km/h] to velocity in [m/s]: $100$[km/h] $=\frac{100 [\textrm{km}]}{1 [\textrm{h}]} \cdot\frac{1000[\textrm{m}]}{1[\textrm{km}]} \cdot\frac{1[\textrm{h}]}{3600[\textrm{s}]}$= 27.8 [m/s]. We fill in the equation with all the desired values $v(5)=27.8$[m/s], $v_i=0$, and $t=5$[s] and solve for $a$: \[ v(5) = 27.8 = a(5) + 0. \] We conclude that your engine has to produce a constant acceleration of $a=5.56$[m/s$^2$] or more.

Some time later, your friend wants to send you another aluminum ball from his apartment located on the 14th floor (height of $44.145$[m]). In order to decrease the time of flight, he throws the ball straight down with an initial velocity of $10$[m/s]. How long does it take before the ball hits the ground?

Imagine the building with the $y$ axis measuring distance upwards starting from the ground floor. We know that the balcony is located at a height of $y_i=44.145$[m], and that at $t=0$[s] the ball starts with $v_i=-10$[m/s]. The initial velocity is negative, because it points in the opposite direction to the $y$ axis. We know that there is an acceleration due to gravity of $a_y=-g=-9.81$[m/s$^2$].

We start by writing out the general UAM equation: \[ y(t) = \frac{1}{2}a_yt^2 + v_i t + y_i. \] We want to find the time when the ball will hit the ground, so $y(t)=0$. To find $t$, we plug in all the known values into the general equation: \[ y(t) = 0 = \frac{1}{2}(-9.81)t^2 -10 t + 44.145, \] which is a quadratic equation in $t$. First rewrite the quadratic equation into the standard form: \[ 0 = \underbrace{4.905}_a t^2 + \underbrace{10.0}_b \ t - \underbrace{44.145}_c, \] and then solve using the quadratic equation: \[ t_{fall} = \frac{-b \pm \sqrt{ b^2 - 4ac }}{2a} = \frac{-10 \pm \sqrt{ 25 + 866.12}}{9.81} = 2.53 \text{ [s]}. \] We ignored the negative-time solution because it corresponds to a time in the past. Comparing with the first Moroccan example, we see that the answer makes sense—throwing a ball downwards will make it fall to the ground faster than just dropping it.

Most kinematics problems you will be asked to solve follow the same pattern as the above examples. You will be given some of the initial values and asked to solve some unknown quantity. It is important to keep in mind the signs of the numbers you plug into the equations. You should always draw the coordinate system and indicate clearly (to yourself) the $x$ axis which measures the displacement. If a velocity or acceleration quantity points in the same direction as the $x$ axis then it is a positive number while quantities that point in the opposite direction are negative numbers.

All this talk of $v(t)$ being the “rate of change of $x(t)$” is starting to get on my nerves. The expression “rate of change of” is an euphemism for the calculus term derivative. We will now take a short excursion into the land of calculus in order to define some basic concepts (derivatives and integrals) so that we can use us this more precise terminology in the remainder of the book.