The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Electrostatics
This section is all about Coulomb's law which tells you how electric charges attract and repulse each other. Coulomb's law is very similar to the universal law of gravitation, the formula has the same shape.
Concepts
Definitions
- $q,Q$: The electric charge of some object. Measured in Coulombs $[C]$.
- $\vec{F}_{e}$: The electric force acting on some object. Measured in Newtons $[N]$.
- $r$: The distance between two objects. Measured in metres $[m]$.
- $\varepsilon_0$: the electric constant. A constant of nature which is also known as “the permittivity of free space”. $\varepsilon_0 = $ 8.854187×10^-12 $\left[A·s/(V·m)\right]$.
- $k_\mathrm{e} = \frac{1}{4 \pi \varepsilon_0}$ = 8.987551787×10^9 $\left[\mathrm{Nm^2 / C^{2}}\right]$, Coulomb's constant.
Vectors
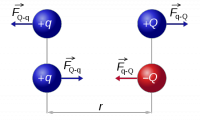
Ok, I hear you saying “Wait now, what is up with this arrow shit on top of the letter F?”. I am not trying to look fancy. I am using the arrow (which means vector) because we really need to use vectors for the calculations here. A vector has a direction – this is all you have to remember. And the reason we say “force is a vector” is because it is a very different thing to be pushed on your chest with a force of 200$[N]$ or being pushed with the same amount of force but on your back. What I am saying is, you can't just add two forces together as if they were numbers. If they are in the same direction, you should add the two numbers. If they are in opposite directions then you have to subtract them!
Constants of nature
$e=1,602x10^{-19}C$
$q_e=-e$
$q_p=+e$
$k= \frac{1}{4\pi\varepsilon o}$
Formulas
Review of Gravitation
$F_g(r)=\frac{MmG}{r^2}[N]$
$\mid F_g \mid = \frac{MmG}{r^2}$
$U_g=\frac{MmG}{r} [J]$
Coulomb's Law
$F=\frac{k\mid qQ\mid}{r^2}$
$k=9,0x10^9N.m^2/c^2$
$F_1=F_{12}+F_{13}+....F_{in}$
$E=\frac{F}{q_{ess}}$
$E=\frac{K\mid Q \mid}{r^2}$
$F=qE$
$V_e=\frac{U_e}{q}$
$U_e=qE_y$
$W_{ext}=q\Delta V$
$\Delta V=+/- Ed$
$dV=\frac{dU}{q}=-E\cdot ds$
$V=\frac{K Q}{r}$
$U=qV$
$\mid F_{elec} \mid=\frac{K\mid Q \mid \mid q \mid}{r^2}[N] $
$F_e=Eq_1$
$\mid E \mid = \frac{KQ}{r^2} [N/C]$
$U_e=\frac{K\mid Q \mid q \mid}{r} [J]$
$U_e=Vq_1$
$V=\frac{K Q}{r}[J/C]$
$4\pir^2= Aire de surface d'une sphere
section 1
section 2
Exemples
exemple 1
voici un exemple.
exemple 2
voici un autre !