The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Magnetic field
Concepts
- $\vec{B}$: Magnetic field strength and direction
- $I$: Electric current
- $r$: Distance between two magnets
- $S$: some surface in space. ex: $S$=spherical shell of radius $r$, $S$=the surface of a ciliner
- $\Phi_S$=Flux: How much magnetic filed $B$ passes through the surface $S$
Formules
Les charges qui bougent causent un champ magnetique. Puisque le champ crée par une particule est tellement petit, on est miex de parler du champ crée par beaucoup d'électrons comme par exemple un fil dans lesquel coule un courant $I$.
Courant
Pour quantifier les charges en mouvement on utilise des diagrammes pis on compte le courant. Le courant se mesure en Coulombs par seconde, une quantité qu'on appelle plus souvent Ampere.
a b
--------------
I= 3 [A]
Le diagramme en haut n'a pas de sens, parce qu'on ne spécifie pas la direciton.
a b
------>-------
I=3 [A]
Ça c'est mieux. Si je dis que $I=3 [A]$, ca veut dire qu'il y a 3 Coulombs de charge qui vont se déplacer du point $a$ au point $b$ chaque seconde dans ce fil. Si je dis que le courant est $I=-1 [A]$, alors il y a des charges qui se déplacent du point $b$ au point $a$ 1 Coulomb par seconde.
La loi de Ampère
Le courant qui passe dans un fil crée un champ magnétique enroulé en cercles tout autour du fil.
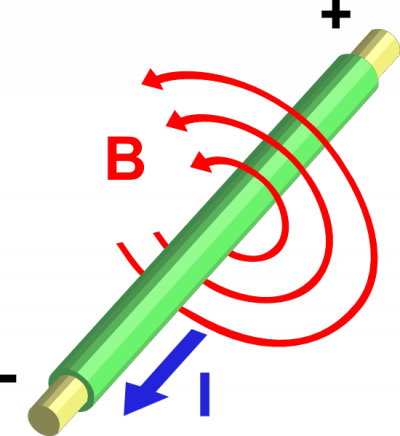
Plus que tu t'éloignes du fil, mois fort le champ magnétique $\vec{B}$ devient.
La formule pour mesurer ça a été découverte par André-Marie Ampère en 1826. Si tu as un fil super long qui porte un courant $I$, pis que tu es placé à une distance de $r$, alors le champ magnétique que tu va ressentir est \[ \vec{B} = \mu_0 \frac{I}{2\pi r} \]
Cette formule sort quand tu prend la contribution do toutes les morceaux du fil. Chaque bout de fil cr/ee un champ magn/etique de force
Lorentz force
\[ \vec{F}_b = q (\vec{v}_q \times \vec{B}), \] cross product !
