The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
<texit info> author=Ivan Savov title=MATH and PHYSICS Funamentals Test backgroundtext=off </texit>
A
You can learn more about the various contexts in which the golden ratio appears from the wikipedia article on that subject.
Testing a dash - like this
Testing an n dash – liek this And this, This is al ink to forces section.
Same thing but with a leading colon Ab and Ab lkjas And this, This is al ink to forces section.
And this, This is al ink to forces: concepts subsection.
lets see
Testin an m dash — like this
Forces
Like a shepherd who brings back stray sheep, we need to rescue the word force and give it precise meaning. In physics force means something very specific. Not “the force” from Star Wars, not the “force of public opinion”, and not the force in the battle of good versus evil.
Force in physics has a precise meaning as an amount of push or pull exerted on an object. Forces are vector quantities measured in Newtons [N]. In this section we will explore all the different kinds of forces.
Concepts
- $\vec{F}$: a force. This is something the object “feels” as a pull or a push. Force is a vector, so you must always keep in mind the direction in which the force $\vec{F}$ acts.
- $k,G,m,\mu_s,\mu_k,\ldots$: parameters on which the force $F$ may depend. Ex: the heavier an object is (large $m$ parameter), the larger its gravitational pull will be: $\vec{W}=-9.81m\hat{\jmath}$, where $\hat{\jmath}$ points towards the sky.
Kinds of forces
We next list all the forces which you are supposed to know about for a standard physics class and define the relevant parameters for each kind of force. You need to practice exercises using each of these forces, until you start to feel how they act.
Gravitation
The force of gravity exists between any two massive objects. The magnitude of the gravitational force between two objects of mass $M$[kg] and $m$[kg] separated by a distance $r$[m] is given by the formula \[ F_g=\frac{GMm}{r^2}, \] where $G=6.67 \times 10^{-11}$[$\frac{\text{Nm}^2}{\text{kg}^2}$] is the gravitational constant. This is the famous one-over-arr-squared law that describes the gravitational pull between two objects. This was Newton's big discovery.
On the surface of the earth, which has mass $M=5.972\times 10^{24}$[kg] and radius $r=6.367\times10^6$[m], the force of gravity on an object of mass $m$ is given by \[ F_g=\frac{GMm}{r^2} = \underbrace{\frac{GM}{r^2}}_{g}m = 9.81 m = W. \] We call this force the weight of the object and to be precise we should write $\vec{W}=-mg\hat{\jmath}$ to indicate that the force acts downwards—in the negative $y$ direction. Verify using your calculator that $\frac{GM}{r^2}=9.81\equiv g$.
Force of a spring
A spring is a piece of metal twisted into a coil that has a certain natural length. The spring will resist any attempts to stretch it or compress it. The force exerted by a spring is given by \[ \vec{F}_s=-k\vec{x}, \] where $x$ is the amount by which the spring is displaced from its natural length and the constant $k$[N/m] is a measure of the strength of the spring. Note the negative sign: if you try to stretch the spring (positive $x$) then the force of a spring will pull against you (in the negative $x$ direction), if you try to compress the spring (negative $x$) it will push back against you (in the positive $x$ direction).
Normal force
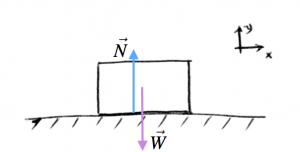
The normal force is the force between two surfaces in contact. The word normal means “perpendicular to the surface of” in this context. The reason why my coffee mug does not fall to the floor right now is that the table exerts a normal force $\vec{N}$ on it keeping in place.
Force of friction
In addition to the normal force between surfaces, there is also the force of friction $\vec{F}_f$ which acts to prevent or slow down any sliding motion between the surfaces. There are two kinds of force of friction and both kinds of are proportional to the amount of normal force between the surfaces: \[ \max \{ \vec{F}_{fs} \}=\mu_s\|\vec{N}\| \ \ \text{(static)}, \qquad \vec{F}_{fk}=\mu_k\|\vec{N}\| \ \ \text{(kinetic)}, \] where $\mu_s$ and $\mu_k$ are the static and dynamic friction coefficients. Note that it makes intuitive sense that the force of friction should be proportional to the magnitude of the normal force $\|\vec{N}\|$: the harder the surfaces push against each other the more difficult it should be to make them slide. The above equations make this intuition precise.
The static force of friction acts on objects that are not moving. It describes the maximum amount of friction that can exist between two objects. If a horizontal force greater than $F_{fs} = \mu_s N$ is applied to the object, then it will start to slip. The kinetic force of friction acts when two objects are sliding relative to each other. It always acts in the direction opposite to the motion.
Tension
A force can also be exerted on an object remotely by attaching a rope to the object. The force exerted on the object will be equal to the tension in the rope $\vec{T}$. Note that tension always pulls away from an object: you can't push a dog on a leash.
Discussion
Viewing the interactions between objects in terms of the forces that act between them is a very powerful way of thinking. In the next section, we will learn how to draw force diagrams which take into account all the forces that act on the object.
Force diagrams
Welcome to Force-Accounting 101. In this section we will learn how to identify all the forces acting on an object and use Newton's 2nd law $\sum \vec{F}=\vec{F}_{net} = m\vec{a}$ to predict the resulting acceleration.
Concepts
Newton's second law describes a relationship between these three quantities:
- $m$: the mass of an object.
- $\vec{F}_{net}$: the net force on the object.
- $\vec{a}$: the acceleration of the object.
Forces and accelerations are vectors. To work with vectors, we work with their components:
- $F_x$: the component of $\vec{F}$ in the $x$ direction.
- $F_y$: the component of $\vec{F}$ in the $y$ direction.
Vectors are meaningless unless it is clear with respect to which coordinate system they are expressed.
- $x$ axis: Usually the $x$ axis is horizontal and to the right, however, for problems with inclines,
it will be more convenient to use an inclined $x$ axis that is parallel to the slope.
- $y$ axis: The $y$ axis is always perpendicular to the $x$ axis.
- $\hat{\imath},\hat{\jmath}$: Unit vectors in the $x$ and $y$ directions. Any vector can be written as $\vec{v}=v_x\hat{\imath}+v_y\hat{\jmath}$ or as $\vec{v}=(v_x,v_y)$.
Provided we have a coordinate system, we can write any force vector in three equivalent ways: \[ \vec{F} \equiv F_x\hat{\imath} + F_y\hat{\jmath} \equiv (F_x,F_y) \equiv \|\vec{F}\|\angle \theta. \]
What types of forces are there in force diagrams?
- $\vec{W}\equiv\vec{F}_{gravity}=m\vec{g}$: The weight. This is the force on a object due to its gravity. The gravitational pull $\vec{g}$ always points downwards – towards the centre of the earth. $g=9.81$[N/kg].
- $\vec{T}$: Tension in a rope. Tension is always pulling away from the object.
- $\vec{N}$: Normal force – the force between two surfaces.
- $\vec{F}_{fs}=\mu_s\|\vec{N}\|$: Static force of friction.
- $\vec{F}_{fk}=\mu_k\|\vec{N}\|$: Kinetic force of friction.
- $\vec{F}_{s}=-kx$: The force (pull or push) of a spring that is displaced (stretched or compressed) by $x$ metres.
Formulas
Newton's 2nd law
The sum of the forces acting on an object, divided by the mass, gives you the acceleration of the object: \[ \sum \vec{F} \equiv \vec{F}_{net}= m\vec{a}. \]
Vector components
If a vector $\vec{v}$ makes an angle $\theta$ with the $x$ axis then: \[ v_x = \|\vec{v}\|\cos\theta, \qquad \text{and} \qquad v_y = \|\vec{v}\|\sin\theta. \] The vector $v_x\hat{\imath}$ corresponds to the part of $\vec{v}$ that points in the $x$ direction.
In what follows, you will be asked a countless number of times to \[ \text{Find the component of } \vec{F} \text{ in the ? direction. } \] Which is another way of asking you to find the number $v_?$.
The answer is usually equal to the length $\|\vec{F}\|$ multiplied by either $\cos$ or $\sin$ and sometimes $-1$ all depending on way the coordinate system is chosen. So don't guess. Look at the coordinate system. If the vector points in the direction where $x$ increases, then $v_x$ should be a positive number. If $\vec{v}$ points in the opposite direction, then $v_x$ should be negative.
To add forces $\vec{F}_1$ and $\vec{F}_2$ you have to add their components: \[ \vec{F}_1 + \vec{F}_2 = (F_{1x},F_{1y}) + (F_{1x},F_{2y}) = (F_{1x}+F_{2x},F_{1y}+F_{2y}) = \vec{F}_{net}. \] Instead of dealing with vectors in the bracket notation as above, when solving force diagrams it is easier to simply write the $x$ equation on one line, and the $y$ equation on a separate line below it: \[ F_{netx} = F_{1x}+F_{2x}, \] \[ F_{nety} = F_{1y}+F_{2y}. \] It is a good idea to always write those two equations together as a block – so it remains clear that you are talking about the same problem, but the first row represents the $x$-dimension and the second row represents the $y$-dimension.
Force check
It is important to account for all the forces acting on an object. Any object with mass on the surface of the earth will feel a downwards gravitational pull of magnitude $F_{g}=W=m\vec{g}$. Then you have to think about which of the other forces might be present: $\vec{T}$, $\vec{N}$, $\vec{F}_{f}$, $\vec{F}_{s}$. Anytime you see a rope tugging on the object, you know there must be some tension $\vec{T}$, which is a force vector pulling on the block. Anytime you have an object sitting on a surface, the surface will push back with a normal force $\vec{N}$. If the object is sliding on the surface there will be a force of friction acting against the direction of the motion: \[ F_{fk}=\mu_k\|\vec{N}\|. \] If the object is not moving, then you have to use $\mu_s$ in the friction force equation, to get the maximum static friction force that the contact between the object and the ground can support before the object starts to slip: \[ \max\{ F_{fs} \}=\mu_s\|\vec{N}\|. \] If you see a spring that is either stretched or compressed by the object, then you must account for the spring force. The force of a spring is restorative: it always acts against the deformation you are making to the spring. If you stretch it by $x$[cm], then it will try to pull itself back to its normal length with a force of: \[ \vec{F}_s = -kx \hat{\imath}. \] The constant of proportionality $k$ is called the spring constant and is measured in [N/m].
Recipe for solving force diagrams
Below we list the steps of the general procedure to follow when solving problems in dynamics.
- Draw a force diagram focussed on the object and indicate all the forces acting on it.
- Choose a coordinate system, and indicate clearly in the diagram what you will call the positive $x$ direction, and what you will call the positive $y$ direction. All quantities in the subsequent equations will be expressed with respect to this coordinate system.
- Write down the following “template”:
\[ \sum F_x = \qquad \qquad \qquad = ma_x, \] \[ \sum F_y = \qquad \qquad \qquad = ma_y. \]
- Fill in the template by calculating the $x$ and $y$ components
of each force acting on the object:
$\vec{W}$, $\vec{N}$, $\vec{T}$, $\vec{F}_{fs}$, $\vec{F}_{fk}$,
$\vec{F}_{s}$ as applicable.
- Solve the equations for the unknown quantities.
I highly recommend that you perform some consistency checks after Step 4. You should check the signs: if the force in the diagram is acting in the $x$ direction, then its component must be positive. If the force is acting in the direction opposite to the $x$ axis, then its component should be negative. You should also check that whenever $F_x \propto \cos\theta$, then $F_y \propto \sin\theta$. If instead we use the angle $\phi$ defined with respect to the $y$ axis, we would have $F_x \propto \sin\phi$, and $F_y \propto \cos\phi$.
We will now illustrate how to use this recipe through a series of examples.
Examples
Block on a table
You place a block of mass $m$ on the table. If it has mass $m$ then it feels its weight $\vec{W}$ pulling down on it, but the table is not letting it drop to the floor. The table pushes back on the block with a normal force $\vec{N}$.
Steps 1,2: We draw the force diagram and choose a coordinate system:
Step 3: Next, we write down the empty equations template: \[ \begin{align*} \sum F_x &= \qquad \qquad = ma_x, \nl \sum F_y &= \qquad \qquad = ma_y. \end{align*} \]
Step 4: There is nothing much going on in the $x$ direction: no forces acting in the $x$ direction and the block is not moving so $a_x=0$. In the $y$ direction we have the force of gravity and the normal force exerted by the table: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \] We set $a_y=0$, because we see that the block is just sitting there on the table without moving. The technical term for situations where $a_x=0, a_y=0$ is called static equilibrium. Force diagrams with static equilibrium are easy to solve, because the entire right-hand side is equal to zero, which means that the forces on the object must be counter-balancing each other.
Step 5: Suppose the teacher was asking you “What is the magnitude of the normal force?”. You can easily answer this by looking at the second equation: “$N=mg$ bro!”
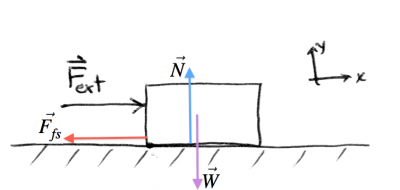
Moving the fridge
You are trying to push your fridge across the kitchen floor. Because it weights quite a lot, it is “gripping” the floor quite a bit. If the static coefficient of friction between the metal “feet” of your fridge and the tiles of the floor is $\mu_s$, how much force $\vec{F}_{ext}$ would it take to get the fridge to start moving?
\[ \begin{align*} \sum F_x &= F_{ext} - F_{fs} = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
If you push with force $F_{ext}=30$[N], the fridge will push back (via its connection to the floor) with a force $F_{fs}=30$[N]. If you push harder, the fridge will push back harder and it will still not move. Only when you reach the slipping threshold will it move. This means you have to push with force equal to the maximum static friction force $F_{fs}=\mu_s N$, so we have: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_s N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
To solve for $F_{ext}$ you first isolate $N=mg$ in the bottom line, and then substitute the value of $N$ in the top line to get $F_{ext} = \mu_s m g$.
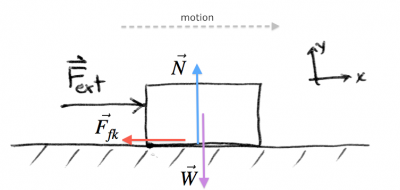
Friction slowing you down
OK, so you have the fridge moving now and you are moving at a steady pace across the room:
Your equation of motion is going to be: \[ \begin{align*} \sum F_x &= F_{ext} - \vec{F}_{fk} = ma_x, \nl \sum F_y &= N - mg = 0. \end{align*} \]
In particular if you want to keep a steady speed ($v=const$) as you move across the room, you will push with such a force just to balance the friction force and keep $a_x=0$.
To find the value of $F_{ext}$ to keep a constant speed we solve: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_k N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
We get a similar expression as above, but with $\mu_k$ instead of $\mu_s$: $F_{ext} = \mu_k m g$. Generally, $\mu_k < \mu_s$ so it takes less force to keep the fridge moving than it took to get it to start moving.
Let us now take a different slant on this whole friction thing.
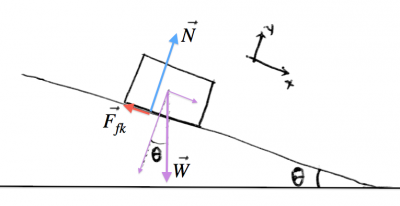
Incline
At this point, my dear readers, we are getting into the main kind of question that will be, without a doubt, asked in your homework or at the final exam. A block sliding down an incline. What is its acceleration?
Step 1: We draw a diagram which includes the weight $\vec{W}$, the normal force $\vec{N}$ and the friction force $\vec{F}_{fk}$.
Step 2: We pick the coordinate system to be tilted along the incline. This is important because this way the motion is purely in the $x$ direction, while the $y$ direction will be static.
Step 3,4: Let's copy the empty template, and fill in the equations: \[ \begin{align*} \sum F_x &= \|\vec{W}\|\sin\theta - F_{fk} = ma_x, \nl \sum F_y &= N - \|\vec{W}\|\cos\theta \ \ = 0, \end{align*} \] or substituting the values that we know: \[ \begin{align*} \sum F_x &= mg\sin\theta - \mu_kN = ma_x, \nl \sum F_y &= N - mg\cos\theta \ \ \ = 0. \end{align*} \]
Step 5: From the $y$ equation, we obtain $N=mg\cos\theta$ and substituting this into the $x$ equation we get: \[ a_x = \frac{1}{m}\left( mg\sin\theta - \mu_k mg\cos\theta \right) = g\sin\theta - \mu_k g\cos\theta. \]
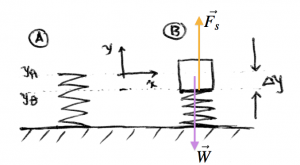
Bathroom scale
You have a spring with spring constant $k$ on which you put a block of mass $m$. By what length $\Delta y$ will the spring be compressed?
Step 1,2: We draw a before and after picture, with the $y$ axis placed at the natural length of the spring.
Step 3,4: Filling in the template we get: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= F_s - mg = 0. \end{align*} \]
Step 5: We know that the force exerted by a spring is proportional to its displacement according to \[ F_s = -k y_B, \] so we can find $y_B = -\frac{mg}{k}$. The length of compression is therefore: \[ |\Delta y| = \frac{mg}{k}. \]
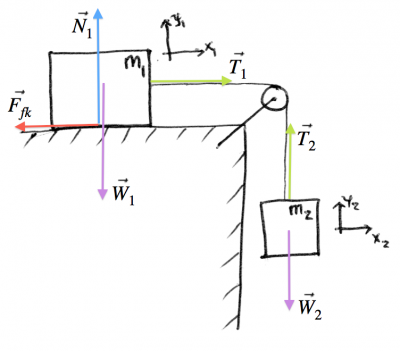
Two blocks
Now for a more involved example with two blocks. One block is sitting on the surface, and another one is falling straight down. The two are connected by a stiff rope. What is the acceleration of the system as a whole?
Steps 1,2: We have two objects, so we have to draw two force diagrams.
Step 3: We also have two sets of equations. One set of equations for the left block, and one for the right block: \[ \begin{align*} & \sum F_{1x} = \qquad\qquad = m_1a_{x_1} & \qquad & \sum F_{2x} = \qquad\quad = m_2a_{x_2} \nl & \sum F_{1y} = \qquad\qquad = m_1a_{y_1} & \qquad & \sum F_{2y} = \qquad\quad = m_2a_{y_2} \end{align*} \]
Steps 4: We fill them in with all the forces drawn in the diagram: \[ \begin{align*} & \sum F_{1x} = -F_{fk} + T_1 = m_1a_{x_1} & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - W_1 = 0 & \qquad & \sum F_{2y} = -W_2 + T_2 = m_2a_{y_2} \end{align*} \]
Step 5: What are the connections between the two blocks? Since it is the same rope that connects the two blocks, this means that the tension in the rope is the same on both ends so $T_1=T_2=T$. Also since the rope is of fixed length we have that the $x_1$ and $y_2$ coordinates are related by a constant (though they point in different directions), so it must be that $a_{x_1}= -a_{y_2} = a$.
Rewriting in terms of the new common variables $T$ and $a$ we have: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - m_1g = 0 & \qquad & \sum F_{2y} = -m_2g + T = - m_2a \end{align*} \]
We isolate $N_1$ on the bottom left, and isolate $T$ on the bottom right: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & N_1 = m_1g & \qquad & T = - m_2a + m_2g \end{align*} \]
Now substitute the values into the top left equation to get \[ \sum F_{1x} = -\mu_k(m_1g) + (- m_2a + m_2g) = m_1 a, \] or moving all the $a$ terms to one side we have \[ -\mu_km_1g + m_2g = m_1 a + m_2 a = (m_1 + m_2) a, \] which makes sense since the “two blocks attached with a rope” is in some sense an object of collective mass $(m_1 + m_2)$ with two external forces on it. From this point of view, the tension $T$ is an internal force of the object and doesn't appear in the external force equation.
The acceleration of the whole two-block system going to be: \[ a = \frac{m_2g - \mu_km_1g}{m_1+m_2}. \]
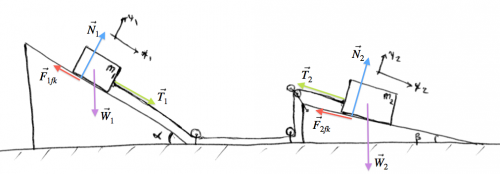
Two inclines
OK, let's just go crazy now! Let's have two inclines, two blocks, a rope, and friction everywhere. We want to find the acceleration as usual.
Steps 1,2: We draw a force diagram with two different coordinate systems each adapted for the angle of the incline:
Steps 3,4: Fill in all force components, and set $a_{y_1}=0,a_{y_2}=0$: \[ \begin{align*} & \sum F_{1x} = W_1\sin\alpha - F_{1fk} + T_1 = m_1a_{x_1}, \nl & \sum F_{1y} = -W_1\cos\alpha + N_1 \quad \ \ \ = 0, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = W_2\sin\beta - F_{2fk} - T_2 = m_2a_{x_2}, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2y} = -W_2\cos\beta + N_2 \quad \ \ \ =0. \end{align*} \]
Step 5: The links between the two worlds are two: the tension in the rope is the same $T=T_1=T_2$ and also the acceleration since the blocks are moving together $a=a_{x_1}=a_{x_2}$. Rewriting and expanding we have: \[ \begin{align*} & \sum F_{1x} = m_1g\sin\alpha - \mu_k N_1 + T = m_1a, \nl & N_1 = m_1g\cos\alpha, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k N_2 - T = m_2a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad N_2 = m_2g\cos\beta. \end{align*} \]
Let's substitute the values of $N_1$ and $N_2$ into the $x$ equations: \[ \begin{align} & \sum F_{1x} = m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k m_2g\cos\beta - T = m_2a. \end{align} \]
There are many ways to solve for the two unknowns in this pair of equations. Either (A) we isolate $T$ in one of the equations and substitute the value of $T$ into the second or (B) we isolate $a$ in both equations and set them equal to each other.
We will use approach (A) and isolate $T$ in the bottom equation to get: \[ \begin{align} & m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a = T. \end{align} \] and finally substitute the expression for $T$ into the top equation to obtain \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + ( m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a) = m_1a, \] which can be rewritten as \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + m_2g\sin\beta - \mu_k m_2g\cos\beta = (m_1 + m_2)a. \] Since we know the values of $m_1$, $m_2$, $\mu_k$, $\alpha$ and $\beta$, we can calculate all the quantities on the left-hand side and solve for $a$.
Other types of problems
All the examples shown asked you to find the acceleration, but sometimes you might be told the acceleration and asked to solve for some other unknown in the equations. Regardless of what you have to solve for, you should always start with the diagram and the sum-of-the-forces template. Once you have these equations in front of you, you will be able to reason about the problem more easily.
Experiment
Suspend an object of known mass (say a 100g chocolate bar) on the spring taken out from a retractable pen. Use a ruler to measure by how much the spring stretches in the process. What is the spring constant $k$?
Discussion
In previous sections we discussed the kinematics problem of finding the position of an object $x(t)$ given the knowledge of its acceleration function $a(t)$ and the initial conditions $x_i$ and $v_i$. In this section we studied the dynamics problem, which involved drawing force diagrams and calculating the net force on the object. Understanding these topics means that you fully understand Newton's equation $F=ma$ which is perhaps the most important equation in this book.
We can summarize the entire procedure for predicting the position of an object $x(t)$ from first principles in the following equation: \[ \frac{1}{m} \underbrace{ \left( \sum \vec{F} = \vec{F}_{net} \right) }_{\text{dynamics}} = \underbrace{ a(t) \ \overset{v_i+ \int\!dt }{\longrightarrow} \ v(t) \ \overset{x_i+ \int\!dt }{\longrightarrow} \ x(t) }_{\text{kinematics}}. \] The left-hand side calculates the net force, which is the cause of acceleration. The right-hand side indicates how we can calculate the equation of motion $x(t)$ from the knowledge of the acceleration and the initial conditions. This means that if you know the forces acting on any object (rocks, projectiles, cars, stars, planets, etc.) then we can predict its motion, which is kind of cool.
Momentum
During a collision between two objects there will be a sudden spike in the contact force between them, which can be difficult to measure and quantify. It is therefore not possible to use Newton's law $F=ma$ to predict the accelerations that occur during collisions. In order to predict the motion of the objects after the collision we must use a momentum calculation. The law of conservation of momentum states that the total amount of momentum before and after the collision is the same. Thus, if we know the momenta of the objects before the collision, it will be possible to calculate their momenta after the collision and from this figure out their subsequent motion.
To illustrate why the notion of momentum is important, consider the following situation. Say you have a 1[g] piece of paper and a 1000[kg] car moving at the same speed 100[km/h]. Which of the two objects would you rather get hit by? Momentum, denoted $\vec{p}$, is the precise physical concept which measures the “amount of moving stuff”. An object of mass $m$ moving with velocity $\vec{v}$ has momentum $\vec{p}\equiv m\vec{v}$. Momentum plays a key role in collisions, so your gut feeling about the piece of paper and the car is correct. The car weights $1000\times1000=10^{6}$ times more than the piece of paper, so it has $10^6$ times more momentum when moving at the same speed. A collision with the car will “hurt” a million times more than the collision with the piece of paper even though they were moving at the same speed.
In this section we will learn how to use the law of conservation of momentum to predict the outcomes of collisions.
Concepts
- $m$: the mass of the moving object.
- $\vec{v}$: the velocity of the moving object.
- $\vec{p}=m\vec{v}$: the momentum of the moving object.
- $\sum \vec{p}_{in}$: the sum of the momenta of particles before a collision.
- $\sum \vec{p}_{out}$: the sum of the momenta after the collision.
Definition
The momentum of a moving object is equal to the velocity of the moving object multiplied by the object's mass: \[ \vec{p} = m\vec{v} \qquad [\text{kg}\:\text{m}/\text{s}]. \] If the velocity of the object is $\vec{v}=20\hat{\imath}=(20,0)$[m/s] and it has a mass of 100[kg] then its momentum is $\vec{p}=2000\hat{\imath}=(2000,0)$[kg$\:$m/s].
Momentum is a vector quantity, so we will often have to convert momentuma from the length-and-direction form to the components form: \[ \vec{p}= \|\vec{p}\| \angle \theta = (\|\vec{p}\|\cos\theta, \|\vec{p}\|\sin\theta) = (p_x, p_y). \] The component form makes it easy to add and subtract vectors: $\vec{p}_1 + \vec{p}_2 = (p_{1x}+p_{2x},p_{1y}+p_{2y})$. To express the final answer, we will have to convert from the component form back to the length-and-direction form using: \[ \|\vec{p}\| = \sqrt{ p_x^2 + p_y^2 }, \qquad \theta = \tan^{-1}\!\left( \frac{ p_{y} }{ p_{x} } \right). \]
Conservation of momentum
Newton's first law states that in the absence of acceleration ($\vec{a}=0$), an object will maintain a constant velocity. This is kind of obvious if you know Calculus, since $\vec{a}$ is the derivative of $\vec{v}$. For example, if an object is stationary and there are no forces on it to cause it to accelerate, then it will remain stationary. If an object is moving with velocity $\vec{v}$ and there is no acceleration (or deceleration), then it will keep moving with velocity $\vec{v}$ forever. In the absence of acceleration, objects will conserve their velocity: \[ \vec{v}_{in}= \vec{v}_{out}. \] This is equivalent to saying that objects conserve their momentum (just multiply the velocity by the constant mass of the object).
More generally, if you have a situation involving multiple moving objects, you can say that the “overall momentum”, i.e., the sum of the momenta of all the interacting particles stays constant. This reasoning is particularly useful when analyzing collisions since it allows us to connect the sum of the momenta before the collision and after the collision: \[ \sum \vec{p}_{in} = \sum \vec{p}_{out}. \] Whatever momentum comes into a collision must come out. This equation is known as the law of conservation of momentum.
This conservation law is one of the furthest reaching laws of physics you will learn in Mechanics. We learned about the conservation of momentum in a simple context of two colliding particles, but the law applies much more generally: for multiple particles, for fluids, for fields, and even for collisions involving atomic particles described by quantum mechanics. The quantity of motion (momentum) cannot be created or destroyed, it can only be exchanged between systems.
Examples
Example 1
You throw a piece of rolled up carton of mass $0.4$[g] from your balcony on a rainy day. You throw it horizontally with a speed of 10[m/s]. Shortly after it leaves your hand it collides with a rain drop of weight $2$[g] falling straight down at a speed of $30$[m/s]. What will be resulting velocity if the two objects stick together after the collision?
The conservation of momentum equation says that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out}. \] Plugging in the values we get \[ 0.4\times (10,0) \ \ + \ \ 2\times (0,-30) \ \ = \ \ 2.4 \times \vec{v}_{out}, \] or solving for $\vec{v}_{out}$ we find: \[ \vec{v}_{out} = \ \frac{ 0.4(10,0) - 2 (0,30)} {2.4} = (1.666, - 25.0) = 1.666\hat{\imath} - 25.0\hat{\jmath}. \]
Example 2: Hipsters on bikes
Two hipsters on single-speed bicycles are headed towards the same intersection. Say they are both speeding down Parc street at 50[km/h] and the first hipster is crossing the street at a diagonal of 30 degrees when they collide. I mean you saw this coming right? Well the second hipster didn't, because he was busy turning the pedals as fast as he can.
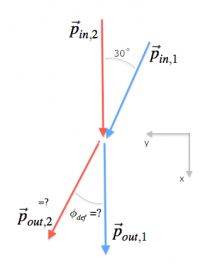 Let us assume that the combined weight of the straight-going hipster and his bike is 100[kg],
whereas the street-crossing-at-30-degrees hipster has a lighter, more expensive bicycle frame.
We put his weight at 90[kg].
Let us assume that the combined weight of the straight-going hipster and his bike is 100[kg],
whereas the street-crossing-at-30-degrees hipster has a lighter, more expensive bicycle frame.
We put his weight at 90[kg].
(I am going to continue with the story, but I want to point out that we have been given, the following information so far: \[ \begin{align*} \vec{p}_{in,1} &= 90\times50 \angle 30=90(50\cos30,50\sin30), \nl \vec{p}_{in,2} &= 100\times50 \angle 0=(5000,0), \end{align*} \] where the $x$ coordinate points down Park street, and the $y$ coordinate is perpendicular to the street.)
Surprisingly, nobody gets hurt in this collision. They bump shoulder-to-shoulder and the one that was trying to cross the street gets redirected straight down the street, while the one going straight down gets deflected to the side and right onto the bike path. I know what you are thinking: couldn't they get hurt at least a little bit? OK, let's say that the whiplash from their shoulder-to-shoulder collision sends their heads flying towards each other and their glasses get smashed. There you have it.
Suppose the velocity of the first hipster after the collision is 60 [km/h], what is the velocity and the deflected direction of the second hipster? (I have just told you that the outgoing momentum of the first hipster is $\vec{p}_{out,1}=(90\times60,0)$, and asked you to find $\vec{p}_{out,2}$.)
We can solve this problem using the conservation of momentum formula, which tells us that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out,1} + \vec{p}_{out,2}. \] We know three of the above quantities so we can solve for the one (vector) unknown by isolating it on one side of the equation: \[ \vec{p}_{out,2} = \vec{p}_{in,1} + \vec{p}_{in,2} - \vec{p}_{out,1}, \] \[ \vec{p}_{out,2} = 90(50\cos30,50\sin30)\ +\ (5000,0)\ - \ (90\times60,0). \] The $x$ component of the momentum $\vec{p}_{out,2}$ is: \[ p_{out,2,x} = 90\times50\cos30 + 5000 - 90\times 60 = 3497.11, \] and the $y$ component is $p_{out,2,y} = 90\times 50\sin30 = 2250$.
The magnitude of the momentum of hipster 2 is given by: \[ \|\vec{p}_{out,2}\| = \sqrt{ p_{out,2,x}^2 + p_{out,2,y}^2 } = 4158.39, \quad \textrm{[kgkm/h]}. \] Note the units we use for the momentum is not the standard choice [kgm/s]. That is fine. So long as you keep in mind which units you are using, you don't have to always convert to SI units.
The final velocity of hipster two is $v_{out,2} = 4158.39/100= 41.58$[km/h]. The deflection angle is obtained by \[ \phi_{def} = \tan^{-1}\!\!\left( \frac{ p_{out,2,y} }{ p_{out,2,x} } \right)= 32.76^\circ. \]
Discussion
We defined the concept of momentum in terms of the velocity of the object, but in fact, momentum is a more fundamental concept than velocity. If you go on to take more advanced physics classes, you will learn that the natural variables to describe the state of a particle are their positions and momenta $(\vec{x}, \vec{p})$. You will also learn that the real form of Newton's second law is written in terms of the momentum: \[ \vec{F} = \frac{d \vec{p} }{dt} \quad \text{for } m \text{ constant } \Rightarrow \quad \vec{F}=\frac{d (m\vec{v}) }{dt}=m\frac{d \vec{v} }{dt} =m\vec{a}. \] In most physics problems the mass of objects will stay constant so using $\vec{F}=m\vec{a}$ is perfectly fine.
The law of conservation of momentum follows from Newton's third law: for each force $\vec{F}_{12}$ exerted by Object 1 on Object 2, there exists a counter force $\vec{F}_{21}$ of equal magnitude and opposite direction, which is the force of Object 2 pushing back on Object 1. Earlier I said that it is difficult to quantify the magnitude of the exact forces $\vec{F}_{12}$ and $\vec{F}_{21}$ that occur during a collision. Indeed, the amount of force suddenly shoots up as the two objects collide and then suddenly drops. Complicated as these forces may be, we know that during the entire collision they obey Newton's third law. Assuming there are no other forces acting on the objects we have: \[ \vec{F}_{12} = -\vec{F}_{21} \quad \text{using the above} \Rightarrow \quad \frac{d \vec{p}_1 }{dt} = -\frac{d \vec{p}_2 }{dt}. \] If now move both terms to the left-hand side we obtain the equation: \[ \frac{d \vec{p}_1 }{dt} + \frac{d \vec{p}_2 }{dt} = \frac{d}{dt}\left( \vec{p}_1 + \vec{p}_2 \right) = 0, \] which implies that quantity $\vec{p}_1 + \vec{p}_2$ is constant over time.
In this section we saw how to use a momentum calculation to predict the motion of the particles after a collision. In the next section, we will learn about the concept of energy which is another useful concept for understanding and predicting the motion of objects.
Links
[ Animations of simple collisions between objects. ]
http://en.wikipedia.org/wiki/Conservation_of_linear_momentum