If you were to put two current-carrying wires close to each other you will see that there will be a force between the wires. If the current is going in the same direction for both wires, then they will attract (buckle inwards), whereas if the currents are in opposite directions, the the wires will be pushed apart (tend to spread apart). This is the magnetic force. The powerful magnetic force is also what makes motors, generators and electromagnets work.

Recall that the electric force will exists between any two charged particles. Recall also how we invented the notion of an electric field $\vec{E}$ as an intermediary phenomenon. The story we told ourselves to explain the emergence of the electric force was as follows. One of the charges, say charge $Q$, creates an electric field $\vec{E}$ in space everywhere around it. The other charge (say $q$), will feel an electric force $F_e = q\vec{E}$ because of the electric field.

In this section we will follow a similar reasoning using a new intermediary concept. To explain the magnetic force between two current carrying wires, we will say that the current in the first wire is causing a magnetic field $\vec{B}$ everywhere in space and that the second current-carrying wire feels a magnetic force because of the magnetic field it is placed in.

A good way to learn about the properties of the magnetic field is to describe what are its causes and what are its effects. This is the approach we take below.

General concepts:

• $I$: Electric current flowing in a wire or a loop.
• $\vec{B}$: Magnetic field strength and direction.
• $r$: Distance between two wires.
• $\vec{F}_b$: Magnetic force acting on another wire.
• $\mu_0$: the magnetic constant, or permeability of free space. It is equal to

$4\pi\times10^{-7}$ [Vs/Am] = $1.2566\times10^{-6}$ [H/m]=[N/A^2]

For solenoids we will have:

• $N$: Number of loops in a windings. Each turn of wire in the winding produces and

reacts to the magnetic field. A winding with $N$ turns produces a magnetic

  field that is $N$ times stronger than a single loop of wire.    
* $L$: The length of a winding.
* $n \equiv N/L$: Is the winding density, how many turns per meter.

Each moving charges causes a magnetic field around it. However, the magnetic field created by a single moving charge is very small, so we will usually discuss magnetic fields created by currents.

Current is measured in Amperes [A], which is a equal to Coulombs per second [C/s]. Consider the following piece of wire with a current $3$[A] in it:

  a            b
  --------------
    I= 3 [A]

The above diagram makes no sense, since it does not specify the direction in whist the current is flowing. Let's fix it:

  a            b
  ------>-------
       I=3 [A]

That is better. When we say $I=3$[A], this means that there are 3[C] of charge flowing through this wire every second. The current enters the wire at $a$, and is confined to flow along the wire and thus it has to leave at point $b$.

If we say that the current is negative, this means that the current is flowing in the opposite direction of which the arrow points.

  a            b         a            b  
  ------>-------    =    ------<-------
       I=-1 [A]              I=1 [A]

In the above diagram the current flows from $b$ to $a$, which is equivalent to saying that a negative current flows from $a$ to $b$.

The magnetic field $\vec{B}$ caused at some point $\vec{r}$ by a piece of wire of length $\ell$ carrying a current $I$ is given by \[ \vec{B} = \frac{k_b\ell I}{r^2} \hat{ I} \times \hat{r} = \frac{\mu_0}{4\pi}\frac{\ell I}{r^2} \hat{I} \times \hat{r}. \]

Don't freak out on me now. I know it looks complicated and there a arrows (vectors), cross products ($\times$), but you shouldn't worry. We will brake it down until it makes sense.

First the magnitude part: \[ |\vec{B}| = \frac{k_b \ell I}{r^2}, \] which doesn't seem quite so foreign no? I mean the electric field was the same story $|\vec{E}| = \frac{k_e Q}{r^2}$, where you have some cause $Q$ and the one-over-r-squared weakening plus some constant of proportionality $k_e=\frac{1}{4\pi \epsilon_0}$. The important thing to remember is that the cause of magnetic field is $\ell I$ the product of the current in the wire times the length of the piece of wire. The longer the wire is, the more magnetic field it will cause. This is the reason that people make “magnetic windings” with hundreds of turns instead of using a single loop.

As for the direction, yes we need to think about that for a moment:

• The direction of the magnetic field ${\hat B} = {\hat I} \times {\hat r}$

is perpendicular to both ${\hat I}$ and ${\hat r}$.

• If ${\hat I}$ and ${\hat r}$ point in the same direction then ${\hat B}=0$.

In general you will want to calculate not the magnetic field of a small piece, but of something more complicated. In this book (and in most E&M books), we will discuss three special cases of the magnetic field produced by:

1. $\infty$-long straight wire.
2. Loop of radius $R$.
3. Solenoid of length $L$ with a total of $N$ windings.

Each of these configurations corresponds to a calculation involving an integral. When you see integral think “adding up the pieces” or “adding up the contributions”. We need an integral to calculate the total $\vec{B}$ field because different parts of the wire may contribute to the magnetic field unevenly. specific integral happens to be a vector integral. You don't need to understand the whole machinery of vector integration just yet, but you do need to know how to use the three formulas given below. If you are interested to see how we derived the formulas, you can check out the Derivations section below.

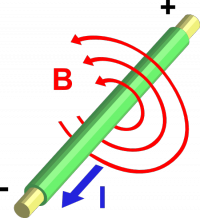If you have take an infinitely long piece of wire and pass a current $I$ through it, you will be creating a magnetic field $\vec{B}$ everywhere around the wire. The magnetic field lines will be circulating around the wire. This is how the magnetic field works.

It is important to get the right direction for the circulation. If you grab a piece of wire with your right hand in such a way that your thumb points in the direction of the current, then the magnetic field lines are circulating around the wire in the same direction as your fingers.

The further away you move from the wire the weaker the magnetic field $\vec{B}$ will get. If a point is $r$ meters away from the wire, the magnitude of the magnetic field at that point will be given by: \[ |\vec{B}| = \mu_0 \frac{I}{2\pi r} \]

This formula was discovered by André-Marie Ampère in 1826.

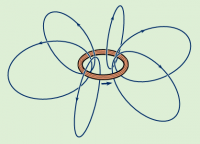If you have a loop of wire that is carrying a current, then the strength of the magnetic field in the centre is going to be: \[ |\vec{B}_{centre}| = 2\pi R \frac{\mu_0}{4\pi} \frac{I}{R^2} = \frac{\mu_0I}{2R}. \]

To get the direction of the magnetic field, you need use the right-hand rule again: grab the loop with your thumb pointed in the same direction of the current and then see which way your fingers point inside the loop.

To create a stronger magnetic field, you can make loop the wire many times to create a winding. Each of the turns in the winding is going to contribute to the magnetic field inside and this way you can get some very strong magnetic fields.

Consider a winding that has $N$ turns and length $L$[m]. We call such a device a solenoid. The magnetic field $\vec{B}$ inside a solenoid is: \[ |\vec{B}| = \mu_0 n I, \] where $n$ is the winding density = number of windings per unit length $n=N/L$ [turns/m].

A charge which is not moving feels no magnetic forces. Only when the charge is moving will it feel a magnetic force, and the faster the charge is moving the stronger the magnetic force will be.

The magnetic force that a charge $q$, moving with velocity $\vec{v}_q$ will field when it is passing through a magnetic field $\vec{B}$ is given by the formula: \[ \vec{F}_b = q (\vec{v}_q \times \vec{B}). \] Observe that the formula involves a cross product. This means that the force on the particle will be perpendicular to both the direction in which it is moving and the direction of the magnetic field. This is the second right-hand rule. Take your open right hand (don't curl your fingers) and place it so that your thumb points in the direction of the velocity and your fingers point in the direction of the magnetic field lines. The magnetic force will be in the direction of your palm.

It is interesting to point out that the magnetic force does zero work. This is because it always acts in a direction perpendicular to the displacement $\vec{d}$: \[ W_b = \vec{F}_b \cdot \vec{d} = 0. \] The magnetic force can change the direction in which the particle is travelling, but not make it go faster or slow it down. Indeed, a moving charged particle placed in a uniform magnetic field will turn around in a circle, because of the centripetal acceleration caused by the magnetic force.

More generally, we can write down the equation for the total electric + magnetic force that a charge feels. The combined force is called the Lorentz force, or electromagnetic force: \[ \vec{F}_{EM} = \underbrace{ q\vec{E} }_{\vec{F}_e} + \underbrace{ q (\vec{v}_q \times \vec{B}) }_{\vec{F}_b}. \]

Consider now a current $I$ flowing in a piece of wire of length $\ell$ placed in a magnetic field $\vec{B}$. The force on the piece of wire will be: \[ \vec{F}_b = \ell \vec{I} \times \vec{B}. \] Observe again that a cross product is used, so we need to use the second right-hand rule again to figure out the direction of the force.

The two scenarios discussed above show how the magnetic field can produce a mechanical force on an object. Magnetic fields can also produce electromotive forces inside a given circuit, that is, the magnetic field can cause (we usually say induce to sound fancy) a voltage inside the circuit and made a current circulate. This phenomenon is called Faraday's law of induction and will be the subject of the next section.

Some of you may feel cheated by this chapter. Here I am telling you to memorizing five formulas without telling you where they come from. Let's fix that.

One of the most important laws for magnetism is Ampere's law. Like Gauss' law electromagnetism, it is not so much a law as a principle from which many laws can be derived.

The statement involves some area of space $A$ with a total current $I_{in}$ passing through that area. Let the closed path $\mathcal{C}$ correspond to the circumference of the area $A$ (the boundary). If you integrate the strength of the magnetic field along the path $\mathcal{C}$ (this is called the circulation), you will find that it is proportional to the total amount of current flowing inside the loop: \[ \oint_{\mathcal{C}} \vec{B} \cdot d\vec{s} = \mu_0 I_{in}. \] Like Gauss' law, Ampere's law simply tells us that we can do the accounting for magnetic phenomena in two different ways: either we calculate the circulation of the magnetic field along the boundary (the path $\mathcal{C}$) or we calculate the total current flowing inside.

The formula of for the strength of the $\vec{B}$ field around an infinitely long wire comes from Ampere's law. Let $\mathcal{C}$ be an imaginary circle of radius $r$ centred on the wire. The $\vec{B}$ field will be constant in magnitude and always pointing along the path of integration so we will get: \[ \oint_{\mathcal{C}} \vec{B} \cdot d\vec{s} = \int_{0}^{2\pi} |\vec{B}| \ r d\theta = |\vec{B}| 2\pi r = \mu_0 I_{in}. \] Solve for $|\vec{B}|$ to obtain the formula for the $\infty$-long wire.

More generally, to calculate the magnetic field produced by some arbitrarily shaped wire $\mathcal{L}$ that is carrying a current $I$ we use the following formula: \[ \vec{B}(\vec{r}) = \int_\mathcal{L}\frac{\mu_0}{4\pi} \frac{I}{|\vec{r}|^2} d\mathbf{l} \times {\hat r}, \] which tells you how strong the magnetic field $\vec{B}$ will be at a point $\vec{r}$. The cause of this field is the current $I$, that is flowing in the length of wire $\mathcal{L}$. The expression is an integral which tells us that we should split the entire length of the wire into little pieces of length $dl$ and add up all their magnetic contributions.

We need an integral because different parts of the wire may contribute to the magnetic field unevenly. This happens to be a vector integral, which you probably have not seen before, and I don't think you need to understand the whole machinery just yet. When you see integral think “adding up the pieces”.

Every time you have a moving charge, there will be a magnetic field $\vec{B}$. Here is a list of real-world phenomena that involve magnetic fields. In each case, when we analyze what is going on we see that some moving charge is causing the magnetic fields.

• light consists of little bundles of energy called photon.

A photon is a wave of EM energy produced by an excited

  electron dropping to a lower energy level in some atom.
* permanent magnets (like a fridge magnet) exhibit magnetic properties 
  because of the many tiny loops of "electron flow" circling around Fe atoms.
* The magnetic field of the earth is caused by the flow of charged 
  magma in the earth's core.

And Mankind saw that magnetic field was good, and decided to make more of it. If moving charges create lots of magnetic field, then let's get lots of charge moving (a current $I$) and then we will have lots of magnetic field!

The following are some practical applications of the magnetic fields and the magnetic forces they produce:

• electromagnet = used to lift cars in the scrap yard, to lock the doors of buildings and to make particles spin around.
• magnetic field inside a motor = used to convert electric energy into mechanical work (think the motor of your elevator, or the one that drops the window down in your car).
• magnetic field inside a generator = used to convert mechanical work into electric energy (think you car's alternator).
• MRI = magnetic resonance imaging allows us to distinguish different molecules

in the human body by using carefully chosen oscillating magnetic fields.

[ Nice pictures of magnetic fields ]
http://en.wikipedia.org/wiki/Magnetic_field
http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/magnetostatics/index.htm

[ An expandable summary of the magnetic field ]
http://www.telescopictext.org/text/pFjkqQY9bmfvQ

[ Good illustrations of the first right-hand rule ]
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html