The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Matrix multiplication
Suppose we are given two matrices A=[abcd],B=[efgh], and we want to multiply them together.
Unlike matrix addition and subtraction, matrix products are not performed element-wise: [abcd][efgh]≠[aebfcgdh].
Instead, the matrix product is computed by taking the dot product of each row of the matrix on the left with each of the columns of the matrix on the right: →r1→r2[abcd] [efgh]→c1 →c2= [→r1⋅→c1→r1⋅→c2→r2⋅→c1→r2⋅→c2] =[ae+bgaf+bhce+dgcf+dh]. Recall that the dot product between to vectors →v and →w is given by →v⋅→w≡∑iviwi.
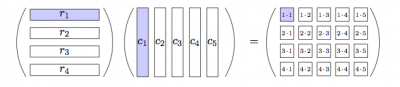
Let's now look at a picture which shows how to compute the product of a matrix with four rows and a matrix with five columns.
The top left entry of the product is computed by taking the dot product of the first row of the matrix on the left and the first column of the matrix on the right:
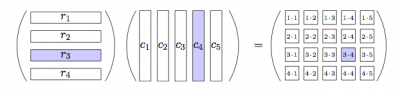
Similarly, the entry on the third row and fourth column of the product is computed by taking the dot product of the third row of the matrix on the left and the fourth column of the matrix on the right:
Note the size of the rows of the matrix on the left must equal the size of the columns of the matrix on the right for the product to be well defined.
Matrix multiplication rules
- Matrix multiplication is associative:
(AB)C=A(BC)=ABC.
- The “touching” dimensions of the matrices must be the same.
For the triple product ABC to exits, the number of rows of A must
be equal to the number of columns of $B$ and the number of rows
of $B$ must equal the number of columns of $C$.
* Given two matrices $A \in \mathbb{R}^{m\times n}$ and $B \in \mathbb{R}^{n\times k}$,
the matrix product $AB$ will be a $m \times k$ matrix.
* The matrix product is //not commutative//:
{{:linear_algebra:linear_algebra--matrix_multiplication_not_commutative.png?300|Matrix multiplication is not commutative.}}
Explanations
Why is matrix multiplication defined like this? We will learn about this more in depth in the linear transformations section, but I don't want you to live in suspense until then, so I will tell you right now. You can think of multiplying some column vector →x∈Rn by a matrix A∈Rm×n as analogous to applying the “vector function” A on the vector input →x to obtain a vector →y: A:Rn→Rm. Applying the vector function A to the input →x is the same as computing the matrix-vector product between A→x: for all →x∈Rn,A(→x)≡A→x. Any linear function from Rn to Rm can be described as a matrix product by some matrix A∈Rm×n.
Okay, so what if you have some vector and you want to apply two linear operations on it. With functions, we call this function composition and we use a little circle to denote it: z=g(f(x))=g∘f(x), where g∘f(x) means that you should apply f to x first to obtain some intermediary value y, and then you apply g to y to get the final output z. The notation g∘f is useful when you don't want to talk about the intermediary variable y and you are interested in the overall functional relationship between x and z. For example, we can define h≡g∘f and then talk about the properties of the function h.
With matrices, B∘A (applying A then B) is equal to applying the product matrix BA: →z=B(A(→x))=(BA)→x. Similar to the case with functions, we can describe the overall map from →x's to →z's by a single entity M≡BA, and not only that, but we can even compute M by taking the product of B and A. So matrix multiplication turns out to be a very useful computational tool. You probably wouldn't have guessed this, given how tedious and boring the actual act of multiplying matrices is. But don't worry, you just have to multiply a couple of matrices by hand to learn how multiplication works. Most of the times, you will let computers multiply matrices for you. They are good at this kind of shit.
This perspective on matrices as linear transformations (functions on vectors) will also allow you to understand why matrix multiplication is not commutative. In general BA≠AB (non-commutativity of matrices), just the same way there is no reason to expect that f∘g will equal g∘f for two arbitrary functions.
Exercises
Basics
Compute the product [1234][5678]=[ ]
Ans: $\left[ \begin{array}{cc}
19&22 \nl
43&50
\end{array}
\right]$