Normal textbooks suck
... so I wrote a better one
Contents
- High school math
- Vectors
- Mechanics
- Derivatives
- Integrals

Contents

Traditional textbooks are too expensive, too long, and too boring.
You don't need to read thousands of pages to learn mechanics and calculus, so why are the required textbooks so long?
Textbook publishers produce such large textbooks
so they can charge you \$150 for each textbook.
They want to get \$300 from you to teach you the basics. That's not cool!
A compact textbook that explains calculus and mechanics concisely and affordably.
Calculus and mechanics are often taught as separate subjects. It shouldn't be like that. If you learn calculus without mechanics, it will be boring. If you learn physics without calculus, you won't truly understand.
By learning both subjects in parallel, you will be able to understand concepts much better.



— Alexandra Shearon, McGill studentIt is literally two heavy textbooks packed into a very light and small book.
— Miriam Aczel, McGill studentFirst of all, I love the book. My only problem has been when I am working through it in the library and start laughing out loud — you have great examples.
— Kevin Del Castillo, studentI like the conversational tone of your writing. It's almost like I'm learning math from a friend.
— Nevenka Peric, studentI found the mechanics part helpful because it summarized the most important points while illustrating some of the less interesting parts — for example, the use of math and physics together. The concepts were reinforced with details which are the essence of solving physics problems.
— Wojciech Pietrzak, developerI'm glad somebody with proper math understanding wrote this excellent piece. The title matches exactly the content, you will not find any boring academic bullshit in this book, but plenty of refreshing learning material about math and physics with charts, diagrams, formulas, and examples.
The book appeared on hacker news,
where it was very well received (topped the homepage for a whole day!).
The book also appeared on reddit.
I was invited to speak about the book on an episode of the TechZing Podcast. The interview is a bit longish, but we discussed a lot of interesting things about the textbook industry and education in general.
Through short tutorials on each of the topics in math, mechanics, and calculus.
In order to learn mechanics, you need to understand calculus. To learn calculus, you need to know about functions and other high school math stuff.
The goal of this book is to be self-contained. Towards this goal, the book begins with a series of tutorials which review the most important concepts of high school math. This is what makes this book special: it comes with prerequisites included.
You are downloading a 720[MB] file from the Internet. At $t=0$[s] you clicked "Save as..." to initiate the download and at $t=600$[s] (10 minutes later) the download completes.
Just start the download and look at the download speed reported by your browser at exactly six minutes and forty seconds.
Let the function $f(t)$ represent the file size of the file.
Suppose that you monitor the file size
during the entire download and observe that it is described by the function:
\[
f(t) = 0.002\,t^2 \qquad \textrm{[MB]}.
\]
We can verify that this function correctly predicts the initial file size at $t=0$[s] ($f(0)=0$[MB])
and the final size at $t=600$[s] ($f(600)=720$[MB]) by plotting its graph:
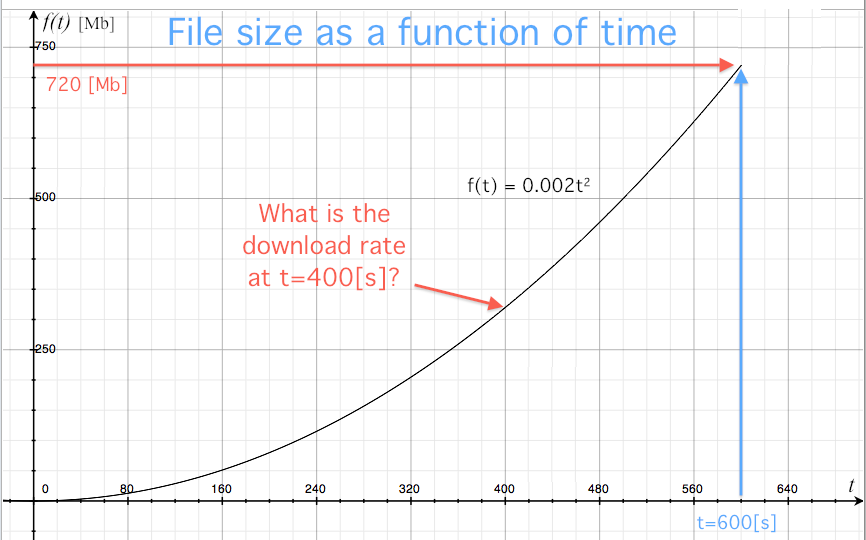
What is the download rate at exactly six minutes and forty seconds into the download?
The download rate corresponds to the slope of the graph of $f(t)$. Recall that the slope of a graph is computed as the rise-over-run for the function. To make the slope calculation easier, you can zoom in on the graph of $f(t)$ near $t=400$[s] and draw a triangle with the same slope as the function.
Observe that that slope of the triangle is exactly the same as the slope of the graph of the function at the point where they touch. The slope of the triangle is equal to the change in $f$ divided by the change in $t$: \[ \textrm{slope}_f(400) = \frac{ \Delta f }{ \Delta t } = \frac{ 255 \textrm{[MB]}}{ 160 \textrm{[s]} } \approx 1.6 \quad \textrm{ [MB/s]}. \] Therefore, the download rate at $t=400$[s] is 1.6[MB/s].
The derivative function $f'(t)$ describes the change in $f(t)$ at all times. In this case, the rate of change of $f(t)$ represents the download speed. Thus, in calculus speak, the questions is asking you to find $f'(400)$.
We will do this in two steps. First we'll compute the derivative using the power-rule formula: \begin{align*} f(t) = a t^n \quad &\Rightarrow \quad f'(t)= a n t^{n-1}. \end{align*} We can use this formula by identifying the variable $a$ with the number $0.002$ and the variable $n$ with the number $2$. The derivative of the file size is: \begin{align*} f(t)=0.002t^2 \textrm{ [MB]} \ \ \Rightarrow \ \ f'(t)=0.004t^1 \textrm{ [MB/s]}. \end{align*}
The second step is to evaluate $f'(t)$ when $t=400$[s]: \[ f'(400) = 0.004(400) = 1.6 \quad \textrm{ [MB/s]}. \] You can verify these calculation using the computer.
It is important to see the connections between the three different ways of finding the answer: the intuitive notion of download speed that we are all familiar with, the graphical notion of "slope of a function," and the abstract notion of the derivative operation which computes the slope of any function. This example serves to illustrate how knowing calculus is useful for solving real world problems. The notion of "rate of change" is crucial to understanding biology, chemistry, business and many other aspects of life.
Trust me on this one, investing some time to learning about abstract concepts like derivatives and integrals is time well spent.
Subscribe to be notified of new book releases and receive exclusive previews of new content.
I've been tutoring math and physics privately for more than 14 years. I did my undergraduate studies at McGill University in electrical engineering, then did a M.Sc. in physics, and recently finished a Ph.D. in compute science. I'm the founder of the ''Minireference Co.'' and I'm on a mission to take over the textbook industry.
