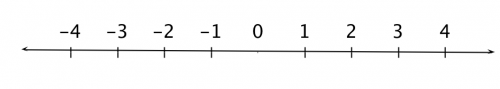<texit info> author=Ivan Savov title=No bullshit guide to MATH and PHYSICS backgroundtext=off </texit>
Front matter
About
This book contains short lessons on topics in math and physics. The coverage of each topic is at the depth required for a university-level course written in a style that is short and to the point. A motivated reader can easily learn enough calculus and mechanics from this book to get an A on the final exam on these subjects. You can learn everything you need to know in two weeks, then you will need another week to practice exercises. Three weeks and you are done.
Calculus and mechanics can be difficult subjects, but they become easy when you break down the concepts into manageable chunks. The most important thing is to learn about the connections between concepts and to understand what is going on intuitively. Every time you learn about some new concept, you need to connect it with all your previous knowledge.
Speaking of previous knowledge...
In order to get off on the right foot, the book begins with a comprehensive review of math fundamentals like algebra, equation solving and functions. Anyone can pick up this book and become proficient in calculus and mechanics regardless of their mathematical background. You can skip the first chapter if you feel comfortable with high school math concepts, though it might still be a good idea for you to do a flyover for review purposes.
Why?
The genesis of this book dates back to my days as an undergraduate student when I was forced to purchase expensive textbooks that were required for my courses. Not only are these textbooks expensive, but they are also long and tedious to read. The standard introductory physics textbook is 1040 pages long and the calculus book is another 1311 pages. I can tell you for a fact that you don't need to read 2300 pages to learn math and physics and calculus, so what is the deal? The reason why mainstream textbooks are so big is that this allows the textbook publishers to suck more money out of you. You wouldn't pay 150 dollars for a 300 page textbook now would you? The fact that a new edition of the textbook comes out every couple of years with almost no changes to the content shows that textbook publishers are not really out to teach you stuff, but only after your money.
Looking at this situation, I said to myself “Something must be done!” and I sat down to write a modern textbook that explains things clearly and concisely. The book you have in your hands.
How?
Each section in this book is like a self-contained private tutorial. Indeed, the lessons you will read grew from my experience as a private tutor. The writing is chill and conversational, but we keep a quick pace through the material. Prerequisites topics are introduced as needed. There are a lot of hands-on explanations through solved examples. We cover the same material as the 400 page textbook in just 40 pages. I call this process information distillation.
Who?
Since this is an “about” section, I will say something about me.
I have been tutoring math and physics privately for more than ten years.
I did my undergraduate studies at McGill University in Electrical Engineering,
then I did a M.Sc. in Physics and I recently completed a Ph.D. in Computer Science.
I have been developing this book in parallel with my studies and,
on the day of my graduation, I founded the Minireference Publishing Co.
revolutionize the textbook industry.
This is the deal. You give me 250 pages of your attention, and I will teach you everything I know about functions, limits, derivatives, integrals, vectors, forces and accelerations. The book which you hold in your hands is the only book you need for the first year of undergraduate studies in science.
Introduction
Before we get started with the equations, it is worthwhile to give a high level overview of the material which we will cover in this book.
In Chapter 1, we
In Chapter 2, we will start to look at how mathematics can be used to describe and model the world around. We will learn about the basic laws which govern the motion of objects in one dimension and the equations that describe them.
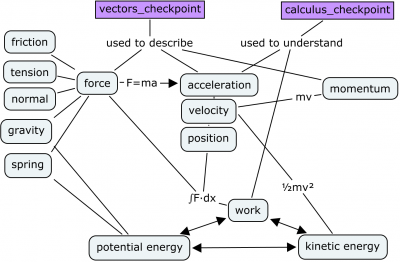
In Chapter 3, we will learn about vectors. Vectors are used to describe directional quantities like, for example, the velocity of a moving object.
Once we know vectors we start to study the motion of objects in the real, three-dimensional world instead of just a single dimension. Chapter 4 is all about Mechanics, which is the study of the motion of objects and more abstract concepts like momentum and energy.
Chapter 5 optics
Chapter 6 covers calculus: limits, derivatives and integrals. Develop these tools….
Finally in Chapter 7 we will study linear algebra
Let's get started.
TODO: ZZZZZ FIX THIS SECTION !
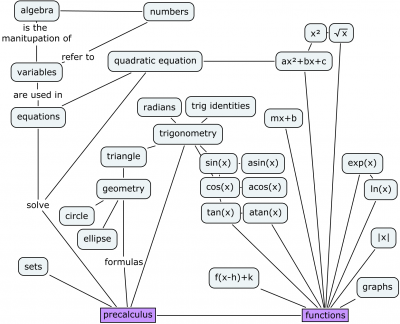
Math fundamentals
In this chapter we will review the fundamental ideas of mathematics like numbers, equations and functions. In order to understand college-level textbooks you need to be comfortable with mathematical calculations. A lot of people have trouble with mathematical calculations, however. Some people say they hate math. Some people are convinced that they could never learn math. Many people carry into their adult life complexes about their math skills as a result of bad grades on math exams they wrote when they were children. If you are carrying any such emotional baggage, you need to drop it right here and right now.
Do not worry about math! You are an adult now, and you can learn math much more easily than when you were in high school. In the next fifty pages we will review everything you need to know about math and, by the end of this chapter, you will see that math is nothing to worry about.
Solving equations
Most math skills boil down to being able to manipulate and solve equations. To solve an equation means to find the value of the unknown in the equation.
Check this shit out: \[ x^2-4=45. \]
To solve the above equation is to answer the question “What is $x$?” More precisely, we want to find the number which can take the place of $x$ in the equation so that the equality holds. In other words, we are asking \[ \text{"Which number times itself minus four gives 45?"} \]
That is quite a mouthful don't you think? To remedy this verbosity, mathematicians often use specialized mathematical symbols. The problem is that the specialized symbols used by mathematicians are confuse people. Sometimes even the simplest concepts are inaccessible if you don't know what the symbols mean.
What are your feelings about math, dear reader? Are you afraid of it? Do you have anxiety attacks because you think it will be too difficult for you? Chill! Relax my brothers and sisters. There is nothing to it. Nobody can magically guess what the solution is immediately. You have to break the problem down into simpler steps.
To find $x$, we can manipulate the original equation until we transform it to a different equation (as true as the first) that looks like this: \[ x= just \ some \ numbers. \]
That's what it means to solve. The equation is solved because you could type the numbers on the right hand side of the equation into a calculator and get the exact value of $x$.
To get $x$, all you have to do is make the right manipulations on the original equation to get it to the final form. The only requirement is that the manipulations you make transform one true equation into another true equation.
Before we continue our discussion, let us take the time to clarify what the equality symbol $=$ means. It means that all that is to the left of $=$ is equal to all that is to the right of $=$. To keep this equality statement true, you have to do everything that you want to do to the left side also to the right side.
In our example from earlier, the first simplifying step will be to add the number four to both sides of the equation: \[ x^2-4 +4 =45 +4, \] which simplifies to \[ x^2 =49. \] You must agree that the expression looks simpler now. How did I know to do this operation? I was trying to “undo” the effects of the operation $-4$. We undo an operation by applying its inverse. In the case where the operation is subtraction of some amount, the inverse operation is the addition of the same amount.
Now we are getting closer to our goal, namely to isolate $x$ on one side of the equation and have just numbers on the other side. What is the next step? Well if you know about functions and their inverses, then you would know that the inverse of $x^2$ ($x$ squared) is to take the square root $\sqrt{ }$ like this: \[ \sqrt{x^2} = \sqrt{49}. \] Notice that I applied the inverse operation on both sides of the equation. If we don't do the same thing on both sides we would be breaking the equality!
We are done now, since we have isolated $x$ with just numbers on the other side: \[ x = \pm 7. \]
What is up with the $\pm$ symbol? It means that both $x=7$ and $x=-7$ satisfy the above equation. Seven squared is 49, and so is $(-7)^2 = 49$ because two negatives cancel out.
If you feel comfortable with the notions of high school math and you could have solved the equation $x^2-4=25$ on your own, then you should consider skipping ahead to Chapter 2. If on the other hand you are wondering how the squiggle killed the power two, then this chapter is for you! In the next sections we will review all the essential concepts from high school math which you will need for the rest of the book. First let me tell you about the different kinds of numbers.
Numbers
We will start the exposition like a philosophy paper and define precisely what we are going to be talking about. At the beginning of all matters we have to define the players in the world of math: numbers.
Definitions
Numbers are the basic objects which you can type into a calculator and which you use to calculate things. Mathematicians like to classify the different kinds of number-like objects into sets:
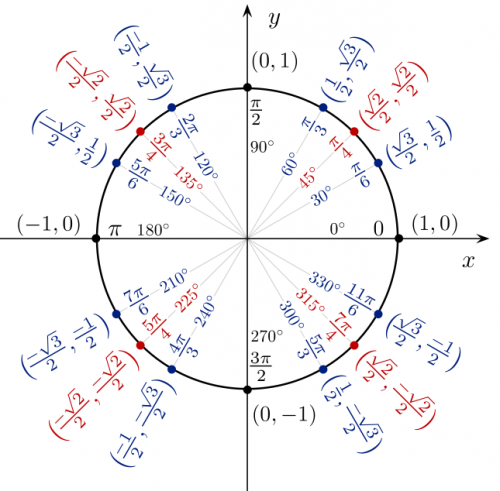
- The Naturals: $\mathbb{N} = \{0,1,2,3,4,5,6,7, \ldots \}$,
- The Integers: $\mathbb{Z} = \{\ldots, -3,-2,-1,0,1,2,3 , \ldots \}$,
- The Rationals: $\mathbb{Q} = \{-1,0,0.125,1,1.5, \frac{5}{3}, \frac{22}{7}, \ldots \} $,
- The Reals: $\mathbb{R} = \{-1,0,1,e,\pi, -1.539..,\ 4.94.., \ \ldots \}$,
- The Complex numbers: $\mathbb{C} = \{ -1, 0, 1, i, 1+i, 2+3i, \ldots \}$.
These categories of numbers should be somewhat familiar to you. Think of them as neat classification labels for everything that you would normally call a number. Each item in the above list is a set. A set is a collection of items of the same kind. Each collection has a name and a precise definition. We don't need to go into the details of sets and set notation for our purposes, but you have to be aware of the different categories. Note also that each of the sets in the above list contains all the sets above it.
Why do you need so many different sets of numbers? The answer is partly historical and partly mathematical. Each of the set of numbers is associated with more and more advanced mathematical problems.
The simplest kind of numbers are the natural numbers $\mathbb{N}$, which are sufficient for all your math needs if all you are going to do is count things. How many goats? Five goats here and six goats there so the total is 11. The sum of any two natural numbers is also a natural number.
However, as soon as you start to use subtraction (the inverse operation of addition), you start to run into negative numbers, which are numbers outside of the set of natural numbers. If the only mathematical operations you will ever use are addition and subtraction then the set of integers $\mathbb{Z} = \{ \ldots, -2, -1, 0, 1, 2, \ldots \}$ would be sufficient. Think about it. Any integer plus or minus any other integer is still an integer.
You can do a lot of interesting math with integers. There is an entire field in math called number theory which deals with integers. However, if you restrict yourself to integers you would be limiting yourself somewhat. You can't use the notion of 2.5 goats for example. You would get totally confused by the menu at Rotisserie Romados which offers $\frac{1}{4}$ of a chicken.
If you want to use division in your mathematical calculations then you will need the rationals $\mathbb{Q}$. The rationals are the set of quotients of two integers: \[ \mathbb{Q} = \{ \text{ all } z \text{ such that } z=\frac{x}{y}, x \text{ is in } \mathbb{Z}, y \text{ is in } \mathbb{N}, y \neq 0 \}. \] You can add, subtract, multiply and divide rational numbers and the result will always be a rational number. However even rationals are not enough for all of math!
In geometry, we can obtain quantities like $\sqrt{2}$ (the diagonal of a square with side 1) and $\pi$ (the ratio between a circle's circumference and its diameter) which are irrational. There are no integers $x$ and $y$ such that $\sqrt{2}=\frac{x}{y}$, therefore, $\sqrt{2}$ is not part of $\mathbb{Q}$. We say that $\sqrt{2}$ is irrational. An irrational number has an infinitely long decimal expansion. For example, $\pi = 3.1415926535897931..$ where the dots indicate that the decimal expansion of $\pi$ continues all the way to infinity.
If you add the irrational numbers to the rationals you get all the useful numbers, which we call the set of real numbers $\mathbb{R}$. The set $\mathbb{R}$ contains the integers, the fractions $\mathbb{Q}$, as well as irrational numbers like $\sqrt{2}=1.4142135..$. You will see that using the reals you can compute pretty much anything you want. From here on in the text, if I say number I will mean an element of the set of real numbers $\mathbb{R}$.
The only thing you can't do with the reals is take the square root of a negative number—you need the complex numbers for that. We defer the discussion on $\mathbb{C}$ until Chapter 3.
Operations on numbers
Addition
You can add and subtract numbers. I will assume you are familiar with this kind of stuff. \[ 2+5=7,\ 45+56=101,\ 65-66=-1,\ 9999 + 1 = 10000,\ \ldots \]
The visual way to think of addition is the number line. Adding numbers is like adding sticks together: the resulting stick has length equal to the sum of the two constituent sticks.
Addition is commutative, which means that $a+b=b+a$. It is also associative, which means that if you have a long summation like $a+b+c$ you can compute it in any order $(a+b)+c$ or $a+(b+c)$ and you will get the same answer.
Subtraction is the inverse operation of addition.
Multiplication
You can also multiply numbers together. \[ ab = \underbrace{a+a+\cdots+a}_{b \ times}=\underbrace{b+b+\cdots+b}_{a \ times}. \] Note that multiplication can be defined in terms of repeated addition.
The visual way to think about multiplication is through the concept of area. The area of a rectangle of base $a$ and height $b$ is equal to $ab$. A rectangle which has height equal to its base is a square, so this why we call $aa=a^2$ “$a$ squared.”
Multiplication of numbers is also commutative $ab=ba$, and associative $abc=(ab)c=a(bc)$. In modern notation, no special symbol is used to denote multiplication; we simply put the two factors next to each other and say that the multiplication is implicit. Some other ways to denote multiplication are $a\cdot b$, $a\times b$ and, on computer systems, $a*b$.
Division
Division is the inverse of multiplication. \[ a/b = \frac{a}{b} = \text{ one } b^{th} \text{ of } a. \] Whatever $a$ is, you need to divide it into $b$ equal pieces and take one such piece. Some texts denote division by $a\div b$.
Note that you cannot divide by $0$. Try it on your
calculator or computer. It will say error divide by zero,
because it simply doesn't make sense.
What would it mean to divide something into zero equal pieces?
Exponentiation
Very often you have to multiply things together many times. We call that exponentiation and denote that with a superscript: \[ a^b = \underbrace{aaa\cdots a}_{b\ times}. \]
We can also have negative exponents. The negative in the exponent does not mean “subtract”, but rather “divide by”: \[ a^{-b}=\frac{1}{a^b}=\frac{1}{\underbrace{aaa\cdots a}_{b\ times}}. \]
An exponent which is a fraction means that it is some sort of square-root-like operation: \[ a^{\frac{1}{2}} \equiv \sqrt{a} \equiv \sqrt[2]{a}, \qquad a^{\frac{1}{3}} \equiv \sqrt[3]{a}, \qquad a^{\frac{1}{4}} \equiv \sqrt[4]{a} = a^{\frac{1}{2}\frac{1}{2}}=\left(a^{\frac{1}{2}}\right)^{\frac{1}{2}} = \sqrt{\sqrt{a}}. \] Square root $\sqrt{x}$ is the inverse operation of $x^2$. Similarly, for any $n$ we define the function $\sqrt[n]{x}$ (the $n$th root of $x$) to be the inverse function of $x^n$.
It is worth clarifying what “taking the $n$th root” means and what this operation can be used for. The $n$th root of $a$ is a number which, when multiplied together $n$ times, will give $a$. So for example a cube root satisfies \[ \sqrt[3]{a} \sqrt[3]{a} \sqrt[3]{a} = \left( \sqrt[3]{a} \right)^3 = a = \sqrt[3]{a^3}. \] Do you see now why $\sqrt[3]{x}$ and $x^3$ are inverse operations?
The fractional exponent notation makes the meaning of roots much more explicit: \[ \sqrt[n]{a} \equiv a^{\frac{1}{n}}, \] which means that $n$th root is equal to one $n$th of a number with respect to multiplication. Thus, if we want the whole number, we have to multiply the number $a^{\frac{1}{n}}$ times itself $n$ times: \[ \underbrace{a^{\frac{1}{n}}a^{\frac{1}{n}}a^{\frac{1}{n}}a^{\frac{1}{n}} \cdots a^{\frac{1}{n}}a^{\frac{1}{n}}}_{n\ times} = \left(a^{\frac{1}{n}}\right)^n = a^{\frac{n}{n}} = a^1 = a. \] The $n$-fold product of $\frac{1}{n}$ fractional exponents of any number products the number with exponent one, therefore the inverse operation of $\sqrt[n]{x}$ is $x^n$.
The commutative law of multiplication $ab=ba$ implies that we can see any fraction $\frac{a}{b}$ in two different ways $\frac{a}{b}=a\frac{1}{b}=\frac{1}{b}a$. First we multiply by $a$ and then divide the result by $b$, or first we divide by $b$ and then we multiply the result by $a$. This means that when we have a fraction in the exponent, we can write the answer in two equivalent ways: \[ a^{\frac{2}{3} }=\sqrt[3]{a^2} = (\sqrt[3]{a})^2, \qquad a^{-\frac{1}{2}}=\frac{1}{a^{\frac{1}{2}}} = \frac{1}{\sqrt{a}}, \qquad a^{\frac{m}{n}} = \left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}. \]
Make sure the above notation makes sense to you. As an exercises try to compute $5^{\frac{4}{3}}$ on your calculator, and check that you get around 8.54987973.. as an answer.
Operator precedence
There is a standard convention for the order in which mathematical operations have to be performed. The three basic operations have the following precedence:
- Exponents and roots.
- Products and divisions.
- Additions and subtractions.
This means that the expression $5\times3^2+13$ is interpreted as “first take the square of $3$, then multiply by $5$ and then add $13$.” If you want the operations to be carried out in a different order, say you wanted to multiply $5$ times $3$ first and then take the square you should use parentheses: $(5\times 3)^2 + 13$, which now shows that the square acts on $(5 \times 3)$ as a whole and not on $3$ alone.
Other operations
We can define all kinds of operations on numbers. The above three are special since they have a very simple intuitive feel to them, but we can define arbitrary transformations on numbers. We call those functions. Before we learn about functions, let us talk about variables first.
Variables
In math we use a lot of variables, which are placeholder names for any number or unknown.
Example
Your friend has some weirdly shaped shooter glasses and you can't quite tell if it is 25[ml] of vodka in there or 50[ml] or somewhere in between. Since you can't say how much booze there is in each shot glass we will say there was $x$[ml] in there. So how much alcohol did you drink over the whole evening? Say you had three shots then you drank $3x$[ml] of vodka. If you want to take it one step further, you can say that you drank $n$ shots then the total amount of alcohol you drank is $nx$[ml].
As you see, variables allow us to talk about quantities without knowing the details. This is abstraction and is very powerful stuff: it allows you to get drunk without knowing how drunk exactly!
Variable names
There are common naming patterns for variables:
- $x$: general name for the unknown in equations. Also used to denote the input to a function
and the position in physics problems.
- $v$: velocity.
- $\theta,\varphi$: the Greek letters “theta” and “phi” are often used to denote angles.
- $x_i,x_f$: Denote initial and final position in physics problems.
- $X$: A random variable in probability theory.
- $C$: Costs in business along with $P$ profit, and $R$ revenues.
Variable substitution
We often need to “change variables” and replace some unknown variable with another. For example, say you don't feel comfortable with square roots. Every time you see a square root, you freak out and you find yourself on an exam trying to solve for $x$ in the following: \[ \frac{6}{5 - \sqrt{x}} = \sqrt{x}. \] Needless to say that you are freaking out big time! Substitution can help with your root phobia. You just write down “Let $u=\sqrt{x}$” and then you are allowed to rewrite the equation in terms of $u$: \[ \frac{6}{5 - u} = u, \] which contains no square roots.
The next step when trying to solve for $u$ is to undo the fraction by multiplying both sides of the equation by $(5-u)$ to obtain: \[ 6 = u(5-u) = 5u - u^2. \] This can be rewritten as a quadratic equation $u^2-5u+6=(u-2)(u-3)=0$ for which $u_1=2$ and $u_2=3$ are the solutions. The last step is to convert our $u$-answers into $x$-answers by using $u=\sqrt{x}$, which is equivalent to $x = u^2$. The final answers are $x=2^2=4$ and $x=3^2=9$. You should try plugging these values of $x$ into the original equation with the square root to verify that they satisfy the equation.
Compact notation
Symbolic manipulation is very powerful, because it allows you to manage complexity. Say you are solving a physics problem in which you are told the mass of an object is $m=140$[kg]. If there are many steps in the calculation, would you rather use the number $140$[kg] in each step, or the shorter variable $m$? It is much better to use the variable $m$ throughout your calculation, and only substitute the value $140$[kg] in the last step when you are computing the final answer.
Functions and their inverses
As we saw in the section on solving equations, the ability to “undo” functions is a key skill to have when solving equations.
Example
Suppose you have to solve for $x$ in the equation \[ f(x) = c. \] where $f$ is some function and $c$ is some constant. Our goal is to isolate $x$ on one side of the equation but there is the function $f$ standing in our way.
The way to get rid of $f$ is to apply the inverse function (denoted $f^{-1}$) which will “undo” the effects of $f$. We find that: \[ f^{-1}\!\left( f(x) \right) = x = f^{-1}\left( c \right). \] By definition the inverse function $f^{-1}$ does the opposite of what the function $f$ does so together they cancel each other out. We have $f^{-1}(f(x))=x$ for any number $x$.
Provided everything is kosher (the function $f^{-1}$ must be defined for the input $c$), the manipulation we made above was valid and we have obtained the answer $x=f^{-1}( c)$.
\[ \ \]
Note the new notation for denoting the function inverse $f^{-1}$ that we introduced in the above example. This notation is borrowed from the notion of “inverse number”. Multiplication by the number $d^{-1}$ is the inverse operation of multiplication by the number $d$: $d^{-1}dx=1x=x$. In the case of functions, however, the negative one exponent does not mean the inverse number $\frac{1}{f(x)}=(f(x))^{-1}$ but functions inverse, i.e., the number $f^{-1}(y)$ is equal to the number $x$ such that $f(x)=y$.
You have to be careful because sometimes the applying the inverse leads to multiple solutions. For example, the function $f(x)=x^2$ maps two input values ($x$ and $-x$) to the same output value $x^2=f(x)=f(-x)$. The inverse function of $f(x)=x^2$ is $f^{-1}(x)=\sqrt{x}$, but both $x=+\sqrt{c}$ and $x=-\sqrt{c}$ would be solutions to the equation $x^2=c$. A shorthand notation to indicate the solutions for this equation is $x=\pm c$.
Formulas
Here is a list of common functions and their inverses:
\[ \begin{align*} \textrm{function } f(x) & \ \Leftrightarrow \ \ \textrm{inverse } f^{-1}(x) \nl x+2 & \ \Leftrightarrow \ \ x-2 \nl 2x & \ \Leftrightarrow \ \ \frac{1}{2}x \nl -x & \ \Leftrightarrow \ \ -x \nl x^2 & \ \Leftrightarrow \ \ \pm\sqrt{x} \nl 2^x & \ \Leftrightarrow \ \ \log_{2}(x) \nl 3x+5 & \ \Leftrightarrow \ \ \frac{1}{3}(x-5) \nl a^x & \ \Leftrightarrow \ \ \log_a(x) \nl \exp(x)=e^x & \ \Leftrightarrow \ \ \ln(x)=\log_e(x) \nl \sin(x) & \ \Leftrightarrow \ \ \arcsin(x)=\sin^{-1}(x) \nl \cos(x) & \ \Leftrightarrow \ \ \arccos(x)=\cos^{-1}(x) \end{align*} \]
The function-inverse relationship is reflexive. This means that if you see a function on one side of the above table (no matter which), then its inverse is on the opposite side.
Example
Let's say your teacher doesn't like you and right away on the first day of classes, he gives you a serious equation and wants you to find $x$: \[ \log_5\left(3 + \sqrt{6\sqrt{x}-7} \right) = 34+\sin(5.5)-\Psi(1). \] Do you see now what I meant when I said that the teacher doesn't like you?
First note that it doesn't matter what $\Psi$ is, since $x$ is on the other side of the equation. We can just keep copying $\Psi(1)$ from line to line and throw the ball back to the teacher in the end: “My answer is in terms of your variables dude. You have to figure out what the hell $\Psi$ is since you brought it up in the first place.” The same goes with $\sin(5.5)$. If you don't have a calculator, don't worry about it. We will just keep the expression $\sin(5.5)$ instead of trying to find its numerical value. In general, you should try to work with variables as much as possible and leave the numerical computations for the last step.
OK, enough beating about the bush. Let's just find $x$ and get it over with! On the right side of the equation, we have the sum of a bunch of terms and no $x$ in them so we will just leave them as they are. On the left-hand side, the outer most function is a logarithm base $5$. Cool. No problem. Looking in the table of inverse functions we find that the exponential function is the inverse of the logarithm: $a^x \Leftrightarrow \log_a(x)$. To get rid of the $\log_5$ we must apply the exponential function base five to both sides: \[ 5^{ \log_5\left(3 + \sqrt{6\sqrt{x}-7} \right) } = 5^{ 34+\sin(5.5)-\Psi(1) }, \] which simplifies to: \[ 3 + \sqrt{6\sqrt{x}-7} = 5^{ 34+\sin(5.5)-\Psi(1) }, \] since $5^x$ canceled the $\log_5 x$.
From here on it is going to be like if Bruce Lee walked into a place with lots of bad guys. Addition of $3$ is undone by subtracting $3$ on both sides: \[ \sqrt{6\sqrt{x}-7} = 5^{ 34+\sin(5.5)-\Psi(1) } - 3. \] To undo a square root you take the square \[ 6\sqrt{x}-7 = \left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2. \] Add $7$ to both sides \[ 6\sqrt{x} = \left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2+7. \] Divide by $6$: \[ \sqrt{x} = \frac{1}{6}\left(\left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2+7\right), \] and then we square again to get the final answer: \[ \begin{align*} x &= \left[\frac{1}{6}\left(\left(5^{ 34+\sin(5.5)-\Psi(1) } - 3\right)^2+7\right) \right]^2. \end{align*} \]
Did you see what I was doing in each step? Next time a function stands in your way, hit it with its inverse, so that it knows not to ever challenge you again.
Discussion
The recipe I have outlined above is not universal. Sometimes $x$ isn't alone on one side. Sometimes $x$ appears in several places in the same equation so can't just work your way towards $x$ as shown above. You need other techniques for solving equations like that.
The bad news is that there is no general formula for solving complicated equations. The good news is that the above technique of “digging towards $x$” is sufficient for 80% of what you are going to be doing. You can get another 15% if you learn how to solve the quadratic equation: \[ ax^2 +bx + c = 0. \]
Solving third order equations $ax^3+bx^2+cx+d=0$ with pen and paper is also possible, but at this point you really might as well start using a computer to solve for the unknown(s).
There are all kinds of other equations which you can learn how to solve: equations with multiple variables, equations with logarithms, equations with exponentials, and equations with trigonometric functions. The principle of digging towards the unknown and applying the function inverse is very important so be sure to practice it.
Basic rules of algebra
It's important for you to know the general rules for manipulating numbers and variables (algebra) so we will do a little refresher on these concepts to make sure you feel comfortable on that front. We will also review some important algebra tricks like factoring and completing the square which are useful when solving equations.
When an expression contains multiple things added together, we call those things terms. Furthermore, terms are usually composed of many things multiplied together. If we can write a number $x$ as $x=abc$, we say that $x$ factors into $a$, $b$ and $c$. We call $a$, $b$ and $c$ the factors of $x$.
Given any four numbers $a,b,c$ and $d$, we can use the following algebra properties:
- Associative property: $a+b+c=(a+b)+c=a+(b+c)$ and $abc=(ab)c=a(bc)$.
- Commutative property: $a+b=b+a$ and $ab=ba$.
- Distributive property: $a(b+c)=ab+ac$.
We use the distributive property every time we expand a bracket. For example $a(b+c+d)=ab + ac + ad$. The opposite operation of expanding is called factoring and consists of taking out the common parts of an expression to the front of a bracket: $ac+ac = a(b+c)$. We will discuss both of these operations in this section and illustrate what they are used for.
Expanding brackets
The distributive property is useful when you are dealing with polynomials: \[ (x+3)(x+2)=x(x+2) + 3(x+2)= x^2 +x2 +3x + 6. \] We can now use the commutative property on the second term $x2=2x$, and then combine the two $x$ terms into a single one to obtain \[ (x+3)(x+2)= x^2 + 5x + 6. \]
This calculation shown above happens so often that it is good idea to see it in more abstract form: \[ (x+a)(x+b) = x(x+b) + a(x+b) = x^2 + (a+b)x + ab. \] The product of two linear terms (expressions of the form $x+?$) is equal to a quadratic expression. Furthermore, observe that the middle term on the right-hand side contains the sum of the two constants on the left-hand side while the third term contains the their product.
It is a very common for people to get this wrong and write down false equations like $(x+a)(x+b)=x^2+ab$ or $(x+a)(x+b)=x^2+a+b$ or some variation of the above. You will never make such a mistake if you keep in mind the distributive property and expand the expression using a step-by-step approach. As a second example, consider the slightly more complicated algebraic expression and its expansion: \[ \begin{align*} (x+a)(bx^2+cx+d) &= x(bx^2+cx+d) + a(bx^2+cx+d) \nl &= bx^3+cx^2+dx + abx^2 +acx +ad \nl &= bx^3+ (c+ab)x^2+(d+ac)x +ad. \end{align*} \] Note how we grouped together all the terms which contain $x^2$ in one term and all the terms which contain $x$ in a second term. This is a common pattern when dealing with expressions which contain different powers of $x$.
Example
Suppose we are asked to solve for $t$ in the following equation \[ 7(3 + 4t) = 11(6t - 4). \] The unknown $t$ appears on both sides of the equation so it is not immediately obvious how to proceed.
To solve for $t$ in the above equation, we have to bring all the $t$ terms to one side and all the constant terms to the other side. The first step towards this goal is to expand the two brackets to obtain \[ 21 + 28t = 66t - 44. \] Now we move things around to get all the $t$s on the right-hand side and all the constants on the left-hand side \[ 21 + 44 = 66t - 28t. \] We see that $t$ is contained in both terms on the right-hand side so we can rewrite the equation as \[ 21 + 44 = (66 - 28)t. \] The answer is now obvious $t = \frac{21 + 44}{66 - 28} = \frac{65}{38}$.
Factoring
Factoring means to take out some common part in a complicated expression so as to make it more compact. Suppose you are given the expression $6x^2y + 15x$ and you are asked to simplify it by “taking out” common factors. The expression has two terms and when we split each terms into it constituent factors we obtain: \[ 6x^2y + 15x = (3)(2)(x)(x)y + (5)(3)x. \] We see that the factors $x$ and $3$ appear in both terms. This means we can factor them out to the front like this: \[ 6x^2y + 15x = 3x(2xy+5). \] The expression on the right is easier to read than the expression on the right since it shows that the $3x$ part is common to both terms.
Here is another example of where factoring can help us simplify an expression: \[ 2x^2y + 2x + 4x = 2x(xy+1+2) = 2x(xy+3). \]
Quadratic factoring
When dealing with a quadratic function, it is often useful to rewrite it as a product of two factors. Suppose you are given the quadratic function $f(x)=x^2-5x+6$ and asked to describe its properties. What are the roots of this function, i.e., for what values of $x$ is this function equal to zero? For which values of $x$ is the function positive and for which values is it negative?
When looking at the expression $f(x)=x^2-5x+6$, the properties of the function are not immediately apparent. However, if we factor the expression $x^2+5x+6$, we will be able to see its properties more clearly. To factor a quadratic expression is to express it as product of two factors: \[ f(x) = x^2-5x+6 = (x-2)(x-3). \] We can now see immediately that its solutions (roots) are at $x_1=2$ and $x_2=3$. You can also see that, for $x>3$, the function is positive since both factors will be positive. For $x<2$ both factors will be negative, but a negative times a negative gives positive, so the function will be positive overall. For values of $x$ such that $2<x<3$, the first factor will be positive, and the second negative so the overall function will be negative.
For some simple quadratics like the above one you can simply guess what the factors will be. For more complicated quadratic expressions, you need to use the quadratic formula. This will be the subject of the next section. For now let us continue with more algebra tricks.
Completing the square
Any quadratic expression $Ax^2+Bx+C$ can be written in the form $A(x-h)^2+k$. This is because all quadratic functions with the same quadratic coefficient are essentially shifted versions of each other. By completing the square we are making these shifts explicit. The value of $h$ is how much the function is shifted to the right and the value $k$ is the vertical shift.
Let's try to find the values $A,k,h$ for the quadratic expression discussed in the previous section: \[ x^2+5x+6 = A(x-h)^2+k = A(x^2-2hx + h^2) + k = Ax^2 - 2Ahx + Ah^2 + k. \]
By focussing on the quadratic terms on both sides of the equation we see that $A=1$, so we have \[ x^2+\underline{5x}+6 = x^2 \underline{-2hx} + h^2 + k. \] Next we look at the terms multiplying $x$ (underlined), and we see that $h=-2.5$, so we obtain \[ x^2+5x+\underline{6} = x^2 - 2(-2.5)x + \underline{(-2.5)^2 + k}. \] Finally, we pick a value of $k$ which would make the constant terms (underlined again) match \[ k = 6 - (-2.5)^2 = 6 - (2.5)^2 = 6 - \left(\frac{5}{2}\right)^2 = 6\times\frac{4}{4} - \frac{25}{4} = \frac{24 - 25}{4} = \frac{-1}{4}. \] This is how we complete the square, to obtain: \[ x^2+5x+6 = (x+2.5)^2 - \frac{1}{4}. \] The right-hand side in the above expression tells us that our function is equivalent to the basic function $x^2$, shifted $2.5$ units to the left, and $\frac{1}{4}$ units downwards. This would be really useful information if you ever had to draw this function, since it is easy to plot the basic graph of $x^2$ and then shift it appropriately.
It is important that you become comfortable with the procedure for completing the square outlined above. It is not very difficult, but it requires you to think carefully about the unknowns $h$ and $k$ and to choose their values appropriately. There is a simple rule you can remember for completing the square in an expression of the form $x^2+bx+c=(x-h)^2+k$: you have to use half of the coefficient of the $x$ term inside the bracket, i.e., $h=-\frac{b}{2}$. You can then work out both sides of the equation and choose $k$ so that the constant terms match. Take out a pen and a piece of paper now and verify that you can correctly complete the square in the following expressions $x^{2} - 6 x + 13=(x-3)^2 + 4$ and $x^{2} + 4 x + 1=(x + 2)^2 -3$.
Solving quadratic equations
What would you do if you were asked to find $x$ in the equation $x^2 = 45x + 23$? This is called a quadratic equation since it contains the unknown variable $x$ squared. The name name comes from the Latin quadratus, which means square. Quadratic equations come up very often so mathematicians came up with a general formula for solving these equations. We will learn about this formula in this section.
Before we can apply the formula, we need to rewrite the equation in the form \[ ax^2 + bx + c = 0, \] where we moved all the numbers and $x$s to one side and left only $0$ on the other side. This is the called the standard form of the quadratic equation. For example, to get the expression $x^2 = 45x + 23$ into the standard form, we can subtract $45x+23$ from both sides of the equation to obtain $x^2 - 45x - 23 = 0$. What are the values of $x$ that satisfy this formula?
Claim
The solutions to the equation \[ ax^2 + bx + c = 0, \] are \[ x_1 = \frac{-b + \sqrt{b^2-4ac} }{2a} \ \ \text{ and } \ \ x_2 = \frac{-b - \sqrt{b^2-4ac} }{2a}. \]
Let us now see how this formula is used to solve the equation $x^2 - 45x - 23 = 0$. Finding the two solutions is a simple mechanical task of identifying $a$, $b$ and $c$ and plugging these numbers into the formula: \[ x_1 = \frac{45 + \sqrt{45^2-4(1)(-23)} }{2} = 45.5054\ldots, \] \[ x_2 = \frac{45 - \sqrt{45^2-4(1)(-23)} }{2} = -0.5054\ldots. \]
Proof of claim
This is an important proof. You should know how to derive the quadratic formula in case your younger brother asks you one day to derive the formula from first principles. To derive this formula, we will use the completing-the-square technique which we saw in the previous section. Don't bail out on me now, the proof is only two pages.
Starting from the equation $ax^2 + bx + c = 0$, our first step will be to move $c$ to the other side of the equation \[ ax^2 + bx = -c, \] and then to divide by $a$ on both sides \[ x^2 + \frac{b}{a}x = -\frac{c}{a}. \]
Now we must complete the square on the left-hand side, which is to say we ask the question: what are the values of $h$ and $k$ for this equation to hold \[ (x-h)^2 + k = x^2 + \frac{b}{a}x = -\frac{c}{a}? \] To find the values for $h$ and $k$, we will expand the left-hand side to obtain $(x-h)^2 + k= x^2 -2hx +h^2+k$. We can now identify $h$ by looking at the coefficients in front of $x$ on both sides of the equation. We have $-2h=\frac{b}{a}$ and hence $h=-\frac{b}{2a}$.
So what do we have so far: \[ \left(x + \frac{b}{2a} \right)^2 = \left(x + \frac{b}{2a} \right)\!\!\left(x + \frac{b}{2a} \right) = x^2 + \frac{b}{2a}x + x\frac{b}{2a} + \frac{b^2}{4a^2} = x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}. \] If we want to figure out what $k$ is, we just have to move that last term to the other side: \[ \left(x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a^2} = x^2 + \frac{b}{a}x. \]
We can now continue with the proof where we left off \[ x^2 + \frac{b}{a}x = -\frac{c}{a}. \] We replace the left-hand side by the complete-the-square expression and obtain \[ \left(x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a^2} = -\frac{c}{a}. \] From here on, we can use the standard procedure for solving equations. We put all the constants on the right-hand side \[ \left(x + \frac{b}{2a} \right)^2 = -\frac{c}{a} + \frac{b^2}{4a^2}. \] Next we take the square root of both sides. Since the square function maps both positive and negative numbers to the same value, this step will give us two solutions: \[ x + \frac{b}{2a} = \pm \sqrt{ -\frac{c}{a} + \frac{b^2}{4a^2} }. \] Let's take a moment to cleanup the mess on the right-hand side a bit: \[ \sqrt{ -\frac{c}{a} + \frac{b^2}{4a^2} } = \sqrt{ -\frac{(4a)c}{(4a)a} + \frac{b^2}{4a^2} } = \sqrt{ \frac{- 4ac + b^2}{4a^2} } = \frac{\sqrt{b^2 -4ac} }{ 2a }. \]
Thus we have: \[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 -4ac} }{ 2a }, \] which is just one step away from the final answer \[ x = \frac{-b}{2a} \pm \frac{\sqrt{b^2 -4ac} }{ 2a } = \frac{-b \pm \sqrt{b^2 -4ac} }{ 2a }. \] This completes the proof.
Alternative proof of claim
To have a proof we don't necessarily need to show the derivation of the formula as we did. The claim was that $x_1$ and $x_2$ are solutions. To prove the claim we could have simply plugged $x_1$ and $x_2$ into the quadratic equation and verified that we get zero. Verify on your own.
Applications
The Golden Ratio
The golden ratio, usually denoted $\varphi=\frac{1+\sqrt{5}}{2}=1.6180339\ldots$ is a very important proportion in geometry, art, aesthetics, biology and mysticism. It comes about from the solution to the quadratic equation \[ x^2 -x -1 = 0. \]
Using the quadratic formula we get the two solutions: \[ x_1 = \frac{1+\sqrt{5}}{2} = \varphi, \qquad x_2 = \frac{1-\sqrt{5}}{2} = - \frac{1}{\varphi}. \]
You can learn more about the various contexts in which the golden ratio appears from the excellent wikipedia article on the subject. We will also see the golden ratio come up again several times in the remainder of the book.
Explanations
Multiple solutions
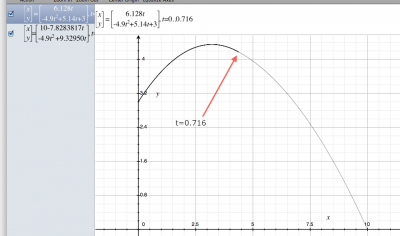
Often times, we are interested in only one of the two solutions to the quadratic equation. It will usually be obvious from the context of the problem which of the two solutions should be kept and which should be discarded. For example, the time of flight of a ball thrown in the air from a height of $3$ meters with an initial velocity of $12$ meters per second is obtained by solving a quadratic equation $0=(-4.9)t^2+12t+3$. The two solutions of the quadratic equation are $t_1=-0.229$ and $t_2=2.678$. The first answer $t_1$ corresponds to a time in the past so must be rejected as invalid. The correct answer is $t_2$. The ball will hit the ground after $t=2.678$ seconds.
Relation to factoring
In the previous section we discussed the quadratic factoring operation by which we could rewrite a quadratic function as the product of two terms $f(x)=ax^2+bx+c=(x-x_1)(x-x_2)$. The two numbers $x_1$ and $x_2$ are called the roots of the function: this is where the function $f(x)$ touches the $x$ axis.
Using the quadratic equation you now have the ability to factor any quadratic equation. Just use the quadratic formula to find the two solutions $x_1$ and $x_2$ and then you can rewrite the expression as $(x-x_1)(x-x_2)$.
Some quadratic expression cannot be factored, however. These correspond to quadratic functions whose graphs do not touch the $x$ axis. They have no solutions (no roots). There is a quick test you can use to check if a quadratic function $f(x)=ax^2+bx+c$ has roots (touches or crosses the $x$ axis) or doesn't have roots (never touches the $x$ axis). If $b^2-4ac>0$ then the function $f$ has two roots. If $b^2-4ac=0$, the function has only one root. This corresponds to the special case when the function touches the $x$ axis only at one point. If $b^2-4ac<0$, the function has no real roots. If you try to use the formula for finding the solutions, you will fail because taking the square root of a negative number is not allowed. Think about it—how could you square a number and obtain a negative number?
Exponents
We often have to multiply together the same number many times in math so we use the notation \[ b^n = \underbrace{bbb \cdots bb}_{n \text{ times} } \] to denote some number $b$ multiplied by itself $n$ times. In this section we will review the basic terminology associated with exponents and discuss their properties.
Definitions
The fundamental ideas of exponents are:
- $b^n$: the number $b$ raised to the power $n$
- $b$: the base
- $n$: the exponent or power of $b$ in the expression $b^n$
By definitions, the zeroth power of any number is equal to one $b^0=1$.
We can also discuss exponential functions of the form $f:\mathbb{R} \to \mathbb{R}$ Define following functions:
- $b^x$: the exponential function base $b$
- $10^x$: the exponential function base $10$
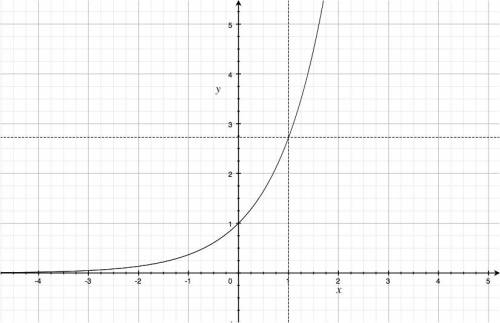
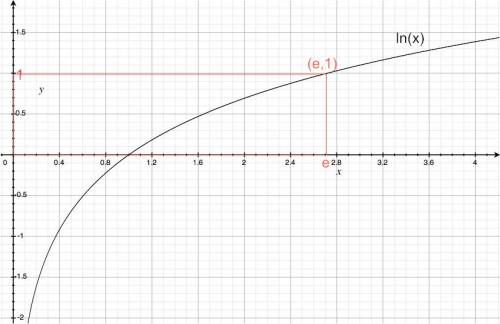
- $\exp(x)=e^x$: the exponential function base $e$. The number $e$ is called Euler's number.
- $2^x$: the exponential function base $2$. This function is very important in computer science.
The number $e=2.7182818\ldots$ is a special base that has lots of applications. We call $e$ the natural base.
Another special base is $10$ because we use the decimal system for our numbers. We can write down very large numbers and very small numbers as powers of $10$. For example, one thousand can be written as $1\:000=10^3$, one million is $1\:000\:000=10^6$ and one billion is $1\:000\:000\:000=10^9$.
Formulas
The following properties follow from the definition of exponentiation as repeated multiplication.
Property 1
Multiplying together two exponential expressions with the same base is the same as adding the exponents: \[ b^m b^n = \underbrace{bbb \cdots bb}_{m \text{ times} } \underbrace{bbb \cdots bb}_{n \text{ times} } = \underbrace{bbbbbbb \cdots bb}_{m + n \text{ times} } = b^{m+n}. \]
Property 2
Division by a number can be expressed as an exponent of minus one: \[ b^{-1} \equiv \frac{1}{b}. \] More generally any negative exponent corresponds to a division: \[ b^{-n} = \frac{1}{b^n}. \]
Property 3
By combining Property 1 and Property 2 we obtain the following rule: \[ \frac{b^m}{b^n} = b^{m-n}. \]
In particular we have $b^{n}b^{-n}=b^{n-n}=b^0=1$. Multiplication by the number $b^{n}$ is the inverse operation of division by the number $b^{n}$. The net effect of the combination of both operations is the same as multiplying by one, i.e., the identity operation.
Property 4
When an exponential expression is exponentiated, the inner exponent and the outer exponent multiply: \[ ({b^m})^n = \underbrace{(\underbrace{bbb \cdots bb}_{m \text{ times} }) (\underbrace{bbb \cdots bb}_{m \text{ times} }) \cdots (\underbrace{bbb \cdots bb}_{m \text{ times} })}_{n \text{ times} } = b^{mn}. \]
Property 5.1
\[ (ab)^n =\underbrace{(ab)(ab)(ab) \cdots (ab)(ab)}_{n \text{ times} } = \underbrace{aaa \cdots aa}_{n \text{ times} } \underbrace{bbb \cdots bb}_{n \text{ times} } = a^n b^n. \]
Property 5.2
\[ \left(\frac{a}{b}\right)^n = \underbrace{\left(\frac{a}{b}\right)\left(\frac{a}{b}\right)\left(\frac{a}{b}\right) \cdots \left(\frac{a}{b}\right)\left(\frac{a}{b}\right)}_{n \text{ times} } = \frac{ \overbrace{aaa \cdots aa}^{n \text{ times} } }{\underbrace{bbb \cdots bb}_{n \text{ times} } } = \frac{a^n}{b^n}. \]
Property 6
Raising a number to the power $\frac{1}{n}$ is equivalent to finding the $n$th root of the number: \[ b^{\frac{1}{n}} = \sqrt[n]{b}. \] In particular, the square root corresponds to the exponent of one half $\sqrt{b}=b^{\frac{1}{2}}$. The cube root (the inverse of $x^3$) corresponds to $\sqrt[3]{b}\equiv b^{\frac{1}{3}}$. We can verify the inverse relationship between $\sqrt[3]{x}$ and $x^3$ using either Property 1: $(\sqrt[3]{x})^3=(x^{\frac{1}{3}})(x^{\frac{1}{3}})(x^{\frac{1}{3}})=x^{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}}=x^1=x$ or using Property 4: $(\sqrt[3]{x})^3=(x^{\frac{1}{3}})^3=x^{\frac{3}{3}}=x^1=x$.
Properties 5.1 and 5.2 also apply for fractional exponents: \[ \sqrt[n]{ab} = \sqrt[n]{a}\sqrt[n]{b}, \] \[ \sqrt[n]{\left(\frac{a}{b}\right)} = \frac{\sqrt[n]{a} }{ \sqrt[n]{b} }. \]
Discussion
Even and odd exponents
The function $f(x)=x^{n}$ behaves differently when the exponent $n$ is an even or odd. If $n$ is odd we have \[ \left( \sqrt[n]{b} \right)^n = \sqrt[n]{ b^n } = b. \]
However if $n$ is even the function $x^n$ destroys the sign of the number (e.g. $x^2$ which maps both $-x$ and $x$ to $x^2$). Thus the successive application of exponentiation by $n$ and the $n$th root has the same effect as the absolute value function: \[ \sqrt[n]{ b^n } = |b|. \] Recall that the absolute value function $|x|$ simply discards the information about the sign of $x$.
The expression $\left( \sqrt[n]{b} \right)^n$ cannot be computed whenever $b$ is a negative number. The reason is that we can't evaluate $\sqrt[n]{b}$ for $b<0$ in terms of real numbers (there is no real number which multiplied times itself an even number of times gives a negative number).
Scientific notation
In science we often have to deal with very large numbers like the speed of light ($c=299\:792\:458$[m/s]), and very small numbers like the permeability of free space ($\mu_0=0.000001256637\ldots$[N/A$^2$]). It can be difficult to judge the magnitude of such numbers and to carry out calculations on them using the usual decimal notation.
Dealing with such numbers is much easier if we use scientific notation. For example the speed of light can be written as $c=2.99792458\times 10^{8}$[m/s] and the the permeability of free space is $\mu_0=1.256637\times 10^{-6}$[N/A$^2$]. In both cases we express the number as a decimal number between $1.0$ and $9.9999\ldots$ followed by the number $10$ raised to some power. The effect of multiplication by $10^8$ is to move the decimal point eight steps to the right thus making the number bigger. The effects of multiplying by $10^{-6}$ has the opposite effect of moving the decimal to the left thus making the number smaller. Scientific notation is very useful because it allows us to see clearly the size of numbers: $1.23\times 10^{6}$ is $1\:230\:000$ whereas $1.23\times 10^{-10}$ is $0.000\:000\:000\:123$. With scientific notation you don't have to count the zeros. Cool no?
The number of decimal places we use when specifying a certain physical quantity is usually an indicator of the precision with which we were able to measure this quantity. Taking into account the precision of the measurements we make is an important aspect of all quantitative research, but going into that right now would be a digression. If you want to read more about this, search for significant digits on the wikipedia page for scientific notation linked to below.
On computer systems, the floating point numbers are represented exactly like in scientific notation—a decimal part and an exponent. To separate the decimal part from exponent when entering a floating point number on the computer we use the character e,
which stands for $\times 10^{?}$. For example to enter the permeability of free space into your calculator you should type 1.256637e-6.
Links
Logarithms
The word “logarithm” makes most people think about some mythical mathematical beast. Surely logarithms are many headed, breathe fire and are extremely difficult to understand. Nonsense! Logarithms are simple. It will take you at most a couple of pages to get used to manipulating them, and that is a good thing because logarithms are used all over the place.
For example, the strength of your sound system is measured in logarithmic units called decibels $[\textrm{dB}]$. This is because your ear is sensitive only to exponential differences in sound intensity. Logarithms allow us to compare very large numbers and very small numbers on the same scale. If we were measuring sound in linear units instead of logarithmic units then your sound system volume control would have to go from $1$ to $1048576$. That would be weird no? This is why we use the logarithmic scale for the volume notches. Using a logarithmic scale, we can go from sound intensity level $1$ to sound intensity level $1048576$ in 20 “progressive” steps. Assume each notch doubles the sound intensity instead of increasing it by a fixed amount, the first notch corresponds to $2$, the second notch is $4$ (still probably inaudible) but by the time you get to sixth notch you are at $2^6=64$ sound intensity (audible music). The tenth notch corresponds to sound intensity $2^{10}=1024$ (medium strength sound) and the finally the twentieth notch will be max power $2^{20}=1048576$ (at this point the neighbours will come knocking to complain).
Definitions
You are probably familiar with these concepts already:
- $b^x$: the exponential function base $b$
- $\exp(x)=e^x$: the exponential function base $e$, Euler's number
- $2^x$: exponential function base $2$
- $f(x)$: the notion of a function $f:\mathbb{R}\to\mathbb{R}$
- $f^{-1}(x)$: the inverse function of $f(x)$. It is defined in terms of
$f(x)$ such that the following holds $f^{-1}(f(x))=x$, i.e.,
if you apply $f$ to some number and get the output $y$,
and then you pass $y$ through $f^{-1}$ the output will be $x$ again.
The inverse function $f^{-1}$ undoes the effects of the function $f$.
NOINDENT In this section we will play with the following new concepts:
- $\log_b(x)$: logarithm of $x$ base $b$. This is the inverse function of $b^x$
- $\ln(x)$; the “natural” logarithm base $e$. This is the inverse of $e^x$
- $\log_2(x)$: the logarithm base $2$ is is the inverse of $2^x$
I say play, because there is nothing much new to learn here: logarithms are just a clever way to talk about the size of number – i.e., how many digits the number has.
Formulas
The main thing to realize is that $\log$s don't really exist on their own. They are defined as the inverses of the corresponding exponential function. The following statements are equivalent: \[ \log_b(x)=m \ \ \ \ \ \Leftrightarrow \ \ \ \ \ b^m=x. \]
For logarithms with base $e$ one writes $\ln(x)$ for “logarithme naturel” because $e$ is the “natural” base. Another special base is $10$ because we use the decimal system for our numbers. $\log_{10}(x)$ tells you roughly the size of the number $x$—how many digits the number has.
Example
When someone working for the system (say someone with a high paying job in the financial sector) boasts about his or her “six-figure” salary, they are really talking about the $\log$ of how much money they make. The “number of figures” $N_S$ in you salary is calculated as one plus the logarithm base ten of your salary $S$. The formula is \[ N_S = 1 + \log_{10}(S). \] So a salary of $S=100\:000$ corresponds to $N_S=1+\log_{10}(100\:000)=1+5=6$ figures. What will be the smallest “seven figure” salary? We have to solve for $S$ given $N_S=7$ in the formula. We get $7 = 1+\log_{10}(S)$ which means that $6=\log_{10}(S)$ and using the inverse relationship between logarithm base ten and exponentiation base ten we find that $S=10^6 = 1\:000\:000$. One million per year. Yes, for this kind of money I see how someone might want to work for the system. But I don't think most system pawns ever make it to the seven figure level. Even at the higher ranks, the salaries are more in the $1+\log_{10}(250\:000) = 1+5.397=6.397$ digits range. There you have it. Some of the smartest people out there selling their brains out to the finance sector for some lousy $0.397$ extra digits. What wankers! And who said you need to have a six digit salary in the first place? Why not make $1+\log_{10}(44\:000)=5.64$ digits as a teacher and do something with your life that actually matters?
Properties
Let us now discuss two important properties that you will need to use when dealing with logarithms. Pay attention because the arithmetic rules for logarithms are very different from the usual rules for numbers. Intuitively, you can think of logarithms as a convenient of referring to the exponents of numbers. The following properties are the logarithmic analogues of the properties of exponents
Property 1
The first property states that the sum of two logarithms is equal to the logarithm of the product of the arguments: \[ \log(x)+\log(y)=\log(xy). \] From this property, we can derive two other useful ones: \[ \log(x^k)=k\log(x), \] and \[ \log(x)-\log(y)=\log\left(\frac{x}{y}\right). \]
Proof: For all three equations above we have to show that the expression on the left is equal to the expression on the right. We have only been acquainted with logarithms for a very short time, so we don't know each other that well. In fact, the only thing we know about $\log$s is the inverse relationship with the exponential function. So the only way to prove this property is to use this relationship.
The following statement is true for any base $b$: \[ b^m b^n = b^{m+n}, \] which follows from first principles. Exponentiation means multiplying together the base many times. If you count the total number of $b$s on the left side you will see that there is a total of $m+n$ of them, which is what we have on the right.
If you define some new variables $x$ and $y$ such that $b^m=x$ and $b^n=y$ then the above equation will read \[ xy = b^{m+n}, \] if you take the logarithm of both sides you get \[ \log_b(xy) = \log_b\left( b^{m+n} \right) = m + n = \log_b(x) + \log_b(y). \] In the last step we used the definition of the $\log$ function again which states that $b^m=x \ \ \Leftrightarrow \ \ m=\log_b(x)$ and $b^n=y \ \ \Leftrightarrow \ \ n=\log_b(y)$.
Property 2
We will now discuss the rule for changing from one base to another. Is a relation between $\log_{10}(S)$ and $\log_2(S)$?
There is. We can express the logarithm in any base $B$ in terms of a ratio of logarithms in another base $b$. The general formula is: \[ \log_{B}(x) = \frac{\log_b(x)}{\log_b(B)}. \]
This means that: \[ \log_{10}(S) =\frac{\log_{10}(S)}{1} =\frac{\log_{10}(S)}{\log_{10}(10)} = \frac{\log_{2}(S)}{\log_{2}(10)}=\frac{\ln(S)}{\ln(10)}. \]
This property is very useful in case when you want to compute $\log_{7}$, but your calculator only gives you $\log_{10}$. You can simulate $\log_7(x)$ by computing $\log_{10}(x)$ and dividing by $\log_{10}(7)$.
Fractions
The set of rational numbers $\mathbb{Q}$ is the set of numbers that can be written as a fraction of two integers: \[ \mathbb{Q} \equiv \left\{ \frac{m}{n}\ \bigg|\ m \in \mathbb{Z}, n \in \mathbb{N}_+ \ \right\}, \] where $\mathbb{Z}$ denotes the set of integers $\mathbb{Z}=\ldots, -1,0,1,2,3,\ldots$ and $\mathbb{N}_+$ denotes the set of positive natural numbers $1,2,3,4,\ldots$. The interpretation is that some whole is cut into a total of $n$ pieces and that we are given $m$ of these pieces.
We read $\frac{1}{4}$ either as one over four or one quarter, which is also equal to $0.25$, but as you can see the notation $\frac{1}{4}$ is more compact and nicer. Why nicer? Well let's take a look at some simple fractions: \[ \begin{align*} \frac{1}{1} &= 1.0 \nl \frac{1}{2} &= 0.5 \nl \frac{1}{3} &= 0.33333\ldots = 0.\overline{3} \nl \frac{1}{4} &= 0.25 \nl \frac{1}{5} &= 0.2 \nl \frac{1}{6} &= 0.166666\ldots = 0.1\overline{6} \nl \frac{1}{7} &= 0.14285714285714285\ldots = 0.\overline{142857} \end{align*} \] Note that a line on top of some numbers means that these numbers are repeated. The fractional notation on the left is preferable, because it shows the underlying structure of the number and it avoids the need to write infinitely long decimals.
Writing down rational numbers as fractions allows us to do precise mathematical calculations easily on pen and paper without the need for a calculator.
Example
Calculate the sum of $\frac{1}{7}$ and $\frac{1}{3}$.
If we use the decimal notation we would have to write our answer as \[ \begin{align*} \textrm{ans} &= 0.\overline{142857} \ + \ 0.\overline{3} \nl &= 0.142\:857\:142\:857\ldots \ + \ 0.333\:333\:333\:333\ldots \nl &= 0.476\:190\:476\:190\:476\ldots \nl & = 0.4\overline{761904}. \end{align*} \] Wow that was complicated! And complicated for nothing too. Let us see how much simpler this calculation is if we use fractions: \[ \frac{1}{7}+\frac{1}{3} = \frac{3\times 1}{3\times 7}+\frac{1 \times 7}{3 \times 7} = \frac{3}{21}+\frac{7}{21} = \frac{3+7}{21} =\frac{10}{21}. \]
Definitions
The fraction $a$ over $b$ can be written in three different ways: \[ a/b \equiv a \div b \equiv \frac{a}{b}. \] The two constituents of the fraction have special names:
- $b$ is the denominator of the fraction and
tells you how many parts there are in the whole.
- $a$ is the numerator and tells you how
many of these parts are given.
Addition of fractions
Consider two fractions $\frac{a}{b}$ and $\frac{c}{d}$ that we want to add together. If the denominators the same, then we can simply add the numerators: \[ \frac{1}{5} + \frac{2}{5} = \frac{3}{5}. \] If the denominators are different however, before we can add the fractions we have rewrite the fractions so that they have a common denominator. An easy way to do this is to cross-multiply: \[ \frac{a}{b} + \frac{c}{d} = \frac{ad}{bd} + \frac{bc}{bd} = \frac{ ad + bc }{bd}. \] The common denominator $bd$ is obtained by multiplying the first fraction by $\frac{d}{d}=1$ and the second fraction by $\frac{c}{c}=1$. Because we multiply both the top and the bottom of the fraction by the same number, this operation does not change the fractions.
More generally, in order to add two fractions we need to find the least common multiple ($\textrm{LCM}$) to use in the common denominator. This is a number obtained by myltiplying the numbers together but removing the common factors: \[ \textrm{LCM}(b,d) = \frac{b \times d}{\textrm{GCD}(b,d) }, \] where $\textrm{GCD}$ is the greatest common divisor: the largest number that divides both $b$ and $d$.
For example if we wanted to add $\frac{1}{6}$ and $\frac{1}{15}$, we could put both fractions on the common denominator $6 \times 15$ (the product of the two denominators), but we could also see that $6=3\times 2$ and $15 =3 \times 5$, which means that $3$ is a common divisor of both $6$ and $15$. The least common multiple is then $\frac{6 \times 15}{3} = 30$, and so we write: \[ \frac{1}{6} + \frac{1}{15} = \frac{5\times 1}{5\times 6} + \frac{1 \times 2}{15 \times 2} = \frac{5}{30} + \frac{2}{30} = \frac{7}{30}. \] Note that all this $\textrm{LCM}$ and $\textrm{GCD}$ business is not required: it is simply the most efficient way of adding the fractions so that you don't get excessively large numbers. If you simply use the product denominator $b\times d$ you will get the same answer after simplification: \[ \frac{1}{6} + \frac{1}{15} = \frac{15\times 1}{15\times 6} + \frac{1 \times 6}{15 \times 6} = \frac{15}{90} + \frac{6}{90} = \frac{21}{90}= \frac{7}{30}. \]
Multiplication of fractions
Fraction multiplication involves multiplying together of the numerators and the denominators: \[ \frac{a}{b} \times \frac{c}{d} = \frac{a\times c}{b \times d} = \frac{ac}{bd}. \]
Division of fractions
To divide two fractions, we compute the product of the first fraction times the second fraction flipped. To illustrate this, consider the following calculation: \[ \frac{ a/b }{ c/d } = \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c} = \frac{a\times d}{b \times c} = \frac{ad}{bc}. \]
The multiplicative inverse of something times that something should give $1$ as the answer. We obtain the multiplicative inverse of a fraction by interchaning the roles of the numerator and the denominators: \[ \left( \frac{c}{d} \right)^{-1} = \frac{d}{c}. \] Thus any fraction times its multiplicative inverse gives $1$: \[ \frac{c}{d} \times \left( \frac{c}{d} \right)^{-1} = \frac{c}{d}\times \frac{d}{c} = \frac{cd}{cd} = 1. \] The “flip and multiply” rule for division comes from the fact that division by a numbers $x$ is the same as multiplication by $\frac{1}{x}$.
Whole and fraction notation
To indicate a fraction like $\frac{5}{3}$ which are greater than one we sometimes use the notation $1\frac{2}{3}$ which is read as “one and two thirds”. Similarly $\frac{22}{7}=3\frac{1}{7}$.
There is nothing wrong with writing fractions like $\frac{5}{3}$ and $\frac{22}{7}$ but some teachers say that this way of writing fractions is improper and demand that they be written in the whole-and-fraction way like $1\frac{2}{3}$ and $3\frac{1}{7}$. Whatever. Either way it is no big deal to me.
Repeated fractions
When written as decimal numbers, certain fractions have infinitely long decimal expansions. We use the “overline” notation to indicate the number(s) which repeat infinitely many times in the expansion: \[ \frac{1}{3} = 0.\bar{3} = 0.333\ldots, \quad \frac{1}{7} = 0.\overline{142857} = 0.14285714285714\ldots. \]
Links
[ The Rappin' Mathematician: Fractions ]
http://www.youtube.com/watch?v=VZQDvb5Yjvw
The number line
The number line is a useful graphical representation for numbers. The integers $\mathbb{Z}$ correspond to the notches on the line while the rationals $\mathbb{Q}$ and the reals $\mathbb{R}$ cover (densely) the whole line:
You can clearly see the ordering of the numbers from the smallest on the left, to largest on the right. The line extends indefinitely on both sides: on the left it goes all the way to negative infinity $-\infty$ and on the right to positive infinity $\infty$.
Intervals
We can represent subsets of the real numbers by setting in bold some section of the real line. For example, the set of numbers that lie strictly between $2$ and $4$, \[ \{ x \in \mathbb{R} | 2 < x < 4 \}, \] is represented graphically as follows.
Note that this subset is described by strict inequalities, which means that it does not contain its endpoints $2$ and $4$. It contains $2.000000001$ and $3.99999999$ but not the limits $2$ and $4$. We say call this kind of endpoints open and use an “empty dot” to denote them on the number line so that it is clear that the limit is not included in the set.
We denote intervals on the number lines which consist of disjoint sets by using the union ($\cup$) notation. For example, the set of numbers \[ \{ x \in \mathbb{R} | -3 \leq x \leq 0 \} \cup \{ x \in \mathbb{R} | 1 \leq x \leq 2 \}, \] can be represented graphically as:
This time we have less-than-or-equal limits so the intervals contain their endpoints. We call these endpoints closed and denote them with a dot that is filled-in on the number line.
Links
[ Better number line diagrams and five great exercises on intervals ]
http://www.sosmath.com/algebra/inequalities/ineq02/ineq02.html
Inequalities
To solve an equation we have to find the one (or many) values of $x$ which satisfy the equation. The solution set for an equation consists of a discrete set of values. For example, the solutions to $(x-3)^2=4$ are $x=1$ and $x=5$.
In this section, we will learn how to solve equations which involve inequalities. The solution to an inequality is usually an entire range of numbers. For example the inequality $(x-3)^2 \leq 4$ is equivalent to asking the question “for which values of $x$ is $(x-3)^2$ less than or equal to $4$.” The answer is the interval $[1,5] \equiv \{ x\in \mathbb{R}\ | \ 1 \leq x \leq 5 \}$.
The techniques used to deal with inequalities are roughly the same as the techniques which we learned for dealing with equations: we have to perform simplifying steps to both sides of the inequality until we obtain the answer.
Definitions
The different type of inequality conditions are:
- $f(x) < g(x)$: a strict inequality. The function $f$ is always strictly less than $g$.
- $f(x) \leq g(x)$: the function $f$ is less than or equal to the function $g$.
- $f(x) > g(x)$: $f$ is strictly greater than $g$.
- $f(x) \geq g(x)$: $f$ is greater than or equal to $g$.
The solutions to an inequality correspond to subsets of the real line. Depending on the type of inequality we are dealing with, the answer will be either a closed or open interval:
- $[a,b]$: the closed interval from $a$ to $b$. This corresponds to the set of numbers between $a$ and $b$ on the real line, including the endpoints $a$ and $b$. $[a,b] = \{ x\in \mathbb{R}\ | \ a \leq x \leq b \}$.
- $(a,b)$: the open interval from $a$ to $b$. This corresponds to the set of numbers between $a$ and $b$ on the real line, not including the $a$ and $b$. $(a,b) = \{ x\in \mathbb{R}\ | \ a < x < b \}$.
- $[a,b)$: the mixed interval which includes the left endpoint $a$, but not the right endpoint $b$.
Sometimes the we will have to deal with intervals which consists of two disjoint parts:
- $[a,b] \cup [c,d]$: The set of all numbers that are either between $a$ and $b$ (inclusive) or between $c$ and $d$ (inclusive).
Formulas
The main idea for solving inequalities is the same as solving equations except for one small special step. When multiplying by a negative number on both sides, the direction of the inequality must be flipped: \[ f(x) \leq g(x) \qquad \Rightarrow \qquad -f(x) \geq -g(x). \]
Example
To solve $(x-3)^2\leq 4$ we must dig towards the $x$ and undo all the operations that stand in our way: \[ \begin{align*} & \ (x-3)^2 \leq 4, \nl -2 \leq & \ (x-3) \leq 2, \nl 1 \leq & \ \ \ \ \ x \ \ \ \ \leq 5. \end{align*} \] where in the first step we took the square root operation (the inverse of the quadratic function) and then we added $3$ to both sides. The final answer is $x\in[1,5]$.
Discussion
As you can see, solving inequalities is not more complicated than solving equations. Indeed, the best way to think about an inequality is in terms of the end points – which correspond to the equality condition.
Cartesian plane
The Cartesian plane, named after René Descartes, the famous philosopher and mathematician, is the graphical representation of the space of pairs of real numbers.
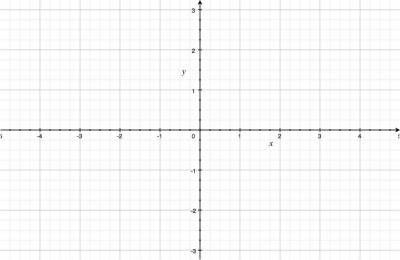
We generally call the horizontal axis “the $x$ axis” and the vertical axis “the $y$ axis.” We put notches at regular intervals on each axis so that we can measure distances. The figure below is an example of an empty Cartesian coordinate system. Think of the coordinate system as an empty canvas. What can you draw on this canvas?
Vectors and points
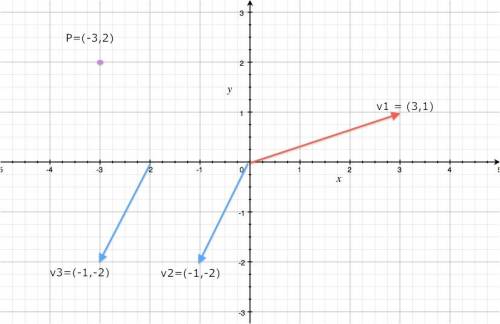
A point $P$ in the Cartesian plane has an $x$-coordinate and a $y$-coordinate. We say $P=(P_x,P_y)$. To find this point, we start from the origin (the point (0,0)) and move a distance $P_x$ on the $x$ axis, then move a distance $P_y$ on the $y$ axis.
Similar to points, a vector $\vec{v}=(v_x,v_y)$ is a pair of displacements, but unlike points, we don't have to necessarily start from the origin. We draw vectors as arrows – so we see explicitly where the vector starts and where it ends.
Here are some examples:
Note that the vectors $\vec{v}_2$ and $\vec{v}_3$ are actually the same vector – the “displace downwards by 2 and leftwards by one” vector. It doesn't matter where you draw this vector, it will always be the same.
Graphs of functions
The Cartesian plane is also a good way to visualize functions \[ f: \mathbb{R} \to \mathbb{R}. \] Indeed, you can think of a function as a set of input-output pairs $(x,f(x))$, and if we identify the output values of the function with the $y$-coordinate we can trace the set of points \[ (x,y) = (x,f(x)). \]
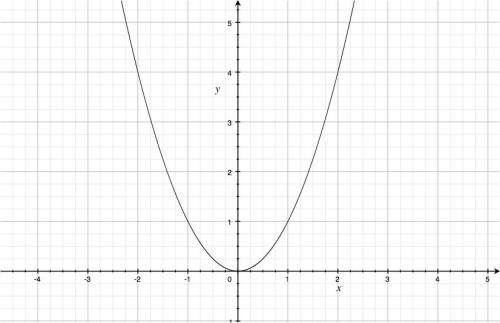
For example, if we have the function $f(x)=x^2$, we can pass a line through the set of points \[ (x,y) = (x, x^2), \] to obtain:
When plotting functions by setting $y=f(x)$, we use a special terminology for the two axes. The $x$ axis is the independent variable (the one that varies freely), whereas the $y$ is the dependent variable since $y=f(x)$ depends on $x$.
Dimensions
Note that a Cartesian plot has two dimensions: the $x$ dimension and the $y$ dimension. If we only had one dimension, then we would use a number line. If we wanted to plot in 3D we can build a three-dimensional coordinate system with $x$, $y$ and $z$ axes.
Functions
Your function vocabulary determines how well you will be able to express yourself mathematically in the same way that your English vocabulary determines how well you can express yourself in English.
The purpose of the following pages is to embiggen your vocabulary a bit so you won't be caught with your pants down when the teacher tries to pull some trick on you at the final. I give you the minimum necessary, but I recommend you explore these functions on your own via wikipedia and by plotting their graphs on Wolfram alpha.
To “know” a function you have to understand and connect several different aspects of the function. First you have to know its mathematical properties (what does it do, what is its inverse) and at the same time have a good idea of its graph, i.e., what it looks like if you plot $x$ versus $f(x)$ in the Cartesian plane. It is also really good idea if you can remember the function values for some important inputs.
Definition
A function is a mathematical object that takes inputs and gives outputs. We use the notation \[ f \colon X \to Y, \] to denote a functions from the set $X$ to the set $Y$. In this book, we will study mostly functions which take real numbers as inputs and give real numbers as outputs: $f\colon\mathbb{R} \to \mathbb{R}$.
We now define some technical terms used to describe the input and output sets.
- The domain of a function is the set of allowed input values.
- The image or range of the function $f$ is the set of all possible
output values of the function.
- The codomain of a function is the type of outputs that the functions has.
To illustrate the subtle difference between the image of a function and its codomain, let us consider the function $f(x)=x^2$. The quadratic function is of the form $f\colon\mathbb{R} \to \mathbb{R}$. The domain is $\mathbb{R}$ (it takes real numbers as inputs) and the codomain is $\mathbb{R}$ (the outputs are real numbers too), however, not all outputs are possible. Indeed, the image the function $f$ consists only of the positive numbers $\mathbb{R}_+$. Note that the word “range” is also sometimes used refer to the function codomain.
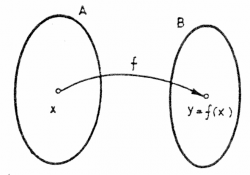
A function is not a number, it is a mapping from numbers to numbers. If you specify a given $x$ as input, we denote as $f(x)$ is the output value of $f$ for that input. Here is a graphical representation of a function with domain $A$ and codomain $B$.
The function corresponds to the arrow in the above picture.
We say that “$f$ maps $x$ to $y=f(x)$” and use the following terminology to classify the type of mapping that a function performs:
- A function is one-to-one or injective if it maps different inputs to different outputs.
- A function is onto or surjective if it covers the entire output set,
i.e., if the image of the function is equal to the function codomain.
- A function is bijective if it is both injective and surjective.
In this case $f$ is a one-to-one correspondence between the input
set and the output set: for each input of the possible outputs $y \in Y$ there exists (surjective part) exactly one input $x \in X$, such that $f(x)=y$ (injective part).
The term injective is a 1940s allusion inviting us to think of injective functions as some form of fluid flow. Since fluids cannot be compressed, the output space must be at least as large as the input space. A modern synonym for injective functions is to say that they are two-to-two. If you imagine two specks of paint inserted somewhere in the “input fluid”, then an injective function will lead to two distinct specks of paint in the “output fluid.” In contrast, functions which are not injective could map several different inputs to the same output. For example $f(x)=x^2$ is not injective since the inputs $2$ and $-2$ both get mapped to output value $4$.
Function names
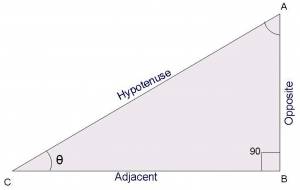
Mathematicians have defined symbols $+$, $-$, $\times$ (usually omitted) and $\div$ (usually denoted as a fraction) for most important functions used in everyday life. We also use the weird surd notation to denote $n$th root $\sqrt[n]{\ }$ and the superscript notation to denote exponents. All other functions are identified and used by their name. If I want to compute the cosine of the angle $60^\circ$ (a function which describes the ratio between the length of one side of a right-angle triangle and the hypotenuse), then I would write $\cos(60^\circ)$, which means that we want the value of the $\cos$ function for the input $60^\circ$.
Incidentally, for that specific angle the function $\cos$ has a nice value: $\cos(60^\circ)=\frac{1}{2}$. This means that seeing $\cos(60^\circ)$ somewhere in an equation is the same as seeing $0.5$ there. For other values of the function like say $\cos(33.13^\circ)$, you will need to use a calculator. A scientific calculator will have a $\cos$ button on it for that purpose.
Handles on functions
When you learn about functions you learn about different “handles” onto these mathematical objects. Most often you will have the function equation, which is a precise way to calculate the output when you know the input. This is an important handle, especially when you will be doing arithmetic, but it is much more important to “feel” the function.
How do you get a feel for some function?
One way is to look at list of input-output pairs $\{ \{ \text{input}=x_1, \text{output}=f(x_1) \},$ $\{ \text{input}=x_2,$ $\text{output}=f(x_2) \},$ $\{ \text{input}=x_3, \text{output}=f(x_3) \}, \ldots \}$. A more compact notation for the input-output pairs $\{ (x_1,f(x_1)),$ $(x_2,f(x_2)),$ $(x_3,f(x_3)), \ldots \}$. You can make a little table of values for yourself, pick some random inputs and record the output of the function in the second column: \[ \begin{align*} \textrm{input}=x \qquad &\rightarrow \qquad f(x)=\textrm{output} \nl 0 \qquad &\rightarrow \qquad f(0) \nl 1 \qquad &\rightarrow \qquad f(1) \nl 55 \qquad &\rightarrow \qquad f(55) \nl x_4 \qquad &\rightarrow \qquad f(x_4) \end{align*} \]
Apart from random numbers it is also generally a good idea to check the value of the function at $x=0$, $x=1$, $x=100$, $x=-1$ and any other important looking $x$ value.
One of the best ways to feel a function is to look at its graph.
A graph is a line on a piece of paper that passes through all input-output
pairs of the function.
What? What line? What points?
Ok let's backtrack a little.
Imagine that you have a piece of paper you have drawn
a coordinate system on the paper.
The horizontal axis will be used to measure $x$, this is also called the abscissa. The vertical axis will be used to measure $f(x)$, but because writing out $f(x)$ all the time is long and tedious, we will invent a short single-letter alias to denote the output value of $f$ as follows: \[ y \equiv f(x) = \text{output}. \]
Now you can take each of the input-output pairs for the function $f$ and think of them as points $(x,y)$ in the coordinate system. Thus the graph of a function is a graphical representation of everything the function does. If you understand the simple “drawing” on this page, you will basically understand everything there is to know about the function.
Another way to feel functions is through the properties of the function: either the way it is defined, or its relation to other functions. This boils down to memorizing facts about the function and its relations to other functions. An example of a mathematical fact is $\sin(30^\circ)=\frac{1}{2}$. An example of a mathematical relation is the equation $\sin^2 x + \cos^2 x =1$, which is a link between the $\sin$ and the $\cos$ functions.
The last part may sound contrary to my initial promise about the book saying that I will not make you memorize stuff for nothing. Well, this is not for nothing. The more you know about any function, the more “paths” you have in your brain that connect to that function. Real math knowledge is not memorization but an establishment of a graph of associations between different areas of knowledge in your brain. Each concept is a node in this graph, and each fact you know about this concept is an edge in the graph. Analytical thought is the usage of this graph to produce calculations and mathematical arguments (proofs). For example, knowing the fact $\sin(30^\circ)=\frac{1}{2}$ about $\sin$ and the relationship $\sin^2 x + \cos^2 x = 1$ between $\sin$ and $\cos$, you could show that $\cos(30^\circ)=\frac{\sqrt{3}}{2}$. Note that the notation $\sin^2(x)$ means $(\sin(x))^2$.
To develop mathematical skills, it is therefore important to practice this path-building between related concepts by solving exercises and reading and writing mathematical proofs. My textbook can only show you the paths between the concepts, it is up to you to practice the exercises in the back of each chapter to develop the actual skills.
Example: Quadratic function
Consider the function from the real numbers ($\mathbb{R}$) to the real numbers ($\mathbb{R}$) \[ f \colon \mathbb{R} \to \mathbb{R} \] given by \[ f(x)=x^2+2x+3. \] The value of $f$ when $x=1$ is $f(1)=1^2+2(1)+3=1+2+3=6$. When $x=2$, we have $f(2)=2^2+2(2)+3=4+4+3=11$. What is the value of $f$ when $x=0$?
Example: Exponential function
Consider the exponential function with base two: \[ f(x) = 2^x. \] This function is of crucial importance in computer systems. When $x=1$, $f(1)=2^1=2$. When $x$ is 2 we have $f(2)=2^2=4$. The function is therefore described by the following input-output pairs: $(0,1)$, $(1,2)$, $(2,4)$, $(3,8)$, $(4,16)$, $(5,32)$, $(6,64)$, $(7,128)$, $(8,256)$, $(9,512)$, $(10,1024)$, $(11, 2048)$, $(12,4096)$, etc. (RAM memory chips come in powers of two because the memory space is exponential in the number of “address lines” on the chip.) Some important input-output pairs for the exponential function are $(0,1)$, because by definition any number to the power 0 is equal to 1, and $(-1,\frac{1}{2^1}=\frac{1}{2}), (-2,\frac{1}{2^2}=\frac{1}{4}$), because negative exponents tells you that you should dividing by that number this many times instead of multiplying.
Function inverse
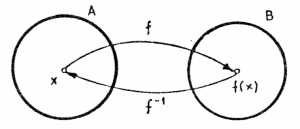 Recall that a bijective function is a one-to-one correspondence between
the set of inputs and the set of output values.
If $f$ is a bijective function, then there exists an inverse function $f^{-1}$,
which performs the inverse mapping of $f$.
Thus, if you start from some $x$, apply $f$ and then apply $f^{-1}$,
you will get back to the original input $x$:
\[
x = f^{-1}\!\left( \; f(x) \; \right).
\]
This is represented graphically in the diagram on the right.
Recall that a bijective function is a one-to-one correspondence between
the set of inputs and the set of output values.
If $f$ is a bijective function, then there exists an inverse function $f^{-1}$,
which performs the inverse mapping of $f$.
Thus, if you start from some $x$, apply $f$ and then apply $f^{-1}$,
you will get back to the original input $x$:
\[
x = f^{-1}\!\left( \; f(x) \; \right).
\]
This is represented graphically in the diagram on the right.
Function composition
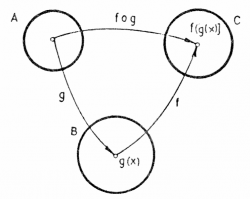 We can combine two simple functions to build a more complicated function
by chaining them together.
The resulting function is denoted
\[
z = f\!\circ\!g \, (x) \equiv z = f\!\left( \: g(x) \: \right).
\]
We can combine two simple functions to build a more complicated function
by chaining them together.
The resulting function is denoted
\[
z = f\!\circ\!g \, (x) \equiv z = f\!\left( \: g(x) \: \right).
\]
The diagram on the left shows a function $g:A\to B$ acting on some input $x$ to produce an intermediary value $y \in B$, which is then input to the function $f:B \to C$ to produce the final output value $z = f(y) = f(g(x))$.
The composition of applying $g$ first followed by $f$ is a function of the form: $f\circ g: A \to C$ defined through the equation $f\circ g(x) = f(g(x))$. Note that “first” in the context of function composition means the first to first to touch the input.
Discussion
In the next sections, we will look into the different functions that you will be dealing with. What we present here is far from and exhaustive list, but if you get a hold of these ones, you will be able to solve any problem a teacher can throw at you.
Links
[ Tank game where you specify the function of the projectile trajectory ]
http://www.graphwar.com/play.html
NOINDENT
[ Gallery of function graphs ]
http://mpmath.googlecode.com/svn/gallery/gallery.html
Function reference
ADDTOCONTENTSTOCPROTECTSETCOUNTERTOCDEPTHTWO
Line
Definition
The equation of a line consists of a multiple of $x$ plus some constant: \[ f(x) = mx+b. \]
Parameters
- $m$ is the slope.
- $b$ is the $y$-intercept. The value of the function when $x=0$.
- $b/m$ is the $x$-intercept. Another word for $x$-intercept is root, i.e., a value where $f(x)=0$.
Properties
- There is a unique linear function that passes through any two points $(x_1,y_1)$ and $(x_2,y_2)$ if $x_1 \neq x_2$.
- The inverse function of $f(x)=\frac{1}{m}(x-b)$.
Graph
Here is the graph of \[ f(x) = 2x - 3. \]
A line can also be described in a more symmetric form. \[ Ax + By = C, \] This is known as the general equation of a line. We have $b=\frac{C}{B}$ and $m=\frac{-A}{B}$.
Square
The square function is also known as the quadratic function, the second degree function, or simply called a parabola.
Definition
The bare quadratic function has the form: \[ f(x)=x^2. \]
Properties
- Inverse of $\sqrt{x}$.
- Never negative: $x^2 \geq 0$, for all $x\in \mathbb{R}$.
- The quadratic function is two-to-one since it sends both $x$ and $-x$ to $x^2=(-x)^2$.
- The quadratic function is convex, i.e., it curves upwards.
Square root
Definition
The function returns a number $y$ such that $y^2=x$: \[ f(x) = \sqrt{x} \equiv x^{\frac{1}{2}} . \]
Graph
The graph of the square root function looks like this:
{{ :math:sqrt_of_x.jpg?500 |The graph of the function $\sqrt{x}$.}}
Properties
- The inverse of $x^2$.
- Since there is no real number $y$ such that
$y^2$ is negative, the function $f(x)=\sqrt{x}$
is not defined for negative inputs $x$.
Parameters
- $2$: the degree of the root operation. More generally
you can have $n$th root $\sqrt[n]{x}$ which is the inverse
function to $x^n$. For example, the inverse function for the
cubic function $f(x)=x^3$ is the //cube root//:
\[
f(x) = \sqrt[3]{x} \equiv x^{\frac{1}{3}}.
\]
So we have $\sqrt[3]{8}=2$ since $2\times2\times2=8$.
Absolute value
The $\textrm{abs}$ function is used when you need to get the size of a number and you don't care if the number is positive or negative. The absolute value just ignores the sign of a number.
Definition
\[ f(x)=|x|= x \text{ if } x>0 \text{ or } -x \text{ if } x<0 \]
Properties
- Always returns a non-negative number.
- The combination of squaring followed by square-root is equivalent
to the absolute value function:
\[
\sqrt{ x^2 } \equiv |x|.
\]
Sine
Contrary to what religious leaders might lead you to believe, there is nothing wrong with $\sin$. At least not with the mathematical $\sin$. The sinus, sine or $\sin$ function tells you the ratio of the lengths of two sides in a right angle triangle.
Definition
Let us not talk about triangles, angles and lengths of sides for now, but think of the $\sin$ function as a generic function of $x$: \[ f(x)=\sin(x). \]
Properties
- The $\sin$ function is odd, which the mathematical term for saying:
\[ f(-x) = -f(x). \]
- The function is periodic, with period $2\pi$, that is:
\[ f(x) = f(x+2\pi). \]
- Relation to $\cos$: $\sin^2 x + \cos^2 x = 1$.
- Relation to $\csc$: $\csc(x) \equiv \frac{1}{\sin x}$ ($\csc$ is read cosecant).
- The inverse function is $\sin^{-1}(x)=\arcsin(x)$, and is not
to be confused with $(\sin(x))^{-1}=\frac{1}{\sin(x)} \equiv \csc(x)$.
Graph
The function starts from zero $\sin(0)=0$, then goes up to take on the value $1$ at $x=\frac{\pi}{4}$, then falls down until it crosses the $x$ axis at $x=\pi$.
After $\pi$ the function drops below the $x$ axis and reaches its minimum value of $-1$ at $x=\frac{3\pi}{2}$ only to come up again and repeat the $2\pi$-long cycle starting from $x=2\pi$.
We have $0=\sin(0)=\sin(\pi)=\sin(2\pi)=\sin(3\pi)=\cdots$, in fact $\sin(x)$ has a root at each multiples of $\pi$.
Cosine
Definition
\[ f(x)=\cos(x). \]
Graph
Cos starts off from $\cos(0)=1$ and then drops down to cross the $x$ axis at $x=\frac{\pi}{2}$. Cos then continues until it reaches its minimum value at $x=\pi$. The function then comes back up, crosses the $x$ axis again at $x=\frac{3\pi}{2}$, and goes back up to its maximum value at $x=2\pi$.
Properties
- The $\cos$ function is even, which means it doesn't care
about the sign of the input:
\[
\cos(-x) = \cos(x).
\]
* The cosine function is a shifted version of the sine function
\[
\cos(x) = \sin(x+\frac{\pi}{2}).
\]
Tangent
Definition
\[ f(x)=\tan(x)\equiv \frac{ \sin(x) } { \cos(x) }. \]
Graph
Properties
- The function $\tan$ is periodic with period $\pi$, not $2\pi$ like $\sin$ and $\cos$.
- The $\tan$ function has asymptotes at all values of $x$ for which the denominator ($\cos$) goes to zero.
- The locations of the asymptotes are $x=\frac{\pi}{2},\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\ldots$.
- At those values, $\tan$ approaches $\infty$ from the left, and $-\infty$ from the right.
- Value at $0$: $\tan(0)=\frac{0}{1}=0$ because $\sin(0)=0$.
- The angle $x=\frac{\pi}{4}$ is special since both $\sin$ and $\cos$ are equal
and we get:
\[
\tan\left(\frac{\pi}{4} \right)
= \frac{ \sin\left(\frac{\pi}{4}\right) }{ \cos\left(\frac{\pi}{4}\right) }
= \frac{ \frac{\sqrt{2}}{2} }{ \frac{\sqrt{2}}{2} }
= 1.
\]
Exponential
Definition
\[ f(x)=Ae^{\gamma x}. \]
Graph
The exponential function graph:
Parameters
- $A$: the initial value, $A=f(0)$. The graph shows the case $A=1$.
- $\gamma$: the rate of the exponential.
For $\gamma > 0$ the function is increasing.
for $\gamma < 0$ the function is decreasing
and tends to zero for large values of $x$.
The case $\gamma=0$ is special since $e^{0}=1$,
and so the exponential becomes the constant function $f(x)=A$.
The graph shows the case $\gamma=1$.
Properties
- The number $e$ is related to the following limit argument
\[ e = \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n, \]
which can be interpreted as a formula for compounding interest.
The limit as $n$ goes to infinity refers to a scenario when
the compounding is performed infinitely often.
* The derivative (slope) of the exponential function is
equal to the exponential function:
\[
f(x) = e^x \ \ \Rightarrow \ \ f'(x)=e^x.
\]
In function $e^x$ is equal to its derivative: $f(x)=f'(x)$.
Links
[ the exponential function $2^x$ for the naturals $x \in \mathbb{N}$ can easily be evaluated by drawing ]
http://www.youtube.com/watch?v=e4MSN6IImpI
Natural logarithm
Definition
\[ f(x)=\ln(x) = \log_e(x). \]
Graph
The natural logarithm function:
Parameters
- $e$: the natural logarithm is the logarithm base $e$.
Properties
- Inverse of the exponential function $e^x$.
Polynomials
Definition
\[ f(x)=a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots + a_nx^n, \] where the $a_i$s are the coefficients.
Parameters
- $n$: the degree of the polynomial. A polynomial of degree $n$ has $n+1$ coefficients $a_i$.
- $a_0$: the constant term.
- $a_1$: the linear coefficient, or first order coefficient.
- $a_2$: the quadratic coefficient.
- $a_3$: the cubic coefficient.
- $a_n$: the $n$th order coefficient.
Properties
- The sum of two polynomials is also a polynomial.
Function transformations
It is often required to adjust the shape of a function by scaling to it or moving it so as to make it pass through certain points. For example, if we wanted to have a function $g$ with the same shape as the absolute value function $f(x)=|x|$, but for which $g(0)=3$, we would use the function $g(x)=|x|+3$.
In this section, we will discuss the four basic transformations you can do on any function $f$ to obtain a transformed function $g$:
- Vertical translation: $g(x) = f(x)+k$.
- Horizontal translation: $g(x) = f(x-h)$.
- Vertical scaling: $g(x) = Af(x)$.
- Horizontal scaling: $g(x) = f(ax)$.
By using these transformations we can move and
stretch a generic function to give it any desired
shape.
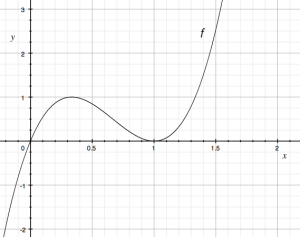 We will illustrate all of the above transformations
on the following function:
\[
f(x) = 6.75(x^3 - 2x^2 +x).
\]
This function is chosen because it has distinctive features
in both the horizontal and vertical directions.
By observing the graph of this function, we see that its
$x$-intercepts are at $x=0$ and $x=1$.
The function $f$ also has a local maximum at $x=\frac{1}{3}$
and the height of the function there is $f(\frac{1}{3})=1$.
We will illustrate all of the above transformations
on the following function:
\[
f(x) = 6.75(x^3 - 2x^2 +x).
\]
This function is chosen because it has distinctive features
in both the horizontal and vertical directions.
By observing the graph of this function, we see that its
$x$-intercepts are at $x=0$ and $x=1$.
The function $f$ also has a local maximum at $x=\frac{1}{3}$
and the height of the function there is $f(\frac{1}{3})=1$.
We can confirm the first observation mathematically by factoring the function as follows: \[ f(x) = 6.75x(x^2 - 2x +1) = 6.75x(x-1)^2, \] where we see clearly that $f(x)=0$ if $x=0$ (the $x$ factor kills it) or $x=1$ (the $(x-1)$ factor kills it).
Vertical translations
If we want to move a function $f$ up by $k$ units, we simply add $k$ to the function: \[ g(x) = f(x) + k. \] The function $g(x)$ will have exactly the same shape as $f(x)$ but it will be translated (the mathematical term for moved) upwards by $k$ units.
Recall the function $f(x) = 6.75(x^3 - 2x^2 +x)$. If we wanted to move the function up by $k=2$ units, we would obtain: \[ g(x) = f(x)+2 = 6.75(x^3 - 2x^2 +x) + 2, \] and the graph of $g(x)$ will be as shown on the right. The original function $f(x)$ crossed the $x$-axis at $x=0$, so we had $f(0)=0$. The transformed function must therefore obey $g(0)=2$. The maximum at $x=\frac{1}{3}$ has similarly shifted in value from $f(\frac{1}{3})=1$ to $g(\frac{1}{3})=3$.
Horizontal translation
We can move a function $f$ to the right by $h$ units by subtracting $h$ from $x$ and using that as the input argument: \[ g(x) = f(x-h). \] The point $(0,f(0))$ on $f(x)$ will now correspond to the point $(h,g(h))$ on $g(x)$.
Consider the graph on the right which shows the function $f(x)= 6.75(x^3 - 2x^2 +x)$ as well as the function $g(x)$ which is shifted to the right by $h=2$ units: \[ g(x) = f(x-2) = 6.75\left[ (x-2)^3 - 2(x-2)^2 +(x-2) \right]. \]
The original function $f$ had $f(0)=0$ and $f(1)=0$ so the new function $g(x)$ must have $g(2)=0$ and $g(3)=0$. The maximum at $x=\frac{1}{3}$ has similarly shifted by two units to the right $g(2+\frac{1}{3})=1$.
Vertical scaling
To stretch or compress the shape of a function vertically, we can multiply it by some constant $A$ and obtain: \[ g(x) = Af(x). \] If $|A|>1$, the function will be stretched, and if $|A|<1$ the function will be compressed. If $A$ is negative, the function will also be flipped upside down (reflection through the $x$-axis).
There is an important difference between vertical translation and vertical scaling. Translation moves all the points of the function the same amount, whereas scaling moves each point proportionally to how far it is from the $x$ axis.
On the right, we see the graph on the function $f(x)= 6.75(x^3 - 2x^2 +x)$ and the function $g(x)$ which is equal to $f(x)$ stretched vertically by a factor of $A=2$: \[ g(x) = 2f(x) = 13.5(x^3 - 2x^2 +x). \]
The $x$-intercepts $f(0)=0$ and $f(1)=0$ didn't move: $g(0)=0$ and $g(1)=0$. The maximum at $x=\frac{1}{3}$ has now doubled in value $g(\frac{1}{3})=2$. Indeed, all values of $f(x)$ have been stretched upwards by a factor of 2, as can be verified with the point $f(1.5)=2.5$ which has become $g(1.5)=5$.
Horizontal scaling
To stretch or compress a function horizontally we can multiply the input value by some constant $a$ to obtain: \[ g(x) = f(ax). \] If $|a|>1$, the function will be compressed, and if $|a|<1$ the function will be stretched. Note that the behaviour here is the opposite of the vertical case. If $a$ is a negative number, the function will also be flipped horizontally (reflection through the $y$-axis).
The graph on the right shows the function $f(x)= 6.75(x^3 - 2x^2 +x)$ and the function $g(x)$ which is $f(x)$ compressed horizontally by a factor of $a=2$: \[ g(x) = f(2x) =6.75\left[ (2x)^3 - 2(2x)^2 +(2x)\right]. \]
The $x$-intercept $f(0)=0$ didn't move since it is on the $y$-axis. The $x$-intercept $f(1)=0$ did move however and we now have $g(0.5)=0$. The maximum at $x=\frac{1}{3}$ has now moved to $g(\frac{1}{6})=1$. All values of $f(x)$ have been compressed towards the $y$-axis by a factor of 2.
General quadratic function
Definition
The general quadratic function has the following form: \[ f(x) = A(x-h)^2 + k, \] where $x$ is the input and $A,h$ and $k$ are the parameters.
Parameters
- $A$: slope multiplier.
- The larger the value of $A$ the steeper the slope.
- If $A<0$ (negative), then the function opens downwards.
- $h$: horizontal displacement of the function centre. Notice that subtracting a
number inside the bracket $(\ )^2$ (i.e. positive $h$) makes the function go to the right.
- $k$: vertical displacement of the function.
If a quadratic crosses the $x$-axis, then it can be written in factored form \[ f(x) = (x-a)(x-b), \] where $a$ and $b$ are the two roots.
Another very common way of writing a quadratic function is \[ f(x) = Ax^2 + Bx + C. \]
Properties
- There is a unique parabola that passes through any three points $(x_1,y_1),$ $(x_2,y_2)$ and $(x_3,y_3)$ if
the points have different $x$ coordinates $x_1 \neq x_2$, $x_2 \neq x_3$ and $x_1 \neq x_3$.
- The derivative of $f(x)=Ax^2 + Bx + C$ is $f'(x)=2Ax + B$.
Graph
When $h=1$ (one unit shifted to the right) and $k=-2$ (two units shifted downwards), we get the following graph:
General sin function
Parameters
Introducing all possible parameters into the sine function we get: \[ f(x) = A\sin( kx - \phi), \] where $A$, $k$ and $\phi$ are the parameters.
- $A$ is the amplitude, which tells you the distance the function will go above and below the $x$ axis as it oscillates.
- $k$ is the wave number and decides how many times the graph goes up and down within one period of $2\pi$. For the “bare” sine, $k=1$ and the function makes one cycle as $x$ goes from $0$ to $2\pi$. If $k=2$ the function will go up and down twice.
- $\phi$ is a phase shift, analogous to the horizontal shift $h$ which we have seen. This is a number which dictates where the oscillation starts. The default sine function has zero phase shift ($\phi=0$), so it starts from zero with an increasing slope.
Instead of counting how many times the function goes up and down, we can instead talk about the wavelength of the function: \[ \lambda \equiv \text{ wavelength} = \{ \text{ the distance form one peak to the next } \}. \] The “bare” sine has wavelength $2\pi$, but when we introduce some wave number multiplier $k$, the wavelength becomes: \[ \lambda = \frac{2\pi}{k}. \]
Hyperbolic cos and sin
If we follow the $x$ and $y$ coordinates of a point $P$ that is on the unit circle, we will see that the $x=\cos(\theta)$ and $y=\sin(\theta)$, where $\theta$ is the angle of the point. This is called circular trigonometry.
We can also have hyperbolic trigonometry, if we replace the circle with a hyperbola. The $x$-coordinate of a point $Q$ that traces out the shape of a hyperbola will have the formula $\cosh$ and its $y$ coordinate will be $\sinh$.
Definition
We can define the hyperbolic functions in terms of the exponential function: \[ \cosh x = \frac{e^{x} + e^{-x}}{2}, \qquad \sinh x = \frac{e^{x} - e^{-x}}{2}. \]
Graph
Parameters
Properties
- $\cosh$ is an even function, while $\sinh$ is odd.
In fact you can think of $\cosh x$ as the “even part of $e^x$,
and $\sinh x$ as the odd part of $e^x$ since \[ e^x = \cosh x + \sinh x. \]
The equivalent of the circular-trigonometric identity $\cos^2 \theta + \sin^2 \theta = 1$, is the following: \[ \cosh^2 x - \sinh^2 x = 1. \]
Applications
A long wire suspended between two lamp posts will sag in the middle producing a curved shape. The exact equation that describes the shape of the cable is the hyperbolic cosine function: $\cosh x$.
ADDTOCONTENTSTOCPROTECTSETCOUNTERTOCDEPTHONE
Polynomials
The polynomials are a very simple and useful family of functions. For example quadratic polynomials of the form $f(x) = ax^2 + bx +c$ often arise in the description of physics phenomena.
Definitions
- $x$: the variable
- $f(x)$: the polynomial. We sometimes sometimes denote polynomials $P(x)$ to
distinguish them from generic function $f(x)$.
- degree of $f(x)$: the largest power of $x$ that appears in the polynomial
- roots of $f(x)$: the values of $x$ for which $f(x)=0$
Polynomials
The most general polynomial of the first degree is a line $f(x) = mx + b$, where $m$ and $b$ are arbitrary constants.
The most general polynomial of second degree is $f(x) = a_2 x^2 + a_1 x + a_0$, where again $a_0$, $a_1$ and $a_2$ are arbitrary constants. We call $a_k$ the coefficient of $x^k$ since this is the number that appears in front of it.
By now you should be able to guess that a third degree polynomial will look like $f(x) = a_3 x^3 + a_2 x^2 + a_1 x + a_0$.
In general, a polynomial of degree $n$ has equation: \[ f(x) = a_n x^n + a_{n-1}x^{n-1} + \cdots + a_2 x^2 + a_1 x + a_0. \] or if you want to use the sum notation we can write it as: \[ f(x) = \sum_{k=0}^n a_kx^k, \] where $\Sigma$ (the capital Greek letter sigma) stands for summation.
Solving polynomial equations
Very often you will have to solve a polynomial equations of the form: \[ A(x) = B(x), \] where $A(x)$ and $B(x)$ are both polynomials. Remember that solving means to find the value of $x$ which makes the equality true.
For example, say the revenue of your company, as function of the number of products sold $x$ is given by $R(x)=2x^2 + 2x$ and the costs you incur to produce $x$ objects is $C(x)=x^2+5x+10$. A very natural question to ask is the amount of product you need to produce to break even, i.e., to make your revenue equal your costs $R(x)=C(x)$. To find the break-even $x$, you will have to solve the following equation: \[ 2x^2 + 2x = x^2+5x+10. \]
This may seem complicated since there are $x$s all over the place and it is not clear how to find the value of $x$ that makes this equation true. No worries though, we can turn this equation into the “standard form” and then use the quadratic equation. To do this, we will move all the terms to one side until we have just zero on the other side: \[ \begin{align} 2x^2 + 2x \ \ \ -x^2 &= x^2+5x+10 \ \ \ -x^2 \nl x^2 + 2x \ \ \ -5x &= 5x+10 \ \ \ -5x \nl x^2 - 3x \ \ \ -10 &= 10 \ \ \ -10 \nl x^2 - 3x -10 &= 0. \end{align} \]
Remember that if we do the same thing on both sides of the equation, it remains true. Therefore, the values of $x$ that satisfy \[ x^2 - 3x -10 = 0, \] namely $x=-2$ and $x=5$, will also satisfy \[ 2x^2 + 2x = x^2+5x+10, \] which was the original problem that we were trying to solve.
This “shuffling of terms” approach will work for any polynomial equation $A(x)=B(x)$. We can always rewrite it as some $C(x)=0$, where $C(x)$ is a new polynomial that has as coefficients the difference of the coefficients of $A$ and $B$. Don't worry about which side you move all the coefficients to because $C(x)=0$ and $0=-C(x)$ have exactly the same solutions. Furthermore, the degree of the polynomial $C$ can be no greater than that of $A$ or $B$.
The form $C(x)=0$ is the standard form of a polynomial and, as you will see shortly, there are formulas which you can use to find the solution(s).
Formulas
The formula for solving the polynomial equation $P(x)=0$ depend on the degree of the polynomial in question.
First
For first degree: \[ P_1(x) = mx + b = 0, \] the solution is $x=b/m$. Just move $b$ to the other side and divide by $m$.
Second
For second degree: \[ P_2(x) = ax^2 + bx + c = 0, \] the solutions are $x_1=\frac{-b + \sqrt{ b^2 -4ac}}{2a}$ and $x_2=\frac{-b - \sqrt{b^2-4ac}}{2a}$.
Note that if $b^2-4ac < 0$, the solutions involve taking the square root of a negative number. In those cases, we say that no real solutions exist.
Third
The solutions to the cubic polynomial equation \[ P_3(x) = x^3 + ax^2 + bx + c = 0, \] are given by \[ x_1 = \sqrt[3]{ q + \sqrt{p} } \ \ + \ \sqrt[3]{ q - \sqrt{p} } \ -\ \frac{a}{3}, \] and \[ x_{2,3} = \left( \frac{ -1 \pm \sqrt{3}i }{2} \right)\sqrt[3]{ q + \sqrt{p} } \ \ + \ \left( \frac{ -1 \pm \sqrt{3}i }{2} \right) \sqrt[3]{ q - \sqrt{p} } \ - \ \frac{a}{3}, \] where $q \equiv \frac{-a^3}{27}+ \frac{ab}{6} - \frac{c}{2}$ and $p \equiv q^2 + \left(\frac{b}{3}-\frac{a^2}{9}\right)^3$.
Note that, in my entire career as an engineer, physicist and computer scientist, I have never used the cubic equation to solve a problem by hand. In math homework problems and exams you will not be asked to solve equations of higher than second degree, so don't bother memorizing the solutions of the cubic equation. I included the formula here just for completeness.
Higher degrees
There is also a formula for polynomials of degree $4$, but it is complicated. For polynomials with order $\geq 5$, there does not exist a general analytical solution.
Using a computer
When solving real world problems,
you will often run into much more complicated equations.
For anything more complicated than the quadratic equation,
I recommend that you use a computer algebra system like
sympy to find the solutions.
Go to http://live.sympy.org and type in:
>>> solve( x**2 - 3*x +2, x) [ shift + Enter ] [1, 2]
Indeed $x^2-3x+2=(x-1)(x-2)$ so $x=1$ and $x=2$ are the two solutions.
Substitution trick
Sometimes you can solve polynomials of fourth degree by using the quadratic formula. Say you are asked to solve for $x$ in \[ g(x) = x^4 - 3x^2 -10 = 0. \] Imagine this comes up on your exam. Clearly you can't just type it into a computer, since you are not allowed the use of a computer, yet the teacher expects you to solve this. The trick is to substitute $y=x^2$ and rewrite the same equation as: \[ g(y) = y^2 - 3y -10 = 0, \] which you can now solve by the quadratic formula. If you obtain the solutions $y=\alpha$ and $y=\beta$, then the solutions to the original fourth degree polynomial are $x=\sqrt{\alpha}$ and $x=\sqrt{\beta}$ since $y=x^2$.
Of course, I am not on an exam, so I am allowed to use a computer:
>>> solve(y**2 - 3*y -10, y) [-2, 5] >>> solve(x**4 - 3*x**2 -10 , x) [sqrt(2)i, -sqrt(2)i, -sqrt(5) , sqrt(5) ]
Note how a 2nd degree polynomial has two roots and a fourth degree polynomial has four roots, two of which are imaginary, since we had to take the square root of a negative number to obtain them. We write $i=\sqrt{-1}$. If this was asked on an exam though, you should probably just report the two real solutions: $\sqrt{5}$ and $-\sqrt{5}$ and not talk about the imaginary solutions since you are not supposed to know about them yet. If you feel impatient though, and you want to know about the complex numbers right now you can skip ahead to the section on complex numbers.
Trigonometry
Put together any three lines and you get a triangle. In particular, if the triangle has one of its angles equal to $90^\circ$, we call this a right angle triangle.
In this section we are going to discuss right angle triangles in great detail and get used to their properties. You will learn how to use fancy Greek words like sinus, cosinus and tangent in order to refer to the various ratios of lengths in the triangle.
Understanding triangles and the trigonometric functions associated with them will be of fundamental importance for your later understanding of mathematics subjects like vectors and complex numbers and physics subjects like oscillations and waves.
Concepts
- $A,B,C$: the three vertices of the triangle
- $\theta$: the angle at the vertex $C$. Angles can be measured in degrees or radians.
- $\text{opp} \equiv \overline{AB}$: the length of the opposite side to $\theta$
- $\text{adj} \equiv \overline{BC}$: the length of side adjacent to $\theta$
- $\text{hyp} \equiv \overline{AC}$: the hypotenuse is longest side in the triangle
- $h$: the “height” of the triangle (in this case $h = \text{opp} = \overline{AB}$)
- $\sin\theta \equiv \frac{\text{opp}}{\text{hyp}}$: the sinus of theta, is the ratio of the lengths of the opposite side and the hypotenuse
- $\cos\theta \equiv \frac{\text{adj}}{\text{hyp}}$: the cosinus of theta, is the ratio of the adjacent and the hypotenuse lengths
- $\tan\theta \equiv \frac{\sin\theta}{\cos\theta} \equiv \frac{\text{opp}}{\text{adj}}$: the tangent is the ratio of the opposite divided by the adjacent
Pythagoras theorem
In a right angle triangle, the length of the hypotenuse squared is equal to the sum of the squares of the lengths of the other sides: \[ |\text{adj}|^2 + |\text{opp}|^2 = |\text{hyp}|^2. \]
If we divide both sides of the above equation by $|\text{hyp}|^2$ we obtain \[ \frac{|\text{adj}|^2}{ |\text{hyp}|^2 } + \frac{|\text{opp}|^2}{ |\text{hyp}|^2 } = 1, \] which can be rewritten as: \[ \cos^2\theta \ + \sin^2\theta = 1. \] This is a powerful trigonometric identity: a relationship between $\sin$ and $\cos$.
Sin and cos
Meet the trigonometric functions, or trigs for short. These are your new friends. Don't be shy now, say hello to them.
“Hello.”
“Hi.”
“Soooooo, you are like functions right?”
“Yep,” sin and cos reply in chorus.
“Okkkkkk, so what do you do?”
“Who me?”, asks cos, “well I tell the ratio.. Hmm..
wait, were you asking what I do as a function or specifically
what I do?”
“Both I guess?”
“Ok so as a function, I take angles as inputs and I give ratios as answers.
More specifically, I tell you how wide a triangle with that angle will be,”
says cos all in one breath.
“What do you mean wide?”, you ask.
“Oh yeah, I forgot to say, the triangle has to have hypotenuse of length 1.
So you see what happens is that, there is like a point $P$ that moves
around on a circle of radius 1, and we imagine a triangle that has
corners the origin, the point $P$ and the point on the $x$ axis that is
right below the point $P$.”
“I am not sure I get it,” you confess.
“Let me try to explain then”, says sin, “cos is always the one
to start off big and confuse people. I will start from zero.”
“OK. Sure. I mean I just don't see what circle cos is talking about.”
“Look on the next page, you will see a circle. The unit circle because
it has radius one. You see it yes?”
“Yes.”
“The circle thing really cool. Imagine a point $P$ which stators from
the point $P(0)=(1,0)$ and moves in a circle of radius one.
The $x$ and $y$ coordinates of the point $P(\theta)=(P_x(\theta),\ P_y(\theta))$
as a function of $\theta$ are given by:
\[
P(\theta)=(P_x(\theta),\ P_y(\theta)) = (\cos\theta, \ \sin\theta ).
\]
So, either you think of us in the context of triangles
or you think of us in the context of the unit circle.”
“OK. Cool. I kind of get it,” you say it to keep conversation,
but in reality you are all weirded out. Talking functions?
“Well, thank you guys. It was nice to meet you, but you
know I have to get going now, so see you later,” you say to
get out the situation.
“OK. Peace out,” says sin, “anyways we are done here, since I told you the most important things.”
“See you later,” says cos.
The unit circle
You should be familiar with the values of $\sin$ and $\cos$ for all the angles that are multiples of $\frac{\pi}{6}$ ($30^\circ$) or $\frac{\pi}{4}$ ($45^\circ$). All of them are shown in the diagram below. For each angle, the $x$ coordinate (the first number in the brackets below) is $\cos$ and the $y$ coordinate is $\sin$.
You might think that there is too much to remember. “Dude”, you say, “I was listening to your advice until now and learning, but now you are telling me to remember all those values with so many square roots in them. How am I to remember all of that?”
Actually, you just have to memorize one fact: \[ \sin(30^\circ) = \sin\!\!\left( \frac{\pi}{6} \right) = \frac{1}{2}. \]
My dad was like “You have to put this in the book”, and he is right. You can figure out all the other angles from this one. Let's start with $\cos(30^\circ)$. We know that the point $P$ on the unit circle at $30^\circ$ has vertical coordinate $\frac{1}{2}=\sin(30^\circ)$, and that by definition the horizontal component is the $\cos$ quantity we are looking for: \[ P = (\cos(30^\circ), \sin(30^\circ) ). \]
The key fact about the unit circle, is that all the points or it are at distance one from the centre. So knowing that $P$ is on the unit circle, and the value of $\sin(30^\circ)$, we can solve for $\cos(30^\circ)$. Indeed we start from the identity: \[ \cos^2\theta \ + \sin^2\theta = 1, \] which is true for all angles $\theta$. Moving things around, we obtain: \[ \cos(30^\circ) = \sqrt{ 1 - \sin^2(30^\circ) } = \sqrt{ 1 - \frac{1}{4} } = \sqrt{ \frac{3}{4} } = \frac{\sqrt{3}}{2}. \]
To get the values of $\cos(60^\circ)$ and $\sin(60^\circ)$, observe the symmetry of the circle. Sixty degrees measured from the $x$ axis, is the same as thirty degrees measured from the $y$ axis. So immediately you know that $\cos(60^\circ)=\sin(30^\circ)=\frac{1}{2}$. Therefore, it must be that $\sin(60^\circ) = \frac{\sqrt{3}}{2}$.
To get the values of sin and cos for angles that are multiples of $45^\circ$, we need to find the value $a$ such that \[ a^2 + a^2 = 1, \] since at $45^\circ$ both the horizontal part and the vertical part will be of the same length. The answer is obviously $a=\frac{1}{\sqrt{2}}$, but because people don't like to see square roots in the denominator we have to write: \[ \frac{\sqrt{2}}{2} = \cos(45^\circ) = \sin(45^\circ). \]
All of the other angles in the circle are just like the above three, but they have a negative sign in one or more of the components. Don't memorize them, but if you ever need one of their values draw a little circle and use the symmetry of the circle to find them. For example, $150^\circ$ is just like $30^\circ$, except the $x$ component is negative.
Non-unit circles
Consider now a point $Q(\theta)$ at an angle of $\theta$ on a circle of radius $R\neq1$. How can we find the $x$ and $y$ coordinates of the point $Q(\theta)$?
We saw that the coefficients $\cos\theta$ and $\sin\theta$ correspond the $x$ and $y$ coordinates of a point on the unit circle ($R=1)$. To obtain the coordinates for a point on a circle of radius $R$ we must scale the coordinates by a factor of $R$: \[ Q(\theta) = (Q_x(\theta), Q_y(\theta) ) = ( R\cos\theta, R\sin\theta ). \]
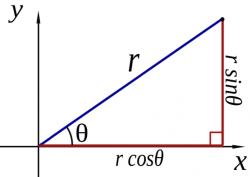 The take home message is that the functions $\cos\theta$ and $\sin\theta$
are generally useful for finding the “horizontal” and “vertical” components
of any length $r$.
The take home message is that the functions $\cos\theta$ and $\sin\theta$
are generally useful for finding the “horizontal” and “vertical” components
of any length $r$.
From this point on in the book, we will always talk about the length of the adjacent side as $r_x=r\cos\theta$ and the opposite side as $r_y = r\sin\theta$. It is extremely important that you get comfortable with this notation.
The reasoning behind the above calculations is as follows: \[ \begin{align*} \cos\theta \equiv \frac{\text{adj}}{\text{hyp}} = \frac{r_x}{r} & \quad \Rightarrow \quad r_x = r \cos\theta, \nl \sin\theta \equiv \frac{\text{opp}}{\text{hyp}}=\frac{r_y}{r} & \quad \Rightarrow \quad r_y = r\sin\theta. \end{align*} \]
Calculators
Make sure your calculator is set to the right units for angles. If you wanted to compute the sinus of 30 degrees what should you type into your calculator?
If you calculator is set to degrees then simply
type sin + 30 + =.
But what if your calculator is set to radians? You have two options:
- Change the
modeof the calculator so it works in degrees. - Convert $30^\circ$ to radians
\[ 30 \ [^\circ] \times \frac{ 2\pi \ [\text{rad}] }{ 360 \ [^\circ] } = \frac{\pi}{6} \ \text{[rad]}, \]
so you should type ''sin'' + $\pi$ + ''/'' + ''6'' + ''='' on your calculator.
Trigonometric identities
There is a number of important relationships between the values of the functions $\sin$ and $\cos$. These are known as trigonometric identities. There are three of them which you should memorize, and about a dozen others which are less important.
Formulas
The trigonometric functions are defined as \[ \cos(\theta)=x_P~~,~~\sin(\theta)=y_P~~,~~\tan(\theta)=\frac{y_P}{x_P}, \] where $P=(x_P,y_P)$ is a point on the unit circle.
The three identities that you must remember are:
1. Unit hypotenuse
\[ \sin^2(x)+\cos^2(x)=1. \] This is true by Pythagoras theorem and the definition of sin and cos. The ratios of the squares of the sides of a triangle is equal to the square of the size of the hypotenuse.
2. sico + sico
\[ \sin(a + b)=\sin(a)\cos(b) + \sin(b)\cos(a). \] The mnemonic for this one is “sico sico”.
3. coco - sisi
\[ \cos(a + b)=\cos(a)\cos(b) - \sin(a)\sin(b). \] The mnemonic for this one is “coco - sisi”—the negative sign is there because it is not good to be a sissy.
Derived formulas
If you remember the above thee formulas, you can derive pretty much all the other trigonometric identities.
Double angle formulas
Starting from the sico-sico identity above, and setting $a=b=x$ we can derive following identity: \[ \sin(2x) = 2\sin(x)\cos(x). \]
Starting from the coco-sisi identity, we derive: \[ \cos(2x) \ =\ 2\cos^2(x) - 1 \ = 2\left(1 - \sin^2(x)\right) - 1 = 1 - 2\sin^2(x), \] or if we rewrite to isolate the $\sin^2$ and $\cos^2$ we get: \[ \cos^2(x) = \frac{1}{2}\left(1+\cos(2x)\right), \qquad \sin^2(x) = \frac{1}{2}\left(1-\cos(2x)\right). \]
Self similarity
Sin and cos are periodic functions with period $2\pi$. So if we add multiples of $2\pi$ to the input, we get the same value: \[ \sin(x + 2\pi)=\sin(x +124\pi) = \sin(x), \qquad \cos(x+2\pi)=\cos(x). \]
Furthermore, sin and cos are self similar within each $2\pi$ cycle: \[ \sin(\pi-x)=\sin(x), \qquad \cos(\pi-x)=-\cos(x). \]
Sin is cos, cos is sin
Now it should come and no surprise if I tell you that actually sin and cos are just $\frac{\pi}{2}$-shifted versions of each other: \[ \cos(x)=\sin\!\left(x\!+\!\frac{\pi}{2}\right)=\sin\!\left(\frac{\pi}{2}\!-\!x\right), \ \ \sin\!\left(x\right) = \cos\left(x\!-\!\frac{\pi}{2}\right) = \cos\left(\frac{\pi}{2}\!-\!x\right). \]
Sum formulas
\[ \sin\!\left(a\right)+\sin\!\left(b\right)=2\sin\!\left(\frac{1}{2}(a+b)\right)\cos\!\left(\frac{1}{2}(a-b)\right), \] \[ \sin\!\left(a\right)-\sin\!\left(b\right)=2\sin\!\left(\frac{1}{2}(a-b)\right)\cos\!\left(\frac{1}{2}(a+b)\right), \] \[ \cos\!\left(a\right)+\cos\!\left(b\right)=2\cos\!\left(\frac{1}{2}(a+b)\right)\cos\!\left(\frac{1}{2}(a-b)\right), \] \[ \cos\!\left(a\right)-\cos\!\left(b\right)=-2\sin\!\left(\frac{1}{2}(a+b)\right)\sin\!\left(\frac{1}{2}(a-b)\right). \]
Product formulas
\[ \sin(a)\cos(b) = {1\over 2}(\sin{(a+b)}+\sin{(a-b)}), \] \[ \sin(a)\sin(b) = {1\over 2}(\cos{(a-b)}-\cos{(a+b)}), \] \[ \cos(a)\cos(b) = {1\over 2}(\cos{(a-b)}+\cos{(a+b)}). \]
Discussion
The above formulas will come in handy in many situations when you have to find some unknown in an equation or when you are trying to simplify a trigonometric expression. I am not saying you should necessarily memorize them, but you should be aware that they exist.
Geometry
Triangles
 The area of a triangle is equal to $\frac{1}{2}$
times the length of the base times the height:
\[
A = \frac{1}{2} a h_a.
\]
Note that $h_a$ is the height of the triangle relative to the side $a$.
The area of a triangle is equal to $\frac{1}{2}$
times the length of the base times the height:
\[
A = \frac{1}{2} a h_a.
\]
Note that $h_a$ is the height of the triangle relative to the side $a$.
The perimeter of the triangle is: \[ P = a + b + c. \]
Consider now a triangle with internal angles $\alpha$, $\beta$ and $\gamma$. The sum of the inner angles in any triangle is equal to two right angles: $\alpha+\beta+\gamma=180^\circ$.
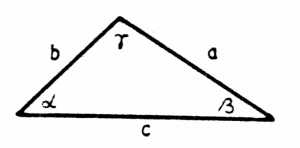 The sine law is:
\[
\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)},
\]
where $\alpha$ is the angle opposite to $a$, $\beta$ is the angle opposite to $b$ and $\gamma$ is the angle opposite to $c$.
The sine law is:
\[
\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)},
\]
where $\alpha$ is the angle opposite to $a$, $\beta$ is the angle opposite to $b$ and $\gamma$ is the angle opposite to $c$.
The cosine rules are: \[ \begin{align} a^2 & =b^2+c^2-2bc\cos(\alpha), \nl b^2 & =a^2+c^2-2ac\cos(\beta), \nl c^2 & =a^2+b^2-2ab\cos(\gamma). \end{align} \]
Sphere
A sphere is described by the equation \[ x^2 + y^2 + z^2 = r^2. \]
Surface area: \[ A = 4\pi r^2. \]
Volume: \[ V = \frac{4}{3}\pi r^3. \]
Cylinder
The surface area of a cylinder consists of the top and bottom circular surfaces plus the area of the side of the cylinder: \[ A = 2 \left( \pi r^2 \right) + (2\pi r) h. \]
The volume is given by product of the area of the base times the height of the cylinder: \[ V = \left(\pi r^2 \right)h. \]
Example
You open the hood of your car and see 2.0L written on top of the engine. The 2[L] refers to the total volume of the four pistons, which are cylindrical in shape. You look in the owner's manual and find out that the diameter of each piston (bore) is 87.5[mm] and the height of each piston (stroke) is 83.1[mm]. Verify that the total volume of the cylinder displacement of your engine is indeed 1998789[mm$^3$] $\approx 2$[L].
Links
[ A formula for calculating the distance between two points on a sphere ]
http://www.movable-type.co.uk/scripts/latlong.html
Circle
The circle is a set of points that are a constant distance from the centre. It is a very simple geometrical shape which comes up in many situations.
Definitions
- $r$: the radius of the circle
- $A$: the area of the circle
- $C$: the circumference of the circle
- $(x,y)$: is a point on the circle
- $\theta$: the angle (measured from the $x$-axis) of some point on the circle.
Formulas
The circle of radius $r$ centred at the origin is described by the following equation: \[ x^2 + y^2 = r^2. \] All points $(x,y)$ which satisfy this equation are part of the circle.
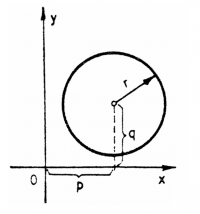 Instead of being centred at the origin, the
centre of the circle could be at any point in the plane $(p,q)$:
\[
(x-p)^2 + (y-q)^2 = r^2.
\]
Instead of being centred at the origin, the
centre of the circle could be at any point in the plane $(p,q)$:
\[
(x-p)^2 + (y-q)^2 = r^2.
\]
Explicit function
The equation of a circle is a relation or an implicit function involving $x$ and $y$. If we want an explicit function $f(x)$ for the circle, we can solve for $y$ to obtain: \[ y = \sqrt{ r^2 - x^2}, \quad -r \leq x \leq r, \] and \[ y = -\sqrt{ r^2 - x^2}, \quad -r \leq x \leq r. \] There are two functions, because a vertical line crosses that circle in two places. The first function corresponds to the top half of the circle and the second function corresponds to the bottom half.
Polar coordinates
Circles are such a common shape in mathematics that mathematicians developed a special “circular coordinate system” in order to describe them more easily.
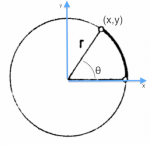 It is possible to specify the coordinates $(x,y)$ of any point on the circle
in terms of the polar coordinates $r\angle\theta$, where $r$ measures the distance of
the point from the origin and $\theta$ is the angle measured from the $x$ axis.
It is possible to specify the coordinates $(x,y)$ of any point on the circle
in terms of the polar coordinates $r\angle\theta$, where $r$ measures the distance of
the point from the origin and $\theta$ is the angle measured from the $x$ axis.
To convert from the polar coordinates $r\angle\theta$ to the $(x,y)$ coordinates we use the trigonometric functions: \[ x = r\cos \theta, \qquad y = r\sin \theta. \]
Parametric equation
We can describe all the points on the circle in we specify a fixed radius $r$ and vary the angle $\theta$ over all angles: $\theta \in [0, 360^\circ)$. A parametric equation specifies the coordinates $(x(\theta), y(\theta))$ for the points on a curve for all values of the paramter $\theta$. The parametric equation for a circle of radius $r$ is given by: \[ \{ (x,y)\in\mathbb{R}^2 \ | \ x=r \cos\theta, y = r\sin\theta, \ \theta \in [0, 360^\circ) \}. \] You should try to visualize the curve traced by the point $(x(\theta),y(\theta))=(r\cos\theta,r\sin\theta)$ as $\theta$ varies from $0$ to $360^\circ$ and convince yourself that it traces out a circle of radius $r$.
If we let the parameter $\theta$ vary over a smaller interval, we will obtain subsets of the circle. For example, the parametric equation for the top half of the circle is: \[ \{ (x,y)\in\mathbb{R}^2 \ | \ x=r \cos\theta, y = r\sin\theta, \ \theta \in [0, 180^\circ] \}. \] The top half of the circle is also described by $\{ (x,y) \in\mathbb{R}^2 \ | \ y = \sqrt{ r^2 - x^2},\ x \in [-r,r] \}$, where the parameter used is the $x$ coordinate.
Area
The area of a circle of radius $r$ is given by \[ A = \pi r^2. \]
Circumference and arc length
The circumference of a circle is \[ C = 2 \pi r. \] This is the total length you would measure out if you were to follow the line of the circle.
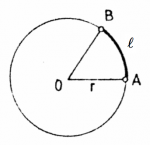 What is the length of a part of the circle?
Say you have a piece of the circle, that corresponds
to the angle $\theta=30^\circ$. What is its length?
If the total length is $C=2 \pi r$ corresponds to
doing a full turn around the circle $360^\circ$, then
the arc length $\ell$ for a portion which corresponds to the angle $\theta$ is
\[
\ell = 2 \pi r \frac{\theta}{360}.
\]
We say that $\ell$ is the act length subtended by the angle $\theta$.
What is the length of a part of the circle?
Say you have a piece of the circle, that corresponds
to the angle $\theta=30^\circ$. What is its length?
If the total length is $C=2 \pi r$ corresponds to
doing a full turn around the circle $360^\circ$, then
the arc length $\ell$ for a portion which corresponds to the angle $\theta$ is
\[
\ell = 2 \pi r \frac{\theta}{360}.
\]
We say that $\ell$ is the act length subtended by the angle $\theta$.
Radians
Though degrees are a commonly used unit for angles, it is much better to measure angles in radians, which is the natural angle parameter. The conversion ratio is: \[ 2\pi \ \text{[radians]} = 360 \ \text{[degrees]}. \] For a circle of radius $r=1$, the arc length is equal to the angle in radians: \[ \ell = \theta_{radians}. \] Measuring radians is equivalent to measuring arc length on a circle of radius one.
Ellipse
The orbit of planet Earth around the Sun is an ellipse.
Definitions
- $a$: the half-length of the ellipse along the $x$ axis, also known as the semi-major axis.
- $b$: the half-length of the ellipse along the $y$ axis.
- $F_1,F_2$: the two focal points of the ellipse.
- $\epsilon$: the eccentricity of the ellipse.
- $(x,y)$: a point on the ellipse.
- $r_1$: the distance from the point $(x,y)$ on the ellipse to $F_1$.
- $r_2$: the distance from the point $(x,y)$ on the ellipse to $F_2$.
Formulas
An ellipse is the curve you get if you trace out all the points such that the sum of the distances to the focal points is a constant length: \[ r_1 + r_2 = \text{const}. \]
There is a really neat way to draw a perfect ellipse using a piece of string and two tacks (pins). Take a piece of string and tack it to a picnic table at two points such that it is loose in the middle. Now take a pencil and without touching the table move the string until both sides are tout. Make a mark at that point. Since the two parts of the string are completely straight, their sum length, $r_1+r_2$ is the length of the whole piece, which plays the role of the constant in the above equation. When you make a mark at every point possible where the two “legs” of string are kept tout you get the following curve:
The mathematical formula for the ellipse is: \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \] where in the above drawing we have $a>b$ so the ellipse is elongated on the $x$ axis.
The coordinates of the focal points are: \[ F_1 = (-e,0), \qquad F_2 = (e,0), \] where $e=\sqrt{a^2 - b^2}$. The focal points correspond to the locations of the two tacks where the string is held fixed.
An important related quantity is the eccentricity: \[ \epsilon \equiv \sqrt{1- \frac{b^2}{a^2} }=\frac{e}{a} , \] which describes the shape of the ellipse in a scale-less fashion. The bigger $\epsilon$ the bigger the difference in the length of the major-axis and the minor-axis. In the special case when $\epsilon=0$, the equation of the ellipse becomes a circle of radius $a$.
Polar coordinates
Polar functions $r(\theta)$ describe the distance of some point from the centre as a function of the angle $\theta$ the point makes with the $x$-axis. Thus in the coordinate system $(r,\theta)$, the independent variable is $\theta$ and the dependent variable is $r$.
If we setup a polar coordinate system with centre at the origin $C=(0,0)$, the equation of the ellipse will be: \[ r(\theta) = \frac{ab}{b^2\cos^2(\theta) + a^2\sin^2(\theta)}. \]
For many applications, it is more convenient to put the centre of the polar coordinates system at $F_1$, the left focal point. Suppose that $(r_1,\phi)$ is a polar coordinate system with centre $C=F_1=(-e,0)$, then the equation of the ellipse is \[ r_1(\phi) = \frac{a(1-\epsilon^2)}{1 - \epsilon\cos(\phi)}, \] where the angle $\phi$ is with respect to the positive $x$-axis.
Applications
Orbit of the Earth around the Sun
To a very good approximation, the motion of the earth around the sun is described by an ellipse with the sun at one focus. The distance of the earth from the sun (positioned at $F_1$, so we are talking about $r_1$) as a function of the angle $\phi$ is given by: \[ r_1(\phi) = \frac{a(1-\epsilon^2)}{1 - \epsilon\cos(\phi)}. \]
The eccentricity of the earth's orbit around the sun is $\epsilon = 0.01671123 $ and the half-length of the major axis is $a=149\:598\:261$[km]. So the distance sun-earth $r_1$ is given by the equation: \[ r_{1}(\phi) = \frac{149556484.56}{1 - 0.01671123\cos(\phi)} \text{[km]}. \]
The moment where the earth is most distant from the sun is called aphelion and occurs around January 3rd. The closet point is called perihelion and it usually occurs around July 4th. The aphelion distance of the earth happens when $\phi=0$ so we have \[ r_{1,aphe}=r_1(0) = \frac{149556483}{1 - 0.01671123\cos(0)} = 152098232 \text{[km]}, \] and the closes pass of the earth near the sun is when $\phi=\pi$ at \[ r_{1,peri} = r_1(\pi) = \frac{149556483}{1 - 0.01671123\cos(\pi)} = 147098290 \text{[km]}. \] If you don't trust me, look up the numbers on wikipedia and compare them with the above predictions.
The angle $\phi$ of the earth relative to the sun, is a function of time. If we measure $t$ in days we have the following lookup table:
| t (day) | 1 | 2 | . | 182 | . | 365 | 365.242199 |
|---|---|---|---|---|---|---|---|
| t (date) | July 3 | July 4 | . | Jan 3 | . | July 2 | ? |
| phi (deg) | 0 | . | 180 | . | 359.761356 | 360 | |
| phi (rad) | 0 | . | pi | . | 6.27902 | 2 pi |
Note the extra amount of “day” that is roughly equal to $\frac{1}{4}=0.25$. Ever wonder why one of every four years is a leap year? That is why.
The exact formula of the function $\phi(t)$ that describes the angle as a function of time is complicated, but computable.
Note that the varying distance of the earth from the sun is not the cause of seasons. Seasons are predominantly caused by the tilt of the earth relative to the plane of its orbit around the sun. The day the tilt of the earth spin axis aligns with sun is either the longest day or the shortest day of the year, depending on which hemisphere you are in (the North or the South). We call those days solstices.
Newton's insight
Contrary to what is commonly believed, Newton did not come up with his theory of gravitation while sitting under a tree because an apple fell on his head. What actually happened is that he started from Kepler's laws of motion which describes the exact elliptical orbit of the Earth as a function of time. Newton asked “what kind of force would cause two bodies to spin around each other in an elliptical orbit” and he deducted that the gravitational force between the sun of mass $M$ and the earth of mass $m$ must be of the form $F_g=\frac{GMm}{r^2}$. We have to give props to the man, for connecting the dots, and we have to give props to Johannes Kepler studying the orbital periods and Tycho Brahe for doing all the astronomical measurements. Above all, we have to give props to the ellipse for being such an awesome shape.
Links
Solving systems of linear equations
You know that to solve equations with one unknown like $2x + 4 = 7x$, you have to manipulate both sides of the equation until you isolate the unknown variable on one side. For the above equation we would subtract $2x$ from both sides to obtain: $4 = 5x$, which means that $x=\frac{4}{5}$.
What if you have two equations and two unknowns? For example: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \] Can you find values of $x$ and $y$ that satisfy these equations?
Concepts
- $x,y$: the two unknowns in the equations.
- $eq1, eq2$: a system of two equations that need to be solved simultaneously.
These equations will look like:
\[
\begin{align*}
a_1x + b_1y & = c_1, \nl
a_2x + b_2y & = c_2,
\end{align*}
\]
where the $a$s, $b$s and $c$s are given constants.
Principles
If you have $n$ equations and $n$ unknowns you can solve the equations simultaneously and find the values of the unknowns. There are different tricks which you can use to solve these equations simultaneously. We learn about three such tricks in this section.
Solution techniques
Solving by equating
We want to solve the following system of equations: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \]
We can isolate $x$ in both equations by moving all other variables and constants to the right sides of the equations: \[ \begin{align*} x & = 5 -2y, \nl x & = \frac{1}{3}(21 - 9y) = 7 - 3y. \end{align*} \]
The variable $x$ is still unknown, but we know two facts about it. We know that $x$ is equal to $5 - 2y$ and also that $x$ is equal to $7 - 3y$. So it must be that: \[ 5 - 2y = 7 -3y. \]
We can now solve for $y$ by adding $3y$ to both sides and subtracting $5$ from both sides to get $y = 2$.
We got $y=2$, but what is $x$? That is easy, we can plug in the value of $y$ that we found into any of the above equations. Say I pick the first one: \[ x = 5 - 2y = 5 - 2(2) = 1. \]
We are done, and $x=1,y=2$ is our solution.
Substitution
Let us go back to our set of equations: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \]
Looking at the first equation we can isolate $x$ to obtain: \[ \begin{align*} x & = 5 - 2y, \nl 3x + 9y & = 21. \end{align*} \]
If we substitute the top equation for $x$ into the bottom equation we will obtain: \[ 3(5-2y) + 9y = 21. \] We have just eliminated one of the unknowns by substitution. Let's do some massaging of this equation now. Expanding the bracket we get: \[ 15 - 6y +9y = 21, \] or \[ 3y = 6, \] which means that $y=2$. To get $x$, we use the original substitution $x = (5-2y)$ to get $x = (5-2(2)) = 1$.
Subtraction
There is a third way to solve the equations: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \]
Observe that we would not change the truth of any equation if we were to multiply it by some constant. For example, we can multiply the first equation by $3$ to obtain an equivalent set of equations: \[ \begin{align*} 3x + 6y & = 15, \nl 3x + 9y & = 21. \end{align*} \]
Why did I pick three as the multiplier? I chose this constant so that the first term (the $x$ term) now has the same coefficient in both equations.
If we subtract two true equations from each other we obtain another true equation. Let's do that. Let's subtract the top equation from the bottom one. We get: \[ 3x - 3x + 9y - 6y = 21 - 15 \quad \Rightarrow \quad 3y = 6. \] Did you see how the $3x$'s cancelled? That is why I originally chose to multiply the first equation by three. Now it is obvious that $y=2$, and substituting back into one of the original equations we have \[ x + 2(2) = 5, \] or moving the $2(2)=4$ to the other side we get $x=1$.
Discussion
These techniques can be extended to as many unknowns as you want. When we get to the chapter on linear algebra, we will learn a much more systematic way of solving this type of equations.
Compound interest
Soon after ancient civilizations invented the notion of numbers, they started computing interest on loans.
Percentages
We often talk about ratios between quantities, instead of the quantities themselves. For example, we can imagine working Joe who invests $1000$ in the stock market and loses $300$, because the boys on Wall Street keep pulling dirty tricks on him. To put the number $300$ into perspective, we can say Joe lost about $0.3$ of his wealth or, alternately, $30\%$ of his wealth.
To obtain the percentage, you simply take the ratio between two quantities and then multiply by $100$. The ratio of loss to investment is: \[ R = 300/1000 = 0.3. \]
The same ratio expressed as a percentage gives \[ R = 300/1000 \times 100 = 30\%. \]
To convert from a percentage to a ratio, you simply have to divide by $100$.
Interest rates
Say you take out a $1000$ dollar loan with interest rate of $6\%$ compounded annually. How much money will you need to pay in interest at the end of the year?
Since $6\%$ corresponds to a ratio of $6/100$, and since you took out $1000$, the interest at the end of the year will be: \[ I_1 = \frac{6}{100}\times 1000 = 60. \]
At the end of the year, you owe the bank a total of \[ L_1 = \left(1 + \frac{6}{100}\right)1000 = (1 + 0.06) 1000 = 1.06\times 1000 = 1060. \]
The total money owed after 6 years is going to be: \[ L_6 = (1.06)^6 \times 1000 = 1418.52. \] Better pay up or else they will have your head soon! Or default maybe? Is your credit rating really that important?
Monthly compounding
The above scenario assumes that the bank computes the interest once per year. Such a compounding schedule is disadvantageous to the bank, and since they write the rules it is never used. Usually, the compounding is done every month.
What is the annual rate then? The bank will quote the nominal APR (annual percentage rate), which is equal to: \[ \text{nAPR} = 12 \times r, \] where $r$ is the monthly interest rate.
Suppose we have an nominal APR of $6\%$, which gives a monthly interest rate of $r=0.5\%$. If you take out a $1000$ loan at that interest rate, you will owe: \[ L_1 = \left(1 + \frac{0.5}{100}\right)^{12} \times 1000 = 1061.68, \] at the end of the first year, and after 6 years you will owe: \[ L_6 = \left(1 + \frac{0.5}{100}\right)^{72}\times 1000 = 1.061677^{6} \times 1000 = 1432.04. \]
Note how the bank tries to pull a fast one on you. The effective APR is actually $6.16\%$ not $6\%$! Indeed, each twelve months, the amount due will increase by the following factor: \[ \textrm{eAPR} = \left(1 + \frac{0.5}{100}\right)^{12} = 1.0616. \] Thus the effective annual percent rate is $\textrm{eAPR} = 6.16\%$.
Compounding infinitely often
For a nominal APR of $6\%$, what would be the effective APR if the bank was to do the compounding $n$ times per year?
The annual growth ratio is going to be: \[ \left(1 + \frac{6}{100n}\right)^{n}, \] since you have interest rate per compounding period is $\frac{6}{n}\%$ and there are $n$ periods in one year.
In the limit of compounding infinitely often, we will see the exponential function emerge: \[ \lim_{n \to \infty} \left(1 + \frac{6}{100n}\right)^{n} = \exp\!\!\left(\frac{6}{100}\right) = 1.0618365, \] or an $\text{eAPR} = 6.183\%$.
With infinitely frequent compounding, the interest after 6 years will be: \[ L_6 = \exp\!\!\left(\frac{6}{100}\right)^6 \times 1000 = \exp\!\!\left(\frac{36}{100}\right) \times 1000 = 1433.33. \]
As you can see, for the same APR of $6\%$, the faster the compounding schedule, the more money you owe at the end of six years. It is a good thing that banks don't know about the exponential function then!
Links
Very good article and notation:
http://plus.maths.org/content/have-we-caught-your-interest
Set notation
A set is mathematically precise way to talk about different groups of objects. To do simple math, you don't need to know about sets, but for more advanced topics you need to know what a set is and how we denote set membership and subset relations between sets.
Definitions
- set: some collection of mathematical objects with a precise definition.
- $S,T$: usual variable names for sets.
- $\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}$: some important sets of numbers. These correspond to the naturals, the integers,
the rationals and the real numbers respectively.
- $\{ definition \}$: The curly brackets are used to surround the definition of a set and the expression inside is supposed
to completely describe what the set is.
NOINDENT Set operations:
- $S\cup T$: the union of two sets. The elements that are either in $S$ or $T$.
- $S \cap T$: the intersection of the two sets. The elements that are in both $S$ and $T$.
- $S \setminus T$: set minus. The elements of $S$ that are not in $T$.
NOINDENT Set relations:
- $\subset$: is a subset of.
- $\subseteq$: is subset or equal to.
NOINDENT Special mathematical shorthand and corresponding meaning in English:
- $\forall$: for all
- $\exists$: there exists
- $\nexists$: there doesn't exist
- $:$ or $|$: such that
- $\in$: is element of
- $\notin$: is not an element of
Sets
A lot of the power of math comes from abstraction: the ability to think meta thoughts and seeing the bigger picture about what math objects have in common. We can think of individual numbers like $3$, $5$ and $222$ or talk about the set of all numbers. You can think of functions like $f(x)=x$, and $f(x)=x^2$ or you can think of the set of all functions $f\colon \mathbb{R} \to \mathbb{R}$ that take real numbers as inputs and give real numbers as outputs.
Example 1: Non-negative numbers
Define $\mathbb{R}_+ \subset \mathbb{R}$ to be the set of non-negative real numbers: \[ \mathbb{R}_+ = \{ \text{all } x \text{ from } \mathbb{R} \text{ such that } x \geq 0 \}, \] or expressed more compactly: \[ \mathbb{R}_+ = \{ x \in \mathbb{R} \ | \ x \geq 0 \}. \]
Example 2: Odd and even
Define the set of even integers as: \[ E = \{ n \in \mathbb{Z} \ | \ \frac{n}{2} \in \mathbb{Z} \} = \{ \ldots, -2, 0, 2, 4, 6, \ldots \}. \] and the set of odd integers as: \[ O = \{ n \in \mathbb{Z} \ | \ \frac{n+1}{2} \in \mathbb{Z} \} = \{ \ldots, -3, -1, 1, 3, 5, \ldots \}. \] In each case the mathematical notation $\{ \ldots \ | \ \ldots \}$ follows the same pattern where you first say what kind of objects we are talking about, followed by the “such that” sign $|$ followed by the conditions which must be satisfied by all elements of the set.
Important sets
The natural numbers are the set of number you can get by starting from $0$ and adding $1$ arbitraryly many times: \[ \mathbb{N} \equiv \{ 0, 1, 2, 3, 4, \ldots \}. \] The integers are the number you get by adding or subtracting 1 arbitrary many times: \[ \mathbb{Z} \equiv \{ \ldots, -3, -2, -1, 0, 1, 2, 3, 4, \ldots \}. \] If you allow for divisions between integers, you get the rational numbers: \[ \mathbb{Q} = \{ -1.5, 1/3, 22/7, 0.125, \ldots \}. \] The more general class of real numbers includes also irrational numbers: \[ \mathbb{R} = \{\pi, e, -1.53929411..,\ 4.99401940129401.., \ \ldots \}. \] Finally we have the set of complex numbers: \[ \mathbb{C} = \{ 1, i, 1+i, 2+3i, \ldots \}= \{ a + bi \ | \ a,b \in \mathbb{R}, i^2=-1 \}. \]
Note the inclusion relationship which holds for these sets: \[ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}. \] Every natural number is also an integer. Every integer is a rational number. Every rational number is a real. Every real number is also a complex number.
New vocabulary
Let's practice the new vocabulary by looking at a simple mathematical proof.
Square-root of two is irrational
Claim: $\sqrt{2} \notin \mathbb{Q}$. This means that there are no integers $m \in \mathbb{Z}$ and $n \in \mathbb{N}$ such that $m/n = \sqrt{2}$. The same sentence in mathematical notation would read: \[ \nexists m \in \mathbb{Z}, n\in\mathbb{N} \ | \ m/n = \sqrt{2}. \]
Proof: Suppose for a contradiction that there existed $m$ and $n$ such that $m/n=\sqrt{2}$. We can further assume that integers $m$ and $n$ are such that they have no common factors: we can always make sure this is the case if we cancel the common factors. In particular this implies that $m$ and $n$ cannot both be even since we would be able to cancel at least one factor of two. We therefore have $\textrm{gcd}(m,n)=1$: the their greatest common divisor is $1$. We will now investigate a simple question which is whether $m$ is an even number $m\in E$ or $m$ is an odd number $m \in O$.
Before we begin, lemme point out the fact that the action of squaring an integers preserves its odd/even nature. Indeed, an even number times an even number gives and even number: if $e \in E$ then $e^2 \in E$. Also an odd number times an odd number also gives an odd number: if $o \in O$ then $o^2 \in O$.
The proof proceeds as follows. We assumed that $m/n = \sqrt{2}$, so if we take the square of this equation we have: \[ \frac{m^2}{n^2} = 2, \qquad m^2 = 2n^2. \] If $m$ is an odd number then $m^2$ is also going to be odd, which contradicts the above equation since we see that $m^2$ “contains” a factor $2$, so $m \notin O$. If $m$ is even then $m^2$ is also an even number, so it can be written as $m=2q$ for some other number $q\in \mathbb{Z}$. The equation would then become: \[ 2^2 q^2 = 2 n^2 \quad \Rightarrow \quad 2 q^2 = n^2. \] This implies that $n \in E$ which leads to a contradiction with the fact that we said $m$ and $n$ cannot both be even. Therefore $m \notin E$, and since $m \notin O$ either, this means that there is no such $m \in \mathbb{Z}$ and therefore $\sqrt{2}$ is irrational.
Set relations and operations
We say that $B \subset A$ if $\forall b \in B$ we also have $b \in A$, and $\exists a \in A$, such that $a \notin B$. We say “$B$ is strictly contained in $A$” which is illustrated graphically in the figure below. Also illustrated in the figure is the union of two sets $A \cup B$ which includes all the elements of $A$ and $B$. We have $e \in A \cup B$, if and only if $e \in A$ or $e \in B$.
The set intersection is $A \cap B$ and set minus $A \setminus B$ are shown below.
Sets related to functions
The set of all functions of a real variable, that return a real variable is denoted: \[ f : \mathbb{R} \to \mathbb{R}. \]
The domain of a function is the set of all possible inputs. An input is not possible if the function is not defined for that input, like in the case of a “divide by zero” error.
The image set of a function is the set of all possible outputs of the function: \[ \textrm{Im}(f) = \{ y \in \mathbb{R} \ | \ \exists x\in\mathbb{R},\ y=f(x) \}. \]
Discussion
Knowledge of the precise mathematical jargon introduced in this section is not crucial to the rest of this book, but I wanted to expose you to it because this is the language in which mathematicians think. Most advanced math textbooks will take it for granted that you understand this kind of notation.
Exercises
Fractions
Compute the sum $1\frac{3}{4} + 1\frac{31}{32}$. Ans: $3\frac{23}{32}$
Fractions 2
Show that the solution for $x$ in the equation $\frac{1}{x}=\frac{1}{a}+\frac{1}{b}$ is $x=\frac{ab}{a+b}$.
Quadratic equation
The golden ratio $\varphi$ is the positive solution to the equation $\varphi^2 - \varphi - 1=0$. Find the golden ratio.
Pythagoras theorem
Consider a right triangle in which the shorter sides are 8cm and 6cm. What is the length of the long side? Ans: 10cm.
Pythagoras theorem 2
An LCD television screen measures 26 inches on the diagonal. The screen height is 13 inches. How wide is the screen? Ans: $22.51$ inches.
Kepler's triangle
Consider a right angle triangle in which the opposite size has length 1 and the adjacent side has length $\sqrt{\phi}$, where $\phi = \frac{\sqrt{5}+1}{2}$ is the golden ratio. Show that the hypotenuse will have length $\phi$.
PDF sizing for iPad
The old iPad screen had a screen resolution of 768 pixels by 1024 pixels and its physical dimensions are 6[in] by 8[in]. The screen has the three-by-four aspect ratio. One might conclude that the best choice of paper size for a PDF for such a screen would be be 6[in] by 8[in]. At first I thought so too, but I forgot about the status bar which is 20 pixels tall. There is actually only an usable screen area of 768 pixels by 1004 pixels.
Assuming the width of the PDF is chosen to be 6[in], what height should the PDF have so that it fits perfectly in the content area of the iPad?
Ans: We want the document to have the $768/1004$ aspect ratio, so the height is going to be $6 \times \frac{1004}{768} = 7.84375$[in].
Formula for the quadratic equation
Find the range of values of the parameter $m$ (a real number) so that the
equation $2x^2 - mx + m = 0$ has no real solutions.
Ans: The equation has no real solutions whenever $0 < m < 8$.
Introduction to physics
Introduction
One of the coolest things about understanding math is that you will automatically start to understand the laws of physics too. Indeed, most physics laws are expressed as mathematical equations. If you know how to manipulate equations and you know how to solve for the unknowns in them, then you know half of physics already.
Ever since Newton figured out the whole $F=ma$ thing, people have used mechanics in order to achieve great technological feats like landing space ships on The Moon and recently even on Mars. You can be part of that too. Learning physics will give you the following superpowers:
- The power to predict the future motion of objects using equations.
It is possible to write down the equation which describes the position of
an object as a function of time $x(t)$ for most types of motion.
You can use this equation to predict the motion at all times $t$,
including the future.
"Yo G! Where's the particle going to be at when $t=1.3$[s]?",
you are asked. "It is going to be at $x(1.3)$[m] bro."
Simple as that. If you know the equation of motion $x(t)$,
which describes the position for //all// times $t$,
then you just have to plug $t=1.3$[s] into $x(t)$
to find where the object will be at that time.
- Special **physics vision** for seeing the world.
You will start to think in term of concepts like force, acceleration and velocity
and use these concepts to precisely describe all aspects of the motion of objects.
Without physics vision, when you throw a ball in the air you will see it go up,
reach the top, then fall down.
Not very exciting.
Now //with// physics vision,
you will see that at $t=0$[s] a ball is thrown into the $+\hat{y}$ direction
with an initial velocity of $\vec{v}_i=12\hat{y}$[m/s]. The ball reaches a maximum
height of $\max\{ y(t)\}= \frac{12^2}{2\times 9.81}=7.3$[m] at $t=12/9.81=1.22$[s],
and then falls back down to the ground after a total flight time of
$t_{f}=2\sqrt{\frac{2 \times 7.3}{9.81}}=2.44$[s].
Why learn physics?
A lot of knowledge buzz awaits you in learning about the concepts of physics and understanding how the concepts are connected. You will learn how to calculate the motion of objects, how to predict the outcomes of collisions, how to describe oscillations and many other things. Once you develop your physics skills, you will be able to use the equations of physics to derive one number (say the maximum height) from another number (say the initial velocity of the ball). Physics is a bit like playing LEGO with a bunch of cool scientific building blocks.
By learning how to solve equations and how to deal with complicated physics problems, you will develop your analytical skills. Later on, you can apply these skills to other areas of life; even if you do not go on to study science, the expertise you develop in solving physics problems will help you deal with complicated problems in general. Companies like to hire physicists even for positions unrelated to physics: they feel confident that if the candidate has managed to get through a physics degree then they can figure out all the business shit easily.
Intro to science
Perhaps the most important reason why you should learn physics is because it represents the golden standard for the scientific method. First of all, physics deals only with concrete things which can be measured. There are no feelings and zero subjectivity in physics. Physicists must derive mathematical models which accurately describe and predict the outcomes of experiments. Above all, we can test the validity of the physical models by running experiments and comparing the outcome predicted by the theory with what actually happens in the lab.
The key ingredient in scientific thinking is skepticism. The scientist has to convince his peers that his equation is true without a doubt. The peers shouldn't need to trust the scientist, but instead carry out their own tests to see if the equation accurately predicts what happens in the real world. For example, let's say that I claim that the equation of motion for the ball thrown up in the air with speed $12$[m/s] is given by $y_c(t)=\frac{1}{2}(-9.81)t^2 + 12t+0$. To test whether this equation is true, you can perform the throwing-the-ball-in-the-air experiment and record the maximum height the ball reaches and the total time of flight and compare them with those predicted by the claimed equation~$y_c(t)$. The maximum height that the ball will attain predicted by the claimed equation occurs at $t=1.22$ and is obtained by substituting this time into the equation of motion $\max_t\{ y_c(t)\}=y_{c}(1.22)=7.3$[m]. If this height matches what you measured in the real world, you can maybe start to trust my equation a little bit. You can also check whether the equation $y_c(t)$ correctly predicts the total time of flight which you measured to be $t=2.44$[s]. To do this you have to check whether $y_c(2.44) = 0$ as it should be when the ball hits the ground. If both predictions of the equation $y_c(t)$ match what happens in the lab, you can start to believe that the claimed equation of motion $y_c(t)$ really is a good model for the real world.
The scientific method depends on this interplay between experiment and theory. Theoreticians prove theorems and derive physics equations, while experimentalists test the validity of the equations. The equations that accurately predict the laws of nature are kept while inaccurate models are rejected.
Equations of physics
The best of the equations of physics are collected and explained in textbooks. Physics textbooks contain only equations that have been extensively tested and are believed to be true. Good physics textbooks also show how the equations are derived from first principles. This is really important, because it is much easier to remember a few general principles at the foundation of physics rather than a long list of formulas. Understanding trumps memorization any day of the week.
In the next section we learn about the equations $x(t)$, $v(t)$ and $a(t)$ which describes the motion of objects. We will also illustrate how the position equation $x(t)=\frac{1}{2}at^2 + v_it+x_i$ can be derived using simple mathematical methods (calculus). Technically speaking, you are not required to know how to derive the equations of physics—you just have to know how to use them. However, learning a bit of theory is a really good deal: reading a few extra pages of theory will give you a deep understanding of, not one, not two, but eight equations of physics.
Kinematics
Kinematics (from the Greek word kinema for motion) is the study of trajectories of moving objects. The equations of kinematics can be used to calculate how long a ball thrown upwards will stay in the air, or to calculate the acceleration needed to go from 0 to 100 km/h in 5 seconds. To carry out these calculations we need to know which equation of motion to use and the initial conditions (the initial position $x_i$ and the initial velocity $v_{i}$). Plug in the knowns into the equations of motion and then you can solve for the desired unknown using one or two simple algebra steps. This entire section boils down to three equations. It is all about the plug-number-into-equation technique.
The purpose of this section is to make sure that you know how to use the equations of motion and understand concepts like velocity and accretion well. You will also learn how to easily recognize which equation is appropriate need to use to solve any given physics problem.
Concepts
The key notions used to describe the motion of an objects are:
- $t$: the time, measured in seconds [s].
- $x(t)$: the position of an object as a function of time—also known as the equation of motion. The position of an object is measured in metres [m].
- $v(t)$: the velocity of the object as a function of time. Measured in [m/s].
- $a(t)$: the acceleration of the object as a function of time. Measured in [m/s$^2$].
- $x_i=x(0), v_i=v(0)$: the initial (at $t=0$) position and velocity of the object (initial conditions).
Position, velocity and acceleration
The motion of an object is characterized by three functions: the position function $x(t)$, the velocity function $v(t)$ and the acceleration function $a(t)$. The functions $x(t)$, $v(t)$ and $a(t)$ are connected—they all describe different aspects of the same motion.
You are already familiar with these notions from your experience driving a car. The equation of motion $x(t)$ describes the position of the car as a function of time. The velocity describes the change in the position of the car, or mathematically \[ v(t) \equiv \text{rate of change in } x(t). \] If we measure $x$ in metres [m] and time $t$ in seconds [s], then the units of $v(t)$ will be metres per second [m/s]. For example, an object moving at a constant speed of $30$[m/s] will have its position change by $30$[m] each second.
The rate of change of the velocity is called the acceleration: \[ a(t) \equiv \text{rate of change in } v(t). \] Acceleration is measured in metres per second squared [m/s$^2$]. A constant positive acceleration means the velocity of the motion is steadily increasing, like when you press the gas pedal. A constant negative acceleration means the velocity is steadily decreasing, like when you press the brake pedal.
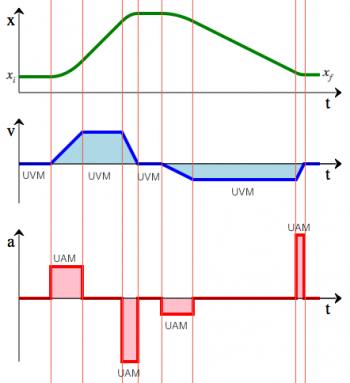 The illustration on the right shows the simultaneous graph of the
position, velocity and acceleration of a car during some time interval.
In a couple of paragraphs, we will discuss the exact mathematical equations which
describe $x(t)$, $v(t)$ and $a(t)$. But before we get to the math,
let us visually analyze the motion illustrated on the right.
The illustration on the right shows the simultaneous graph of the
position, velocity and acceleration of a car during some time interval.
In a couple of paragraphs, we will discuss the exact mathematical equations which
describe $x(t)$, $v(t)$ and $a(t)$. But before we get to the math,
let us visually analyze the motion illustrated on the right.
The car starts off with an initial position $x_i$ and just sits there for some time. The driver then floors the pedal to produce a maximum acceleration for some time, picks up speed and then releases the accelerator, but keeps it pressed enough to maintain a constant speed. Suddenly the driver sees a police vehicle in the distance and slams on the brakes (negative acceleration) and shortly afterwards brings the car to a stop. The driver waits for a few seconds to make sure the cops have passed. The car then accelerates backwards for a bit (reverse gear) and then maintains a constant backwards speed for an extended period of time. Note how “moving backwards” corresponds to negative velocity. In the end the driver slams on the brakes again to bring the car to a stop. The final position is $x_f$.
In the above example, we can observe two distinct types of motion. Motion at a constant velocity (uniform velocity motion, UVM) and motion with constant acceleration (uniform acceleration motion, UAM). Of course, there could be many other types of motion, but for the purpose of this section you are only responsible for these two.
- UVM: During times when there is no acceleration,
the car maintains a uniform velocity, that is,
$v(t)$ will be a constant function.
Constant velocity means that the position function
will be a line with a constant slope because, by definition, $v(t)= \text{slope of } x(t)$.
* UAM: During times where the car experiences a constant acceleration $a(t)=a$,
the velocity of the function will change at a constant rate.
The rate of change of the velocity is constant $a=\text{slope of } v(t)$,
so the velocity function must look like a line with slope $a$.
The position function $x(t)$ has a curved shape (quadratic) during moments of
constant acceleration.
Formulas
There are basically four equations that you need to know for this entire section. Together, these three equations fully describe all aspects of any motion with constant acceleration.
Uniform acceleration motion (UAM)
If the object undergoes a constant acceleration $a(t)=a$, like your car if you floor the accelerator, then its motion will be described by the following equations: \[ \begin{align*} x(t) &= \frac{1}{2}at^2 + v_i t + x_i, \nl v(t) &= at + v_i, \nl a(t) &= a, \end{align*} \] where $v_i$ is the initial velocity of the object and $x_i$ is its initial position.
There is also another useful equation to remember: \[ [v(t)]^2 = v_i^2 + 2a[x(t)- x_i], \] which is usually written \[ v_f^2 = v_i^2 + 2a\Delta x, \] where $v_f$ denotes the final velocity and $\Delta x$ denotes the change in the $x$ coordinate.
That is it. Memorize these equations, plug-in the right numbers, and you can solve any kinematics problem humanly imaginable. Chapter done.
Uniform velocity motion (UVM)
The special case where there is zero acceleration ($a=0$), is called uniform velocity motion or UVM. The velocity stays uniform (constant) because there is no acceleration. The following three equations describe the motion of the object under uniform velocity: \[ \begin{align} x(t) &= v_it + x_i, \nl v(t) &= v_i, \nl a(t) &= 0. \end{align} \] As you can see, these are really the same equations as in the UAM case above, but because $a=0$, some terms are missing.
Free fall
We say that an object is in free fall if the only force acting on it is the force of gravity. On the surface of the earth, the force of gravity produces a constant acceleration of $a=-9.81$[m/s$^2$]. The negative sign is there because the gravitational acceleration is directed downwards, and we assume that the $y$ axis points upwards. The motion of an object in free fall is described by the UAM equations.
Examples
We will now illustrate how the equations of kinematics are used to solve physics problems.
Moroccan example
Suppose your friend wants to send you a ball wrapped in aluminum foil from his balcony, which is located at a height of $x_i=44.145$[m]. How long does it take for the ball to hit the ground?
We recognize that this is a problem with acceleration, so we start by writing out the general UAM equations: \[ \begin{align*} y(t) &= \frac{1}{2}at^2 + v_i t + y_i, \nl v(t) &= at + v_i. \end{align*} \] To find the answer, we substitute the known values $y(0)=y_i=44.145$[m], $a=-9.81$ and $v_i=0$[m/s] (since the ball was released from rest) and solve for $t_{fall}$ in the equation $y(t_{fall}) = 0$ since we are interested in the time when the ball will reach a heigh of zero. The equation is \[ y(t_{fall}) = 0 = \frac{1}{2}(-9.81)(t_{fall})^2+0(t_{fall}) + 44.145, \] which has solution $t_{fall} = \sqrt{\frac{44.145\times 2}{9.81}}= 3$[s].
0 to 100 in 5 seconds
Suppose you want to be able to go from $0$ to $100$[km/h] in $5$ seconds with your car. How much acceleration does your engine need to produce, assuming it produces a constant amount of acceleration.
We can calculate the necessary $a$ by plugging the required values into the velocity equation for UAM: \[ v(t) = at + v_i. \] Before we get to that, we need to convert the velocity in [km/h] to velocity in [m/s]: $100$[km/h] $=\frac{100 [\textrm{km}]}{1 [\textrm{h}]} \cdot\frac{1000[\textrm{m}]}{1[\textrm{km}]} \cdot\frac{1[\textrm{h}]}{3600[\textrm{s}]}$= 27.8 [m/s]. We fill in the equation with all the desired values $v(5)=27.8$[m/s], $v_i=0$, and $t=5$[s] and solve for $a$: \[ v(5) = 27.8 = a(5) + 0. \] We conclude that your engine has to produce a constant acceleration of $a=5.56$[m/s$^2$] or more.
Moroccan example II
Some time later, your friend wants to send you another aluminum ball from his apartment located on the 14th floor (height of $44.145$[m]). In order to decrease the time of flight, he throws the ball straight down with an initial velocity of $10$[m/s]. How long does it take before the ball hits the ground?
Imagine the building with the $y$ axis measuring distance upwards starting from the ground floor. We know that the balcony is located at a height of $y_i=44.145$[m], and that at $t=0$[s] the ball starts with $v_i=-10$[m/s]. The initial velocity is negative, because it points in the opposite direction to the $y$ axis. We know that there is an acceleration due to gravity of $a_y=-g=-9.81$[m/s$^2$].
We start by writing out the general UAM equation: \[ y(t) = \frac{1}{2}a_yt^2 + v_i t + y_i. \] We want to find the time when the ball will hit the ground, so $y(t)=0$. To find $t$, we plug in all the known values into the general equation: \[ y(t) = 0 = \frac{1}{2}(-9.81)t^2 -10 t + 44.145, \] which is a quadratic equation in $t$. First rewrite the quadratic equation into the standard form: \[ 0 = \underbrace{4.905}_a t^2 + \underbrace{10.0}_b \ t - \underbrace{44.145}_c, \] and then solve using the quadratic equation: \[ t_{fall} = \frac{-b \pm \sqrt{ b^2 - 4ac }}{2a} = \frac{-10 \pm \sqrt{ 25 + 866.12}}{9.81} = 2.53 \text{ [s]}. \] We ignored the negative-time solution because it corresponds to a time in the past. Comparing with the first Moroccan example, we see that the answer makes sense—throwing a ball downwards will make it fall to the ground faster than just dropping it.
Discussion
Most kinematics problems you will be asked to solve follow the same pattern as the above examples. You will be given some of the initial values and asked to solve some unknown quantity. It is important to keep in mind the signs of the numbers you plug into the equations. You should always draw the coordinate system and indicate clearly (to yourself) the $x$ axis which measures the displacement. If a velocity or acceleration quantity points in the same direction as the $x$ axis then it is a positive number while quantities that point in the opposite direction are negative numbers.
All this talk of $v(t)$ being the “rate of change of $x(t)$” is starting to get on my nerves. The expression “rate of change of” is an euphemism for the calculus term derivative. We will now take a short excursion into the land of calculus in order to define some basic concepts (derivatives and integrals) so that we can use us this more precise terminology in the remainder of the book.
Introduction to calculus
Calculus is the study of functions. We use calculus in order to describe how quantities change over time (derivatives $\frac{d}{dt}$) or to find the total amount of quantities that vary over time (integration $\int\cdot\;dt$).
Derivatives
The derivative function $f'(t)$ is a description of how the function $f(t)$ changes over time. The derivative encodes the information about rate of change or the slope of the function $f(t)$: \[ f'(t) \equiv \text{slope}_f(t) = \frac{ \text{change in} \ f(t) }{ \text{change in}\ t } = \frac{ f(t+\Delta t) - f(t) }{ \Delta t }. \] If the slope of $f(t)$ is big at some value of $t$, this means that the function changes very quickly at that time. At the other extreme we have the points where $f'(t)=0$ which correspond to locations where the function is flat—it is neither increasing nor decreasing.
Derivatives are used widely in many areas of science, so there are many names and symbols used to denote this operation: $Df(t) = f'(t)=\frac{df}{dt}=\frac{d}{dt}\!\left\{ f(t) \right\}=\dot{f}$. You shouldn't think of $f'(t)$ as a separate entity from $f(t)$, but as a property of the function $f(t)$. Indeed, it is best to think of the derivative as an operator $\frac{d}{dt}$ which can be applied to any function in order to obtain the slope information.
Integrals
 An integral corresponds to the computation of an area
under a curve $f(t)$ between two points:
\[
A(a,b) \equiv \int_{t=a}^{t=b} f(t)\;dt.
\]
The symbol $\int$ is a mnemonic for sum,
since the area under the curve corresponds in some
sense to the sum of the values of the function $f(t)$
between $t=a$ and $t=b$.
The integral is the total amount of $f$ between $a$ and $b$.
An integral corresponds to the computation of an area
under a curve $f(t)$ between two points:
\[
A(a,b) \equiv \int_{t=a}^{t=b} f(t)\;dt.
\]
The symbol $\int$ is a mnemonic for sum,
since the area under the curve corresponds in some
sense to the sum of the values of the function $f(t)$
between $t=a$ and $t=b$.
The integral is the total amount of $f$ between $a$ and $b$.
Example 1
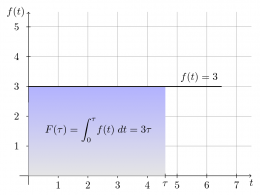 We can easily find the area under the constant function $f(t) = 3$
between any two points because the region under the curve is rectangular.
We choose to use $t=0$ as the reference point and compute
the indefinite integral $F(\tau)$ which corresponds to the
area under $f(t)$ starting from $t=0$ and going until $t=\tau$:
\[
F(\tau) \equiv A(0,\tau) = \! \int_0^\tau \!\! f(t)\;dt = 3 \tau.
\]
Indeed the area is equal to the height times the length of the rectangle.
We can easily find the area under the constant function $f(t) = 3$
between any two points because the region under the curve is rectangular.
We choose to use $t=0$ as the reference point and compute
the indefinite integral $F(\tau)$ which corresponds to the
area under $f(t)$ starting from $t=0$ and going until $t=\tau$:
\[
F(\tau) \equiv A(0,\tau) = \! \int_0^\tau \!\! f(t)\;dt = 3 \tau.
\]
Indeed the area is equal to the height times the length of the rectangle.
Example 2
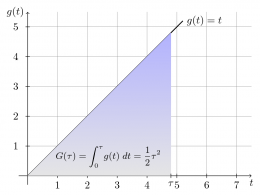 We can also easily compute the area under the line $g(t)=t$
since the region under the curve is triangular.
Recall that the area of a triangle is given by the length of
the base times the height divided by two.
We can also easily compute the area under the line $g(t)=t$
since the region under the curve is triangular.
Recall that the area of a triangle is given by the length of
the base times the height divided by two.
We choose $t=0$ as our starting point again and find the area: \[ G(\tau) \equiv A(0,\tau) = \int_0^\tau g(t) \; dt = \frac{\tau\times\tau}{2} = \frac{1}{2}\tau^2. \]
We were able to compute the above integrals thanks to the simple geometry of the areas under the curves. Later on in this book we will develop techniques for finding integrals of more complicated functions. In fact, there is an entire course, Calculus II, which is dedicated to the task of finding integrals.
What I need you to remember for now is that the integral of a function gives you the area under the curve, which is in some sense the total amount of the function accumulated during that period.
You should also remember the following two formulas: \[ \int_0^\tau a \;dt = a\tau, \qquad \int_0^\tau at \;dt = \frac{1}{2}a\tau^2. \] The second formula is a generalization of the formula we saw in Example 2.
Using the above formulas in combination, you can now compute the integral under an arbitrary line $h(t)=mt+b$ as follows: \[ H(\tau)= \int_0^\tau h(t)\;dt = \int_0^\tau (mt + b)\;dt = \int_0^\tau \!mt\;dt\ + \int_0^\tau \!b\;dt = \frac{1}{2}m\tau^2 + b \tau. \]
Why do we need integrals? How often do you need to compute the area below a function $f(t)$ in the real life?
Inverse operations
The integral is the inverse operation of the derivative. You are already familiar with the inverse relationship between functions. When solving equations, we use inverse functions to undo the effects of functions that stand in the way. Similarly, we use the integral operation to undo the effects of the derivative operation. For example, if you want to find the function $f(t)$ in an equation of the form \[ \frac{d}{dt} \left\{ f(t) \right\} = g(t), \] you have to apply the integration operation on both sides of the equation. The integral operation will undo the derivative operation on the left so we will obtain: \[ \int \frac{d}{dt} \left\{ f(t) \right\} \;dt = f(t) = \int g(t) \; dt. \]
From now on, every time you want to undo a derivative, you can apply the integral operation: \[ \text{int}\!\left( \text{diff}( f(x) ) \right) = \int_0^x \left( \frac{d}{dt} f(t) \right) \; dt = \int_0^x \! f'(t) \; dt = f(x) + C. \] Note that integration always introduces an additive constant term $+C$. This is because the derivative operation destroys the information about the initial value of the function. The functions $f(x)+1$ and $f(x)+2$ have same derivative $f'(x)$ so when we solve the inverse problem of finding $f(x)$ from $f'(x)$, we must state our answer as $f(x)+C$ for some constant $C$.
Banking example
In order to illustrate how derivative and integral operations can be used in the real world, we will draw an analogy with a scenario that every student is familiar with. Consider the function $\textrm{ba}(t)$ which represents your bank account balance at time $t$, and the function $\textrm{tr}(t)$ which corresponds to the transactions (deposits and withdraws) on your account.
The function $\textrm{tr}(t)$ is the derivative of the function $\textrm{ba}(t)$. Indeed, if you ask “how does my balance change over time”, the answer will be the function $\textrm{tr}(t)$. Using the mathematical symbols, we can represent this relationship as follows: \[ \textrm{tr}(t) = \frac{d}{dt} \left\{ \textrm{ba}(t) \right\}. \] If the derivative is big (and negative), your account balance will be depleted quickly.
Suppose now, that you have the record of all the transactions on your account $\textrm{tr}(t)$ and you want to compute the final account balance at the end of the month. Since $\textrm{tr}(t)$ is the derivative of $\textrm{ba}(t)$, you can use an integral (the inverse operation to the derivative) in order to obtain $\textrm{ba}(t)$. Knowing the balance of your account at the beginning of the month, you can calculate the balance at the end of the month by calculating the following integral: \[ \textrm{ba}(30)=\textrm{ba}(0)+\int_0^{30} \textrm{tr}(t)\:dt. \] This calculation makes sense intuitively since $\textrm{tr}(t)$ represents the instantaneous change in $\textrm{ba}(t)$. If you want to find the overall change from day 0 until day 30, you need to compute the total of all the changes on the account. More generally, the integrals are used every time you need to calculate the total of some quantity over a time period.
In the next section we will see how the integration techniques learned in this section can be applied to the subject of kinematics. We will see how the equations of motion for UAM are derived from first principles.
Kinematics with calculus
To carry out kinematics calculations, all we need to do is plug the initial conditions into the correct equation of motion and then read out the answer. It is all about the plug-number-into-equation skill. But where do the equations of motion come from? Now that you know a little bit of calculus, you can see how the equations of motion are derived.
Concepts
Recall the concepts related to the motion of objects (kinematics):
- $t$: the time, measured in seconds [s].
- $x(t)$: the position as a function of time, also known as the equation of motion.
- $v(t)$: the velocity.
- $a(t)$: the acceleration.
- $x_i=x(0), v_i=v(0)$: the initial conditions.
Position, velocity and acceleration revisited
Recall that the purpose of the equations of kinematics is to predict the motion of objects. Suppose that you know the acceleration of the object $a(t)$ at all times $t$. How could you find $x(t)$ starting from $a(t)$?
The equations of motion $x(t)$, $v(t)$ and $a(t)$ are related: \[ a(t) \overset{\frac{d}{dt} }{\longleftarrow} v(t) \overset{\frac{d}{dt} }{\longleftarrow} x(t). \] The velocity is the derivative of the position function and the acceleration is the derivative of the velocity.
General procedure
If you know the acceleration of an object $a(t)$ as a function of time and its initial velocity $v_i=v(0)$, you can find its velocity $v(t)$ function at all later times. This is because the acceleration function $a(t)$ describes the change in the velocity of the object. If you know that the object started with an initial velocity of $v_i \equiv v(0)$, the velocity at a later time $t=\tau$ is equal to $v_i$ plus the total acceleration of the object between $t=0$ and $t=\tau$: \[ v(\tau)=v_i+\int_0^\tau a(t)\;dt. \]
If you know the initial position $x_i$ and the velocity function $v(t)$ you can find the position function $x(t)$ by using integration again. We find the position at time $t=\tau$ by adding up all the velocity (changes in the position) that occurred between $t=0$ and $t=\tau$: \[ x(\tau) = x_i + \int_0^\tau v(t)\:dt. \]
The procedure for finding $x(t)$ starting from $a(t)$ can be summarized as follows: \[ a(t) \ \ \overset{v_i + \int\!dt}{\longrightarrow} \ \ v(t) \ \ \overset{x_i+ \int\!dt }{\longrightarrow} \ \ x(t). \]
We will now illustrate how to apply this procedure for the important special case of motion with constant acceleration.
Derivation of the UAM equations of motion
Consider an object undergoing uniform acceleration motion (UAM) with acceleration function $a(t) =a$. Suppose that we know the initial velocity of $v_i \equiv v(0)$, and you want to find the velocity at later time $t=\tau$. We have to compute the following integral: \[ v(\tau) =v_i+ \int_0^\tau a(t)\;dt = v_i + \int_0^\tau a \ dt = v_i + a\tau. \] The velocity as a function of time is given by the initial velocity $v_i$ plus the integral of the acceleration.
If you know the initial position $x_i$ and the velocity function $v(t)$ you can find the position function $x(t)$ by using integration again. The formula is \[ x(\tau) = x_i + \int_0^\tau v(t)\:dt = x_i + \int_0^\tau (at+v_i) \; dt = x_i + \frac{1}{2}a\tau^2 + v_i\tau. \]
Note that the above calculations required the knowledge of the initial conditions $x_i$ and $v_i$. This is because the integral calculations tell us the change in the quantities relative to their initial values.
The fourth equation
The fourth equation of motion \[ v_f^2 = v_i^2 + 2a(x_f-x_i) \] can be derived by combining the equations of motion $v(t)$ and $x(t)$.
Consider squaring both sides of the velocity equation $v_f = v_i + at$ to obtain \[ v_f^2 = (v_i + at)^2 = v_i^2 + 2av_it + a^2t^2 = v_i^2 + 2a(v_it + \frac{1}{2}at^2). \] We can recognize the term in the bracket is equal to $\Delta x = x(t)-x_i=x_f-x_i$.
Discussion
Forces are the causes of acceleration
According to Newton's second law of motion, forces are the cause of acceleration and the formula that governs this relationship is \[ F_{net}=ma, \] where $F_{net}$ is the magnitude of the net force on the object.
In a later chapter, we will learn about dynamics which is the study of the different kinds of forces that can act on objects: the gravitational force $\vec{F}_g$, the spring force $\vec{F}_s$, the friction force $\vec{F}_f$, the electric force $\vec{F}_e$, the magnetic force $\vec{F}_b$ and many others. To find the acceleration on an object we must add together (as vectors) all of the forces which are acting on the object and divide by the mass \[ \sum \vec{F} = F_{net}, \qquad \Rightarrow \qquad a = \frac{1}{m} F_{net}. \]
The physics procedure for predicting the motion of objects can be summarized as follows: \[ \frac{1}{m} \underbrace{ \left( \sum \vec{F} = \vec{F}_{net} \right) }_{\text{dynamics}} = \underbrace{ a(t) \ \overset{v_i+ \int\!dt }{\longrightarrow} \ v(t) \ \overset{x_i+ \int\!dt }{\longrightarrow} \ x(t) }_{\text{kinematics}}. \]
Free fall revisited
The force of gravity on a object of mass $m$ on the surface of the earth is given by $\vec{F}_g=-mg\hat{y}$, where $g=9.81$[m/s$^2$] is the gravitational constant. Recall that we said that an object is in free fall when the only force acting on it is the force of gravity. In this case, Newton's second law tells us that \[ \begin{align*} \vec{F}_{net} &= m\vec{a} \nl -mg\hat{y} &= m\vec{a}. \end{align*} \] Dividing both sides by the mass we see that the acceleration of an object in free fall is $\vec{a} = -9.81\hat{y}$.
It is interesting to note that the mass of the object does
not affect its acceleration during free fall.
The force of gravity is proportional to the mass of the object,
but the acceleration is inversely proportional to the mass of the object
so overall we get $a_y = -g$ for objects in free fall regardless of their mass.
This observation was first made by Galileo in his famous Leaning Tower of Pisa experiment
during which he dropped a wooden ball and a metal ball (of same shape but different mass)
from the Leaning Tower of Pisa and observed that they fall to the ground in the same time.
Search for “Apollo 15 feather and hammer drop” on YouTube to see a similar experiment
performed on The Moon.
What next?
You may have noticed that in the last couple of paragraphs we started putting little arrows on top of certain quantities. The arrow is used to remind you that forces are vector quantities. Before we proceed with the physics lessons, we must make a mathematical digression and introduce vectors.
Vectors
In this chapter we will learn how to manipulate multi-dimensional objects called vectors. Vectors are useful when you want to describe directions, velocities, or in general any kind of data that has many components. You can think of vectors as lists of numbers, but you need to also learn about their geometrical properties.
Great outdoors
Vectors are directions. Directions are “recipes” for getting from point A to point B. Directions can be given in terms of street names and visual landmarks or with respect to a coordinate system.
While on vacation in BC, you want to visit a certain outdoor location which you friend has told you about. Your friend is not available to take you there himself, but he has sent you directions for how to get to the place from the bus stop:
Sup G. Go to bus stop number 345. Bring a compass. Walk 3km North then 4km East. U will find X there.
This text message is all that you need in order to find $X$.
Act 1: Directions
You get to the bus station. A beautiful field spreads in front of you. The bus stop at the top of a small hill so from up here you can see the whole valley. The field is full of very tall crops which prevent anyone walking in them to see very far; good thing you have a compass. You align the compass needle to the marks on the glass so that the red arrow points North. You walk 3km Northward and then you turn to the right (East) and walk another 4km. You get to X.
OK, back to vectors. In this case, the directions recipe can be written as a directions vector $\vec{d}$ as follows: \[ \vec{d} = 3\textrm{km}\: \hat{N} + 4\textrm{km}\: \hat{E}, \] which is the mathematical expression that corresponds to the directions “walk 3km North then 4km East.” Here $\hat{N}$ is a direction and the number in front of the direction tells me the distance that I should walk in that direction.
Act 2: Equivalent directions
Later on in your vacation, you decide to return to the location. When you arrive at the bus stop, you see that there is a slight problem. From your position you can see that, just a kilometre north of you, there is a group of armed and threatening looking men waiting in ambush on what has now become a trail in the crops. Clearly the word has spread about X and several people have come here promoting too much attention to the location.
Well, technically speaking, there is no problem with X. The problem is on the route that starts off North and goes through the ambush. Could you find an alternate route to get to X?
"Use math, Luke! Use math!"
For numbers we have $a+b=b+a$, maybe we can do the same thing with vectors: \[ \vec{d} = 3\textrm{km}\: \hat{N} + 4\textrm{km}\: \hat{E} = 4\textrm{km}\: \hat{E} + 3\textrm{km}\: \hat{N}. \] Yes you can. You walk the 4[km] East first then 3[km] North and get to X again. This equivalent set of directions completely avoids the ambush.
Act 3: Efficiency
It takes $7$[km] of walking to get from the bus stop to X and another $7$[km] to get back. Thus, it takes a total of $14$[km] walking every time you want to go to X. Could you find a shorter route? What is the shortest route to the destination? If you take the diagonal it will certainly be quicker. Using Pythagoras theorem you can even calculate how long the diagonal is when the sides are $4$ and $3$ in length. The diagonal has length $\sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5$. The direction you need to walk in at $53^\circ$ (on a compass degrees are measured from the $\hat{N}$ direction, starting towards East). The direct route is $5$ km long which means that you are saving a whole 2 km of walking in each direction.
But perhaps seeking efficiency is not always necessary! You could take a longer path and give yourself time to enjoy the great outdoors.
Discussion
Vectors are directions for getting from one point to another point. For directions on maps, we use the four cardinal directions: $\hat{N}$, $\hat{S}$, $\hat{E}$, $\hat{W}$, but in math we will use just two of them: $\hat{E}\equiv\hat{x}$ and $\hat{N}\equiv\hat{y}$, since they fit nicely with the usual way of drawing the cartesian plane. We don't need an $\hat{S}$ direction because we can represent downward distances as negative distances in the $\hat{N}$ direction. Similarly, $\hat{W}$ is just negative $\hat{E}$.
From now on, when we talk about vectors they will always be represented in the standard coordinate system $\hat{x}$ and $\hat{y}$ so we can use a bracket notation: \[ (v_x, v_y) \equiv v_x \: \hat{x} \ + \ v_y\:\hat{y}. \]
The bracket notation is very compact, which is good if you are going to be doing a lot of calculations with vectors. Instead of writing down explicitly the basis elements (the directions), you simply assume that the first number in the bracket is the $\hat{x}$ distance and the second number is the $\hat{y}$ distance.
Vectors
Vectors are mathematical objects that have multiple components. The vector $\vec{v}$ is equivalent to a pair of numbers \[ \vec{v} \equiv (v_x, v_y), \] where $v_x$ is the $x$ component of $\vec{v}$ and $v_y$ is the $y$ component.
Just like numbers, you can add vectors \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y), \] subtract them \[ \vec{v}-\vec{w} = (v_x, v_y) - (w_x, w_y) = (v_x-w_x, v_y-w_y), \] and solve all kinds of equations where the unknown variable is a vector.
This might sound like a formidably complicated new development in mathematics, but it is not. Doing arithmetic calculations on vectors is simply doing arithmetic operations on their components.
Thus, if I told you that $\vec{v}=(4,2)$ and $\vec{w}=(3,7)$, then \[ \vec{v}-\vec{w} = (4, 2) - (3, 7) = (1, -5). \]
Vectors are extremely useful in all areas of life. In physics, for example, to describe phenomena in the three-dimensional world we use vectors with three components: $x,y$ and $z$. It is of no use to say that we have a force of 20[N] pushing on a block unless we specify in which direction the force acts. Indeed, both of these vectors have length 20 \[ \vec{F}_1 = (20,0,0), \qquad \vec{F}_2=(0,20,0), \] but one points along the $x$ axis, and the other along the $y$ axis, so they are completely different vectors.
Definitions
- $\hat{x},\hat{y},\hat{z}$: the usual coordinate system. Every vector is implicitly defined in terms of this coordinate system. When you and I talk about the point $P=(3,4,2)$,
we are really saying “start from the origin, $(0,0,0)$, move 3 units in the $x$ direction, then move 4 units in the $y$ direction, and finally move 2 units in the $z$ direction.” Obviously it is simpler to just say $(3,4,2)$, but keep in mind that these numbers are relative to the coordinate system $\hat{x}\hat{y}\hat{z}$.
- $\hat{\imath},\hat{\jmath},\hat{k}$: is an alternate way of describing the $xyz$-coordinate system
in terms of three unit length vectors:
\[\hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1).\]
Any number multiplied by $\hat{\imath}$ corresponds to a vector
with that number in the first coordinate. For example, $\vec{v}=3\hat{\imath}\equiv(3,0,0)$.
* $\vec{v}=(v_x,v_y,v_z)=v_x\hat{\imath} + v_y \hat{\jmath}+v_z\hat{k}$:
A //vector// expressed in terms of components and in terms of $\hat{\imath}$, $\hat{\jmath}$ and $\hat{k}$.
In two dimensions there are two equivalent ways to denote vectors:
- In component notation $\vec{v} =(v_x, v_y)$,
which describes the vector as seen from the $x$ axis and the $y$ axis.
- As a length and direction $\vec{v}=\|\vec{v}\|\angle \theta$, where $\|\vec{v}\|$
is the length of the vector and $\theta$ is the angle that the vector
makes with the $x$ axis.
Vector dimension
The most common types of vectors are $2$-dimensional vectors (like the ones in the Cartesian plane), and $3$-dimensional vectors (directions in 3D space). These kinds of vectors are easier to work with since we can visualize them and draw them in diagrams. Vectors in general can exist in any number of dimensions. An example of a $n$-dimensional vector is \[ \vec{v} = (v_1, v_2, \ldots, v_n) \in \mathbb{R}^n. \]
Vector arithmetic
Addition of vectors is done component wise \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y). \] Vector subtraction works the same way: component by component.
The length of a vector is obtained from Pythagoras theorem. Imagine a triangle with one side of length $v_x$ and the other side of length $v_y$. The length of the vector is equal to the length of the hypotenuse: \[ \|\vec{v}\| = \sqrt{ v_x^2 + v_y^2 }. \]
We can also scale a vector by any number $\alpha \in \mathbb{R}$: \[ \alpha \vec{v} = (\alpha v_x, \alpha v_y), \] where we see that each component gets multiplied by the scaling factor $\alpha$. If $\alpha>1$ the vector will get longer, if $0\leq \alpha <1 $ then the vector will shrink. If $\alpha$ is a negative number, then the resulting vector will point in the opposite direction.
A particularly useful scaling is to divide a vector $\vec{v}$ by its length $\|\vec{v}\|$ to obtain a unit length vector that points in the same direction as $\vec{v}$: \[ \hat{v} = \frac{\vec{v}}{ \|\vec{v}\| }. \] Unit-length vectors (denoted with a hat instead of an arrow) are useful when you want to describe a direction in space.
Vector geometry
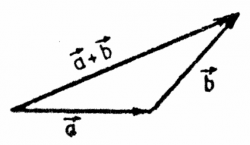 You can think of a vectors as arrows, and addition
as putting together of vectors head-to-tail
as shown in the diagram.
You can think of a vectors as arrows, and addition
as putting together of vectors head-to-tail
as shown in the diagram.
The negative of a vector—a vector multiplied by $\alpha=-1$—is a vector of same length but in the opposite direction. So the graphical subtraction of vectors is also possible.
Length and direction of vectors
 We have seen so far how to represent vectors as coefficients.
There is also another way of expressing vectors: we can
specify their length $||\vec{v}||$ and their orientation—the angle they
make with the $x$ axis.
For example,
the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$.
It is useful to represent vectors in the
magnitude and direction notation because their physical
size becomes easier to see.
We have seen so far how to represent vectors as coefficients.
There is also another way of expressing vectors: we can
specify their length $||\vec{v}||$ and their orientation—the angle they
make with the $x$ axis.
For example,
the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$.
It is useful to represent vectors in the
magnitude and direction notation because their physical
size becomes easier to see.
There are formulas for converting between the two notations. To convert the length-and-direction vector $\|\vec{r}\|\angle\theta$ to components $(r_x,r_y)$ use: \[ r_x=\|\vec{r}\|\cos\theta, \qquad\qquad r_y=\|\vec{r}\|\sin\theta. \] To convert from component notation $(r_x,r_y)$ to length-and-direction $\|\vec{r}\|\angle\theta$ use \[ r=\|\vec{r}\|=\sqrt{r_x^2+r_y^2}, \qquad\quad \theta=\tan^{-1}\!\left(\frac{r_y}{r_x}\right). \]
Note that the second part of the equation involves the arctangent (or inverse tan) function which by convention returns values between $\pi/2$ and $\mbox{-}\pi/2$ and must be used carefully for vectors that have direction outside of this range.
Alternate notation
A vector $\vec{v}=(v_x, v_y, v_z)$ is really a prescription to “go a distance $v_x$ in the $x$-direction, then a distance $v_y$ in the $y$-direction and $v_z$ in the $z$-direction.”
A more explicit notation for denoting vectors is as multiples of the basis vectors $\hat{\imath}, \hat{\jmath}$ and $\hat{k}$, which are unit length vectors pointing in the $x$, $y$ and $z$ direction respectively: \[ \hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1). \]
People who do a lot of numerical calculations with vectors often prefer to use the following alternate notation: \[ v_x \hat{\imath} + v_y\hat{\jmath} + v_z \hat{k} \qquad \Leftrightarrow \qquad \vec{v} \qquad \Leftrightarrow \qquad (v_x, v_y, v_z) . \]
The addition rule looks as follows in the new notation: \[ \underbrace{2\hat{\imath}+ 3\hat{\jmath}}_{\vec{v}} \ \ + \ \ \underbrace{ 5\hat{\imath} - 2\hat{\jmath}}_{\vec{w}} \ = \ \underbrace{ 7\hat{\imath} + 1\hat{\jmath} }_{\vec{v}+\vec{w}}. \] It is the same story repeating: adding $\hat{\imath}$s with $\hat{\imath}$s and $\hat{\jmath}$s with $\hat{\jmath}$s.
Examples
Vector addition example
You are heading to your physics class after a safety meeting with a friend and looking forward to two hours of amazement and absolute awe of the laws of Mother nature. As it turns out, there is no enlightenment to be had that day because there is going to be an in-class midterm. The first question you have to solve involves a block sliding down an incline. You look at it, draw a little diagram and then wonder how the hell you are going to find the net force acting on the block (this is what they are asking you to find). The three forces acting on the block are $\vec{W} = 30 \angle -90^{\circ} $, $\vec{N} = 200 \angle -290^{\circ} $ and $\vec{F}_f = 50 \angle 60^{\circ} $.
You happen to remember the formula: \[ \sum \vec{F} = \vec{F}_{net} = m\vec{a}. \qquad \text{[ Newton's \ 2nd law ]} \]
You get the feeling that this is the answer to all your troublems. You know that because the keyword “net force” that appeared in the question appears in this equation also.
The net force is simply the sum of all the forces acting on the block: \[ \vec{F}_{net} = \sum \vec{F} = \vec{W} + \vec{N} + \vec{F}_f. \]
All that separates you from the answer is the addition of these vectors. Vectors right. Vectors have components, and there is the whole sin cos thing for decomposing length and direction vectors in terms of their components. But can't you just add them together as arrows too? It is just a sum, of things right, should be simple.
OK, chill. Let's do this one step at a time. The net force must have and $x$-component which, according to the equation, must be equal to the sum of the $x$ components of all the forces: \[ \begin{align*} F_{net,x} & = W_x + N_x + F_{f,x} \nl & = 30\cos(-90^{\circ}) + 200\cos(-290^{\circ})+ 50\cos(60^{\circ}) \nl & = 93.4[\textrm{N}]. \end{align*} \] You find the $y$ component of the net force using the $\sin$ of the angles: \[ \begin{align*} F_{net,y} & = W_y + N_y + F_{f,y} \nl & = 30\sin(-90) + 200\sin(-290)+ 50\sin(60) \nl & = 201.2[\textrm{N}]. \end{align*} \]
Combining the two components of the victor, we get the final answer: \[ \vec{F}_{net} = (F_{net,x},F_{net,y}) =(93.4,201.2) =93.4 \hat{\imath} + 201.2 \hat{\jmath}. \] Bam! Just like that you are done because you overstand them mathematics. Nuh problem. What-a-di next question fi me?
Relative motion example
A boat can reach a top speed of 12 knots in calm seas. Instead of being in a calm sea, however, it is trying to sail up the St-Laurence river. The speed of the current is 5 knots.
If the boat goes directly upstream at full throttle 12$\vec{\imath}$, then the speed of the boat relative to the shore will be \[ 12\hat{\imath} - 5 \hat{\imath} = 7\hat{\imath}, \] since we have to “deduct” the speed of the current from the speed of the boat relative to the water.
 If the boat wants to cross the river perpendicular to
the current flow, then it can use some
of its thrust to counterbalance the current, and the other
part to push across.
What direction should the boat sail in so that it moves
in the across-the-river direction?
We are looking for the direction of $\vec{v}$ the boat
should take such that, after adding the current
component, the boat moves in a straight line
between the two banks (the $\hat{\jmath}$ direction).
If the boat wants to cross the river perpendicular to
the current flow, then it can use some
of its thrust to counterbalance the current, and the other
part to push across.
What direction should the boat sail in so that it moves
in the across-the-river direction?
We are looking for the direction of $\vec{v}$ the boat
should take such that, after adding the current
component, the boat moves in a straight line
between the two banks (the $\hat{\jmath}$ direction).
The geometrical picture is necessary so draw a river and a triangle in the river with the long side perpendicular to the current flow. Make the short side of length $5$ and the hypotenuse of length $12$. We will take the up-the-river component of the speed $\vec{v}$ to be equal to $5\hat{\imath}$ so that it cancels exactly the $-5\hat{\imath}$ flow of the river. We have also labeled the hypotenuse as 12 since this is the ultimate speed that the boat can have relative to the water.
From all of this we can answer the questions like professionals. You want the angle? OK, well we have that $12\sin(\theta)=5$, where $\theta$ is the angle of the boat's course relative to the straight line between the two banks. We can use the inverse-sin function to solve for the angle: \[ \theta = \sin^{-1}\!\left(\frac{5}{12} \right) = 24.62^\circ. \] The accross-the-river component speed can be calculated from $v_y = 12\cos(\theta)$, or from Pythagoras Theorem if you prefer $v_y = \sqrt{ \|\vec{v}\|^2 - v_x^2 } = \sqrt{ 12^2 - 5^2 }=10.91$.
Throughout this section we have used the $x$, $y$ and $z$ axes and described vectors as components along each of these directions. It is very convenient to have perpendicular axes like this, and a set of unit vectors pointing in each of the three directions like the vectors $\{\hat{\imath},\hat{\jmath},\hat{k}\}$.
More generally, we can express vectors in terms of any basis $\{ \hat{e}_1, \hat{e}_2, \hat{e}_3 \}$ for the space of three-dimensional vectors $\mathbb{R}^3$. What is a basis you ask? I am glad you asked, because it is a very important concept.
Basis
One of the most important concepts in the study of vectors is the concept of a basis. In the English language, the word basis carries the meaning of criterion. Thus, in the sentence “The students were selected on the basis of their results in the MEQ exams” means that the numerical results of some stupid test were used in order to classify the worth of the candidates. Sadly, this type of thing happens a lot and people often disregard the complex characteristics of a person and focus on a single criterion. The meaning of basis in mathematics is more holistic. A basis is a set of criteria that collectively capture all the information about an object.
Let's start with a simple example. If one looks at the HTML code behind the average
web-page there will certainly be at least one mention of a colour like
background-color:#336699; which should be read as a triplet of values $(33,66,99)$,
each one describing how much red, green and blue is needed to create the given colour.
The triple $(33,66,99)$ describes the colour “hotmail blue.”
This convention for colour representation is called
the RGB scale or something I would like to call this the RGB basis. A basis is a
set of elements which can be used together to express something more
complicated. In our case we have the R, G and B elements which are pure colours
and when mixed appropriately they can create any colour. Schematically we can
write this as:
\[
{\rm RGB\_color}(33,66,99)=33{\mathbf R}+66{\mathbf G}+99{\mathbf B},
\]
where we are using the coefficients to determine the strength of each
colour component.
To create the colour, we combine its components and
the $+$ operation symbolizes the mixing of the colours.
The reason why we are going into such detail is to illustrate that the
coefficients by themselves do not mean much. In fact they do not mean
anything unless we know the basis that is being used.
Another colour scheme that is commonly used is the cyan, magenta and yellow (CMY) colour basis. We would get a completely different colour if we were to interpret the same triplet of coordinates $(33,66,99)$ with respect to the CMY basis. To express the “hotmail blue” colour in the CMY basis you would need the following coefficients: \[ {\rm Hotmail Blue} = (33,66,99)_{RGB} = (222,189,156)_{CMY}. \]
A basis is a mapping which converts mathematical objects like the triple $(a,b,c)$ into real world ideas like colours. If there is ever an ambiguity about which basis is being used for a given vector, we can indicate the basis as a subscript after the bracket as we did above.
The ijk Basis
Look at the bottom left corner of the room you are in. Let's call “the $x$ axis” the edge between the wall that is to your left and the floor. The right wall and the floor meet at the $y$ axis. Finally, the vertical line where the two walls meet will be called the $z$ axis. This is a right-handed $xyz$ coordinate system. It is used by everyone in math and physics. It has three very nice axes. They are nice because they are orthogonal (perpendicular, i.e., at 90$^\circ$ with each other) and orthoginal is good for your life. We will see why that is shortly.
Now take an object of fixed definite length, say the size of your foot. We will call this the unit length. Measure a unit length along the $x$ axis. This is the $\hat{\imath}$ vector. Repeat the same procedure with the $y$ axis and you will have the $\hat{\jmath}$ vector. Using these two vectors and the property of addition, we can build new vectors. For example, I can describe a vector pointing at 45$^\circ$ with both the $x$ axis and the $y$ axis by the following expression: \[ \vec{v}=1\:\hat{\imath}+ 1\:\hat{\jmath}, \] which means measure one step out on the $x$ axis, one step out on the $y$ axis. Using our two basis vectors we can express any vector in the plane of the floor by a linear combination like \[ \vec{v}_{\mathrm{spoint\ on\ the\ floor}}=a\:\hat{\imath}+b\:\hat{\jmath}. \] The precise mathematical statement that describtes this situation is that the basis formed by the pair $\hat{\imath}$,$\hat{\jmath}$ span the two dimensional space of the floor. We can extend this idea to three dimensions by specifying the coordinates of any point in room as a weighted sum of the three basis vectors: \[ \vec{v}_{\mathrm{point\ in\ the\ room}}=a\:\hat{\imath}+b\:\hat{\jmath}+c\:\hat{k}, \] where $\hat{k}$ is the unit length vector along the $z$ axis.
Choice of basis
In the case where it is clear which coordinate system we are using in a particular situation, we can take the liberty to omit the explicit mention of the basis vectors and simply write $(a,b,c)$ as an ordered triplet which contains only the coefficients. When there is more than one basis in some context (like in problems where you have to change basis, then for every tuple of numbers we should be explicit about which basis it refers to. We can do this by putting a subscript after the tuple. For example, the vector $\vec{v}=a\:\hat{\imath} + b\:\hat{\jmath}+c\:\hat{k}$ in the standard basis is referred to as $(a,b,c)_{\hat{\imath}\hat{\jmath}\hat{k}}$.
Discussion
It is hard to over-emphasize the importance of the notion of a basis. Every time you solve a problem with vectors, you need to be consistent in your choice of basis, because all the numbers and variables in your equations will depend on it. The basis is the bridge between real world vector quantities and their mathematical representation in terms of components.
Vector products
If addition of two vectors $\vec{v}$ and $\vec{w}$ is given by the equation $(v_x+w_x, v_y+w_y,v_z+w_z)$, you might think that the product of two vectors is $(v_xw_x, v_yw_y,v_zw_z)$, but you would be wrong. This way of multiplying vectors is not used in practice. We will define two other useful ways to multiply vectors in this section.
The dot product tells you how similar two vectors are to each other: \[ \vec{v}\cdot\vec{w}\equiv v_xw_x+v_yw_y+v_zw_z \equiv \|\vec{v}\|\|\vec{w}\|\cos(\varphi) \quad \in \mathbb{R}, \] where $\varphi$ is the angle between the two vectors. The factor $\cos(\varphi)$ is largest when the two vectors point in the same direction.
The formula for the cross product is more complicated so I will not show it to you just yet. What is important is that the cross product of two vectors is another vector: \[ \vec{v}\times\vec{w} = \{ \text{ a vector perpendicular to both } \vec{v} \text{ and } \vec{w} \ \} \quad \in \mathbb{R}^3. \] If you take the $\times$ product of one vector that points in the $x$ direction with another vector in the $y$ direction, you will get a vector in the $z$ direction.
Dot product
The dot product between two vectors is given by the formula: \[ \vec{v}\cdot\vec{w}\equiv v_xw_x+v_yw_y+v_zw_z \equiv \|\vec{v}\|\|\vec{w}\|\cos(\varphi) \in \mathbb{R}, \] where $\varphi$ is the angle between the two vectors. This operation is also known as the inner product or scalar product. The name scalar comes from the fact that the result of the dot product is a scalar number: a number that does not change when the basis changes.
The signature for the dot product operation is \[ \cdot : \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}. \] The dot product takes two vectors as inputs and outputs a real number.
The geometric factor $\cos(\varphi)$ depends on the relative orientation of the two vectors:
- If the vectors point in the same direction, then
$\cos(\varphi)=\cos(0^\circ) = 1$ and so
$\vec{v}\cdot\vec{w}=\|\vec{v}\|\|\vec{w}\|$.
* If the vectors are perpendicular to each other,
$\cos(\varphi)=\cos(90^\circ) = 0$ and so
$\vec{v}\cdot\vec{w}=\|\vec{v}\|\|\vec{w}\|(0)=0$.
* If the vectors point in exactly opposite directions, then
$\cos(\varphi)=\cos(180^\circ) = -1$ and so
$\vec{v}\cdot\vec{w}=-\|\vec{v}\|\|\vec{w}\|$.
Cross product
The cross product takes as inputs two vectors and returns another vector: \[ \times : \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}^3. \] The fact that the output of this operation is a vector is why we sometimes refer to the cross product as the vector product.
The cross products of the individual basis elements is defined as follows: \[ \hat{\imath}\times\hat{\jmath} =\hat{k}, \ \ \ \hat{\jmath}\times\hat{k} =\hat{\imath}, \ \ \ \hat{k}\times \hat{\imath}= \hat{\jmath}. \]
The cross product is anti-symmetric in its inputs, which means that swapping the order of the inputs introduces a negative sign in the output: \[ \hat{\jmath}\times \hat{\imath} =-\hat{k}, \ \ \ \hat{k}\times\hat{\jmath} =-\hat{\imath}, \ \ \ \hat{\imath}\times \hat{k} = -\hat{\jmath}. \] I bet you had not seen an anti-symmetric product before. Most products you have seen so far in math are commutative, which means that the order of the inputs doesn't matter. The product of two numbers is commutative $ab=ba$, the dot product is commutative $\vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$, but the cross product of two vectors is non commutative $\hat{\imath}\times \hat{\jmath} \neq \hat{\jmath}\times \hat{\imath}$.
For two arbitrary vectors $\vec{a}=(a_x,a_y,a_z)$ and $\vec{b}=(b_x,b_y,b_z)$, the cross product is calculated as follows: \[ \vec{a}\times\vec{b}=\left( a_yb_z-a_zb_y, \ a_zb_x-a_xb_z, \ a_xb_y-a_yb_x \right). \]
The length of the output of the cross product is proportional to the $\sin$ of the angle between the vectors: \[ \|\vec{a}\times\vec{b}\|=\|\vec{a}\|\|\vec{b}\|\sin(\varphi). \] The direction of the vector $\vec{a}\times\vec{b}$ is perpendicular to both $\vec{a}$ and $\vec{b}$.
Complex numbers
You have no doubt heard about the complex numbers $\mathbb{C}$. The word “complex” is an intimidating word. Surely it must be a complex task to learn about the complex numbers. That may be true in general, but not if you know about vectors. Complex numbers are similar to two-dimensional vectors $\vec{v} \in \mathbb{R}^2$. We add and subtract complex numbers like vectors. Complex numbers also have components, length and “direction”. If you understand vectors then you will understand complex numbers at almost no additional mental cost.
Example
Suppose you are asked to solve the following quadratic equation: \[ x^2 + 1 = 0. \] You are looking for a number $x$, such that $x^2=-1$ so that adding one to $x^2$ we get zero. If you are only allowed to give real answers (the set of real numbers is denoted $\mathbb{R}$), then there is no answer to this question. In other words, this equation has no solution. This is because the quadratic function $f(x)=x^2 + 1$ does not cross the $x$ axis.
We are not going to take that though. We will imagine a new number called $i$ which fits this requirement. By definition $i^2=-1$. And we call $i$ the unit imaginary number. The solutions to the equation are going to be $x=i$ and $x=-i$. Remember that a quadratic equation has two solutions. We can check $i^2 + 1 = -1 +1 = 0$ and also $(-i)^2 +1 = (-1)^2i^2 + 1 = i^2 +1 = 0$.
Definitions
- $i$: The unit imaginary number $i \equiv \sqrt{-1}$ or $i^2 = -1$.
- $bi$: An imaginary number that is equal to $b$ times $i$.
- $\mathbb{R}$: The set of real numbers.
- $\mathbb{C}$: The set of complex numbers $\mathbb{C} = \{ a + bi \ | \ a,b \in \mathbb{R} \}$.
- $z=a+bi$: A complex number (has a real part and an imaginary part).
- $\textrm{Re}\{ z \}=a$: The real part of $z$.
- $\textrm{Im}\{ z \}=b$: The imaginary part of $z$.
- $\bar{z}$: The complex conjugate of $z$. If $z=a+bi$, then $\bar{z}=a-bi$.
NOINDENT When using the polar representation of complex numbers we have:
- $z= |z|\angle \phi_z= |z|\cos\phi_z + i|z|\sin\phi_z$.
- $|z|=\sqrt{ \bar{z}z }=\sqrt{a^2+b^2}$: The magnitude of $z=a+bi$.
- $\phi_z=\tan^{-1}(b/a)$: The phase of $z=a+bi$.
- $\textrm{Re}\{ z \} = |z|\cos(\phi_z)$.
- $\textrm{Im}\{ z \} = |z|\sin(\phi_z)$.
Formulas
Addition and subtraction
Just like the addition of vectors is done component wise, the addition of complex numbers is done reals-part-with-real-part and imaginary-part-with-imaginary-part: \[ (a+bi) + (c+di) = (a+c) + (b+d)i. \]
Polar representation
A geometrical interpretation of the complex numbers is to extend the real number line that stretches from $-\infty$ to $\infty$ into a two-dimensional plane. The horizontal axis (where the $x$-axis is usually) will measure the real part of the number. The vertical axis will measure the imaginary component. Complex numbers are vectors in the complex plane.
It is possible to represent any complex number $z=a+bi$ in terms of length and direction notation: \[ z= |z|\angle \phi_z = (|z|\cos\phi_z) + (|z|\sin\phi_z)i. \]
The magnitude of a complex number $z=a+bi$ is \[ |z|=\sqrt{a^2+b^2}. \] This corresponds to the distance of from the origin. The formula is obtained by using Pythagoras theorem.
The phase of the complex number is \[ \phi_z=\tan^{-1}(b/a). \] This corresponds to the angle that $z$ makes with the real axis.
Multiplication
The product of two complex numbers is computed using the usual rules of algebra: \[ (a+bi)(c+di) = (ac - bd) + (ad + bc)i. \] In the polar representation, the product is \[ (p\angle \phi)(q\angle \psi) = pq \angle (\phi + \psi). \]
Cardan's example
One of the first examples of reasoning using complex numbers was given by Jerome Cardan in his Ars Magna. “If someone says to you, divide 10 into two parts, one of which multiplied into the other shall produce 40, it is evident that this case or question is impossible.” What is required is to find wo numbers $x_1$ and $x_2$ such that $x_1+x_2=10$ and $x_1x_2=40$. This sounds kind of impossible. Or is it?
“Nevertheless,” Cardan says, “we shall solve it in this fashion: \[ x_1 = 5 + \sqrt{15}i, \ \ \text{and} \ \ x_2 = 5 - \sqrt{15}i. \] When you add $x_1 + x_2$ you get 10, and when you multiply them you get \[ x_1x_2=\left(5 + \sqrt{15}i\right)\left(5 - \sqrt{15}i\right) = 25 - \sqrt{15}^2i^2 = 25 + 15 = 40. \] Hence this product is 40.”[1]
Example
Both $i$ and $-1$ have a magnitude of $1$, but $i$ has an argument of $\pi/2$ ($90^\circ$) while $-1$ has an argument of $\pi$ ($180^\circ$). \[ (i)(-1) = (1\angle \frac{\pi}{2})(1 \angle \pi) = 1 \angle \frac{3\pi}{2} = -i. \] Effectively, multiplication by $i$ is like rotation by $90$ degrees leftward.
Division
Let me now show you the procedure for dividing complex numbers: \[ \frac{(a+bi)}{(c+di)} = \frac{(a+bi)}{(c+di)}\frac{(c-di)}{(c-di)} = (a+bi)\frac{(c-di)}{(c^2+d^2)} = (a+bi)\frac{\overline{c+di}}{|c+di|^2}. \] In other words, if you want to divide the number $z$ by the complex number $s$, you should compute $\bar{s}$ and $|s|^2=s\bar{s}$ and then use: \[ z/s = z\frac{ \bar{s} }{ |s|^2 }. \] You can think of $\frac{ \bar{s} }{ |s|^2 }$ as being equivalent to $s^{-1}$.
Fundamental theorem of algebra
The solutions to any polynomial equation $a_0 + a_1x + a_2x^2 + \cdots a_nx^n=0$ are of the form: \[ z=a+bi. \] In other words, any polynomial $P(x)$ of $n^\textrm{th}$ degree can be written as \[ P(x) = (x - z_1)(x - z_2) \cdots (x-z_n), \] where $z_i \in \mathbb{C}$ are its complex roots.
Before today, you would say that the equation $x^2 + 1 =0$ had no solutions. Now you know that actually it has solutions, but the solutions are complex numbers: $x_1=i$ and $x_2=-i$.
Euler's formula
We know that $\sin(\theta)$ is just a shifted version of $\cos(\theta)$, so clearly these two functions are related. The exponential function, however, seems kind of unrelated to $\sin$ and $\cos$. Lo and behold Euler's formula: \[ \exp(i\theta) \equiv e^{i\theta} = \cos(\theta) + i\sin(\theta), \] where $i = \sqrt{-1}$ is the unit imaginary number. An imaginary input number to the exponential function produces a complex number as output which contains both $\cos$ and $\sin$. Euler's formula gives us a more natural notation for the polar representation of complex numbers: $z=|z|\angle\phi_z = |z|e^{i\phi_z}$
If you want to impress your friends with you math knowledge, you can plug $\theta=\pi$ into the above equation to get \[ \exp(i\pi) = \cos(\pi) + i\sin(\pi)= -1, \] which can be rearranged into this form: $e^{\pi i} + 1 = 0$. This equation shows a relationship between the five most important numbers in all of mathematics: Euler's number $e=2.71828...$, $\pi=3.14…$, the imaginary number $i$, one and zero.
de Moivre's theorem
We can replace $\theta$ in Euler's formula with $n\theta$, we obtain de Moivre's theorem: \[ \left( \cos \theta + i \sin \theta \right)^n = \cos n\theta + i \sin n\theta. \]
De Moivre's Theorem seems obvious if you think of the multiplication law in the polar representation of the complex number as $z=|z|e^{i\theta}$ which is simply raised to the $n$th power $(\cos \theta + i \sin \theta)^n=z^n = (|z|e^{i\theta})^n = |z|^ne^{in\theta}=\cos n\theta + i \sin n\theta$.
Using $n=2$ in de Moivre's formula, we can derive the double angle formulas as the real an imaginary part of the following equation: \[ (\cos^2 \theta - \sin^2 \theta) + (2\sin \theta \cos \theta )i = \cos(2\theta) + \sin(2\theta)i. \]
Links and references
[ Mini tutorial ]
http://paste.lisp.org/display/133628
[ Pretty pictures of the Mandelbrot set ]
https://christopherolah.wordpress.com/2011/08/08/the-real-3d-mandelbrot-set/
NOINDENT [1] Girolamo Cardan, The Great Art or The Rules of Algebra, trans. and ed. by T. Richard Widmer (Cambridge: Massachusetts Institute of Technology Press, 1968), pp. 219–20.
Mechanics
Introduction
Mechanics is the precise study of the motion of objects, the forces acting on them and more abstract concepts such as momentum and energy. You probably have an intuitive understanding of these concepts already. In this chapter we will learn how to use precise mathematical equations to support your intuition.
Newton's laws
Mechanics is the part of physics that is most well understood. Starting from three simple principles known as Newton's laws, we can figure out pretty much everything about the motion of the objects around us. Newton's three laws are:
- In the absence of external forces, objects will maintain their velocity and their direction of motion.
- A force acting on an object causes an acceleration inversely proportional to the mass of the object: $\vec{F}=m\vec{a}$.
- For each force $\vec{F}_{12}$ applied by Object 1 on Object 2,
there is an equal and opposite force $\vec{F}_{21}$ that Object 2 exerts on Object 1. This ability to express the laws of Nature as simple principles like the above is what makes Physics fascinating. Complicated phenomena can be broken down and understood in terms of simple theories.
The laws of physics are expressed in terms of mathematical equations. There are about twenty such equations (see the back of the book). In this chapter we will learn how to use each of these equations in order to solve physics problems.
Motion
To solve a physics problem is to obtain the equation of motion $x(t)$, which describes the position of the object as a function of time. Once you know $x(t)$, you can answer any question pertaining to the motion of the object. To find the initial position $x_i$ of the object, you simply plug $t=0$ into the equation of motion $x_i = x(0)$. To find the time(s) when the object reaches a distance of 20[m] from the origin, you simply solve for $t$ in $x(t)=20$[m]. Many of the problems on the mechanics final exam will be of this form so, if you know how to find $x(t)$, you will be in good shape to ace the exam.
In Chapter 2, we learned about the kinematics of objects moving in one dimension. More specifically, we showed how the process of integration over time (twice) can be used to obtain the position of a particle starting from the knowledge of its acceleration: \[ a(t) \ \ \ \overset{v_i+ \int\!dt }{\longrightarrow} \ \ \ v(t) \ \ \ \overset{x_i+ \int\!dt }{\longrightarrow} \ \ \ x(t). \] But how do we obtain the acceleration?
Dynamics is the study of forces
The first step towards finding $x(t)$ is to calculate all the forces that act on the object. Forces are the cause of acceleration so if you want to find the acceleration, you need to calculate the forces acting on the object. Newton's second law $F=ma$ states that a force acting on an object produces an acceleration inversely proportional to the mass of the object. There are many kinds of forces: the weight of an object $\vec{W}$ is a type of force, the force of friction $\vec{F}_f$ is another type of force, the tension in a rope $\vec{T}$ is yet another type of force and there are many others. Note the little arrow on top of each force, which is there to remind you that forces are vector quantities. To find the net force acting on the object you have to calculate the sum of all the forces acting on the object $\vec{F}_{net} \equiv \sum \vec{F}$.
Once you have the net force, you can use the formula $\vec{a}(t) = \frac{\vec{F}_{net}}{m}$ to find the acceleration of the object. Once you have the acceleration $a(t)$, you can compute $x(t)$ using the calculus steps we learned in Chapter 2. The entire procedure for predicting the motion of objects can be summarized as follows: \[ \frac{1}{m} \underbrace{ \left( \sum \vec{F} = \vec{F}_{net} \right) }_{\text{dynamics}} = \underbrace{ a(t) \ \ \ \overset{v_i+ \int\!dt }{\longrightarrow} \ \ \ v(t) \ \ \ \overset{x_i+ \int\!dt }{\longrightarrow} \ \ \ x(t) }_{\text{kinematics}}. \] If you understand the above equation, then you understand mechanics. The goal of this chapter is to introduce you to all the concepts that appear in this equation and the relationships between them.
Other stuff
Apart from dynamics and kinematics, we will discuss a number of other physics topics in this chapter.
Newton's second law can also be applied to the study of objects in rotation. Angular motion is described by the angle of rotation $\theta(t)$, the angular velocity $\omega(t)$ and the angular acceleration $\alpha(t)$. The causes of angular acceleration are angular force, which we call torque $\mathcal{T}$. Apart from this change to angular quantities, the principles behind circular motion are exactly the same as those for linear motion.
During a collision between two objects, there will be a sudden spike in the contact force between them which can be difficult to measure and quantify. It is therefore not possible to use Newton's law $F=ma$ to predict the accelerations that occur during collisions.
In order to predict the motion of the objects after the collision we must use a momentum calculation. An object of mass $m$ moving with velocity $\vec{v}$ has momentum $\vec{p}\equiv m\vec{v}$. The principle of conservation of momentum states that the total amount of momentum before and after the collision is conserved. Thus, if two objects with initial momenta $\vec{p}_{i1}$ and $\vec{p}_{i2}$ collide, the total momentum before the collision must be equal to the total momentum after the collision: \[ \sum \vec{p}_i = \sum \vec{p}_f \qquad \Rightarrow \qquad \vec{p}_{i1} + \vec{p}_{i2} = \vec{p}_{f1} + \vec{p}_{f2}. \] Using this equation, it is possible to calculate the final momenta $\vec{p}_{f1}$, $\vec{p}_{f2}$ of the objects after the collision.
Another way of solving physics problems is to use the concept of energy. Instead of trying to describe the entire motion of the object, we can focus only on the initial parameters and the final parameters. The law of conservation of energy states that the total energy of the system is conserved. Knowing the total initial energy of a system allows us to find the final energy, and from this calculate the final motion parameters.
Units
In math we just deal with numbers, that is, we solve questions where the answer is just a dimensionless number like $3$, $5$ or $55.3$. The universal power of math comes precisely from this high level of abstraction. We could be solving for the number of sheep in a pen, the surface area of a sphere or the annual revenue of your startup and in all the cases the same mathematical techniques can be used despite the fact that the numbers refer to very different kinds of quantities.
In physics we use numbers too, but because we are talking about the real world the numbers always have some dimension and measurement unit attached to them. An answer in physics is a number which is either a length, a time, a velocity, an acceleration, or some other physical quantity. We must distinguish between these different types of numbers. It doesn't make sense to add a time and a mass, because the two numbers are measuring different kinds of quantities.
Here is a list of some of the kinds of quantities that will be discussed in this chapter. \[ \begin{array}{lllll} \mathbf{Dimension} & \mathbf{SI\ unit} & \mathbf{Other\ units} & \mathbf{Measured\ with} \nl \textrm{time} & [\textrm{s}] & [\mathrm{h}], [\mathrm{min}] & \textrm{clock} \nl \textrm{length} & [\textrm{m}] & [\mathrm{cm}], [\mathrm{mm}], [\mathrm{ft}], [\mathrm{in}] & \textrm{metre tape} \nl \textrm{velocity} &[\textrm{m}/\textrm{s}]& [\mathrm{km}/\mathrm{h}], [\mathrm{mi}/\mathrm{h}] & \textrm{speedometer} \nl \textrm{acceleration} &[\textrm{m}/\textrm{s}^2]& & \textrm{acceleroometer} \nl \textrm{mass} &[\textrm{kg}] & [\mathrm{g}], [\mathrm{lb}] & \textrm{scale} \nl \end{array} \]
You should always try to “check the units” in your equations. Sometimes you will be able to catch a numerical mistake because the units will not be correct. If I ask you to calculate the maximum height that a ball will reach, I expect that your answer will be a length measured in [m] and not some other kind of quantity like a velocity $[\textrm{m}/\textrm{s}]$ or an acceleration $[\textrm{m}/\textrm{s}^2]$ or a surface area $[\textrm{m}^2]$. An answer in $[\mathrm{ft}]$ would also be acceptable since this is also a length, and it can be converted to metres using $1[\mathrm{ft}]=0.3048[\mathrm{m}]$. Learn to watch out for the units/dimensions of physical quantities, and you will have an easy time in physics. They are an excellent error checking mechanism.
The units of physical quantities in this book are indicated in square brackets throughout the lessons in this book.
\[ \ \]
We will begin our physics journey by starting from the familiar subject of kinematics which we studied in Chapter 2. Now that you know about vectors, we can study kinematics problems in two dimensions like the motion of a projectile: $\vec{r}(t)=[x(t),y(t)]$.
Projectile motion
Ever since the invention of gun powder, generation after generation of men have thought of countless different ways of hurtling shrapnel and explosives at each other. Indeed, mankind has been stuck to the idea of two dimensional projectile motion like flies on shit. So long as there is money to be made in selling weapons, and TV stations to keep justifying the legitimacy of the use of these weapons, it is likely that the trend will continue.
It is therefore imperative for anyone interested in reversing this trend to learn about the physics of projectile motion. You need to know the techniques of the enemy (the industrial military complex) before you can fight them. We will see that projectile motion is nothing more than two parallel one-dimensional kinematics problems: UVM in the $x$ direction and UAM in the $y$ direction.
Concepts
The basic concepts of kinematics in two dimensions are:
- $\hat{x},\hat{y}$: a coordinate system.
- $t$: time, measured in seconds.
- $\vec{r}(t)\equiv (x(t),y(t))$: the position (vector) of the object at time $t$.
- $\vec{v}(t) \equiv (v_x(t), v_y(t) ) $: the velocity of the object as a function of time.
- $\vec{a}(t) \equiv (a_x(t), a_y(t) ) $: the acceleration as a function of time.
When solving some problem, where we calculate the motion of an object that starts form an initial point an goes to a final point, we will use the following terminology:
- $t_i=0$: initial time (the beginning of the motion).
- $t_f$: final time (when the motion stops).
- $\vec{v}_{i}=\vec{v}(0)=(v_x(0),v_y(0))=(v_{ix},v_{iy})$: the initial velocity at $t=0$.
- $\vec{r}_i=\vec{r}(0)=(x(0),y(0))=(x_i,y_i)$: the initial position at $t=0$.
- $\vec{r}_f=\vec{r}(t_f)=(x(t_f),y(t_f))=(x_f,y_f)$: the final position at $t=t_f$.
Formulas
Motion in two dimensions
Sometimes you have to describe both the $x$ and the $y$ coordinate of the motion of a particle: \[ \vec{r}(t)=(x(t), y(t)). \] We choose $x$ to be the horizontal component of the projectile motion and $y$ to be its height.
The velocity of the projectile will be \[ \vec{v}(t) = \frac{d}{dt}\left(\vec{r}(t)\right) = \left(\frac{dx(t)}{dt}, \frac{dy(t)}{dt} \right) = (v_x(t),v_y(t)), \] and the initial velocity is: \[ \vec{v}_i = \vec{v}(0) = \|\vec{v}_i\|\angle \theta = (v_x(0), v_y(0)) = (v_{ix}, v_{iy})= (\|\vec{v}_i\|\cos\theta, \|\vec{v}_i\|\sin\theta). \]
The acceleration of the projectile will be: \[ \vec{a}(t) = \frac{d}{dt}\left(\vec{v}(t)\right) = (a_x(t),a_y(t)) = (0,-9.81). \] Note how we have zero acceleration in the $x$ direction (ignoring air friction) so we can use the UVM equations of motion for $x(t)$ and $v_x(t)$. In the $y$ direction we have a uniform downward acceleration due to gravity.
Projectile motion
The equations of motion of a projectile are the following. First in the $x$ direction we have: \[ \begin{align} x(t) & = v_{ix}t + x_i, \nl v_x(t) & =v_{ix}. \end{align} \]
In the $y$ direction, you have the constant pull of gravity downwards which gives us a uniformly accelerated motion (UAM): \[ \begin{align} y(t) & = \frac{1}{2}(-9.81)t^2 + v_{iy}t + y_i, \nl v_y(t) & = -9.81 t + v_{iy}, \nl v_{yf}^2 & = v_{iy}^2 + 2(-9.81)(\Delta y). \end{align} \]
Example
![An object is thrown with 8.96[m/s] at an angle of 51.3 degrees from a height of 1[m].
What will be the maximum height reached and distance travelled by the object? An object is thrown with 8.96[m/s] at an angle of 51.3 degrees from a height of 1[m].
What will be the maximum height reached and distance travelled by the object?](/_media/physics/projecticle-concepts_tikz-0.png?w=400) Let us now consider an example in which we analyze all aspects of the motion of a projectile.
An object is thrown with an initial velocity $8.96$[m/s] at an angle of $51.3^\circ$
with the ground from an initial height of $1$[m].
You are asked to calculate the maximum height $h$ that the object will reach,
and the distance $d$ where the object will hit the ground.
Let us now consider an example in which we analyze all aspects of the motion of a projectile.
An object is thrown with an initial velocity $8.96$[m/s] at an angle of $51.3^\circ$
with the ground from an initial height of $1$[m].
You are asked to calculate the maximum height $h$ that the object will reach,
and the distance $d$ where the object will hit the ground.
Your first step when reading any physics problem should be to extract the information from the problem statement. The initial position is $\vec{r}(0)=(x_i,y_i)=(0,1)$[m]. The initial velocity is $\vec{v}_i=8.96\angle51.3^\circ$[m/s], which is $\vec{v}_i = (8.96\cos51.3^\circ, 8.96\sin51.3^\circ)= (5.6,7)$[m/s] in component form.
You can now plug the values of $\vec{r}_i$ and $\vec{v}_i$ into the equations of motion and find the desired quantities. When the object reaches its maximum height, it will have zero velocity in the $y$ direction: $v_{y}(t_{top})=0$. We can use this fact, and the $v_y(t)$ equation in order to find $t_{top} = 7/9.81= 0.714$[s]. The maximum height is then obtained by evaluating the function $y(t)$ at $t=t_{top}$. We obtain $h = y(t_{top})= 1 + 7(0.714) + \tfrac{1}{2}(-9.81)(0.714)^2 = 3.5$[m].
To find $d$, we must solve the quadratic equation $0=y(t_f)=1 + 7(t_f) + \tfrac{1}{2}(-9.81)(t_f)^2$ to find the time $t_f$ when the object hits the ground. The solution is $t_f=1.55$[s]. We then plug this value into the equation for $x(t)$ to obtain $d= x(t_f)=0 + 5.6(1.55)=8.68$[m]. You can verify that these answers match the trajectory illustrated in the figure.
Explanations
Coordinate system
Before you start to solve any problem, you need to make a diagram of what is going on. On that diagram indicate clearly the coordinate system with respect to which you will measure $x$ and $y$, and $v_x$ and $v_y$. The values you plug into the equations of motion are measured with respect to this coordinate system: a velocity $v_x$ in the opposite direction of the $x$ axis is represented as a negative number.
Uniform velocity motion in the $x$ direction
Ignoring the effects of air friction, there is zero acceleration in the $x$ direction so $a_x=0$. As a consequence, the velocity will be constant. Whatever $x$ velocity you give the projectile when you throw it, it will keep it. Therefore the UVM equations describe its motion in the $x$ direction: \[ \begin{align*} a_x(t) &=0, \nl v_x(t) &= v_{ix}, \nl x(t) &= v_{ix}t + x_{i}. \end{align*} \]
Uniform acceleration motion in the y-direction
We have the pull of gravity in the $y$ direction which is a constant acceleration $a=-9.81$[m/s$^2$], the equations of motion are: \[ \begin{align*} a_y(t) &= - g, \nl v_y(t) &= -gt + v_{iy}, \nl y(t) &= \frac{1}{2}(-g)t^2 + v_{iy}t + y_i, \end{align*} \] where $g=9.81$[m/s$^2$] is the gravitational acceleration on the surface on Earth.
Furthermore we have another useful equation relating the initial and final velocity in the $y$ direction: \[ v_{fy}^2 = v_{iy}^2 + 2a(\Delta y). \] This equation is useful because it does not contain the time.
Examples
Freedom and democracy
An American F-18 is flying above Iraq. It is carrying two bombs. One bomb is called “freedom” and weighs 200[kg], the other “democracy” with mass 500[kg]. If the plane is flying with speed $v_i=300$ [m/s] and drops both bombs from a height of $2000$[m]. How far will the bombs travel? Which city is going to get democracy and which will get freedom?
The equations of motion are: \[ \begin{align*} x(t) &= v_{ix}t + x_{i} = 300 t + 0, \nl y(t) &= \frac{1}{2}(-9.81)t^2 + v_{iy}t + y_{Ai}= -4.9 t^2 + 2000. \end{align*} \] Solving for $t$ in the second equation we get $t=20.20$[s]. We use this value of $t$ in the first equation to find the final $x$ position where the bombs hit the ground $x_f=x(20.20) = 6060$[m]. Both bombs hit the same town, the one which is $6.06$[km] from the launch point. Observe that the masses of the bombs did not play any part in the final equations of motion.
The above scenario is basically what the people in the US state administration are talking about when they say they are bringing freedom and democracy to the Middle East. We have to get those crooked warmongering bastards out of power and quickly. In fact the entire industrial military complex needs to be dismantled because they are the ones who ultimately benefit from the World conflicts. What can we do to stop them you ask? In my opinion, the best way to fight the system is not to work for the system.
Roach throw
You are standing comfortably on a picnic bench in the Parc Mt-Royal and, not far from you, there is a garbage bin. Feeling lazy and relaxed, you decide that you want to throw a particle $r$ into the bin instead of walking over and dropping it in. The particle $r$ (for the French rebut) is a piece of carton rolled upon itself and wrapped in a paper. Imagine a coordinate system centred below your feet. We will denote as $(0,0)$ the point where your right toe touches the ground and the point $(x=0,y=1.4)$[m] is the initial position of the carton $r$ as you are about to flick it with your finger towards the garbage.
Suppose that the garbage bin is 3 metres away from you and that it is 1 metre tall. Can you calculate the initial velocity that the roach needs to have to land in the garbage bin? Assume that you send it flying purely along the $x$-axis, in other words you do not give it any initial $y$-velocity: $v_{iy}=0$. Can you solve for $v_{ix}$ necessary for the roach to fall into the garbage bin?
All that you need to describe the motion of $r$ are the initial
position $\vec{r}(0)=(x(0), y(0))$ and the initial
velocity $\vec{v}_i = \vec{v}(0) = (v_x(0), v_y(0))$,
which you can then plug into the equations of motion:
\[
\begin{align*}
x(t) &= v_{ix}t + x_i, \nl
y(t) &= y_i + v_{iy}t + \frac{1}{2}a_y t^2.
\end{align*}
\]
Most physics word problems will follow this pattern.
The problem statement gives you some information
about the initial conditions and the desired final conditions
and then ask you to solve for the unknown,
i.e., the one variable which they didn't give you.
Can you carry out the necessary calculations in this case? I don't mean to stress you out, but sitting next to you is your 110kg pure-muscle Chilean friend who has two kids and really gets pissed off at people who throw garbage around in the park. You don't want to piss him off so you better get that initial velocity right!
OK, from now on we can switch into high gear because we have everything setup nicely for us. We know that the general equations of motion for UVM in $x$ and UAM in $y$ are: \[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}a_y t^2, \end{align*} \] and more specifically we know that the $y$ acceleration is due to gravity so we have: \[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}(-9.81)t^2. \end{align*} \]
We also know that the position at $t=0$ is $(x_i, y_i) = (0,1.4)$ and that at some $t_f>0$ we will be flying through the bin at $(x(t_f), y(t_f)) = (3,1)$.
Thus we have: \[ \begin{align*} x(t_f) = 3 &= v_{ix}t_f + 0, \nl y(t_f) = 1 &= 1.4 + v_{iy}t_f + \frac{1}{2}(-9.81)t_f^2. \end{align*} \]
Furthermore, since the problem specified it, we can assume that
the initial velocity of $r$ was purely horizontal ($v_{iy}=0$).
Thus, the equations we have to solve are:
\[
\begin{align*}
\qquad \ \ \: 3 &= v_{ix}t_f, \nl
\qquad \ \ \: 1 &= 1.4 -4.9 t^2_f,
\end{align*}
\]
where $v_{ix}$ and $t_f$ are the two unknowns.
From here on, it should be clear where the story is going. First we solve for $t_f$ in the second equation: \[ t_f = \sqrt{ \frac{(1-1.4)}{-4.9} } = \sqrt{ \frac{-0.4}{-4.9} } = \sqrt{ 4/49} = 2/7 \approx 0.28571.. , \qquad \text{[s]} \] and plug that into the first equation to solve for $v_{ix}$ as follows: \[ v_{ix} = \frac{3}{t_f} = \frac{3\cdot 7}{2} = \frac{21}{2} = 10.5 \qquad \text{ [m/s]. } \]
You flick $r$ with you finger at an initial velocity of exactly $\vec{v}_i =(10.5,0)$[m/s] and the roach flies right into the garbage bin. Success!
Interception
With all those people lunging explosive projectiles at each other, a need develops for interception systems which can throw a counter-projectile at the incoming projectile and knock it out of the air.
Let us study how we can intercept an incoming ball (A) launched from $\vec{r}_{Ai}=(0,3)$ with initial velocity $\vec{v}_{Ai}=(8\cos(40), 8\sin(40))$. As interception device, you have at your disposal a ball launcher placed at $\vec{r}_{Bi}=(10,0)$ with a fixed firing angle of $50^\circ$ placed so that it faces the incoming ball. The ball launcher has a variable launch speed $w$[m/s], which you can choose. You want to fire an intercepting ball, which will have initial velocity $\vec{v}_{Bi}=(-w\cos(50), w\sin(50))$ so as to intercept the ball (A) in mid-air. What is the required initial velocity $w$ for the balls to hit each other? At which time $t$ will the collision take place?
As far as kinematics is concerned, this is a standard projectile motion problem times two. You have ball (A) which has equations of motion: \[ \begin{align*} x_A(t) &= v_{Aix}t + x_{Ai} = 8\cos(40) t + 0, \nl y_A(t) &= \frac{1}{2}(-9.81)t^2 + v_{Aiy}t + y_{Ai}= -4.9 t^2 + 8\sin(40) t + 3, \end{align*} \] and ball (B) which has equations of motion: \[ \begin{align*} x_B(t) &= v_{Bix}t + x_{Bi} = - w \cos(50) t + 10, \nl y_B(t) &= \frac{1}{2}(-9.81)t^2 + v_{Biy}t + y_{Bi}= -4.9 t^2 + w\sin(50) t + 0. \end{align*} \]
The fact that we want the balls to collide, means that at some point they will have the same coordinates $\vec{r}_A = \vec{r}_B$, which is another way of saying \[ (x_A(t), y_A(t)) = (x_B(t), y_B(t)). \] The $x$-coordinates have to match, and the $y$-coordinates have to match, so this gives us two equations: \[ \begin{align} 8\cos(40) t + 0 &= - w \cos(50) t + 10, \nl -4.9 t^2 + 8\sin(40) t + 3 &= -4.9 t^2 + w\sin(50) t + 0. \end{align} \]
We can cancel the $-4.9 t^2$ on both sides of the bottom equation to get: \[ \begin{align} 8\cos(40) t &= - w \cos(50) t + 10, \nl 8\sin(40) t + 3 &= w\sin(50) t. \end{align} \]
This is a set of two equations with two unknowns, so we can solve it. It is not going to be easy to do this, because we can't isolate either of $t$ or $w$ in a clean way using the standard substitution techniques. There is a trick though: we can divide the two equations! If $A=B$ and $C=D\neq 0$ then $A/C = B/D$ so this is what we will use. In preparation for this step, let me rearrange the equations a bit to have all the $w$-containing terms alone on the right side: \[ \begin{align} 10 - 8\cos(40) t &= w \cos(50) t , \nl 8\sin(40) t + 3 &= w \sin(50) t. \end{align} \]
We will now divide the bottom equation by the top equation to obtain: \[ \frac{ 8\sin(40) t + 3 }{10 - 8\cos(40) t} = \frac{ w \sin(50) t }{ w \cos(50) t} = \tan(50). \]
Rearranging the expression we get \[ 8\sin(40) t + 3 = \tan(50)( 10 - 8\cos(40) t ). \] We now collect all the $t$ terms to one side to obtain: \[ [8\sin(40) + 8\cos(40)\tan(50)] t = 10\tan(50) - 3, \] and finally \[ t = \frac{10\tan(50) - 3}{ 8\sin(40) + 8\cos(40)\tan(50) } = 0.7165 \text{[s]}. \]
We can now plug into any of the above equations to find the value of $w$. For example plugging the value of $t=0.7165$ into \[ 10 - 8\cos(40) t = w \cos(50) t, \] we will get \[ 10 - 8\cos(40)(0.7165) = w \cos(50)(0.7165), \] and so $w = \frac{10 - 8\cos(40)(0.7165)}{ \cos(50)(0.7165)} = 12.1788$ [m/s].
OK. Now let's check our answer. If we use the initial velocity $12.1788$ and substitute that into the equations of motion for ball (B), and plot the two trajectories on the computer:
They do meet indeed and at the specified time $t=0.7165$[s].
Discussion
I want to point out that there is no new physics necessary to understand the motion of projectiles. Projectile motion is a two-dimensional kinematics problem which can be broken down into two parts: the $x$ direction (described by the UVM equations) and the $y$ direction (described by the UAM equations).
Links
[ Eisenhower on the danger posed by the industrial military complex. ]
Quote: “Only an alert and knowledgeable citizenry can compel the proper
meshing of the huge industrial and military machinery of defence with
our peaceful methods and goals.”
http://www.youtube.com/watch?v=8y06NSBBRtY
Forces
Like a shepherd who brings back stray sheep, we need to rescue the word force and give it precise meaning. In physics force means something very specific. Not “the force” from Star Wars, not the “force of public opinion”, and not the force in the battle of good versus evil.
Force in physics has a precise meaning as an amount of push or pull exerted on an object. Forces are vector quantities measured in Newtons [N]. In this section we will explore all the different kinds of forces.
Concepts
- $\vec{F}$: a force. This is something the object “feels” as a pull or a push. Force is a vector, so you must always keep in mind the direction in which the force $\vec{F}$ acts.
- $k,G,m,\mu_s,\mu_k,\ldots$: parameters on which the force $F$ may depend. Ex: the heavier an object is (large $m$ parameter), the larger its gravitational pull will be: $\vec{W}=-9.81m\hat{\jmath}$, where $\hat{\jmath}$ points towards the sky.
Kinds of forces
We next list all the forces which you are supposed to know about for a standard physics class and define the relevant parameters for each kind of force. You need to practice exercises using each of these forces, until you start to feel how they act.
Gravitation
The force of gravity exists between any two massive objects. The magnitude of the gravitational force between two objects of mass $M$[kg] and $m$[kg] separated by a distance $r$[m] is given by the formula \[ F_g=\frac{GMm}{r^2}, \] where $G=6.67 \times 10^{-11}$[$\frac{\text{Nm}^2}{\text{kg}^2}$] is the gravitational constant. This is the famous one-over-arr-squared law that describes the gravitational pull between two objects. This was Newton's big discovery.
On the surface of the earth, which has mass $M=5.972\times 10^{24}$[kg] and radius $r=6.367\times10^6$[m], the force of gravity on an object of mass $m$ is given by \[ F_g=\frac{GMm}{r^2} = \underbrace{\frac{GM}{r^2}}_{g}m = 9.81 m = W. \] We call this force the weight of the object and to be precise we should write $\vec{W}=-mg\hat{\jmath}$ to indicate that the force acts downwards—in the negative $y$ direction. Verify using your calculator that $\frac{GM}{r^2}=9.81\equiv g$.
Force of a spring
A spring is a piece of metal twisted into a coil that has a certain natural length. The spring will resist any attempts to stretch it or compress it. The force exerted by a spring is given by \[ \vec{F}_s=-k\vec{x}, \] where $x$ is the amount by which the spring is displaced from its natural length and the constant $k$[N/m] is a measure of the strength of the spring. Note the negative sign: if you try to stretch the spring (positive $x$) then the force of a spring will pull against you (in the negative $x$ direction), if you try to compress the spring (negative $x$) it will push back against you (in the positive $x$ direction).
Normal force
The normal force is the force between two surfaces in contact. The word normal means “perpendicular to the surface of” in this context. The reason why my coffee mug does not fall to the floor right now is that the table exerts a normal force $\vec{N}$ on it keeping in place.
Force of friction
In addition to the normal force between surfaces, there is also the force of friction $\vec{F}_f$ which acts to prevent or slow down any sliding motion between the surfaces. There are two kinds of force of friction and both kinds of are proportional to the amount of normal force between the surfaces: \[ \max \{ \vec{F}_{fs} \}=\mu_s\|\vec{N}\| \ \ \text{(static)}, \qquad \vec{F}_{fk}=\mu_k\|\vec{N}\| \ \ \text{(kinetic)}, \] where $\mu_s$ and $\mu_k$ are the static and dynamic friction coefficients. Note that it makes intuitive sense that the force of friction should be proportional to the magnitude of the normal force $\|\vec{N}\|$: the harder the surfaces push against each other the more difficult it should be to make them slide. The above equations make this intuition precise.
The static force of friction acts on objects that are not moving. It describes the maximum amount of friction that can exist between two objects. If a horizontal force greater than $F_{fs} = \mu_s N$ is applied to the object, then it will start to slip. The kinetic force of friction acts when two objects are sliding relative to each other. It always acts in the direction opposite to the motion.
Tension
A force can also be exerted on an object remotely by attaching a rope to the object. The force exerted on the object will be equal to the tension in the rope $\vec{T}$. Note that tension always pulls away from an object: you can't push a dog on a leash.
Discussion
Viewing the interactions between objects in terms of the forces that act between them is a very powerful way of thinking. In the next section, we will learn how to draw force diagrams which take into account all the forces that act on the object.
Force diagrams
Welcome to Force-Accounting 101. In this section we will learn how to identify all the forces acting on an object and use Newton's 2nd law $\sum \vec{F}=\vec{F}_{net} = m\vec{a}$ to predict the resulting acceleration.
Concepts
Newton's second law describes a relationship between these three quantities:
- $m$: the mass of an object.
- $\vec{F}_{net}$: the net force on the object.
- $\vec{a}$: the acceleration of the object.
Forces and accelerations are vectors. To work with vectors, we work with their components:
- $F_x$: the component of $\vec{F}$ in the $x$ direction.
- $F_y$: the component of $\vec{F}$ in the $y$ direction.
Vectors are meaningless unless it is clear with respect to which coordinate system they are expressed.
- $x$ axis: Usually the $x$ axis is horizontal and to the right, however, for problems with inclines,
it will be more convenient to use an inclined $x$ axis that is parallel to the slope.
- $y$ axis: The $y$ axis is always perpendicular to the $x$ axis.
- $\hat{\imath},\hat{\jmath}$: Unit vectors in the $x$ and $y$ directions. Any vector can be written as $\vec{v}=v_x\hat{\imath}+v_y\hat{\jmath}$ or as $\vec{v}=(v_x,v_y)$.
Provided we have a coordinate system, we can write any force vector in three equivalent ways: \[ \vec{F} \equiv F_x\hat{\imath} + F_y\hat{\jmath} \equiv (F_x,F_y) \equiv \|\vec{F}\|\angle \theta. \]
What types of forces are there in force diagrams?
- $\vec{W}\equiv\vec{F}_{gravity}=m\vec{g}$: The weight. This is the force on a object due to its gravity. The gravitational pull $\vec{g}$ always points downwards – towards the centre of the earth. $g=9.81$[N/kg].
- $\vec{T}$: Tension in a rope. Tension is always pulling away from the object.
- $\vec{N}$: Normal force – the force between two surfaces.
- $\vec{F}_{fs}=\mu_s\|\vec{N}\|$: Static force of friction.
- $\vec{F}_{fk}=\mu_k\|\vec{N}\|$: Kinetic force of friction.
- $\vec{F}_{s}=-kx$: The force (pull or push) of a spring that is displaced (stretched or compressed) by $x$ metres.
Formulas
Newton's 2nd law
The sum of the forces acting on an object, divided by the mass, gives you the acceleration of the object: \[ \sum \vec{F} \equiv \vec{F}_{net}= m\vec{a}. \]
Vector components
If a vector $\vec{v}$ makes an angle $\theta$ with the $x$ axis then: \[ v_x = \|\vec{v}\|\cos\theta, \qquad \text{and} \qquad v_y = \|\vec{v}\|\sin\theta. \] The vector $v_x\hat{\imath}$ corresponds to the part of $\vec{v}$ that points in the $x$ direction.
In what follows, you will be asked a countless number of times to \[ \text{Find the component of } \vec{F} \text{ in the ? direction. } \] Which is another way of asking you to find the number $v_?$.
The answer is usually equal to the length $\|\vec{F}\|$ multiplied by either $\cos$ or $\sin$ and sometimes $-1$ all depending on way the coordinate system is chosen. So don't guess. Look at the coordinate system. If the vector points in the direction where $x$ increases, then $v_x$ should be a positive number. If $\vec{v}$ points in the opposite direction, then $v_x$ should be negative.
To add forces $\vec{F}_1$ and $\vec{F}_2$ you have to add their components: \[ \vec{F}_1 + \vec{F}_2 = (F_{1x},F_{1y}) + (F_{1x},F_{2y}) = (F_{1x}+F_{2x},F_{1y}+F_{2y}) = \vec{F}_{net}. \] Instead of dealing with vectors in the bracket notation as above, when solving force diagrams it is easier to simply write the $x$ equation on one line, and the $y$ equation on a separate line below it: \[ F_{netx} = F_{1x}+F_{2x}, \] \[ F_{nety} = F_{1y}+F_{2y}. \] It is a good idea to always write those two equations together as a block – so it remains clear that you are talking about the same problem, but the first row represents the $x$-dimension and the second row represents the $y$-dimension.
Force check
It is important to account for all the forces acting on an object. Any object with mass on the surface of the earth will feel a downwards gravitational pull of magnitude $F_{g}=W=m\vec{g}$. Then you have to think about which of the other forces might be present: $\vec{T}$, $\vec{N}$, $\vec{F}_{f}$, $\vec{F}_{s}$. Anytime you see a rope tugging on the object, you know there must be some tension $\vec{T}$, which is a force vector pulling on the block. Anytime you have an object sitting on a surface, the surface will push back with a normal force $\vec{N}$. If the object is sliding on the surface there will be a force of friction acting against the direction of the motion: \[ F_{fk}=\mu_k\|\vec{N}\|. \] If the object is not moving, then you have to use $\mu_s$ in the friction force equation, to get the maximum static friction force that the contact between the object and the ground can support before the object starts to slip: \[ \max\{ F_{fs} \}=\mu_s\|\vec{N}\|. \] If you see a spring that is either stretched or compressed by the object, then you must account for the spring force. The force of a spring is restorative: it always acts against the deformation you are making to the spring. If you stretch it by $x$[cm], then it will try to pull itself back to its normal length with a force of: \[ \vec{F}_s = -kx \hat{\imath}. \] The constant of proportionality $k$ is called the spring constant and is measured in [N/m].
Recipe for solving force diagrams
Below we list the steps of the general procedure to follow when solving problems in dynamics.
- Draw a force diagram focussed on the object and indicate all the forces acting on it.
- Choose a coordinate system, and indicate clearly in the diagram what you will call the positive $x$ direction, and what you will call the positive $y$ direction. All quantities in the subsequent equations will be expressed with respect to this coordinate system.
- Write down the following “template”:
\[ \sum F_x = \qquad \qquad \qquad = ma_x, \] \[ \sum F_y = \qquad \qquad \qquad = ma_y. \]
- Fill in the template by calculating the $x$ and $y$ components
of each force acting on the object:
$\vec{W}$, $\vec{N}$, $\vec{T}$, $\vec{F}_{fs}$, $\vec{F}_{fk}$,
$\vec{F}_{s}$ as applicable.
- Solve the equations for the unknown quantities.
I highly recommend that you perform some consistency checks after Step 4. You should check the signs: if the force in the diagram is acting in the $x$ direction, then its component must be positive. If the force is acting in the direction opposite to the $x$ axis, then its component should be negative. You should also check that whenever $F_x \propto \cos\theta$, then $F_y \propto \sin\theta$. If instead we use the angle $\phi$ defined with respect to the $y$ axis, we would have $F_x \propto \sin\phi$, and $F_y \propto \cos\phi$.
We will now illustrate how to use this recipe through a series of examples.
Examples
Block on a table
You place a block of mass $m$ on the table. If it has mass $m$ then it feels its weight $\vec{W}$ pulling down on it, but the table is not letting it drop to the floor. The table pushes back on the block with a normal force $\vec{N}$.
Steps 1,2: We draw the force diagram and choose a coordinate system:
Step 3: Next, we write down the empty equations template: \[ \begin{align*} \sum F_x &= \qquad \qquad = ma_x, \nl \sum F_y &= \qquad \qquad = ma_y. \end{align*} \]
Step 4: There is nothing much going on in the $x$ direction: no forces acting in the $x$ direction and the block is not moving so $a_x=0$. In the $y$ direction we have the force of gravity and the normal force exerted by the table: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \] We set $a_y=0$, because we see that the block is just sitting there on the table without moving. The technical term for situations where $a_x=0, a_y=0$ is called static equilibrium. Force diagrams with static equilibrium are easy to solve, because the entire right-hand side is equal to zero, which means that the forces on the object must be counter-balancing each other.
Step 5: Suppose the teacher was asking you “What is the magnitude of the normal force?”. You can easily answer this by looking at the second equation: “$N=mg$ bro!”
Moving the fridge
You are trying to push your fridge across the kitchen floor. Because it weights quite a lot, it is “gripping” the floor quite a bit. If the static coefficient of friction between the metal “feet” of your fridge and the tiles of the floor is $\mu_s$, how much force $\vec{F}_{ext}$ would it take to get the fridge to start moving?
\[ \begin{align*} \sum F_x &= F_{ext} - F_{fs} = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
If you push with force $F_{ext}=30$[N], the fridge will push back (via its connection to the floor) with a force $F_{fs}=30$[N]. If you push harder, the fridge will push back harder and it will still not move. Only when you reach the slipping threshold will it move. This means you have to push with force equal to the maximum static friction force $F_{fs}=\mu_s N$, so we have: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_s N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
To solve for $F_{ext}$ you first isolate $N=mg$ in the bottom line, and then substitute the value of $N$ in the top line to get $F_{ext} = \mu_s m g$.
Friction slowing you down
OK, so you have the fridge moving now and you are moving at a steady pace across the room:
Your equation of motion is going to be: \[ \begin{align*} \sum F_x &= F_{ext} - \vec{F}_{fk} = ma_x, \nl \sum F_y &= N - mg = 0. \end{align*} \]
In particular if you want to keep a steady speed ($v=const$) as you move across the room, you will push with such a force just to balance the friction force and keep $a_x=0$.
To find the value of $F_{ext}$ to keep a constant speed we solve: \[ \begin{align*} \sum F_x &= F_{ext} - \mu_k N = 0, \nl \sum F_y &= N - mg = 0. \end{align*} \]
We get a similar expression as above, but with $\mu_k$ instead of $\mu_s$: $F_{ext} = \mu_k m g$. Generally, $\mu_k < \mu_s$ so it takes less force to keep the fridge moving than it took to get it to start moving.
Let us now take a different slant on this whole friction thing.
Incline
At this point, my dear readers, we are getting into the main kind of question that will be, without a doubt, asked in your homework or at the final exam. A block sliding down an incline. What is its acceleration?
Step 1: We draw a diagram which includes the weight $\vec{W}$, the normal force $\vec{N}$ and the friction force $\vec{F}_{fk}$.
Step 2: We pick the coordinate system to be tilted along the incline. This is important because this way the motion is purely in the $x$ direction, while the $y$ direction will be static.
Step 3,4: Let's copy the empty template, and fill in the equations: \[ \begin{align*} \sum F_x &= \|\vec{W}\|\sin\theta - F_{fk} = ma_x, \nl \sum F_y &= N - \|\vec{W}\|\cos\theta \ \ = 0, \end{align*} \] or substituting the values that we know: \[ \begin{align*} \sum F_x &= mg\sin\theta - \mu_kN = ma_x, \nl \sum F_y &= N - mg\cos\theta \ \ \ = 0. \end{align*} \]
Step 5: From the $y$ equation, we obtain $N=mg\cos\theta$ and substituting this into the $x$ equation we get: \[ a_x = \frac{1}{m}\left( mg\sin\theta - \mu_k mg\cos\theta \right) = g\sin\theta - \mu_k g\cos\theta. \]
Bathroom scale
You have a spring with spring constant $k$ on which you put a block of mass $m$. By what length $\Delta y$ will the spring be compressed?
Step 1,2: We draw a before and after picture, with the $y$ axis placed at the natural length of the spring.
Step 3,4: Filling in the template we get: \[ \begin{align*} \sum F_x &= 0 = 0, \nl \sum F_y &= F_s - mg = 0. \end{align*} \]
Step 5: We know that the force exerted by a spring is proportional to its displacement according to \[ F_s = -k y_B, \] so we can find $y_B = -\frac{mg}{k}$. The length of compression is therefore: \[ |\Delta y| = \frac{mg}{k}. \]
Two blocks
Now for a more involved example with two blocks. One block is sitting on the surface, and another one is falling straight down. The two are connected by a stiff rope. What is the acceleration of the system as a whole?
Steps 1,2: We have two objects, so we have to draw two force diagrams.
Step 3: We also have two sets of equations. One set of equations for the left block, and one for the right block: \[ \begin{align*} & \sum F_{1x} = \qquad\qquad = m_1a_{x_1} & \qquad & \sum F_{2x} = \qquad\quad = m_2a_{x_2} \nl & \sum F_{1y} = \qquad\qquad = m_1a_{y_1} & \qquad & \sum F_{2y} = \qquad\quad = m_2a_{y_2} \end{align*} \]
Steps 4: We fill them in with all the forces drawn in the diagram: \[ \begin{align*} & \sum F_{1x} = -F_{fk} + T_1 = m_1a_{x_1} & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - W_1 = 0 & \qquad & \sum F_{2y} = -W_2 + T_2 = m_2a_{y_2} \end{align*} \]
Step 5: What are the connections between the two blocks? Since it is the same rope that connects the two blocks, this means that the tension in the rope is the same on both ends so $T_1=T_2=T$. Also since the rope is of fixed length we have that the $x_1$ and $y_2$ coordinates are related by a constant (though they point in different directions), so it must be that $a_{x_1}= -a_{y_2} = a$.
Rewriting in terms of the new common variables $T$ and $a$ we have: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & \sum F_{1y} = N_1 - m_1g = 0 & \qquad & \sum F_{2y} = -m_2g + T = - m_2a \end{align*} \]
We isolate $N_1$ on the bottom left, and isolate $T$ on the bottom right: \[ \begin{align*} & \sum F_{1x} = -\mu_kN_1 + T = m_1a & \qquad & \sum F_{2x} = 0 =0 \nl & N_1 = m_1g & \qquad & T = - m_2a + m_2g \end{align*} \]
Now substitute the values into the top left equation to get \[ \sum F_{1x} = -\mu_k(m_1g) + (- m_2a + m_2g) = m_1 a, \] or moving all the $a$ terms to one side we have \[ -\mu_km_1g + m_2g = m_1 a + m_2 a = (m_1 + m_2) a, \] which makes sense since the “two blocks attached with a rope” is in some sense an object of collective mass $(m_1 + m_2)$ with two external forces on it. From this point of view, the tension $T$ is an internal force of the object and doesn't appear in the external force equation.
The acceleration of the whole two-block system going to be: \[ a = \frac{m_2g - \mu_km_1g}{m_1+m_2}. \]
Two inclines
OK, let's just go crazy now! Let's have two inclines, two blocks, a rope, and friction everywhere. We want to find the acceleration as usual.
Steps 1,2: We draw a force diagram with two different coordinate systems each adapted for the angle of the incline:
Steps 3,4: Fill in all force components, and set $a_{y_1}=0,a_{y_2}=0$: \[ \begin{align*} & \sum F_{1x} = W_1\sin\alpha - F_{1fk} + T_1 = m_1a_{x_1}, \nl & \sum F_{1y} = -W_1\cos\alpha + N_1 \quad \ \ \ = 0, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = W_2\sin\beta - F_{2fk} - T_2 = m_2a_{x_2}, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2y} = -W_2\cos\beta + N_2 \quad \ \ \ =0. \end{align*} \]
Step 5: The links between the two worlds are two: the tension in the rope is the same $T=T_1=T_2$ and also the acceleration since the blocks are moving together $a=a_{x_1}=a_{x_2}$. Rewriting and expanding we have: \[ \begin{align*} & \sum F_{1x} = m_1g\sin\alpha - \mu_k N_1 + T = m_1a, \nl & N_1 = m_1g\cos\alpha, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k N_2 - T = m_2a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad N_2 = m_2g\cos\beta. \end{align*} \]
Let's substitute the values of $N_1$ and $N_2$ into the $x$ equations: \[ \begin{align} & \sum F_{1x} = m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & \qquad \qquad \qquad \qquad \qquad \qquad \sum F_{2x} = m_2g\sin\beta - \mu_k m_2g\cos\beta - T = m_2a. \end{align} \]
There are many ways to solve for the two unknowns in this pair of equations. Either (A) we isolate $T$ in one of the equations and substitute the value of $T$ into the second or (B) we isolate $a$ in both equations and set them equal to each other.
We will use approach (A) and isolate $T$ in the bottom equation to get: \[ \begin{align} & m_1g\sin\alpha - \mu_k m_1g\cos\alpha + T = m_1a, \nl & m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a = T. \end{align} \] and finally substitute the expression for $T$ into the top equation to obtain \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + ( m_2g\sin\beta - \mu_k m_2g\cos\beta - m_2a) = m_1a, \] which can be rewritten as \[ m_1g\sin\alpha - \mu_k m_1g\cos\alpha + m_2g\sin\beta - \mu_k m_2g\cos\beta = (m_1 + m_2)a. \] Since we know the values of $m_1$, $m_2$, $\mu_k$, $\alpha$ and $\beta$, we can calculate all the quantities on the left-hand side and solve for $a$.
Other types of problems
All the examples shown asked you to find the acceleration, but sometimes you might be told the acceleration and asked to solve for some other unknown in the equations. Regardless of what you have to solve for, you should always start with the diagram and the sum-of-the-forces template. Once you have these equations in front of you, you will be able to reason about the problem more easily.
Experiment
Suspend an object of known mass (say a 100g chocolate bar) on the spring taken out from a retractable pen. Use a ruler to measure by how much the spring stretches in the process. What is the spring constant $k$?
Discussion
In previous sections we discussed the kinematics problem of finding the position of an object $x(t)$ given the knowledge of its acceleration function $a(t)$ and the initial conditions $x_i$ and $v_i$. In this section we studied the dynamics problem, which involved drawing force diagrams and calculating the net force on the object. Understanding these topics means that you fully understand Newton's equation $F=ma$ which is perhaps the most important equation in this book.
We can summarize the entire procedure for predicting the position of an object $x(t)$ from first principles in the following equation: \[ \frac{1}{m} \underbrace{ \left( \sum \vec{F} = \vec{F}_{net} \right) }_{\text{dynamics}} = \underbrace{ a(t) \ \overset{v_i+ \int\!dt }{\longrightarrow} \ v(t) \ \overset{x_i+ \int\!dt }{\longrightarrow} \ x(t) }_{\text{kinematics}}. \] The left-hand side calculates the net force, which is the cause of acceleration. The right-hand side indicates how we can calculate the equation of motion $x(t)$ from the knowledge of the acceleration and the initial conditions. This means that if you know the forces acting on any object (rocks, projectiles, cars, stars, planets, etc.) then we can predict its motion, which is kind of cool.
Momentum
During a collision between two objects there will be a sudden spike in the contact force between them, which can be difficult to measure and quantify. It is therefore not possible to use Newton's law $F=ma$ to predict the accelerations that occur during collisions. In order to predict the motion of the objects after the collision we must use a momentum calculation. The law of conservation of momentum states that the total amount of momentum before and after the collision is the same. Thus, if we know the momenta of the objects before the collision, it will be possible to calculate their momenta after the collision and from this figure out their subsequent motion.
To illustrate why the notion of momentum is important, consider the following situation. Say you have a 1[g] piece of paper and a 1000[kg] car moving at the same speed 100[km/h]. Which of the two objects would you rather get hit by? Momentum, denoted $\vec{p}$, is the precise physical concept which measures the “amount of moving stuff”. An object of mass $m$ moving with velocity $\vec{v}$ has momentum $\vec{p}\equiv m\vec{v}$. Momentum plays a key role in collisions, so your gut feeling about the piece of paper and the car is correct. The car weights $1000\times1000=10^{6}$ times more than the piece of paper, so it has $10^6$ times more momentum when moving at the same speed. A collision with the car will “hurt” a million times more than the collision with the piece of paper even though they were moving at the same speed.
In this section we will learn how to use the law of conservation of momentum to predict the outcomes of collisions.
Concepts
- $m$: the mass of the moving object.
- $\vec{v}$: the velocity of the moving object.
- $\vec{p}=m\vec{v}$: the momentum of the moving object.
- $\sum \vec{p}_{in}$: the sum of the momenta of particles before a collision.
- $\sum \vec{p}_{out}$: the sum of the momenta after the collision.
Definition
The momentum of a moving object is equal to the velocity of the moving object multiplied by the object's mass: \[ \vec{p} = m\vec{v} \qquad [\text{kg}\:\text{m}/\text{s}]. \] If the velocity of the object is $\vec{v}=20\hat{\imath}=(20,0)$[m/s] and it has a mass of 100[kg] then its momentum is $\vec{p}=2000\hat{\imath}=(2000,0)$[kg$\:$m/s].
Momentum is a vector quantity, so we will often have to convert momentuma from the length-and-direction form to the components form: \[ \vec{p}= \|\vec{p}\| \angle \theta = (\|\vec{p}\|\cos\theta, \|\vec{p}\|\sin\theta) = (p_x, p_y). \] The component form makes it easy to add and subtract vectors: $\vec{p}_1 + \vec{p}_2 = (p_{1x}+p_{2x},p_{1y}+p_{2y})$. To express the final answer, we will have to convert from the component form back to the length-and-direction form using: \[ \|\vec{p}\| = \sqrt{ p_x^2 + p_y^2 }, \qquad \theta = \tan^{-1}\!\left( \frac{ p_{y} }{ p_{x} } \right). \]
Conservation of momentum
Newton's first law states that in the absence of acceleration ($\vec{a}=0$), an object will maintain a constant velocity. This is kind of obvious if you know Calculus, since $\vec{a}$ is the derivative of $\vec{v}$. For example, if an object is stationary and there are no forces on it to cause it to accelerate, then it will remain stationary. If an object is moving with velocity $\vec{v}$ and there is no acceleration (or deceleration), then it will keep moving with velocity $\vec{v}$ forever. In the absence of acceleration, objects will conserve their velocity: \[ \vec{v}_{in}= \vec{v}_{out}. \] This is equivalent to saying that objects conserve their momentum (just multiply the velocity by the constant mass of the object).
More generally, if you have a situation involving multiple moving objects, you can say that the “overall momentum”, i.e., the sum of the momenta of all the interacting particles stays constant. This reasoning is particularly useful when analyzing collisions since it allows us to connect the sum of the momenta before the collision and after the collision: \[ \sum \vec{p}_{in} = \sum \vec{p}_{out}. \] Whatever momentum comes into a collision must come out. This equation is known as the law of conservation of momentum.
This conservation law is one of the furthest reaching laws of physics you will learn in Mechanics. We learned about the conservation of momentum in a simple context of two colliding particles, but the law applies much more generally: for multiple particles, for fluids, for fields, and even for collisions involving atomic particles described by quantum mechanics. The quantity of motion (momentum) cannot be created or destroyed, it can only be exchanged between systems.
Examples
Example 1
You throw a piece of rolled up carton of mass $0.4$[g] from your balcony on a rainy day. You throw it horizontally with a speed of 10[m/s]. Shortly after it leaves your hand it collides with a rain drop of weight $2$[g] falling straight down at a speed of $30$[m/s]. What will be resulting velocity if the two objects stick together after the collision?
The conservation of momentum equation says that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out}. \] Plugging in the values we get \[ 0.4\times (10,0) \ \ + \ \ 2\times (0,-30) \ \ = \ \ 2.4 \times \vec{v}_{out}, \] or solving for $\vec{v}_{out}$ we find: \[ \vec{v}_{out} = \ \frac{ 0.4(10,0) - 2 (0,30)} {2.4} = (1.666, - 25.0) = 1.666\hat{\imath} - 25.0\hat{\jmath}. \]
Example 2: Hipsters on bikes
Two hipsters on single-speed bicycles are headed towards the same intersection. Say they are both speeding down Parc street at 50[km/h] and the first hipster is crossing the street at a diagonal of 30 degrees when they collide. I mean you saw this coming right? Well the second hipster didn't, because he was busy turning the pedals as fast as he can.
 Let us assume that the combined weight of the straight-going hipster and his bike is 100[kg],
whereas the street-crossing-at-30-degrees hipster has a lighter, more expensive bicycle frame.
We put his weight at 90[kg].
Let us assume that the combined weight of the straight-going hipster and his bike is 100[kg],
whereas the street-crossing-at-30-degrees hipster has a lighter, more expensive bicycle frame.
We put his weight at 90[kg].
(I am going to continue with the story, but I want to point out that we have been given, the following information so far: \[ \begin{align*} \vec{p}_{in,1} &= 90\times50 \angle 30=90(50\cos30,50\sin30), \nl \vec{p}_{in,2} &= 100\times50 \angle 0=(5000,0), \end{align*} \] where the $x$ coordinate points down Park street, and the $y$ coordinate is perpendicular to the street.)
Surprisingly, nobody gets hurt in this collision. They bump shoulder-to-shoulder and the one that was trying to cross the street gets redirected straight down the street, while the one going straight down gets deflected to the side and right onto the bike path. I know what you are thinking: couldn't they get hurt at least a little bit? OK, let's say that the whiplash from their shoulder-to-shoulder collision sends their heads flying towards each other and their glasses get smashed. There you have it.
Suppose the velocity of the first hipster after the collision is 60 [km/h], what is the velocity and the deflected direction of the second hipster? (I have just told you that the outgoing momentum of the first hipster is $\vec{p}_{out,1}=(90\times60,0)$, and asked you to find $\vec{p}_{out,2}$.)
We can solve this problem using the conservation of momentum formula, which tells us that: \[ \vec{p}_{in,1} + \vec{p}_{in,2} = \vec{p}_{out,1} + \vec{p}_{out,2}. \] We know three of the above quantities so we can solve for the one (vector) unknown by isolating it on one side of the equation: \[ \vec{p}_{out,2} = \vec{p}_{in,1} + \vec{p}_{in,2} - \vec{p}_{out,1}, \] \[ \vec{p}_{out,2} = 90(50\cos30,50\sin30)\ +\ (5000,0)\ - \ (90\times60,0). \] The $x$ component of the momentum $\vec{p}_{out,2}$ is: \[ p_{out,2,x} = 90\times50\cos30 + 5000 - 90\times 60 = 3497.11, \] and the $y$ component is $p_{out,2,y} = 90\times 50\sin30 = 2250$.
The magnitude of the momentum of hipster 2 is given by: \[ \|\vec{p}_{out,2}\| = \sqrt{ p_{out,2,x}^2 + p_{out,2,y}^2 } = 4158.39, \quad \textrm{[kgkm/h]}. \] Note the units we use for the momentum is not the standard choice [kgm/s]. That is fine. So long as you keep in mind which units you are using, you don't have to always convert to SI units.
The final velocity of hipster two is $v_{out,2} = 4158.39/100= 41.58$[km/h]. The deflection angle is obtained by \[ \phi_{def} = \tan^{-1}\!\!\left( \frac{ p_{out,2,y} }{ p_{out,2,x} } \right)= 32.76^\circ. \]
Discussion
We defined the concept of momentum in terms of the velocity of the object, but in fact, momentum is a more fundamental concept than velocity. If you go on to take more advanced physics classes, you will learn that the natural variables to describe the state of a particle are their positions and momenta $(\vec{x}, \vec{p})$. You will also learn that the real form of Newton's second law is written in terms of the momentum: \[ \vec{F} = \frac{d \vec{p} }{dt} \quad \text{for } m \text{ constant } \Rightarrow \quad \vec{F}=\frac{d (m\vec{v}) }{dt}=m\frac{d \vec{v} }{dt} =m\vec{a}. \] In most physics problems the mass of objects will stay constant so using $\vec{F}=m\vec{a}$ is perfectly fine.
The law of conservation of momentum follows from Newton's third law: for each force $\vec{F}_{12}$ exerted by Object 1 on Object 2, there exists a counter force $\vec{F}_{21}$ of equal magnitude and opposite direction, which is the force of Object 2 pushing back on Object 1. Earlier I said that it is difficult to quantify the magnitude of the exact forces $\vec{F}_{12}$ and $\vec{F}_{21}$ that occur during a collision. Indeed, the amount of force suddenly shoots up as the two objects collide and then suddenly drops. Complicated as these forces may be, we know that during the entire collision they obey Newton's third law. Assuming there are no other forces acting on the objects we have: \[ \vec{F}_{12} = -\vec{F}_{21} \quad \text{using the above} \Rightarrow \quad \frac{d \vec{p}_1 }{dt} = -\frac{d \vec{p}_2 }{dt}. \] If now move both terms to the left-hand side we obtain the equation: \[ \frac{d \vec{p}_1 }{dt} + \frac{d \vec{p}_2 }{dt} = \frac{d}{dt}\left( \vec{p}_1 + \vec{p}_2 \right) = 0, \] which implies that quantity $\vec{p}_1 + \vec{p}_2$ is constant over time.
In this section we saw how to use a momentum calculation to predict the motion of the particles after a collision. In the next section, we will learn about the concept of energy which is another useful concept for understanding and predicting the motion of objects.
Links
[ Animations of simple collisions between objects. ]
http://en.wikipedia.org/wiki/Conservation_of_linear_momentum
Energy
Instead of thinking about velocities $v(t)$ and motion trajectories $x(t)$, we can solve physics problems using energy calculations. In this section, we will define precisely the different kinds of energies that exist and then learn the rules of converting one energy into another. The key idea in this section is the principle of total energy conservation, which tells us that, in any physical process, the sum of the initial energies is equal to the sum of the final energies.
Example
Say you drop a ball from a height $h$[m] and you want to predict its speed right before it hits the ground. Using the kinematics approach, you would go for the general equation of motion: \[ v_f^2 = v_i^2 + 2a(y_f-y_i), \] and substitute $y_i=h$, $y_f=0$, $v_i=0$ and $a=-g$ to obtain the answer $v_f = \sqrt{2gh}$ for the final velocity at impact.
Alternately, you could use an energy calculation. Initially the ball starts from a height $h$, which means it has $U_i=mgh$[J] of potential energy. As the ball falls, the potential energy is converted into kinetic energy. Right before the ball hits the ground, it will have a final kinetic energy equal to the initial potential enegy: $K_f=U_i$ [J]. Since the formula for kinetic energy is $K=\frac{1}{2}mv^2$, we have $\frac{1}{2}mv_f^2 = mgh$. After cancelling the mass on both sides of the equation and solving for $v_f$ we obtain $v_f=\sqrt{2gh}$.
Both methods of solving the example problem come to the same conclusion, but the energy reasoning is arguably more intuitive than plugging values into a formula. In science, it is really important to know different ways for arriving at some answer. Knowing about these alternate routes will allow you to check your answers and to understand concepts better.
Concepts
Energy is measured in Joules [J] and it arises in several different contexts:
- $K =$ kinetic energy.
This is the type of energy that objects have by virtue of their motion.
- $W$ = work.
This is the amount of energy that an external
force adds or subtracts from a system. Positive work corresponds to energy being added to the system while negative work corresponds to energy being withdrawn from the system. * $U_g=$ **gravitational potential energy**. This is the energy that an object has by virtue of its position above the ground. We say this energy is //potential// because it is a form of //stored work//. The potential energy corresponds to the amount of work that the force of gravity will add to an object when you let the object fall to the ground. * $U_s= $ **spring potential energy.** This is the energy stored in a spring when it is displaced from its relaxed position. * There are many kinds other kinds of energy: electrical energy, magnetic energy, sound energy, thermal energy, etc. In this section, however, we limit out focus only on the //mechanical// energy concepts described above.
Formulas
Kinetic energy
An object of mass $m$ moving at velocity $\vec{v}$ has a kinetic energy of \[ K=\frac{1}{2}m\|\vec{v}\|^2 \qquad \text{[J]}. \] Note that the kinetic energy only depends on the speed $\|\vec{v}\|$ of the object and not the direction of motion.
Work
If an external force $\vec{F}$ acts on a object as it moves through a distance $\vec{d}$, the work done by this force is \[ W=\vec{F}\cdot \vec{d} = \|\vec{F}\| \|\vec{d}\|\cos \theta \qquad \text{[J]}, \] where the second equality follows from the geometrical interpretation of the dot product: $\vec{u}\cdot \vec{v} = \|\vec{u}\| \|\vec{v}\|\cos \theta$, with $\theta$ is the angle between $\vec{u}$ and $\vec{v}$.
If the force $\vec{F}$ acts in the same direction as the displacement $\vec{d}$, then it will do positive work ($\cos(180^\circ)=+1$)—the force will be adding energy to the system. If the force acts in the direction opposite to the displacement, then the work done will be negative ($\cos(180^\circ)=-1$), which means that energy is being withdrawn from the system.
Gravitational potential energy
An object raised to a height $h$ above the ground has a gravitational potential energy given by: \[ U_g(h) = mgh \qquad \text{[J]}, \] where $m$ is the mass of the object and $g=9.81$[m/s$^2$] is the gravitational acceleration on the surface of Earth.
Spring potential energy
The potential energy stored in a spring when it is displaced by $\vec{x}$[m] from its relaxed position is given by \[ U_{s} = \frac{1}{2}k\|\vec{x}\|^2 \qquad \text{[J]}, \] where $k$[N/m] is the spring constant.
Note that it doesn't matter whether the spring is stretched or compressed by a certain length: only the magnitude of the displacement matters $\|\vec{x}\|$.
Conservation of energy
Consider a system which starts from an initial state (i), undergoes some motion and arrives at a final state (f). The law of conservation of energy states that energy cannot be created or destroyed in any physical process. This means that the initial energy of the system plus the work that was input into the system must equal the final energy of the system plus any work that the was output: \[ \sum E_{i} \ \ + W_{in} \ \ \ = \ \ \ \sum E_{f} \ \ + W_{out}. \] The expression $\sum E_{(a)}$ corresponds to the sum of the different types of energy the system has in state (a). If we write down the equation in full we have: \[ K_i + U_{gi} + U_{si} \ \ \ + W_{in} \ \ \ = \ \ \ K_f + U_{gf} + U_{sf} \ \ \ + W_{out}. \] Usually, some of the terms in the above expression can be dropped. For example, we do not need to consider the spring potential energy $U_s$ in physics problems that do not involve springs.
Explanations
Work and energy are measured in Joules [J]. Joules can be expressed in terms of the fundamental units as follows: \[ [\text{J}] = [\text{N}\:\text{m}] = [\text{kg}\:\text{m}^2/\text{s}^{2}]. \] The first equality follows from the definition of work as force times displacement. The second equality comes from definition of the Newton [N]$=[\text{kg}\:\text{m}/\text{s}^2]$ via $F=ma$.
Kinetic energy
A moving object has energy $K=\frac{1}{2}m\|\vec{v}\|^2$[J], which we call kinetic energy from the Greek word for motion kinema.
Note that velocity $\vec{v}$ and speed $\|\vec{v}\|$ are not the same as energy. Suppose you have two objects of the same mass and one is moving twice faster than the other. The faster object will have twice the velocity, but four times more kinetic energy.
Work
When hiring someone to help you move, you have to pay them for the work they do. Work is the product of how much force is necessary for the move and the distance of the move. The more force, the more work there will be for a fixed displacement. The more displacement (think moving to the South Shore versus moving next door) the more money the movers will ask for.
The amount of work done by a force $\vec{F}$ on an object which moves along some path $p$ is given by: \[ W = \int_p \vec{F}(x) \cdot d\vec{x}, \] where we account for the fact that the magnitude and direction of the force might change throughout the motion.
If the force is constant and the displacement path is a straight line, the formula for work simplifies to: \[ W = \int_0^d \vec{F}\cdot d\vec{x} = \vec{F}\cdot\int_0^d d\vec{x} = \vec{F}\cdot \vec{d} = \|\vec{F}\|\|\vec{d}\|\cos\theta. \] Note the use of the dot product to obtain only the part of $\vec{F}$ that is pushing in the direction of the displacement $\vec{d}$. A force which acts perpendicular to the displacement produces no work, since it neither speeds up or slows down the motion.
Potential energy is stored work
Some kinds of work are just a waste of your time, like working in a bank for example. You work and you get your paycheque, but nothing remains with you at the end of the day. Other kinds of work leave you with some resource at the end of the work day. Maybe you learn something, or you network with a lot of good people.
In physics, we make a similar distinction. Some types of work, like work against friction, are called dissipative since they just waste energy. Other kinds of work are called conservative since the work you do is not lost: it is converted into potential energy.
The gravitational force and the spring force are conservative forces. Any work you do while lifting an object up into the air against the force of gravity is not lost but stored in the height of the object. You can get all the work/energy back if you let go of the object. The energy will come back in the form of kinetic energy since the object will pick up speed during the fall.
The negative of the work done against a conservative force is called potential energy. For any conservative force $\vec{F}_?$, we can define the associated potential energy $U_?$ through the formula: \[ U_?(d) = -W_{done} = - \int_0^d \vec{F}_? \cdot d\vec{x}. \] We will discuss two specific examples of this general formula below: the gravitational and spring potential energies. Being high in the air means you have a lot of potential to fall, and compressing a spring by a certain distance means it has the potential to spring back to its normal position. Let us look now at the exact formulas for these two cases.
Gravitational potential energy
The force of gravity is given by: \[ \vec{F}_g = -mg \hat{\jmath}. \] The direction of the gravitational force is downwards, towards the centre of the Earth.
The gravitational potential energy of lifting an object from a height of $y=0$ to a height of $y=h$ is given by: \[ \begin{align*} U_g(h) &\equiv - W_{done} \nl &= - \!\int_0^h \! \vec{F}_g \cdot d\vec{y} = - \!\int_0^h \!\!(-mg \hat{\jmath})\cdot \hat{\jmath} \; dy = mg \!\int_0^h \!\!\! 1\:dy = mg y\big\vert_{y=0}^{y=h} = mgh. \end{align*} \]
Spring energy
The force of a spring when stretched a distance $\vec{x}$[m] form its natural position is given by: \[ \vec{F}_s(\vec{x}) = - k\vec{x}. \]
The potential energy stored in a spring as it is compressed from $y=0$ to $y=x$[m] is given by: \[ \begin{align*} U_s(x) &= -W_{done} \nl &=-\!\int_0^x \!\vec{F}_{s}(y) \cdot d\vec{y} = \int_0^x \!\! ky dy = k\int_0^x \!\! y dy = k\frac{1}{2}y^2\big\vert_{y=0}^{y=x} = \frac{1}{2}kx^2. \end{align*} \]
Conservation of energy
Energy cannot be created or destroyed. It can only be transforms from one form to another. If there are no external forces acting on the system, then we have conservation of energy: \[ \sum E_i \ \ = \ \ \sum E_f. \]
If there are external forces like friction that do work on the system, we must take their energy contributions into account as well: \[ \sum E_i \ +\ W_{in} = \sum E_f, \quad \text{or} \quad \sum E_i = \sum E_f \ +\ W_{out}. \]
This is one of the most important equations you will find in this book, because it will allow you to solve very complicated problems simply by accounting for all the different kinds of energy involved in the problem.
Examples
Banker dropped
An investment banker is dropped (from rest) from a 100[m] tall building. What is his speed when he hits the ground?
We start from: \[ \begin{align*} \sum E_i \ \ &= \ \ \sum E_f, \nl K_i + U_i \ \ & = \ \ K_f + U_f, \end{align*} \] and plugging in the numbers we get: \[ 0 + m \times9.81 \times100 = \frac{1}{2}mv^2 + 0. \] After cancelling the mass $m$ from both sides of the equation we are left with \[ 9.81\times 100 = \frac{1}{2}v_f^2. \] Solving for $v_f$ in the above equation, we find that the banker will be going at $v_f =\sqrt{ 2\times 9.81\times 100}=44.2945$[m/s] when he hits the ground. This is like $160$[km/h]. Ouch! That will definitely hurt.
Bullet speedometer
 An incoming bullet at speed $v$ hits a mass $M$ suspended on two strings.
Use conservation of momentum and conservation of energy principles to
find the speed $v$ of the bullet if the block rises to a height $h$ after
it is hit by the bullet.
An incoming bullet at speed $v$ hits a mass $M$ suspended on two strings.
Use conservation of momentum and conservation of energy principles to
find the speed $v$ of the bullet if the block rises to a height $h$ after
it is hit by the bullet.
First we use the conservation of momentum principle to find the (horizontal) speed of the block and mass right after the bullet hits: \[ \vec{p}_{in,m} + \vec{p}_{in,M} = \vec{p}_{out}, \] \[ m v + 0 = (m+M) v_{out}, \] so the velocity of the block with the bullet embedded in it is $v_{out}= \frac{mv}{M+m}$ right after collision.
Next we use the conservation of energy principle to relate the initial kinetic energy of the block-plus-bullet and the height $h$ by which it rises: \[ K_i + U_i = K_f + U_f, \] \[ \frac{1}{2}(M+m)v_{out}^2 + 0 = 0 + (m+M)gh. \] Isolating $v_{out}$ in the above equation and setting it equal to the $v_{out}$ we got from the momentum calculation we get: \[ v_{out} = \frac{mv}{M+m} = \sqrt{2gh} = v_{out}. \] We can use this equation to find the speed of the incoming bullet: \[ v = \frac{M+m}{m}\sqrt{2gh}. \]
Incline and spring
A block of mass $m$ is released from rest at point (A) on the top of an incline at a coordinate $y=y_i$. It slides down the frictionless incline to the point (B) $y=0$. The coordinate $y=0$ corresponds to the relaxed length of a spring of spring constant $k$. The block then compresses the spring all the way to point (C ), corresponding to $y=y_f$, when the block comes to rest again. The angle of the slope is $\theta$.
What is the speed of the block at $y=0$? How far does the spring get compressed $y_f$? Bonus points if you can express your answer for $y_f$ in terms of $\Delta h$, the difference in height between $y_i$ and $y_f$.
We have essentially two problems: the motion from (A) to (B) in which the gravitational potential energy of the block is converted into kinetic energy and the motion from (B) to (C ) in which the all the energy of the block gets converted into spring potential energy.
In both cases, there is no friction so we can use the conservation of energy formula: \[ \sum E_i \ \ = \ \ \sum E_f. \]
For the motion from (A) to (B) we have: \[ K_i + U_i = K_f + U_f. \] The block starts from rest so $K_i=0$. The difference in potential energy is equal to $mgh$ and in this case the block is $|y_i|\sin\theta$ [m] higher at (A) than it is at (B), so we can write: \[ 0 + mg|y_i|\sin\theta = \frac{1}{2}mv_B^2 + 0. \] The above formula uses the point (B) at $y=0$ as reference for the gravitational potential energy. The potential at point (A) is $U_i=mgh=mg|y_i-0|\sin\theta$ relative to point (B) since the point (A) is $h=|y_i-0|\sin\theta$ metres higher than the point (B).
Solving for $v_B$ in this equation gives us the answer to the first part of the question: \[ v_{B} = \sqrt{ 2 g|y_i|\sin\theta }. \]
Now for the second part of the motion. The law of conservation of energy dictates that: \[ K_i + U_{gi} + U_{si} = K_f + U_{gf} + U_{sf}, \] where now $i$ refers to the moment (B) and $f$ refers to the moment (C ). Initially the spring is uncompressed so $U_{si}=0$, and by the end of the motion the spring is compressed by a total of $\Delta y=|y_f-0|$[m], so its spring potential energy is $U_{sf}=\frac{1}{2}k|y_f|^2$. We choose the height of (C ) as the reference potential energy and thus $U_{gf}=0$. Since the difference in gravitational potential energy is $U_{gi} - U_{gf}=mgh=|y_f-0|\sin\theta$, we can fill-in the entire energy equation: \[ \frac{1}{2}m v_B^2 + mg|y_f|\sin\theta + 0 = 0 + 0 + \frac{1}{2}k|y_f|^2. \] Since $k$ and $m$ are given and we know $v_B$ from the first part of the question, we can solve for $|y_f|$ (a quadratic equation).
To obtain the answer $|y_f|$ in terms of $\Delta h$ we can use $\sum E_i = \sum E_f$ again, but this time $i$ will refer moment (A) and $f$ refers to the moment (C ). The energy equation becomes $mg\Delta h = \frac{1}{2}k|y_f|$ from which we obtain $|y_f|=\frac{ 2 mg\Delta h}{k}$.
Energy lost to friction
You have a block of mass 50[kg] on an incline. The force of friction between the block and the incline is 30N. The block slides for 200[m] down the incline. The incline is at a slope $\theta=30^\circ$ so the total vertical displacement of the block is $200\sin30=100$[m]. What is its speed as it reaches the bottom of the incline?
This is a problem in which initial energies are converted into final energies and some lost work: \[ \sum E_i = \sum E_f + W_{lost}. \] The term $W_{lost}$ represents the energy lost due to the friction.
Another (better) way of describing the situation is that the block had a negative amount of word done on it \[ \sum E_i + \underbrace{W_{done}}_{ \textrm{negative} } = \sum E_f. \] The quantity $W_{done}$ is negative because during the entire motion the friction force on the object was acting in the opposite direction to the motion: \[ W_{done} = \vec{F}\cdot \vec{d} = \|\vec{F}_f\|\|\vec{d}\|\cos(180^\circ) = - F_f\|\vec{d}\|, \] where $\vec{d}$ is the $200$[m] of sliding distance during which the friction acts. Since we are told that $F_f = 30$[N], we can calculate $W_{done} = W_{friction} = -30[\text{N}]\times 200[\text{m}] = -6000$[J].
We can now substitute this value into the conservation of energy equation: \[ \begin{align*} K_i + U_i + W_{done} &= K_f + U_f, \nl 0 + mgh + (-F_f|d|) &= \frac{1}{2}mv_f^2 + 0, \end{align*} \] where we have used the formula $mgh= U_i- U_f$ for the difference in gravitational potential energy. Substituting all the values we know we get \[ 0 + 50 \times 9.81 \times 100 - 6000 = \frac{1}{2}(50)v_f^2 + 0, \] which can be solved for $v_f$.
Discussion
In this section we saw that describing physical situation in terms of the energies involved is a useful way of thinking. The law of conservation of energy allows us to do simple “energy accounting” and calculate the values of unknown quantities.
Uniform circular motion
In this section we will learn about the circular motion of objects. Circular motion is different from linear motion and we will have to develop new techniques and concepts which are better suited for the description of circular motion.
Imagine a rock of mass $m$ is swinging around in a horizontal circle attached at the end of a rope. The rock is flying through the air at a constant (uniform) speed of $v_t$[m/s] along a circular path of radius $R$[m] at a height $h$[m] above the ground. What is the tension $T$ in the rope?
Consider a coordinate system which has the $x$ and $y$ axis placed on the ground level at the centre of the circle of motion are the $z$ axis measuring the height above the ground. In that coordinate system, the trajectory of the rock is described by the equation \[ \vec{r}(t) =(x(t),y(t),z(t)) = \left(R\cos\!\left(\frac{v_t}{R}\:t\right),\ R\sin\!\left(\frac{v_t}{R}\:t\right), \ h\right). \] You will agree with me that this expression looks somewhat complicated. This complexity stems from the fact that the $(x,y,z)$ coordinate system is not very well adapted for the description of circular paths.
A new coordinate system
Instead of the usual coordinate system $\hat{x},\hat{y},\hat{z}$ which is static, we can use a new coordinate system $\hat{t},\hat{r},\hat{z}$ that is “attached” to the rotating object.
Three important directions can be identified:
- $\hat{t}$: the tangential direction in the instantaneous direction of motion of the object.
The name comes from the Greek word for “touch” (imagine a straight line “touching” the circle).
- $\hat{r}$: the radial direction always points towards the centre of the circle of rotation.
- $\hat{z}$: the usual $\hat{z}$ direction, which is perpendicular to the plane of rotation.
From the point of view of a static observer, the tangential and radial directions constantly change their orientation as the object rotates around in a circle. From the point of view of the rotating object, the tangential and radial directions are fixed. The tangential direction is always “forward” and the radial direction is always to the side.
We can use the new coordinate system to describe the position, velocity and acceleration of the object undergoing circular motion:
- $\vec{v}=(v_r,v_t)_{\hat{r}\hat{t}}$: the velocity of object expressed with respect to
the $\hat{r}\hat{t}$ coordinates.
- $\vec{a}=(a_r,a_t)_{\hat{r}\hat{t}}$: The acceleration of the object in the $\hat{r}\hat{t}$ coordinates.
The most important parameters of motion are the tangential velocity $v_t$, the radial acceleration $a_r$ and the radius of the circle of motion $R$. We have $v_r=0$ since the motion is entirely in the $\hat{t}$ direction, and $a_t=0$ because we assumed that the tangential velocity $v_t$ remains constant (uniform circular motion).
In the next section we will learn how to calculate the radial acceleration $a_r$.
Radial acceleration
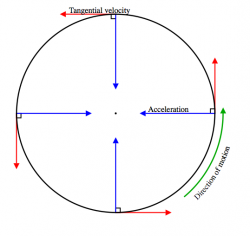 The defining feature of circular motion is the presence of an acceleration
that acts perpendicularly to direction of motion.
At each instant, the object wants to continue moving along the tangential direction,
but the radial acceleration causes the velocity to change direction.
The result of this constant inward acceleration is that the object will
follow a circular path.
The defining feature of circular motion is the presence of an acceleration
that acts perpendicularly to direction of motion.
At each instant, the object wants to continue moving along the tangential direction,
but the radial acceleration causes the velocity to change direction.
The result of this constant inward acceleration is that the object will
follow a circular path.
The radial acceleration $a_r$ of an object moving in a circle of radius $R$ with a tangential velocity $v_t$ is given by: \[ a_r = \frac{v^2_t}{ R }. \] This is an important equation which relates the three key parameters of circular motion.
According to Newton's second law $\vec{F}=m\vec{a}$, the radial acceleration of the object must be caused by a radial force. We can calculate the magnitude of this radial force $F_r$ as follows: \[ F_{r} = ma_r = m \frac{v^2_t}{ R }. \] The above formula allows us to connect the observable aspects of the circular motion $v_t$ and $R$ with its cause: the force $F_r$ which always acts towards the centre of rotation.
To put it differently, we can say that circular motion requires a radial force. From now on, every time you see an object undergoing circular motion, you should try to visualize the radial force which is causing the circular motion.
In the rock-on-a-rope example described in the beginning of this section, the circular motion was caused by the tension of the rope which always acts in the radial direction (towards the centre of rotation). We are now in a position to calculate the value of the tension $T$ in the rope using the equation: \[ F_{r} = T = ma_r, \qquad \Rightarrow \qquad T=m \frac{v^2_t}{ R }. \]
Example
During a student protest, a young activist called David is stationed on the rooftop of a building of height $12$[m]. A mob of blood-thirsty neoconservatives is slowly approaching his position determined to lynch him because of his leftist views. David has put together a make-shift weapon by attaching a 0.3[kg] rock to the end of a shoelace of length $1.5$[m]. The maximum tension that the shoelace can support is 500[N]. What is the maximum tangential velocity $\max\{v_t\}$ that the shoelace can support? What is the maximum range for this projectile when it is launched from the roof?
The first part of the question is answered easily using the $T=m \frac{v^2_t}{ R }$ formula: $\max\{v_t\} = \sqrt{ \frac{R T}{m} }= \sqrt{ \frac{1.5\times 500}{0.3} }=50$[m/s]. To answer the second question, we must solve for the distance travelled by a projectile with initial velocity $\vec{v}_i=(v_{ix},v_{iy})=(50,0)$[m/s] launched from $\vec{r}_i=(x_i,y_i)=(0,12)$[m]. First we solve for the total time of flight $t_f=\sqrt{2\times 12/9.81}=1.56$[s]. Then we find the range by multiplying this time by the horizontal speed $x(t_f)=0+v_{ix} t_f = 50\times 1.56=78.20$[m].
After carrying out these calculations on a piece of paper, David starts to spin-up the rock and waits for the neocons to come into range.
Circular motion parameters
We now introduce some further terminology used to describe circular motion:
- $C=2\pi R$[m]: The circumference of the circle of motion.
- $T$: The period of the motion is how long it takes for the object to complete one full circle.
The period is measured in seconds [s].
- $f=\frac{1}{T}$: The frequency of rotation. How many times per second does the object pass by
some reference point on the circle. Frequency is measured in Hertz [Hz]=[1/s].
We sometimes describe the frequency of rotation in //revolutions per minute// (RPM).
* $\omega\equiv\frac{v_t}{R}=2\pi f$: The //angular velocity// describes how fast the
object is rotating. Angular velocity is measured in [rad/s].
Recall that a circle of radius $R$ has circumference $C = 2 \pi R$. The period $T$ is defined as how long it will take the object to complete one full turn around the circle: \[ T = \frac{\text{distance}}{\text{speed}} = \frac{C}{v_t} = \frac{2\pi R}{v_t}, \] where $C=2\pi R$ is total distance that must be travelled to compete one turn and $v_t$ is the velocity of the object along the curve. The object will complete one full turn every $T$ seconds.
Another way of describing the motion is to talk about the frequency: \[ f=\frac{1}{T} = \text{[Hz]}. \] The frequency tells you how many turns the object completes in one second. If the object competes one turn in $T=0.2$[s], then the motion has frequency $f=5$[Hz], or $f=60\times 5 = 300$[RPM].
The most natural parameter for describing rotation is in terms of the angular velocity $\omega$[rad/s]. We know that one full turn corresponds to an angle of rotation of $2\pi$[rad], so the angular velocity is obtained by dividing $2\pi$ by the time it takes to complete one turn: \[ \omega = \frac{2\pi}{T} = 2\pi f = \frac{v_t}{R}. \]
The angular velocity $\omega$ is very useful because it describes the speed of the circular motion without any reference to the radius. If we know that the angular velocity of an object is $\omega$, we can obtain the tangential velocity by multiplying times the radius: $v_t=R\omega$[m/s].
Let us now look at some examples in which we are asked to compute some angular velocities.
Bicycle odometer
Imagine that you place a small speed detector gadget on one of the spokes of the front wheel of your bicycle. Your bike's wheels have a radius $R=14$[in] and the gadget is attached at a distance of $\frac{3}{4}R$[m] from the centre of the wheel. Find the angular velocity $\omega$, period $T$, and frequency $f$ of rotation for the wheel when the speed of the bicycle relative to the ground is $40$[km/h]. What is the tangential velocity $v_t$ of the detector gadget?
The velocity of the bicycle relative to the ground $v_{bike}=40$[km/h] is equal to the tangential velocity of the rim of the wheel: \[ v_{bike} = v_{rim} = 40 [\text{km/h}] \times \frac{ 1000 [\text{m}] }{ 1 [\text{km}]} \times \frac{ 1 [\text{h}] }{ 3600 [\text{s}]} = 11.11 [\text{m/s}]. \] We can find the angular velocity using $\omega = \frac{v_{rim}}{R}$ and the radius of the wheel $R=14[\text{in}]=0.355$[m]. We obtain $\omega = \frac{11.11}{0.355}= 31.24[\text{rad/s}]$. From this we can easily calculate $T=\frac{2\pi}{\omega}=0.20$[s] and $f=\frac{1}{0.20}=5$[Hz]. Finally, to compute the tangential velocity of the gadget we multiply the angular velocity $\omega$ by its radius of rotation to obtain $v_{det}= \omega \times \frac{3}{4}R = 8.333$[m/s].
Rotation of the Earth
It takes exactly 23 hours, 56 minutes and 4.09 seconds for the Earth to compete one full turn ($2\pi$ radians) around its axis of rotation. What is its angular velocity? What is the tangential speed at a latitude of $45^\circ$ (Montreal)?
We can find $\omega$ by carrying out a simple conversion: \[ \frac{2\pi \text{ [rad]}}{ 1 \text{ [day]} } \cdot \frac{1 \text{ [day]}}{ 23.93447 \text{ [h]} } \cdot \frac{1 \text{ [h]}}{ 3600 \text{ [s]} } = 7.2921\times 10^{-5} \text{ [rad/s]}. \]
The radius of the trajectory traced out by someone at a latitude of $45^\circ$ (Montreal) is given by $r=R\cos(45^\circ)=4.5025\times 10^6$[m], where $R=6.3675×10^6$[m] is the radius of the Earth. Thus, though it may seem that you are not moving right now, in reality you are hurtling through space at a speed of \[ v_t = r \omega = 4.5025\times 10^6 \times 7.2921\times 10^{-5} = 464.32 \text{ [m/s]}. \] Which is $1671.56$[km/h]. Just try to imagine that for a second. You can try to use this fact if you get stopped by the cops one day for a speeding infraction: “Yes officer, I was doing 130[km/h], but this is really a negligible speed relative to the 1671[km/h] that the Earth is doing around the sun.”
Three dimensions
For some problems involving circular motion, it will be necessary to consider the $z$ direction in the force diagram. The best approach in this case is to draw the force diagram as a cross section, which is perpendicular to the tangential direction. The diagram will show the $\hat{r}$ and $\hat{z}$ axes.
Using the force diagram, you should be able to find all the forces in the radial and vertical directions and solve for accelerations $a_r$, $a_z$. Remember that you can always use the relation $a_r=\frac{v_t^2}{R}$ which connects the value of $a_r$ with the tangential velocity $v_t$ and the radius of rotation $R$.
Example
Japanese people of the future want to design a giant racetrack for retired superconducting speed trains. The shape of the race track is a big circle with radius $R=3$[km]. Because the trains are magnetically levitated, there is no friction between the track and the train $\mu_s=0, \mu_k=0$. What is the bank angle required for the race track so that trains moving at a speed of exactly $400$[km/h] will stay on the track without moving laterally?
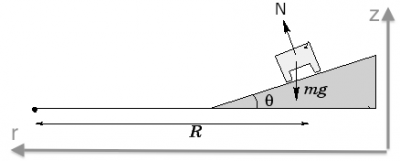 We begin by drawing a force diagram which shows a cross-cut of the
train in the $\hat{r}$ and $\hat{z}$ directions.
The bank angle of the racetrack is $\theta$. This is the unknown we are looking for.
Because of the frictionless-ness of levitated superconducting suspension
there cannot be any force of friction $F_f$ so the only forces on the
train will be it weight $\vec{W}$ and the normal force $\vec{N}$.
We begin by drawing a force diagram which shows a cross-cut of the
train in the $\hat{r}$ and $\hat{z}$ directions.
The bank angle of the racetrack is $\theta$. This is the unknown we are looking for.
Because of the frictionless-ness of levitated superconducting suspension
there cannot be any force of friction $F_f$ so the only forces on the
train will be it weight $\vec{W}$ and the normal force $\vec{N}$.
The next step is to write down the force equations for the two directions: \[ \begin{align*} \sum F_r &= N\sin\theta = m a_r = m \frac{v_t^2}{R} \quad \Rightarrow \quad N\sin\theta = m \frac{v_t^2}{R}, \nl \sum F_z &= N\cos\theta - mg = 0 \ \ \quad \quad \Rightarrow \quad N\cos\theta = mg. \end{align*} \] Note how the normal force $\vec{N}$ is split into two parts: the vertical component counter balances the weight of the train, while the component in the $\hat{r}$ direction is the force that is responsible for causing the rotational motion of the train around the track.
We want to solve for $\theta$ in the above equations. A commonly used trick for solving equations containing multiple trigonometric functions is to divide one equation by the other. We obtain: \[ \frac{ N \sin\theta }{ N\cos\theta } =\frac{ m \frac{v_t^2}{R} }{ mg} \quad \Rightarrow \quad \tan\theta = \frac{ v_t^2 }{ Rg }. \] The final answer is $\theta = \tan^{-1}\!\!\left(\frac{v_t^2}{gR} \right) = \tan^{-1}\!\!\left(\frac{(400\times\frac{1000}{3600})^2}{9.81 \times 3000} \right) = 22.76^\circ$. If the angle were any steeper, the trains would fall towards the centre. If the bank angle were any shallower, the trains would fly off to the side. The angle $22.76^\circ$ is just right.
Discussion
Radial acceleration
In the kinematics section we studied problems involving linear acceleration: in which an acceleration $a$ was acting in the same direction as the velocity and was thus causing a change the magnitude of the velocity $v$.
Circular motion deals with a different situation in which the speed $\|\vec{v}\|$ of the object remains constant but the velocity $\vec{v}$ changes direction. At each point along the circle, the velocity of the object points along the tangential direction and during each instant the radial acceleration pulls the object inwards and causes it to rotate.
Another term for radial acceleration is centripetal acceleration, which literally means “tending towards the centre”.
Centrifugal force
When a car makes a left turn, the passenger riding shotgun will feel pushed towards the right: into the passenger door. Some people erroneously attribute this effect to a centrifugal force, which acts away from the centre of rotation. During a sharp turn, these people feel as though they are being flung out of the car and therefore they conclude that there must be some force which is responsible for this.
The reason why we feel as though we are being thrown out of the car is due to Newton's first law which says that, in the absence of external forces, an object will continue moving in a straight line. Since your initial motion is in the $\hat{t}$ direction, your body will naturally continue moving in that direction because of Newton's first law. The force of the car door pushes you inwards and keeps you in the circular trajectory. If it weren't for the door, you would fly straight on.
Radial forces do no work
An interesting property of radial forces is that they do zero work. Recall that the work done by a force $\vec{F}$ during a displacement $\vec{d}$ is computed using the dot product $W=\vec{F}\cdot \vec{d}$. For circular motion, the displacement is always in the $\hat{t}$ direction, whereas the radial force is in the $\hat{r}$ direction so the dot product of the two is zero.
This is why it is possible for the speed of the object undergoing circular motion to remain constant despite the fact that it is being accelerated. The effects of the radial acceleration do not increase the speed: they only act to change the direction of the velocity.
Exercises
Staying in touch
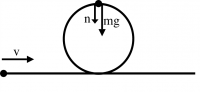 A vertical loop of radius 5[m] is placed on a racetrack.
What is the minimum speed $v$ for a motorcyclist to come into
the loop and make it around? The motorcyclist will “lose contact” with the top of the ramp if the magnitude of the normal force becomes zero.
A vertical loop of radius 5[m] is placed on a racetrack.
What is the minimum speed $v$ for a motorcyclist to come into
the loop and make it around? The motorcyclist will “lose contact” with the top of the ramp if the magnitude of the normal force becomes zero.
Solution. Find $v_{top}$ when $\vec{N}=0$ and then use conservation of energy to find $v$ in terms of $v_{top}$. Ans: $v=\sqrt{5g+20g}=5\sqrt{g}$.
Links
[ Banked curve exercise ]
http://www.chaostoy.com/cd/html/banked_e.htm
Angular motion
We will now study the physics of objects in rotation. A simple example of this kind of motion is a rotating disk. Other examples include rotating bicycle wheels, spinning footballs and spinning figure skaters.
As you will see shortly, the basic concepts used to describe angular motion are directly analogous to the concepts for linear motion: position, velocity, acceleration, force, momentum and energy.
Review of linear motion
It is instructive to begin our discussion with a brief review of the concepts and formulas used to describe the linear motion of objects.
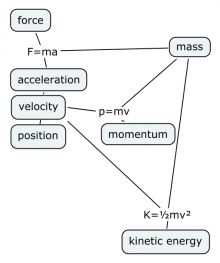 The linear motion of an object is described by its position $x(t)$,
velocity $v(t)$ and acceleration $a(t)$ as functions of time.
The position function tells you where the object is,
the velocity tells you how fast it is moving and
the acceleration measures the change in the velocity of the object.
The linear motion of an object is described by its position $x(t)$,
velocity $v(t)$ and acceleration $a(t)$ as functions of time.
The position function tells you where the object is,
the velocity tells you how fast it is moving and
the acceleration measures the change in the velocity of the object.
The motion of objects is governed by Newton's first and second laws. In the absence of external forces, objects will maintain a uniform velocity (UVM) which corresponds to the equations of motion: $x(t)=x_i+v_it$, $v(t)=v_i$. If there is a net force $\vec{F}$ acting on the object, the force will cause the object to accelerate and the magnitude of the acceleration is obtained using the formula $F=ma$. A constant force acting on an object will produce a constant acceleration (UAM), which corresponds to the equations of motion: $x(t)=x_i+v_it+\frac{1}{2}at^2$, $v(t)=v_i + at$.
We also learned how to quantify the momentum $\vec{p}=m\vec{v}$ and the kinetic energy $K=\frac{1}{2}mv^2$ of moving objects. The momentum vector is the natural measure of the “quantity of motion,” which plays a key role in collisions. The kinetic energy measures how much energy the object has by virtue of its motion.
The mass of the object $m$ is an important factor in many of the equations of physics. In the equation $F=ma$, the mass $m$ measures the objects inertia, i.e., how much resistance the object offers to being accelerated. The mass of the object also appears in the formulas for momentum and kinetic energy: the heavier the object is, the larger its momentum and its kinetic energy will be.
Concepts
We now introduce the new concepts used to describe the angular motion of objects.
- The kinematics of rotating objects is described in terms of angular quantities:
- $\theta(t)$[rad]: The angular position.
- $\omega(t)$[rad/s]: The angular velocity.
- $\alpha(t)$[rad/s$^2$]: The angular acceleration.
- $I$[kg m$^2$]: The moment of inertia of an object tells you how difficult it is to make it turn.
The quantity $I$ plays the same role in angular motion as the mass $m$ plays in linear motion.
- $\mathcal{T}$[N$\:$m]: The torque is a measures angular force.
Torque is the cause of angular acceleration.
The angular equivalent of Newton's second law $\sum F=ma$ is given by the equation
$\sum\mathcal{T}=I\alpha$.
In words, this law states that applying an angular force (torque) $\mathcal{T}$
will produce an amount of angular acceleration $\alpha$ which is
inversely proportional to the moment of inertia $I$ of the object.
* $L=I\omega$[kg$\:$m$^2$/s]: The //angular momentum// of a rotating object describes
the "quantity of spinning stuff."
* $K_r=\frac{1}{2}I\omega^2$[J]: The //angular// or //rotational// kinetic energy
quantifies the amount of energy an object has by virtue of its rotational motion.
Formulas
Angular kinematics
Instead of talking about position $x$, velocity $v$ and acceleration $a$, we will now talk about the angular position $\theta$, angular velocity $\omega$ and angular acceleration $\alpha$. Except for this change of ingredients, the recipe for fining the equations of motion remains the same: \[ \alpha(t) \ \ \overset{\omega_i + \int\!dt}{\longrightarrow} \ \ \omega(t) \ \ \overset{\theta_i+ \int\!dt }{\longrightarrow} \ \ \theta(t). \] Given the knowledge of the angular acceleration $\alpha(t)$, the initial velocity $\omega_i$ and the initial position $\theta_i$, we can use integration in order to find the equation of motion $\theta(t)$ which describes the angular position of the rotating object at all times.
Though this recipe can be applied to any form of angular acceleration function, you are only required to know the equations of motion for two special cases: the case of constant angular acceleration $\alpha(t)=\alpha$ and the case of zero angular acceleration $\alpha(t)=0$. These are the angular analogues of uniform acceleration motion and uniform velocity motion which we studied in the kinematics section.
The equations which describe uniformly accelerated angular motion are: \[ \begin{align*} \alpha(t) &= \alpha, \nl \omega(t) &= \alpha t + \omega_i, \nl \theta(t) &= \frac{1}{2}\alpha t^2 + \omega_it + \theta_i, \nl \omega_f^2 &= \omega_i^2 + 2\alpha(\theta_f - \theta_i). \end{align*} \] Note how the form of the equations is identical to the UAM equations. This should come as no surprise since the both sets of equations are obtained from the same integrals.
The equations of motion for uniform velocity angular motion are: \[ \begin{align*} \alpha(t) &= 0, \nl \omega(t) &= \omega_i, \nl \theta(t) &= \omega_it + \theta_i. \end{align*} \]
Relation to linear quantities
The angular quantities $\theta$, $\omega$ and $\alpha$ are the natural parameters for describing the motion of rotating objects. In certain situations, however, we may want to relate the angular quantities to linear quantities like distance, velocity and linear acceleration. This can be accomplished by multiplying the angular quantity by the radius of motion: \[ d = R\theta, \quad v = R\omega, \quad a = R\alpha. \]
For example, suppose you have a spool of network cable with radius 20[cm] and you need to measure out a length of 20[m] so as to connect your computer to your neighbours' computer. How many turns from the spool will you need? To find out, we can solve for $\theta$ in the formula $d=R\theta$ and obtain $\theta = 20/0.2=100$[rad] which corresponds to 15.9 turns.
Torque
Torque is angular force. In order to make an object rotate, you must exert a torque on it. Torque is measured in Newton metres [N$\:$m].
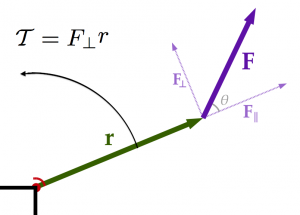 The torque produced by a force depends on how far from the centre of rotation it is applied:
\[
\mathcal{T} = F_{\!\perp}\: r = \|\vec{F}\|\sin\theta\; r,
\]
where $r$ is called the leverage.
Note that only the $F_{\perp}$ component of the force creates a torque.
The torque produced by a force depends on how far from the centre of rotation it is applied:
\[
\mathcal{T} = F_{\!\perp}\: r = \|\vec{F}\|\sin\theta\; r,
\]
where $r$ is called the leverage.
Note that only the $F_{\perp}$ component of the force creates a torque.
To understand the meaning of the torque equation, you should stop reading right now and go experiment with a door. If you push the door close to the hinges, it will take a lot more force to make it move than if you push far from the hinges. The more leverage $r$ you have, the more torque you will produce. Also, if you pull on the door handle away from the hinges, your force will have only a $F_{||}$ component so no matter how hard you pull, you will not cause the door to move.
The standard convention is to call torques that produce counter-clockwise motion positive and torques that cause clockwise rotation negative.
The relationship between torque and force can also be used in the other direction. If an electric motor produces a torque of $\mathcal{T}$[N$\:$m] and is attached to a chain wheel of radius $R$ then the tension in the chain will be: \[ T = F_{\perp} = \mathcal{T}/R \qquad [\text{N}]. \] Using this equation, you could compute the maximum pulling force produced by your car. You will have to lookup the value of the maximum torque produced by your car's engine and then divide by the radius of your wheels.
Moment of inertia
The momentum of inertia of an object describes how difficult it is to make the object rotate: \[ I = \{ \text{ how difficult it is to make an object turn } \}. \]
The calculation of the moment of inertia takes into account the mass distribution of the object. An object which has most of its mass close to the centre will have a smaller moment of inertia, whereas objects which have their mass far from the centre will have a large moment of inertia.
The formula for calculating the moment of inertia is: \[ I = \sum m_i r_i^2 = \int_{obj} r^2 \; dm \qquad [\text{kg}\:\text{m}^2]. \] The above equation indicates that we need to weight each part of the object by the squared distance of that part from the centre, hence the units $[\text{kg}\:\text{m}^2]$.
We rarely calculate the moment of inertia of objects using the above formula. Most of the physics problems you will have to solve will involve geometrical shapes for which the moment of inertia is given by simple formulas: \[ I_{disk} = \frac{1}{2}mR^2, \quad I_{ring}=mR^2, \] \[ I_{sphere} = \frac{2}{5} mR^2, \quad I_{sph. shell} = \frac{2}{3} mR^2. \] When you learn more about calculus, you will be able to derive each of the above formulas on your own. For now, just try to remember the formulas for the inertia of the disk and the ring as they are likely to come up in problems.
The quantity $I$ plays the same role in the equations of angular motion as the mass $m$ plays in the equations of linear motion.
Torques cause angular acceleration
Recall Newton's second law $F=ma$ which describes the amount of acceleration produced by a given force acting on an object. The angular analogue of Newton's second law is the following equation: \[ \mathcal{T} = I \alpha. \] This equation indicates that the angular acceleration produced by the a toque $\mathcal{T}$ is inversely proportional to the object's moment of inertia. Torque is the cause of angular acceleration.
Angular momentum
The angular momentum of a spinning object measures the “amount of rotational motion” that the object has. The formula for the angular momentum of a an object with moment of inertia $I$ rotating at an angular velocity $\omega$ is: \[ L = I \omega \qquad [\text{kg}\:\text{m}^2/\text{s}]. \]
The angular momentum of an object is a conserved quantity in the absence of external torques: \[ L_{in} = L_{out}. \] This is similar to the way momentum $\vec{p}$ is a conserved quantity in the absence of external forces.
Rotational kinetic energy
The kinetic energy of a rotating object is calculated as follows: \[ K_r = \frac{1}{2} I \omega^2 \qquad [\text{J}]. \] This is the rotational analogue to the linear kinetic energy $\frac{1}{2}mv^2$.
The amount of work produced by a torque $\mathcal{T}$ which is applied during an angular displacement of $\theta$ is given by: \[ W = \mathcal{T}\theta \qquad [\text{J}]. \]
Using the above equations, we can now include the energy and work associated with rotational motion into conservation of energy calculations.
Examples
Rotational UVM
A disk is spinning at a constant angular velocity of $12$[rad/s]. How many turns will the disk complete in one minute?
Since the angular velocity is constant, we can use the equation $\theta(t) = \omega t + \theta_i$ to find the total angular displacement after one minute. We obtain $\theta(60)=12\times 60=720$[rad]. To obtain the number of turns, we divide this number by $2\pi$ and obtain 114.6[turns].
Rotational UAM
A solid disk of mass $20$[kg] and radius $30$[cm] is initially spinning with an angular velocity of $20$[rad/s]. A brake pad applied to the edge of the disk produces a friction force of 60[N]. How long before the disk stops?
To solve the kinematics problem, we need to find the angular acceleration produced by the brake. We can do this using the equation $\mathcal{T}=I\alpha$. We must find $\mathcal{T}$ and $I_{disk}$ and solve for $\alpha$. The torque produced by the brake is calculated using the force-times-leverage formula: $\mathcal{T}=F_{\perp}r= 60\times 0.3=18$[N$\:$m]. The moment of inertia of a disk is given by $I_{disk} = \frac{1}{2}mR^2=\frac{1}{2}(20)(0.3)^2=0.9$[kg m$^2$]. Thus we have $\alpha=20$[rad/s$^2$]. We can now use the UAM formula for the angular velocity $\omega(t) = \alpha t + \omega_i$ and solve for the time when the motion will stop: $0 = \alpha t + \omega_i$. The disk will come to a stop after $t=\omega_i/\alpha = 1$[s].
Combined motion
A pulley of radius $R$ and moment of inertia $I$ has a rope wound around it and a mass $m$ attached at the end of the rope. What will be the angular acceleration of the disk if we let the mass drop to the ground while unwinding the rope.
A force diagram on the mass tells us that $mg-T=ma_y$ (where $\hat{y}$ points downwards). The torque diagram on the disk tells us that $TR = I \alpha$. Adding $R$ times the first equation to the second we get: \[ R({mg - T}) + T R = R m a_y + I \alpha, \] or after simplification we get: \[ R m g = R m a_y + I \alpha. \] But we know that the rope forms a solid connection between the disk and the mass block, so we must also have $R \alpha = a_y$, so if we substitute for $a_y$ we get: \[ R m g = R m R \alpha + I \alpha = (R^2 m + I) \alpha. \] Solving for $\alpha$ we obtain: \[ \alpha = \frac{ R m g }{ R^2 m + I }. \] This answer makes sense intuitively. The numerator is the “cause” of the motion while the denominator is the effective moment of inertia of the mass-pulley system as a whole.
Conservation of angular momentum
A spinning figure skater starts from an initial angular velocity of $\omega_i=12$[rad/s] with her arms far away from her body. The moment of inertia of her body in this configuration is $I_i=3$[kg$\:$m$^2$]. She then brings her arms close to her body and in the process her moment of inertia changes to $I_f=0.5$[kg$\:$m$^2$]. What will be her new angular velocity?
We will solve this problem using the law of conservation of angular momentum: \[ L_i = L_f \qquad \Rightarrow \qquad I_i\omega_i = I_f \omega_f, \] which we can solve for the final angular velocity $\omega_f$. The answer is $\omega_f = I_i\omega_i/I_f= 3\times 12/0.5=72$[rad/s], which corresponds to 11.46 turns per second.
Conservation of energy
A 14[in] bicycle wheel with mass $m=4$[kg] with all its mass concentrated near the rim is set in rolling motion at a velocity of 20[m/s] up an incline. How far up the incline will the wheel reach before it stops?
We will solve this problem using the principle of conservation of energy $\sum E_i = \sum E_f$. We must take into account both the linear and rotational kinetic energies of the wheel: \[ \begin{align*} K_i \ \ + \ \ K_{ri} \ + U_i & = K_f + K_{rf} + U_f \nl \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2 + 0 \ & = \ 0 \ + \ 0 \ + mgh. \end{align*} \]
The first step is to calculate $I_{wheel}$ using the formula $I_{wheel} = mR^2 = 4 \times (0.355)^2=0.5$[kg m$^2$]. If the linear velocity of the wheel is 20[m/s], then its angular velocity is $\omega=v_t/R=20/0.355=56.34$[rad/s]. We can now use these values in the energy equation: \[ \frac{1}{2}(4)(20)^2 + \frac{1}{2}(0.5)(56.34)^2 + 0 = 800.0 + 793.55 = (4)(9.81)h. \] The maximum height reached will be $h=40.61$[m].
Note that roughly half of the kinetic energy of the wheel was stored in the rotational motion. This shows that it is important to take into account $K_r$ when solving problems using energy principles.
Static equilibrium
We say that a system is in equilibrium when all the forces and torques acting on the system balance each other out. Since there is no net force on the system, it will just sit there motionless.
Conversely, if you see an object that is not moving, then the forces on it must be in equilibrium: \[ \sum F_x = 0, \quad \sum F_y = 0, \quad \sum \mathcal{T} = 0. \] There must be zero net force in the $x$ direction, zero net force in the $y$ direction and zero net torque on the object.
Example: Walking the plank
A heavy wooden plank is placed so that one third of its length protrudes from the side of a pirate ship. The plank has a length of 12[m] and total weight 120[kg]: this means that 40[kg] of its weight is suspended above the ocean, while 80[kg] is lying on the ship's deck. How far out on the plank can a 80[kg] person walk before the plank tips over?
We will use the torque equilibrium equation $\sum \mathcal{T}_E = 0$ where we calculate the torques relative to the edge of the ship. The torque produced by person when he has walked a distance of $x$[m] from the edge of ship is $\mathcal{T}_1 = -80x$. The torque produced by the weight of the plank is given by $\mathcal{T}_2=120\times 2=240$[N$\:$m] since the weight acts in the centre of gravity of the plank, which is located $2$[m] from the edge. The maximum distance that can be walked before the plank tips over is therefore $x=240/80=3$[m]. After that it is all sharks.
Discussion
Our coverage of the ideas of rotational motion has been very brief. The reason for this, is that there was no new physics to be learned. In this section we used the techniques and ideas developed in the context of linear motion to describe the rotational motion of objects.
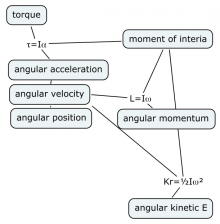 It is really important that you see the parallels between
the new rotational concepts and their linear counterparts.
To help you see the connections,
you can compare the diagram shown on the right with the diagram from the beginning of this section.
It is really important that you see the parallels between
the new rotational concepts and their linear counterparts.
To help you see the connections,
you can compare the diagram shown on the right with the diagram from the beginning of this section.
Let us summarize. If you know the torque acting on an object, then you can calculate its angular acceleration $\alpha$. Knowing the angular acceleration $\alpha(t)$ and the initial conditions $\theta_i$ and $\omega_i$, you can then calculate the equations of motion $\omega(t)$ and $\theta(t)$ at all times.
Furthermore, the angular velocity $\omega$ is related to the angular momentum $L=I\omega$ and the rotational kinetic energy $K_r=\frac{1}{2}I \omega^2$ of the rotating object. The angular momentum measures the “quantity of rotational motion”, while the rotational kinetic energy measures how much energy the object has by virtue of its rotational motion.
The moment of inertia $I$ plays the role of the mass $m$ in the rotational equations. In the equation $\mathcal{T}=I\alpha$, the moment of inertia $I$ measures how difficult it is to make the object turn. The moment of inertia also appears in the formulas for the angular momentum and rotational kinetic energy.
Simple harmonic motion
Vibrations and oscillations are all around us. White light is made up of many oscillations of the electromagnetic field at different frequencies (colors). Sounds are made up of a combination of many air vibrations with different frequencies and strengths. In this section we will learn about simple harmonic motion, which describes the oscillation of a mechanical system at a fixed frequency and with a constant amplitude. By studying oscillations in their simplest form, you will pick up important intuition which you can apply to all other types of oscillations.
 The canonical example of simple harmonic motion is the motion of a mass-spring system
illustrated in the figure on the right. The block is free to slide along
the horizontal frictionless surface. If the system is disturbed from its
equilibrium position, it will start to oscillate back and forth at
a certain natural frequency, which depends on the mass of the block and the stiffness of the spring.
The canonical example of simple harmonic motion is the motion of a mass-spring system
illustrated in the figure on the right. The block is free to slide along
the horizontal frictionless surface. If the system is disturbed from its
equilibrium position, it will start to oscillate back and forth at
a certain natural frequency, which depends on the mass of the block and the stiffness of the spring.
In this section we will focus our attention on two mechanical systems: the mass-spring system and the simple pendulum. We will follow the usual approach and describe the positions, velocities, accelerations and energies associated with this type of motion. The notion of simple harmonic motion (SHM) is far more important than just these two systems. The equations and intuition developed for the analysis of the oscillation of these simple mechanical systems can be applied much more generally to sound oscillations, electric current oscillations and even quantum oscillations. Pay attention, that is all I am saying.
Concepts
- $A$: The amplitude of the movement, how far the object goes back and forth relative to the centre position.
- $x(t)$[m], $v(t)$[m/s], $a(t)$[m/s$^2$]: The position, velocity and acceleration of the object as functions of time.
- $T$[s]: The period of the motion, i.e., how long it takes for the motion to repeat.
- $f$[Hz]: The frequency of the motion.
- $\omega$[rad/s]: The angular frequency of the simple harmonic motion.
- $\phi$[rad]: The phase constant. The Greek letter $\phi$ is pronounced “phee”.
Simple harmonic motion
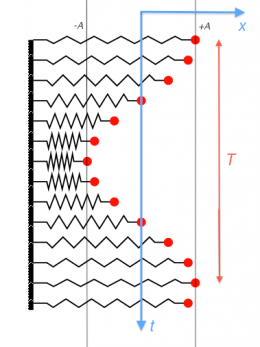 The figure on the right illustrates a mass-spring system undergoing simple harmonic motion.
Observe that the position of the mass as a function of time behaves like the cosine function.
From the diagram, we can also identify two important parameters of the motion: the amplitude $A$,
which describes the maximum displacement of the mass from the centre position,
and the period $T$, which describes how long it takes for the mass to come back to its initial position.
The figure on the right illustrates a mass-spring system undergoing simple harmonic motion.
Observe that the position of the mass as a function of time behaves like the cosine function.
From the diagram, we can also identify two important parameters of the motion: the amplitude $A$,
which describes the maximum displacement of the mass from the centre position,
and the period $T$, which describes how long it takes for the mass to come back to its initial position.
The equation which describes the position of the object as a function of time is the following: \[ x(t)=A\cos(\omega t + \phi). \] The constant $\omega$ (omega) is called the angular frequency of the motion. It is related to the period $T$ by the equation $\omega = \frac{2\pi}{T}$. The additive constant $\phi$ (phee) is called the phase constant or phase shift and its value depends on the initial condition for the motion $x_i\equiv x(0)$.
I don't want you to be scared by the formula for simple harmonic motion. I know there are a lot of Greek letters that appear in it, but it is actually pretty simple. In order to understand the purpose of the three parameters $A$, $\omega$ and $\phi$, we will do a brief review of the properties of the $\cos$ function.
Review of sin and cos functions
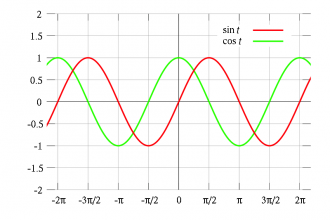 The functions $f(t)=\sin(t)$ and $f(t)=\cos(t)$ are periodic functions
which oscillate between $-1$ and $1$ with a period of $2\pi$.
Previously we used the functions $\cos$ and $\sin$ in order to find the horizontal and vertical components of vectors,
and called the input variable $\theta$ (theta).
However, in this section the input variable is the time $t$ measured in seconds.
Look carefully at the plot of the function $\cos(t)$.
As $t$ goes from $t=0$ to $t=2\pi$, the function $\cos(t)$ completes one full cycle.
The period of $\cos(t)$ is $T=2\pi$ because this is how long it takes
(in radians) for a point to go around the unit circle.
The functions $f(t)=\sin(t)$ and $f(t)=\cos(t)$ are periodic functions
which oscillate between $-1$ and $1$ with a period of $2\pi$.
Previously we used the functions $\cos$ and $\sin$ in order to find the horizontal and vertical components of vectors,
and called the input variable $\theta$ (theta).
However, in this section the input variable is the time $t$ measured in seconds.
Look carefully at the plot of the function $\cos(t)$.
As $t$ goes from $t=0$ to $t=2\pi$, the function $\cos(t)$ completes one full cycle.
The period of $\cos(t)$ is $T=2\pi$ because this is how long it takes
(in radians) for a point to go around the unit circle.
Time-scaling
To describe periodic motion with a different period, we can still use the $\cos$ function but we must add a multiplier in front of the variable $t$ inside the $\cos$ function. This multiplier is called the angular frequency and is usually denoted $\omega$ (omega). The input-scaled $\cos$ function: \[ f(t) = \cos(\omega t ), \] has a period of $T=\frac{2\pi}{\omega}$.
If you want to have a periodic function with period $T$, you should use the multiplier constant $\omega = \frac{2\pi}{T}$ inside the $\cos$ function. When you vary $t$ from $0$ to $T$, the function $\cos(\omega t )$ will go through one cycle because the quantity $\omega t$ goes from $0$ to $2\pi$. You shouldn't just take my word for this: try this for yourself by building a cos function with a period of 3 units.
The frequency of periodic motion describes how many times per second the motion repeats. The frequency is equal to the inverse of the period: \[ f=\frac{1}{T}=\frac{\omega}{2\pi} \text{ [Hz].} \] The relation between $f$ (frequency) and $\omega$ (angular frequency) is a factor of $2\pi$. This multiplier is needed since the natural cycle length of the $\cos$ function is $2\pi$ radians.
Output-scaling
If we want to have oscillations that go between $-A$ and $+A$ instead of between $-1$ and $+1$, we can multiply the $\cos$ function by the appropriate amplitude: \[ f(t)=A\cos(\omega t). \] The above function has period $T=\frac{2\pi}{\omega}$ and oscillates between $-A$ and $A$ on the $y$ axis.
Time-shifting
The function $A\cos(\omega t)$ starts from its maximum value at $t=0$. In the case of the mass-spring system, this corresponds to the case when the motion begins with the spring maximally stretched $x_i\equiv x(0)=A$.
In order to describe other starting positions for the motion, it may be necessary to introduce a phase shift inside the $\cos$ function: \[ f(t)=A\cos(\omega t + \phi). \] The constant $\phi$ must be chosen so that at $t=0$, the function $f(t)$ correctly describes the initial position of the system.
For example, if the harmonic motion starts from the centre $x_i \equiv x(0)=0$ and is initially going in the positive direction, then the equation of motion is described by the function $A\sin(\omega t)$. However, since $\sin(\theta)=\cos(\theta - \frac{\pi}{2})$ we can equally well describe the motion in terms of a shifted $\cos$ function: \[ x(t) = A\cos\!\left(\omega t - \frac{\pi}{2}\right) = A\sin(\omega t). \] Note that the function $x(t)$ correctly describes the initial position: $x(0)=0$.
By now, the meaning of all the parameters in the simple harmonic motion equation should be clear to you. The constant in front of the $\cos$ tells us the amplitude $A$ of the motion, the multiplicative constant $\omega$ inside the $\cos$ is related to the period/frequency of the motion $\omega = \frac{2\pi}{T} = 2\pi f$. Finally, the additive constant $\phi$ is chosen depending on the initial conditions.
Mass and spring
OK, enough math. It is time to learn about the first physical system which exhibits simple harmonic motion: the mass-spring system.
An object of mass $m$ is attached to a spring with spring constant $k$. If disturbed from rest, this mass-spring system will undergo simple harmonic motion with angular frequency: \[ \omega = \sqrt{ \frac{k}{m} }. \] A stiff spring attached to a small mass will result in very rapid oscillations. A weak spring or a large mass will result in slow oscillations.
A typical exam question will tell you $k$ and $m$ and ask about the period $T$. If you remember the definition of $T$, you can easily calculate the answer: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{ \frac{m}{k} }. \]
Equations of motion
The general equations of motion for the mass-spring system are as follows: \[ \begin{align} x(t) &= A\cos(\omega t + \phi), \nl v(t) &= -A\omega \sin(\omega t + \phi), \nl a(t) &= -A\omega^2\cos(\omega t + \phi). \end{align} \]
The general shape of the function $x(t)$ is $\cos$-like. The angular frequency $\omega$ parameter is governed by the physical properties of the system. The parameters $A$ and $\phi$ describe the specifics of the motion, namely, the size of the oscillation and where it starts from.
The function $v(t)$ is obtained, as usual, by taking the derivative of $x(t)$. The function $a(t)$ is obtained by taking the derivative of $v(t)$, which corresponds to the second derivative of $x(t)$.
Motion parameters
The velocity and the acceleration of the object are also periodic functions.
We can find the maximum values of the velocity and the acceleration by reading off the coefficient in front of the $\sin$ and $\cos$ in the functions $v(t)$ and $a(t)$.
- The maximum velocity of the object is
\[ v_{max} = A \omega. \]
- The maximum acceleration is
\[ a_{max} = A \omega^2. \] The velocity is maximum as the object passes through the centre, while the acceleration is maximum when the spring is maximally stretched (compressed).
You will often be asked to solve for the quantities $v_{max}$ and $a_{max}$ in exercises and exams. This is an easy task if you remember the above formulas and you know the values of the amplitude $A$ and the angular frequency $\omega$.
Energy
The potential energy stored in a spring which is stretched (compressed) by a length $x$ is given by the formula $U_s=\frac{1}{2}k x^2$. Since we know $x(t)$, we can obtain the potential energy of the mass-spring system as a function of time: \[ U_s(t)= \frac{1}{2} kx(t)^2 =\frac{1}{2}kA^2\cos^2(\omega t +\phi). \] The potential energy reaches its maximum value $U_{s,max}=\frac{1}{2}kA^2$ when the spring is fully stretched or fully compressed.
The kinetic energy of the mass as a function of time is given by: \[ K(t)= \frac{1}{2} mv(t)^2 = \frac {1}{2}m\omega^2A^2\sin^2(\omega t +\phi). \] The kinetic energy is maximum when the mass passes through the centre position. The maximum kinetic energy is given by $K_{max} = \frac{1}{2} mv_{max}^2= \frac{1}{2}mA^2\omega^2$.
Conservation of energy
The conservation of energy equation tells us that the total energy of the mass-spring system is conserved. The sum of the potential energy and the kinetic energy at any two instants $t_1$ and $t_2$ is the same: \[ U_{s1} + K_2 = U_{s2} + K_2. \]
It is also useful to calculate the total energy of the system $E_T = U_s(t) + K(t) = \text{const}$. This means that even if $U_s(t)$ and $K(t)$ change over time, the total energy of the system always remains constant.
We can use the identity $\cos^2\theta + \sin^2\theta =1$ to verify that the total energy is indeed a constant and that it is equal $U_{s,max}$ and $K_{max}$: \[ \begin{align} E_{T} &= U_s(t) + K(t) \nl &= \frac{1}{2}kA^2\cos^2(\omega t) + \frac {1}{2}m\omega^2A^2\sin^2(\omega t) \nl &= \frac{1}{2}m\omega^2A^2\cos^2(\omega t ) + \frac {1}{2}m\omega^2A^2\sin^2(\omega t ) \ \ \ (\text{since } k = m\omega^2 )\nl &= \frac{1}{2}m\underbrace{\omega^2A^2}_{v_{max}^2}\underbrace{\left[ \cos^2(\omega t) + \sin^2(\omega t)\right]}_{=1} = \frac{1}{2}mv_{max}^2 = K_{max} \nl & =\frac{1}{2}m(\omega A)^2 = \frac{1}{2}(m \omega^2) A^2 =\frac{1}{2}kA^2 = U_{s,max}. \end{align} \]
The best way to understand SHM is to visualize how the energy of the system shifts between the potential energy of the spring and the kinetic energy of the moving mass. When the spring is maximally stretched $x=\pm A$, the mass will have zero velocity and hence zero kinetic energy $K=0$. At this moment all the energy of the system is stored in the spring $E_T= U_{s,max}$. The other important moment is when the mass has zero displacement but maximal velocity $x=0, U_s=0, v=\pm A\omega, E_T=K_{max}$, which corresponds to all the energy being stored as kinetic energy.
Pendulum motion
We now turn our attention to another simple mechanical system whose motion is also described by the simple harmonic motion equations.
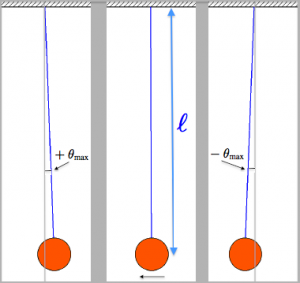 Consider a mass suspended at the end of a long string of length $\ell$ in a gravitational field of strength $g$.
If we start the pendulum from a certain angle $\theta_{max}$ away from the vertical position and then release it,
the pendulum will swing back and forth undergoing simple harmonic motion.
Consider a mass suspended at the end of a long string of length $\ell$ in a gravitational field of strength $g$.
If we start the pendulum from a certain angle $\theta_{max}$ away from the vertical position and then release it,
the pendulum will swing back and forth undergoing simple harmonic motion.
The period of oscillation is given by the following formula: \[ T = 2\pi \sqrt{ \frac{\ell}{g} }. \] Note that the period does not depend on the amplitude of the oscillation (how far the pendulum swings) nor the mass of the pendulum. The only factor that plays a role is the length of the string $\ell$. The angular frequency for a pendulum of length $\ell$ is going to be: \[ \omega \equiv \frac{2\pi}{T} = \sqrt{ \frac{g}{\ell} }. \]
We describe the position of the pendulum in terms of the angle $\theta$ that it makes with the vertical. The equations of motion are described in terms of angular variables: the angular position $\theta$, the angular velocity $\omega_\theta$ and the angular acceleration $\alpha_\theta$: \[ \begin{align} \theta(t) &= \theta_{max} \: \cos\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right), \nl \omega_\theta(t) &= -\theta_{max}\sqrt{ \frac{g}{\ell} } \: \sin\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right), \nl \alpha_\theta(t) &= -\theta_{max}\frac{g}{\ell} \: \cos\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right). \end{align} \] The angle $\theta_{max}$ describes the maximum angle that the pendulum swings to. Note how we had to use a new variable name $\omega_\theta$ for the angular velocity of the pendulum $\omega_\theta(t)=\frac{d}{dt}\!\left(\theta(t)\right)$, so as not to confuse it with the constant $\omega=\sqrt{ \frac{g}{\ell} }$ inside the $\cos$ function, which describes angular frequency of the periodic motion.
Energy
The motion of the pendulum is best understood by imagining how the energy of the system shifts between the gravitational potential energy of the mass and its kinetic energy.
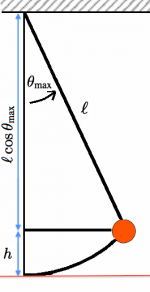 The pendulum will have a maximum potential energy when it swings to the side by the angle $\theta_{max}$.
At that angle, the vertical position of the mass will be increased by a height $h$ above the lowest point.
We can calculate $h$ as follows:
\[
h = \ell - \ell \cos \theta_{max}.
\]
Thus the maximum gravitational potential energy of the mass is therefore:
\[
U_{g,max}= mgh= mg\ell(1-\cos\theta_{max}).
\]
The pendulum will have a maximum potential energy when it swings to the side by the angle $\theta_{max}$.
At that angle, the vertical position of the mass will be increased by a height $h$ above the lowest point.
We can calculate $h$ as follows:
\[
h = \ell - \ell \cos \theta_{max}.
\]
Thus the maximum gravitational potential energy of the mass is therefore:
\[
U_{g,max}= mgh= mg\ell(1-\cos\theta_{max}).
\]
By the conservation of energy principle, the maximum kinetic energy of the pendulum must be equal to the maximum of the gravitational potential energy: \[ mg\ell(1-\cos\theta_{max}) = U_{g,max} = K_{max} = \frac{1}{2} mv_{max}^2, \] where $v_{max}=\ell \omega_\theta$ is the linear velocity of the mass as it swings through the centre.
Explanations
It is worthwhile to understand how the equations of simple harmonic motion come about. In this subsection, we will discuss how the equations are derived from Newton's second law $F=ma$.
Trigonometric derivatives
The slope (derivative) of the function $\sin(t)$ varies between $-1$ and $1$. The slope is largest when $\sin$ passes through the $x$ axis and the slope is zero when it reaches its maximum and minimum values. A careful examination of the graphs of the bare functions $\sin$ and $\cos$ reveals that the derivative of the function $\sin(t)$ is described by the function $\cos(t)$ and vice versa: \[ f(t) = \sin(t) \:\qquad \Rightarrow \qquad f'(t) = \cos(t), \] \[ f(t) = \cos(t) \qquad \Rightarrow \qquad f'(t) = -\sin(t). \] When you learn more about calculus you will know how to find the derivative of any function you want, but for now just take my word that the above two formulas are true.
The chain rule for derivatives tells us that the derivative of a composite function $f(g(x))$ is given by $f'(g(x))\cdot g'(x)$, i.e., you must take the derivative of the outer function and then multiply by the derivative of the inner function. We can use the chain rule to the find derivative of the simple harmonic motion position function: \[ x(t)=A\cos(\omega t +\phi) \ \ \Rightarrow \ \ v(t) \equiv x^{\prime}(t)=-A\sin(\omega t +\phi)(\omega) = -A\omega\sin(\omega t +\phi), \] where the outer function is $f(x)=A\cos(x)$ with derivative $f'(x)=-A\sin(x)$ and the inner function is $g(x)=\omega x +\phi$ with derivative $g'(x)=\omega$.
The same reasoning is used to obtain the second derivative: \[ a(t)\equiv \frac{d}{dt}\!\left\{ v(t) \right\} =-A\omega^2 \cos(\omega t +\phi) = -\omega^2 x(t). \] Note that $a(t)=x^{\prime\prime}(t)$ has the same form as $x(t)$, but always acts in the opposite direction.
I hope this clarifies for you how we obtained the functions $v(t)$ and $a(t)$: we simply took the derivative of the function $x(t)$.
Derivation of the mass-spring SHM equation
You may be wondering where the equation $x(t)=A\cos(\omega t + \phi)$ comes from. This formula looks very different from the kinematics equations for linear motion $x(t) = x_i + v_it + \frac{1}{2}at^2$, which we obtained starting from Newton's second law $F=ma$ after two integration steps.
In this section, we pulled the $x(t)=A\cos(\omega t + \phi)$ formula out of thin air, as if by revelation. Why did we suddenly start talking about $\cos$ functions and Greek letters with dubious names like phase. Are you phased by all of this? When I was first learning about simple harmonic motion, I was totally phased because I didn't see where the $\sin$ and $\cos$ came from.
The $\cos$ also comes from $F=ma$, but the story is a little more complicated this time. The force exerted by a spring is $F_{s} = -kx$. If you draw a force diagram on the mass, you will see that the force of the spring is the only force acting on it so we have: \[ \sum F = F_s =ma \qquad \Rightarrow \qquad -kx = ma. \] Recall that the acceleration is the second derivative of the position: \[ a=\frac{dv(t)}{dt} = \frac{d^2x(t)}{dt^2} = x^{\prime\prime}(t). \]
We now rewrite the equation $-kx = ma$ in terms of the function $x(t)$ and its second derivative: \[ \begin{align*} -kx(t) &= m\frac{d^2x(t)}{dt^2} \nl 0 & = m\frac{d^2x(t)}{dt^2}+ kx(t) \nl 0 & = \frac{d^2x(t)}{dt^2}+ \frac{k}{m}x(t). \end{align*} \]
This is called a differential equation. Instead of looking for an unknown number as in normal equations, in differential equations we are looking for an unknown function $x(t)$. We do not know what $x(t)$ is but we do know one of its properties, namely, that its second derivative $x^{\prime\prime}(t)$ is equal to the negative of $x(t)$ multiplied by some constant.
To solve a differential equation, you have to guess which function $x(t)$ satisfies this property. There is an entire course called Differential Equations, in which engineers and physicists learn how to do this guessing thing. Can you think of a function which, when multiplied by $\frac{k}{m}$, is equal to its second derivative?
OK, I thought of one: \[ x_1(t)=A_1 \cos\!\left( \sqrt{ \frac{k}{m}}t \right). \] Come to think of it, there is also a second one which works: \[ x_2(t)=A_2 \sin\!\left( \sqrt{ \frac{k}{m}}t \right). \] You should try this for yourself: verify that $x^{\prime\prime}_1(t) + \frac{k}{m}x_1(t)=0$ and $x^{\prime\prime}_2(t) + \frac{k}{m}x_2(t)=0$, which means that these functions are both solutions to the differential equation $x^{\prime\prime}(t)+\frac{k}{m} x(t)=0$. Since both $x_1(t)$ and $x_2(t)$ are solutions, any combination of them must also be a solution: \[ x(t) = A_1\cos(\omega t) + A_2\sin(\omega t). \] This is kind of the answer we were looking for. I say kind of because the function $x(t)$ is specified in terms of the coefficients $A_1$ and $A_2$ instead of the usual parameters: the amplitude $A$ and a phase $\phi$.
Lo and behold, using the trigonometric identity $\cos(a + b)=\cos(a)\cos(b) - \sin(a)\sin(b)$ we can express the function $x(t)$ as a time-shifted trigonometric function: \[ x(t)=A\cos(\omega t + \phi) = A_1\cos(\omega t) + A_2\sin(\omega t). \] The expression on the left is the preferred way of describing SHM because the parameters $A$ and $\phi$ corresponds to observable aspects of the motion.
Let me go over what just happened here one more time. Our goal was to find the equation of motion which predicts the position of an object as a function of time $x(t)$. To understand what is going on, let us draw an analogy with a situation which we have seen previously. In linear kinematics, uniform accelerated motion with $a(t)=a$ is described by the equation $x(t)=x_i+v_it + \frac{1}{2}at^2$ in terms of parameters $x_i$ and $v_i$. Depending on the initial velocity and the initial position of the object, we obtain different trajectories. Simple harmonic motion with angular frequency $\omega$ is described by the equation $x(t)=A\cos(\omega t + \phi)$ in terms of the parameters $A$ and $\phi$, which are the natural parameters for describing SHM. We obtain different harmonic motion trajectories depending on the values of the parameters $A$ and $\phi$.
Derivation of the pendulum SHM equation
To see how the SHM equation of motion arises in the case of the pendulum, we need to start from the torque equation $\mathcal{T}=I\alpha$.
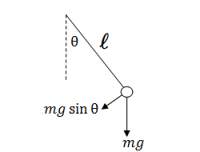 The diagram on the right illustrates how we can calculate the torque on the pendulum
which is caused by the force of gravity as a function of the displacement angle $\theta$.
Recall that the torque calculation only takes into account the $F_{\!\perp}$ component
of any force, since it is the only part which causes rotation:
\[
\mathcal{T}_\theta = F_{\!\perp} \ell = mg\sin\theta \ell.
\]
If we now substitute this into the equation $\mathcal{T}=I\alpha$,
we obtain the following:
\[
\begin{align*}
\mathcal{T} &= I \alpha \nl
mg\sin\theta(t) \ell &= m\ell^2 \frac{d^2\theta(t)}{dt^2} \nl
g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2}
\end{align*}
\]
The diagram on the right illustrates how we can calculate the torque on the pendulum
which is caused by the force of gravity as a function of the displacement angle $\theta$.
Recall that the torque calculation only takes into account the $F_{\!\perp}$ component
of any force, since it is the only part which causes rotation:
\[
\mathcal{T}_\theta = F_{\!\perp} \ell = mg\sin\theta \ell.
\]
If we now substitute this into the equation $\mathcal{T}=I\alpha$,
we obtain the following:
\[
\begin{align*}
\mathcal{T} &= I \alpha \nl
mg\sin\theta(t) \ell &= m\ell^2 \frac{d^2\theta(t)}{dt^2} \nl
g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2}
\end{align*}
\]
What follows is something which is not mathematically rigorous, but will allow us to continue and solve this problem. When $\theta$ is a small angle we can use the following approximation: \[ \sin(\theta)\ \approx \ \theta, \qquad \qquad \text{ for } \theta \ll 1. \] This type of equation is called a small angle approximation. You will see where it comes from later on when you learn about Taylor series approximations to functions. For now, you can convince yourself of the above formula by zooming many times on the graph of the function $\sin$ near the origin to see that $y=\sin(x)$ will look very much like $y=x$. Try this out.
Using the small angle approximation for $\sin\theta$ we can rewrite the equation involving $\theta(t)$ and its second derivative as follows: \[ \begin{align*} g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2} \nl g\theta(t) &\approx \ell \frac{d^2\theta(t)}{dt^2} \nl 0 &= \frac{d^2\theta(t)}{dt^2}+ \frac{g}{\ell}\theta(t). \end{align*} \]
At this point we recognize that we are dealing with the same differential equation as in the case of the mass-spring system: $\theta^{\prime\prime}(t)+\omega^2 \theta(t)=0$, which has solution: \[ \theta(t) = \theta_{max}\cos(\omega t + \phi), \] where the constant inside the $\cos$ function is $\omega=\sqrt{\frac{g}{\ell}}$.
Examples
When asked to solve word problems, you will usually be told the initial amplitude $x_i=A$ or the initial velocity $v_i=\omega A$ of the SHM and the question will ask you to calculate some other quantity. Answering these problems shouldn't be too difficult provided you write down the general equations for $x(t)$, $v(t)$ and $a(t)$, fill-in the knowns quantities and then solve for the unknowns.
Standard example
You are observing a mass-spring system build from a $1$[kg] mass and a 250[N/m] spring. The amplitude of the oscillation is 10[cm]. Determine (a) the maximum speed of the mass, (b) the maximum acceleration, and (c ) the total mechanical energy of the system.
First we must find the angular frequency for this system $\omega = \sqrt{k/m}=\sqrt{250/1}=15.81$[rad/s]. To find (a) we use the equation $v_{max} = \omega A = 15.81 \times 0.1=1.58$[m/s]. Similarly, we can find the maximum acceleration using $a_{max} = \omega^2 A = 15.81^2 \times 0.1=25$[m$^2$/s]. There are two equivalent ways for solving (c ). We can obtain the total energy of the system by considering the potential energy of the spring when it is maximally extended (compressed) $E_T=U_s(A) = \frac{1}{2}kA^2 = 1.25$[J], or we can obtain the total energy from the maximum kinetic energy $E_T=K=\frac{1}{2}m v_{max}^2 = 1.25$[J].
Discussion
In this section we learned about simple harmonic motion, which is described by the equation $x(t)=A\cos(\omega t + \phi)$. You may be wondering what non-simple harmonic motion is. A simple extension of what we learned would be to study oscillating systems where the energy is slowly dissipating. This is known as damped harmonic motion for which the equation of motion looks like $x(t)=Ae^{-\gamma t}\cos(\omega t + \phi)$, which describes an oscillation whose magnitude slowly decreases. The coefficient $\gamma$ is known as the damping coefficient and indicates how fast the energy of the system is dissipated.
The concept of SHM comes up in many other areas of physics. When you learn about electric circuits, capacitors and inductors, you will run into equations of the form $v^{\prime\prime}(t)+\omega^2 v(t)=0$, which indicates that the voltage in a circuit is undergoing simple harmonic motion. Guess what, the same equation used to describe the mechanical motion of the mass-spring system will be used to describe the voltage in an oscillating circuit!
Links
[ Plot of the simple harmonic motion using a can of spray-paint. ]
http://www.youtube.com/watch?v=p9uhmjbZn-c
NOINDENT
[ 15 pendulums with different lengths. ]
http://www.youtube.com/watch?v=yVkdfJ9PkRQ
Conclusion
The fundamental purpose of mechanics is to predict the motion of objects using equations. In the beginning of the chapter, I made the claim that there are only twenty equations that you need to know in order to solve any physics problem. Let us now verify this claim and review the material.
Our goal was to find $x(t)$ for all times $t$. However, there are no equations of physics which will tell us $x(t)$ directly. Instead, we have Newton's second law $F=ma$, which tells us that the acceleration of the object $a(t)$ is equal to the net force acting on the object divided by the object's mass. In order to find $x(t)$ starting from $a(t)$ we must use integration (twice).
We studied kinematics in several different contexts. We originally looked at kinematics problems in one dimension, and derived the UAM and UVM equations. We also studied the problem of projectile motion by decomposing it into two separate kinematics subproblems: one in the $x$ direction (UVM) and one in the $y$ direction (UAM). Later, we studied the circular motion of objects and stated equation $a_r=\frac{v_t^2}{r}$ which describes an important relationship between the radial acceleration, the tangential velocity and the radius of the circle of rotation. We also studied rotational motion using angular kinematics quantities $\theta(t)$, $\omega(t)$ and $\alpha(t)$. We defined the concept of torque and used this concept to write down the angular equivalent of Newton's second law $\mathcal{T}=I\alpha$. Finally, we studied the equation which describes simple harmonic motion: $x(t)=A\cos(\omega t + \phi)$ and showed the formula $\omega = \sqrt{ \frac{k}{m} }$, which is used to find the angular frequency of a mass-spring system.
We also discussed three conservation laws: the conservation of linear momentum law $\sum\vec{p}_{i} = \sum\vec{p}_{f}$, the conservation of angular momentum law $L_{i} = L_{f}$ and the conservation of energy law $\sum E_{i} = \sum E_{f}$. Each of these three fundamental quantities is conserved overall and cannot be created nor destroyed. Momentum calculations are used to analyze collisions, while energy formulas like equations $K=\frac{1}{2}mv^2$, $U_g=mgh$ and $U_s=\frac{1}{2}kx^2$ can be used to analyze the motion of objects in terms of energy principles.
As you can see, twenty equations really are enough for all of Mechanics. The next step for you should be to practice solving exercises in order to solidify your understanding.
Exercises
In this section we present some physics exercises which you can use to test your understanding. Don't be discouraged if you find the exercises difficult—these are meant to be hard.
When solving the exercises, I recommend that you use the following approach:
- Figure out what type of problem you are dealing with (kinematics? angular motion? energy?).
- Draw a diagram which describes the physical situation. Label things clearly.
- Copy over from your formula sheet all the equations which you plan to use.
- Substitute the known quantities into the equations and analyze which is the
unknown you are looking for. Visualize the steps (plug what into what?) which
you will use to solve for the unknowns. - Solve for the unknowns.
Make sure you attempt to do each of the exercises on your own before looking at the solutions.
Simple ones
Simple kinematics
A ball is thrown from the ground upwards with an initial velocity of 20[m/s]. How long will it stay in the air before it comes back to the ground?
Sol: This is a kinematics question. Using the equation $v(t) = at+v_i$ we can find $t_{top}$ (we know that $v(t_{top})= 0$). Ans: $t_{flight} = 2t_{top}=4.1$[s].
Good ones
Turntable slug
A disk is rotating with an angular velocity of $\omega=5$[rad/s]. A slug is sliding along the surface of the disk in the radial direction. Imagine the slug starting from the centre of the disk an moving outwards. If the coefficient of friction between the slug and the disk is $\mu_k = 0.4$, how far will the slug be able to slide to before it flies off the surface?
Ans: The normal force of the between the slug and the turntable is $N=mg$. The friction force available is $F_f=0.4mg$. The centripetal acceleration required to keep the slug on the disk when it is at a radius $R$ is $F_r=ma_r=m\frac{(R\omega)^2}{R}$. The slug will fly off when the friction force is not sufficient to keep it turning, which happens at distance $R=\frac{0.4g}{\omega^2}$ from the centre of the disk.
Word problems
Elevator fridge
You are moving your fridge and you have it loaded on the elevator. Because of static friction, a force is required to start the fridge sliding across the floor of the elevator. Rank the forces required, from smallest to largest, in three situations: (a) a stationary elevator, (b) when the elevator is accelerating upwards, © when the elevator is accelerating downwards.
Ans: $F_{fs}$ (upwards) $ > F_{fs}$ (static) $> F_fs$ downwards. The equation for F_fs is $F_{fs} = \mu_s N$, where $N$ is the normal force (contact force between the box and the floor of the elevator). In the $y$ direction the force diagram on the match box reads $\sum F_y = N - mg = ma_y$. When the elevator is static we have a_y = 0 so N = mg. If $a_y > 0$ (accelerating upwards) then we must have $N > mg$ hence the friction force will be larger than when static. When $a_y < 0$ (accelerating downwards) $N$ must be smaller than $mg$ and consequently there will be less $F_{fs}$.
More turntable stuff
Three coins are placed on a rotating turntable. One coin is placed at $5$[cm] from the centre, another is placed at $10$[cm] from the centre and the third is at $15$[cm] from the centre. Initially, due to static friction, the pennies are moving together with the turntable as it starts to rotate. The angular speed $\omega$ is then increased slowly. Assuming each penny has the same coefficients of friction with the turntable surface, which penny starts to slide first?
Sol: This is a circular motion question. The penny that is furthest from the centre will fly off the first. That is because the centripetal force required to keep it turning is the largest. Recall that $F_r = ma_r$, that $a_r = v^2/R$ and that $v =\omega R$. If the turn table is turning with angular velocity $\omega$, then the centripetal acceleration required to keep a coin turning in a circle of radius $R$ is $F_r = m \omega^2 R$. This centripetal force must be supplied by the static force of friction $F_{fs}$ between the coin and the turn table. Large $R$ requires more $F_{fs}$ hence the coin furthest will fly off first.
Keep you v
Three identical balls (a, b, and c) are thrown upwards with identical speeds but different angles. Ball is (a) is thrown directly upwards, ball (b) is thrown at an angle of $30^\circ$ with the vertical while ball (c ) is thrown at an angle of $45^\circ$. Rank the balls in order of their speed when they have reached a height of one meter. Assume all of the balls have enough energy to get to this height.
Sol: This is a projectile question. The vertically-thrown ball (a) will have the largest $v_iy$ and zero $v_ix$. The angled shots trade decreased $v_iy$ for ininitial $v_ix$. For the $y$ direction we have $v_{fy}^2 = v_{iy}^2 + 2(-9.81)y$. For the $x$ direction we have $v_{fx} = v_{ix}$. Any investment you put into $v_ix$ is conserved, while investments in $v_iy$ get transformed by the function $f(a) = \sqrt{ a^2 - \textrm{ const} } < |a|$ so you are better off investing in $v_ix$ than in $v_iy$. To maximize the speed of the ball when it reaches a height of one meter you should choose the ball with the largest horizontal velocity (c ).
Leverage is key
Two identical (same moment of inertia) pulleys have strings wound around them. The first pulley has the string wound around the outer radius $R$, while the sting on the second pulley is wound on a smaller radius $r < R$. The same force F is used to rotate the pulleys. After a fixed time $t$, which pulley has the larger speed? Which puck has the larger rotational kinetic energy?
Sol: This is an angular motion question. The two pucks have identical rotational resistance: they have the same moment of inertia $I$. The torque produced by the string is larger for the pulley which has the string wound around the larger radius $R$. Higher torque will produce a more angular acceleration and hence a bigger angular velocity (and KE).
Integration tests
These following exercises will require you to mix techniques from different sections.
Disk brakes
The disk brake pads on your new bicycle squeeze the brake disks
with a force of 5000[N] (from each side) and you have one on each tire.
The coefficient of friction between brake pads and brake disk is $\mu_k=0.3$.
The brake disks have radius $r=6$[cm] while the tire has a radius $R=20$[cm].
1. What is the total force of friction in each brake?
2. What is the torque exerted by each brake?
3. How many turns of wheels will it take before to stop
if you are moving with 10[m/s] and apply broth brakes.
Assume that the combined mass of you and your bicycle is 100[kg]?
4. What will be the braking distance?
Sol: 1. The friction force is proportional to the normal force so we have $F_f=0.3\times 5000=1500$[N] of friction on each side of the disk for a total force of $F_f=3000$[N] per wheel. 2. This friction force of the brakes acts with a leverage of $0.06$[m] so the torque produced by each brake is $\mathcal{T} = 0.06 \times 3000 = 180$[N$\:$m]. 3. The kinetic energy of a 100kg object moving at 10[m/s] is equal to $K_i=\frac{1}{2}100(10)^2=5000$[J]. We will use $K_i - W = 0$ where $W$ is the work done by the brakes. Denote $\theta_{stop}$ the angle rotation of the tires. The work done by each brake is $180\theta_{stop}$ so to it will take a total of $\theta_{stop} = \frac{5000}{360}=13.\overline{8}$[rad] to stop the bike. This is 2.21 turns of the wheels. 4. Your stopping distance is $13.\overline{8}\times 0.20=2.\overline{7}$[m]. Yey for disk brakes!
Tarzan
A half-naked dude swings from a long rope attached to the ceiling. The rope has length 6.00[m], the dude swings from an initial angle of $-50.0^\circ$ ($50^\circ$ to the left of the vertical line) all the way to the angle $+10.0^\circ$ at which point he lets go of the rope. How far will Tarzan fall (as measured from the centre position of the swing), i.e., I am asking you to find $x_f = 6\sin(10) + d$ where $d$ is the distance travelled by the “projectile”.
Sol: This is an energy problem followed by a projectile motion problem. The energy equations is $\sum E_i = \sum E_f$ which in this case is $U_i = U_f + K_f$ or $mg(6-6\cos50^\circ)=mg(6-6\cos10^\circ)+\frac{1}{2}mv^2$ which can be simplified to $v^2 = 12g(\cos10^\circ - \cos50^\circ)$, and solving for $v$ we find $v=4.48$[m/s]. Now for the projectile motion part. The initial velocity is $4.48$[m/s] at an angle of $10^\circ$ with respect to the ground so $v_i=(4.42,0.778)$[m/s]. The initial position is $(x_i,y_i) = ( 6\sin(10), 6[1-\cos(10)] )= (1.04, 0.0911)$[m]. To find the total time of flight we solve for $t$ in $0=-4.9 t^2+ 0.778t+ 0.0911$ and we find $t=0.237$[s]. The final position will be $x_f = 6\sin(10)+ 4.42\times 0.237=2.08$[m].
Advanced
Pendulum painting
Two disgruntled airport employees decide to vandalize a long moving sidewalk by suspending a leaking-paint-bucket pendulum on top of the moving sidewalk and letting it run. The oscillations of the pendulum are small and transverse to the direction of the motion of the sidewalk. The pendulum is composed of a long cable (considered massless) and a paint bucket with a hole in the bottom. Find the equation $y(x)$ of the the resulting pattern of pain on the moving sidewalk in terms of the pendulum's maximum (angular) displacement $\theta_{max}$, its length $\ell$, and the speed of the sidewalk $v$. Assume that $x$ measures distances along the sidewalk and $y$ denotes the transversal displacement of the pendulum. Does the loss of pendulum mass affect the waveform you see on the moving sidewalk?
Sol: This is a simple harmonic motion question involving a pendulum. We can therefore begin by writing down the general equation of motion for a pendulum $\theta(t) = \theta_{max} \cos( \omega t )$, where $\omega=\sqrt{ g/\ell }$. Enter sidewalk. The sidewalk is moving to the left at velocity $v$. If we choose the $x=0$ coordinate at a time when $\theta(t) = \theta_{max}$, then the pattern on the sidewalk will be described by the equation $y(x) = \ell \sin(\theta_{max})\cos( kx )$ where $k=2\pi/\lambda$ and $\lambda$ is how long (as a distance in the $x$ direction) it takes to complete one cycle. One full swing of the bucket takes $T = 2\pi/\omega$[s]. In that time, the moving sidewalk will have moved a distance of $vT$ meters. So one cycle in space (one wavelength) is $\lambda=vT = v 2\pi/\omega$. We conclude that the equation of the paint on the moving sidewalk is $y(x) = \ell \sin(\theta_max) \cos( (\omega/v) x )$. Observe that the the angular frequency parameters $\omega=\sqrt{ g/\ell }$ does not depend on the mass of the pendulum, thus the change in mass (as the paint leaks out) will not affect the motion.
A derivation
A ball of radius $r$ is rolling back and forth inside a ramp. The ramp opens upwards and is circular in shape with an radius $R$. The ball rolls to one side, slows down, stops, then rolls back to the centre of the ramp and continues rolling up the other side and so on and so forth. What is the period of this oscillation?
Links
[ Physics exercises. ]
http://en.wikibooks.org/wiki/Physics_Exercises
http://en.wikibooks.org/wiki/A-level_Physics_(Advancing_Physics)
NOINDENT
[ Word problems ]
http://www.physics.umd.edu/perg/abp/think/mech/mechdyn.htm
NOINDENT
[ Lots of worked examples. ]
http://farside.ph.utexas.edu/teaching/301/lectures/lectures.html
Calculus
Calculus is useful math. It is useful for solving problems in physics, chemistry, computing, biology, business and many other areas of life. You need calculus in order to do quantitative analysis of how functions change over time (derivatives) or sum up all kinds of contributions that add up to a total (integration). Calculating the slope of a function is a very common task. The inverse problem of finding a function given its slope is equally common. The language of calculus will will allow you to speak precisely about the following properties of functions: their slopes, their curvatures, their asymptotes, their areas under the curve, etc.
Introduction
In the physics chapter we developed an intuitive understanding of integrals since we used this concept in order to calculate the position and the velocity of an object given the knowledge of its acceleration. It is now time to study the techniques of calculus more closely and with more mathematical rigour. Real math is not so much about calculating things, but about seeing patterns and relationships between concepts.
The only prerequisite knowledge for calculus is functions. You see, most problems that you will find on a calculus exam involve some function $f(t)$ and ask you to calculate some property of the function, hence the name calculus. Let us now look at two real-world examples where calculus ideas are used.
Download example
Suppose you are downloading a large file to your computer. At $t=0$ you clicked “Save as” in your browser and started the download. Let $f(t)$ represent the size of the downloaded data. The number $f(t)$ is what you would see if, at time $t$, you clicked on the partially-downloaded file and checked how much space it takes on your disk. If you are downloading a $700$[Mb] file, then the download progress bar at time $t$ will correspond to the fraction $\frac{f(t)}{700 \text{[Mb]}}$.
The derivative function $f^\prime(t)$ is a description of how the function $f(t)$ changes over time. In our example $f^\prime(t)$ is the download speed. Indeed, if you are downloading at 100 [kb/s], then the function $f(t)$ must increase by 100[kb] each second. If you maintain this download speed the file size will grow uniformly: $f(0)=0$[kb], $f(1)=100$[kb], $f(2)=200$[kb], $\ldots$, f(100)=10[Mb]. The “estimated time remaining” is calculated by dividing the size of the part remaining to be downloaded by the current download speed: \[ \text{time remaining } = \frac{ 700 - f(t) }{ f^\prime(t) } [s]. \] The bigger the derivative is, the faster the download will finish.
Inverse problem
Let us now consider this problem from the point of view of the router which connects you to the Internet. The router knows what download rate $f^\prime(t)$[kb/s] you had at all times during the download because it was sending you the data. What is the download speed for you is the upload speed for the router.
The router does not have access to your computer and therefore does not know the actual file size $f(t)$ on your computer. Nevertheless, the router can infer the information about the size of the file $f(t)$ from the transmission rate $f^\prime(t)$. The sum (integral) of the download rate between $t=0$ and $t=\tau$ corresponds to the total new downloaded data that appeared on your computer. During this period, the change in the file size was \[ \Delta f = f(\tau)-f(0) = \int_0^\tau f'(t)\; dt. \] Assuming that the file size starts from zero $f(0)=0$[kb] at $t=0$, the router can use the integration procedure to find $f(\tau)$, the file size on your computer at $t=\tau$: \[ f(\tau) = \int_0^\tau f^\prime(t)\; dt. \]
This example illustrates two very important ideas. The first is the notion of an integral $\int_a^b\cdot dt$ which is the calculation of the total of a function during the time period from $t=a$ until $t=b$. The second idea illustrated is the inverse relationship between the integral and the derivative operations. If you know the slope of a function $f^\prime(t)$, you can find the value of the function $f(t)$ by integrating.
Definitions
Calculus is the study of functions $f(x)$ over the real numbers $\mathbb{R}$: \[ f: \mathbb{R} \to \mathbb{R}. \] The function $f$ takes as input some number, usually called $x$ and gives as output another number $f(x)=y$. You are familiar with many functions and have used them in many problems.
In this chapter we will learn about different operations that can be performed on functions. It worth understanding these operations because of the numerous applications which they have.
Differential calculus
Differential calculus is all about derivatives:
- $f'(x)$: the derivative of $f(x)$ is the rate of change of $f$ at $x$.
The derivative is also a function of the form
\[
f': \mathbb{R} \to \mathbb{R},
\]
The output of $f'(x)$ represents the //slope// of
a line parallel (tangent) to $f$ at the point $(x,f(x))$.
Integral calculus
Integral calculus is all about integration:
- $\int_a^b f(x)\:dx$: the integral of $f(x)$ from $x=a$ to $x=b$
corresponds to the area under $f(x)$ between $a$ and $b$:
\[
A(a,b) = \int_a^b f(x) \: dx.
\]
The $\int$ sign is a mnemonic for //sum//.
The integral is the "sum" of $f(x)$ over that interval.
* $F(x)=\int f(x)\:dx$: the anti-derivative of the function $f(x)$
contains the information about the area under the curve for
//all// limits of integration.
The area under $f(x)$ between $a$ and $b$ is computed as the
difference between $F(b)$ and $F(a)$:
\[
A(a,b) = \int_a^b f(x)\;dx = F(b)-F(a).
\]
Sequences and series
Functions are usually defined for continuous inputs $x\in \mathbb{R}$, but there are also functions which are defined only for natural numbers $n \in \mathbb{N}$. Sequences are the discrete analogue functions.
- $a_n$: sequence of numbers $\{ a_0, a_1, a_2, a_3, a_4, \ldots \}$.
You can think about each sequence as a function
\[
a: \mathbb{N} \to \mathbb{R},
\]
where the input $n$ is an integer (index into the sequence) and
the output is $a_n$ which could be any number.
NOINDENT The integral of a sequence is called a series.
- $\sum$: sum.
The summation sign is the short way to express
the sum of several objects:
\[
a_3 + a_4 + a_5 + a_6 + a_7
\equiv \sum_{3 \leq i \leq 7} a_i
\equiv \sum_{i=3}^{7} a_i.
\]
Note that summations could go up to infinity.
* $\sum a_i$: the series corresponds to the running total of a sequence until $n$:
\[
S_n = \sum_{i=1}^{n} a_i = a_1 + a_2 + \cdots + a_{n-1} + a_n.
\]
* $f(x)=\sum_{i=0}^\infty a_i x^i$: a //power series// is a series
which contains powers of some variable $x$.
Power series give us a way to express any function $f(x)$ as
an infinitely long polynomial.
For example, the power series of $\sin(x)$ is
\[
\sin(x)
= x - \frac{x^3}{3!} + \frac{x^5}{5!}
- \frac{x^7}{7!} + \frac{x^9}{9!}+ \ldots.
\]
Don't worry if you don't understand all the notions and the new notation in the above paragraphs. I just wanted to present all the calculus actors in the first scene. We will talk about each of them in more detail in the following sections.
Limits
Actually, we have not mentioned the main actor yet: the limit. In calculus, we do a lot of limit arguments in which we take some positive number $\epsilon>0$ and we make it progressively smaller and smaller:
- $\displaystyle\lim_{\epsilon \to 0}$: the mathematically rigorous
way of saying that the number $\epsilon$ becomes smaller and smaller. We can also take limits to infinity, that is, we imagine some number $N$ and we make that number bigger and bigger:
- $\displaystyle\lim_{N \to \infty}$: the mathematical
way of saying that the number $N$ will get larger and larger.
Indeed, it wouldn't be wrong to say that calculus is the study of the infinitely small and the infinitely many. Working with infinitely small quantities an infinitely large numbers can be tricky business but it is extremely important that you become comfortable with the concept of a limit which is the rigorous way of talking about infinity. Before we learn about derivatives, integrals and series we will spend some time learning about limits.
Infinity
Let's say you have a length $\ell$ and you want to divide it into infinitely many, infinitely short segments. There are infinitely many of them, but they are infinitely short so they add up to the total length $\ell$.
OK, that sounds complicated. Let's start from something simpler. We have a piece of length $\ell$ and we want to divide this length into $N$ pieces. Each piece will have length: \[ \delta = \frac{\ell}{N}. \] Let's check that, together, the $N$ pieces of length $\delta$ add up to the total length of the string: \[ N \delta = N \frac{\ell}{N} = \ell. \] Good.
Now imagine that $N$ is a very large number. In fact it can take on any value, but always larger and larger. The larger $N$ gets, the more fine grained the notion of “small piece of string” becomes. In this case we would have: \[ \lim_{N\to \infty} \delta = \lim_{N\to \infty} \frac{\ell}{N} = 0, \] so effectively the pieces of string are infinitely small. However, when you add them up you will still get: \[ \lim_{N\to \infty} \left( N \delta \right) = \lim_{N\to \infty} \left( N \frac{\ell}{N} \right) = \ell. \]
The lesson to learn here is that, if you keep things well defined you can use the notion of infinity in your equations. This is the central idea of this course.
Infinitely large
The number $\infty$ is really large. How large? Larger than any number you can think of! Say you think of a number $n$, then it is true that $\infty > n$. But no, you say, actually I thought of a different number $N > n$, well still it will be true that $\infty > N$. In fact any finite number you can think of, no matter how large will always be strictly smaller than $\infty$.
Infinitely small
If instead of a really large number, we want to have a really small number $\epsilon$, we can simply define it as the reciprocal of (one over) a really large number $N$: \[ \epsilon = \lim_{N \to \infty \atop N \neq \infty} \frac{1}{N}. \] However small $\epsilon$ must get, it remains strictly greater than zero $\epsilon > 0$. This is ensured by the condition $N\neq \infty$, otherwise if we would have $\lim_{N \to \infty} \frac{1}{N} = 0$.
The infinitely small $\epsilon>0$ is a new beast like nothing you have seen before. It is a non-zero number that is smaller than any number you can think of. Say you think $0.00001$ is pretty small, well it is true that $0.00001 > \epsilon > 0$. Then you say, no actually I was thinking about $10^{-16}$, a number with 15 zeros after the decimal point. It will still be true that $10^{-16} > \epsilon$, or even $10^{-123} > \epsilon > 0$. Like I said, I can make $\epsilon$ smaller than any number you can think of simply by choosing $N$ to be larger and larger, yet $\epsilon$ always remains non-zero.
Infinity for limits
When evaluating a limit, we often make the variable $x$ go to infinity. This is useful information, for example if we want to know what the function $f(x)$ looks like for very large values of $x$. Does it get closer and closer to some finite number, or does it blow up? For example the negative-power exponential function tends to zero for large values of $x$: \[ \lim_{x \to \infty} e^{-x} = 0. \] In the above examples we also saw that the inverse-$x$ function also tends to zero: \[ \lim_{x \to \infty} \frac{1}{x} = 0. \]
Note that in both cases, the functions will never actually reach zero. They get closer and closer to zero but never actually reach it. This is why the limit is a useful quantity, because it says that the functions get arbitrarily close to 0.
Sometimes infinity might come out as an answer to a limit question: \[ \lim_{x\to 3^-} \frac{1}{3-x} = \infty, \] because as $x$ gets closer to $3$ from below, i.e., $x$ will take on values like $2.9$, $2.99$, $2.999$, and so on and so forth, the number in the denominator will get smaller and smaller, thus the fraction will get larger and larger.
Infinity for derivatives
The derivative of a function is its slope, defined as the “rise over run” for an infinitesimally short run: \[ f'(x) = \lim_{\epsilon \to 0} \frac{\text{rise}}{\text{run}} = \lim_{\epsilon \to 0} \frac{f(x+\epsilon)\ - \ f(x)}{x+\epsilon \ - \ x}. \]
Infinity for integrals
The area under the curve $f(x)$ for values of $x$ between $a$ and $b$, can be though of as consisting of many little rectangles of width $\epsilon$ and height $f(x)$: \[ \epsilon f(a) + \epsilon f(a+\epsilon) + \epsilon f(a+2\epsilon) + \cdots + \epsilon f(b-\epsilon). \] In the limit where we take infinitesimally small rectangles, we obtain the exact value of the integral \[ \int_a^b f(x) \ dx= A(a,b) = \lim_{\epsilon \to 0}\left[ \epsilon f(a) + \epsilon f(a+\epsilon) + \epsilon f(a+2\epsilon) + \cdots + \epsilon f(b-\epsilon) \right], \]
Infinity for series
For a given $|r|<1$, what is the sum \[ S = 1 + r + r^2 + r^3 + r^4 + \ldots = \sum_{k=0}^\infty r^k \ \ ? \] Obviously, taking your calculator and performing the summation is not practical since there are infinitely many terms to add.
For several such infinite series, there is actually a closed form formula for their sum. The above series is called the geometric series and its sum is $S=\frac{1}{1-r}$. How were we able to tame the infinite? In this case, we used the fact that $S$ is similar to a shifted version of itself $S=1+rS$, and then solved for $S$.
Limits
To understand the ideas behind derivatives and integrals, you need to understand what a limit is and how to deal with the infinitely small, infinitely large and the infinitely many. In practice, using calculus doesn't actually involve taking limits since we will learn direct formulas and algebraic rules that are more convenient than doing limits. Do not skip this section though just because it is “not on the exam”. If you do so, you will not know what I mean when I write things like $0,\infty$ and $\lim$ in later sections.
Introduction in three acts
Zeno's paradox
The ancient greek philosopher Zeno once came up with the following argument. Suppose an archer shoots an arrow and sends it flying towards a target. After some time it will have travelled half the distance, and then at some later time it will have travelled the half of the remaining distance and so on always getting closer to the target. Zeno observed that no matter how little distance remains to the target, there will always be some later instant when the arrow will have travelled half of that distance. Thus, he reasoned, the arrow must keep getting closer and closer to the target, but never reaches it.
Zeno, my brothers and sisters, was making some sort of limit argument, but he didn't do it right. We have to commend him for thinking about such things centuries before calculus was invented (17th century), but shouldn't repeat his mistake. We better learn how to take limits, because limits are important. I mean a wrong argument about limits could get you killed for God's sake! Imagine if Zeno tried to verify experimentally his theory about the arrow by placing himself in front of one such arrow!
Two monks
Two young monks were sitting in silence in a Zen garden one autumn afternoon.
“Can something be so small as to become nothing?” asked one of the monks, braking the silence.
“No,” replied the second monk, “if it is something then it is not nothing.”
“Yes, but what if no matter how close you look you cannot see it, yet you know it is not nothing?”, asked the first monk, desiring to see his reasoning to the end.
The second monk didn't know what to say, but then he found a counterargument. “What if, though I cannot see it with my naked eye,
I could see it using a magnifying glass?”.
The first monk was happy to hear this question, because he had already prepared a response for it. “If I know that you will be looking with a magnifying glass, then I will make it so small that you cannot see with you magnifying glass.”
“What if I use a microscope then?”
“I can make the thing so small that even with a microscope you cannot see it.”
“What about an electron microscope?”
“Even then, I can make it smaller, yet still not zero.” said the first monk victoriously and then proceeded to add “In fact, for any magnifying device you can come up with, you just tell me the resolution and I can make the thing smaller than can be seen”.
They went back to concentrating on their breathing.
Epsilon and delta
The monks have the right reasoning but didn't have the right language to express what they mean. Zeno has the right language, the wonderful Greek language with letters like $\epsilon$ and $\delta$, but he didn't have the right reasoning. We need to combine aspects of both of the above stories to understand limits.
Let's analyze first Zeno's paradox. The poor brother didn't know about physics and the uniform velocity equation of motion. If an object is moving with constant speed $v$ (we ignore the effects of air friction on the arrow), then its position $x$ as a function of time is given by \[ x(t) = vt+x_i, \] where $x_i$ is the initial location where the object starts from at $t=0$. Suppose that the archer who fired the arrow was at the origin $x_i=0$ and that the target is at $x=L$ metres. The arrow will hit the target exactly at $t=L/v$ seconds. Shlook!
It is true that there are times when the arrow will be $\frac{1}{2}$, $\frac{1}{4}$, $\frac{1}{8}$th, $\frac{1}{16}$th, and so forth distance from the target. In fact there infinitely many of those fractional time instants before the arrow hits, but that is beside the point. Zeno's misconception is that he thought that these infinitely many timestamps couldn't all fit in the timeline since it is finite. No such problem exists though. Any non-zero interval on the number line contains infinitely many numbers ($\mathbb{Q}$ or $\mathbb{R}$).
Now let's get to the monks conversation. The first monk was talking about the function $f(x)=\frac{1}{x}$. This function becomes smaller and smaller but it never actually becomes zero: \[ \frac{1}{x} \neq 0, \textrm{ even for very large values of } x, \] which is what the monk told us.
Remember that the monk also claimed that the function $f(x)$ can be made arbitrarily small. He wants to show that, in the limit of large values of $x$, the function $f(x)$ goes to zero. Written in math this becomes \[ \lim_{x\to \infty}\frac{1}{x}=0. \]
To convince the second monk that he can really make $f(x)$ arbitrarily small, he invents the following game. The second monk announces a precision $\epsilon$ at which he will be convinced. The first monk then has to choose an $S_\epsilon$ such that for all $x > S_\epsilon$ we will have \[ \left| \frac{1}{x} - 0 \right| < \epsilon. \] The above expression indicates that $\frac{1}{x}\approx 0$ at least up to a precision of $\epsilon$.
The second monk will have no choice but to agree that indeed $\frac{1}{x}$ goes to 0 since the argument can be repeated for any required precision $\epsilon >0$. By showing that the function $f(x)$ approaches $0$ arbitrary closely for large values of $x$, we have proven that $\lim_{x\to \infty}f(x)=0$.
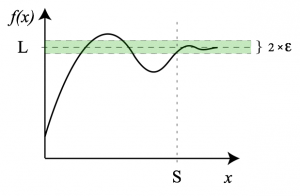 More generally, the function $f(x)$ can converge to any number $L$
for as $x$ takes on larger and larger values:
\[
\lim_{x \to \infty} f(x) = L.
\]
The above expressions means that, for any precision $\epsilon>0$,
there exists a starting point $S_\epsilon$,
after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision:
\[
\left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon.
\]
More generally, the function $f(x)$ can converge to any number $L$
for as $x$ takes on larger and larger values:
\[
\lim_{x \to \infty} f(x) = L.
\]
The above expressions means that, for any precision $\epsilon>0$,
there exists a starting point $S_\epsilon$,
after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision:
\[
\left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon.
\]
Example
You are asked to calculate $\lim_{x\to \infty} \frac{2x+1}{x}$, that is you are given the function $f(x)=\frac{2x+1}{x}$ and you have to figure out what the function looks like for very large values of $x$. Note that we can rewrite the function as $\frac{2x+1}{x}=2+\frac{1}{x}$ which will make it easier to see what is going on: \[ \lim_{x\to \infty} \frac{2x+1}{x} = \lim_{x\to \infty}\left( 2 + \frac{1}{x} \right) = 2 + \lim_{x\to \infty}\left( \frac{1}{x} \right) = 2 + 0, \] since $\frac{1}{x}$ tends to zero for large values of $x$.
In a first calculus course you are not required to prove statements like $\lim_{x\to \infty}\frac{1}{x}=0$, you can just assume that the result is obvious. As the denominator $x$ becomes larger and larger, the fraction $\frac{1}{x}$ becomes smaller and smaller.
Types of limits
Limits to infinity
\[ \lim_{x\to \infty} f(x) \] what happens to $f(x)$ for very large values of $x$.
Limits to a number
The limit of $f(x)$ approaching $x=a$ from above (from the right) is denoted: \[ \lim_{x\to a^+} f(x) \] Similarly, the expression \[ \lim_{x\to a^-} f(x) \] describes what happens to $f(x)$ as $x$ approaches $a$ from below (from the left), i.e., with values like $x=a-\delta$, with $\delta>0, \delta \to 0$. If both limits from the left and from the right of some number are equal, then we can talk about the limit as $x\to a$ without specifying the direction: \[ \lim_{x\to a} f(x) = \lim_{x\to a^+} f(x) = \lim_{x\to a^-} f(x). \]
Example 2
You now asked to calculate $\lim_{x\to 5} \frac{2x+1}{x}$. \[ \lim_{x\to 5} \frac{2x+1}{x} = \frac{2(5)+1}{5} = \frac{11}{5}. \]
Example 3
Find $\lim_{x\to 0} \frac{2x+1}{x}$. If we just plug $x=0$ into the fraction we get an error divide by zero $\frac{2(0)+1}{0}$ so a more careful treatment will be required.
Consider first the limit from the right $\lim_{x\to 0+} \frac{2x+1}{x}$. We want to approach the value $x=0$ with small positive numbers. The best way to carry out the calculation is to define some small positive number $\delta>0$, to choose $x=\delta$, and to compute the limit: \[ \lim_{\delta\to 0} \frac{2(\delta)+1}{\delta} = 2 + \lim_{\delta\to 0} \frac{1}{\delta} = 2 + \infty = \infty. \] We took it for granted that $\lim_{\delta\to 0} \frac{1}{\delta}=\infty$. Intuitively, we can imagine how we get closer and closer to $x=0$ in the limit. When $\delta=10^{-3}$ the function value will be $\frac{1}{\delta}=10^3$. When $\delta=10^{-6}$, $\frac{1}{\delta}=10^6$. As $\delta \to 0$ the function will blow up—$f(x)$ will go up all the way to infinity.
If we take the limit from the left (small negative values of $x$) we get \[ \lim_{\delta\to 0} f(-\delta) =\frac{2(-\delta)+1}{-\delta}= -\infty. \] Therefore, since $\lim_{x\to 0^+}f(x)$ does not equal $\lim_{x\to 0^-} f(x)$, we say that $\lim_{x\to 0} f(x)$ does not exist.
Continuity
A function $f(x)$ is continuous at $a$ if the limit of $f$ as $x\to a$ converges to $f(a)$: \[ \lim_{x \to a} f(x) = f(a). \]
Most functions we will study in calculus are continuous, but not all functions are. For example, functions which make sudden jumps are not continuous. Another examples is the function $f(x)=\frac{2x+1}{x}$ which is discontinuous at $x=0$ (because the limit $\lim_{x \to 0} f(x)$ doesn't exist and $f(0)$ is not defined). Note that $f(x)$ is continuous everywhere else on the real line.
Formulas
We now switch gears into reference mode, as I will state a whole bunch known formulas for limits of various kinds of functions. You are not meant to know why these limit formulas are true, but simply understand what they mean.
The following statements tell you about the relative sizes of functions. If the limit of the ratio of two functions is equal to $1$, then these functions must behave similarly in the limit. If the limit of the ratio goes to zero, then one function must be much larger than the other in the limit.
Limits of trigonometric functions: \[ \lim_{x\rightarrow0}\frac{\sin(x)}{x}=1,\quad \lim_{x\rightarrow0} \cos(x)=1,\quad \lim_{x\rightarrow 0}\frac{1-\cos x }{x}=0, \quad \lim_{x\rightarrow0}\frac{\tan(x)}{x}=1. \]
The number $e$ is defined as one of the following limits: \[ e \equiv \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n = \lim_{\epsilon\to 0 }(1+\epsilon)^{1/\epsilon}. \] The first limit corresponds to a compound interest calculation, with annual interest rate of $100\%$ and compounding performed infinitely often.
For future reference, we state some other limits involving the exponential function: \[ \lim_{x\rightarrow0}\frac{{\rm e}^x-1}{x}=1,\qquad \quad \lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n={\rm e}^x. \]
These are some limits involving logarithms: \[ \lim_{x\rightarrow 0^+}x^a\ln(x)=0,\qquad \lim_{x\rightarrow\infty}\frac{\ln^p(x)}{x^a}=0, \ \forall p < \infty \] \[ \lim_{x\rightarrow0}\frac{\ln(x+a)}{x}=a,\qquad \lim_{x\rightarrow0}\left(a^{1/x}-1\right)=\ln(a). \]
A polynomial of degree $p$ and the exponential function base $a$ with $a > 1$ both go to infinity as $x$ goes to infinity: \[ \lim_{x\rightarrow\infty} x^p= \infty, \qquad \qquad \lim_{x\rightarrow\infty} a^x= \infty. \] Though both functions go to infinity, the exponential function does so much faster, so their relative ratio goes to zero: \[ \lim_{x\rightarrow\infty}\frac{x^p}{a^x}=0, \qquad \mbox{for all } p \in \mathbb{R}, |a|>1. \] In computer science, people make a big deal of this distinction when comparing the running time of algorithms. We say that a function is computable if the number of steps it takes to compute that function is polynomial in the size of the input. If the algorithm takes an exponential number of steps, then for all intents and purposes it is useless, because if you give it a large enough input the function will take longer than the age of the universe to finish.
Other limits: \[ \lim_{x\rightarrow0}\frac{\arcsin(x)}{x}=1,\qquad \lim_{x\rightarrow\infty}\sqrt[x]{x}=1. \]
Limit rules
If you are taking the limit of a fraction $\frac{f(x)}{g(x)}$, and you have $\lim_{x\to\infty}f(x)=0$ and $\lim_{x\to\infty}g(x)=\infty$, then we can informally write: \[ \lim_{x\to \infty} \frac{f(x)}{g(x)} = \frac{\lim_{x\to \infty} f(x)}{ \lim_{x\to \infty} g(x)} = \frac{0}{\infty} = 0, \] since both functions are helping to drive the fraction to zero.
Alternately if you ever get a fraction of the form $\frac{\infty}{0}$ as a limit, then both functions are helping to make the fraction grow to infinity so we have $\frac{\infty}{0} = \infty$.
L'Hopital's rule
Sometimes when evaluating limits of fractions $\frac{f(x)}{g(x)}$, you might end up with a fraction like \[ \frac{0}{0}, \qquad \text{or} \qquad \frac{\infty}{\infty}. \] These are undecidable conditions. Is the effect of the numerator stronger or the effect of the denominator stronger?
One way to find out, is to compare the ratio of their derivatives. This is called L'Hopital's rule: \[ \lim_{x\rightarrow a}\frac{f(x)}{g(x)} \ \ \ \overset{\textrm{H.R.}}{=} \ \ \ \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}. \]
Derivatives
The derivative of a function $f(x)$ is another function, which we will call $f'(x)$ that tells you the slope of $f(x)$. For example, the constant function $f(x)=c$ has slope $f'(x)=0$, since a constant function is flat. What is the derivative of a line $f(x)=mx+b$? The derivative is the slope right, so we must have $f'(x)=m$. What about more complicated functions?
Definition
The derivative of a function is defined as: \[ f'(x) \equiv \lim_{ \epsilon \rightarrow 0}\frac{f(x+\epsilon)-f(x)}{\epsilon}. \] You can think of $\epsilon$ as a really small number. I mean really small. The above formula is nothing more than the rise-over-run rule for calculating the slope of a line, \[ \frac{ rise } { run } = \frac{ \Delta y } { \Delta x } = \frac{y_f - y_i}{x_f - x_i} = \frac{f(x+\epsilon)\ - \ f(x)}{x + \epsilon \ -\ x}, \] but by taking $\epsilon$ to be really small, we will get the slope at the point $x$.
Derivatives occur so often in math that people have come up with many different notations for them. Don't be fooled by that. All of them mean the same thing $Df(x) = f'(x)=\frac{df}{dx}=\dot{f}=\nabla f$.
Applications
Knowing how to take derivatives is very useful in life. Given some phenomenon described by $f(x)$ you can say how it changes over time. Many times we don't actually care about the value of $f'(x)$, just its sign. If the derivative is positive $f'(x) > 0$, then the function is increasing. If $f'(x) < 0$ then the function is decreasing.
When the function is flat at a certain $x$ then $f'(x)=0$. The points where $f'(x)=0$ (the roots of $f'(x)$) are very important for finding the maximum and minimum values of $f(x)$. Recall how we calculated the maximum height $h$ that projectile reaches by first finding the time $t_{top}$ when its velocity in the $y$ direction was zero $y^\prime(t_{top})=v(t_{top})=0$ and then substituting this time in $y(t)$ to obtain $h=\max\{ y(t) \} =y(t_{top})$.
Example
Now let's take a derivative of $f(x)=2x^2 + 3$ to see how that complicated-looking formula works: \[ f'(x)=\lim_{\epsilon \rightarrow 0} \frac{f(x+\epsilon)-f(x)}{\epsilon} = \lim_{\epsilon \rightarrow 0} \frac{2(x+\epsilon)^2+3 \ \ - \ \ 2x^2 + 3}{\epsilon}. \] Let's simplify the right-hand side a bit \[ \frac{2x^2+ 4x\epsilon +\epsilon^2 - 2x^2}{\epsilon} = \frac{4x\epsilon +\epsilon^2}{\epsilon}= \frac{4x\epsilon}{\epsilon} + \frac{\epsilon^2}{\epsilon}. \] Now when we take the limit, the second term disappears: \[ f'(x) = \lim_{\epsilon \rightarrow 0} \left( \frac{4x\epsilon}{\epsilon} + \frac{\epsilon^2}{\epsilon} \right) = 4x + 0. \] Congratulations, you have just taken your first derivative! The calculations were not that complicated, but it was pretty long and tedious. The good news is that you only need to calculate the derivative from first principles only once. Once you find a derivative formula for a particular function, you can use the formula every time you see a function of that form.
A derivative formula
\[ f(x) = x^n \qquad \Rightarrow \qquad f'(x) = n x^{n-1}. \]
Example
Use the above formula to find the derivatives of the following three functions: \[ f(x) = x^{10}, \quad g(x) = \sqrt{x^3}, \qquad h(x) = \frac{1}{x^3}. \] In the first case, we use the formula directly to find the derivative $f'(x)=10x^9$. In the second case, we first use the fact that square root is equivalent to an exponent of $\frac{1}{2}$ to rewrite the function as $g(x)=x^{\frac{3}{2} }$, then using the formula we find that $g'(x)=\frac{3}{2}x^{\frac{1}{2} } =\frac{3}{2}\sqrt{x}$. We can also rewrite the third function as $h(x)=x^{-3}$ and then compute the derivative $h'(x)=-3x^{-4}=\frac{-3}{x^4}$ using the formula.
Discussion
In the next section we will develop derivative formulas for other functions.
Derivative formulas
The table below shows the derivative formulas for a number of commonly used functions. You will be using these derivative formulas a lot in the remainder of this chapter so it might be a good idea to memorize them.
Formulas to memorize
\[ \begin{align*} F(x) & \ - \textrm{ diff. } \to \quad F'(x) \nl \int f(x)\;dx & \ \ \leftarrow \textrm{ int. } - \quad f(x) \nl a &\qquad\qquad\qquad 0 \nl x &\qquad\qquad\qquad 1 \nl af(x) &\qquad\qquad\qquad af'(x) \nl f(x)+g(x) &\qquad\qquad\qquad f'(x)+g'(x) \nl x^n &\qquad\qquad\qquad nx^{n-1} \nl 1/x=x^{-1} &\qquad\qquad\qquad -x^{-2} \nl \sqrt{x}=x^{\frac{1}{2}} &\qquad\qquad\qquad \frac{1}{2}x^{-\frac{1}{2}} \nl {\rm e}^x &\qquad\qquad\qquad {\rm e}^x \nl a^x &\qquad\qquad\qquad a^x\ln(a) \nl \ln(x) &\qquad\qquad\qquad 1/x \nl \log_a(x) &\qquad\qquad\qquad (x\ln(a))^{-1} \nl \sin(x) &\qquad\qquad\qquad \cos(x) \nl \cos(x) &\qquad\qquad\qquad -\sin(x) \nl \tan(x) &\qquad\qquad\qquad \sec^2(x)\equiv\cos^{-2}(x) \nl \csc(x) \equiv \frac{1}{\sin(x)} &\qquad\qquad\qquad -\sin^{-2}(x)\cos(x) \nl \sec(x) \equiv \frac{1}{\cos(x)} &\qquad\qquad\qquad \tan(x)\sec(x) \nl \cot(x) \equiv \frac{1}{\tan(x)} &\qquad\qquad\qquad -\csc^2(x) \nl \sinh(x) &\qquad\qquad\qquad \cosh(x) \nl \cosh(x) &\qquad\qquad\qquad \sinh(x) \nl \sin^{-1}(x) &\qquad\qquad\qquad \frac{1}{\sqrt{1-x^2}} \nl \cos^{-1}(x) &\qquad\qquad\qquad \frac{-1}{\sqrt{1-x^2}} \nl \tan^{-1}(x) &\qquad\qquad\qquad \frac{1}{1+x^2} \end{align*} \]
There is a complete table of derivative formulas in the back of the book.
Links
[ An even longer list of derivative formulas ]
http://en.wikipedia.org/wiki/Lists_of_integrals
Derivative rules
Taking derivatives is a simple task: you just have to lookup the appropriate formula in the table of derivative formulas. However the tables of derivatives usually don't have the formulas for composite functions. In this section, we will learn about some important rules for derivatives, so that you will know how to handle derivatives of composite functions.
Formulas
Linearity
The derivative of a sum of two functions is the sum of the derivatives: \[ \left[f(x) + g(x)\right]^\prime= f^\prime(x) + g^\prime(x), \] and for any constant $a$, we have \[ \left[a f(x)\right]^\prime= a f^\prime(x). \] The fact that the derivative operation obeys these two conditions means that derivatives are linear operations.
Product rule
The derivative of a product of two functions is obtained as follows: \[ \left[ f(x)g(x) \right]^\prime = f^\prime(x)g(x) + f(x)g^\prime(x). \]
Quotient rule
As a special case the product rule, we obtain the derivative rule for a fraction of two functions: \[ \frac{d}{dx}\left[ \frac{f(x)}{g(x)}\right]^\prime=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}. \]
Chain rule
If you have a situation with an inner function and outer function like $f(g(x))$, then the derivative is obtained in a two step process: \[ \left[ f(g(x)) \right]^\prime = f^\prime(g(x))g^\prime(x). \] In the first step you leave $g(x)$ alone and focus on taking the derivative of the outer function. Just copy over whatever $g(x)$ is inside the $f'$ expression. The second step is to multiply the resulting expression by the derivative of the inner function $g'(x)$.
In words, the chain rule tells us that the rate of change of a composite function can be calculated as the product of the rate of change of the components.
Example
\[ \frac{d}{dx}\left[ \sin(x^2)) \right] = \cos(x^2)[x^2]' = \cos(x^2)2x. \]
More complicated example
The chain rule also applies to functions of functions of functions $f(g(h(x)))$. To take the derivative, just start from the outermost function and then work your way towards $x$. \[ \left[ f(g(h(x))) \right]' = f'(g(h(x))) g'(h(x)) h'(x). \] Now let's try this \[ \frac{d}{dx} \left[ \sin( \ln( x^3) ) \right] = \cos( \ln(x^3) ) \frac{1}{x^3} 3x^2 = \cos( \ln(x^3) ) \frac{3}{x}. \] Simple right?
Examples
The above rules are all that you need to take the derivative of any function no matter how complicated. To convince you of this, I will now show you some examples of really hairy functions. Don't be scared by complexity: as long as you follow the rules, you will get the right answer in the end.
Example
Calculate the derivative of \[ f(x) = e^{x^2}. \] We just need the chain rule for this one: \[ \begin{align} f'(x) & = e^{x^2}[x^2]' \nl & = e^{x^2}2x. \end{align} \]
Example 2
\[ f(x) = \sin(x)e^{x^2}. \] We will need the product rule for this one: \[ \begin{align} f'(x) & = \cos(x)e^{x^2} + \sin(x)2xe^{x^2}. \end{align} \]
Example 3
\[ f(x) = \sin(x)e^{x^2}\ln(x). \] This is still the product rule, but now we will have three terms. In each term, we take the derivative of one of the functions and multiply by the other two: \[ \begin{align} f'(x) & = \cos(x)e^{x^2}\ln(x) + \sin(x)2xe^{x^2}\ln(x) + \sin(x)e^{x^2}\frac{1}{x}. \end{align} \]
Example 4
Ok let's go crazy now: \[ f(x) = \sin\!\left( \cos\!\left( \tan(x) \right) \right). \] We need a triple chain rule for this one: \[ \begin{align} f'(x) & = \cos\!\left( \cos\!\left( \tan(x) \right) \right) \left[ \cos\!\left( \tan(x) \right) \right]^\prime \nl & = -\cos\!\left( \cos\!\left( \tan(x) \right) \right) \sin\!\left( \tan(x) \right)\left[ \tan(x) \right]^\prime \nl & = -\cos\!\left( \cos\!\left( \tan(x) \right) \right) \sin\!\left( \tan(x) \right)\sec^2(x). \end{align} \]
Explanations
Proof of the product rule
By definition, the derivative of $f(x)g(x)$ is \[ \left( f(x)g(x) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(x+\epsilon)g(x+\epsilon)-f(x)g(x)}{\epsilon}. \] Consider the numerator of the fraction. If we add and subtract $f(x)g(x+\epsilon)$, we can factor the expression into two terms like this: \[ \begin{align} & f(x+\epsilon)g(x+\epsilon) \ \overbrace{-f(x)g(x+\epsilon) +f(x)g(x+\epsilon)}^{=0} \ - f(x)g(x) \nl & \ \ \ = [f(x+\epsilon)-f(x) ]g(x+\epsilon) + f(x)[ g(x+\epsilon)- g(x)], \end{align} \] thus the expression for the derivative of the product becomes \[ \left( f(x)g(x) \right)' = \left\{ \lim_{\epsilon \rightarrow 0} \frac{[f(x+\epsilon)-f(x) ]}{\epsilon}g(x+\epsilon) + f(x) \frac{[ g(x+\epsilon)- g(x)]}{\epsilon} \right\}. \] This looks almost exactly like the product rule formula, except that we have $g(x+\epsilon)$ instead of $g(x)$. This is not a problem, though, since we assumed that $f(x)$ and $g(x)$ are differentiable functions, which implies that they are continuous functions. For continuous functions, we have $\lim_{\epsilon \rightarrow 0}g(x+\epsilon) = g(x)$ and we obtain the final form of the product rule: \[ \left( f(x)g(x) \right)' = f'(x)g(x) + f(x)g'(x). \]
Proof of the chain rule
Before we begin the proof, I want to make a remark on the notation used in the definition of the derivative. I like the greek letter epsilon $\epsilon$ so I defined the derivative of $f(x)$ as \[ f'(x)=\lim_{\epsilon \rightarrow 0} \frac{f(x+\epsilon)-f(x)}{\epsilon}, \] but I could have used any other variable instead: \[ f'(x) \equiv \lim_{\delta \rightarrow 0} \frac{f(x+\delta)-f(x)}{\delta} \equiv \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}. \] All that matters is that we divide by the same quantity that is added to $x$ in the numerator, and that this quantity goes to zero.
The derivative of $f(g(x))$ is \[ \left( f(g(x)) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(g(x+\epsilon))-f(g(x))}{\epsilon}. \] The trick is to define a new quantity \[ \delta = g(x+\epsilon)-g(x), \] and then substitute $g(x+\epsilon) = g(x) + \delta$ into the expression for the derivative as follows \[ \left( f(g(x)) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\epsilon}. \] This is starting to look more like a derivative formula, but the quantity added in the input is different from the quantity by which we divide. To fix this we will multiply and divide by $\delta$ to obtain \[ \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\epsilon}\frac{\delta}{\delta} = \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\delta}\frac{\delta}{\epsilon}. \] We now use the definition of the quantity $\delta$ and rearrange the fraction as follows: \[ \left( f(g(x)) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\delta}\frac{g(x+\epsilon)-g(x)}{\epsilon}. \] This is starting to look a lot like $f'(g(x))g'(x)$, and in fact it is: taking the limit $\epsilon \to 0$ implies that the quantity $\delta(\epsilon) \to 0$. This is because the function $g(x)$ is continuous: $\lim_{\epsilon \rightarrow 0} g(x+\epsilon)-g(x)=0$. And so the quantity $\delta$ is just as good as $\epsilon$ for taking a derivative. Thus, we have proved that: \[ \left( f(g(x)) \right)' = f'(g(x))g'(x). \]
Alternate notation
The presence of so much primes and brackets in the above expressions can make them difficult to read. This is why we sometimes use a different notation for derivatives. The three rules of derivatives in the alternate notation are as follows:
Linearity: \[ \frac{d}{dx}(\alpha f(x) + \beta g(x))= \alpha\frac{df}{dx} + \beta\frac{dg}{dx}. \] Product rule: \[ \frac{d}{dx}(f(x)g(x)) = \frac{df}{dx}g(x) + f(x)\frac{dg}{dx}. \] Chain rule: \[ \frac{d}{dx}\left( f(g(x)) \right) = \frac{df}{dg}\frac{dg}{dx}. \]
Higher derivatives
In the previous section we learned how to calculate the derivative $f^{\prime}(x)$ of any function $f(x)$. The second derivative of $f(x)$ is the derivative of the derivative of $f(x)$ and it is denoted as: \[ f^{\prime\prime}(x) \equiv \left[ f^{\prime}(x) \right]^\prime \equiv \frac{d}{dx} f^{\prime}(x). \equiv \frac{d^2}{dx^2} f(x). \] This process can be continued further in order to calculate higher derivatives of $f(x)$.
In practice, the first and second derivatives are most important because they have a geometrical interpretation. The first derivative of $f(x)$ describes the slope of $f(x)$ while the second derivative describes the curvature of $f(x)$.
Definitions
- $f(x)$: A function.
- $f^{\prime}(x)$: The first derivative of the function $f(x)$.
The first derivatives contains the information about the slope of the function.
- $f^{\prime\prime}(x)$: The second derivative of the function $f(x)$.
The second derivative contains the information about the curvature of the function $f(x)$.
- If $f^{\prime\prime}(x)>0$, then the function $f(x)$ is convex (opens upwards).
- If $f^{\prime\prime}(x)<0$, then the function $f(x)$ is concave (opens downwards).
- $f^{\prime\prime\prime}(x)\equiv f^{(3)}(x)$: The third derivative of the function $f(x)$.
- $f^{(n)}(x)$: The n$^\textrm{th}$ derivative of the function $f(x)$.
Second derivative
The second derivative describes the change in the value of the first derivative. To obtain $f^{\prime\prime}(x)$ we compute the derivative of $f'(x)$.
The second derivative tells you about the “curvature” of the function $f(x)$. If the curvature of a function is positive ($f^{\prime\prime}(x)>0$), this means that the slope of the function is increasing so the function must be curving upwards. Negative curvature means the function curves downwards.
Example
Calculate the second derivatives of the functions $u(x)=x^2$ and $d(x)=-x^2$ and comment on the shape of these functions.
To solve this problem, we first calculate the first derivative $u^{\prime}(x)=2x$ and $d^{\prime}(x)=-2x$. We obtain the second derivatives by taking the derivative of the first derivative: $u^{\prime\prime}(x)=2$ and $d^{\prime\prime}(x)=-2$. The fact that the second derivative is positive means that the curvature of the function $u(x)$ is always positive. The function $u(x)$ is convex: it opens upwards. On the other hand $d(x)$ is concave: it opens downwards.
The function $u(x)$ and $d(x)$ are canonical examples of functions with positive and negative curvature. If a function $f(x)$ has positive curvature at a point $x^*$ ($f^{\prime\prime}(x^*) > 0$), then the function locally resembles $u(x-x^*)=(x-x^*)^2$. If on the other hand the second derivative of $f(x)$ is negative at $x^*$, then the function locally resembles $d(x-x^*)=-(x-x^*)^2$. In other words, the terms convex and concave refer to the $u$-likeness vs. $d$-likeness property of functions.
Higher derivatives
If we take the derivative of the derivative of the derivative of $f(x)$ we obtain the third derivative of the function. This process can be continued further to obtain the n$^\textrm{th}$ derivative of the function: \[ f^{(n)}(x) \equiv \frac{d^n}{dx^n} f(x) \equiv \underbrace{ \frac{d}{dx} \frac{d}{dx} \cdots \frac{d}{dx} }_{n} f(x). \]
Higher derivatives do not have an obvious geometrical interpretation. However, if you are given a function $f(x)$ such that $f^{\prime\prime\prime}(x)>0$, then the function $f(x)$ must be $+x^3$-like. Alternately, if $f^{\prime\prime\prime}(x)<0$, then the function must resemble $-x^3$.
Later in this chapter, we will learn how to compute the Taylor series of a function, which is a procedure used to find polynomial approximations to any function $f(x)$: \[ f(x) \ \approx \ a_0 + a_1x + a_2x^2 + a_3x^3 + a_4x^4 + \cdots + a_n x^n. \] The values of the coefficients $a_0$, $a_1$, $\ldots$, $a_n$ in the approximation will require computing higher derivatives of $f(x)$. The coefficient $a_n$ tells us whether $f(x)$ is more similar to $+x^n$ or $-x^n$.
Example
Compute the third derivative of $f(x)=\sin(x)$.
The first derivative is $f^{\prime}(x)=\cos(x)$. The second derivative will be $f^{\prime\prime}(x)=-\sin(x)$ and so the third derivative must be $f^{\prime\prime\prime}(x)=-\cos(x)$.
Optimization: calculus' killer app
The reason why you need to learn about derivatives is that this skill will allow you to optimize any function. Suppose you have control over the input of the function $f(x)$ and you want to pick the best value of $x$. Best usually means maximum (if the function measures something good like profits) or minimum (if the function describes something bad like costs).
Example
The drug boss for the whole of lower Chicago area has recently had a lot of problems with the police intercepting his people on the street. It is clear that the more drugs he sells the more, money he will make, but if he starts to sell too much, the police arrests start to become more frequent and he loses money.
Fed up with this situation, he decides he needs to find the optimal amount of drugs to put out on the streets: as much as possible, but not too much for the police raids to kick in. So one day he tells his brothers and sisters in crime to leave the room and picks up a pencil and a piece of paper to do some calculus.
If $x$ is the amount of drugs he puts out on the street every day, then the amount of money he makes is given by the function: \[ f(x) = 3000x e^{-0.25x}, \] where the linear part $3000x$ represents his profits if there is no police and the $e^{-0.25x}$ represents the effects of the police stepping up their actions when more drugs is pumped on the street.
Looking at the function he asks “What is the value of $x$ which will give me the most profits from my criminal dealings?” Stated mathematically, he is asking for \[ \mathop{\text{argmax}}_x \ 3000x e^{-0.25x} \ = \ ?, \] which is read “find the value of the argument $x$ that gives the maximum value of $f(x)$.”
He remembers the steps required to find the maximum of a function from a conversation with a crooked stock trader he met in prison. First he must take the derivative of the function. Because the function is a product of two functions, he has to use the product rule $(fg)' = f'g+fg'$. When he takes the derivative of $f(x)$ he gets: \[ f'(x) = 3000e^{-0.25x} + 3000x(-0.25)e^{-0.25x}. \]
Whenever $f'(x)=0$ this means the function $f(x)$ has zero slope. A maximum is just the kind of place where there is zero slope: think of the peak of a mountain that has steep slopes to the left and to right, but right at the peak it is momentarily horizontal.
So when is the derivative zero? \[ f'(x) = 3000e^{-0.25x} + 3000x(-0.25)e^{-0.25x} = 0. \] We can factor out the $3000$ and the exponential function to get \[ 3000e^{-0.25x}( 1 -0.25x) = 0. \] Now $3000\neq0$ and the exponential function $e^{-0.25x}$ is never equal to zero either so it must be the term in the bracket which is equal to zero: \[ (1 -0.25x) = 0, \] or $x=4$. The slope of $f(x)$ is equal to zero when $x=4$. This correspond to the peak of the curve.
Right then and there the crime boss called his posse back
into the room and proudly announced that from now on his
organization will put out exactly four kilograms of drugs
on the street per day.
“Boss, how much will we make per day if we sell four kilograms?”, asks
one of the gangsters in sweatpants.
“We will make the maximum possible!”, replies the boss.
“Yes I know Boss, but how much money is the maximum?”
The dude in sweatpants is asking a good question.
It is one thing to know where the maximum occurs and it is another to know
the value of the function at this point.
He is asking the following mathematical question:
\[
\max_x \ 3000x e^{-0.25x} \ = \ ?.
\]
Since we already know the value $x^*=4$ where the maximum occurs,
we simply have to plug it into the function $f(x)$ to get:
\[
\max_x f(x) = f(4) = 3000(4)e^{-0.25(4)} = \frac{12000}{e} \approx 4414.55.
\]
After that conversation, everyone, including the boss, started to question
their choice of occupation in life.
Is crime really worth it when you do the numbers?
As you may know, the system is obsessed with this whole optimization thing. Optimize to make more profits, optimize to minimize costs, optimize stealing of natural resources from Third World countries, optimize anything that moves basically. Therefore, the system wants you, the young and powerful generation of the future, to learn this important skill and become faithful employees in the corporations. They want you to know so that you can help them optimize things, so that the whole enterprise will continue to run smoothly.
Mathematics makes no value judgments about what should and should not be optimized; this part is up to you. If, like me, you don't want to use optimization for system shit, you can use calculus for science. It doesn't matter whether it will be physics or medicine or building your own business, it is all good. Just stay away from the system. Please do this for me.
Optimization algorithm
In this section we show and explain the details of the algorithm for finding the maximum of a function. This is called optimization, as in finding the optimal value(s).
Say you have the function $f(x)$ that represents a real world phenomenon. For example, $f(x)$ could represent how much fun you have as a function of alcohol consumed during one evening. We all know that too much $x$ and the fun stops and you find yourself, like the Irish say, “talking to God on the big white phone.” Too little $x$ and you might not have enough Dutch courage to chat up that girl/guy from the table across the room. To have as much fun as possible, you want to find the alcohol consumption $x^*$ where $f$ takes on its maximum value.
This is one of the prominent applications of calculus (optimization not alcohol consumption). This is why you have been learning about all those limits, derivative formulas and differentiation rules in the previous sections.
Definitions
- $x$: the variable we have control over.
- $[x_i,x_f]$: some interval of values where $x$ can be chosen from, i.e., $x_i \leq x \leq x_f$. These are the constraints on the optimization problem. (For the drinking optimization problem $x\geq 0$ since you can't drink negative alcohol, and probably $x<2$ (in litres of hard booze) because roughly around there you will die from alcohol poisoning. So we can say we are searching for the optimal amount of alcohol $x$ in the interval $[0,2]$.)
- $f(x)$: the function we want to optimize. This function has to be differentiable, meaning that we can take its derivative.
- $f'(x)$: The derivative of $f(x)$. The derivative contains the information about the slope of $f(x)$.
- maximum: A place where the function reaches a peak. Furthermore, when there are multiple peaks, we call the highest of them the global maximum, while all others are called local maxima.
- minimum: A place where the function reaches a low point: the bottom of a valley. The global minimum is the lowest point overall, whereas a local minimum is only the minimum in some neighbourhood.
- extremum: An extremum is a general term that includes maximum and minimum.
- saddle point: A place where $f'(x)=0$ but that point is neither a max nor a min. Ex: $f(x)=x^5$ when $x=0$.
Suppose some function $f(x)$ has a global maximum at $x^*$ and the value of that maximum is $f(x^*)=M$. The following mathematical notations apply:
- $\mathop{\text{argmax}}_x \ f(x)=x^*$, to refer the location (the argument) where the maximum occurs.
- $\max_x \ f(x) = M$, to refer to the maximum value.
Algorithm for finding extrema
Input: Some function $f(x)$ and a constraint region $C=[x_i,x_f]$.
Output: The location and value of all maxima and minima of $f(x)$.
You should proceed as follows to find the extrema of a function:
- First look at $f(x)$. If you can, plot it. If not, just try to imagine it.
- Find the derivative $f'(x)$.
- Solve the equation $f'(x)=0$. There will usually be multiple solutions. Make a list of them. We will call this the list of candidates.
- For each candidate $x^*$ in the list check if is a max, a min or a saddle point.
- If $f'(x^*-0.1)$ is positive and $f'(x^*+0.1)$ is negative, then the point $x^*$ is a max.
The function was going up, then flattens at $x^*$ then goes down after $x^*$. Therefore $x^*$ must be a peak.
- If $f'(x^*-0.1)$ is negative and $f'(x^*+0.1)$ is positive, then the point $x^*$ is a min.
The function goes down, flattens then goes up, so the point must be a minimum.
- If $f'(x^*-0.1)$ and $f'(x^*+0.1)$ have the same sign, then the point $x^*$ is a saddle point. Remove it from the list of candidates.
- Now go through the list one more time and reject all candidates $x^*$ that do not satisfy the constraints C. In other words if $x\in [x_i,x_f]$ it stays, but if $x \not\in [x_i,x_f]$, we remove it since it is not feasible. For example, if you have a candidate solution in the alcohol consumption problem that says you should drink 5[L] of booze, you have to reject it, because otherwise you would die.
- Add $x_i$ and $x_f$ to the list of candidates. These are the boundaries of the constraint region and should also be considered. If no constrain was specified use the default constraint $x \in \mathbb{R}\equiv[-\infty,\infty]$ and add $-\infty$ and $\infty$ to the list.
- For each candidate $x^*$, calculate the function value $f(x^*)$.
The resulting list is a list of local extrema: maxima, minima and endpoints. The global maximum is the largest value from the list of local maxima. The global minimum is the smallest of the local minima.
Note that in dealing with points at infinity like $x^*=\infty$, you are not actually calculating a value but the limit $\lim_{x\to\infty}f(x)$. Usually the function either blows up $f(\infty)=\infty$ (like $x$, $x^2$, $e^x$, $\ldots$), drops down indefinitely $f(\infty)=-\infty$ (like $-x$, $-x^2$, $-e^x$, $\ldots$), or reaches some value (like $\lim_{x\to\infty} \frac{1}{x}=0, \ \lim_{x\to\infty} e^{-x}=0$). If a function goes to positive $\infty$ it doesn't have a global maximum: it simply keeps growing indefinitely. Similarly, functions that go towards negative $\infty$ don't have a global minimum.
Example 1
Find all the maxima and minima of the function \[ f(x)=x^4-8x^2+356. \]
Since no interval is specified we will use the default interval $x \in \mathbb{R}= -\infty,\infty$. Let's go through the steps of the algorithm.
- We don't know how a $x^4$ function looks like, but it is probably similar to the $x^2$ – it goes up to infinity on the far left and the far right.
- Taking the derivative is simple for polynomials:
\[ f'(x)=4x^3-16x. \]
- Now we have to solve
\[ 4x^3-16x=0, \]
which is the same as
\[
4x(x^2-4)=0,
\]
which is the same as
\[
4x(x-2)(x+2)=0.
\]
So our list of candidates is $\{ x=-2, x=0, x=2 \}$.
- For each of these we have to check if it is a max, a min or a saddle point.
- For $x=-2$, we check $f'(-2.1)=4(-2.1)(-2.1-2)(-2.1+2) < 0$ and
$f'(-1.9)=4(-1.9)(-1.9-2)(-1.9+2) > 0$ so $x=-2$ must be minimum.
- For $x=0$ we try $f'(-0.1)=4(-0.1)(-0.1-2)(-0.1+2) > 0$ and
$f'(0.1)=4(0.1)(0.1-2)(0.1+2) < 0$ so we have a maximum.
- For $x=2$, we check $f'(1.9)=4(1.9)(1.9-2)(1.9+2) < 0$
and $f'(2.1)=4(2.1)(2.1-2)(2.1+2) > 0$ so $x=2$ must be a minimum.
- We don't have any constraints so all of the above candidates make the cut.
- We add the two constraint boundaries $-\infty$ and $\infty$ to the list of candidates. At this point our final shortlist of candidates contains $\{ x=-\infty, x=-2, x=0, x=2, x=\infty \}$.
- We now evaluate the function $f(x)$ for each of the values to
get location-value pairs $(x,f(x))$ like so: $\{ (-\infty,\infty),$ $(-2,340),$ $(0,356),$ $(2,340),$ $(\infty,\infty) \}$.
Note that $f(\infty)=\lim_{x\to\infty} f(x) =$ $\infty^4 - 8\infty^2+356$ $= \infty$ and same for $f(-\infty)=\infty$.
We are done now. The function has no global maximum since it goes up to infinity. It has a local maximum at $x=0$ with value $356$ and two global minima at $x=-2$ and $x=2$ both of which have value $340$. Thank you, come again.
Alternate algorithm
Instead of checking nearby points to the left and to the right of each critical point, we can use an alternate Step 4 of the algorithm known as the second derivative test. Recall that the second derivative tells you the curvature of the function: if the second derivative is positive at a critical point $x^*$, then the point $x^*$ must be a minimum. If on the other hand the second derivative at a critical point is negative, then the function must be a maximum at $x^*$. If the second derivative is zero, the test is inconclusive.
Alternate Step 4
- For each candidate $x^*$ in the list check if is a max, a min or a saddle point.
- If $f^{\prime\prime}(x^*) < 0$ then $x^*$ is a max.
- If $f^{\prime\prime}(x^*) > 0$ then $x^*$ is a min.
- If $f^{\prime\prime}(x^*) = 0$ then, revert back to checking nearby values: $f'(x^*-\epsilon)$ and $f'(x^*+\epsilon)$,
to determine if $x^*$ is max, min or saddle point.
Limitations
The above optimization algorithm applies to differentiable functions of a single variable. It just happens to be that most functions you will face in life are of this kind, so what you have learned is very general. Not all functions are differentiable however. Functions with sharp corners like the absolute value function $|x|$ are not differentiable everywhere and therefore we cannot use the algorithms above. Functions with jumps in them (like the Heaviside step function) are not continuous and therefore not differentiable either so the algorithm cannot be used on them either.
There are also more general kinds of functions and optimization scenarios. We can optimize functions of multiple variables $f(x,y)$. You will learn how to do this in multivariable calculus. The techniques will be very similar to the above, but with more variables and intricate constraint regions.
At last, I want to comment on the fact that you can only maximize one function. Say the Chicago crime boss in the example above wanted to maximize his funds $f(x)$ and his gangster street cred $g(x)$. This is not a well posed problem, either you maximize $f(x)$ or you maximize $g(x)$, but you can't do both. There is no reason why a single $x$ will give the highest value for $f(x)$ and $g(x)$. If both functions are important to you, you can make a new function that combines the other two $F(x)=f(x)+g(x)$ and maximize $F(x)$. If gangster street cred is three times more important to you than funds, you could optimize $F(x)=f(x)+3g(x)$, but it is mathematically and logically impossible to maximize two things at the same time.
Exercises
The function $f(x)=x^3-2x^2+x$ has a local maximum on the interval $x \in [0,1]$. Find where this maximum occurs and the value of $f$ at that point. ANS:$\left(\frac{1}{3},\frac{4}{27}\right)$.
Implicit differentiation
You can take the derivative $\frac{dy}{dx}$ of any relation involving $y$ and $x$ in order to find the slope.
As an example, consider the relation that describes a circle of radius $R$: \[ x^2 + y^2 = R^2. \] We are given a point $P=(x_P,y_P)$ that lies on the circle and asked to find the slope of the circle at that point. We begin by taking the implicit derivative of the relation that describes the circle \[ \begin{align*} \big[\ x^2 \ + \ \ y^2 \ \ \ &= R^2 \big]' \nl 2x + 2y\frac{dy}{dx} &= 0. \end{align*} \] After rearranging the terms a bit, we find that the slope of the circle at point $P=(x_P,y_P)$ is given by \[ \frac{dy}{dx} = - \frac{x_P}{y_P}. \] You can check that the slope predicted at $P=(0,R)$ is $0$ (the circle is flat at the top) and that at $P=(R,0)$, the slope is infinite since the tangent to the circle is vertical.
As you can see there is nothing fancy going on, we just went through and took the derivative of each term in the equation, and then used the result to isolate the slope $\frac{dy}{dx}$. In particular we didn't have to explicitly find the $y$ as a function of $x$, (which is actually possible $y=f(x)=\pm \sqrt{R^2-x^2}$). We took the derivative directly on expression describing the circle treating implicitly $y$ is a function of $x$.
Definitions
- $g(x,y)=0$: a relation between the variables $x$ and $y$.
- $\big[ g(x,y) \big]' = 0$: the implicit derivative of the
expression with respect to the variable $x$.
Examples
Corporate Joe
In corporate America, a man's ego $E$ is related to his salary $S$ by the following equation: \[ E^2 = S^3. \] Assume that both $E$ and $S$ are implicitly functions of time. What is the rate of change of the ego of dirty Joe the insurance analyst, when he is making 60k and his salary is increasing at a rate of 5k per year?
We are told that $\frac{dS}{dt}=5000$ and we are asked to find $\frac{dE}{dt}$ when $S=60000$. To do this we first take the implicit derivative of the salary-to-ego relation as follows: \[ 2E \frac{dE}{dt} = 3 S^2 \frac{dS}{dt}. \] We are interested in the point where $S=60000$. To find Joe's ego at that point, we use the original relation $ E^2 = S^3$ and solving for $E$ we find $E=\sqrt{ 60000^3}= 14696938.46$ ego points. Substituting all these values into the derivative of the relation we find that \[ 2(14696938.46)\frac{dE}{dt} = 3 (60 000)^2 (5000). \] Joe's ego is growing at $\frac{dE}{dt}=\frac{3 (60 000)^2 (5000)}{2(14696938.46)} = 1837117.31$ ego points per year. Yey ego points! I wonder what you can redeem these for…
Error bars
You want to calculate the precision associated with your measurement of the kinetic energy of some particle. Recall that the formula for the kinetic energy is $K = \frac{1}{2}m v^2$. Your measurement of the mass $m$ has precision 3%, and the measurement of the velocity has precision 2%. What will be the precision of your calculation for the kinetic energy?
The precision of any measurement is defined as ratio of the error divided by the quantity itself. We report our measurement of some quantity $Q$ as $Q \pm dQ$. The relative error (in percent) is $\frac{dQ}{Q}$.
In this case we want to find $\frac{dK}{K}$ and we are told $\frac{dm}{m}=0.03$ and $\frac{dv}{v}=0.02$. We proceed by calculus, taking the implicit derivative of the expression for kinetic energy: \[ dK = d\left( \frac{1}{2}m v^2 \right) = \frac{1}{2}(dm) v^2 + m v (dv), \] where we used the product rule of derivatives. In order to obtain ratios, we divide both sides by $K$ to obtain: \[ \frac{dK}{K} = \frac{\frac{1}{2}dm v^2 \ + \ m v dv}{ \frac{1}{2}m v^2 } = \frac{dm}{m} + 2 \frac{dv}{v}, \] so the precision of the kinetic energy measurement is $\frac{dK}{K}=0.03+ 2(0.02)=0.07$ or 7%.
Explanations
The above examples illustrate that derivative rules are applicable very generally. Indeed we can talk about the differential or “change in” $dQ$ for any quantity $Q$.
Integrals
We now begin our discussion of integrals, which is the second topic in calculus. Integrals are a fancy way to add up the value of a function to get “the whole” or the sum of its values over some interval. Normally integral calculus is taught as a separate course after differential calculus, but this separation is not necessary and can be even counter-productive.
The derivative $f'(x)$ measures the change in $f(x)$, i.e., the derivative measures the differences in $f$ for an $\epsilon$-small change in the input variable $x$: \[ \text{derivative } \ \propto \ \ f(x+\epsilon)-f(x). \] Integrals, on the other hand, measure the sum of the values of $f$, between $a$ and $b$ at regular intervals of $\epsilon$: \[ \text{integral } \propto \ \ \ f(a) + f(a+\epsilon) + f(a+2\epsilon) + \ldots + f(b-2\epsilon) + f(b-\epsilon). \] The best way to understand integration is to think of it as the opposite operation of differentiation: adding up all the changes in function gives you the function value.
In Calculus I we learned how to take a function $f(x)$ and find its derivative $f'(x)$. In integral calculus, we will be given a function $f(x)$ and we will be asked to find its integral on various intervals.
Definitions
These are some concepts that you should already be familiar with:
- $\mathbb{R}$: The set of real numbers.
- $f(x)$: A function:
\[ f: \mathbb{R} \to \mathbb{R}, \]
which means that $f$ takes as input some number (usually we call that number $x$)
and it produces as an output another number $f(x)$ (sometimes we also give an alias for the output $y=f(x)$).
* $\lim_{\epsilon \to 0}$: limits are the mathematically rigorous
way of speaking about very small numbers.
* $f'(x)$: the derivative of $f(x)$ is the rate of change of $f$ at $x$:
\[
f'(x) = \lim_{\epsilon \to 0} \frac{f(x+\epsilon)\ - \ f(x)}{\epsilon}.
\]
The derivative is also a function of the form
\[
f': \mathbb{R} \to \mathbb{R}.
\]
The function $f'(x)$ represents the //slope// of
the function $f(x)$ at the point $(x,f(x))$.
NOINDENT These are the new concepts:
- $x_i=a$: where the integral starts, i.e., some given point on the $x$ axis.
- $x_f=b$: where the integral stops.
- $A(x_i,x_f)$: The value of the area under the curve $f(x)$ from $x=x_i$ to $x=x_f$.
- $\int f(x)\; dx$: the integral of $f(x)$.
More precisely we can define the antiderivative of $f(x)$ as follows:
\[
F(b) = \int_0^b f(x) dx \ \ + \ \ F(0).
\]
The area $A$ of the region under $f(x)$ from $x=a$ to $x=b$ is given by:
\[
\int_a^b f(x) dx = F(b) - F(a) = A(a,b).
\]
The $\int$ sign is a mnemonic for //sum//.
Indeed the integral is nothing more than the "sum" of $f(x)$ for all values of $x$ between $a$ and $b$:
\[
A(a,b) = \lim_{\epsilon \to 0}\left[ \epsilon f(a) + \epsilon f(a+\epsilon) + \ldots + \epsilon f(b-2\epsilon) + \epsilon f(b-\epsilon) \right],
\]
where we imagine the total area broken-up into thin rectangular
strips of width $\epsilon$ and height $f(x)$.
* The name antiderivative comes from the fact that
\[
F'(x) = f(x),
\]
so we have:
\[
F(x) \!= \text{int}\!\left( \text{diff}( F(x) ) \right)= \int_0^x \left( \frac{d}{dt} F(t) \right) \ dt = \int_0^x \! f'(t) \ dt = F(x).
\]
Indeed, the //fundamental theorem of calculus//,
tells us that the derivative and integral are //inverse operations//,
so we also have:
\[
f(x) \!= \text{diff}\!\left( \text{int}( f(x) ) \right)
= \frac{d}{dx}\left[\int_0^x f(t) dt\right]
= \frac{d}{dx}\left[ F(x) - F(0) \right]
= f(x).
\]
Formulas
Riemann Sum
The Riemann sum is a good way to define the integral from first principles. We will brake up the area under the curve into many little strips of height varying according to $f(x)$. To obtain the total area, we sum-up all the areas of the rectangles. We will discuss Riemann sums in the next section, but first we look at the properties of integrals.
Area under the curve
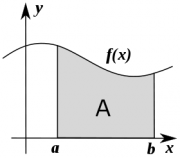 The value of an integral corresponds to the area $A$,
under the curve $f(x)$ between $x=a$ and $x=b$:
\[
A(a,b) = \int_a^b f(x) \; dx.
\]
The value of an integral corresponds to the area $A$,
under the curve $f(x)$ between $x=a$ and $x=b$:
\[
A(a,b) = \int_a^b f(x) \; dx.
\]
For certain functions it is possible to find an anti-derivative function $F(\tau)$, which describes the “running total” of the area under the curve starting from some arbitrary left endpoint and going all the way until $t=\tau$. We can compute the area under $f(t)$ between $a$ and $b$ by looking at the change in $F(\tau)$ between $a$ and $b$. \[ A(a,b) = F(b) - F(a). \]
We can illustrate the reasoning behind the above formula graphically:
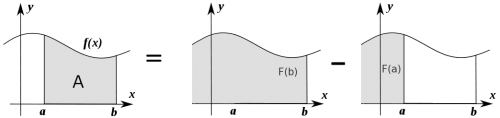 The area $A(a,b)$ is equal to the “running total” until $x=b$
minus the running total until $x=a$.
The area $A(a,b)$ is equal to the “running total” until $x=b$
minus the running total until $x=a$.
Indefinite integral
The problem of finding the anti-derivative is also called integration. We say that we are finding an indefinite integral, because we haven't defined the limits $x_i$ and $x_f$.
So an integration problem is one in which you are given the $f(x)$, and you have to find the function $F(x)$. For example, if $f(x)=3x^2$, then $F(x)=x^3$. This is called “finding the integral of $f(x)$”.
Definite integrals
A definite integral specifies the function to integrate as well as the limits of integration $x_i$ and $x_f$: \[ \int_{x_i=a}^{x_f=b} f(x) \; dx = \int_{a}^{b} f(x) \; dx. \]
To find the value of the definite integral first calculate the indefinite integral (the antiderivative): \[ F(x) = \int f(x)\; dx, \] and then use it to compute the area as the difference of $F(x)$ at the two endpoints: \[ A(a,b) = \int_{x=a}^{x=b} f(x) \; dx = F(b) - F(a) \equiv F(x)\bigg|_{x=a}^{x=b}. \]
Note the new “vertical bar” notation: $g(x)\big\vert_{\alpha}^\beta=g(\beta)-g(\alpha)$, which is shorthand notation to denote the expression to the left evaluated at the top limit minus the same expression evaluated at the bottom limit.
Example
What is the value of the integral $\int_a^b x^2 \ dx$? We have \[ \int_a^b x^2 dx = \frac{1}{3}x^3\bigg|_{x=a}^{x=b} = \frac{1}{3}(b^3-a^3). \]
Signed area
If $a < b$ and $f(x) > 0$, then the area \[ A(a,b) = \int_{a}^{b} f(x) \ dx, \] will be positive.
However if we swap the limits of integration, in other words we start at $x=b$ and integrate backwards all the way to $x=a$, then the area under the curve will be negative! This is because $dx$ will always consist of tiny negative steps. Thus we have that: \[ A(b,a) = \int_{b}^{a} f(x) \ dx = - \int_{a}^{b} f(x) \ dx = - A(a,b). \] In all expressions involving integrals, if you want to swap the limits of integration, you have to add a negative sign in front of the integral.
The area could also come out negative if we integrate a negative function from $a$ to $b$. In general, if $f(x)$ is above the $x$ axis in some places these will be positive contributions to the total area under the curve, and places where $f(x)$ is below the $x$ axis will count as negative contributions to the total area $A(a,b)$.
Additivity
The integral from $a$ to $b$ plus the integral from $b$ to $c$ is equal to the integral from $a$ to $c$: \[ A(a,b) + A(b,c) = \int_a^b f(x) \; dx + \int_b^c f(x) \; dx = \int_a^c f(x) \; dx = A(a,c). \]
Linearity
Integration is a linear operation: \[ \int [\alpha f(x) + \beta g(x)]\; dx = \alpha \int f(x)\; dx + \beta \int g(x)\; dx, \] for arbitrary constants $\alpha, \beta$.
Recall that this was true for differentiation: \[ [\alpha f(x) + \beta g(x)]' = \alpha f'(x) + \beta g'(x), \] so we can say that the operations of calculus as a whole are linear operations.
The integral as a function
So far we have looked only at definite integrals where the limits of integration were constants $x_i=a$ and $x_f=b$, and so the integral was a number $A(a,b)$.
More generally, we can have one (or more) variable integration limits. For example we can have $x_i=a$ and $x_f=x$. Recall that area under the curve $f(x)$ is, by definition, computed as a difference of the anti-derivative function $F(x)$ evaluated at the limits: \[ A(x_i,x_f) = A(a,x) = F(x) - F(a). \]
The expression $A(a,x)$ is a bit misleading as a function name since it looks like both $a$ and $x$ are variable when in fact $a$ is a constant parameter, and only $x$ is the variable. Let's call it $A_a(x)$ instead. \[ A_a(x) = \int_a^x f(t) \; dt = F(x) - F(a). \]
Two observations. First, note that $A_a(x)$ and $F(x)$ differ only by a constant, so in fact the anti-derivative is the integral up to a constant which is usually not important. Second, note that because the variable $x$ appears in the upper limit of the expression, I had to use a dummy variable $t$ inside the integral. If we don't use a different variable, we could confuse the running variable inside the integral, with the limit of integration.
Fundamental theorem of calculus
Let $f(x)$ be a continuous function, and let $F(x)$ be its antiderivative on the interval $[a,b]$: \[ F(x) = \int_a^x f(t) \; dt, \] then, the derivative of $F(x)$ is equal to $f(x)$: \[ F'(x) = f(x), \] for any $x \in (a,b)$.
We see that differentiation and integration are inverse operations: \[ F(x) \!= \text{int}\left( \text{diff}( F(x) ) \right)= \int_0^x \left( \frac{d}{dt} F(t) \right) \; dt = \int_0^x f(t) \; dt = F(x) + C, \] \[ f(x) \!= \text{diff}\left( \text{int}( f(x) ) \right) = \frac{d}{dx}\left[\int_0^x f(t) dt\right] = \frac{d}{dx}\left[ F(x) - F(0) \right] = f(x). \]
We can think of the inverse operators $\frac{d}{dt}$ and $\int\cdot dt$ symbolically on the same footing as the other mathematical operations that you know about. The usual equation solving techniques can then be applied to solve equations which involve derivatives. For example, suppose that you want to solve for $f(t)$ in the equation \[ \frac{d}{dt} \; f(t) = 100. \] To get to $f(t)$ we must undo the $\frac{d}{dt}$ operation. We apply the integration operation to both sides of the equation: \[ \int \left(\frac{d}{dt}\; f(t)\right) dt = f(t) = \int 100\;dt = 100t + C. \] The solution to the equation $f'(t)=100$ is $f(t)=100t+C$ where $C$ is called the integration constant.
Gimme some of that
OK, enough theory. Let's do some anti-derivatives. But how does one do anti-derivatives? It's in the name, really. Derivative and anti. Whatever the derivative does, the integral must do the opposite. If you have: \[ F(x)=x^4 \qquad \overset{\frac{d}{dx} }{\longrightarrow} \qquad F'(x)=4x^3 \equiv f(x), \] then it must be that: \[ f(x)=4x^3 \qquad \overset{\ \int\!dx }{\longrightarrow} \qquad F(x)=x^4 + C. \] Each time you integrate, you will always get the answer up to an arbitrary additive constant $C$, which will always appear in your answers.
Let us look at some more examples:
- The integral of $\cos\theta$ is:
\[ \int \cos\theta \ d\theta = \sin\theta + C, \]
since $\frac{d}{d\theta}\sin\theta = \cos\theta$,
and similarly the integral for $\sin\theta$ is:
\[
\int \sin\theta \ d\theta = - \cos\theta + C,
\]
since $\frac{d}{d\theta}\cos\theta = - \sin\theta$.
* The integral of $x^n$ for any number $n \neq -1$ is:
\[
\int x^n \ dx = \frac{1}{n+1}x^{n+1} + C,
\]
since $\frac{d}{d\theta}x^n = nx^{n-1}$.
* The integral of $x^{-1}=\frac{1}{x}$ is
\[
\int \frac{1}{x} \ dx = \ln x + C,
\]
since $\frac{d}{dx}\ln x = \frac{1}{x}$.
I could go on but I think you get the point: all the derivative formulas you learned can be used in the opposite direction as an integral formula.
With limits now
What is the area under the curve $f(x)=\sin(x)$, between $x=0$ and $x=\pi$? First we take the anti derivative \[ F(x) = \int \sin(x) \ dx = - \cos(x) + C. \] Now we calculate the difference between $F(x)$ at the end-point minus $F(x)$ at the start-point: \[ \begin{align} A(0,\pi) & = \int_{x=0}^{x=\pi} \sin(x) \ dx \nl & = \underbrace{\left[ - \cos(x) + C \right]}_{F(x)} \bigg\vert_0^\pi \nl & = [- \cos\pi + C] - [- \cos(0) + C] \nl & = \cos(0) - \cos\pi \ \ = \ \ 1 - (-1) = 2. \end{align} \]
The constant $C$ does not appear in the answer, because it is in both the upper and the lower limits.
What next
If integration is nothing more than backwards differentiation and you already know differentiation inside out from differential calculus, you might be wondering what you are going to do during an entire semester of integral calculus. For all intents and purposes, if you understood the conceptual material in this section, then you understand integral calculus. Give yourself a tap on the back—you are done.
The establishment, however, doesn't just want you to know the concepts of integral calculus, but also wants you to know how to apply them in the real world. Thus, you need not only understand, but also practice the techniques of integration. There are a bunch of techniques, which allow you to integrate complicated functions. For example, if I asked you to integrate $f(x)=\sin^2(x) = (\sin(x))^2$ from $0$ to $\pi$ and you look in the formula sheet you won't find a function $F(x)$ who's derivative equals $f(x)$. So how do we solve: \[ \int_0^\pi \sin^2(x) \ dx = ?. \] One way to approach this problem is to use the trigonometric identity which says that $\sin^2(x)=\frac{1-\cos(2x)}{2}$ so we will have \[ \int_0^\pi \! \sin^2(x) dx = \int_0^\pi \left[ \frac{1}{2} - \frac{1}{2}\cos(2x) \right] dx = \underbrace{ \frac{1}{2} \int_0^\pi 1 \ dx}_{T_1} - \underbrace{ \frac{1}{2} \int_0^\pi \cos(2x) \ dx }_{T_2}. \] The fact that we can split the integral into two parts, and factor out the constant $\frac{1}{2}$ comes from the fact that integration is linear.
Let's continue the calculation of our integral, where we left off: \[ \int_0^\pi \sin^2(x) \ dx = T_1 - T_2. \] The value of the integral in the first term is: \[ T_1 = \frac{1}{2} \int_0^\pi 1 \ dx = \frac{1}{2} x \bigg\vert_0^\pi = \frac{\pi-0}{2} =\frac{\pi}{2}. \] The value of the second term is \[ T_2 =\frac{1}{2} \int_0^\pi \cos(2x) \ dx = \frac{1}{4} \sin(2x) \bigg\vert_0^\pi = \frac{\sin(2\pi) - \sin(0) }{4} = \frac{0 - 0 }{4} = 0. \] Thus we find the final answer for the integral to be: \[ \int_0^\pi \sin^2(x) \ dx = T_1 - T_2 = \frac{\pi}{2} - 0 = \frac{\pi}{2}. \]
Do you see how integration can quickly get tricky? You need to learn all kinds of tricks to solve integrals. I will teach you all the necessary tricks, but to become proficient you can't just read: you have to practice the techniques. Promise me you will practice! As my student, I expect nothing less than a total ass kicking of the questions you will face on the final exam.
Riemann sum
We defined the integral operation $\int f(x)\;dx$ as the inverse operation of $\frac{d}{dx}$, but it is important to know how to think of the integral operation on its own. No course on calculus would be complete without a telling of the classical “rectangles story” of integral calculus.
Definitions
- $x$: $\in \mathbb{R}$, the argument of the function.
- $f(x)$: a function $f \colon \mathbb{R} \to \mathbb{R}$.
- $x_i$: where the sum starts, i.e., some given point on the $x$ axis.
- $x_f$: where the sum stops.
- $A(x_i,x_f)$: Exact value of the area under the curve $f(x)$ from $x=x_i$ to $x=x_f$.
- $S_n(x_i,x_f)$: An approximation to the area $A$ in terms of
$n$ rectangles.
- $s_k$: Area of $k$-th rectangle when counting from the left.
 In the picture on the right, we are approximating the function $f(x)=x^3-5x^2+x+10$ between $x_i=-1$ and $x_f=4$ using $n=12$ rectangles.
The sum of the areas of the 12 rectangles is what we call $S_{12}(-1,4)$.
We say that $S_{12}(-1,4) \approx A(-1,4)$.
In the picture on the right, we are approximating the function $f(x)=x^3-5x^2+x+10$ between $x_i=-1$ and $x_f=4$ using $n=12$ rectangles.
The sum of the areas of the 12 rectangles is what we call $S_{12}(-1,4)$.
We say that $S_{12}(-1,4) \approx A(-1,4)$.
Formulas
The main formula you need to know is that the combined area approximation is given by the sum of the areas of the little rectangles: \[ S_n = \sum_{k=1}^{n} s_k. \]
Each of the little rectangles has an area $s_k$ given by its height multiplied by its width. The height of each rectangle will vary, but the width is constant. Why constant? Riemann figured that having each rectangle with a constant width $\Delta x$ would make it very easy to calculate the approximation. The total length of the interval from $x_i$ to $x_f$ is $(x_f-x_i)$. If we divide this length into $n$ equally spaced segments, each of width $\Delta x$ given by: \[ \Delta x = \frac{x_f - x_i}{n}. \]
OK, we have the formula for the width figured out, let's see what the height will be for the $k$-th rectangle, where $k$ is our counter from left to right in the sequence of rectangles. The height of the function varies as we move along the $x$ axis. For the rectangles, we pick isolated “samples” of $f(x)$ for the following values \[ x_k = x_i + k\Delta x, \textrm{ for } k \in \{ 1, 2, 3, \ldots, n \}, \] all of them equally spaced $\Delta x$ apart.
The area of each rectangle is height times width: \[ s_k = f(x_i + k\Delta x)\Delta x. \]
Now, my dear students, I want you to stare at the above equation and do some simple calculations to check that you understand. There is no point in continuing if you are just taking my word for it. Verify that when $k=1$, the formula gives the area of the first little rectangle. Verify also that when $k=n$, the formula for the $x_n$ gives the right value ($x_f$).
Ok let's put our formula for $s_k$ in the sum where it belongs. The Riemann sum approximation using $n$ rectangles is given by \[ S_n = \sum_{k=1}^{n} f(x_i + k\Delta x)\Delta x, \] where $\Delta x =\frac{|x_f - x_i|}{n}$.
Let us get back to the picture where we try to approximate the area under the curve $f(x)=x^3-5x^2+x+10$ by using 12 pieces.
For this scenario the value we would get for the 12-rectangle
approximation to the area under the curve with
\[
S_{12} = \sum_{k=1}^{12} f(x_i + k\Delta x)\Delta x = 11.802662.
\]
You shouldn't trust me though, but always check for yourself using
live.sympy.org by typing in the following expressions:
>>> n=12.0; xk = -1 + k*5/n; sk = (xk**3-5*xk**2+xk+10)*(5/n);
>>> summation( sk, (k,1,n) )
11.802662...
More is better
Who cares though? This is such a crappy approximation! You can clearly see that some rectangles lie outside of the curve (overestimates), and some are too far inside (underestimates). You might be wondering why I wasted so much of your time to achieve such a lousy approximation. We have not been wasting our time. You see, the Riemann sum formula $S_n$ gets better and better as you cut the region into smaller and smaller rectangles.
With $n=25$, we get a more fine grained approximation
in which the sum of the rectangles is given by:
\[
S_{25} = \sum_{k=1}^{25} f(x_i + k\Delta x)\Delta x = 12.4.
\]
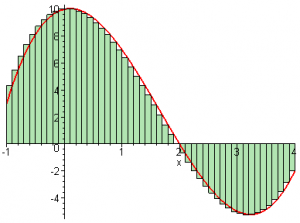 Then for $n=50$ we get:
\[
S_{50} = 12.6625.
\]
Then for $n=50$ we get:
\[
S_{50} = 12.6625.
\]
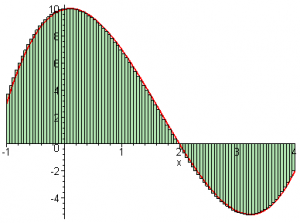 For $n=100$ the sum of the rectangles areas is starting to look pretttttty much like the function.
The calculation gives us $S_{100} = 12.790625$.
For $n=100$ the sum of the rectangles areas is starting to look pretttttty much like the function.
The calculation gives us $S_{100} = 12.790625$.
For $n=1000$ we get $S_{1000} = 12.9041562$ which is very close to the actual value of the area under the curve: \[ A(-1,4) = 12.91666\ldots \]
You see in the long run, when $n$ gets really large the rectangle approximation (Riemann sum) can be made arbitrarily good. Imagine you cut the region into $n=10000$ rectangles, wouldn't $S_{10000}(-1,4)$ be a pretty accurate approximation of the actual area $A(-1,4)$?
Integral
The fact that you can approximate the area under the curve with a bunch of rectangles is what integral calculus is all about. Instead of mucking about with bigger and bigger values of $n$, mathematicians go right away for the kill and make $n$ go to infinity.
In the limit of $n \to \infty$, you can get arbitrarily close approximations to the area under the curve. All this time, that which we were calling $A(-1,4)$ was actually the “integral” of $f(x)$ between $x=-1$ and $x=4$, or written mathematically: \[ A(-1,4) \equiv \int_{-1}^4 f(x)\;dx \equiv \lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \sum_{k=1}^{n} f(x_i + k\Delta x)\Delta x. \]
While it is not computationally practical to make $n \to \infty$,
we can convince ourselves that the approximation becomes better and
better as $n$ becomes larger. For example the approximation using $n=1$M rectangles is accurate up to the fourth decimal place as
can be verified using the following commands on live.sympy.org:
>>> n=1000000.0; xk = -1 + k*5/n; sk = (xk**3-5*xk**2+xk+10)*(5/n);
>>> summation( sk, (k,1,n) )
12.9166541666563
>>> integrate( x**3-5*x**2+x+10, (x,-1,4) ).evalf()
12.9166666666667
In practice, when we want to compute the area under the curve, we don't use Riemann sums. There are formulas for directly calculating the integrals of functions. In fact, you already know the integration formulas: they are simply the derivative formulas used in the opposite direction. In the next section we will discuss the derivative-integral inverse relationship in more details.
Links
[ Riemann sum wizard ]
http://mathworld.wolfram.com/RiemannSum.html
Fundamental theorem of calculus
Though it may not be apparent at first, the study of derivatives (Calculus I) and integrals (Calculus II) are intimately related. Differentiation and integration are inverse operations.
You have previously studied the inverse relationship for functions. Recall that for any bijective function $f$ (a one-to-one relationship) there exists an inverse functions $f^{-1}$ which undoes the effects of $f$: \[ (f^{-1}\!\circ f) (x) \equiv f^{-1}(f(x)) = x. \] and \[ (f \circ f^{-1}) (y) \equiv f(f^{-1}(y)) = y. \] The circle $\circ$ stands for composition of functions, i.e., first you apply one function and then you apply the second function. When you apply a function followed by its inverse to some input you get back the original input.
The integral is the “inverse operation” to the derivative. If perform the integral operation followed by the derivative operation on some function, you will get back the same function. This is stated more formally as the Fundamental Theorem of Calculus.
Statement
Let $f(x)$ be a continuous function and let $F(x)$ be its antiderivative on the interval $[a,b]$: \[ F(x) = \int_a^x f(t) \; dt, \] then, the derivative of $F(x)$ is equal to $f(x)$: \[ F'(x) = f(x), \] for any $x \in (a,b)$.
Thus, we see that differentiation is the inverse operation of integration. We obtained $F(x)$ by integrating $f(x)$. If we then take the derivative of $F(x)$ we get back to $f(x)$. It works the other way too. If you integrate a function and then take its derivative, you get back to the original function. Differential calculus and integral calculus are two sides of the same coin. If you understand this fact, then you understand something very deep about calculus.
Note that $F(x)$ is not a unique anti-derivative. We can add an arbitrary constant $C$ to $F(x)$ and it will still satisfy the above conditions since the derivative of a constant is zero.
Formulas
If you are given some function $f(x)$, you take its integral and then take the derivative of the result, you will get back the same function: \[ \left(\frac{d}{dx} \circ \int dx \right) f(x) \equiv \frac{d}{dx} \int_a^x f(t) dt = f(x). \] Alternately, you can first take the derivative, and then take the integral, and you will get back the function (up to a constant): \[ \left( \int dx \circ \frac{d}{dx}\right) f(x) \equiv \int_a^x f'(t) dt = f(x) - f(a). \]
Note that we had to use a dummy variable $t$ inside the integral since $x$ is used in the limit. Indeed, all integrals are functions of their limits and the inner variable is not important: we could write $\int_a^x f(y)\;dy$ or $\int_a^x f(z)\;dz$ or even $\int_a^x f(\xi)\;d\xi$ and the answer for all of these will be $F(x)-F(a)$.
Discussion
As a consequence of the Fundamental theorem, you can reuse all your knowledge of differential calculus to solve integrals.
Example: Reverse engineering
Suppose you are asked find this integral: \[ \int x^2 dx. \] Using the Fundamental theorem, we can rephrase this question as the search for some function $F(x)$ such that \[ F'(x) = x^2. \] Now since you remember your derivative formulas well, you will guess right away that $F(x)$ must contain a $x^3$ term. This is because you get back quadratic term when you take the derivative of cubic term. So we must have $F(x)=cx^3$, for some constant $c$. We must pick the constant that makes this work out: \[ F'(x) = 3cx^2 = x^2, \] therefore $c=\frac{1}{3}$ and the integral is: \[ \int x^2 dx = \frac{1}{3}x^3 + C. \] Did you see what just happened? We were able to take an integral using only derivative formulas and “reverse engineering”. You can check that, indeed, $\frac{d}{dx}\left[\frac{1}{3}x^3\right] = x^2$.
You can also use the Fundamental theorem to check your answers.
Example: Integral verification
Suppose a friend tells you that
\[
\int \ln(x) dx = x\ln(x) - x + C,
\]
but he is a shady character and you don't trust him.
How can you check his answer?
If you had a smartphone handy, you can check on live.sympy.org,
but what if you just have pen and paper?
If $x\ln(x) - x$ is really the antiderivative of $\ln(x)$, then
by the Fundamental theorem of calculus, if we take the derivative
we should get back $\ln(x)$. Let's check:
\[
\frac{d}{dx}\!\left[ x\ln(x) - x \right] = \underbrace{\frac{d}{dx}\!\left[x\right]\ln(x)+ x \left[\frac{d}{dx} \ln(x) \right]}_{\text{product rule} } - \frac{d}{dx}\left[ x \right] = 1\ln(x) + x\frac{1}{x} - 1 = \ln(x).
\]
OK, so your friend is correct.
Proof of the Fundamental theorem
There exists an unspoken rule in mathematics which states that if the word theorem appears in your writing, it has to be followed by the word proof. We therefore have to look into the proof of the Fundamental Theorem of Calculus (FTC). It is not that important that you understand the details of the proof, but I still recommend that you read this section for your general math culture. If you are in a rush though, feel free to skip it.
Before we get to the proof of the FTC, let me first introduce the squeezing principle, which will be used in the proof. Suppose you have three functions $f, \ell$, and $u$, such that: \[ \ell(x) \leq f(x) \leq u(x) \qquad \text{ for all } x. \] We say that $\ell(x)$ is a lower bound on $f(x)$ since its graph is always below that of $f(x)$. Similarly $u(x)$ is an upper bound on $f(x)$. Whatever the value of $f(x)$ is, we know that it is in between that of $\ell(x)$ and $u(x)$.
Suppose that $u(x)$ and $\ell(x)$ both converge to the same limit $L$: \[ \lim_{x\to a} \ell(x) = L, \quad \text{and} \quad \lim_{x\to a} u(x) = L, \] then it must be true that $f(x)$ also converges to the same limit: \[ \lim_{x\to a} f(x) = L. \] This is true because the function $f$ is squeezed between $\ell$ and $u$; it has no other choice than to converge to the same limit.
Proof
The formula for the derivative of $F(x)$ looks like this:
\[
F'(x) = \lim_{\epsilon \to 0} \frac{ F(x+\epsilon) - F(x) }{ \epsilon }.
\]
Let us look more closely at the term in the numerator, and express it in
terms of the definition of $F(x)$:
\[
\begin{align*}
{\color{red} F(x+\epsilon) - F(x) }
&= \int_a^{x+\epsilon} f(t) \ dt - \int_a^x f(t) \; dt \nl
&= {\color{red} \int_x^{x+\epsilon} f(t) \;dt }.
\end{align*}
\]
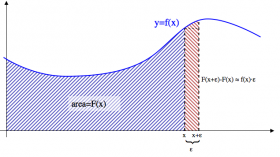 Thus the difference of $F(x+\epsilon)$ and $F(x)$ is just the integral of $f(x)$ between
$x$ and $x+\epsilon$.
The region which corresponds to this difference looks like a long narrow strip
of width $\epsilon$ and height varying according to $f(x)$:
\[
{\color{red} \int_x^{x+\epsilon} f(t) \ dt} \approx \underbrace{\text{width}}_{\epsilon}\times \underbrace{\text{height}}_?.
\]
Thus the difference of $F(x+\epsilon)$ and $F(x)$ is just the integral of $f(x)$ between
$x$ and $x+\epsilon$.
The region which corresponds to this difference looks like a long narrow strip
of width $\epsilon$ and height varying according to $f(x)$:
\[
{\color{red} \int_x^{x+\epsilon} f(t) \ dt} \approx \underbrace{\text{width}}_{\epsilon}\times \underbrace{\text{height}}_?.
\]
Let us define the maximum and minimum values of the height of the function $f(x)$ on that interval: \[ M \equiv \max_{t\in[x,x+\epsilon]} f(t), \qquad \qquad m \equiv \min_{t\in[x,x+\epsilon]} f(t). \] By definition, the quantities $m$ and $M$ provide a lower and an upper bound on the quantity we are trying to study: \[ \epsilon m \leq {\color{red} \int_x^{x+\epsilon} f(t) \ dt } \leq \epsilon M. \]
Recall that we said that $f$ is continuous in the theorem statement. If $f$ is continuous then as $\epsilon \to 0$ we will have: \[ \lim_{\epsilon \to 0} f(x+\epsilon ) = f(x). \]
In fact, as $\epsilon \to 0$ all the values of $f$ on the shortening interval $[x, x+\epsilon]$ will approach $f(x)$. In particular, both the minimum value $m$ and the maximum value $M$ will approach $f(x)$: \[ \lim_{\epsilon \to 0} f(x+\epsilon ) = f(x) = \lim_{\epsilon \to 0} m = \lim_{\epsilon \to 0} M. \]
So starting from the inequality, \[ \epsilon m \leq \int_x^{x+\epsilon} f(t) \ dt \leq \epsilon M, \] and taking the limit as $\epsilon \to 0$ we get: \[ \begin{align} \lim_{\epsilon \to 0} \epsilon m \leq & \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt \leq \lim_{\epsilon \to 0} \epsilon M, \nl \lim_{\epsilon \to 0} \epsilon f(x) \leq & \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt \leq \lim_{\epsilon \to 0} \epsilon f(x), \end{align} \]
Using the squeezing principle, we can affirm that \[ \qquad \qquad \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt = \lim_{\epsilon \to 0} \epsilon f(x). \qquad \qquad \qquad \qquad (\dagger) \]
To complete the proof, we substitute this expression into the derivative formula: \[ \begin{align} F'(x) & = \lim_{\epsilon \to 0} \frac{ F(x+\epsilon) - F(x) }{ \epsilon } \nl & = \lim_{\epsilon \to 0} \frac{\int_x^{x+\epsilon} f(t) \ dt }{\epsilon} \qquad \qquad \text{( by the definition of } F) \nl & = \lim_{\epsilon \to 0} \frac{ \epsilon f(t) }{\epsilon} \qquad \qquad \qquad \ \ \ ( \text{ by using equation } (\dagger)\ ) \nl & = f(x) \lim_{\epsilon \to 0} \frac{ \epsilon }{\epsilon} \nl & = f(x). \end{align} \]
We have thus proved that, for all continuous functions $f(x)$, we have: \[ \left(\frac{d}{dx} \circ \int dx \right) f(x) \equiv \frac{d}{dx} \int_a^x f(t) dt = f(x). \]
Integrals look at the “accumulation” of some quantity, whereas derivatives look at the incremental changes. In words, the Fundamental theorem says that the change in the accumulation of $f$ is just $f$ itself. Taking the derivative after taking an integral is as if someone asked you to add up a long list of numbers, and in each step state by how much the sum has changed. You don't need to add or subtract anything, just read out loud all the values in the list.
Links
Techniques of integration
The operation of “taking the integral” of some function is usually much more complicated than that of taking the derivative. In fact, you can take the derivative of any function – no matter how complex – simply by using the product rule, the chain rule and the derivative formulas. The same is not true for integrals.
There are plenty of integrals for which there is no closed form solution, which means that the function doesn't have an anti-derivative. There simply doesn't exist a simple procedure to follow, such that you input a function and you “turn the crank” until the integral comes out. Integration is a bit of an art.
What can we integrate then and how? Back in the day, scientists used to collect big tables with integral formulas for various complicated functions. That is what you can lookup-integrate.
There are also some integration techniques which can help you make complicated integrals simpler. Think of the techniques below, as adapters you need to use for cases when the function you are trying to integrate doesn't appear in your table of integrals, but a similar one is in the table.
The intended audience for this chapter are Calculus II students. This is exactly the kind of skills which you will be asked to show on the final. Instead of using the table of integrals to lookup some complicated integral, you have know how to make your own table.
For people interested in learning physics, I will honestly tell
you that if you skip this section you won't miss much.
You should just read the section on substitution which is the important one,
but don't bother reading the details of all the recipes for
integrating things.
For most intents and purposes, once you understand
what an integral is, you can use a computer to calculate it.
A good tool for this is the computer algebra system at live.sympy.org.
>>> integrate( sin(x) )
-cos(x)
>>> integrate( x**2*exp(x) )
x**2*exp(x) - 2*x*exp(x) + 2*exp(x)
You can use sympy for all your integration needs.
For those of you reading this book for general culture and who want to understand what calculus is without having to write a final exam on it, consider the next couple of pages as an ethnographic survol of the academic realities in which bright first year students are forced to integrate things they don't want to integrate and this for many long hours. Just picture some unlucky science student locked up in her room doing calculus and hundreds of dangling integrals grabbing at her with their hooks, keeping her away from her friends.
Actually, it is not that bad. There are, like, four tricks to learn and if you practice you can learn all of them in a week or so. Mastering these four tricks is essentially the entire Calculus II class. If you understand the material in this section, you will be done with integral calculus and you will have two months to chill.
Substitution
Say you are integrating some complicated function which contains a square root $\sqrt{x}$. You are wondering how to go about computing this integral: \[ \int \frac{1}{x - \sqrt{x}} \; dx \ = \ ? \]
Sometimes you can simplify the integral by substituting a new variable in the expression. Let $u=\sqrt{x}$. Substitution is like search-and-replace in a word processor. Every time you see the expression $\sqrt{x}$, you have to replace it with $u$: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{1}{u^2 - u} \; dx. \] Note that we also replaced $x=(\sqrt{x})^2$ with $u^2$.
We are not done yet. When you change from the $x$ variable to the $u$ variable, you have to be thorough. You have to change the $dx$ to a $du$ also. Can we just replace $dx$ with $du$? Unfortunately no, otherwise it would be like saying that the “short step” $du$ is equal in length to the “short step” $dx$, which is only true for the trivial substitution $u=x$.
To find the relation between the infinitesimals we take the derivative: \[ u(x) = \sqrt{x} \quad \Rightarrow \quad u'(x) = \frac{du}{dx} = \frac{1}{2\sqrt{x}}. \] For the next step, I need you to stop thinking about the expression $\frac{du}{dx}$ as a whole, but think about it as a rise-over-run fraction which can be split. Lets take the run $dx$ to the other side of the equation: \[ du = \frac{1}{2\sqrt{x}} \; dx, \] and to isolate $dx$, we multiply both sides by $2\sqrt{x}$: \[ dx = 2\sqrt{x} \; du = 2u \; du, \] where in the last step we used the fact that $u=\sqrt{x}$ again.
Now we have an expression for $dx$ entirely in terms of $u$'s. Let's see what that gives: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{1}{u^2 - u} 2u \; du = \int \frac{2}{u - 1} \; du. \]
We can now recognize the general form $\frac{1}{x}$ which has integral $\ln(x)$, but we have to account for the $-1$ shift inside the function. The integral therefore is: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{2}{u - 1} \; du = 2\ln(u-1) = 2\ln(\sqrt{x}-1). \] Note that in the last step we changed back to the $x$ variable, to give the final answer. The variable $u$ exists only in our calculation. We invented it out of thin air, when we said “Let $u=\sqrt{x}$” in the beginning. It is only natural to convert back to the original variable $x$ in the last step.
Notice what happened thanks to the substitution? The integral got simpler since we got rid of the square roots. On the outside we had just an extra $u$ appearing, which ends up cancelling with the $u$ in the denominator making things even simpler. In practice, substituting inside $f$ is the easy part. The hard part is making sure that our choice of substitution leads to a replacement for $dx$ which helps to make the integral simpler.
For definite integrals, i.e., integrals that have explicit limits, there is an extra step that we need to take when changing variables: we have to change the $x$ limits of integration to $u$ limits. In our expression, when changing to the $u$ variable, we would have to write: \[ \int_a^b \frac{1}{x - \sqrt{x}} \; dx = \int_{u(a)}^{u(b)} \frac{2}{u - 1} \; du. \] If the integral had asked for the integral between $x_i=4$ and $x_f=9$, then the new limits will be $u_i=\sqrt{4}=2$ and $u_f=\sqrt{9}=3$, so we will have: \[ \int_4^9 \frac{1}{x - \sqrt{x}} \; dx = \int_{2}^{3} \frac{2}{u - 1} \; du = 2\ln(u-1)\bigg|_2^3 = 2(\ln(2) - \ln(1)) = 2\ln(2). \]
OK, so let's recap. Substitution involves three steps:
- Replace all occurrences of $u(x)$ with $u$.
- Replace $dx$ with $\frac{1}{u'(x)}du$.
- If there are limits, replace the $x$ limits with $u$ limits.
If the resulting integral is simpler to solve then good for you!
Example
We are asked to find $\int \tan(x)\; dx$. We know that $\tan(x)=\frac{\sin(x)}{\cos(x)}$, so we can use the substitution $u=\cos(x)$, $du=-\sin(x)dx$ as follows: \[ \begin{eqnarray} \int \tan(x)dx &=& \int \frac{\sin(x)}{\cos(x)} dx \nl &=& \int \frac{-1}{u} du \nl &=& -\ln |u| + C \nl &=& -\ln |\cos(x) | + C. \end{eqnarray} \]
Integrals of trig functions
Because $\sin$, $\cos$, $\tan$ and the other trig functions are related, we can often express one function in terms of another in order to simplify integrals.
Recall the trigonometric identity: \[ \cos^2(x) + \sin^2(x) = 1, \] which is the statement of Pythagoras theorem.
If we choose to make the substitution $u=\sin(x)$, then we can replace all kinds of trigonometric terms with the new variable $u$: \[ \begin{align*} \sin^2(x) &= u^2, \nl \cos^2(x) &= 1 - \sin^2(x) = 1 - u^2, \nl \tan^2(x) &= \frac{\sin^2(x)}{\cos^2(x)} = \frac{u^2}{1-u^2}. \end{align*} \]
Of course the change of variable $u=\sin(x)$ means that you have to change the $du=u'(x) dx= \cos(x) dx$ so there better be something to cancel this $\cos(x)$ term in the integral.
Let me show you one example when things work out perfectly. Suppose $m$ is some arbitrary number, and you have to integrate: \[ \int \left(\sin(x)\right)^{m}\cos^{3}(x) \; dx \equiv \int \sin^{m}(x)\cos^{3}(x) \; dx. \] This integral contains $m$ powers of the $\sin$ function and a three powers of the $\cos$ function. Let us split the $\cos$ term into two parts: \[ \int \sin^{m}(x)\cos^{3}(x) \; dx = \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx. \]
Making the change of variable $u=\sin(x)$, $du=\cos(x)dx$ means that we can replace $\sin^m(x)$ by $u^m$, and $\cos^2(x)=1-u^2$ in the above expression to get: \[ \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx = \int u^{m} \left(1-u^2\right) \cos(x) \; dx. \]
Conveniently we happen to have $du= \cos(x)dx$ so the complete change of variable step is: \[ \begin{align*} \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx & = \int u^{m} \left(1-u^2\right) \; du. \end{align*} \] This is what I was talking about earlier about “having an extra $\cos(x)$” to cancel the one that will appear from the $dx \to du$ change.
What is the answer then? It is a simple integral of a polynomial: \[ \begin{align*} \int u^{m} \left(1-u^2\right) \; du & = \int \left( u^{m} - u^{m+2} \right) \; du \nl & = \frac{1}{m+1}u^{m+1} - \frac{1}{m+3}u^{m+3} \nl & = \frac{1}{m+1}\sin^{m+1}(x) - \frac{1}{m+3}\sin^{m+3}(x). \end{align*} \]
You might be wondering how useful this substitution technique really is. I mean, how often do you have to integrate such a particular combinations of $\sin$ and $\cos$ powers so that the substitution works out perfectly. You would surprised! Sins and cos functions are used a lot in this thing called the Fourier transform, which is a way of expressing a sound wave $f(t)$ in terms of the frequencies it contains. Also on exams, they love to test this kinds of things. Teachers often want to check if you can do integrals and substitutions and they check if you remember all the trigonometric identities, which you are supposed to have learned in high school.
What other trigonometric functions should you know how to integrate? On an exam you should try any possible substitution you can think of, combined with any trigonometric identity that seems to simplify things. Some common ones are described below.
Cos
Just as we can substitute $\sin$, we can also substitute $u=\cos(x)$ and use $\sin^2(x)=1-u^2$. Again, this substitution only makes sense if you have a $\sin$ left over somewhere in the integral to cancel with the $du = -\sin(x)dx$.
Tan and sec
We can get some more mileage out of $\cos^2(x) + \sin^2(x) = 1$. If we divide both sides by $\cos^2(x)$ we get: \[ 1 + \tan^2(x) = \sec^2(x) \equiv \frac{1}{\cos^2(x)}, \] which is useful because $u=\tan(x)$ gives $du=\sec^2(x)dx$ so you can often “kill off” even powers of $\sec^2(x)$ in integrals of the form \[ \int\tan^m(x)\sec^n(x)\,dx. \]
Even powers of sin and cos
There are other trigonometric identities called half-angle and double-angle formulas which give you formulas like: \[ \sin^2(x)=\frac{1}{2}(1-\cos(2x)), \qquad \cos^2(x)=\frac{1}{2}(1+\cos(2x)). \]
These are useful if you have to integrate even powers of $\sin$ and $\cos$.
Example
Let's see how we would find $I=\int\sin^2(x)\cos^4(x)\,dx$: \[ \begin{eqnarray} I &=& \int\sin^2(x)\cos^4(x)\;dx \nl &=& \int \left( {1 \over 2}(1 - \cos(2x)) \right) \left( {1 \over 2}(1 + \cos(2x)) \right)^2 \;dx, \nl &=& \frac{1}{8} \int \left( 1 - \cos^2(2x) + \cos(2x)- \cos^3(2x) \right) \;dx. \nl & = & \frac{1}{8} \int \left( 1 - \cos^2(2x) + \cos(2x) -\cos^2(2x) \cos(2x) \right)\; dx \nl & = & \frac{1}{8} \int \left( 1 - \frac{1}{2} (1 + \cos(4x)) + \underline{\cos(2x)} - (\underline{1}-\sin^2(2x))\underline{\cos(2x)} \right) \; dx \nl & = & \frac{1}{8} \int \left( \frac{1}{2} - \frac{1}{2} \cos(4x) + \underbrace{\sin^2(2x)}_{u^2}\cos(2x) \right) \;dx \nl & = & \frac{1}{8} \left( \frac{x}{2} - \frac{\sin(4x)}{8} + \frac{\sin^3(2x)}{6} \right) \nl &=& \frac{x}{16}-\frac{\sin(4x)}{64} + \frac{\sin^3(2x)}{48}+C. \end{eqnarray} \]
There is no limit to the number of combinations of simplification steps you can try. On a homework question or an exam, the teacher will ask for something simple. You just have to find the right substitution.
Sneaky example
Sometime, the substitution is not obvious at all, as in the case of $\int \sec(x)dx$. To find the integral you need to know the following trick: multiply and divide by $\tan(x) +\sec(x) $.
What we get is \[ \begin{eqnarray} \int \sec(x) \, dx &=& \int \sec(x)\ 1 \, dx \nl &=& \int \sec(x)\frac{\tan(x) +\sec(x)}{\tan(x) +\sec(x)} \; dx \nl &=& \int \frac{\sec^2(x) + \sec(x) \tan(x)}{\tan(x) +\sec(x)} \; dx\nl &=& \int \frac{1}{u} du \nl &=& \ln |u| + C \nl &=& \ln |\tan(x) + \sec(x) | + C, \end{eqnarray} \] where in the fourth line we used the substitution $u=\tan(x)+\sec(x)$ and $du = (\sec^2(x) + \tan(x)\sec(x))dx$.
I highly recommend you view and practice all the examples you can get your hands on. Don't bother memorizing any recipes though, you will do just as well with trial and error.
Trig substitution
Often times when doing integrals for physics we get terms of the form $\sqrt{a^2-x^2}$, $\sqrt{a^2+x^2}$ or $\sqrt{x^2-a^2}$ which are not easy to handle. In each of the above three cases, we can do a trig substitution, in which we substitute $x$ with one of the trigonometric functions $a\sin(\theta)$, $a\tan(\theta)$ or $a\sec(\theta)$, and the resulting integral becomes much simpler.
Sine substitution
Consider an integral which contains an expression of the form $\sqrt{a^2-x^2}$. If we use the substitution $x=a\sin \theta$, the complicated square-root expression will get simpler: \[ \sqrt{a^2-x^2} = \sqrt{a^2-a^2\sin^2\theta} = a\sqrt{1-\sin^2\theta} = a\cos\theta, \] because we have $\cos^2\theta = 1 - \sin^2\theta$. The transformed integral now involves a trigonometric function which we know how to integrate.
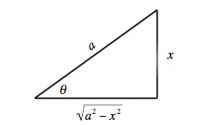 Once we find the integral in terms of $\theta$, we have to convert
the various $\theta$ expressions in the answer back
to the original variables $x$ and $a$:
\[
\sin\theta = \frac{x}{a}, \ \
\cos\theta = \frac{\sqrt{a^2-x^2}}{a}, \ \
\tan\theta = \frac{x}{\sqrt{a^2-x^2}}, \ \
\]
\[
\csc\theta = \frac{a}{x}, \ \
\sec\theta = \frac{a}{\sqrt{a^2-x^2}}, \ \
\cot\theta = \frac{\sqrt{a^2-x^2}}{x}. \ \
\]
Once we find the integral in terms of $\theta$, we have to convert
the various $\theta$ expressions in the answer back
to the original variables $x$ and $a$:
\[
\sin\theta = \frac{x}{a}, \ \
\cos\theta = \frac{\sqrt{a^2-x^2}}{a}, \ \
\tan\theta = \frac{x}{\sqrt{a^2-x^2}}, \ \
\]
\[
\csc\theta = \frac{a}{x}, \ \
\sec\theta = \frac{a}{\sqrt{a^2-x^2}}, \ \
\cot\theta = \frac{\sqrt{a^2-x^2}}{x}. \ \
\]
Example 1
Suppose you are asked to calculate $\int \sqrt{1-x^2}\; dx$.
We will approach the problem by making the substitution \[ x=\sin \theta, \qquad dx=\cos \theta \; d\theta, \] which is the simplest case of the sine substitution with $a=1$.
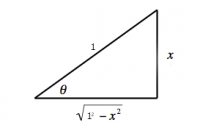 We proceed as follows:
\[
\begin{eqnarray}
\int \sqrt{1-x^2} \; dx
& = & \int \sqrt{1-\sin^2 \theta} \cos \theta \; d\theta \nl
& = & \int \cos^2 \theta \; d\theta \nl
& = & \frac{1}{2} \int \left[ 1+ \cos 2\theta \right] \; d\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{4}\sin2\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{2}\sin\theta\cos\theta \nl
& = & \frac{1}{2}\sin^{-1}\!\left(x \right)
+\frac{1}{2}\frac{x}{1}\frac{\sqrt{1-x^2}}{1}.
\end{eqnarray}
\]
We proceed as follows:
\[
\begin{eqnarray}
\int \sqrt{1-x^2} \; dx
& = & \int \sqrt{1-\sin^2 \theta} \cos \theta \; d\theta \nl
& = & \int \cos^2 \theta \; d\theta \nl
& = & \frac{1}{2} \int \left[ 1+ \cos 2\theta \right] \; d\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{4}\sin2\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{2}\sin\theta\cos\theta \nl
& = & \frac{1}{2}\sin^{-1}\!\left(x \right)
+\frac{1}{2}\frac{x}{1}\frac{\sqrt{1-x^2}}{1}.
\end{eqnarray}
\]
Note how in the last step we used the triangle diagram to “read off” the values of $\theta$, $\sin\theta$ and $\cos\theta$ from the triangle. The substitution $x = \sin\theta$ means the hypotenuse in the diagram should be of length 1, and the opposite side is of length $x$.
Example 2
We want to compute $\int \sqrt{ \frac{a+x}{a-x}} \; dx$. We can rewrite this fraction as follows: \[ \sqrt{\frac{a+x}{a-x}} = \sqrt{\frac{a+x}{a-x} \frac{1}{1}} = \sqrt{\frac{a+x}{a-x} \frac{a+x}{a+x}} =\frac{a+x}{\sqrt{a^2-x^2}}. \]
Next we can make the substitution \[ x=a \sin \theta, \qquad dx=a\cos \theta d\theta, \]
 \[
\begin{eqnarray}
\int \frac{a+x}{\sqrt{a^2-x^2}} dx
& = & \int \frac{a+a\sin \theta}{a\cos \theta} a \cos \theta \, d\theta \nl
& = & a \int \left[ 1+ \sin \theta \right] d\theta \nl
& = & a \left[ \theta - \cos \theta \right] \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - a\frac{\sqrt{a^2-x^2}}{a} \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - \sqrt{a^2-x^2}.
\end{eqnarray}
\]
\[
\begin{eqnarray}
\int \frac{a+x}{\sqrt{a^2-x^2}} dx
& = & \int \frac{a+a\sin \theta}{a\cos \theta} a \cos \theta \, d\theta \nl
& = & a \int \left[ 1+ \sin \theta \right] d\theta \nl
& = & a \left[ \theta - \cos \theta \right] \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - a\frac{\sqrt{a^2-x^2}}{a} \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - \sqrt{a^2-x^2}.
\end{eqnarray}
\]
Tan substitution
When an integral contains $\sqrt{a^2+x^2}$, we use the substitution: \[ x = a \tan \theta, \qquad dx = a \sec^2 \theta d\theta. \]
Because of the identity $1+\tan^2\theta=\sec^2\theta$, the square root expression will simplify drastically: \[ \sqrt{a^2+x^2} = \sqrt{a^2+a^2 \tan^2 \theta} = a\sqrt{1+\tan^2 \theta} = a \sec \theta. \] Simplification is a good thing. You are much more likely to be able to find the integral in terms of $\theta$, using trig identities, than in terms of $\sqrt{a^2+x^2}$.
Once you calculate the integral in terms of $\theta$, you will want to convert the answer back into $x$ coordinates. To do this, you need to use a triangle labeled according to our substitution: \[ \tan\theta = \frac{x}{a} = \frac{\text{opp}}{\text{adj}}. \] The equivalent of $\sin\theta$ in terms of $x$ is going to be $\sin\theta \equiv \frac{\text{opp}}{\text{hyp}} = \frac{x}{\sqrt{a^2+x^2}}$. Similarly, the other trigonometric functions are defined as various ratios of $a$, $x$ and $\sqrt{a^2+x^2}$.
Example
Calculate $\int\frac{1}{x^2+1}\,dx$.
The denominator of this function is equal to $\left(\sqrt{1+x^2}\right)^2$. This suggests that we try to substitute $\displaystyle x=\tan \theta\,$ and use the identity $\displaystyle 1 + \tan^2 \theta =\sec^2 \theta\,$. With this substitution, we obtain that $\displaystyle dx= \sec^2 \theta\, d\theta$ and thus: \[ \begin{align} \int\frac{1}{x^2+1}\,dx & =\int\frac{1}{\tan^2 \theta+1} \sec^2 \theta\,d\theta \nl & =\int\frac{1}{\sec^2 \theta} \sec^2 \theta\,d\theta \nl & =\int 1\;d\theta \nl &=\theta \nl &=\tan^{-1}(x) + C. \end{align} \]
Obfuscated example
What if we don't have $x^2 + 1$ in the denominator (a second degree polynomial with a missing linear term), but a full second degree polynomial like: \[ \frac{1}{y^2 - 6y + 10}. \] How would you integrate something like this? If there were no $-2y$, you would be able to use the tan substitution as above – or perhaps you can lookup the formula $\int \frac{1}{x^2+1}dx = \tan^{-1}(x)$ in the table of integrals. But there is no formula for \[ \int \frac{1}{y^2 - 6y + 10} \; dy, \] in the table so how should you proceed.
We will use the good old substitution technique $u=\ldots$ and a high-school algebra trick called “completing the square” in order to rewrite the fraction inside the integral so that it looks like $(y-h)^2 + k$, i.e., with no middle term.
The first step is to find “by inspection” the values of $h$ and $k$: \[ \frac{1}{y^2 - 6y + 10} = \frac{1}{(y-h)^2+k} = \frac{1}{(y-3)^2+1}. \] The “square completed” quadratic expression has no linear term, which is what we wanted. We can now use the substitution $x=y-3$ and $dx=dy$ to obtain an integral which we know how to solve: \[ \!\int \!\! \frac{1}{y^2 - 6y + 10}\; dy \!= \!\int \!\! \frac{1}{(y-3)^2+1}\; dy \!= \!\int \!\!\frac{1}{x^2+1}\; dx = \tan^{-1}(x) = \tan^{-1}(y-3). \]
Sec substitution
In the last two sections we learned how to deal with $\sqrt{a^2-x^2}$, $\sqrt{x^2+a^2}$ and so only the last option remains: $\sqrt{x^2-a^2}$.
Recall the trigonometric identity $1+\tan^2\theta=\sec^2\theta$, or rewritten differently we get \[ \sec^2\theta - 1 = \tan^2\theta. \]
The appropriate substitution for terms like $\sqrt{x^2-a^2}$, is the following: \[ x = a \sec \theta, \qquad dx = a \tan \theta \sec \theta \; d\theta. \]
The substitution method and procedure is the same as in both previous cases, so we will not get into the details. We label the sides of the triangle in the appropriate fashion, namely: \[ \sec\theta = \frac{x}{a} = \frac{\text{hyp}}{\text{opp}}, \] and use this triangle when we are converting back from $\theta$ to $x$ in the final steps.
Interlude
By now, things are starting to get pretty tight for your Calculus teacher. You are starting to know how to “handle” any kind of integral he can throw at you: polynomials, fractions with $x^2$ plus or minus $a^2$ and square roots. He can't even use the dirty old trigonometric tricks, with the $\sin$, the $\cos$ and the $\tan$ since you know that too. What options are there left for him to come up with an integral that you wouldn't know how to solve?
OK, I am exaggerating, but you should at least feel, by now, that you know how to do some integrals that you didn't know before. Just remember to come back to this section when you are hit with some complicated integral. When this happens, check to see which of the examples in this section looks the most similar and use the same approach. Don't bother memorizing the steps in each problem. The substitution $u=\ldots$ may be different from any problem that you have seen so far. You should think of “integration techniques” like general recipe ideas which you must adapt depending on the ingredients that you have to work with.
The most important integration techniques is substation. Recall the steps involved: (1) the change of variable $u=\ldots$, (2) the associated $dx$ to $du$ change and (3) the change in the limits of integration required for definite integrals. With medium to advanced substitution skills you will get at least an 80% on your Calculus II final.
Where is the remaining 20% of the exam going to come from? There are two more recipes to go. I know all these tricks that I have been throwing at you during the last ten pages may seem arduous and difficult to understand, but this is what you got yourself into when you signed-up for the course “Integral Calculus”: there are integrals and you calculate them.
The good news is that we are almost done. There is just one more “trick” to go, and finally I will tell you about “integration by parts”, which is kind of the analogue of the product rule for derivatives $(fg)'=f'g + fg'$.
Partial fractions
Suppose you have to integrate a rational function $\frac{P(x)}{Q(x)}$, where $P$ and $Q$ are polynomials.
For example, you could be asked to integrate \[ \frac{P(x)}{Q(x)} = \frac{Dx+E}{Fx^2 + G x + H}, \] where $D$, $E$, $F$, $G$ and $H$ are arbitrary constants. To get even more specific, let's say you are asked to calculate: \[ \int {3x+ 1 \over x^2+x} \; dx. \]
By magical powers, I can transform the function in this integral into two partial fractions as follows: \[ \int {3x+ 1 \over x^2+x} \; dx = \int \left( \frac{1}{x} + \frac{2}{x+1} \right) \; dx = \int \frac{1}{x} \; dx \ + \ \int \frac{2}{x+1} \; dx, \] in which both terms will give something $\ln$-like when integrated (since $\frac{d}{dx}\ln(x)=\frac{1}{x}$). The final answer is: \[ \int {3x+ 1 \over x^2+x} \; dx = \ln \left| x \right| + 2 \ln \left| x+1 \right| + C. \]
How did I split the problem into partial fractions? Is it really magic or is there a method? There is a little bit of both. The method part is that I assumed that there exist constants $A$ and $B$ such that \[ {3x+ 1 \over x^2+x}={3x+ 1 \over x(x+1)}= {A \over x}+ {B \over x+1}, \] and then I solved the above equation for $A$ and $B$, by computing the sum of the two fractions: \[ {3x+1 \over x(x+1)} = {{A(x+1) + Bx} \over {x(x+1)}}. \]
The magic part is the fact that you can solve for two unknowns in one equation. The relevant part of the equation is just the numerator because both sides have the same denominator. To find $A$ and $B$ we have to solve \[ 3x+1 = (3)x + (1)1 = A(x+1)+Bx = (A+B)x + (A)1. \] To solve this you just have to group the unknown constants into bunches and then read off their value from the equation. The bunch of numbers in front of the constant 1 on the left-hand side is (1) and the coefficient of 1 on the right-hand side is $A$, so $A=1$. Similarly you can deduce that $B=2$ from $A+B=3$ having found that $A=1$ in the first step.
Another way of looking at this, is that the equation \[ 3x+1 = A(x+1)+Bx \] must hold for all values of the variable $x$. If we put in $x=0$ we get $1 = A$ and putting $x=-1$ gives $-2=-B$ so $B=2$.
The above problem highlights the power of the partial fractions method for attacking integrals of polynomial fractions $\frac{P(x)}{Q(x)}$. Most of the work goes into some high-school math (factoring and finding unknowns) and then you do some simple calculus steps once you have split the problem into partial fractions. Some people call this method separation of quotients, but whatever you call it, it is clear that having a way to split a fraction into multiple parts is a good thing: \[ \frac{3x+ 1}{x^2+x} = \frac{A}{x} + \frac{B}{x+1}. \]
How many parts are there going to be for a fraction $\frac{P(x)}{Q(x)}$? What will each part look like? The answer is that there will be as many as the degree of the polynomial $Q(x)$, which is in the denominator of the fraction. Each part will consist of one of the factors of $Q(x)$.
Here is the general procedure:
- Split the denominator $Q(x)$ into the product of parts (factorize),
and for each part assume an appropriate partial fraction term
on the right.
You will get three types of fractions:
* Simple factors like $(x-\alpha)^1$. For each of these
you should //assume// a partial fraction of the form:
\[
\frac{A}{x-\alpha},
\]
as in the above example.
* Repeated factors like $(x-\beta)^n$ for which we have to
assume $n$ different terms on the right-hand side:
\[
\frac{B}{x-\beta} + \frac{C}{(x-\beta)^2} + \cdots + \frac{F}{(x-\beta)^n}.
\]
* If the denominator contains a portion $ax^2+bx+c$ that cannot be factored, like
$x^2+1$ for example, we have to keep it as whole
and assume that a term of the form:
\[
\frac{Gx + H}{ax^2+bx+c}
\]
exists on the right-hand side. A polynomial $ax^2+bx+c$ cannot be factored
if $b^2 < 4ac$, which means it has no real roots $r_1$, $r_2$
such that $ax^2+bx+c=(x-r_1)(x-r_2)$.
- Add together all the parts on the right-hand side by first
cross multiplying them to set all the fractions to a
common denominator. If you followed the steps
correctly in Part 1, the //least common denominator// (LCD) will turn
out to be $Q(x)$,
so both sides will have the same denominator.
Solve for the unknown coefficients $A, B, C, \ldots$
in the numerators. Find the coefficients
of each power of $x$ on the right-hand side and set them
equal to the corresponding coefficient in the numerator $P(x)$ of the left-hand side.
- Use the appropriate integral formula for each kind of term:
* For simple factors we have
\[
\int \frac{1}{x-\alpha} \; dx= A \ln|x-\alpha| + C.
\]
* For higher powers in the denominator we have
\[
\int \frac{1}{(x-\beta)^m} \; dx= \frac{1-m}{(x-\beta)^{m-1}} + C.
\]
* For the quadratic denominator terms with "matching" numerator
terms we can obtain:
\[
\int \frac{2ax+b}{ax^2+bx+c} \; dx= \ln|ax^2+bx+c| + C.
\]
For quadratic terms with just a constant on top we use
a two step substitution process.
First we change to a complete-the-square variable $y=x-h$:
\[
\int \frac{1}{ax^2+bx+c} \; dx
=
\int \frac{1/a}{(x-h)^2+k} \; dx
=
\frac{1}{a}\int \frac{1}{y^2+k} \; dy,
\]
and then we use a trig substitution $y = \sqrt{k}\tan\theta$ to get
\[
\frac{1}{a} \int \frac{1}{y^2+k} \; dy =
\frac{\sqrt{k}}{a}\tan^{-1}\!\!\left(\frac{y}{\sqrt{k}} \right) =
\frac{\sqrt{k}}{a}\tan^{-1}\!\!\left(\frac{x-h}{\sqrt{k}} \right).
\]
Example
Find $\int {1 \over (x+1)(x+2)^2}dx$?
Here $P(x)=1$ and $Q(x)=(x+1)(x+2)^2$. If I wanted to be sneaky, I could have asked for $\int {1 \over x^3+5x^2+8x+4}dx$, instead – which is actually the same question, but you have to do the factoring yourself.
According to the recipe outlined above, we have to look for a split fraction of the form: \[ \frac{1}{(x+1)(x+2)^2}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}. \] To make the equation more explicit, let us add the fractions on the right. We set all of them to a the least common denominator and add up: \[ \begin{align} \frac{1}{(x+1)(x+2)^2} & =\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2} \nl &= \frac{A(x+2)^2}{(x+1)(x+2)^2}+\frac{B(x+1)(x+2)}{(x+1)(x+2)^2}+\frac{C(x+1)}{(x+1)(x+2)^2} \nl & = \frac{A(x+2)^2+B(x+1)(x+2)+C(x+1)}{(x+1)(x+2)^2}. \end{align} \]
The denominators are the same on both sides in the above equation, so we can focus our attention on the numerator: \[ A(x+2)^2+B(x+1)(x+2)+C(x+1) = 1. \] We choose three different values of $x$ in order to find the values of $A$, $B$ and $C$: \[ \begin{matrix} x=0 & 1= 2^2A +2B+C \nl x=-1 & 1=A \nl x=-2 & 1= -C \end{matrix} \] so $A=1$, $B=-1$, $C=-1$, and thus \[ \frac{1}{(x+1)(x+2)^2}=\frac{1}{x+1}-\frac{1}{x+2}-\frac{1}{(x+2)^2}. \]
We can now calculate the integral by integrating each of the terms: \[ \int \frac{1}{(x+1)(x+2)^2} dx= \ln(x+1) - \ln({x+2}) + \frac{1}{x+2} +C. \]
Integration by parts
Suppose you have to integrate the product of two functions. If one of the functions happens to look like the derivative of a function that you recognize, then you can do the following trick: \[ \int f(x) g'(x) \; dx \ \ = \ \ f(x) g(x) \ \ \ \ - \int f'(x)g(x) \; dx. \]
This means that you can shift the work to evaluating a different integral where one function is replaced by its derivative and another is replaced by its integral.
Derivatives tend to simplify functions whereas integrals make functions more complicated, so such shifting of work can be quite beneficial: you will save yourself some work on integrating the $f$ part, but you will do more work on the $g$ part.
It is easier to remember the integration by parts formula in the shorthand notation: \[ \int u\; dv = uv - \int v\; du. \] In fact, you can think of integration by parts as a form of “double substitution”, where you replace $u$ and $dv$ at the same time. To be sure of what is going on, I recommend you always make a little table like this: \[ \begin{align} u &= & \qquad dv &= \nl du &= & \qquad v &= \end{align} \] and fill in the blanks. The first row consists of the two parts that you see in your original problem. Then you differentiate in the left column, and integrate in the right column. If you do this, using the integration by parts formula will be really easy since you have all your expressions ready.
For definite integrals the integration by parts rule needs to take into account the evaluation at the limits: \[ \int_a^b u\; dv = \left(uv\right)\Big|_a^b \ \ - \ \ \int_a^b v \; du, \] which tells us to evaluate the difference of the value of $uv$ at the two endpoints and then subtract the switched integral with the same endpoints.
Example 1
Find $\int x e^x \, dx$. We identify the good candidates for $u$ and $dv$ in the original expression, and perform all the work necessary for the substitution: \[ \begin{align} u &=x & \qquad dv &= e^x \; dx, \nl du &=dx & \qquad v &= e^x. \end{align} \] Next we apply the integration by parts formula \[ \int u\; dv = uv - \int v\; du, \] to get the following: \[ \begin{align} \int xe^x \, dx &= x e^x - \int e^x \; dx \nl &= x e^x - e^x + C. \end{align} \]
Example 2
Find $\int x \sin x \; dx$. We choose $u=x$ and $dv=\sin x dx$. With these choices, we have $du=dx$ and $v=-\cos x$, and integrating by parts we get: \[ \begin{align} \int x \sin x \, dx &= -x \cos x - \int \left(-\cos x\right) \; dx \nl &= -x \cos x + \int \cos x \; dx \nl &= -x \cos x + \sin x + C. \end{align} \]
Example 3
Often times, you have to integrate by parts multiple times. To calculate $\int x^2 e^x \, dx$, we start by choosing: \[ \begin{align} u &=x^2 & \qquad dv &= e^x \; dx \nl du &= 2x \; dx & \qquad v &= e^x, \end{align} \] which gives the following after integration by parts: \[ \int x^2 e^x \; dx = x^2 e^x \ - \ 2 \int x e^x \; dx. \] We apply integration by parts again on the remaining integral this time using $u=x$ and $dv=e^x\; dx$, which gives $du = dx$ and $v=e^x$.
\[ \begin{align} \int x^2 e^x \; dx &= x^2 e^x - 2 \int x e^x \; dx \nl &= x^2 e^x - 2\left(x e^x - \int e^x \; dx \right) \nl &= x^2 e^x - 2x e^x + 2e^x + C. \end{align} \]
By now I hope you are starting to see that this integration by parts thing is good. If you always write down the substitutions clearly (who is who in $\int u dv$), and use the formula correctly ($=uv-\int v du$) you can do damage to any integral. Sometimes the choice of $u$ and $dv$ you make might not be good: if the integral $\int v du$ is not simpler than the original $\int u dv$ then what is the point of integrating by parts?
Sometimes, however, you can get into a weird self-referential loop when doing integration by parts. After a couple of integration-by-parts steps you might end up back with an integral you started with! The way out of this loop is best shown by example.
Example 4
Evaluate the integral $ \int \sin(x) e^x\; dx$. First we let $u = \sin(x) $ and $dv=e^x \; dx$, which gives $dv=\cos(x)dx$ and $v=e^x$. Using integration by parts gives \[ \int \sin(x) e^x\, dx = e^x\sin(x)- \int \cos(x)e^x\, dx. \]
We integrate by parts again. This time we set $u = \cos(x)$, $dv=e^x dx$ and $du=-\sin(x)dx$, $v=e^x$. We obtain \[ \underbrace{ \int \sin(x) e^x\, dx}_I \ = \ e^x\sin(x) - e^x\cos(x)\ \ -\ \ \underbrace{\int e^x \sin(x)\, dx}_I. \] Do you see the Ouroboros? We could continue integrating by parts indefinitely like that.
Let us define clearly what we are doing here. The question asked us to find $I$ where \[ I = \int \sin(x) e^x\, dx, \] and after doing two integration by parts steps we obtain the following equation: \[ I = e^x\sin(x) - e^x\cos(x) - I. \] OK, good. Now just move all the I's to one side: \[ 2I = e^x\sin(x) - e^x\cos(x), \] or finally \[ \int \sin(x) e^x\, dx = I = \frac{1}{2} e^x\left(\sin(x) - \cos(x) \right) +C. \]
Derivation of the Integration by parts formula
Remember the product rule for derivatives? \[ \frac{d}{dx}(f(x)g(x)) = \frac{df}{dx}g(x) + f(x)\frac{dg}{dx}. \] We can rewrite this as: \[ f(x)\frac{dg}{dx} = \frac{d}{dx}(f(x)g(x)) \ -\ \frac{df}{dx}g(x) . \] Now we take the integral on both sides \[ \int f(x)\frac{dg}{dx} \ dx \ = \ \int \left[ \frac{d}{dx}(f(x)g(x)) \; dx - \frac{df}{dx}g(x) \; dx \right]. \]
At this point, you need to recall the Fundamental Theorem of Calculus, which says that taking the derivative and taking an integral are inverse operations \[ \int \frac{d}{dx} h(x) \; dx = h(x). \] We use this to simplify the product rule equation as follows: \[ \int f(x)\frac{dg}{dx} \; dx \ = \ f(x)g(x) \ \ - \ \ \int \frac{df}{dx}g(x) \; dx. \]
Outro
We are done. Now you know all the integration techniques. I know it took a while, but we had to go through a lot of tricks. In any case, I must say I am glad to be done writing this section. My job of teaching you is done. Now your job begins. Do all the examples you can find. Do all the exercises. Practice the tricks.
Here is a suggestion for you. Make your own formula-sheet-slash-trophy-case where you record any complex integral that you have personally calculated from first principles in homework assignments. If by the end of the class you trophy case has 50 integrals which you calculated yourself, then you will get $100\%$ on your final. Another thing to try is to go over the integral formulas in the back of the book and see how many of them you can derive.
Links
[ More examples of integration techniques ]
http://en.wikibooks.org/wiki/Calculus/Integration_techniques/
Applications of integration
Integration is used in many areas of science.
Applications to mechanics
Calculus was kind of invented for mechanics, so it is not surprising that there will be many links between the two subjects.
Kinematics
Suppose that an object of mass $m$ has a constant force $F_{net}$ applied to it. Newton's second law tells us that the acceleration of the object will be $a =\frac{F_{net}}{m}$.
If the net force is constant, then the acceleration will also be constant. We can find the equations of motion of the object $x(t)$ by integrating $a(t)$ twice since $a(t)=x^{\prime\prime}(t)$.
We start with the acceleration function $a(t) = a$ and integrate once to obtain: \[ v(\tau) = \int_0^\tau a(t) \; dt = a t + v_i, \] where $v_i=v(0)$ is the initial velocity of the object at $t=0$. We obtain the position function by integrating the velocity function and adding the initial position $x_i=x(0)$: \[ x(\tau) = \int v(t) \; dt = \int ( a t + v_i )\; dt = \frac{1}{2}a\tau^2 + v_i\tau + x_i. \]
Non-constant acceleration
If net force on the object is not constant then the acceleration will not be constant either. In general both the force and the mass could change over time so the acceleration will also change over time $a(t)=\frac{F_{net}(t)}{m(t)}$. This sort of problem is usually not covered in the first mechanics course because the establishment assume that it would be too complicated for you to handle.
Now that you know more about integrals, you can learn how to predict the motion of the object with an arbitrary acceleration function $a(t)$. To find the velocity at time $t=\tau$, we need sum up all acceleration felt by the object between $t=0$ and $t=\tau$: \[ v(\tau) = v_i + \int_0^\tau a(t)\; dt. \] The equation of motion $x(t)$ is obtained by integrating the velocity $v(t)$: \[ x(s) = x_i + \int_0^s v(\tau) \; d\tau = \int_0^s \left[ v_i + \int_0^\tau a(t)\; dt \right] \; d\tau. \] The above expression looks quite intense, but in fact it is nothing more complicated than the simple integrals used in UAM. The expression just looks complicated because we have three different variables which are used to represent the time and two consecutive integration steps. Computer games often include a “physics engine” to simulates the motion of objects in the real world using the equation described above.
Gravitational potential
By definition, the integral of a conservative force over some distance $d$ gives you the potential energy of that force. Since gravity $\vec{F}_g$ is a conservative force, we can integrate it to obtain the gravitational potential energy $U_g$.
On the surface of the earth we have $\vec{F}_g = -gm \hat{\jmath}$, where the negative sign means that it acts in the opposite direction to “upwards” as represented by the $\hat{\jmath}$ unit vector, which points in the positive $y$-direciton (towards the sky). In particular the gravitational force as a function of height $\vec{F}_g(y)$ is a constant $\vec{F}_g(y)=\vec{F}_g$. By definition, the gravitational potential energy is the negative of the integral of the force over some distance, say from height $y_i=0$ to height $y_f=h$: \[ \Delta U_{g} = U_{gf} - U_{gi} = - \int_{y_i}^{y_f} \vec{F}_g \cdot \hat{\jmath} \ dy = - \int_{0}^{h} - mg \ dy = \left[ mg y \right]_{0}^{h} = mgh. \]
More generally, i.e., not on the surface of the earth, the gravitational force acting on an object of mass $m$ due to another object of mass $M$ is given by Newton's famous one-over-$r$-squared law: \[ \vec{F}_g = \frac{GMm}{r^2} \hat{r}, \] where $r$ is the distance between the objects and $\hat{r}$ points towards the other object. The general formula for gravitational potential is obtained, again, by taking the integral of the gravitational force over some distance. We will start the object of mass $m$ from a distance $r=r_i$ and move it away until it is infinitely far away. The change in the gravitational potential from $r=r_i$ to $r=\infty$ is: \[ \begin{align} \Delta U_g & = \int_{r=r_i}^{r=\infty} \frac{GMm}{r^2} \ dr \nl & = GMm \int_{r_i}^{\infty} \frac{1}{r^2} \ dr \nl & = GMm \left[ \frac{-1}{r} \right]_{r_i}^{\infty} \nl & = GMm \left[ \frac{-1}{\infty} - \frac{-1}{r_i} \right] \nl & = \frac{GMm}{r_i}. \end{align} \]
Integrals over circular objects
Consider the circular region $S = \{x,y \in \mathbb{R} : x^2 + y^2 \leq R^2\}$. In polar coordinates we would describe this region as $r \leq R$, where it is implicit that the angle $\theta$ varies between $0$ and $2 \pi$. Because this region is two dimensional, in order to integrate it, we would need a double integral.
Even before you learn about double integrals, you can still integrate over the circular region if you brake it up into little pieces of circle $dS$. In fact, this is the whole point of this subsection.
 A natural way to break up the circular region is in
terms of thin
circular strips at a different radius and with width $dr$.
Each circular strip will have an area of:
\[
dS = 2\pi r dr,
\]
where $2\pi r$ is the circumference of a circle with radius $r$.
A natural way to break up the circular region is in
terms of thin
circular strips at a different radius and with width $dr$.
Each circular strip will have an area of:
\[
dS = 2\pi r dr,
\]
where $2\pi r$ is the circumference of a circle with radius $r$.
Using this way of braking up the circle, we can check that indeed we get a total area of $\pi R^2$ when we add up all the pieces $dS$: \[ A_{circle} = \int_S \ dS = \int_{r=0}^{r=R} 2\pi r \ dr = 2\pi \int_{0}^{R} r \ dr = \pi R^2. \]
The following sections discuss different extensions of this idea. We use the circular symmetry of various objects to integrate over them by breaking them into thin circular strips of thickness $dr$.
In all circular integrals, you can think of the object as being described by a rotation, or revolution of some function around one of the axes, thus, this kind of integrals are called integrals of revolution.
Total mass of a disk
Suppose you have a disk of total mass $m$ and radius $R$. You can think of the disk as being made of parts, each of mass $\Delta m$, such that when you add them all up you get the total mass: \[ \int_{disk} \Delta m = m. \]
The mass density is defined as the total mass divided by the area of the disk: $\sigma = \frac{m}{A_{disk}} = \frac{m}{\pi R^2}$. The mass density corresponds to the amount of mass per unit area. Let's split the disk into concentric circular strips of width $dr$. The mass contribution of a strip as a function of the radius will be $\Delta m({r}) = \sigma 2\pi r dr $, since the stip at radius $r$ has circumference $2\pi r$ and width $dr$. Let's check that when we add up the pieces we get the total mass: \[ m = \int_0^R \Delta m ({r}) = \int_0^R \sigma 2 \pi r \ dr = 2\pi\sigma \left[ \frac{r^2}{2} \right]_0^R = 2\pi \frac{m}{\pi R^2} \frac{R^2-0}{2} = m. \]
Moment of inertia of a disk
The moment of inertia of an object is a measure of how difficult it is to make it turn. It appears in the rotational version of $F=ma$, in place of the inertial mass $m$: \[ \mathcal{T} = I \alpha. \]
To compute the moment of inertia of an object you need to add up all the mass contributions $\Delta m$ and weight them by $r^2$, where $r$ is the distance of the piece $\Delta m$ from the centre: \[ I = \int_{disk} r^2 \Delta m. \]
We can perform the integral over the whole disk, by adding up the contributions of all the strips: \[ I_{disk} = \int_0^R r^2 \Delta m ({r}) = \int_0^R r^2 \sigma 2 \pi r \ dr = \int_0^R r^2 \frac{m}{\pi R^2} 2 \pi r \ dr = \] \[ \qquad = \frac{2m}{R^2} \int_0^R r^3 \ dr = \frac{2m}{R^2} \left[ \frac{r^4}{4} \right]_0^R = \frac{2m}{R^2} \frac{R^4}{4} = \frac{1}{2}mR^2. \]
Arc lengths of a curve
Given a function $y=f(x)$ and an interval $x \in [x_i, x_f]$, how can you calculate the total length $\ell$ of the curve $f(x)$ between these two points?
If the curve were a straight line, then we would simply take the hypotenuse of the change in $x$ and the change in $y$: $\sqrt{ \text{run}^2 + \text{rise}^2 }=$ $\sqrt{ (x_f-x_i)^2 + (f(x_f)-f(x_i))^2}$.
If the function is not a straight line, however, we have to do this hypotenuse thing on each piece of the curve $d\ell = \sqrt{ dx^2 + dy^2}$, and add up all the contributions as an integral.
The arc length $\ell$ of a curve $y = f(x)$ is given by: \[ \ell=\int d\ell = \int_{x_i}^{x_f} \sqrt{1+\left(\frac{df(x)}{dx}\right)^2} \ dx. \]
Surface of revolution
We can use the above formula for arc-length to ask how much surface area $A$ a solid of revolution with boundary $f(x)$ would have.
Each piece of length $d\ell$, must be multiplied by $2 \pi f(x)$ since it is being rotated around the $x$-axis in a circle of radius $f(x)$. The area of the surface of revolution traced out by $f(x)$ rotated around the $x$-axis is given by the following integral: \[ A= \int 2\pi f(x) d\ell = \int_{x_i}^{x_f} 2\pi f(x)\ \sqrt{1+\left(\frac{df(x)}{dx}\right)^2} \ dx. \]
Volumes of revolution
Next we raise the stakes. We already showed that we can express two dimensional integrals with circular symmetry as one dimensional integrals. Now we move on to three dimensional integrals: integrals over volumes. We will use the circular symmetry to calculate the volume using a single integral again.
Washer method
We can split any volume into a number of disks of thickness $dx$ and with radius proportional to the function $f(x)$.
 The volume $V$ of a solid of traced out by
some $f(x)$ as revolution is:
\[
V
= \int A_{disk}(x) \times h_{disk}
= \int \pi f^2(x) \ dx.
\]
The volume $V$ of a solid of traced out by
some $f(x)$ as revolution is:
\[
V
= \int A_{disk}(x) \times h_{disk}
= \int \pi f^2(x) \ dx.
\]
If we want the volume of revolution in between two functions $g(x)$ and $f(x)$, then we have to imagine splitting the volume into washers: disks of inner radius $f(x)$, outer radius $g(x)$ and thickness $dx$: \[ V = \int A_{washer}(x) \; dx = \int \pi [f^2(x)-g^2(x)] \; dx. \] Each washer consist of a disk of are $\pi f^2(x)$ from which a circular piece of area $\pi g^2(x)$ has been cut out.
Example
Let's calculate the volume of a sphere of radius $r$ using the disk method. Our generating region will be the region bounded by the curve $f(x)=\sqrt{r^2-x^2}$ and the line $y=0$. Our limits of integration will be the $x$-values where the curve intersects the line $y=0$, namely, $x=\pm r$. We have: \[ \begin{align} V_{sphere}&=\int_{-r}^r \pi(r^2-x^2)dx \nl &=\pi(\int_{-r}^r r^2 dx-\int_{-r}^r x^2 dx)\nl &=\pi(r^2 x\bigr|_{-r}^r - \frac{x^3}{3}\biggr|_{-r}^r)\nl &=\pi(r^2 (r-(-r)) - (\frac{r^3}{3}-\frac{(-r)^3}{3})\nl &=\pi(2r^3-\frac{2r^3}{3})\nl &=\pi\frac{6r^3-2r^3}{3}\nl &=\frac{4\pi r^3}{3}. \end{align} \]
Cylindrical shell method
Alternately we can split any circularly symmetric volume into thin cylindrical shells of thickness $dr$. If the volume has a circular symmetry and is bounded from above by $F(r )$ and from below by $G(r )$, then the integral over the volume will be: \[ \begin{align*} V & = \int C_{shell}(r ) \: h_{shell}(r ) \; dr \nl & = \int_a^b 2\pi r | F(r ) - G(r ) | \; dr, \end{align*} \] where $2\pi r$ is the circumference of each cylindrical shell and $|F(r )-G(r )|$ is its height.
Example
 Calculate the volume of a sphere of radius $R$ using the cylindrical
shell method. We are talking about the region enclosed by the
surface $x^2 + y^2 + z^2 = R^2$.
Calculate the volume of a sphere of radius $R$ using the cylindrical
shell method. We are talking about the region enclosed by the
surface $x^2 + y^2 + z^2 = R^2$.
The shell at radius $r=\sqrt{x^2+y^2}$ will have a roof of $z=F(r)=2\sqrt{R^2-r^2}$, a floor of $z=G(r)=-2\sqrt{R^2-r^2}$, circumference $2\pi r$ and a width of $dr$. The integral will proceed as follows: \[ \begin{align*} V &= \int_0^R 2\pi r | F(r ) - G(r ) | \; dr \nl &= \int_0^R 2 \pi r 2\sqrt{R^2-r^2} \ dr \nl &= - 2\pi \int_{R^2}^0 \sqrt{u} \ du \nl &= - 2\pi \frac{2}{3} u^{3/2}\bigg|_{R^2}^0 \nl &= - 2\pi [ 0 - \frac{2}{3}R^3] \nl &= \frac{4\pi R^3}{3}, \end{align*} \] where in the second line we carried out the substitution $u=R^2-r^2, du = -2r dr$.
Exercises
Exercise 1
Calculate the volume of the cone with radius $R$ and height $h$ which is generated by the revolution of the region bounded by $y=R-\frac{R}{h}x$ and the lines $y=0$ and $x=0$ around the $x$-axis. Answer: $\frac{\pi R^2 h}{3}$.
Exercise 2
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curve $y=x^2$ and the lines $x=1$ and $y=0$ around the $x$-axis. Answer:$\frac{\pi}{5}$.
Exercise 3
Use the washer method to find the volume of a cone containing a central hole formed by revolving the region bounded by $y=R-\frac{R}{h}x$ and the lines $y=r$ and $x=0$ around the $x$-axis. Answer:$\pi h\left(\frac{R^2}{3}-r^2\right)$.
Exercise 4
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curves $y=x^2$ and $y=x^3$ and the lines $x=1$ and $y=0$ around the $x$-axis. Answer: $\frac{2\pi}{35}$.
Exercise 5
Find the volume of a cone with radius $R$ and height $h$ by using the shell method on the appropriate region which, when rotated around the $y$-axis, produces a cone with the given characteristics. Answer:$\frac{\pi r^2 h}{3}$.
Exercise 6
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curve $y=x^2$ and the lines $x=1$ and $y=0$ around the $y$-axis. Answer:$\frac{\pi}{2}$.
Improper integrals
Imagine you want to find the area under the function $f(x)=\frac{1}{x^2}$ from $x=1$ all the way to infinity $x=\infty$. This kind of calculation is known as an improper integral since one of the endpoints of the integration is not a regular number, but infinity.
Nevertheless we can compute this integral: \[ \int_1^\infty \frac{1}{x^2}\;dx \equiv \lim_{b\to\infty} \int_1^b\frac{1}{x^2}\; dx = \lim_{b\to\infty} \left[ \frac{-1}{x} \right]_1^b = \lim_{b\to\infty} \left[-\frac{1}{b} + \frac{1}{1}\right] = 1. \]
Definitions
An improper integral is one in which one or more of the limits of integration is infinite. Such integrals are to be evaluated as regular integrals where the infinity is replaced by a dummy variable, followed by a limit calculation in which the the dummy variable is taken to infinity: \[ \int_a^\infty f(x) \; dx \equiv \lim_{b\to \infty} \int_a^b f(x) \; dx = \lim_{b\to \infty} [ F(b) - F(a) ], \] where $F(x)$ is the anti-derivative function of $f(x)$.
Applications
Later in this chapter, we will learn about the “integral test” for the convergence of a series, which requires the evaluation of an improper integral.
Sequences
A sequence is and ordered list of numbers, usually following some pattern like the “find the pattern” questions on IQ tests. We will study the properties of these sequences. For example, we can check whether the sequence converges to some limit.
Understanding sequences is also a prerequisite for understanding series, which is an important topic we will discuss in the next section.
Definitions
- $\mathbb{N}$: The set of natural numbers $\{0, 1, 2, 3, \ldots \}$.
- $\mathbb{N}^*=\mathbb{N} \setminus \{0\}$:
The set of strictly positive natural numbers $\{1, 2, 3, \ldots \}$,
which is the same as the above, but we skip zero.
* $a_n$: sequence of numbers $a_0, a_1, a_2, a_3, a_4, \ldots$.
You can also think about each sequence as a function
\[
a: \mathbb{N} \to \mathbb{R},
\]
where the input is $n$ an integer (the //index// into the sequence) and
the output is some number $a_n \in \mathbb{R}$.
Examples
Consider the following common sequences.
Arithmetic progression
Consider a sequence in which successive terms differ by one: \[ 1, \ 2,\ 3, \ 4, \ 5, \ 6, \ \ldots \] which is described by the formula: \[ a_n = n, \qquad n \in \mathbb{N}^*. \]
More generally, an arithmetic sequence can start at any value $a_0$ and make jumps of size $d$ at each step: \[ a_n = a_0 + nd, \qquad n \in \mathbb{N}. \]
Harmonic sequence
If we choose to make the sequence elements inversely proportional to the index $n$ we obtain the harmonic sequence: \[ 1, \ \frac{1}{2},\ \frac{1}{3}, \ \frac{1}{4}, \ \frac{1}{5}, \ \frac{1}{6}, \ \ldots \] \[ a_n = \frac{1}{n}, \qquad n \in \mathbb{N}^*. \]
More generally, we can define a $p$-sequence in which the index $n$ appears in the denominator raised to the power $p$: \[ a_n = \frac{1}{n^p}, \qquad n \in \mathbb{N}^*. \]
For example, when $p=2$ we get the sequence of inverse squares of the integers: \[ 1, \ \frac{1}{4}, \ \frac{1}{9}, \ \frac{1}{16}, \ \frac{1}{25}, \ \frac{1}{36}, \ \ldots. \]
Geometric sequence
If we use the index as an exponent to a fixed number $r$ we obtain the geometric series: \[ a_n = r^n, \ \ n \in \mathbb{N}, \] which is a sequence of the form \[ 1, r, r^2, r^3, r^4, r^5, r^6, \ldots. \]
Suppose we choose $r=\frac{1}{2}$, then the geometric series with this ratio will be: \[ 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}, \frac{1}{128}, \ldots. \]
Fibonacci
\[ a_0 =1, a_1 = 1, \qquad \ a_n = a_{n-1} + a_{n-2}, \ \ n > 1. \] \[ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \ldots. \]
Convergence
We say a sequence $a_n$ converges to a limit $L$, or written mathematically: \[ \lim_{n \to \infty} a_n \ = \ L, \] if for large $n$ the sequence values get arbitrarily close to the value $L$.
More precisely, the limit notation means that for any choice of precisions $\epsilon>0$, we can pick a number $N_\epsilon$ such that: \[ | a_n - L | < \epsilon, \qquad \forall n \geq N_\epsilon. \]
The notion of a limit of a sequence is the same as that of a limit of a function. The same way we learned how to calculate which number the function $f(x)$ tends to for large $x$, we can study which number the sequence $a_n$ tends to for large $n$. Indeed, sequences are functions that are defined only at integer values of $x$.
Ratio convergence
The numbers in the Fibonacci sequence grow indefinitely large ($\lim_{n \to \infty} a_n = \infty$), but the ratio of $\frac{a_n}{a_{n-1}}$ converges to a constant: \[ \lim_{n \to \infty}\frac{a_n}{a_{n-1}} = \phi = \frac{1+\sqrt{5}}{2} \approx 1.618033\ldots, \] which is known as the golden ratio.
Calculus on sequences
If a sequence $a_n$ is like a function $f(x)$, then we should be able to do calculus on it. We already saw we can take limits of sequences, but can we also compute derivatives and integrals of sequences? Derivatives are a no-go, because they depend on the function $f(x)$ being continuous and sequences are only defined for integer values. We can take integrals of sequences, however, and this is the subject of the next section.
Series
Can you compute $\ln(2)$ using only a basic
calculator with four operations: [+], [-], [$\times$], [$\div$]?
I can tell you one way. Simply compute the following sum:
\[
1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} + \ldots.
\]
We can compute the above sum for large values of $n$ using live.sympy.org:
>>> def axn_ln2(n): return 1.0*(-1)**(n+1)/n
>>> sum([ axn_ln2(n) for n in range(1,100) ])
0.69(817217931)
>>> sum([ axn_ln2(n) for n in range(1,1000) ])
0.693(64743056)
>>> sum([ axn_ln2(n) for n in range(1,1000000) ])
0.693147(68056)
>>> ln(2).evalf()
0.693147180559945
As you can see, the more terms you add in this series, the more accurate the series approximation of $\ln(2)$ becomes. A lot of practical mathematical computations are done in this iterative fashion. The notion of series is a powerful way to calculate quantities to arbitrary precision by summing together more and more terms.
Definitions
- $\mathbb{N}$: $ = \{0, 1, 2, 3, 4, 5, 6, \ldots \}$.
- $\mathbb{N}^*=\mathbb{N} \setminus \{0\}$: = $\{1, 2, 3, 4, 5, 6, \ldots \}$.
- $a_n$: sequence of numbers $a_0, a_1, a_2, a_3, a_4, \ldots$.
- $\sum$: sum. Means to take the sum of several objects
put together. The summation sign is the short way to express
certain long expressions:
\[
a_3 + a_4 + a_5 + a_6 + a_7 = \sum_{3 \leq i \leq 7} a_i = \sum_{i=3}^7 a_i.
\]
* $\sum a_i$: series. The running total of a sequence until $n$:
\[
S_n = \sum_{i=1}^n a_i = a_1 + a_2 + \ldots + a_{n-1} + a_n.
\]
Most often, we take the sum of all the terms in the sequence:
\[
S_\infty = \sum_{i=1}^\infty = a_1 + a_2 + a_{3} + a_4 + \ldots.
\]
* $n!$: the //factorial// function: $n!=n(n-1)(n-2)\cdots 3\cdot2\cdot1$.
* $f(x)=\sum_{n=0}^\infty a_n x^n$: //Taylor series// approximation
of the function $f(x)$. It has the form of an infinitely long polynomial
$a_0 + a_1x + a_2x^2 + a_3x^3 + \ldots$ where the coefficients $a_n$ are
chosen so as to encode the properties of the function $f(x)$.
Exact sums
There exist formulas for calculating the exact sum of certain series. Sometimes even infinite series can be calculated exactly.
The sum of the geometric series of length $n$ is: \[ \sum_{k=0}^n r^k = 1 + r + r^2 + \cdots + r^n =\frac{1-r^{n+1}}{1-r}. \]
If $|r|<1$, we can take the limit as $n\to \infty$ in the above expression to obtain: \[ \sum_{k=0}^\infty r^k=\frac{1}{1-r}. \]
Example
Consider the geometric series with $r=\frac{1}{2}$. If we apply the above formula formula we obtain \[ \sum_{k=0}^\infty \left(\frac{1}{2}\right)^k=\frac{1}{1-\frac{1}{2}} = 2. \]
You can also visualize this infinite summation graphically. Imagine you start with a piece of paper of size one-by-one and then you add next to it a second piece of paper with half the size of the first, and a third piece with half the size of the second, etc. The total area that this sequence of pieces of papers will occupy is:
\[ \ \]
The sum of the first $N+1$ terms in arithmetic progression is given by: \[ \sum_{n=0}^N (a_0+nd)= a_0(N+1)+\frac{N(N+1)}{2}d. \]
We have the following closed form expression involving the first $N$ integers: \[ \sum_{k=1}^N k = \frac{N(N+1)}{2}, \qquad \quad \sum_{k=1}^N k^2=\frac{N(N+1)(2N+1)}{6}. \]
Other series which have exact formulas for their sum are the $p$-series with even values of $p$: \[ \sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}, \quad \sum_{n=1}^\infty\frac{1}{n^4}=\frac{\pi^4}{90}, \quad \sum_{n=1}^\infty\frac{1}{n^6}=\frac{\pi^6}{945}. \] These series are computed by Euler's method.
Other closed form sums: \[ \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^2}=\frac{\pi^2}{12}, \qquad \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n}=\ln(2), \] \[ \sum_{n=1}^\infty\frac{1}{4n^2-1}=\frac{1}{2}, \] \[ \sum_{n=1}^\infty\frac{1}{(2n-1)^2}=\frac{\pi^2}{8}, \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{(2n-1)^3}=\frac{\pi^3}{32}, \quad \sum_{n=1}^\infty\frac{1}{(2n-1)^4}=\frac{\pi^4}{96}. \]
Convergence and divergence of series
Even when we cannot compute an exact expression for the sum of a series it is very important to distinguish series that converge from series that do not converge. A great deal of what you need to know about series is different tests you can perform on a series in order to check whether it converges or diverges.
Note that convergence of a series is not the same as convergence of the underlying sequence $a_i$. Consider the sequence of partial sums $S_n = \sum_{i=0}^n a_i$: \[ S_0, S_1, S_2, S_3, \ldots , \] where each of these corresponds to \[ a_0, \ \ a_0 + a_1, \ \ a_0 + a_1 + a_2, \ \ a_0 + a_1 + a_2 + a_3, \ldots. \]
We say that the series $\sum a_i$ converges if the sequence of partial sums $S_n$ converges to some limit $L$: \[ \lim_{n \to \infty} S_n = L. \]
As with all limits, the above statement means that for any precision $\epsilon>0$, there exists an appropriate number of terms to take in the series $N_\epsilon$, such that \[ |S_n - L | < \epsilon,\qquad \text{ for all } n \geq N_\epsilon. \]
Sequence convergence test
The only way the partial sums will converge is if the entries in the sequences $a_n$ tend to zero for large $n$. This observation gives us a simple series divergence test. If $\lim\limits_{n\rightarrow\infty}a_n\neq0$ then $\sum\limits_n a_n$ diverges. How could an infinite sum of non-zero quantities add up to a finite number?
Absolute convergence
If $\sum\limits_n|a_n|$ converges, $\sum\limits_n a_n$ also converges. The opposite is not necessarily true, since the convergence of $a_n$ might be due to some negative terms cancelling with the positive ones.
A sequence $a_n$ for which $\sum_n |a_n|$ converges is called absolutely convergent. A sequence $b_n$ for which $\sum_n b_n$ converges, but $\sum_n |b_n|$ diverges is called conditionally convergent.
Decreasing alternating sequences
An alternating series of which the absolute values of the terms are decreasing and go to zero converges.
p-series
The series $\displaystyle\sum_{n=1}^\infty \frac{1}{n^p}$ converges if $p>1$ and diverges if $p\leq1$.
Limit comparison test
Suppose $\displaystyle\lim_{n\rightarrow\infty}\frac{a_n}{b_n}=p$, then the following is true:
- if $p>0$ then $\sum\limits_{n}a_n$ and $\sum\limits_{n}b_n$ either both converge or both diverge.
- if $p=0$ holds: if $\sum\limits_{n}b_n$ converges, then $\sum\limits_{n}a_n$ also converges.
n-th root test
If $L$ is defined by $\displaystyle L=\lim_{n\rightarrow\infty}\sqrt[n]{|a_n|}$ then $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Ratio test
$\displaystyle L=\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|$, then is $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Radius of convergence for power series
In a power series $a_n=c_nx^n$, the $n$th term is multiplied by the $n$th power of $x$. For such series, the convergence or divergence of the series depends on the choice of the variable $x$.
The radius of convergence $\rho$ of $\sum\limits_n c_n$ is given by: $\displaystyle\frac{1}{\rho}=\lim_{n\rightarrow\infty}\sqrt[n]{|c_n|}= \lim_{n\rightarrow\infty}\left|\frac{c_{n+1}}{c_n}\right|$. For all $-\rho < x < \rho$ the series $a_n$ converges.
Integral test
If $\int_a^{\infty}f(x)dx<\infty$, then $\sum\limits_n f(n)$ converges.
Taylor series
The Taylor series approximation to the function $\sin(x)$ to the 9th power of $x$ is given by \[ \sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!}. \] If we want to get rid of the approximate sign, we have to take infinitely many terms in the series: \[ \sin(x) = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \frac{x^{11}}{11!} + \ldots . \]
This kind of formula is known as a Taylor series approximation. The Taylor series of a function $f(x)$ around the point $a$ is given by: \[ \begin{align*} f(x) & =f(a)+f'(a)(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3+\cdots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n. \end{align*} \]
The McLaurin series of $f(x)$ is the Taylor series expanded at $a=0$: \[ \begin{align*} f(x) & =f(0)+f'(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3 + \ldots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n . \end{align*} \]
Taylor series of some common functions: \[ \begin{align*} \cos(x) &= 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} + \ldots \nl e^x &= 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots \nl \ln(x+1) &= x - \frac{x^2}2 + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} - \frac{x^6}{6} + \ldots \nl \cosh(x) &= 1 + \frac{x^2}{2} + \frac{x^4}{4!} + \frac{x^6}{6!} + \frac{x^8}{8!} + \frac{x^{10} }{10!} + \ldots \nl \sinh(x) &= x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!} + \frac{x^9}{9!} + \frac{x^{11} }{11!} + \ldots \end{align*} \] Note the similarity in the Taylor series of $\sin$, $\cos$ and $\sinh$ and $\cosh$. The formulas are the same, but the hyperbolic version do not alternate.
Explanations
Taylor series
The names Taylor series and McLaurin series are used interchangeably. Another synonym for the same concept is a power series. Indeed, we are talking about a polynomial approximation with coefficients $a_n=\frac{f^{(n)}(0)}{n!}$ in front of different powers of $x$.
If you remember your derivative rules correctly, you can calculate the McLaurin series of any function simply by writing down a power series $a_0 + a_1x + a_2x^2 + \ldots$ taking as the coefficients $a_n$ the value of the n'th derivative divided by the appropriate factorial. The more terms in the series you compute, the more accurate your approximation is going to get.
The zeroth order approximation to a function is \[ f(x) \approx f(0). \] It is not very accurate in general, but at least it is correct at $x=0$.
The best linear approximation to $f(x)$ is its tangent $T(x)$, which is a line that passes through the point $(0, f(0))$ and has slope equal to $f'(0)$. Indeed, this is exactly what the first order Taylor series formula tells us to compute. The coefficient in front of $x$ in the Taylor series is obtained by first calculating $f'(x)$ and then evaluating it at $x=0$: \[ f(x) \approx f(0) + f'(0)x = T(x). \]
To find the best quadratic approximation to $f(x)$, we find the second derivative $f^{\prime\prime}(x)$. The coefficient in front of the $x^2$ term will be $f^{\prime\prime}(0)$ divided by $2!=2$: \[ f(x) \approx f(0) + f'(0)x + \frac{f^{\prime\prime}(0)}{2!}x^2. \]
If we continue like this we will get the whole Taylor series of the function $f(x)$. At step $n$, the coefficient will be proportional to the $n$th derivative of $f(x)$ and the resulting $n$th degree approximation is going to imitate the function in its behaviour up the $n$th derivative.
Proof of the sum of the geometric series
We are looking for the sum $S$ given by: \[ S = \sum_{k=0}^n r^k = 1 + r + r^2 + r^3 + \cdots + r^n. \] Observe that there is a self similar pattern in the expanded summation $S$ where each term to the right has an additional power of $r$. The effects of multiplying by $r$ will therefore to “shift” all the terms of the series: \[ rS = r\sum_{k=0}^n r^k = r + r^2 + r^3 + \cdots + r^n + r^{n+1}, \] we can further add one to both sides to obtain \[ 1 + rS = \underbrace{1 + r + r^2 + r^3 + \cdots + r^n}_S + r^{n+1} = S + r^{n+1}. \] Note how the sum $S$ appears as the first part of the expression on the right-hand side. The resulting equation is quite simple: $1 + rS = S + r^{n+1}$. Since we wanted to find $S$, we just isolate all the $S$ terms to one side: \[ 1 - r^{n+1} = S - rS = S(1-r), \] and then solve for $S$ to obtain $S=\frac{1-r^{n+1}}{1-r}$. Neat no? This is what math is all about, when you see some structure you can exploit to solve complicated things in just a few lines.
Examples
An infinite series
Compute the sum of the infinite series \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n. \] This may appear complicated, but only until you recognize that this is a type of geometric series $\sum ar^n$, where $a=\frac{1}{N+1}$ and $r=\frac{N}{N+1}$: \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n = \sum_{n=0}^\infty a r^n = \frac{a}{1-r} = \frac{1}{N+1}\frac{1}{1-\frac{N}{N+1}} = 1. \]
Calculator
How does a calculator compute $\sin(40^\circ)=0.6427876097$ to ten decimal places? Clearly it must be something simple with addition and multiplication, since even the cheapest scientific calculators can calculate that number for you.
The trick is to use the Taylor series approximation of $\sin(x)$: \[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} + \ldots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}. \]
To calculate sin of 40 degrees we just compute the sum of the series on the right with $x$ replaced by 40 degrees (expressed in radians). In theory, we need to sum infinitely many terms to satisfy the equality, but in practice you calculator will only have to sum the first seven terms in the series in order to get an accuracy of 10 digits after the decimal. In other words, the series converges very quickly.
Let me show you how this is done in Python.
First we define the function for the $n^{\text{th}}$ term:
\[
a_n(x) = \frac{(-1)^nx^{2n+1}}{(2n+1)!}
\]
>>> def axn_sin(x,n): return (-1.0)**n * x**(2*n+1) / factorial(2*n+1)
Next we convert $40^\circ$ to radians:
>>> forti = (40*pi/180).evalf()
0.698131700797732 # 40 degrees in radians
NOINDENT These are the first 10 coefficients in the series:
>>> [ axn_sin( forti ,n) for n in range(0,10) ] [(0, 0.69813170079773179), # the values of a_n for Taylor(sin(40)) (1, -0.056710153964883062), (2, 0.0013819920621191727), (3, -1.6037289757274478e-05), (4, 1.0856084058295026e-07), (5, -4.8101124579279279e-10), (6, 1.5028144059670851e-12), (7, -3.4878738801065803e-15), (8, 6.2498067170560129e-18), (9, -8.9066666494280343e-21)]
NOINDENT To compute $\sin(40^\circ)$ we sum together all the terms:
>>> sum( [ axn_sin( forti ,n) for n in range(0,10) ] )
0.642787609686539 # the Taylor approximation value
>>> sin(forti).evalf()
0.642787609686539 # the true value of sin(40)
Discussion
You can think of the Taylor series as “similarity coefficients” between $f(x)$ and the different powers of $x$. By choosing the coefficients as we have $a_n = \frac{f^{(n)}(?)}{n!}$, we guarantee that Taylor series approximation and the real function $f(x)$ will have identical derivatives. For a McLaurin series the similarity between $f(x)$ and its power series representation is measured at the origin where $x=0$, so the coefficients are chosen as $a_n = \frac{f^{(n)}(0)}{n!}$. The more general Taylor series allow us to build an approximation to $f(x)$ around any point $x_o$, so the similarity coefficients are calcualted to match the derivatives at that point: $a_n = \frac{f^{(n)}(x_o)}{n!}$.
Another way of looking at the Taylor series is to imagine that it is a kind of X-ray picture for each function $f(x)$. The zeroth coefficient $a_0$ in the power series tells you how much of the constant function there is in $f(x)$. The first coefficient, $a_1$, tells you how much of the linear function $x$ there is in $f$, the coefficient $a_2$ tells you about the $x^2$ contents of $f$, and so on and so forth.
Now get ready for some crazy shit. Using your new found X-ray vision for functions, I want you to go and take a careful look at the power series for $\sin(x)$, $\cos(x)$ and $e^x$. As you will observe, it is as if $e^x$ contains both $\sin(x)$ and $\cos(x)$, except for the alternating negative signs. How about that? This is a sign that these three functions are somehow related in a deeper mathematical sense: recall Euler's formula.
Exercises
Derivative of a series
Show that \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n n = N. \] Hint: take the derivative with respect to $r$ on both sides of the formula for the geometric series.
End matter
Conclusion
I would like to go on telling you about other math and physics stuff, but at some point we have to take a brake. This time is now.
We managed to cover a lot of ground in terms of topics and concepts in a relatively small textbook. We reviewed high school math and discussed calculus and mechanics in depth. Above all, we presented the math and physics material in an integrated manner.
It will sound a little cheesy, but it is the truth so I will go ahead and say it.
I am writing this book for you so if you liked/hated it, be sure to send me feedback.
Feedback is very important for me so I know how to adjust the writing,
the content and the attitude in the book.
Please take the time to drop me a line and let me know what you think about this book.
My email address is: ivan.savov@gmail.com.
You can also find me on twitter: http://twitter.com/minireference
and Facebook http://facebook.com/pages/Math-and-Physics-Minireference/189157377884715.
There is also the company blog at http://minireference.com/blog/ where I
discuss the business side of things.
Acknowledgments
This book would not have been possible without the support and encouragement of the people around me. I have been fortunate enough to grow up surrounded by good people who knew the value of math and encouraged me in my studies and with this project. In this section, I want to big up all the people who deserve it.
First and foremost in this list are my parents who brought me up well, educated me and taught me how to think critically.
Next in line are all my teachers. I want to thank my CEGEP teachers: Karnig Bedrossian from whom I learned calculus, Paul Kenton from whom I leaned how to think about physics in a chill manner and Benoit Larose who taught me that more dimensions does not mean things get more complicated. I want to thank Kohur GowriSankaran, Frank Ferrie, Mourad El-Gamal, Ioannis Psaromiligkos for teaching me how to be an Engineer, Guy Moore and Zaven Altounian who taught me a lot about advanced physics. I owe many thanks to Patrick Hayden, David Avis and Doina Precup for their support and advice on matters of research. I also want to thank Igor Khavkine, Juan Pablo Di Lelle, Andie Sigler, Omar Fawzi and Mark M. Wilde for teaching me a great many things.
Preparing this book took a lot of effort. Afton Lewis, Oleg Zhoglo and Alexandra Foty helped me proofread early drafts and suggested many clarifications. Their comments and feedback were much appreciated and contributed to make this book better.
Last but not least, I want to thank all my students for their endless questions and demands for explanations. If I have developed any skill for explaining things, it is to them that I owe it.
Further reading
You have reached the end of this book, but you are only at the beginning of the journey of scientific discovery. There are a lot of cool things left for you to learn about. Below are some recommendation of subjects which you might be interested in.
Electricity and Magnetism
Electrostatics is the study of the electric force $\vec{F}_e$ and the associated electric potential $U_e$. You will also learn about the electric field $\vec{E}$ and electric potential $V$.
Magnetism is the study of the magnetic force $\vec{F}_b$ and the magnetic field $\vec{B}$, which is caused by electric currents flowing in wires. The current $I$ is the total number of electrons passing through a cross-section of the wire in one second. By virtue of its motion through space, each electron contributes to the strength of the magnetic field surrounding the wire.
The beauty of electromagnetism is that the entire theory can be describes in just four equations: \[ \begin{align*} \nabla \cdot \vec{E} &= \frac {\rho} {\varepsilon_0} & \textrm{Gauss's law} \nl \nabla \cdot \vec{B} &= 0 & \textrm{ Gauss's law for magnetism} \nl \nabla \times \vec{E} &= -\frac{\partial \vec{B}} {\partial t} & \textrm{Faraday's law of induction } \nl \nabla \times \vec{B} &= \mu_0\vec{J} + \mu_0 \varepsilon_0 \frac{\partial \vec{E}} {\partial t} & \textrm{ Ampère's circuital law } \end{align*} \] Together, these are known as Maxwell's equations.
Vector calculus
You may be wondering what the triangle thing is $\nabla$. The symbol $\nabla$ (nabla) is the vector derivative operation. Guess what, you can also do calculus with vectors.
In vector calculus you will learn about path integrals, surface integrals and volume integrals of vector quantities. You will also learn about vector-derivatives and two vector equivalents of the Fundamental Theorem of Calculus:
- Stokes' Theorem:
\[ \iint_{\Sigma} \nabla \times \vec{F} \cdot d\vec{\Sigma} = \int_{\partial\Sigma} \vec{F} \cdot d \vec{r}, \]
which relates the integral of the $\textrm{curl} \vec{F} \equiv \nabla \times \vec{F}$
of the field $\vec{F}$ over the surface $\Sigma$ to the
circulation of $\vec{F}$ along the boundary of the surface
$\partial\Sigma$.
* Gauss' Divergence Theorem:
\[
\iiint_{\mathrm{V}} \nabla \cdot \vec{F} \ d\mathrm{V}
= \int\!\!\!\int_{\partial \mathrm{V}} \vec{F} \cdot d \vec{\Sigma},
\]
which relates the integral of the divergence $\textrm{div} \vec{F} \equiv \nabla \cdot \vec{F}$
of the field $\vec{F}$ over the volume $\mathrm{V}$ to the
flux of $\vec{F}$ through the volume boundary $\partial\mathrm{V}$.
Both of the above theorems relate the total of some derivative quantity over some region $R$ to the quantity on the boundary of the region $R$, which we denote as $\partial R$. The Fundamental Theorem of Calculus can also be interpreted in the same manner: \[ \int_I F^\prime(x) \; dx = \int_a^b F^\prime(x) \; dx = F_{\partial I} = F(b) - F(a), \] where $I=[a,b]$ is the interval from $a$ to $b$ on the real line and the two points $a$ and $b$ form its boundary $\partial I$.
Only physicists and engineers have to take this course.
Multivariable calculus
Of wider interest is the course which studies calculus with functions which have more than one input variable. Consider as an example the function $f(x,y)$ which has two input variables $x$ and $y$. You can plot this function as a surface, where the height $z$ of the function above the point $(x,y)$ is given by the function value $z=f(x,y)$.
There is no new math to learn in multivariable calculus: it is just the same stuff as Calculus I (derivatives) and Calculus 2 (integrals) but with more variables. For a function $f(x,y)$ there will be an “$x$-derivative” $\frac{\partial}{\partial x}$ and a “$y$-derivative” $\frac{\partial}{\partial y}$. The operator $\nabla$ is a combination of both the $x$ and $y$ derivatives: $\nabla f(x,y) = [ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial x}]$. Note that $\nabla$ acts on a function $f(x,y)$ to produce a vector. This is known as the gradient vector, which tells you the “slope” of the function. More specifically it tells you the direction of maximum increase of the function. If you think of $z=f(x,y)$ as the height of a mountain at a particular $(x,y)$ coordinates on a map then the gradient vector $\nabla f(x,y)$ always points uphill.
If you understood derivatives and integrals well, then you should definitely take this course (usually called Calculus III) as it is perhaps the easiest science course you will ever take.
Probability
Probability distribution are a fundamental tool for modelling non-deterministic behaviour. A discrete random variable $X$ is associated with a probability mass function $p_X(x) \equiv \textrm{Pr}\{ X = x \}$, which assigns a “probability mass” to each of the possible outcomes $x \in \mathcal{X}$. For example, if $X$ represents a fair die, then the possible outcomes are $\mathcal{X}=\{ 1, 2, 3, 4, 5, 6 \}$ and the probability mass function has the values $p_X(x)=\frac{1}{6}$, $\forall x \in \mathcal{X}$.
Probability theory is used all over the place: statistics, machine learning, quantum mechanics, gambling, risk analysis, etc.
General mathematics
Mathematics is a very broad field. There are all kinds of topics to learn about: some of them fun, some of them useful, some of them boring and some which have been know historically to drive people insane. Like, literally.
I recently found a very interesting book which covers many topics of general interest and serves as a great overview of the various areas of mathematics. I highly recommend that you take a look at this book if you are interested in math. It is written for the general audience so it is very accessible.
NOINDENT [BOOK] Richard Elwes. Mathematics 1001: Absolutely Everything That Matters About Mathematics in 1001 Bite-Sized Explanations, Firefly Books, 2010, ISBN 1554077192.
General physics
If you want to more about physics, I highly recommend the Feynman lectures on physics. This three-tome collection covers all of undergraduate physics with countless links to more advanced topics:
NOINDENT [BOOK] Richard P. Feynman, Robert B. Leighton, Matthew Sands. The Feynman Lectures on Physics including Feynman's Tips on Physics: The Definitive and Extended Edition, Addison Wesley, 2005, ISBN 0805390456.
While on the Feynman note, I want to also recommend his other book with life stories.
NOINDENT [BOOK] Richard P. Feynman. Surely You're Joking, Mr. Feynman! (Adventures of a Curious Character), W. W. Norton & Company, 1997, ISBN 0393316041.
Lagrangian mechanics
In this book we learned about Newtonian mechanics, that is, Mechanics starting from Newton's laws. There is a much more general framework known as Lagrangian mechanics which can be used to analyze more complex mechanical systems. The following is an excellent book on the subject.
NOINDENT [BOOK] Herbert Goldstein, Charles P. Poole Jr., John L. Safko. Classical Mechanics, Addison-Wesley, Third edition, 2001, ISBN 0201657023.
Quantum mechanics
Quantum mechanics describes the physics of all things is small: photons, electrons and atoms. An absolutely approachable and readable introduction to the subject is Richard Feynman's QED book.
NOINDENT [BOOK] Richard P. Feynman. QED: The strange theory of light and matter. Princeton University Press, 2006, ISBN 0691125759.
For a deeper understanding of quantum mechanics, I recommend the book by Sakurai. If you understand linear algebra, then you can understand quantum mechanics.
NOINDENT [BOOK] Jun John Sakurai. Modern Quantum Mechanics, Second Edition, Addison-Wesley, 2010, ISBN 0805382917.
If you want to read Sakurai, it would be a good idea to first learn about Lagrangian mechanics from Goldstein. Goldstein followed by Sakurai is an excellent combo.
Information theory
Claude Shannon developed a mathematical framework for studying the problems of information storage and information transmission. Using statistical notions such as entropy, we can quantify the information content of data sources and the information transmitting abilities of noisy communication channels.
We can arrive at an operational interpretation of the information carrying capacity of a noisy communication channel in terms of our ability to convert it into a noiseless channel. Channels with more noise have a smaller capacity for carrying information. Consider a channel which allows us to send data at the rate of 1 MB/sec on which half of the packets sent get lost due to the effects of noise on the channel. It is not true that the capacity of such a channel is 1MB/sec, because we also have to account for the need to retransmit lost packets. In order to correctly characterize the information carrying capacity of a channel, we must consider the rate of the end-to-end code which converts many uses of the noisy channel into an effectively noiseless communication channel.
Channel coding is one are the fundamental problems studied in information theory. The book by Cover and Thomas is an excellent textbook on the subject, which I highly recommend.
NOINDENT [BOOK] Thomas M. Cover, Joy A. Thomas. Elements of Information Theory, Wiley, 2006, ISBN 0471241954.
With this book, I tried to equip you with as much tools as I could, so that the remainder of your science studies will be enjoyable and pain free. Remember to always take it easy. Play with math and never take things too seriously. Grades don't matter. Big paycheques don't matter. Never settle for a boring job just because it is well paid. Try to work only on projects which you care about.
I want you to be confident in your ability to handle math, physics and other complicated stuff that life will throw at you. You have the tools to do anything you want. Choose your own adventure. And if the banks come-a-knocking one day, offering you a big paycheque for the application of your analytical skills to their avaricious schemes, send them-a-walking.