Ever since the invention of gun powder, generation after generation of men have thought of countless different ways of hurtling shrapnel and explosives at each other. Indeed, mankind has been stuck to the idea of two dimensional projectile motion like flies on shit. So long as there is money to be made in selling weapons, and TV stations to keep justifying the legitimacy of the use of these weapons, it is likely that the trend will continue.

It is therefore imperative for anyone interested in reversing this trend to learn about the physics of projectile motion. You need to know the techniques of the enemy (the industrial military complex) before you can fight them. We will see that projectile motion is nothing more than two parallel one-dimensional kinematics problems: UVM in the $x$ direction and UAM in the $y$ direction.

The basic concepts of kinematics in two dimensions are:

• $\hat{x},\hat{y}$: a coordinate system.
• $t$: time, measured in seconds.
• $\vec{r}(t)\equiv (x(t),y(t))$: the position (vector) of the object at time $t$.
• $\vec{v}(t) \equiv (v_x(t), v_y(t) ) $: the velocity of the object as a function of time.
• $\vec{a}(t) \equiv (a_x(t), a_y(t) ) $: the acceleration as a function of time.

When solving some problem, where we calculate the motion of an object that starts form an initial point an goes to a final point, we will use the following terminology:

• $t_i=0$: initial time (the beginning of the motion).
• $t_f$: final time (when the motion stops).
• $\vec{v}_{i}=\vec{v}(0)=(v_x(0),v_y(0))=(v_{ix},v_{iy})$: the initial velocity at $t=0$.
• $\vec{r}_i=\vec{r}(0)=(x(0),y(0))=(x_i,y_i)$: the initial position at $t=0$.
• $\vec{r}_f=\vec{r}(t_f)=(x(t_f),y(t_f))=(x_f,y_f)$: the final position at $t=t_f$.

Sometimes you have to describe both the $x$ and the $y$ coordinate of the motion of a particle: \[ \vec{r}(t)=(x(t), y(t)). \] We choose $x$ to be the horizontal component of the projectile motion and $y$ to be its height.

The velocity of the projectile will be \[ \vec{v}(t) = \frac{d}{dt}\left(\vec{r}(t)\right) = \left(\frac{dx(t)}{dt}, \frac{dy(t)}{dt} \right) = (v_x(t),v_y(t)), \] and the initial velocity is: \[ \vec{v}_i = \vec{v}(0) = \|\vec{v}_i\|\angle \theta = (v_x(0), v_y(0)) = (v_{ix}, v_{iy})= (\|\vec{v}_i\|\cos\theta, \|\vec{v}_i\|\sin\theta). \]

The acceleration of the projectile will be: \[ \vec{a}(t) = \frac{d}{dt}\left(\vec{v}(t)\right) = (a_x(t),a_y(t)) = (0,-9.81). \] Note how we have zero acceleration in the $x$ direction (ignoring air friction) so we can use the UVM equations of motion for $x(t)$ and $v_x(t)$. In the $y$ direction we have a uniform downward acceleration due to gravity.

The equations of motion of a projectile are the following. First in the $x$ direction we have: \[ \begin{align} x(t) & = v_{ix}t + x_i, \nl v_x(t) & =v_{ix}. \end{align} \]

In the $y$ direction, you have the constant pull of gravity downwards which gives us a uniformly accelerated motion (UAM): \[ \begin{align} y(t) & = \frac{1}{2}(-9.81)t^2 + v_{iy}t + y_i, \nl v_y(t) & = -9.81 t + v_{iy}, \nl v_{yf}^2 & = v_{iy}^2 + 2(-9.81)(\Delta y). \end{align} \]

Let us now consider an example in which we analyze all aspects of the motion of a projectile. An object is thrown with an initial velocity $8.96$[m/s] at an angle of $51.3^\circ$ with the ground from an initial height of $1$[m]. You are asked to calculate the maximum height $h$ that the object will reach, and the distance $d$ where the object will hit the ground.

Your first step when reading any physics problem should be to extract the information from the problem statement. The initial position is $\vec{r}(0)=(x_i,y_i)=(0,1)$[m]. The initial velocity is $\vec{v}_i=8.96\angle51.3^\circ$[m/s], which is $\vec{v}_i = (8.96\cos51.3^\circ, 8.96\sin51.3^\circ)= (5.6,7)$[m/s] in component form.

You can now plug the values of $\vec{r}_i$ and $\vec{v}_i$ into the equations of motion and find the desired quantities. When the object reaches its maximum height, it will have zero velocity in the $y$ direction: $v_{y}(t_{top})=0$. We can use this fact, and the $v_y(t)$ equation in order to find $t_{top} = 7/9.81= 0.714$[s]. The maximum height is then obtained by evaluating the function $y(t)$ at $t=t_{top}$. We obtain $h = y(t_{top})= 1 + 7(0.714) + \tfrac{1}{2}(-9.81)(0.714)^2 = 3.5$[m].

To find $d$, we must solve the quadratic equation $0=y(t_f)=1 + 7(t_f) + \tfrac{1}{2}(-9.81)(t_f)^2$ to find the time $t_f$ when the object hits the ground. The solution is $t_f=1.55$[s]. We then plug this value into the equation for $x(t)$ to obtain $d= x(t_f)=0 + 5.6(1.55)=8.68$[m]. You can verify that these answers match the trajectory illustrated in the figure.

Before you start to solve any problem, you need to make a diagram of what is going on. On that diagram indicate clearly the coordinate system with respect to which you will measure $x$ and $y$, and $v_x$ and $v_y$. The values you plug into the equations of motion are measured with respect to this coordinate system: a velocity $v_x$ in the opposite direction of the $x$ axis is represented as a negative number.

Ignoring the effects of air friction, there is zero acceleration in the $x$ direction so $a_x=0$. As a consequence, the velocity will be constant. Whatever $x$ velocity you give the projectile when you throw it, it will keep it. Therefore the UVM equations describe its motion in the $x$ direction: \[ \begin{align*} a_x(t) &=0, \nl v_x(t) &= v_{ix}, \nl x(t) &= v_{ix}t + x_{i}. \end{align*} \]

We have the pull of gravity in the $y$ direction which is a constant acceleration $a=-9.81$[m/s$^2$], the equations of motion are: \[ \begin{align*} a_y(t) &= - g, \nl v_y(t) &= -gt + v_{iy}, \nl y(t) &= \frac{1}{2}(-g)t^2 + v_{iy}t + y_i, \end{align*} \] where $g=9.81$[m/s$^2$] is the gravitational acceleration on the surface on Earth.

Furthermore we have another useful equation relating the initial and final velocity in the $y$ direction: \[ v_{fy}^2 = v_{iy}^2 + 2a(\Delta y). \] This equation is useful because it does not contain the time.

An American F-18 is flying above Iraq. It is carrying two bombs. One bomb is called “freedom” and weighs 200[kg], the other “democracy” with mass 500[kg]. If the plane is flying with speed $v_i=300$ [m/s] and drops both bombs from a height of $2000$[m]. How far will the bombs travel? Which city is going to get democracy and which will get freedom?

The equations of motion are: \[ \begin{align*} x(t) &= v_{ix}t + x_{i} = 300 t + 0, \nl y(t) &= \frac{1}{2}(-9.81)t^2 + v_{iy}t + y_{Ai}= -4.9 t^2 + 2000. \end{align*} \] Solving for $t$ in the second equation we get $t=20.20$[s]. We use this value of $t$ in the first equation to find the final $x$ position where the bombs hit the ground $x_f=x(20.20) = 6060$[m]. Both bombs hit the same town, the one which is $6.06$[km] from the launch point. Observe that the masses of the bombs did not play any part in the final equations of motion.

The above scenario is basically what the people in the US state administration are talking about when they say they are bringing freedom and democracy to the Middle East. We have to get those crooked warmongering bastards out of power and quickly. In fact the entire industrial military complex needs to be dismantled because they are the ones who ultimately benefit from the World conflicts. What can we do to stop them you ask? In my opinion, the best way to fight the system is not to work for the system.

You are standing comfortably on a picnic bench in the Parc Mt-Royal and, not far from you, there is a garbage bin. Feeling lazy and relaxed, you decide that you want to throw a particle $r$ into the bin instead of walking over and dropping it in. The particle $r$ (for the French rebut) is a piece of carton rolled upon itself and wrapped in a paper. Imagine a coordinate system centred below your feet. We will denote as $(0,0)$ the point where your right toe touches the ground and the point $(x=0,y=1.4)$[m] is the initial position of the carton $r$ as you are about to flick it with your finger towards the garbage.

Suppose that the garbage bin is 3 metres away from you and that it is 1 metre tall. Can you calculate the initial velocity that the roach needs to have to land in the garbage bin? Assume that you send it flying purely along the $x$-axis, in other words you do not give it any initial $y$-velocity: $v_{iy}=0$. Can you solve for $v_{ix}$ necessary for the roach to fall into the garbage bin?

All that you need to describe the motion of $r$ are the initial position $\vec{r}(0)=(x(0), y(0))$ and the initial velocity $\vec{v}_i = \vec{v}(0) = (v_x(0), v_y(0))$, which you can then plug into the equations of motion:
\[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}a_y t^2. \end{align*} \] Most physics word problems will follow this pattern. The problem statement gives you some information about the initial conditions and the desired final conditions and then ask you to solve for the unknown, i.e., the one variable which they didn't give you.

Can you carry out the necessary calculations in this case? I don't mean to stress you out, but sitting next to you is your 110kg pure-muscle Chilean friend who has two kids and really gets pissed off at people who throw garbage around in the park. You don't want to piss him off so you better get that initial velocity right!

OK, from now on we can switch into high gear because we have everything setup nicely for us. We know that the general equations of motion for UVM in $x$ and UAM in $y$ are: \[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}a_y t^2, \end{align*} \] and more specifically we know that the $y$ acceleration is due to gravity so we have: \[ \begin{align*} x(t) &= v_{ix}t + x_i, \nl y(t) &= y_i + v_{iy}t + \frac{1}{2}(-9.81)t^2. \end{align*} \]

We also know that the position at $t=0$ is $(x_i, y_i) = (0,1.4)$ and that at some $t_f>0$ we will be flying through the bin at $(x(t_f), y(t_f)) = (3,1)$.

Thus we have: \[ \begin{align*} x(t_f) = 3 &= v_{ix}t_f + 0, \nl y(t_f) = 1 &= 1.4 + v_{iy}t_f + \frac{1}{2}(-9.81)t_f^2. \end{align*} \]

Furthermore, since the problem specified it, we can assume that the initial velocity of $r$ was purely horizontal ($v_{iy}=0$). Thus, the equations we have to solve are:
\[ \begin{align*} \qquad \ \ \: 3 &= v_{ix}t_f, \nl \qquad \ \ \: 1 &= 1.4 -4.9 t^2_f, \end{align*} \] where $v_{ix}$ and $t_f$ are the two unknowns.

From here on, it should be clear where the story is going. First we solve for $t_f$ in the second equation: \[ t_f = \sqrt{ \frac{(1-1.4)}{-4.9} } = \sqrt{ \frac{-0.4}{-4.9} } = \sqrt{ 4/49} = 2/7 \approx 0.28571.. , \qquad \text{[s]} \] and plug that into the first equation to solve for $v_{ix}$ as follows: \[ v_{ix} = \frac{3}{t_f} = \frac{3\cdot 7}{2} = \frac{21}{2} = 10.5 \qquad \text{ [m/s]. } \]

You flick $r$ with you finger at an initial velocity of exactly $\vec{v}_i =(10.5,0)$[m/s] and the roach flies right into the garbage bin. Success!

With all those people lunging explosive projectiles at each other, a need develops for interception systems which can throw a counter-projectile at the incoming projectile and knock it out of the air.

Let us study how we can intercept an incoming ball (A) launched from $\vec{r}_{Ai}=(0,3)$ with initial velocity $\vec{v}_{Ai}=(8\cos(40), 8\sin(40))$. As interception device, you have at your disposal a ball launcher placed at $\vec{r}_{Bi}=(10,0)$ with a fixed firing angle of $50^\circ$ placed so that it faces the incoming ball. The ball launcher has a variable launch speed $w$[m/s], which you can choose. You want to fire an intercepting ball, which will have initial velocity $\vec{v}_{Bi}=(-w\cos(50), w\sin(50))$ so as to intercept the ball (A) in mid-air. What is the required initial velocity $w$ for the balls to hit each other? At which time $t$ will the collision take place?

As far as kinematics is concerned, this is a standard projectile motion problem times two. You have ball (A) which has equations of motion: \[ \begin{align*} x_A(t) &= v_{Aix}t + x_{Ai} = 8\cos(40) t + 0, \nl y_A(t) &= \frac{1}{2}(-9.81)t^2 + v_{Aiy}t + y_{Ai}= -4.9 t^2 + 8\sin(40) t + 3, \end{align*} \] and ball (B) which has equations of motion: \[ \begin{align*} x_B(t) &= v_{Bix}t + x_{Bi} = - w \cos(50) t + 10, \nl y_B(t) &= \frac{1}{2}(-9.81)t^2 + v_{Biy}t + y_{Bi}= -4.9 t^2 + w\sin(50) t + 0. \end{align*} \]

The fact that we want the balls to collide, means that at some point they will have the same coordinates $\vec{r}_A = \vec{r}_B$, which is another way of saying \[ (x_A(t), y_A(t)) = (x_B(t), y_B(t)). \] The $x$-coordinates have to match, and the $y$-coordinates have to match, so this gives us two equations: \[ \begin{align} 8\cos(40) t + 0 &= - w \cos(50) t + 10, \nl -4.9 t^2 + 8\sin(40) t + 3 &= -4.9 t^2 + w\sin(50) t + 0. \end{align} \]

We can cancel the $-4.9 t^2$ on both sides of the bottom equation to get: \[ \begin{align} 8\cos(40) t &= - w \cos(50) t + 10, \nl 8\sin(40) t + 3 &= w\sin(50) t. \end{align} \]

This is a set of two equations with two unknowns, so we can solve it. It is not going to be easy to do this, because we can't isolate either of $t$ or $w$ in a clean way using the standard substitution techniques. There is a trick though: we can divide the two equations! If $A=B$ and $C=D\neq 0$ then $A/C = B/D$ so this is what we will use. In preparation for this step, let me rearrange the equations a bit to have all the $w$-containing terms alone on the right side: \[ \begin{align} 10 - 8\cos(40) t &= w \cos(50) t , \nl 8\sin(40) t + 3 &= w \sin(50) t. \end{align} \]

We will now divide the bottom equation by the top equation to obtain: \[ \frac{ 8\sin(40) t + 3 }{10 - 8\cos(40) t} = \frac{ w \sin(50) t }{ w \cos(50) t} = \tan(50). \]

Rearranging the expression we get \[ 8\sin(40) t + 3 = \tan(50)( 10 - 8\cos(40) t ). \] We now collect all the $t$ terms to one side to obtain: \[ [8\sin(40) + 8\cos(40)\tan(50)] t = 10\tan(50) - 3, \] and finally \[ t = \frac{10\tan(50) - 3}{ 8\sin(40) + 8\cos(40)\tan(50) } = 0.7165 \text{[s]}. \]

We can now plug into any of the above equations to find the value of $w$. For example plugging the value of $t=0.7165$ into \[ 10 - 8\cos(40) t = w \cos(50) t, \] we will get \[ 10 - 8\cos(40)(0.7165) = w \cos(50)(0.7165), \] and so $w = \frac{10 - 8\cos(40)(0.7165)}{ \cos(50)(0.7165)} = 12.1788$ [m/s].

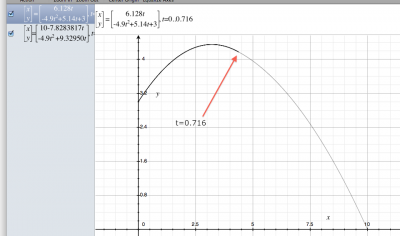
OK. Now let's check our answer. If we use the initial velocity $12.1788$ and substitute that into the equations of motion for ball (B), and plot the two trajectories on the computer:

They do meet indeed and at the specified time $t=0.7165$[s].

I want to point out that there is no new physics necessary to understand the motion of projectiles. Projectile motion is a two-dimensional kinematics problem which can be broken down into two parts: the $x$ direction (described by the UVM equations) and the $y$ direction (described by the UAM equations).

[ Eisenhower on the danger posed by the industrial military complex. ]
Quote: “Only an alert and knowledgeable citizenry can compel the proper meshing of the huge industrial and military machinery of defence with our peaceful methods and goals.”
http://www.youtube.com/watch?v=8y06NSBBRtY