The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Series
Can you compute $\ln(2)$ using only a basic
calculator with four operations: [+], [-], [$\times$], [$\div$]?
I can tell you one way. Simply compute the following sum:
\[
1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} + \ldots.
\]
We can compute the above sum for large values of $n$ using live.sympy.org:
>>> def axn_ln2(n): return 1.0*(-1)**(n+1)/n
>>> sum([ axn_ln2(n) for n in range(1,100) ])
0.69(817217931)
>>> sum([ axn_ln2(n) for n in range(1,1000) ])
0.693(64743056)
>>> sum([ axn_ln2(n) for n in range(1,1000000) ])
0.693147(68056)
>>> ln(2).evalf()
0.693147180559945
As you can see, the more terms you add in this series, the more accurate the series approximation of $\ln(2)$ becomes. A lot of practical mathematical computations are done in this iterative fashion. The notion of series is a powerful way to calculate quantities to arbitrary precision by summing together more and more terms.
Definitions
- $\mathbb{N}$: $ = \{0, 1, 2, 3, 4, 5, 6, \ldots \}$.
- $\mathbb{N}^*=\mathbb{N} \setminus \{0\}$: = $\{1, 2, 3, 4, 5, 6, \ldots \}$.
- $a_n$: sequence of numbers $a_0, a_1, a_2, a_3, a_4, \ldots$.
- $\sum$: sum. Means to take the sum of several objects
put together. The summation sign is the short way to express
certain long expressions:
\[
a_3 + a_4 + a_5 + a_6 + a_7 = \sum_{3 \leq i \leq 7} a_i = \sum_{i=3}^7 a_i.
\]
* $\sum a_i$: series. The running total of a sequence until $n$:
\[
S_n = \sum_{i=1}^n a_i = a_1 + a_2 + \ldots + a_{n-1} + a_n.
\]
Most often, we take the sum of all the terms in the sequence:
\[
S_\infty = \sum_{i=1}^\infty = a_1 + a_2 + a_{3} + a_4 + \ldots.
\]
* $n!$: the //factorial// function: $n!=n(n-1)(n-2)\cdots 3\cdot2\cdot1$.
* $f(x)=\sum_{n=0}^\infty a_n x^n$: //Taylor series// approximation
of the function $f(x)$. It has the form of an infinitely long polynomial
$a_0 + a_1x + a_2x^2 + a_3x^3 + \ldots$ where the coefficients $a_n$ are
chosen so as to encode the properties of the function $f(x)$.
Exact sums
There exist formulas for calculating the exact sum of certain series. Sometimes even infinite series can be calculated exactly.
The sum of the geometric series of length $n$ is: \[ \sum_{k=0}^n r^k = 1 + r + r^2 + \cdots + r^n =\frac{1-r^{n+1}}{1-r}. \]
If $|r|<1$, we can take the limit as $n\to \infty$ in the above expression to obtain: \[ \sum_{k=0}^\infty r^k=\frac{1}{1-r}. \]
Example
Consider the geometric series with $r=\frac{1}{2}$. If we apply the above formula formula we obtain \[ \sum_{k=0}^\infty \left(\frac{1}{2}\right)^k=\frac{1}{1-\frac{1}{2}} = 2. \]
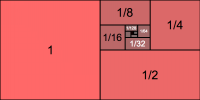
You can also visualize this infinite summation graphically. Imagine you start with a piece of paper of size one-by-one and then you add next to it a second piece of paper with half the size of the first, and a third piece with half the size of the second, etc. The total area that this sequence of pieces of papers will occupy is:
\[ \ \]
The sum of the first $N+1$ terms in arithmetic progression is given by: \[ \sum_{n=0}^N (a_0+nd)= a_0(N+1)+\frac{N(N+1)}{2}d. \]
We have the following closed form expression involving the first $N$ integers: \[ \sum_{k=1}^N k = \frac{N(N+1)}{2}, \qquad \quad \sum_{k=1}^N k^2=\frac{N(N+1)(2N+1)}{6}. \]
Other series which have exact formulas for their sum are the $p$-series with even values of $p$: \[ \sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}, \quad \sum_{n=1}^\infty\frac{1}{n^4}=\frac{\pi^4}{90}, \quad \sum_{n=1}^\infty\frac{1}{n^6}=\frac{\pi^6}{945}. \] These series are computed by Euler's method.
Other closed form sums: \[ \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^2}=\frac{\pi^2}{12}, \qquad \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n}=\ln(2), \] \[ \sum_{n=1}^\infty\frac{1}{4n^2-1}=\frac{1}{2}, \] \[ \sum_{n=1}^\infty\frac{1}{(2n-1)^2}=\frac{\pi^2}{8}, \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{(2n-1)^3}=\frac{\pi^3}{32}, \quad \sum_{n=1}^\infty\frac{1}{(2n-1)^4}=\frac{\pi^4}{96}. \]
Convergence and divergence of series
Even when we cannot compute an exact expression for the sum of a series it is very important to distinguish series that converge from series that do not converge. A great deal of what you need to know about series is different tests you can perform on a series in order to check whether it converges or diverges.
Note that convergence of a series is not the same as convergence of the underlying sequence $a_i$. Consider the sequence of partial sums $S_n = \sum_{i=0}^n a_i$: \[ S_0, S_1, S_2, S_3, \ldots , \] where each of these corresponds to \[ a_0, \ \ a_0 + a_1, \ \ a_0 + a_1 + a_2, \ \ a_0 + a_1 + a_2 + a_3, \ldots. \]
We say that the series $\sum a_i$ converges if the sequence of partial sums $S_n$ converges to some limit $L$: \[ \lim_{n \to \infty} S_n = L. \]
As with all limits, the above statement means that for any precision $\epsilon>0$, there exists an appropriate number of terms to take in the series $N_\epsilon$, such that \[ |S_n - L | < \epsilon,\qquad \text{ for all } n \geq N_\epsilon. \]
Sequence convergence test
The only way the partial sums will converge is if the entries in the sequences $a_n$ tend to zero for large $n$. This observation gives us a simple series divergence test. If $\lim\limits_{n\rightarrow\infty}a_n\neq0$ then $\sum\limits_n a_n$ diverges. How could an infinite sum of non-zero quantities add up to a finite number?
Absolute convergence
If $\sum\limits_n|a_n|$ converges, $\sum\limits_n a_n$ also converges. The opposite is not necessarily true, since the convergence of $a_n$ might be due to some negative terms cancelling with the positive ones.
A sequence $a_n$ for which $\sum_n |a_n|$ converges is called absolutely convergent. A sequence $b_n$ for which $\sum_n b_n$ converges, but $\sum_n |b_n|$ diverges is called conditionally convergent.
Decreasing alternating sequences
An alternating series of which the absolute values of the terms are decreasing and go to zero converges.
p-series
The series $\displaystyle\sum_{n=1}^\infty \frac{1}{n^p}$ converges if $p>1$ and diverges if $p\leq1$.
Limit comparison test
Suppose $\displaystyle\lim_{n\rightarrow\infty}\frac{a_n}{b_n}=p$, then the following is true:
- if $p>0$ then $\sum\limits_{n}a_n$ and $\sum\limits_{n}b_n$ either both converge or both diverge.
- if $p=0$ holds: if $\sum\limits_{n}b_n$ converges, then $\sum\limits_{n}a_n$ also converges.
n-th root test
If $L$ is defined by $\displaystyle L=\lim_{n\rightarrow\infty}\sqrt[n]{|a_n|}$ then $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Ratio test
$\displaystyle L=\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|$, then is $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Radius of convergence for power series
In a power series $a_n=c_nx^n$, the $n$th term is multiplied by the $n$th power of $x$. For such series, the convergence or divergence of the series depends on the choice of the variable $x$.
The radius of convergence $\rho$ of $\sum\limits_n c_n$ is given by: $\displaystyle\frac{1}{\rho}=\lim_{n\rightarrow\infty}\sqrt[n]{|c_n|}= \lim_{n\rightarrow\infty}\left|\frac{c_{n+1}}{c_n}\right|$. For all $-\rho < x < \rho$ the series $a_n$ converges.
Integral test
If $\int_a^{\infty}f(x)dx<\infty$, then $\sum\limits_n f(n)$ converges.
Taylor series
The Taylor series approximation to the function $\sin(x)$ to the 9th power of $x$ is given by \[ \sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!}. \] If we want to get rid of the approximate sign, we have to take infinitely many terms in the series: \[ \sin(x) = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \frac{x^{11}}{11!} + \ldots . \]
This kind of formula is known as a Taylor series approximation. The Taylor series of a function $f(x)$ around the point $a$ is given by: \[ \begin{align*} f(x) & =f(a)+f'(a)(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3+\cdots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n. \end{align*} \]
The McLaurin series of $f(x)$ is the Taylor series expanded at $a=0$: \[ \begin{align*} f(x) & =f(0)+f'(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3 + \ldots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n . \end{align*} \]
Taylor series of some common functions: \[ \begin{align*} \cos(x) &= 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} + \ldots \nl e^x &= 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots \nl \ln(x+1) &= x - \frac{x^2}2 + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} - \frac{x^6}{6} + \ldots \nl \cosh(x) &= 1 + \frac{x^2}{2} + \frac{x^4}{4!} + \frac{x^6}{6!} + \frac{x^8}{8!} + \frac{x^{10} }{10!} + \ldots \nl \sinh(x) &= x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!} + \frac{x^9}{9!} + \frac{x^{11} }{11!} + \ldots \end{align*} \] Note the similarity in the Taylor series of $\sin$, $\cos$ and $\sinh$ and $\cosh$. The formulas are the same, but the hyperbolic version do not alternate.
Explanations
Taylor series
The names Taylor series and McLaurin series are used interchangeably. Another synonym for the same concept is a power series. Indeed, we are talking about a polynomial approximation with coefficients $a_n=\frac{f^{(n)}(0)}{n!}$ in front of different powers of $x$.
If you remember your derivative rules correctly, you can calculate the McLaurin series of any function simply by writing down a power series $a_0 + a_1x + a_2x^2 + \ldots$ taking as the coefficients $a_n$ the value of the n'th derivative divided by the appropriate factorial. The more terms in the series you compute, the more accurate your approximation is going to get.
The zeroth order approximation to a function is \[ f(x) \approx f(0). \] It is not very accurate in general, but at least it is correct at $x=0$.
The best linear approximation to $f(x)$ is its tangent $T(x)$, which is a line that passes through the point $(0, f(0))$ and has slope equal to $f'(0)$. Indeed, this is exactly what the first order Taylor series formula tells us to compute. The coefficient in front of $x$ in the Taylor series is obtained by first calculating $f'(x)$ and then evaluating it at $x=0$: \[ f(x) \approx f(0) + f'(0)x = T(x). \]
To find the best quadratic approximation to $f(x)$, we find the second derivative $f^{\prime\prime}(x)$. The coefficient in front of the $x^2$ term will be $f^{\prime\prime}(0)$ divided by $2!=2$: \[ f(x) \approx f(0) + f'(0)x + \frac{f^{\prime\prime}(0)}{2!}x^2. \]
If we continue like this we will get the whole Taylor series of the function $f(x)$. At step $n$, the coefficient will be proportional to the $n$th derivative of $f(x)$ and the resulting $n$th degree approximation is going to imitate the function in its behaviour up the $n$th derivative.
Proof of the sum of the geometric series
We are looking for the sum $S$ given by: \[ S = \sum_{k=0}^n r^k = 1 + r + r^2 + r^3 + \cdots + r^n. \] Observe that there is a self similar pattern in the expanded summation $S$ where each term to the right has an additional power of $r$. The effects of multiplying by $r$ will therefore to “shift” all the terms of the series: \[ rS = r\sum_{k=0}^n r^k = r + r^2 + r^3 + \cdots + r^n + r^{n+1}, \] we can further add one to both sides to obtain \[ 1 + rS = \underbrace{1 + r + r^2 + r^3 + \cdots + r^n}_S + r^{n+1} = S + r^{n+1}. \] Note how the sum $S$ appears as the first part of the expression on the right-hand side. The resulting equation is quite simple: $1 + rS = S + r^{n+1}$. Since we wanted to find $S$, we just isolate all the $S$ terms to one side: \[ 1 - r^{n+1} = S - rS = S(1-r), \] and then solve for $S$ to obtain $S=\frac{1-r^{n+1}}{1-r}$. Neat no? This is what math is all about, when you see some structure you can exploit to solve complicated things in just a few lines.
Examples
An infinite series
Compute the sum of the infinite series \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n. \] This may appear complicated, but only until you recognize that this is a type of geometric series $\sum ar^n$, where $a=\frac{1}{N+1}$ and $r=\frac{N}{N+1}$: \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n = \sum_{n=0}^\infty a r^n = \frac{a}{1-r} = \frac{1}{N+1}\frac{1}{1-\frac{N}{N+1}} = 1. \]
Calculator
How does a calculator compute $\sin(40^\circ)=0.6427876097$ to ten decimal places? Clearly it must be something simple with addition and multiplication, since even the cheapest scientific calculators can calculate that number for you.
The trick is to use the Taylor series approximation of $\sin(x)$: \[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} + \ldots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}. \]
To calculate sin of 40 degrees we just compute the sum of the series on the right with $x$ replaced by 40 degrees (expressed in radians). In theory, we need to sum infinitely many terms to satisfy the equality, but in practice you calculator will only have to sum the first seven terms in the series in order to get an accuracy of 10 digits after the decimal. In other words, the series converges very quickly.
Let me show you how this is done in Python.
First we define the function for the $n^{\text{th}}$ term:
\[
a_n(x) = \frac{(-1)^nx^{2n+1}}{(2n+1)!}
\]
>>> def axn_sin(x,n): return (-1.0)**n * x**(2*n+1) / factorial(2*n+1)
Next we convert $40^\circ$ to radians:
>>> forti = (40*pi/180).evalf()
0.698131700797732 # 40 degrees in radians
NOINDENT These are the first 10 coefficients in the series:
>>> [ axn_sin( forti ,n) for n in range(0,10) ] [(0, 0.69813170079773179), # the values of a_n for Taylor(sin(40)) (1, -0.056710153964883062), (2, 0.0013819920621191727), (3, -1.6037289757274478e-05), (4, 1.0856084058295026e-07), (5, -4.8101124579279279e-10), (6, 1.5028144059670851e-12), (7, -3.4878738801065803e-15), (8, 6.2498067170560129e-18), (9, -8.9066666494280343e-21)]
NOINDENT To compute $\sin(40^\circ)$ we sum together all the terms:
>>> sum( [ axn_sin( forti ,n) for n in range(0,10) ] )
0.642787609686539 # the Taylor approximation value
>>> sin(forti).evalf()
0.642787609686539 # the true value of sin(40)
Discussion
You can think of the Taylor series as “similarity coefficients” between $f(x)$ and the different powers of $x$. By choosing the coefficients as we have $a_n = \frac{f^{(n)}(?)}{n!}$, we guarantee that Taylor series approximation and the real function $f(x)$ will have identical derivatives. For a McLaurin series the similarity between $f(x)$ and its power series representation is measured at the origin where $x=0$, so the coefficients are chosen as $a_n = \frac{f^{(n)}(0)}{n!}$. The more general Taylor series allow us to build an approximation to $f(x)$ around any point $x_o$, so the similarity coefficients are calcualted to match the derivatives at that point: $a_n = \frac{f^{(n)}(x_o)}{n!}$.
Another way of looking at the Taylor series is to imagine that it is a kind of X-ray picture for each function $f(x)$. The zeroth coefficient $a_0$ in the power series tells you how much of the constant function there is in $f(x)$. The first coefficient, $a_1$, tells you how much of the linear function $x$ there is in $f$, the coefficient $a_2$ tells you about the $x^2$ contents of $f$, and so on and so forth.
Now get ready for some crazy shit. Using your new found X-ray vision for functions, I want you to go and take a careful look at the power series for $\sin(x)$, $\cos(x)$ and $e^x$. As you will observe, it is as if $e^x$ contains both $\sin(x)$ and $\cos(x)$, except for the alternating negative signs. How about that? This is a sign that these three functions are somehow related in a deeper mathematical sense: recall Euler's formula.
Exercises
Derivative of a series
Show that \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n n = N. \] Hint: take the derivative with respect to $r$ on both sides of the formula for the geometric series.