To understand the ideas behind derivatives and integrals, you need to understand what a limit is and how to deal with the infinitely small, infinitely large and the infinitely many. In practice, using calculus doesn't actually involve taking limits since we will learn direct formulas and algebraic rules that are more convenient than doing limits. Do not skip this section though just because it is “not on the exam”. If you do so, you will not know what I mean when I write things like $0,\infty$ and $\lim$ in later sections.

The ancient greek philosopher Zeno once came up with the following argument. Suppose an archer shoots an arrow and sends it flying towards a target. After some time it will have travelled half the distance, and then at some later time it will have travelled the half of the remaining distance and so on always getting closer to the target. Zeno observed that no matter how little distance remains to the target, there will always be some later instant when the arrow will have travelled half of that distance. Thus, he reasoned, the arrow must keep getting closer and closer to the target, but never reaches it.

Zeno, my brothers and sisters, was making some sort of limit argument, but he didn't do it right. We have to commend him for thinking about such things centuries before calculus was invented (17th century), but shouldn't repeat his mistake. We better learn how to take limits, because limits are important. I mean a wrong argument about limits could get you killed for God's sake! Imagine if Zeno tried to verify experimentally his theory about the arrow by placing himself in front of one such arrow!

Two young monks were sitting in silence in a Zen garden one autumn afternoon.
“Can something be so small as to become nothing?” asked one of the monks, braking the silence.
“No,” replied the second monk, “if it is something then it is not nothing.”
“Yes, but what if no matter how close you look you cannot see it, yet you know it is not nothing?”, asked the first monk, desiring to see his reasoning to the end.
The second monk didn't know what to say, but then he found a counterargument. “What if, though I cannot see it with my naked eye, I could see it using a magnifying glass?”.
The first monk was happy to hear this question, because he had already prepared a response for it. “If I know that you will be looking with a magnifying glass, then I will make it so small that you cannot see with you magnifying glass.”
“What if I use a microscope then?”
“I can make the thing so small that even with a microscope you cannot see it.”
“What about an electron microscope?”
“Even then, I can make it smaller, yet still not zero.” said the first monk victoriously and then proceeded to add “In fact, for any magnifying device you can come up with, you just tell me the resolution and I can make the thing smaller than can be seen”.
They went back to concentrating on their breathing.

The monks have the right reasoning but didn't have the right language to express what they mean. Zeno has the right language, the wonderful Greek language with letters like $\epsilon$ and $\delta$, but he didn't have the right reasoning. We need to combine aspects of both of the above stories to understand limits.

Let's analyze first Zeno's paradox. The poor brother didn't know about physics and the uniform velocity equation of motion. If an object is moving with constant speed $v$ (we ignore the effects of air friction on the arrow), then its position $x$ as a function of time is given by \[ x(t) = vt+x_i, \] where $x_i$ is the initial location where the object starts from at $t=0$. Suppose that the archer who fired the arrow was at the origin $x_i=0$ and that the target is at $x=L$ metres. The arrow will hit the target exactly at $t=L/v$ seconds. Shlook!

It is true that there are times when the arrow will be $\frac{1}{2}$, $\frac{1}{4}$, $\frac{1}{8}$th, $\frac{1}{16}$th, and so forth distance from the target. In fact there infinitely many of those fractional time instants before the arrow hits, but that is beside the point. Zeno's misconception is that he thought that these infinitely many timestamps couldn't all fit in the timeline since it is finite. No such problem exists though. Any non-zero interval on the number line contains infinitely many numbers ($\mathbb{Q}$ or $\mathbb{R}$).

Now let's get to the monks conversation. The first monk was talking about the function $f(x)=\frac{1}{x}$. This function becomes smaller and smaller but it never actually becomes zero: \[ \frac{1}{x} \neq 0, \textrm{ even for very large values of } x, \] which is what the monk told us.

Remember that the monk also claimed that the function $f(x)$ can be made arbitrarily small. He wants to show that, in the limit of large values of $x$, the function $f(x)$ goes to zero. Written in math this becomes \[ \lim_{x\to \infty}\frac{1}{x}=0. \]

To convince the second monk that he can really make $f(x)$ arbitrarily small, he invents the following game. The second monk announces a precision $\epsilon$ at which he will be convinced. The first monk then has to choose an $S_\epsilon$ such that for all $x > S_\epsilon$ we will have \[ \left| \frac{1}{x} - 0 \right| < \epsilon. \] The above expression indicates that $\frac{1}{x}\approx 0$ at least up to a precision of $\epsilon$.

The second monk will have no choice but to agree that indeed $\frac{1}{x}$ goes to 0 since the argument can be repeated for any required precision $\epsilon >0$. By showing that the function $f(x)$ approaches $0$ arbitrary closely for large values of $x$, we have proven that $\lim_{x\to \infty}f(x)=0$.

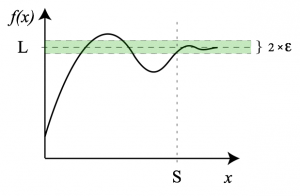More generally, the function $f(x)$ can converge to any number $L$ for as $x$ takes on larger and larger values: \[ \lim_{x \to \infty} f(x) = L. \] The above expressions means that, for any precision $\epsilon>0$, there exists a starting point $S_\epsilon$, after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision: \[ \left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon. \]

You are asked to calculate $\lim_{x\to \infty} \frac{2x+1}{x}$, that is you are given the function $f(x)=\frac{2x+1}{x}$ and you have to figure out what the function looks like for very large values of $x$. Note that we can rewrite the function as $\frac{2x+1}{x}=2+\frac{1}{x}$ which will make it easier to see what is going on: \[ \lim_{x\to \infty} \frac{2x+1}{x} = \lim_{x\to \infty}\left( 2 + \frac{1}{x} \right) = 2 + \lim_{x\to \infty}\left( \frac{1}{x} \right) = 2 + 0, \] since $\frac{1}{x}$ tends to zero for large values of $x$.

In a first calculus course you are not required to prove statements like $\lim_{x\to \infty}\frac{1}{x}=0$, you can just assume that the result is obvious. As the denominator $x$ becomes larger and larger, the fraction $\frac{1}{x}$ becomes smaller and smaller.

\[ \lim_{x\to \infty} f(x) \] what happens to $f(x)$ for very large values of $x$.

The limit of $f(x)$ approaching $x=a$ from above (from the right) is denoted: \[ \lim_{x\to a^+} f(x) \] Similarly, the expression \[ \lim_{x\to a^-} f(x) \] describes what happens to $f(x)$ as $x$ approaches $a$ from below (from the left), i.e., with values like $x=a-\delta$, with $\delta>0, \delta \to 0$. If both limits from the left and from the right of some number are equal, then we can talk about the limit as $x\to a$ without specifying the direction: \[ \lim_{x\to a} f(x) = \lim_{x\to a^+} f(x) = \lim_{x\to a^-} f(x). \]

You now asked to calculate $\lim_{x\to 5} \frac{2x+1}{x}$. \[ \lim_{x\to 5} \frac{2x+1}{x} = \frac{2(5)+1}{5} = \frac{11}{5}. \]

Find $\lim_{x\to 0} \frac{2x+1}{x}$. If we just plug $x=0$ into the fraction we get an error divide by zero $\frac{2(0)+1}{0}$ so a more careful treatment will be required.

Consider first the limit from the right $\lim_{x\to 0+} \frac{2x+1}{x}$. We want to approach the value $x=0$ with small positive numbers. The best way to carry out the calculation is to define some small positive number $\delta>0$, to choose $x=\delta$, and to compute the limit: \[ \lim_{\delta\to 0} \frac{2(\delta)+1}{\delta} = 2 + \lim_{\delta\to 0} \frac{1}{\delta} = 2 + \infty = \infty. \] We took it for granted that $\lim_{\delta\to 0} \frac{1}{\delta}=\infty$. Intuitively, we can imagine how we get closer and closer to $x=0$ in the limit. When $\delta=10^{-3}$ the function value will be $\frac{1}{\delta}=10^3$. When $\delta=10^{-6}$, $\frac{1}{\delta}=10^6$. As $\delta \to 0$ the function will blow up—$f(x)$ will go up all the way to infinity.

If we take the limit from the left (small negative values of $x$) we get \[ \lim_{\delta\to 0} f(-\delta) =\frac{2(-\delta)+1}{-\delta}= -\infty. \] Therefore, since $\lim_{x\to 0^+}f(x)$ does not equal $\lim_{x\to 0^-} f(x)$, we say that $\lim_{x\to 0} f(x)$ does not exist.

A function $f(x)$ is continuous at $a$ if the limit of $f$ as $x\to a$ converges to $f(a)$: \[ \lim_{x \to a} f(x) = f(a). \]

Most functions we will study in calculus are continuous, but not all functions are. For example, functions which make sudden jumps are not continuous. Another examples is the function $f(x)=\frac{2x+1}{x}$ which is discontinuous at $x=0$ (because the limit $\lim_{x \to 0} f(x)$ doesn't exist and $f(0)$ is not defined). Note that $f(x)$ is continuous everywhere else on the real line.

We now switch gears into reference mode, as I will state a whole bunch known formulas for limits of various kinds of functions. You are not meant to know why these limit formulas are true, but simply understand what they mean.

The following statements tell you about the relative sizes of functions. If the limit of the ratio of two functions is equal to $1$, then these functions must behave similarly in the limit. If the limit of the ratio goes to zero, then one function must be much larger than the other in the limit.

Limits of trigonometric functions: \[ \lim_{x\rightarrow0}\frac{\sin(x)}{x}=1,\quad \lim_{x\rightarrow0} \cos(x)=1,\quad \lim_{x\rightarrow 0}\frac{1-\cos x }{x}=0, \quad \lim_{x\rightarrow0}\frac{\tan(x)}{x}=1. \]

The number $e$ is defined as one of the following limits: \[ e \equiv \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n = \lim_{\epsilon\to 0 }(1+\epsilon)^{1/\epsilon}. \] The first limit corresponds to a compound interest calculation, with annual interest rate of $100\%$ and compounding performed infinitely often.

For future reference, we state some other limits involving the exponential function: \[ \lim_{x\rightarrow0}\frac{{\rm e}^x-1}{x}=1,\qquad \quad \lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n={\rm e}^x. \]

These are some limits involving logarithms: \[ \lim_{x\rightarrow 0^+}x^a\ln(x)=0,\qquad \lim_{x\rightarrow\infty}\frac{\ln^p(x)}{x^a}=0, \ \forall p < \infty \] \[ \lim_{x\rightarrow0}\frac{\ln(x+a)}{x}=a,\qquad \lim_{x\rightarrow0}\left(a^{1/x}-1\right)=\ln(a). \]

A polynomial of degree $p$ and the exponential function base $a$ with $a > 1$ both go to infinity as $x$ goes to infinity: \[ \lim_{x\rightarrow\infty} x^p= \infty, \qquad \qquad \lim_{x\rightarrow\infty} a^x= \infty. \] Though both functions go to infinity, the exponential function does so much faster, so their relative ratio goes to zero: \[ \lim_{x\rightarrow\infty}\frac{x^p}{a^x}=0, \qquad \mbox{for all } p \in \mathbb{R}, |a|>1. \] In computer science, people make a big deal of this distinction when comparing the running time of algorithms. We say that a function is computable if the number of steps it takes to compute that function is polynomial in the size of the input. If the algorithm takes an exponential number of steps, then for all intents and purposes it is useless, because if you give it a large enough input the function will take longer than the age of the universe to finish.

Other limits: \[ \lim_{x\rightarrow0}\frac{\arcsin(x)}{x}=1,\qquad \lim_{x\rightarrow\infty}\sqrt[x]{x}=1. \]

If you are taking the limit of a fraction $\frac{f(x)}{g(x)}$, and you have $\lim_{x\to\infty}f(x)=0$ and $\lim_{x\to\infty}g(x)=\infty$, then we can informally write: \[ \lim_{x\to \infty} \frac{f(x)}{g(x)} = \frac{\lim_{x\to \infty} f(x)}{ \lim_{x\to \infty} g(x)} = \frac{0}{\infty} = 0, \] since both functions are helping to drive the fraction to zero.

Alternately if you ever get a fraction of the form $\frac{\infty}{0}$ as a limit, then both functions are helping to make the fraction grow to infinity so we have $\frac{\infty}{0} = \infty$.

Sometimes when evaluating limits of fractions $\frac{f(x)}{g(x)}$, you might end up with a fraction like \[ \frac{0}{0}, \qquad \text{or} \qquad \frac{\infty}{\infty}. \] These are undecidable conditions. Is the effect of the numerator stronger or the effect of the denominator stronger?

One way to find out, is to compare the ratio of their derivatives. This is called L'Hopital's rule: \[ \lim_{x\rightarrow a}\frac{f(x)}{g(x)} \ \ \ \overset{\textrm{H.R.}}{=} \ \ \ \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}. \]