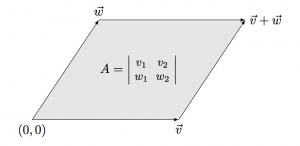
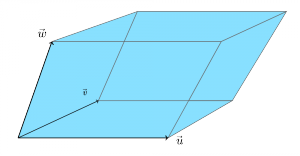
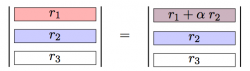
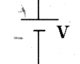<texit info> author=Ivan Savov title=MATH and PHYSICS Funamentals backgroundtext=off </texit>
Long division
When there are large numbers, we need to follow a procedure to divide them.
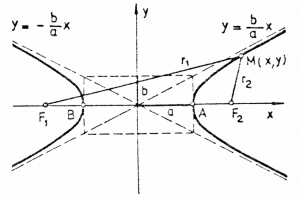
Hyperbolas
No not exaggerated figures of speech, but the mathematical shape.
Formulas
Applications
Repulsive collision of two particles.
Links
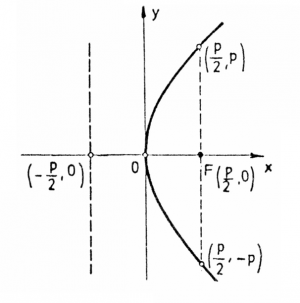
Parabola
Geometry
The shape of the quadratic function is called a parabola and obeys a very important rule. Say we have a sideways parabola: \[ x = f(y) = Ay^2. \]
Imagine rays (show pic!) of light coming from infinity from the right and striking the surface of the parabola. All the rays will be reflected towards the point $F=(\frac{p}{2},0)$ where $p = \frac{1}{2A}$.
( probably need a better drawing.)
Satellite dishes
You put the receiver in the focus point, and you get all the power incident on the dish concentrated right on your receiver.
Base representation
other topics:
working in base 2 and base 16 discrete exponentiation Hamming distance (& friends)
modular arithmetic primality testing basic stats (standard deviation & variance)
Number systems
Decimal system
Binary system
Hexadecimal system
Formulas
Discussion
maybe as a review – sequences/circuits/polynomials ?
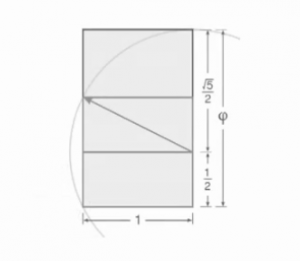
Golden ratio
The golden ratio, usually denoted $\phi\approx 1.6180339887$ is very important proportion in geometry, art, aesthetics, biology and mysticism. If you have a stick of length $1$m and you wan to cut it into two pieces, say from $0$ (the left) to $x$ and from $x$ to $1$ (the right end). You have to pick the point $x$ closer to the right end, such that the ratio of the lengths of the short piece and the long piece is the same as the ratio of the long piece and the whole stick. Mathematically, this means this: \[ \frac{l_{\text{remaining short}}} {l_{\text{long}}} \equiv \frac{1-x}{x} = \frac{x}{1m} \equiv \frac{l_{\text{long}}}{l_{\text{whole}}}. \]
To see how the quadratic equation comes about, just multiply both sides by $x$ to get: \[ 1-x = x^2, \] which after moving all the terms to one side becomes \[ x^2 +x -1 = 0. \]
Using the quadratic formula we get the two solutions which are \[ x_1 = \frac{-1+\sqrt{5}}{2} = \frac{1}{\phi} \approx 0.618030, \qquad x_2 = \frac{-1-\sqrt{5}}{2} = -\phi \approx - 1.61803. \] The solution $x_2$ is some negative number, so it cannot be the $x$ we want – we wanted a ratio, i.e., $0 \leq x\leq 1$. The golden ration then is \[ \begin{align*} \phi &= \frac{1}{x_1} = \frac{2}{\sqrt{5}-1} \nl &= \frac{2}{\sqrt{5}-1}\frac{\sqrt{5}+1}{\sqrt{5}+1} = \frac{2(\sqrt{5}+1)}{5-1} = \frac{\sqrt{5}+1}{2}. \end{align*} \]
Geometry
Trigonometric functions
\[ \cos \left( \frac {\pi} {5} \right) = \cos 36^\circ={\sqrt{5}+1 \over 4} = \frac{\varphi }{2} \]
\[ \sin \left( \frac {\pi} {10} \right) = \sin 18^\circ = {\sqrt{5}-1 \over 4} = {\varphi - 1 \over 2} = {1 \over 2\varphi} \]
Fibonacci connection
The Fibonacci sequence, is defined by the recurrence relation: $F_n=F_{n-1}+F_{n-2}$ with $F_1=1$, and $F_2=1$.
Binet's formula
The $n$th term in the Fibonacci sequence has a closed formed expression \[ F_n=\frac{\phi^n-(1-\phi)^n}{\sqrt{5}}, \] where $\phi=\frac{1+\sqrt{5}}{2}$ is the golden ratio.
in the limit of large $n$, this term will dominate the rate of growth of the Fibonacci sequence. Consider the ratio between $F_n$ and $F_{n-1}$, i.e. at what rate is the sequence growing? \[ \frac{F_n}{F_{n-1}} = \frac{\phi^n-(1-\phi)^n}{\phi^{n-1} - (1- \phi)^{n-1} } \]
http://en.wikipedia.org/wiki/Fibonacci_number#Closed-form_expression
Five-pointed star
The golden ratio also appears in the ratios of two lengths in the pentagram, or five-pointed star. I am choosing not to discuss this here, because the five-pointed star is a symbol associated with satanism, freemasonry and communism, and I want nothing to do with any of these.
Electronic circuits
Links
[ The golden ratio in web design ]
http://www.pearsonified.com/2011/12/golden-ratio-typography.php
FOR MECHANICS
TODO: leverage = mechanical advantage / force conversion TODO: Bicycle Gears = torque converters —> need notion of work torque wrench?
TODO: Pulley problems in force diagrams
TODO: toilet paper now I think of Torque
Waves and optics
Polar coordinates
Definitions
Formulas
To convert the polar coordinates $r\angle\theta$ to components notation $(x,y)$ use: \[ x=r\cos\theta\qquad\qquad y=r\sin\theta. \]
To convert from the cartesian coordinates $(x,y)$ to polar coordinates $r\angle\theta$ use \[ r=\sqrt{x^2+y^2}\qquad\qquad \theta=\tan^{-1}\left(\frac{y}{x}\right) \]
Explanations
Discussion
Examples
sin review travelling pulses
sound travelling waves standing waves
Optics
Introduction
A camera consists essentially of two parts: a detector and a lens construction. The detector is some surface that can record the light which hits it. Old-school cameras used the chemical reaction of silver-oxidation under light, whereas modern cameras use electronic photo-detectors.
While the detector is important, that which really makes or brakes a camera is the lens. The lens' job is to take the light reflected off some object (that which you are taking a picture of) and redirect it in an optimal way so that a faithful image forms on the detection surface. The image has to form exactly at the right distance $d_i$ (so that it is in focus) and have exactly the right height $h_i$ (so it fits on the detector).
To understand how lenses transform light, there is just one equation you need to know: \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}, \] where $d_o$ is the distance from the object to the lens, $d_i$ is the distance from the lens to the image and $f$ is called the focal length of the lens. This entire chapter is dedicated to this equation and its applications. It turns out that curved mirrors behave very similarly to lenses, and the same equation can be used to calculate the properties of the images formed by mirrors. Before we talk about curved mirrors and lenses, we will have to learn about the basic properties of light and the laws of reflection and refraction.
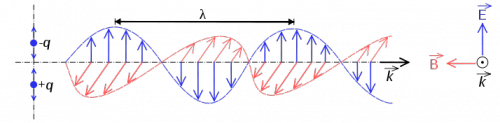
Light
Light is pure energy stored in the form of a travelling electromagnetic wave.
The energy of a light particle is stored in the electromagnetic oscillation. During one moment, light is a “pulse” of electric field in space, and during the next instant it is a “pulse” of pure magnetic energy. Think of sending a “wrinkle pulse” down a long rope – where the pulse of mechanical energy is traveling along the rope. Light is like that, but without the rope. Light is just an electro-magnetic pulse and such pulses happen even in empty space. Thus, unlike most other waves you may have seen until now, light does not need a medium to travel in: empty space will do just fine.
The understanding of light as a manifestation of electro-magnetic energy (electromagnetic radiation) is some deep stuff, which is not the subject of this section. We will get to this, after we cover the concept of electric and magnetic fields, electric and magnetic energy and Maxwell's equations. For the moment, when I say “oscillating energy”, I want you to think of a mechanical mass-spring system in which the energy oscillates between the potential energy of the spring and the kinetic energy of the mass. A photon is a similar oscillation between a “magnetic system” part and the “electric system” part, which travels through space at the speed of light.
In this section, we focus on light rays. The vector $\hat{k}$ in the figure describes the direction of travel of the light ray.
Oh light ray, light ray! Where art thou, on this winter day.
Definitions
Light is made up of “light particles” called photons:
- $p$: a photon.
- $E_p$: the Energy of the photon.
- $\lambda$: the wavelength the photon.
- $f$: the frequency of the photon. (Denoted $\nu$ in some texts.)
- $c$: the speed of light in vacuum. $c=2.9979\times 10^{8}$[m/s].
NOINDENT The speed of light depends on the material in which it travels:
- $v_x$: the speed of light in material $x$.
- $n_x$: the diffraction index of material $x$,
which tells you how much slower light is in that material
relative to the speed of light in vacuum.
$v_x=c/n_x$.
Air is pretty much like vacuum,
so $v_{air} \approx c$ and $n_{air}\approx 1$.
There are different types of glass used in
lens-manifacturing with $n$ values ranging from 1.4 to 1.7.
Equations
Like all travelling waves, the propagation speed of light is equal to the product of its frequency times its wavelength. In vacuum we have \[ c = \lambda f. \]
For example, red light of wavelength $\lambda=700$n[m], has frequency $f=428.27$THz since the speed of light is $c=2.9979\times 10^{8}$[m/s].
The energy of a beam of light is proportional to the intensity of the light (how many photon per second are being emitted) and the energy carried by each photon. The energy of a photon is proportional to its frequency: \[ E_p = \hbar f, \] where $\hbar=1.05457\times 10^{-34}$ is Plank's constant. The above equation is a big deal, since it applies not just to light but to all forms of electromagnetic radiation. The higher the frequency, the more energy per photon there is. Einstein got a Nobel prize for figuring out the photoelectric effect which is a manifestation of the above equation.
The speed of light in a material $x$ with refractive index $n_x$ is \[ v_x = \frac{c}{n_x}. \]
Here is a list of refractive indices for some common materials: $n_{vacuum}\equiv 1.00$, $n_{air} = 1.00029$, $n_{ice}=1.31$, $n_{water}=1.33$, $n_{fused\ quartz}=1.46$, $n_{NaCl}=1.54$, Crown glass 1.52-1.62, Flint glass 1.57-1.75, $n_{sapphire}=1.77$, and $n_{diamond}=2.417$.
Discussion
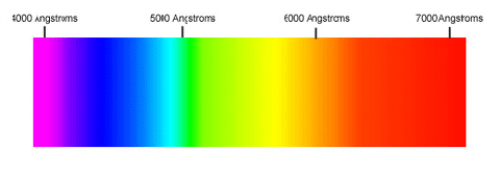
Visible light
Our eyes are able to distinguish certain wavelengths of light as different colours.
| Color | Wavelength (nm) |
|---|---|
| Red | 780 - 622 |
| Orange | 622 - 597 |
| Yellow | 597 - 577 |
| Green | 577 - 492 |
| Blue | 492 - 455 |
| Violet | 455 - 390 |
Note that units of wavelength are tiny numbers like: nanometers $1[\textrm{nm}]=10^{-9}[\textrm{m}]$ or Armstrongs $1[\textrm{A}]=10^{-10}[\textrm{m}]$.
The electromagnetic spectrum
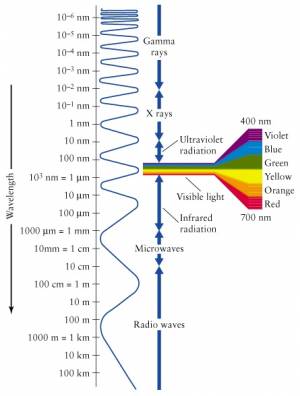 Visible light is only a small part of the electromagnetic spectrum.
Waves with frequency higher than that of violet light are called
ultraviolet (UV) radiation and cannot be seen by the human eye.
Also, frequencies lower than that of red light (infrared)
are not seen, but can sometimes be felt as heat.
Visible light is only a small part of the electromagnetic spectrum.
Waves with frequency higher than that of violet light are called
ultraviolet (UV) radiation and cannot be seen by the human eye.
Also, frequencies lower than that of red light (infrared)
are not seen, but can sometimes be felt as heat.
The EM spectrum extends to all sorts of frequencies (and therefore wavelengths, by $c=\lambda f$). We have different names for the different parts of the EM spectrum. The highest energy particles (highest frequency $\to$ shortest wavelength) are called gamma rays ($\gamma$-rays). We are constantly bombarded by gamma rays coming from outer space with tremendous energy. These $\gamma$-rays are generated by nuclear reactions inside distance stars.
Particles with less energy than $\gamma$-rays are called X-rays. These are still energetic enough that they easily pass through most parts of your body like a warm knife through butter. Only your bones offer some resistance, which is kind of useful in medical imaging since all bone structure can be seen in contrast when taking an X-ray picture.
The frequencies below the visible range (wavelengths longer than that of visible light) are populated by radio waves. And when I say radio, I don't mean specifically radio, but any form of wireless communication. Starting from 4G (or whatever cell phones have gotten to these days), then the top GSM bands at 2.2-2.4GHz, the low GSM bands 800-900MHz, and then going into TV frequencies, FM frequencies (87–108MHz) and finally AM frequencies (153kHz–26.1MHz). It is all radio. It is all electromagnetic radiation emitted by antennas, travelling through space and being received by other antennas.
Light rays
In this section we will study how light rays get reflected off the surfaces of objects and what happens when light rays reach the boundary between two different materials.
Definitions
The speed of light depends on the material where it travels:
- $v_x$: the speed of light in material $x$.
- $n_x$: the diffraction index of material $x$,
which tells you how much slower light is in that material.
$v_x=c/n_x$.
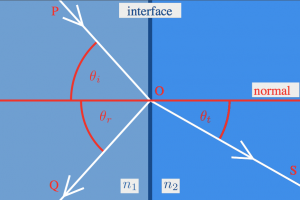
When an incoming ray of light comes to the surface of a transparent object, part of it will be reflected and part of it will be transmitted. We measure all angles with respect to the normal, which is the direction perpendicular to the interface.
- $\theta_{i}$: The incoming or incidence angle.
- $\theta_{r}$: The reflection angle.
- $\theta_{t}$: The transmission angle:
the angle of the light that goes into the object.
Formulas
Reflection
Light that hits a reflective surface will bounce back exactly at the same angle as it came in on: \[ \theta_{i} = \theta_{r}. \]
Refraction
The transmission angle of light when it goes into a material with different refractive index can be calculated from Snell's law: \[ n_i \sin\theta_{i} = n_t \sin \theta_{t}. \]
Total internal refraction
Light coming in from a medium with low refraction index into a medium with high refraction index gets refracted towards the normal. If the light travels in the opposite direction (from high $n$, to low $n$), then it will get deflected away from the normal. In the latter case, an interesting phenomenon called total internal refraction occurs, whereby light rays incident at sufficiently large angles with the normal get trapped inside the material. The angle at which this phenomenon starts to kick in is called the critical angle $\theta_{crit}$.
Consider a light ray inside a material of refractive indeed $n_x$ surrounded by a material with smaller refractive index $n_y$, $n_x > n_y$. To make this more concrete, think of a trans-continental underground optical cable made of glass $n_x=1.7$ surrounded by some plastic with $n_y=1.3$. All light at an angle greater than: \[ \theta_{crit} = \sin^{-1}\left( \frac{n_y}{n_{x}} \underbrace{\sin(90^\circ)}_{=1} \right) = \sin^{-1}\!\left( \frac{n_y}{n_{x}} \right) = \sin^{-1}\!\left( \frac{1.3}{1.7} \right) = 49.88^\circ, \] will get reflected every time it reaches the surface of the optical cable. Thus, if you shine a laser pointer into one end of such a fibre-optical cable in California, 100% of that laser light will come out in Japan. Most high-capacity communication links around the world are based around this amazing property of light. In other words: no total internal refraction means no internet.
Examples
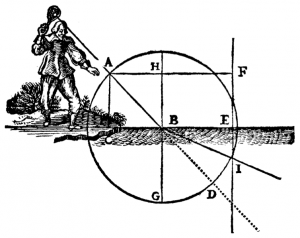
What is wrong in this picture?
Here is an illustration from one of René Descartes' books, which shows a man in funny pants with some sort of lantern which produces a light ray that goes into the water.
Q: What is wrong with the picture?
Hint: Recall that $n_{air}=1$ and $n_{water}=1.33$, so $n_i < n_t$.
Hint 2: What should happen to the angles of the light ray?
A: Suppose that the line $\overline{AB}$, is at $45^\circ$ angle, then after entering the water at $B$, the ray should be deflected towards the normal, i.e., it should pass somewhere between $G$ and $D$. If you wanted to be precise and calculate the transmission angle then we would use: \[ n_i \sin\theta_{i} = n_t \sin \theta_{t}, \] filled in with the values for air and water \[ 1 \sin(45^\circ) = 1.33 \sin( \theta_{t} ), \] and solved for $\theta_{t}$ (the refracted angle) we would get: \[ \theta_{t} = \sin^{-1}\left( \frac{\sqrt{2}}{2\times1.33} \right) = 32.1^\circ. \] The mistake apparently is due to Descartes' printer who got confused and measured angles with respect to the surface of the water. Don't make that mistake: remember to always measure angles with respect to the normal. The correct drawing should have the light ray going at an angle of $32.1^\circ$ with respect to the line $\overline{BG}$.
Explanations
Refraction
To understand refraction you need to imagine “wave fronts” perpendicular to the light rays. Because light comes in at an angle, one part of the wave front will be in material $n_i$ and the other will be in material $n_t$. Suppose $n_i < n_t$, then the part of the wavefront in the $n_t$ material will move slower so angles of the wavefronts will change. The precise relationship between the angles will depend on the refractive indices of the two materials:
\[ n_i \sin\theta_{i} = n_t \sin \theta_{t}. \]
Total internal refraction
Whenever $n_i > n_t$, we reach a certain point where the formula: \[ n_i \sin\theta_{i} = n_t \sin \theta_{t}, \] brakes down. If the transmitted angle $\theta_t$ becomes greater than $90^\circ$ (the critical transmission angle) it will not be transmitted at all. Instead, 100% of the light ray will get reflected back into the material.
To find the critical incident angle solve for $\theta_i$ in: \[ n_i \sin\theta_{i} = n_t \sin 90^\circ, \] \[ \theta_{crit} = \sin^{-1}\left( \frac{n_t}{n_{i}} \right). \]
The summary of the “what happens when a light ray comes to a boundary”-story is as follows:
- If $-\theta_{crit} < \theta_i < \theta_{crit}$, then some part of the light will be
transmitted at an angle $\theta_t$ and some part will be reflected at an angle $\theta_r=\theta_i$.
- If $\theta_i \geq \theta_{crit}$, then all the light will get reflected at an angle $\theta_r=\theta_i$.
Note that when going from a low $n$ medium into a high $n$ medium, there is no critical angle – there will always be some part of the light that is transmitted.
Parabolic shapes
The parabolic curve has a special importance in optics. Consider for example a very weak radio signal coming from a satellite in orbit. If you use just a regular radio receiver, the signal will be so weak as to be indistinguishable from the background noise. However, if you use a parabolic satellite dish to collect the power from a large surface area and focus it on the receiver, then you will be able to detect the signal. This works because of the parabolic shape of the satellite dish: all radio wave coming in from far away will get reflected towards the same point—the focal point of the parabola. Thus, if you put your receiver at the focal point, it will have the signal power from the whole dish redirected right to it.
Depending on the shape of the parabola (which way it curves and how strong the curvature is) the focal point or focus will be at a different place. In the next two sections, we will study parabolic mirrors and lenses. We will use the “horizontal rays get reflected towards the focus”-fact to draw optics diagrams and calculate where images will be formed.
Mirrors
Definitions
To understand how curved mirrors work, we imagine some test object (usually drawn as an arrow, or a candle) and the test image it forms.
- $d_o$: The distance of the object from the mirror.
- $d_i$: The distance of the image from the mirror.
- $f$: The focal length of the mirror.
- $h_o$: The height of the object.
- $h_i$: The height of the image.
- $M$: The magnification $M=h_i/h_o$.
When drawing optics diagrams with mirrors, we can draw the following three rays:
- $R_\alpha$: A horizontal incoming ray which gets redirected towards
the focus after it hits the mirror.
- $R_\beta$: A ray that passes through the focus and gets redirected horizontally
after it hits the mirror.
- $R_\gamma$: A ray that hits the mirror right in the centre and bounces back
at the same angle at which it came in.
Formulas
The following formula can be used to calculate where an image will be formed, given that you know the focal length of the mirror and the distance $d_o$ of the object: \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}. \]
We follow the convention that distances measured from the reflective side of the mirror are positive, and distances behind the mirror are negative.
The magnification is defined as: \[ M = \frac{h_i}{h_o} = \frac{|d_i|}{|d_o|} \] How much bigger is the image compared to the object?
Though it might sound confusing, we will talk about magnification even when the image is smaller than the object; in those cases we say we have fractional magnification.
Examples
Visual examples
Mirrors reflect light, so it is usual to see an image formed on the same side as where it came from. This leads to the following convention:
- If the image forms on the usual side (in front of the mirror),
then we say it has positive distance $d_i$.
- If the image forms behind the mirror, then it has negative $d_i$.
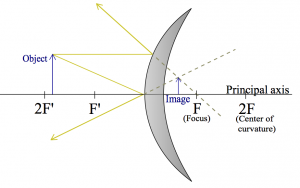
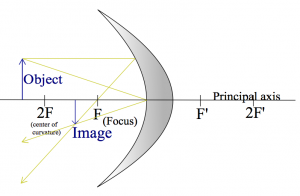
Let us first look at the kind of mirror that you see in metro tunnels: convex mirror. These mirrors will give you a very broad view, and if someone is coming around the corner the hope is that your peripheral vision will be able to spot them in the mirror and you won't bump into each other.
I am going to draw $R_\alpha$ and $R_\gamma$:
Note that the image is “virtual”, since it appears to form inside the mirror.
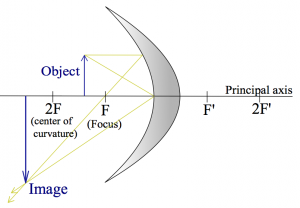
Here is a drawing of a concave mirror instead, with the rays $R_\alpha$ and $R_\gamma$ drawn again.
Can you add the ray $R_\beta$ (through the focus)? As you can see, any two rays out of the three are sufficient to figure out where the image will be: just find the point where the rays meet.
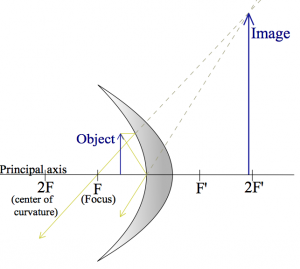
Here are two more examples where the object its placed closer and closer to the mirror.
These are meant to illustrate that the same curved surface, and the same object can lead to very different images depending on where the object is placed relative to the focal point.
Numerical example 1
OK, let's do an exercise of the “can you draw straight lines using a ruler” type now. You will need a piece of white paper, a ruler and a pencil. Go get this stuff, I will be waiting right here.
Q: A convex mirror (like in the metro) is placed at the origin. An object of height 3[cm] is placed $x=5$[cm] away from the mirror. Where will the image be formed?
Geometric answer: Instead of trying to draw a curved mirror, we will draw a straight line. This is called the thin lens approximation (in this case, thin mirror) and it will make the drawing of lines much simpler. Take out the ruler and draw the two rays $R_\alpha$ and $R_\gamma$ as I did:
Then I can use the ruler to measure out $d_i\approx 1.7cm$.
Formula Answer: Using the formula \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}, \] with the appropriate values filled in \[ \frac{1}{5} + \frac{1}{d_i} = \frac{1}{-2.6}, \] or \[ d_i = 1.0/(-1.0/2.6 - 1.0/5) = -1.71 \text{[cm]}. \] Nice.
Observe that (1) I used a negative focal point for the mirror since in some sense the focal point is “behind” the mirror, and (2) the image is formed behind the mirror, which means that it is virtual: this is where the arrow will appear to an the observing eye drawn in the top left corner.
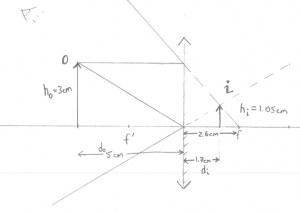
Numerical example 2
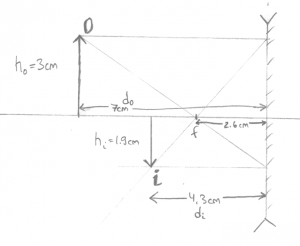
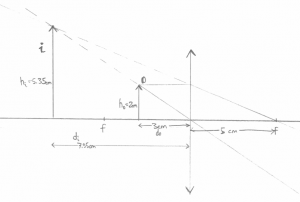
Now we have a concave mirror with focal length $f=2.6cm$ and we measure the distances the same way (positive to the left).
Q: An object is placed at $d_0=7$[cm] from the mirror. Where will the image form? What is the height of the image?
Geometric answer: Taking out the ruler, you can choose to draw any of the three rays. I picked $R_\alpha$ and $R_\beta$ since they are the easiest to draw:
Then measuring with the ruler I find that $d_i \approx 4.3$[cm], and that the image is height $h_i\approx-1.9$[cm], where negative height means that the image is upside down.
Formula Answer: With the formula now. We start from \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}, \] and fill in what we know \[ \frac{1}{7} + \frac{1}{d_i} = \frac{1}{2.6}, \] then solve for $d_i$: \[ d_i = 1.0/(1.0/2.6 - 1.0/7.0) = 4.136 \text{[cm]}. \] To find the height of the image we use \[ \frac{h_i}{h_o} = \frac{d_i}{d_o}, \] so \[ h_i = 3 \times \frac{4.136}{7.0} = 3 \times 4.13/7.0 = 1.77 \text{[cm]}. \] You still need the drawing to figure out that the image is inverted though.
Generally, I would trust the numeric answers from the formula more, but read the signs of the answers from the drawing. Distances in front of the mirror are positive whereas images formed behind the mirror have negative distance.
Links
Lenses
Definitions
To understand how lenses work, we imagine again some test object. (an arrow) and the test image it forms.
- $d_o$: The distance of the object from the lens.
- $d_i$: The distance of the image from the lens.
- $f$: The focal length of the lens.
- $h_o$: The height of the object.
- $h_i$: The height of the image.
- $M$: The magnification $M=h_i/h_o$.
When drawing lens diagrams, we use the following representative rays:
- $R_\alpha$: A horizontal incoming ray which gets redirected towards
the focus after it passes through the lens.
- $R_\beta$: A ray that passes through the focus and gets redirected horizontally
after the lens.
- $R_\gamma$: A ray that passes exactly through the centre of the lens
and travels in a straight line.
Formulas
\[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \]
\[ M = \frac{h_i}{h_o} = \frac{|d_i|}{|d_o|} \]
Examples
Visual
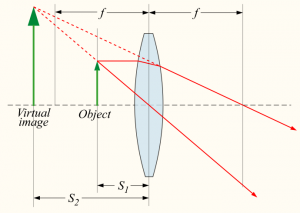
Fist consider the typical magnifying glass situation. You put the object close to the lens, and looking from the side, the object will appear magnified.
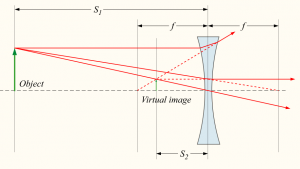
A similar setup with a diverging lens. This time the image will appear to the observer to be smaller than the object.
Note that in the above two examples, if you used the formula you would get a negative $d_i$ value since the image is not formed on the “right” side. We say the image is virtual.
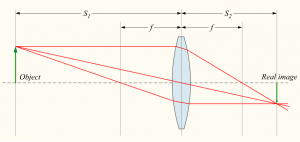
Now for an example where a real image is formed:
In this example all the quantities $f$, $d_o$ and $d_i$ are positive.
Numerical
An object is placed at a distance of 3[cm] from a magnifying glass of focal length 5[cm]. Where will the object appear to be?
You should really try this on your own. Just reading about light rays is kind of useless. Try drawing the above by yourself with the ruler. Draw the three kinds of rays: $R_\alpha$, $R_\beta$, and $R_\gamma$.
Here is my drawing.
Numerically we get \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}, \] \[ \frac{1}{3.0} + \frac{1}{d_i} = \frac{1}{5.0}, \] \[ d_i = 1.0/(1.0/5.0 - 1.0/3.0) = -7.50 \text{[cm]}. \]
As you can see, drawings are not very accurate. Always trust the formula for the numeric answers to $d_o$, $d_i$ type of questions.
Multiple lenses
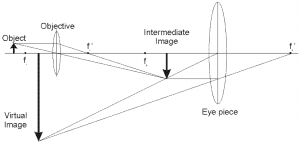
Imagine that the “output” image formed by the first lens is the “input” image to a second lens.
It may look complicated, but if you solve the problem in two steps (1) how the object forms an intermediary image, and (2) how the intermediary image forms the final image you will get things right.
You can also trace all the rays as they pass through the double-lens apparatus:
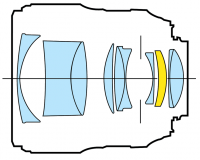 We started this chapter talking about real cameras, so I want to
finish on that note too. To form a clear image, with variable focus and
possibly zoom functionality, we have to use a whole series of lenses,
not just one or two.
We started this chapter talking about real cameras, so I want to
finish on that note too. To form a clear image, with variable focus and
possibly zoom functionality, we have to use a whole series of lenses,
not just one or two.
For each lens though, we can use the formula and calculate the effects of that lens on the light coming in.
Note that the real world is significantly more complicated than the simple ray picture which we have been using until now. For one, each frequency of light will have a slightly different refraction angle, and sometimes the lens shapes will not be perfect parabolas, so the light rays will not be perfectly redirected towards the focal point.
Discussion
Fresnel lens
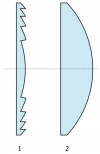 Thicker lenses are stronger. The reason is that the curvature
of a thick lens is bigger and thus light will be refracted more
when it hits the surface.
The actual thickness of the lens is of no importance.
The way rays get deflected by lenses only depends on the angles of
incidence. Indeed, we can cut out all the middle part
of the lens and leave a highly curved surface parts.
This is called a Fresnel lens and it is used in car headlights.
Thicker lenses are stronger. The reason is that the curvature
of a thick lens is bigger and thus light will be refracted more
when it hits the surface.
The actual thickness of the lens is of no importance.
The way rays get deflected by lenses only depends on the angles of
incidence. Indeed, we can cut out all the middle part
of the lens and leave a highly curved surface parts.
This is called a Fresnel lens and it is used in car headlights.
interference diffraction double slit expriment dispersion
Electricity and Magnetism
Electricity & magnetism
This course is about all things electrical and magnetic. Every object which has a mass $m$ will be affected by gravity. Similarly, every object which has a charge $q$ will feel the electric force $\vec{F}_e$. Furthermore, if a charge is moving then it will also be affected by the magnetic force $\vec{F}_b$. The formula for the electric force between objects is very similar to the formula for the gravitational force, but the magnetism stuff is totally new. Get read for some mind expansion!
Understanding the laws of electricity and magnetism will make you very powerful. Have you heard of Nikola Tesla? He is a pretty cool guy, and he was a student of electricity and magnetism just like you:
This course requires a good understanding of vector and basic calculus techniques. If you are feel a little rusty on these subjects, I highly recommend that you review the general ideas of vectors and integration before you start reading the material.
Below is a short overview of the topics which we will discuss.
Electricity
We start of with a review of Newton's formula for the gravitation force ($F_g=\frac{GMm}{r^2}$), then learn about electrostatics ($F_e=\frac{kQq}{r^2}$) and discuss three related concepts: the electric potential energy $U_e=\frac{kQq}{r}$, the electric field ($E=\frac{GQ}{r^2}$, $F_e=qE$) and the electric potential ($V=\int E\;dx$, $\vec{E}=\frac{dV}{dx}$).
Circuits
Electrostatic interactions between two points in space A and B take on a whole new nature if a charge-conducting wire is used to connect the two points. Charge will be able to flow from one point to the other along the wire. This flow of charge is called electric current. Current is denoted as $I$[A] and measured in Amperes.
The flow of current is a abstract way of describing moving charges. If you understand that well, you can start to visualize stuff and it will be all simple. The current $I$[A] is the “total number of electrons” passing in the wire in one second.
Electric current can be “accumulated” in charge containers called capacitors.
Magnetism
 Understanding current is very important because each electron by virtue of its motion through
space is creating a magnetic field around it.
The strength of the magnetic field created by each electron is tiny—we could just ignore it.
Understanding current is very important because each electron by virtue of its motion through
space is creating a magnetic field around it.
The strength of the magnetic field created by each electron is tiny—we could just ignore it.
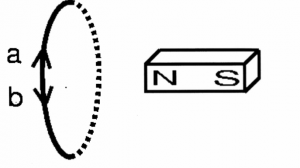
However if there is a current of 1[A] flowing through the wire, you know how many electrons that makes? It means there is a flow of $6.242 \times 10^{18}$ electrons per second in that wire. This is something we can't ignore. The magnetic field created by this wire will be quite powerful. You can use the magnetic field to build electromagnets (to lift cars in junk yards, or for magnetic locks—when you are fighting the front doors of McConnell to get into Blues Pub after 9PM—you are fighting with the magnetic force). You can also have two magnets push on each other while turning an engine forward—this is called an electric motor (think electric cars).
But hey, you don't have time to learn all of this now. Read a couple of pages and then go practice on the exams from previous years! If you have any problems come ask here: http://bit.ly/XYOhE1 (only on April 21st, 22nd, and 23rd)
Links
Electrostatics
Electrostatics is the study of charge and the electric forces that exist between charges. The same way that the force of gravity exists between any two objects with mass, the electric force (Coulomb force) exists between any two charged objects. We will see, however, that unlike gravity which is always attractive (tends to bring masses closer together), the electrostatic force can sometimes be repulsive (tends to push charges apart).
Electrostatics is a big deal. You are alive right now, because of the electric forces that exist between the amino acid chains (proteins) in your body. The attractive electric force that exists between protons and electrons helps to make atoms stable. The electric force is also an important factor in many chemical reactions.
The study of charged atoms and their chemistry can be kind of complicated. Each atom contains many charged particles: the positively charged protons in the negatively charged electrons. For example, a single iron atom has 26 positively charged particles (protons) in the nucleus and 26 negatively charged electrons in various energy shells surrounding the nucleus. To keep things simple, in this course we will study the electric force and potential energy of only a few charges at a time.
Example: Cathode ray tube
When I was growing up, television sets and computer monitors were bulky objects in which electrons were accelerated and crashed onto a phosphorescent surface to produce the image on the screen. A cathode ray tube (CRT) is a vacuum tube containing an electron gun (a source of electrons). What is the speed of the electrons which produce the image on an old-school TV?
Suppose the Voltage used to drive the electron gun is $4000$[V]. Since voltage is energy per unit charge, this means that each electron that goes through the electron gun will lose the following amount of potential energy \[ U_e = q_e V = 1.602\times10^{-19} \ \times \ 4000 \qquad \text{[J]}. \] In fact the potential energy is not lost but converted to kinetic energy \[ U_e \to K_e = \frac{1}{2}m_e v^2 = \frac{1}{2}(9.109\times10^{-31})v^2, \] where we have used the formula for the kinetic energy of an object with mass $m_e = 9.109\times10^{-31}$ [Kg]. Numerically we get: \[ 1.602\times10^{-19} \ \times \ 4000 = \frac{1}{2}(9.109\times10^{-31})v^2 \qquad \text{[J]}, \] where $v$, the velocity of the electrons, is the only unknown in the equation. Solving for $v$ we find that the elections inside the TV are flying at \[ v = \sqrt{\frac{2 q_e V}{m_e}} = \sqrt{\frac{2 \times 1.602\times10^{-19} \times 4000 }{9.109\times10^{-31}}} = 3.751\times 10^{7} \text{[m/s]}. \] This is pretty fast.
Concepts
- $q$: Electric charge of some particle or object. It is measured in Coulombs $[C]$. If there are multiple charges in the proble we can call them $q,Q$ or $q_1, q_2, q_3$ to distinguish them.
- $\vec{r}$: The vector-distance between two charges.
- $r \equiv |\vec{r}|$: Distance between two charges, measured in meters $[m]$
- $\hat{r} \equiv \frac{ \vec{r} }{ |\vec{r}|}$: A direction vector (unit length vector) in the $\vec{r}$ direction.
- $\vec{F}_e$: Electic force strength and direction, measured in Newtons $[N]$
- $U_e$: The electric potential energy, measured in Joules $[J]=[N*m]$
- $\varepsilon_0=8.8542\ldots\times 10^{-12}$ $\left[\frac{\mathrm{F}}{\mathrm{m}}\right]$: The permittivity of free space, which is one of the fundamental constants of Nature.
- $k_e=8.987551\times 10^9$ $\left[\frac{\mathrm{Nm^2}}{\mathrm{C}^{2}}\right]$: The electric constant. It is related to the permittivity of free space by $k_e=\frac{1}{4 \pi \varepsilon_0}$.
Charge
One of the fundamental properties of matter is charge, which is measured in Coulombs [C]. An electron has the charge $q_e=-1.602\times10^{-19}$ [C]. The electric charge of the nucleus of a Helium atom is $q_{He}=2\times1.602\times10^{-19}$, because it contains two protons and each proton has a charge of $1.602\times10^{-19}$ [C].
Unlike mass, of which there is only one kind, there are two kinds of charge: positive and negative. Using the sign (positive vs. negative) to denote the “type” of charge is nothing more than a convenient mathematical trick. We could have instead called the two types of charges “hot” and “cold”. The important thing is that there are two kinds with “opposite” properties in some sense. In what sense opposite? In the sense of their behaviour in physical experiments. If the two charges are of the same kind, then they try to push each other away, but if the two charges are of different kinds then they will attract each other.
Formulas
Coulomb's law
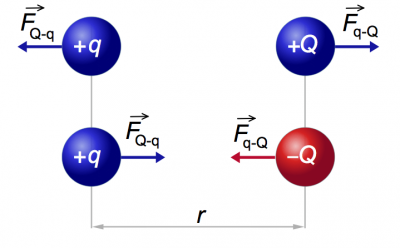 Two point charges $Q$ and $q$ placed at a distance $r$ meters apart will interact
via the electric force.
The magnitude of the electric force is given by the following formula
\[
|\vec{F}_e({r})| = \frac{k_eQq}{r^2} \qquad \text{[N]},
\]
which is known as Coulomb's law.
Two point charges $Q$ and $q$ placed at a distance $r$ meters apart will interact
via the electric force.
The magnitude of the electric force is given by the following formula
\[
|\vec{F}_e({r})| = \frac{k_eQq}{r^2} \qquad \text{[N]},
\]
which is known as Coulomb's law.
If the charges are different (one positive and one negative) then the force will be attractive – it will tend to draw the two charges together. If the two charges are of the same sign then the force will be repulsive.
Electric potential energy
Every time you have a force, you can calculate the potential energy associated with that force, which represents the total effect (the integral) of the force over some distance. We now define the electric potential energy $U_e$, i.e., how much potential energy is stored in the configuration of two charges $Q$ and $q$ separated by a distance of $r$. The formula is \[ U({r}) = \frac{kQq}{r} \qquad \text{[J]}, \] which is very similar to the formulate for $|\vec{F}_e(Q,q,r)|$ above, but with a one-over-r relationship instead of a one-over-r-squared.
We learned in mechanics, that often times the most elegant way to solve problems in physics is not to calculate the forces involved directly, but to use the principle of conservation of energy. By simple accounting of the different types of energy: kinetic (K), potential (U) and the work done (W), we can often arrive at the answer.
In mechanics we studied the gravitational potential energy $U_g=mgh$ and the spring potential energy $U_s=\frac{1}{2}kx^2$ associated with the gravitational force and spring force respectively. Now you have a new kind of potential energy to account for: $U_e=\frac{kQq}{r}$.
Examples
Example 1
A charge $Q=20$[$\mu$C] is placed 2.2 [m] away from a second charge $q=3$[$\mu$C]. What will be the magnitude of the force between them? Is the force attractive or repulsive?
Example 2
A charge $Q=6$[$\mu$C] is placed at the origin $(0,0)$ and a second charge $q=-5$[$\mu$C] is placed at $(3,0)$ [m]. What will be the force on $q$. Express your answer as a vector.
If the charge $q$ was placed instead at $(0,3)$[m], what would be the resulting electric vector?
What if the charge $q$ is placed at $(2,4)$[m]. What will be the electric force on $q$ then? Express your answer both in terms of magnitude-and-direction and in component notation.
Example 3
A fixed charge of $Q=3$[$\mu$C] and a movable charge $q=2$ [$\mu$C] are placed at a distance of 30 [cm] apart. If the charge $q$ is released it will fly off into the distance. How fast will it be going when it is $4$[m] away from $Q$?
Explanations
Coulomb's law
The electric force is a vector quantity so the real formula for the electric force must be written as a vector.
Let $\vec{r}$ be the vector distance from $Q$ to $q$. The electric force on the charge $q$ is \[ \vec{F}_e({r}) = \frac{k_eQq}{r^2}\hat{r} \qquad \text{[N]}, \] where $\hat{r}$ is a direction vector pointing away from $Q$. This formula will automatically take care of the direction of the vector in both the attractive and repulsive cases. If $Q$ and $q$ are of the same charge the force will be in the positive $\hat{r}$ direction (repulsive force), but if the charges have opposite sign, the force will be in the negative $\hat{r}$ direction.
In general, it is easier to think of the magnitude of the electric force, and then add the vector part manually by thinking in terms of attractive/repulsive rather than to depend on the sign in the vector equation to figure out the direction for you.
From force to potential energy
The potential energy of a configuration of charges is defined as the negative of the amount of work which would be necessary in order to bring the charges into this configuration: $U_e = - W_{done}$.
To derive the potential energy formula for charges $Q$ and $q$ separated by a distance $R$ in meters, we can imagine that $Q$ is at the origin and the charge $q$ starts off infinitely far away on the $x$-axis and is brought to a distance of $R$ from the origin slowly. The electric potential energy is given by the following integral: \[ \Delta U_e = - W_{done} = - \int_{r=\infty}^{r=R} \vec{F}_{ext}({r}) \cdot d\vec{s}. \] By bringing the charge $q$ from infinitely far away we make sure that the initial potential energy is going to be zero. Just like with all potentials, we need to specify a reference point with respect to which we will measure it. We define the potential at infinity to be zero, so that $\Delta U_e = U_e({R})-U_e(\infty) = U_e({R})-0= U_e({R})$.
OK, so the charge $q$ starts at $(\infty,0)$ and we sum-up all the work that will be necessary to bring it to the coordinate $(R,0)$. Note that we need an integral an integral to calculate the work, because the strength of the force changes during the process.
Before we do the integral, we have to think about the direction of the force and the direction of the integration steps. If we want to obtain the correct sign, we better be clear about all the negative signs in the expression:
- The negative sign in the front of the integral comes from the definition $U_e \equiv - W_{done}$.
- The electric force on the charge $q$ when it is a distance $x$ away
will be $\vec{F}_e({x}) = \frac{k_eQq}{x^2}\hat{x}$.
Therefore if we want to move the charge $q$ towards $Q$ we have
to apply an external force $\vec{F}_{ext}$ on the charge in the opposite direction.
The magnitude of the external force needed
to hold the charge in place (or to move it towards the origin at a constant speed)
is given by $\vec{F}_{ext}({x}) = -\frac{k_eQq}{x^2}\hat{x}$.
* The displacement vector $d\vec{s}$ always points in the
negative direction, since we start from $+\infty$ and move back to the origin.
Therefore, in terms of the positive $x$-direction the displacements
are small negative steps $d\vec{s} = - dx\; \hat{x}$.
The negative of the $W_{done}$ from $\infty$ to $R$ is given by the following integral: \[ \begin{align} \Delta U_e & = - W_{done} = - \int_{r=\infty}^{r=R} \vec{F}_{ext}({r}) \cdot d\vec{s} \nl & = -\int_{x=\infty}^{x=R} \left( - \frac{k_eQq}{x^2}\hat{x}\right) \cdot \left( -\hat{x}dx\right) \nl & = - \int_{\infty}^{R} \frac{k_eQq}{x^2} \ (\hat{x}\cdot\hat{x}) \ dx \nl & = - k_eQq \int_{\infty}^{R} \frac{1}{x^2} \ 1 \ dx \nl & = - k_eQq \left[ \frac{-1}{x} \right]_{\infty}^{R} \nl & = k_eQq \left[ \frac{1}{R} - \frac{1}{\infty} \right] \nl & = \frac{k_eQq}{R}. \end{align} \]
So we have that we have \[ \Delta U_e \equiv U_{ef} - U_{ei} = U_e({R}) - U_e(\infty), \] and since $U_e(\infty)=0$ we have derived that \[ U_e({R}) = \frac{k_eQq}{R}. \]
We say that the work done to bring the two charges together is stored in the electric potential energy $U_e({r})$ because if we were to let go of these charges they would fly away from each other, and give back all that energy as kinetic energy.
From potential to force
We can also use the relationship between force and potential energy in the other direction. If I were to tell you that the potential energy of two charges is \[ U({r}) = \frac{k_eQq}{r}, \] then, by definition, the force associated with that potential is given by \[ \vec{F}({r}) \equiv - \frac{dU({r}) }{dr} = \frac{k_eQq}{r^2} \hat{r}. \]
Discussion
More intuition about charge
Opposite charges cancel out. If you have a sphere with $5$[$\mu$C] of charge on it, and you add some negative charge to it, say $-1$[$\mu$C], then the resulting charge on the sphere will be $4$[$\mu$C].
Charged particles will redistribute themselves between different objects brought into contact so as to minimize the repulsive force between them. This means that charge is always maximally spread out over the entire surface of the object. For example, if charge is placed on a metal ball made of conducting material the charge will all go to the surface of the body and will not penetrate into the interior.
As another example, consider two metal spheres that are connected by a conducting wire with a total charge $Q$ placed on the system. Because charge is free to move along the wire, it will end up distributed uniformly over the total area $A =A_1 +A_2$, where $A_1$ and $A_2$ are the surface areas of the two spheres. The surface charge density will be $\sigma = Q/A$ [C/m$^2$]. The charge on each sphere will be proportional to the surface area of the object: \[ Q_1 = \sigma A_1 = \frac{A_1}{A_1+A_2} Q, \qquad Q_2 = \sigma A_2 = \frac{A_2}{A_1+A_2} Q. \qquad \textrm{[C]} \] Note that the $Q_1 + Q_2=Q$ as expected.
Links
Electric field
We will now discuss a new language for dealing with electrostatic problems.
So far we saw that the electric force, $\vec{F}_e$, exists between two charges $Q$ and $q$, and that the formula is given by Coulomb's law $\vec{F}_e=\frac{k_eQq}{r^2}\hat{r}$. How exactly this force is produced, we don't know. We just know from experience that it exists.
The electric field is an intuitive way to explain how the electric force works. We imagine that the charge $Q$ creates an electric field everywhere in space described by the formula $\vec{E} = \frac{k_eQ}{r^2}\hat{r}$ $[N/C]$. We further say that any charge placed in an electric field will feel an electric force proportional to the strength of the electric field. A charge $q$ placed in an electric field of strength $\vec{E}$ will feel an electric force $\vec{F}_e = q \vec{E}=\frac{k_eQq}{r^2}\hat{r}$.
This entire chapter is about this change of narrative when explaining electrostatic phenomena. There is no new physics. The electric field is just a nice way of thinking in terms of cause and effect. The charge $Q$ caused the electric field $\vec{E}$ and the electric field $\vec{E}$ caused the force $\vec{F}_e$ on the charge $q$.
You have to admit that this new narrative is nicer, than just saying that somehow the electric force “happens”.
Concepts
Recall the concepts from electrostatics:
- $q,Q,q_1,q_2$: The electric charge of some particle or object. It is measured in Coulombs $[C]$.
- $\vec{F}$: Electic force strength and direction, measured in Newtons $[N]$
- $U$: Potential energy (electrical), measured in Joules $[J]=[N*m]$
- $\vec{r}$: The vector-distance between two charges.
- $r \equiv |\vec{r}|$: Distance between two charges, measured in meters $[m]$
- $\hat{r}$: A direction vector (unit length vector) in the $\vec{r}$ direction.
In this section we will introduce a new language to talk about the same ideas.
- $\vec{E}$: Electric field strength and direction, measured in $[V/m]$ or Gauss
- $V$: Electric potential, measured in Volts $[V]$
Formulas
Electric field
The electric field caused by a charge $Q$ at a distance $r$ is given by \[ \vec{E}({r}) = \frac{kQ}{r^2}\hat{r} \qquad \text{[N/C]=[V/m]}. \]
Electric force
When asked to calculate the force between two particles we simply have to multiply the electric field times the charge \[ \vec{F}_e({r}) = q\vec{E}({r}) = q\frac{kQ}{r^2}\hat{r} = \frac{kQq}{r^2}\hat{r} \qquad \text{[N]}. \]
Electric potential
The electric potential $V$ (not to be confused with the electric potential energy $U_e$) of a charge $Q$ is given by \[ V({r})= \frac{kQ}{r} \qquad \text{[V]} \equiv \text{[J/C]} \]
Electric potential energy
The electric potential energy necessary to bring charge $q$ to point where an electric potential $V({r})$ exists is given by \[ U_e({r}) = q V({r}) = q\frac{kQ}{r} = \frac{kQq}{r} \qquad \text{[J]}. \]
Relations between the above four quantities
We can think of the electric field $\vec{E}$ as an electric force per unit charge. Indeed the dimensions of the electric field is $\text{[N/C]}$, so the electric field tells us the amount of force that a test charge of $q=1$[C] would feel at that point. Similarly, the electric potential is $V$ is the electric potential energy per unit charge, as can be seen from the dimensions: $\text{[V]}=\text{[J/C]}$.
In the electrostatics chapter we saw that, \[ U_e({R}) = - W_{done} = - \int_{\infty}^R \vec{F}_e({r}) \cdot d\vec{s}, \qquad \qquad \vec{F}_e({r}) = - \frac{dU({r}) }{dr}. \]
An analogous relation exists between the per unit charge quantities. \[ V({R}) = - \int_{\infty}^R \vec{E}({r}) \cdot d\vec{s}, \qquad \qquad \qquad \qquad \ \ \vec{E}({r}) = - \frac{dV({r}) }{dr}. \]
Explanations
Electric potential
A major issue in understanding the ideas of electromagnetism is to get an intuitive understanding of the concept of electric potential $V$. First, there is the naming problem. There are at least four other terms for the concept: voltage, potential difference, electromotive force and even electromotance! Next, we have the possible source of confusion with the concept of electric potential energy, which doesn't help the situation. Perhaps the biggest problem with the concept of electric potential is that it doesn't exist in the real world: like the electric field to which it is related, it is simply a construct of the mind, which we use to solve problems and do calculations.
Despite the seemingly unsurmountable difficulty of describing the nature of something which doesn't exist, I will persist in this endeavour. I want to give you a proper intuition about voltage, because this concept will play an extremely important role in circuits. While it is true that voltage doesn't exist, energy does exist and energy is just $U=qV$. Voltage, therefore, is electric potential energy per unit charge, and we can talk about the voltage in the language of energy.
Every time you need to think about some electric potential, just imagine what would happen to a unit test charge: q=1[C], and then think in terms of energy. If the potential difference between point (a) and point (b) is $V_{ab}=16$[V], this means that a charge of 1[C] that goes from (a) to (b) will gain 16[J] of energy. If you have some circuit with a 3[V] battery in it, then each Coulomb of charge that is pumped through the battery gains $3$[J] of energy. This is the kind of reasoning we used in the opening example in the beginning of electrostatics, in which we calculated the kinetic energy of the electrons inside an old-school TV.
Field lines
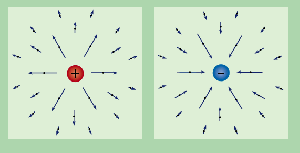 We can visualize the electric field caused by some charge as
electric field lines everywhere around it.
For a positive charge ($Q>0$), the field lines will be leaving it
in all directions towards negative charges or expanding to infinity.
We say that a positive charge is a source of electric field lines
and that a negative charge ($Q<0$) is a sink for electric field lines,
i.e., it will have electric field lines going into it
The diagram on the right illustrates the field lines for two isolated
charges. If these charges were placed next to each other, then
the field lines leaving the (+) charge would all curve around and go into the (-) charge.
We can visualize the electric field caused by some charge as
electric field lines everywhere around it.
For a positive charge ($Q>0$), the field lines will be leaving it
in all directions towards negative charges or expanding to infinity.
We say that a positive charge is a source of electric field lines
and that a negative charge ($Q<0$) is a sink for electric field lines,
i.e., it will have electric field lines going into it
The diagram on the right illustrates the field lines for two isolated
charges. If these charges were placed next to each other, then
the field lines leaving the (+) charge would all curve around and go into the (-) charge.
Links
[ A guided tour of the electie vield lines ]
http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/electrostatics/index.htm
{{page>electricity:electron_gun}}
{{page>electricity:crt}}
Electrostatic integrals
The electric field produced by a point charge $Q$ placed at the origin is given by $\vec{E}(\vec{r})=\frac{k_eQ}{r^2}\hat{r}$. What if the charge is not a point but some continuous object? It could be a line-charge, or some charged surface. How would you calculate the electric field produced by such an object $O$?
What you will do is cut up the object into little pieces $dO$ and calculate the electric field produced by each piece and then add up all the contribution. In other words you need to do an integral.
Concepts
- $Q$: the total charge. The units are Coulombs [C].
- $\lambda$: linear charge density. The units are coulombs per meter [C/m].
The charge density of a long wire of length $L$ is $\lambda = \frac{Q}{L}$.
- $\sigma$: the surface charge density. Units are [C/m$^2$].
The charge density of a disk with radius $R$ is $\sigma = \frac{Q}{\pi R^2}$.
The charge on a sphere of radius $R$ made of conducting material will be concentrated
on its surface and will have density $\rho =\frac{Q}{4 \pi R^2}$.
* $\rho$: the volume charge density. Units are [C/m$^3$].
The charge density of a cube of uniform charge and side length $c$ is $\rho = \frac{Q}{c^3}$.
The charge density of a solid sphere made of insulator with a uniform
charge distribution will be $\rho = \frac{Q}{\frac{4}{3} \pi R^3}$.
One-over-r-squared quantities:
- $\vec{F}_e$: Electric force.
- $\vec{E}$: Electric field.
One-over-r quantities:
- $U$: electric potential energy.
- $V$: electric potential.
Integration techniques review
Both the formulas for electric force (field) and potential energy (electric potential) contain a denominator of the form $r\equiv |\vec{r}| = \sqrt{x^2 + y^2}$. As you can imagine, these kind of integrals will be quite hairy to calculate if you don't know what you are doing.
But you know what you are doing! Well, you know if you remember your techniques_of_integration. Now I realize we saw this quite a long time ago so a little refresher is in order.
The reason why they make you practice all those trigonometric substitutions is that they will be useful right now. For example, how would you evaluate the integral \[ \int_{-\infty}^{\infty} \frac{1}{(1+x^2)^{\frac{3}{2}} } \ dx, \] if you were forced to – like on an exam question or something. Relax. You are not in an exam. I just said that to get your attention. The above integral may look complicated, but actually you will see that it is not too hard: we just have to use a trig substitution trick. You will see that all that time spent learning about integration techniques was not wasted.
Recall that the trigonometric substitution trick necessary to handle the terms like $\sqrt{1 + x^2}$is to use the identity: \[ 1 + \tan^2 \theta = \sec^2 \theta, \] which comes from $\cos^2 \theta + \sin^2 \theta = 1$ divided by $\cos^2 \theta$.
If we make the substitution $x=\tan\theta$, $dx=\sec^2\theta \ d\theta$ in the above integral we will get \[ 1 + x^2 = \sec^2 \theta. \] But we don't just have $1+x^2$, but $(1+x^2)^{\frac{3}{2}}$. So we need to take the $\frac{3}{2}$th power of the above equation, which is equivalent to taking the square root and then raising to the third power: \[ (1+x^2)^{\frac{3}{2}} = (\sec^2\theta)^{\frac{3}{2}} = \left( \sqrt{ \sec^2\theta} \right)^{3} = (\sec\theta)^{3} = \sec^3\theta. \] Next, we have to calculate the new limits of integration due to the change of variable $x=\tan\theta$. The upper limit $x_f=+\infty$ becomes $\theta_f = \tan^{-1}(+\infty)=\frac{\pi}{2}$ and the lower limit $x_i=-\infty$ becomes $\theta_i = \tan^{-1}(-\infty)=-\frac{\pi}{2}$.
Ok now let's see how all of this comes together: \[ \begin{align} \int_{x=-\infty}^{x=\infty} \frac{1}{(1+x^2)^{\frac{3}{2}} } \ dx &= \int_{ \theta=-\frac{\pi}{2} }^{ \theta=\frac{\pi}{2} } \frac{1}{(1+\tan^2\theta)^{\frac{3}{2}} } \sec^2 \theta \ d\theta \nl &= \int_{ -\frac{\pi}{2} }^{ \frac{\pi}{2} } \frac{1}{\sec^3\theta} \sec^2 \theta \ d\theta \nl &= \int_{ -\frac{\pi}{2} }^{ \frac{\pi}{2} } \cos \theta \ d\theta \nl &= \sin \theta \bigg|_{ -\frac{\pi}{2} }^{ \frac{\pi}{2} } = \sin\left( \frac{\pi}{2} \right) - \sin\left( - \frac{\pi}{2} \right) = 1 - (-1) = 2. \end{align} \]
Exercise
Now I need you to put the book down for a moment and try to reproduce the above steps by practicing on the similar problem: \[ \int_{-\infty}^{\infty} \frac{a}{(a^2+x^2)^{\frac{3}{2}} } \ dx, \] where $a$ is some fixed constant. Hint: substitute $x = a \tan\theta$. This integral corresponds to the strength of the electric field at a distance $a$ from an infinitely long line charge. Ans: $\frac{2}{a}$. We will use this result in Example 1 below, so go take a piece of paper and do it.
The tan substation is also useful when calculating the electric potential, but the denominator will be of the form $\frac{1}{(1+x^2)^{\frac{1}{2}} }$ instead of $\frac{1}{(1+x^2)^{\frac{3}{2}} }$. We show how to compute this integral in Example 3.
Formulas
Let $\vec{E} = ( E_x, E_y )=( \vec{E}\cdot \hat{x}, \vec{E}\cdot \hat{y} )$ be the electric field strength at some point $P$ due to the charge on some object $O$. We can calculate the total electric field by analyzing the individual contribution $dE$ due to each tiny part of the object $dO$.
The total field strength in the $\hat{x}$ direction is given by \[ E_x = \int dE_x = \int_O \vec{E}\cdot \hat{x}\ dO. \]
The above formula is too abstract to be useful. Think of it more as a general statement of the principle that the electric field due to the object as a whole, is equal to sum of the electric field due to its parts.
Charge density
The linear charge density of an object of length $L$ with charge $Q$ on it is \[ \lambda = \frac{Q}{L}, \qquad \textrm{ [C/m] } \] where $\lambda$ is the Greek letter lambda which is also used to denote wavelength.
Similarly the surface charge density is defined as the total charge divided by the total area and the volume charge density as the total charge divided by the total volume: \[ \sigma = \frac{Q}{A} \ \ \ \left[ \frac{\textrm{C}} { \textrm{m}^2} \right], \qquad \rho = \frac{Q}{V} \ \ \ \left[ \frac{ \textrm{C} }{ \textrm{m}^3} \right], \] where $\sigma$ and $\rho$ are the Greek letters sigma and rho.
Examples
Example 1: Electric field of an infinite line charge
Consider a horizontal line charge of charge density $\lambda$ [C/m]. What is the strength of the electric field strength at a distance $a$ from the wire?
The wire has a line symmetry so we can choose any point along the wire, so long as it is $a$[m] away from it. Suppose we pick the point $P=(0,a)$ which lies on the $y$ axis. We want to calculate $\vec{E}({P}) = ( E_x, E_y )=( \vec{E}\cdot \hat{x}, \vec{E}\cdot \hat{y} )$.
Consider first the term $E_y$. It is given by the following integral: \[ \begin{align} E_y & = \int dE_y = \int d\vec{E} \cdot \hat{y} \nl & = \int_{x=-\infty}^{x=\infty} \vec{E}(dx) \cdot \hat{y} \nl & = \int_{x=-\infty}^{x=\infty} \frac{ k_e (\lambda dx)} { r^2} \hat{r} \cdot \hat{y} \nl & = \int_{x=-\infty}^{x=\infty} \frac{ k_e \lambda dx} { r^2} \hat{r} \cdot \hat{y} \nl & = \int_{-\infty}^{\infty} \frac{k_e \lambda}{(a^2+x^2)} ( \hat{r} \cdot \hat{y} ) \ dx \nl & = \int_{-\infty}^{\infty} \frac{k_e \lambda}{(a^2+x^2)} \left( \frac{ a }{ \sqrt{ a^2+x^2} } \right) \ dx \nl & = \int_{-\infty}^{\infty} \frac{k_e \lambda a}{(a^2+x^2)^{\frac{3}{2}} } \ dx. \end{align} \]
We showed how to compute this integral in the review section on integration techniques. If you did as I asked you, you will know that \[ \int_{-\infty}^{\infty} \frac{a}{(a^2+x^2)^{\frac{3}{2}} } \ dx \ = \ \frac{2}{a}. \]
The total electric field in the $y$ direction is therefore given by: \[ E_y = k_e \lambda \int_{-\infty}^{\infty} \frac{ a}{(a^2+x^2)^{\frac{3}{2}} } \ dx \ = \ \frac{ 2 k_e \lambda }{ a }. \]
By symmetry $E_x=0$, since there is an equal amount of charge to the left and to the right of the origin. Therefore, the electric field $\vec{E}({P})$ at the point $P$ at a distance $a$ from the line charge is given by $\vec{E}({P})=(E_x, E_y) = \left( 0, \frac{ 2 k_e \lambda }{ a } \right)$.
Example 2: Charged disk
What is the electric field in the $z$ direction directly above the a disk with charge density $\sigma$[C/m$^2$] and radius $R$ that is lying in the centre of the $xy$-plane?
Example 3: Electric potential of a line charge of finite length
Consider a line charge of length $2L$ and linear charge density $\lambda$. The integral in that case will be \[ \begin{align} \int_{-L}^{L} \frac{1}{ \sqrt{ 1+x^2} } \ dx &= \int \frac{1}{ \sqrt{ 1+\tan^2\theta} } \sec^2 \theta \ d\theta \nl &= \int \frac{1}{\sec\theta} \sec^2 \theta \ d\theta \nl &= \int \sec \theta \ d\theta. \end{align} \] To proceed we need to remember a sneaky trick, which is to use the substitution $u = \tan\theta +\sec\theta$, $du=\sec^\theta + \tan\theta\sec\theta$ and to multiply top and bottom by $\tan\theta +\sec\theta$. \[ \begin{eqnarray} \int \sec(\theta) \, dx &=& \int \sec(\theta)\ 1 \, d\theta \nl &=& \int \sec(\theta)\frac{\tan(\theta) +\sec(\theta)}{\tan(\theta) +\sec(\theta)} \ d\theta \nl &=& \int \frac{\sec^2(\theta) + \sec(\theta) \tan(\theta)}{\tan(\theta) +\sec(\theta)} \ d\theta\nl &=& \int \frac{1}{u} du \nl &=& \ln |u| \nl &=& \ln |\tan(\theta) + \sec(\theta) | \nl &=& \ln \left| x + {\sqrt{ 1 + x^2} } \right| \bigg|_{-L}^L \nl &=& \ln \left| L + {\sqrt{ 1 + L^2}} \right| - \ln \left| -L + {\sqrt{ 1 + L^2} } \right| \nl &=& \ln \left| \frac{ L + {\sqrt{ 1 + L^2} } } { -L + {\sqrt{ 1 + L^2} } } \right|. \end{eqnarray} \]
Exercise: The above calculation is showing the important calculus core of the problem. The necessary physical constants like $\lambda$ (charge density) and $a$ (distance from wire) are missing. Add them to obtain the final answer. You can check your answer in the link below.
Discussion
If you find the steps in this chapter complicated, then you are not alone. I had to think quite hard to get all the things right so don't worry: you won't be expected to do this on an exam on your own. In a homework problem maybe.
The important things to remember is to split the object $O$ into pieces $dO$ and then keep in mind the vector nature of $\vec{E}$ and $\vec{F}_e$ (two integrals: one for the $x$ component of the quantity and one for the $y$ component).
An interesting curiosity is that the electric potential at a distance $a$ from an infinitely long wire is infinite. The potential scales as $\frac{1}{r}$ and so integrating all the way to infinity makes it blow up. This is why we had to choose a finite length $2L$ in Example 3.
Links
Gauss' law
We saw in the previous chapters that the electric field $\vec{E}$ is a useful concept in order to visualize the electromagnetic effects produced by charged objects. More specifically, we imagined electric field lines which are produced by positive charges $+Q$ and end up on negative charges $-Q$. The number of field lines produced by a charge $+2Q$ is the double of the number of field lines produced by a charge $+Q$.
In this section, we learn how to count the number of field lines passing through a surface (electric flux) and infer facts about the amount of charge that the surface contains. The relationship between the electric flux leaving a surface and the amount of charge contained in that surface is called Gauss' law.
Consider the following reasoning. To keep the numbers simple, let us say that a charge of 1[C] produces exactly 10 electric field lines. Someone has given you a closed box $B$ with surface area $S$. Using a special instrument for measuring flux, you find that there are exactly 42 electric field lines leaving the box. You can then infer that there must be a net charge of 4.2[C] contained in the box.
In some sense, Gauss' law is nothing more than a statement of the principle of conservation of field lines. Whatever field lines are created within some surface must leave that surface at some point. Thus we can do our accounting in two equivalent ways: either we do a volume accounting to find the total charge inside the box, or we do a surface accounting and measure the number of field lines leaving the surface of the box.
Concepts
- $Q$: Electric charge of some particle or object. It is measured in Coulombs $[C]$.
- $S$: Some closed surface in a three dimensional space. ex: box, sphere, cylinder.
- $A$: The area of the surface $S$.
- $dA$: A small piece of surface area used for integration. We have that $A=\int_S dA$.
- $d\vec{A}=\hat{n}dA$: A oriented piece of area, which is just $dA$ combined with
a vector $\hat{n}$ which points perpendicular to the surface at that point.
- $\Phi_S$= The electric flux is the total amount of electric field $\vec{E}$ passing through the surface $S$.
- $\varepsilon_0=8.8542\ldots\times 10^{-12}$ $\left[\frac{\mathrm{F}}{\mathrm{m}}\right]$: The permittivity of free space, which is one of the fundamental constants of Nature.
Instead of a point charge $Q$, we can have charge spread out:
- $\lambda$: linear charge density. The units are coulombs per meter [C/m].
The charge density of a long wire of length $L$ is $\lambda = \frac{Q}{L}$.
- $\sigma$: the surface charge density. Units are [C/m$^2$].
The charge density of a disk with radius $R$ is $\sigma = \frac{Q}{\pi R^2}$.
- $\rho$: the volume charge density. Units are [C/m$^3$].
The charge density of a cube of uniform charge and side length $c$ is $\rho = \frac{Q}{c^3}$.
Formulas
Volumes and surface areas
Recall the following basic facts about volumes and surface areas of some geometric solids. The volume of a parallelepiped (box) of sides $a$, $b$, and $c$ is given by $V=abc$, and the surface area is given by $A=2ab+2bc+2ac$. The volume of a sphere of radius $r$ is $V_s=\frac{4}{3}\pi r^3$ and the surface area is $A_s=4\pi r^2$. A cylinder of height $h$ and radius $r$ has volume $V_c=h\pi r^2$, and surface area $A_c=(2\pi r)h + 2 (\pi r^2)$.
Electric flux
For any surface $S$, the electric flux passing through $S$ is given by the following vector integral \[ \Phi_S = \int_S \vec{E} \cdot d\vec{A}, \] where $d\vec{A}=\hat{n} dA$, $dA$ is a piece of surface area and $\hat{n}$ points perpendicular to the surface.
I know what you are thinking “Whooa there Johnny! Hold up, hold up. I haven't seen vector integrals yet, and this expression is hurting my brain because it is not connected to anything else I have seen.” Ok you got me! You will learn about vector integrals for real in the course Vector Calculus, but you already have all the tools you need to understand the above integral: the dot product and integrals. Besides, in first electromagnetism course you will only have to do this integral for simple surfaces like a box, a cylinder or a sphere.
In the case of simple geometries where the strength of the electric field is constant everywhere on the surface and its orientation is always perpendicular to the surface (\hat{E}\cdot\hat{n}=1) the integral simplifies to: \[ \Phi_S = \int_S \vec{E} \cdot d\vec{A} = |\vec{E}| \int_S (\hat{E} \cdot \hat{n}) dA = |\vec{E}| \int_S 1 dA = |\vec{E}|A. \]
In all problems and exams in first year electricity and magnetism we will
have $\Phi_S = |\vec{E}|A$ or $\Phi_S = 0$ (if $\vec{E}$ is parallel to the surface),
so essentially you don't have to worry about the vector integral.
I had to tell you the truth though, because this is the minireference way.
Gauss' law
Gauss' law states that the electric flux $\Phi_S$ leaving some closed surface $S$ is proportional to the total amount of charge $Q_{in}$ enclosed inside the surface: \[ \frac{Q_{in}}{\varepsilon_0} = \Phi_S \equiv \int_S \vec{E} \cdot d\vec{A}. \] The proportionality constant is $\varepsilon_0$, the permittivity of free space.
Examples
Sphere
Consider a spherical surface $S$ of radius $r$ enclosing a charge $Q$ at its centre. What is the strength of the electric field strength, $|\vec{E}|$, on the surface of that sphere?
We can find this using Gauss' law as follows: \[ \frac{Q}{\varepsilon_0} = \Phi_S \equiv \int_S \vec{E} \cdot d\vec{A} = |\vec{E}| A = |\vec{E}| 4 \pi r^2. \] Solving for $|\vec{E}|$ we find: \[ |\vec{E}| = \frac{Q}{4 \pi \varepsilon_0 r^2} = \frac{k_eQ}{r^2}. \] I bet you have seen that somewhere before. Coulomb's law can be derived from Gauss' law, and this is why the electric constant is $k_e=\frac{1}{4\pi \epsilon_0}$.
Line charge and cylindrical surface
Consider line charge of charge density $\lambda$ [C/m]. Imagine a charged wire which has 1[C] of charge on each meter of it. What is the strength of the electric field strength at a distance $r$ from the wire?
This is a classical example of a bring your own surface (BYOS) problem: the problem statement didn't mention any surface $S$, so we have to choose it ourselves. Let $S$ be the surface are of a cylinder of radius $r$ and height $h=1$[m] that encloses the line charge at its centre. We now write down Gauss' law for that cylinder: \[ \begin{align} \frac{\lambda (1 [\textrm{m}])}{\varepsilon_0} & = \Phi_S \equiv \int_S \vec{E} \cdot d\vec{A} \nl & = \vec{E}({r}) \cdot \vec{A}_{side} + \vec{E}_{top} \cdot \vec{A}_{top} + \vec{E}_{bottom} \cdot \vec{A}_{bottom} \nl & = (|\vec{E}|\hat{r}) \cdot \hat{r} 2 \pi r (1 [\textrm{m}]) + 0 + 0 \nl & = |\vec{E}| (\hat{r}\cdot \hat{r}) 2 \pi r (1 [\textrm{m}]) \nl & = |\vec{E}| 2 \pi r (1 [\textrm{m}]). \end{align} \]
Solving for $|\vec{E}|$ in the above equation we find \[ |\vec{E}| = \frac{ \lambda }{ 2 \pi \varepsilon_0 r } = \frac{ 2 k_e \lambda }{ r }. \]
Which you should also have seen before (Example 1 in electrostatic_integrals ).
Electric field inside a capacitor
Assume you have two large metallic plates of opposite charges (a capacitor). The (+) plate has charge density $+\sigma$[C/m$^2$] and the (-) plate has $-\sigma$[C/m$^2$]. What is the strength of the electric field between the two plates?
Consider first a surface $S_1$ which makes a cross section of area $A$ that contains sections of both plates. This surface contains no net charge, so by Gauss' law, we conclude that there are no electric field lines entering or leaving this surface. An electric field $\vec{E}$ exits between the two plates and nowhere outside of the capacitor. This is, by the way, why capacitors are useful: since they store a lot of energy in a confined space.
Consider now a surface $S_2$ which also makes a cross section of area $A$, but only goes halfway through the capacitor, enclosing only the (+) plate. The total charge inside the surface $S_2$ is $\sigma A$, therefore by Gauss' law \[ \frac{\sigma A}{\varepsilon_0} = |\vec{E}|A, \] we conclude that the electric field strength inside the capacitor is $|\vec{E}| = \frac{\sigma }{\varepsilon_0}$.
We will see in capacitors, that this result can also be derived by thinking of the electric field as the spacial derivative of the voltage on the capacitor. You should check that the two approaches lead to the same answer for some physical device with area $A$, plate separation $d$.
Explanations
Surface integral
The flux $\Phi_S$ is a measure of the strength of the electric field lines passing through the surface $S$. To compute the flux, we need the concept of directed area, that is, we split the surface $S$ into little pieces of area $d\vec{A} = \hat{n} dA$ where $dA$ is the surface area of a little piece of surface and $\hat{n}$ is a vector that points perpendicular to the surface. We need this kind of vector to calculate the flux leaving through $dA$: \[ d\Phi_{dA} = \vec{E} \cdot \hat{n} dA, \] where the dot product is necessary to account for the relative orientation of the piece surface are and the direction of the electric field. For example if the piece-of-area-perpendicular vector $\hat{n}$ points outwards on the surface and an electric field of strength $|\vec{E}|$ is leaving the surface then the flux integral will be positive. If on the other hand electric field lines are entering the surface, the integral will come out negative since $\vec{E}$ and $d\vec{A}$ will point in opposite directions. Of particular importance are surfaces where the electric field lines are parallel to the surface: in that case $\vec{E} \cdot \hat{n} dA = 0$.
Implications
Have you ever wondered why the equation for the strength of the electric field $|\vec{E}|(r )$ at a function of the distance $r$ is given by the formula $|\vec{E}(r )|=\frac{kQ}{r^2}$? Why is it one-over-$r$-squared exactly? Why not one over $r$ to the third power or the seventh?
The one-over-$r$-squared comes from Gauss' law. The flux $\Phi$ is a conserved quantity in this situation. The field lines emanating from the charge $Q$ (assumed $Q$ is positive) flow outwards away from the charge and uniformly in all directions. Since we know that $\Phi = |\vec{E}|A_s$, then it must be that that $|\vec{E}| \propto 1/A_s$. The surface area of sphere is
Imagine now applying Gauss' law to a small surface which tightly wraps the charge (small $r$) and a larger spherical surface (big $r$). The total flux of electric field through both surfaces is the same. The flux near the charge is due to a very strong electric field that flows out of a small surface area. The flux far away from the charge is due to a very weak field over a very large surface area.
Discussion
So what was this chapter all about? We started with crazy stuff like vector integrals (more specifically surface integrals) denoted by fancy Greek letters like $\Phi$, but in the end we derived only three results which we already knew. What is the point?
The point is that we have elevated our understanding from the formula level to a principle. Gauss' law is a super-formula: a formula that generates formulas. The understanding of such general principles that exist in Nature is what physics is all about.
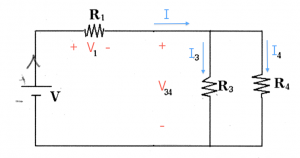
Circuits
Electric circuits are contraptions in which electric current flows through various pipes (wires) and components (resistors, capacitors, inductors, on-off switches, etc.). Because the electric current cannot escape the wire, it is forced to pass through each of the components along its path.
Your sound system is a circuit. Your computer power supply is a circuit. Even the chemical reactions involved in neuronal spiking can be modelled as an electric circuit.
Concepts
$I$: the electric current. It flows through all circuit components. We measure current in Amperes $[A]$.
We use wires to guide the flow of currents: to make them go where we want.
* {{ :electricity:circuit-element-voltage.png|}}
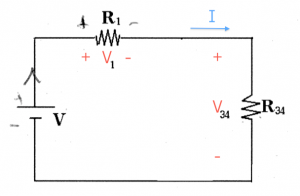
$V$: the electric potential difference between two points. We say //voltage// for short instead of "electric potential difference". There is no notion of "absolute" voltage, we only measure potential difference between //two// points. Thus if you should always label a (+) side and a (-) side when reporting a voltage. Conveniently, the unit of Voltage is the Volt [V], after Volta.
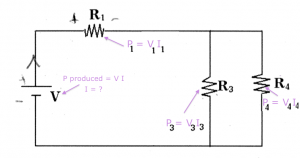
* $P$: the power consumed or produced by some component. Measured in Watts [W].
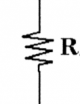
* $R$: the //resistance// value of a resistor. For resistors, the voltage across the leads is linearly related to current flowing in the resistor. We call //resistance// the ratio between the voltage and the current:
\[
R=\frac{V}{I}.
\]
We measure resistance in Ohms [$\Omega$].
Circuit components
The basic building blocks of circuits are called electric components. In this section we will learn how to use the following components.
\[ V_{\text{wire}} = \text{any}, \quad \qquad I_{\text{wire}} = \text{any} \]
Battery: This is a voltage source. Can provide any current, but always keeps a constant voltage of V volts.
\[
V_{\text{batt}} = V, \qquad \qquad I_{\text{batt}} = \text{any}
\]
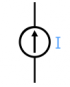
Current source: This device pushes a constant current of $I$ [A], no matter what circuit it is connected to. The current source is allowed to have any voltage across its terminals.
\[
V_{\text{source}} = \text{any}, \quad \qquad I_{\text{source}} = I
\]
Resistor: Can carry any current $I$, and has a voltage across its terminals of $V=RI$ where $R$ is the resistance measured in Ohmns [$\Omega$].
\[
V_{\text{resistor}} = I_{\text{resistor}}R, \qquad \qquad I_{\text{resistor}} = \frac{V_{\text{resistor}}}{R}
\]
The energy of the electrons (the voltage) right before entering the resistor is $IR$ [V] higher than when they leave the resistor. It is important to label the positive and negative terminals of the resistor. The positive terminal is where the current enters, the negative where the current leaves.
An on-off switch.
When the switch is //off// (we also say //the switch is open// like in the figure on the right), then the two pieces of wires are disconnected and no current is allowed to flow through. When the switch is //on// (or //closed//), then it acts like a piece of wire and will let current through.
General principles
Ohm's law
The voltage across the terminals of a resistor is proportional to the current
flowing through. The more current flowing through, the more voltage will be dropped.
The constant of proportionality is called resistance of the element.
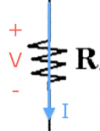 \[
V= IR, \qquad \text{or} \qquad I = \frac{V}{R}, \qquad \text{or} \qquad R = \frac{V}{I}
\]
This is obey Ohm's law.
\[
V= IR, \qquad \text{or} \qquad I = \frac{V}{R}, \qquad \text{or} \qquad R = \frac{V}{I}
\]
This is obey Ohm's law.
Electric power
The power consumed by an electric component is given by \[ P = V I, \] where $I$ is the current going into the (+) terminal of the device. The logic behind this formula is as follows. Each electron passing through the device will have lost $V$ volts of electric potential by passing through the device, and the more of them that are flowing (high current) then more power will be consumed.
For batteries, usually the current leaves the (+) terminal instead of entering it, which is equivalent to saying that a negative current flows into the (+) terminal. The expression for the power consumed will therefore be negative: which makes sense since batteries supply energy to the circuit.
For resistors, the current always flows into the (+) side, so power is always consumed. Furthermore, since we know that $V=IR$, we can rewrite the power formula in two other equivalent forms: \[ P = V I, \qquad P = \frac{V^2}{R} \qquad P = RI^2. \] These forms are useful when only the current or the voltage of a resistor is known.
Kirchhoff's loop law
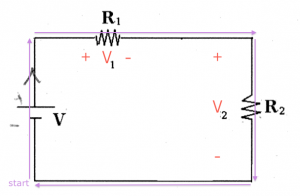 Let's follow the life of a charge going around in the circuit.
It's kind of like a reality show, but with a really simple character.
The journey of the charge begins at $\color{blue}{\text{start}}$, and we will say that the electric potential of this point is $0$[V].
The charge goes up and as it passes through the battery it gains $V$ volts of potential.
We know this, because this is what batteries do: they take charges at the (-) terminal and push them out of (+) terminal with $V$ volts more electric potential.
Next the charge goes right and passes through the resistor $R_1$. The result of this is a change of $-V_1$ in electric potential. This is because the charge dissipated some energy as it passed thought the resistor.
Some more voltage is dropped as it passes through the second resistor. The change in potential is $-V_{2}$,
because the change enters the (+) side and leaves at the (-) side.
Then the charge comes back to $\color{blue}{\text{start}}$, and so its potential must be zero again:
\[
0 + V - V_1 - V_{2} = 0.
\]
By doing this imaginary journey we have established a connection between the battery voltage and the total voltage dropped in the circuit loop.
Let's follow the life of a charge going around in the circuit.
It's kind of like a reality show, but with a really simple character.
The journey of the charge begins at $\color{blue}{\text{start}}$, and we will say that the electric potential of this point is $0$[V].
The charge goes up and as it passes through the battery it gains $V$ volts of potential.
We know this, because this is what batteries do: they take charges at the (-) terminal and push them out of (+) terminal with $V$ volts more electric potential.
Next the charge goes right and passes through the resistor $R_1$. The result of this is a change of $-V_1$ in electric potential. This is because the charge dissipated some energy as it passed thought the resistor.
Some more voltage is dropped as it passes through the second resistor. The change in potential is $-V_{2}$,
because the change enters the (+) side and leaves at the (-) side.
Then the charge comes back to $\color{blue}{\text{start}}$, and so its potential must be zero again:
\[
0 + V - V_1 - V_{2} = 0.
\]
By doing this imaginary journey we have established a connection between the battery voltage and the total voltage dropped in the circuit loop.
Kirchhoff's law says that the sum of the voltage gains and drops along any loop must add up to zero: \[ \sum_{\text{loop}} V_i = 0. \]
Kirchhoff current law
 If you have one current going into a junction, and two currents leaving the junction then:
\[
I = I_3 + I_4.
\]
This is implied by conservation of charge: charge can't be created or destroyed so the sum of the currents coming into a junction, must equal the sum of the currents leaving the junction:
\[
\sum I_{\text{in}} = \sum I_{\text{out}}.
\]
If you have one current going into a junction, and two currents leaving the junction then:
\[
I = I_3 + I_4.
\]
This is implied by conservation of charge: charge can't be created or destroyed so the sum of the currents coming into a junction, must equal the sum of the currents leaving the junction:
\[
\sum I_{\text{in}} = \sum I_{\text{out}}.
\]
Resistances in series
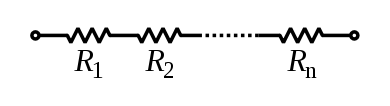 If you have several resistors attached together in series, then the
equivalent resistance of the three resistors is
\[
R_{eq} = R_1 + R_2 + \ldots + R_n.
\]
If you have several resistors attached together in series, then the
equivalent resistance of the three resistors is
\[
R_{eq} = R_1 + R_2 + \ldots + R_n.
\]
Note that in this configuration the same current flows through all the resistors.
Example 1
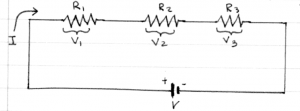 Suppose you have connected three resistors $R_1=1[\Omega]$, $R_2=3[\Omega]$ and $R_3=5[\Omega]$ in series to a 16[V] battery.
Q: What is the equivalent resistance of the circuit?
Suppose you have connected three resistors $R_1=1[\Omega]$, $R_2=3[\Omega]$ and $R_3=5[\Omega]$ in series to a 16[V] battery.
Q: What is the equivalent resistance of the circuit?
A: The equivalent resistance that the battery sees is $R_{eq}=R_1+R_2+R_3 = 8[\Omega]$.
Q: What will be the current $I$ in the circuit?
A: The current flowing in the circuit can be found by using Ohm's law V=IR. In this case $I=\frac{V}{R}=\frac{16}{8} = 2$[A].
Q: What is the voltage drop across $R_3$?
A: The voltage is $V_3=IR_3=(2[A])(5[\Omega]) = 10$[V].
Resistances in parallel
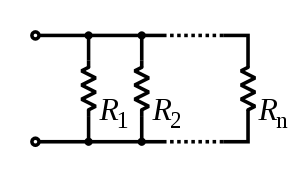 For resistors in parallel, the equivalent resistance is:
\[
R_{eq} = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\ldots+\frac{1}{R_n}}.
\]
Because all the resistors are connected to the same (+) and (-)
endpoints, they will all have the same voltage across them.
For resistors in parallel, the equivalent resistance is:
\[
R_{eq} = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\ldots+\frac{1}{R_n}}.
\]
Because all the resistors are connected to the same (+) and (-)
endpoints, they will all have the same voltage across them.
When there are just two resistors in parallel, the equation simplifies to: \[ R_{eq} = \frac{1}{ \frac{1}{R_1}+\frac{1}{R_2} } = \frac{R_1R_2}{R_1+R_2}. \] We sometimes denote the equivalent resistance of $R_1$ and $R_2$ in parallel as $R_1 \| R_2$.
Example 2
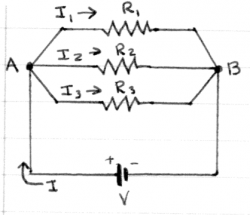 Suppose you have connected three resistors $R_1=1[\Omega]$, $R_2=3[\Omega]$ and $R_3=5[\Omega]$ in parallel to a 16[V] battery.
Q: What is the equivalent resistance of the circuit?
Suppose you have connected three resistors $R_1=1[\Omega]$, $R_2=3[\Omega]$ and $R_3=5[\Omega]$ in parallel to a 16[V] battery.
Q: What is the equivalent resistance of the circuit?
A: The equivalent resistance as seen by the battery is: $R_{eq}=\left(\frac{1}{1}+\frac{1}{3}+\frac{1}{5}\right)^{-1}$.
We can calculate it by finding the least common denominator.
$R_{eq} = \left(\frac{15}{15}+\frac{5}{15}+\frac{3}{15}\right)^{-1} =
\left(\frac{23}{15}\right)^{-1}=\frac{15}{23}\approx 0.652[\Omega]$.
Q: What will be the current $I$ drawn from the battery?
A: The battery will supply $I=\frac{V}{R_{eq}}$ Amperes.
In this case $I=\frac{V}{R}=\frac{16}{15/23} = 368/15\approx 24.533$[A].
Q: What are the currents $I_1$, $I_2$ and $I_3$ flowing through each resistor?
A: All three resistors are connected across the same voltage $V=16$[V], so we can use Ohm's law on each individually to find the current. $I_1 = \frac{16}{1}=16$[A], $I_1 = \frac{16}{3}\approx 5.333$[A],
and $I_3 = \frac{16}{5}=3.2$[A]. Note that $I_1+I_2+I_3=I$ as required by Kirchhoff's current law for points A and B.
Q: What is the voltage drop across $R_3$?
A: This is a trick question. $R_3$ is connected across the $16$[V] battery, so the voltage drop across it is 16[V].
Units
I want to also give you some intuition about the quantities we normally see in circuit. Most electronics work with milliamperes [mA] and small voltages like 3V or 5V. On the other hand, an electric radiator can draw about 10$[A]$ or current easily. The voltage that is used for power transport over long distances is on the order of 50000$[V]$ – this is why they call them high-voltage lines.
Worked example
You have in your hands the following circuit. There is a voltage source of $V$[V] and four loads $R_1$, $R_2$, $R_3$ and $R_4$, which could be light bulbs, heating elements or any other kind of device. Assume that the value of the resistances are given to you and you are given the following task: Find the value of of the current flowing through resistor $R_4$?
First observe that the switch $S$ is open, so effectively that entire branch of the circuit is completely disconnected and we can ignore it. We have to find all the currents and voltages in this circuit. To do this we will use Ohm's law ($V=IR$) three times, each time applying the rule to different sections of the circuit. Let's get started.
Step 1: The first step is to simplify the circuit. Since $R_3$ and $R_4$ are in parallel, we can replace them with their equivalent resistance: \[ R_{34} = \frac{R_3R_4}{R_3+R_4}. \] The equivalent circuit looks much simpler now, and in particular there is only one current: the current $I$ flowing around the loop.
Step 2: To calculate the value of the current, we divide the value of the voltage source $V$ by the total resistance of the circuit $R_{tot} = R_1 + R_{34}$: \[ I = \frac{V}{R_1+R_{34}} = \frac{V_{tot}}{R_{tot}}. \]
Step 3: Now that we know the current flowing in this loop we can compute the voltages dropped on $R_1$ and $R_{34}$ respectively. To calculate these voltages, we use $V=IR$ again: \[ V_1 = IR_1 = \frac{V}{R_1+R_{34}}R_1, \qquad V_{34} = IR_{34} = \frac{V}{R_1+R_{34}}R_{34}. \]
Step 4: It is time to de-simplify the circuit and replace the equivalent resistance $R_{34}$ with the real circuit which had $R_3$ and $R_4$ in parallel. In doing so, we introduce two new variables $I_3$ and $I_4$, the currents flowing in each branch of the circuit.
Step 4: In this last step we have to find the current $I_4$. This is easy to do since we know the value of the voltage $V_{34}$ across it leads. Indeed we can find both currents $I_3$ and $I_4$ by using the $V=IR$ formula again: \[ I_3 = \frac{V_{34}}{R_3}, \qquad I_4 = \frac{V_{34}}{R_4}. \] Note that the two resistors in parallel have the same voltage across them.
We were able to carry out the entire calculation using variables. This is a good approach to follow, rather than solving with the numerical values of the resistors. Let's say that your teacher wants you to answer the problem for a particular set of parameters: the voltage source has $V=7[V]$ and $R_1=3[\Omega]$, $R_2=356[\Omega]$, $R_3=8[\Omega]$ and $R_4=8[\Omega]$. In that case we would have: \[ R_{34} = 8\|8 = \!\!\frac{8\times 8}{8\ + \ 8} = 4[\Omega],\ \ I = \frac{7}{3+4}=1[A], \ \ V_{34} = IR_{34} = 4[V], \ \ I_4 = \frac{V_{34}}{R_4} = \frac{4}{8} = 0.5[A]. \]
Bonus Step: Since we have all the voltages and currents calculated, let's calculate the power $P=IV$ consumed by the different elements of the circuit.
We first calculate the power consumed by the battery. We have to put a negative current into the equation for power, since the current $I$ is leaving the (+) terminal: \[ P_{\text{batt}} = IV = (-1[A])(7[V])=-7[W]. \] We say that the battery generates 7[W], since negative power consumed, means that this device is actually inputting power into the circuit rather than consuming it.
For the resistors we can use any one of these expressions: $P=IV=IR^2=V^2/R$. \[ P_1 = I^2R_1 = 3[W], \ P_2 = 0, \ P_3 = I_3V_{34} = 0.5[A]4[V]=2[W], \ P_4 = I_4V_{34} = 2[W]. \] Note that we have overall conservation of power in the circuit. The battery produces 7[W] and the resistors consume a total of 7[W].
Electric measurement tools
How do we measure all these things that we have been plugging into equations? Currents, voltages, resistances: how do we see them?
Voltmeter
________
| |
| [ V] |
| |
| + - |
|_|____|_|
| |
\== \_==
The voltmeter measures the voltage difference between two points in the circuit. The voltage measured tell us how much electric potential energy the electrons gain (or lose) by going from the point attached to + to the point attached to -.
Observations:
- If you connect the two leads + and - together, then you will measure 0 [V].
There is no potential difference, since you are at the same point.
- Say you have an AA battery. If you connect a voltmeter (+) to the battery (+) and the voltmeter (-) to the battery (-), the voltmeter will report 1.5V. This means that an electric charge gains 1.5V of potential energy when it goes from one terminal to the other.
- If you connect the voltmeter (+) to the battery (-) and vice versa, then it will read -1.5V.
- If you connect 10 AA batteries head to tail, then the voltage between the (+) of the first one and the (-) of the last the voltmeter will measure 15[V].
How does a voltmeter work? It diverts a tiny quantity of electrons from the main circuit and measures the change in their energy as they pass from the (+) side to the (-) side.
Amperemeter
|
_|______
| + |
| |
| [ A] |
| |
| - |
|______|_|
|
\____
To measure the current in some wire, you need to open the circuit and connect an ampermeter in series. Thus, the current you are trying to measure will have to pass through the ampermeter and you will be able to measure how big that current is.
Ohmmeter
If you want to measure the resistance, then you use an Ohm-meter.
________
| |
| [ Ω] |
| |
| |
|_|____|_|
| |
\ \___
\___
If you put the two leads across a resistor, this device will compute the equivalent resistance $R_{eq}$ for that device. It does this by passing a small current through, and measuring the resulting voltage. The Ohmmetter is essentially the combination of a voltmeter and an ampermeter and it reports the ratio $R_{eq} = V_{\text{resulting}}I_{\text{pushed}}$.
If you want to measure the resistance of a resistor, you have to disconnect it from the rest of the circuit. If you don't do that, the Ohmmeter will report the effective resistance of the whole circuit.
Discussion
We have seen how to solve simple circuits involving resistors. In the next chapter, we will learn how to deal with more complicated arrangements of resistors and in the chapters after that we can learn about the properties of new circuit elements like capacitors or inductors.
Links
More circuits
More complicated circuits cannot be solved by simple finding the equivalent resistance and simplyfing in each step. In general, we have to use the Kirchoff's loop law (the sum of thr voltages gained or lost around any loop in the circuit must add up to zero) and the Kirchoff junction law (the sum of the currents entering a junction is equal to the sum of the currents leaving the junction). The general procedure is to label all the unknown voltages and currents and then simultaneously solve the equations to find the unknowns.
Concepts
$I$: the electric current. It flows through all circuit components. We measure current in Amperes $[A]$.
We use wires to guide the flow of currents: to make them go where we want.
* {{ :electricity:circuit-element-voltage.png|}}
$V$: the electric potential difference between two points. We say //voltage// for short instead of "electric potential difference". There is no notion of "absolute" voltage, we only measure potential difference between //two// points. Thus if you should always label a (+) side and a (-) side when reporting a voltage. Conveniently, the unit of Voltage is the Volt [V], after Volta.
* $P$: power consumed or produced by some component. Measured in Watts [W].
* $R$: For resistors, the voltage across the leads is linearly related to current flowing in the resistor. We call //resistance// the ratio between the voltage and the current:
\[
R=\frac{V}{I}.
\]
We measure resistance in Ohms [$\Omega$].
Circuit components
Recall the basic building blocks for circuits are:
- wires
- batteris
- current sources
- resistors = light bulbs
- switches
General principles
Ohm's law
Electric power
The power consumed by an electric component is given by \[ P = V I, \] where $I$ is the current going into the (+) terminal of the device.
Kirchhoff's loop law
Kirchhoff's law says that the sum of the voltage gains and drops along any loop must add up to zero: \[ \sum_{\text{loop}} V_i = 0. \]
Kirchhoff current law
This is implied by conservation of charge: charge can't be created or destroyed so the sum of the currents coming into a junction, must equal the sum of the currents leaving the junction: \[ \sum I_{\text{in}} = \sum I_{\text{out}}. \]
Capacitors
Capacitors are used to store electric energy. We can also call them condensers, since they condense a lot of charge in one place. We saw already that the capacity of an object to store electric charge is proportional to the surface area the object. To store a lot of charge, therefore, you need large objects, but it is impractical to carry around huge metallic spheres.
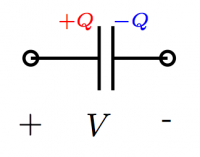 A more successful way to store charge is the parallel
plate capacitor which has two plates: one side will
store positive charge and the other negative charge.
We can imagine that some a voltage source of $V$[V] is
used to charge the capacitor by stripping electrons
from the (+) side and moving them over to the (-) side.
When the capacitor is disconnected, it will then store
the charge $+Q$ and $-Q$ on its plates.
The capacitance, $C$[F], is a property of the capacitor
which tells us how much charge it will store for a
given voltage $V$ applied to it: $Q=CV$.
A more successful way to store charge is the parallel
plate capacitor which has two plates: one side will
store positive charge and the other negative charge.
We can imagine that some a voltage source of $V$[V] is
used to charge the capacitor by stripping electrons
from the (+) side and moving them over to the (-) side.
When the capacitor is disconnected, it will then store
the charge $+Q$ and $-Q$ on its plates.
The capacitance, $C$[F], is a property of the capacitor
which tells us how much charge it will store for a
given voltage $V$ applied to it: $Q=CV$.
Inside every camera there is a simple electronic circuit that uses a capacitor in order to provide a sudden burst of electricity to the light bulb. When you turn on the flash, the circuit starts by connecting the capacitor to the battery in order to charge the capacitor. If your camera uses two AA batteries, then the charging voltage will be 3[V]. During this time, a blinking yellow light will indicate to you that you should wait. The camera is saying “Wait a minute please while I pump some charge into the capacitor”. When the charging is done and you take the picture, all the electric energy stored in the capacitor will be released in one burst (a current spike) into the flash lightbulb thus resulting in moment of super high light intensity unlike one that would be possible if you simply connected the light bulb to the batteries.
Concepts
- $Q$: The amount of charge on the capacitor. The (+) plate will have charge $+Q$[C],
while the (-) plate will have $-Q$[C].
- $V$: The voltage access the capacitor.
- C: the capacitance of the capacitor.
For a parallel plate capacitor, the capacitance $C$ is a function of the following physical properties of the capacitor:
- $A$: the area of the plates.
- $d$: the distance between the plates.
- $\varepsilon=\varepsilon_r\varepsilon_0$: The permittivity of the material between the plates,
where $\varepsilon_0$ is the permittivity of free space and $\varepsilon_r$ is the relative permittivity
of the material.
We will also study the electric potential ($V$) and the electric field $\vec{E}$ at different points in the capacitor:
- $x$: a variable that indicates the distance from the (+) plate inside the capacitor. $x\in[0,d]$.
- $V(x)$: the voltage (electric potential) in the capacitor at position $x$.
- $\vec{E}(x)$: the electric field at position $x$ inside the capacitor.
To study the process of charging and discharging, we must describe the state of the capacitor as a function of time:
- $q(t)$: the charge on the (+) plate as a function of time.
- $v_c(t)$: the voltage between the plates of the capacitor as a function of time.
- $i_c(t)$: the current entering the (+) side of the capacitor.
Formulas
Definition of capacitance
The charge stored on a capacitor of capacitance $C$[F] when charged to a voltage $V$[V] is given by: \[ Q = CV. \] The units of capacitance are Farads [F]=[C/V].
Physics properties
Consider a capacitor of area $A$, plate separation $d$ and material of dielectric constant $\varepsilon$ inserted between the plates. The capacitance of such a device is \[ C = \frac{\epsilon A}{d}. \qquad [\textrm{F}] \]
Voltage-current relationship
Because charge cannot simply be created from thin air, any amount of charge that appears on the (+) plate must have come into the capacitor as an electric current of charge. We define the current entering the capacitor $i_c(t)$ as the derivative of the charge on in the capacitor: \[ i_c(t) \equiv \frac{dq(t)}{dt}. \qquad [\textrm{A}] = [\textrm{C}/\textrm{s}] \] The bigger the current flowing into the (+) side of the capacitor, the faster the charge will build up. By using the definition of capacitance $Q=CV$, we also get the following relation \[ i_c(t) = C \frac{dv_c(t)}{dt}, \] which relates $i_c(t)$ and $v_c(t)$ the two quantities which we usually measure in circuits.
Another way of looking at the above differential relation is to say that the charge on the plate, $q(t)$, is equal to the initial charge $q(0)$ plus the sum (integral) of all the current that has gone into the capacitor: \[ q(t) = q(0) \ + \ \int_0^t i_c(\tau) d\tau. \] We can use the relation $Q=CV$ rewritten as $V=\frac{1}{C}Q$ to obtain the equation: \[ v_c(t) = v_c(0) \ + \ \frac{1}{C}\int_0^t i_c(\tau) d\tau. \]
Recall from calculus that a necessary condition for a function to have a well defined derivative is for the function to be continuous. The fact that we have $i_c(t) = C \frac{dv_c(t)}{dt}$ means that the capacitor voltage $v_c(t)$ must be continuous: it cannot suddenly jump in value or else this would correspond to infinite amount of current, which is impossible. Because of this voltage-smoothing property of capacitors, they are used in electronics and sound equipment in order to filter out voltage spikes.
Energy stored in a capacitor
The energy stored in a capacitor is given by \[ E = \frac{1}{2} Q V = \frac{1}{2} \frac{Q^2}{C} = \frac{1}{2} CV^2. \qquad [\textrm{J}] \]
Equivalent capacitors
We will now study what happens if we connect multiple capacitors together. We will see two formulas for finding the equivalent capacitance of the capacitors taken together as a whole.
Capacitors in parallel
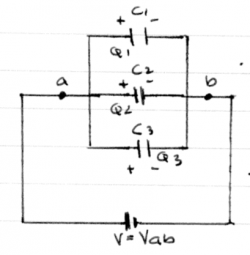 If you take several capacitors and connect them to the
same voltage source we get the parallel configuration.
In this setup, all the capacitors will have the same voltage
across their plates:
\[
V_1 = V_2 = V_3 = V_{ab}.
\]
Effectively, you have build a
capacitor that has a combined surface area of the
three capacitors.
It should not be a surprise that the formula for
the equivalent capacitance of the three capacitors
taken together is
\[
C_{eq} = C_1 + C_2 + C_3.
\]
If you take several capacitors and connect them to the
same voltage source we get the parallel configuration.
In this setup, all the capacitors will have the same voltage
across their plates:
\[
V_1 = V_2 = V_3 = V_{ab}.
\]
Effectively, you have build a
capacitor that has a combined surface area of the
three capacitors.
It should not be a surprise that the formula for
the equivalent capacitance of the three capacitors
taken together is
\[
C_{eq} = C_1 + C_2 + C_3.
\]
Furthermore, because we know the voltage on each of the capacitors is $V_{ab}$ we can use $Q=CV$ to find the charge on each of the capacitors: \[ Q_1 = C_1 V_{ab}, \qquad Q_2 = C_2 V_{ab}, \qquad Q_3 = C_3 V_{ab}. \]
Capacitors in series
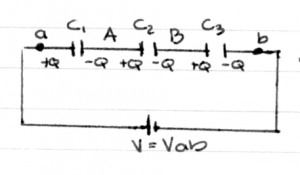 Consider now three capacitors connected one after the other.
We say that the capacitors are connected in series.
Consider the region labelled (A), which consists
of the (-) plate of $C_1$ and the (+) plate of $C_2$.
Because the region (A) started off initially uncharged,
it must be so after the battery is connected. Whatever
negative charge exists on the (-) plate of $C_1$,
therefore, must have comes from the (+) plate of $C_2$.
The same is true for the region (B).
This means that the charge on all the capacitors must
be the same:
\[
Q_1 = Q_2 = Q_3 = Q.
\]
Consider now three capacitors connected one after the other.
We say that the capacitors are connected in series.
Consider the region labelled (A), which consists
of the (-) plate of $C_1$ and the (+) plate of $C_2$.
Because the region (A) started off initially uncharged,
it must be so after the battery is connected. Whatever
negative charge exists on the (-) plate of $C_1$,
therefore, must have comes from the (+) plate of $C_2$.
The same is true for the region (B).
This means that the charge on all the capacitors must
be the same:
\[
Q_1 = Q_2 = Q_3 = Q.
\]
Since the capacitors are connected in series, the battery voltage $V_{ab}$ must be shared between all the capacitors. By Kirchhoff's voltage rule we have that: \[ V_{ab} = V_1 + V_2 + V_3. \]
We can now use the relationship $V=Q/C$ to obtain: \[ V_{ab} = \frac{Q}{C_1} +\frac{Q}{C_2} + \frac{Q}{C_3}. \] The effective capacitance $C_{eq} = \frac{Q}{V_{ab}}$ can therefore be calculated as follows: \[ C_{eq} = \frac{Q}{V_{ab}} = \frac{Q}{ \frac{Q}{C_1} +\frac{Q}{C_2} + \frac{Q}{C_3} } = \left( \frac{1}{C_1} +\frac{1}{C_2} + \frac{1}{C_3} \right)^{-1}. \] The last equation is called the harmonic sum, and also appears when calculating the equivalent resistance of resistors connected in parallel. The series and parallel addition formulas for capacitors and resistors are opposite.
Electric field inside a capacitor
Recall from the section on the electric_field that there is a relationship between the strength of the electric field $\vec{E}$ and the electric potential $V$. The voltage $V({r})$ at a point $r$ is defined as the integral per unit charge of the work you would have to do to bring a test charge to the point $r$. Because $\vec{E}({r})$ corresponds to the force per unit charge, we obtained the following relation: \[ V({R}) = - \int_{\infty}^R \vec{E}({r}) \cdot d\vec{s}, \] where $d\vec{s}$ describes the steps of the path which we took to bring the charge to the point $R$.
In this section we will use the differential version of the above relationship: \[ \vec{E}({r}) = - \; \frac{dV({r})}{ dr }, \] which states that the electric field is the gradient (derivative in space) of the electric potential.
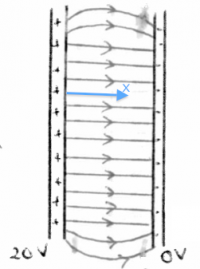 Consider the capacitor shown on the right,
which has a voltage of 20[V] between its (+) plate
and its (-) plate.
Using the (-) plate as a potential reference,
we can say that the voltage at (-) is 0[V],
and that the voltage at (+) is 20[V].
Assuming the material between the plates is uniform,
the voltage between the plates must vary continuously
as we go from one plate to the other.
The electric potential inside the capacitor is
\[
V(x) = 20 - \frac{20}{d}x,
\]
where $d$ is the plate separation and $x$ is a coordinate
which measures the distance from the (+) plate.
Check that $V(x)$ gives the correct potential at $x=0$ and
$x=d$.
Consider the capacitor shown on the right,
which has a voltage of 20[V] between its (+) plate
and its (-) plate.
Using the (-) plate as a potential reference,
we can say that the voltage at (-) is 0[V],
and that the voltage at (+) is 20[V].
Assuming the material between the plates is uniform,
the voltage between the plates must vary continuously
as we go from one plate to the other.
The electric potential inside the capacitor is
\[
V(x) = 20 - \frac{20}{d}x,
\]
where $d$ is the plate separation and $x$ is a coordinate
which measures the distance from the (+) plate.
Check that $V(x)$ gives the correct potential at $x=0$ and
$x=d$.
The strength of the electric field inside the capacitor is therefore given by the derivative of the voltage with respect to $x$: \[ \vec{E}(x) = - \frac{d}{dx} V(x) = \frac{20}{d}. \qquad [\textrm{V}/\textrm{m}] \]
We generally report the units of electric field as $[\textrm{V}/\textrm{m}]$ instead of the equivalent $[\textrm{N}/\textrm{C}]$. This is an indicator of the fact that relationship $\vec{E}(x) = - \frac{d}{dx} V(x)$ is used more often than the relationship between $\vec{F}_e = q\vec{E}$ in practice.
Charging and discharging
The currents and voltages associated with the process of charging and discharging a capacitor can be described mathematically. In this section we will find the equation for the current $i_c(t)$ as a function of time by using principles from circuits and solving a simple differential equation.
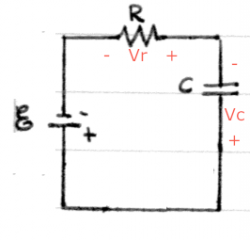 Consider a circuit which connects a battery, a capacitor and a resistor.
This is called an RC circuit.
The voltages across each of the elements have been indicated.
By Kirchhoff's voltage law (KVL) the voltage gains/drops
in this loop must add up to zero so we have:
\[
+ V_{\mathcal{E}} - v_c - v_r = 0.
\]
Consider a circuit which connects a battery, a capacitor and a resistor.
This is called an RC circuit.
The voltages across each of the elements have been indicated.
By Kirchhoff's voltage law (KVL) the voltage gains/drops
in this loop must add up to zero so we have:
\[
+ V_{\mathcal{E}} - v_c - v_r = 0.
\]
We now rewrite this equation in terms of the current $i(t)$ that will flow around the loop. We know that the voltage of a resistor is $v_r(t) = Ri(t)$ and we also know that $v_c(t)=\frac{1}{C}\int i(t) dt$, so the equation becomes: \[ + V_{\mathcal{E}} - \frac{1}{C}\int i(t) dt - Ri(t) = 0. \]
Now we take the derivative of this equation to obtain \[ + 0 - \frac{1}{C}i(t) - Ri'(t) = 0, \] where the first terms is zero because $V_{\mathcal{E}}$ is constant and the second term follows from the fundamental theorem of calculus (the derivative is the inverse operation of the integral).
We still haven't found $i(t)$ but we know that it must obey the following differential equation: \[ i'(t) = -\frac{1}{RC}i(t). \]
Can you think of any function $f(x)$ which is equal to the negative of its derivative up to a constant? The only function which has this property is of the form $f(x) = \alpha e ^{-\beta x}$, where $\beta > 0$ and $\alpha$ is an arbitrary constant.
By choosing the constant in the exponent appropriately, namely $\beta = \frac{1}{RC}$, we obtain the formula for the current in the circuit as a function of time \[ i(t) = \alpha e^{-\frac{t}{RC}}. \] Check that this function satisfies the differential equation $i'(t) = -\frac{1}{RC}i(t)$.
Now that we have the current $i(t)$ in the circuit, we can calculate the voltage of the capacitor by integration: \[ v_c(t) = \int i(t) dt = \beta e^{-\frac{t}{RC}} + \gamma, \] where $\beta=-\alpha RC$ and $\gamma$ is an arbitrary constant of integration.
We now discuss how to set the constants $\beta$ and $\gamma$ in the above equation so that it will describe the charging and discharging voltage of a capacitor.
Charging capacitor
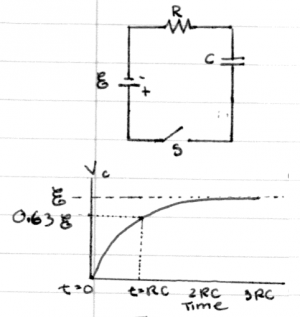 Consider capacitor of capacitance $C$ being charged
by a battery of $V_{\mathcal{E}}$ volts through a resistance
of $R$ ohms as illustrated in the circuit on the right.
We want to find the equation of
the voltage of the capacitor as a function of time.
Consider capacitor of capacitance $C$ being charged
by a battery of $V_{\mathcal{E}}$ volts through a resistance
of $R$ ohms as illustrated in the circuit on the right.
We want to find the equation of
the voltage of the capacitor as a function of time.
We know that the general formula for the voltage in an RC circuit is given by \[ v_c(t) = \beta e^{-\frac{t}{RC}} + \gamma, \] so we have to just choose the constants $\beta$ and $\gamma$ appropriately by taking into account the boundary conditions. The first boundary condition is at $t=\infty$, when the capacitor will have fully charged to the voltage of the battery $V_{\mathcal{E}}$. Using this fact we can deduce that $\gamma=V_{\mathcal{E}}$ from the equation \[ v_c(\infty) = V_{\mathcal{E}} = \beta e^{-\frac{\infty}{RC}} + \gamma =\beta \times 0 + \gamma = \gamma. \]
The second boundary condition (we need two since there are two unknown constants) is that the capacitor starts completely discharged. Thus, when we close the switch at $t=0$, the initial voltage on the capacitor is $v_c(0)=0$. We can now use the equation \[ v_c(0) = 0 = \beta e^{-\frac{0}{RC}} + \gamma = \beta \times 1 + \gamma = \beta + \gamma \] and our previous findings that $\gamma=V_{\mathcal{E}}$ to deduce that $\beta=-V_{\mathcal{E}}$.
The function describing the voltage of a charging capacitor as function of time is therefore given by: \[ v_c(t) = V_{\mathcal{E}} - V_{\mathcal{E}} e^{-\frac{t}{RC}} =V_{\mathcal{E}} \left[ 1 - e^{-\frac{t}{RC}} \right]. \]
Recalling that $i_c(t) \equiv C\frac{dv_c(t)}{dt}$ we can also derive the current of the capacitor \[ i_c(t) = C\frac{d}{dt}\left[ V_{\mathcal{E}} - V_{\mathcal{E}} e^{-\frac{t}{RC}} \right] = \frac{V_{\mathcal{E}}}{R} e^{-\frac{t}{RC}}. \] The constant $\frac{V_{\mathcal{E}}}{R}=i_c(0)$, which we previously called $\alpha$, corresponds to the maximum charging current that will flow in the circuit.
Discharging capacitor
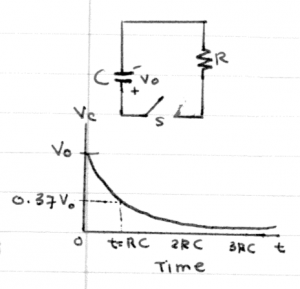 Consider now a capacitor charged to voltage $V_o$ which
discharges into a resistor of resistance $R$ starting at $t=0$,
when the switch is closed.
Consider now a capacitor charged to voltage $V_o$ which
discharges into a resistor of resistance $R$ starting at $t=0$,
when the switch is closed.
We start off from the general equation again \[ v_c(t) = \beta e^{-\frac{t}{RC}} + \gamma. \] The boundary conditions in this case are that the initial voltage $v_c(0)=V_o$ and the final voltage $v_c(\infty)=0$, which corresponds to the time when the capacitor has discharged completely. By plugging in the boundary conditions into the general equation we find that $\beta=V_o$ and $\gamma=0$. The equation for the voltage of a discharging capacitor is: \[ v_c(t) = V_o e^{-\frac{t}{RC}}. \]
We can also find the value of the capacitor current: \[ i_c(t) = C \frac{d}{dt} v_c(t) = -\frac{V_o}{R} e^{-\frac{t}{RC}}. \] The maximum discharge current is given by $-\frac{V_o}{R}=i_c(0)$. The negative sign indicates that the current is leaving the (+) plate of the capacitor.
In both of the above scenarios, the parameter $\tau=RC = \frac{1}{\beta}$ describes the time scale for the capacitor to charge or discharge. We call this quantity the time constant and measure it in seconds [s]. When charging, the time constant tells us how long it takes the capacitor to charge to $63\%=0.63=1-e^{-1}$ times its maximum voltage $V_{\mathcal{E}}$. When discharging, the time constant $\tau$ tells us how long it will take for the capacitor to reach $37\%=0.37=e^{-1}$ of its initial voltage $V_o$.
Explanations
Voltage continuity
The relationship between the current $i_c(t)$ and the voltage $v_c(t)$ is the defining features of a capacitors. More generally, we say that any circuit element is capacitive if the current of the device is proportional to the derivative of the voltage.
Capacitor energy derivation
We can equate the energy stored in a capacitor with the total energy consumed by the capacitor as while it charges up.
Consider some small amount of charge $dq$ which we want to add to the capacitor. The energy associated with moving this charge is given by $dE = dq v_c(t)$. This comes from the definition of power $\frac{dE}{dt} \equiv P(t) =i_c(t)v_c(t)$ and identifying the movement of charge $dq$ as the amount of current $i_c(t)=\frac{dq}{dt}$.
The total energy stored in the capacitor is calculated by taking the integral over the variable $q$. We sum up the individual contributions $dE$ for each of the $dq$s as the capacitor goes from $q=0$ to $q=Q$. \[ E = \int_{q=0}^{q=Q} v_c(q) \ dq = \int_{q=0}^{q=Q} \frac{q}{C} \ dq = \frac{1}{C} \frac{q^2}{2} \bigg|_{q=0}^{q=Q} = \frac{1}{2} \frac{Q^2}{C}. \] The other forms of the energy equation are obtained by using $Q=CV$.
Exercises
1. Capacitor charge
You are given a 5 [mF] capacitor and asked to produce a charging circuit which will charge the capacitors to 97% of the maximum voltage in 3[s]. What value should you use for the resistor?
2. Diff that for me will you?
Using a voltmeters, you observe that the voltage across a capacitor of capacitance $7$[$\mu$F] varies as the function $v_c(t) = 7\sin(120\pi t)$ [V]. What is the equation of current $i_c(t)$?
Magnetic field
If you were to put two current-carrying wires close to each other you will see that there will be a force between the wires. If the current is going in the same direction for both wires, then they will attract (buckle inwards), whereas if the currents are in opposite directions, the the wires will be pushed apart (tend to spread apart). This is the magnetic force. The powerful magnetic force is also what makes motors, generators and electromagnets work.
Recall that the electric force will exists between any two charged particles. Recall also how we invented the notion of an electric field $\vec{E}$ as an intermediary phenomenon. The story we told ourselves to explain the emergence of the electric force was as follows. One of the charges, say charge $Q$, creates an electric field $\vec{E}$ in space everywhere around it. The other charge (say $q$), will feel an electric force $F_e = q\vec{E}$ because of the electric field.
In this section we will follow a similar reasoning using a new intermediary concept. To explain the magnetic force between two current carrying wires, we will say that the current in the first wire is causing a magnetic field $\vec{B}$ everywhere in space and that the second current-carrying wire feels a magnetic force because of the magnetic field it is placed in.
A good way to learn about the properties of the magnetic field is to describe what are its causes and what are its effects. This is the approach we take below.
Concepts
General concepts:
- $I$: Electric current flowing in a wire or a loop.
- $\vec{B}$: Magnetic field strength and direction.
- $r$: Distance between two wires.
- $\vec{F}_b$: Magnetic force acting on another wire.
- $\mu_0$: the magnetic constant, or permeability of free space. It is equal to
$4\pi\times10^{-7}$ [Vs/Am] = $1.2566\times10^{-6}$ [H/m]=[N/A^2]
For solenoids we will have:
- $N$: Number of loops in a windings. Each turn of wire in the winding produces and
reacts to the magnetic field. A winding with $N$ turns produces a magnetic
field that is $N$ times stronger than a single loop of wire. * $L$: The length of a winding. * $n \equiv N/L$: Is the winding density, how many turns per meter.
Currents
Each moving charges causes a magnetic field around it. However, the magnetic field created by a single moving charge is very small, so we will usually discuss magnetic fields created by currents.
Current is measured in Amperes [A], which is a equal to Coulombs per second [C/s]. Consider the following piece of wire with a current $3$[A] in it:
a b
--------------
I= 3 [A]
The above diagram makes no sense, since it does not specify the direction in whist the current is flowing. Let's fix it:
a b
------>-------
I=3 [A]
That is better. When we say $I=3$[A], this means that there are 3[C] of charge flowing through this wire every second. The current enters the wire at $a$, and is confined to flow along the wire and thus it has to leave at point $b$.
If we say that the current is negative, this means that the current is flowing in the opposite direction of which the arrow points.
a b a b
------>------- = ------<-------
I=-1 [A] I=1 [A]
In the above diagram the current flows from $b$ to $a$, which is equivalent to saying that a negative current flows from $a$ to $b$.
Currents cause magnetic fields
The magnetic field $\vec{B}$ caused at some point $\vec{r}$ by a piece of wire of length $\ell$ carrying a current $I$ is given by \[ \vec{B} = \frac{k_b\ell I}{r^2} \hat{ I} \times \hat{r} = \frac{\mu_0}{4\pi}\frac{\ell I}{r^2} \hat{I} \times \hat{r}. \]
Don't freak out on me now. I know it looks complicated and there a arrows (vectors), cross products ($\times$), but you shouldn't worry. We will brake it down until it makes sense.
First the magnitude part: \[ |\vec{B}| = \frac{k_b \ell I}{r^2}, \] which doesn't seem quite so foreign no? I mean the electric field was the same story $|\vec{E}| = \frac{k_e Q}{r^2}$, where you have some cause $Q$ and the one-over-r-squared weakening plus some constant of proportionality $k_e=\frac{1}{4\pi \epsilon_0}$. The important thing to remember is that the cause of magnetic field is $\ell I$ the product of the current in the wire times the length of the piece of wire. The longer the wire is, the more magnetic field it will cause. This is the reason that people make “magnetic windings” with hundreds of turns instead of using a single loop.
As for the direction, yes we need to think about that for a moment:
- The direction of the magnetic field ${\hat B} = {\hat I} \times {\hat r}$
is perpendicular to both ${\hat I}$ and ${\hat r}$.
- If ${\hat I}$ and ${\hat r}$ point in the same direction then ${\hat B}=0$.
In general you will want to calculate not the magnetic field of a small piece, but of something more complicated. In this book (and in most E&M books), we will discuss three special cases of the magnetic field produced by:
- $\infty$-long straight wire.
- Loop of radius $R$.
- Solenoid of length $L$ with a total of $N$ windings.
Each of these configurations corresponds to a calculation involving an integral. When you see integral think “adding up the pieces” or “adding up the contributions”. We need an integral to calculate the total $\vec{B}$ field because different parts of the wire may contribute to the magnetic field unevenly. specific integral happens to be a vector integral. You don't need to understand the whole machinery of vector integration just yet, but you do need to know how to use the three formulas given below. If you are interested to see how we derived the formulas, you can check out the Derivations section below.
1. Magnetic field of a long wire
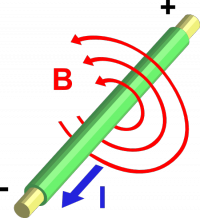 If you have take an infinitely long piece of wire and pass a current $I$ through it,
you will be creating a magnetic field $\vec{B}$ everywhere around the wire.
The magnetic field lines will be circulating around the wire.
This is how the magnetic field works.
If you have take an infinitely long piece of wire and pass a current $I$ through it,
you will be creating a magnetic field $\vec{B}$ everywhere around the wire.
The magnetic field lines will be circulating around the wire.
This is how the magnetic field works.
It is important to get the right direction for the circulation. If you grab a piece of wire with your right hand in such a way that your thumb points in the direction of the current, then the magnetic field lines are circulating around the wire in the same direction as your fingers.
The further away you move from the wire the weaker the magnetic field $\vec{B}$ will get. If a point is $r$ meters away from the wire, the magnitude of the magnetic field at that point will be given by: \[ |\vec{B}| = \mu_0 \frac{I}{2\pi r} \]
This formula was discovered by André-Marie Ampère in 1826.
2. Magnetic field of a winding
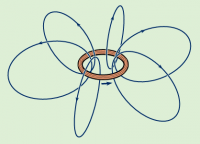 If you have a loop of wire that is carrying a current, then the strength of the magnetic field
in the centre is going to be:
\[
|\vec{B}_{centre}| = 2\pi R \frac{\mu_0}{4\pi} \frac{I}{R^2} = \frac{\mu_0I}{2R}.
\]
If you have a loop of wire that is carrying a current, then the strength of the magnetic field
in the centre is going to be:
\[
|\vec{B}_{centre}| = 2\pi R \frac{\mu_0}{4\pi} \frac{I}{R^2} = \frac{\mu_0I}{2R}.
\]
To get the direction of the magnetic field, you need use the right-hand rule again: grab the loop with your thumb pointed in the same direction of the current and then see which way your fingers point inside the loop.
3. Magnetic field of a solenoid
To create a stronger magnetic field, you can make loop the wire many times to create a winding. Each of the turns in the winding is going to contribute to the magnetic field inside and this way you can get some very strong magnetic fields.
Consider a winding that has $N$ turns and length $L$[m]. We call such a device a solenoid. The magnetic field $\vec{B}$ inside a solenoid is: \[ |\vec{B}| = \mu_0 n I, \] where $n$ is the winding density = number of windings per unit length $n=N/L$ [turns/m].
Effects of magnetic field
Force on a moving charge
A charge which is not moving feels no magnetic forces. Only when the charge is moving will it feel a magnetic force, and the faster the charge is moving the stronger the magnetic force will be.
The magnetic force that a charge $q$, moving with velocity $\vec{v}_q$ will field when it is passing through a magnetic field $\vec{B}$ is given by the formula: \[ \vec{F}_b = q (\vec{v}_q \times \vec{B}). \] Observe that the formula involves a cross product. This means that the force on the particle will be perpendicular to both the direction in which it is moving and the direction of the magnetic field. This is the second right-hand rule. Take your open right hand (don't curl your fingers) and place it so that your thumb points in the direction of the velocity and your fingers point in the direction of the magnetic field lines. The magnetic force will be in the direction of your palm.
It is interesting to point out that the magnetic force does zero work. This is because it always acts in a direction perpendicular to the displacement $\vec{d}$: \[ W_b = \vec{F}_b \cdot \vec{d} = 0. \] The magnetic force can change the direction in which the particle is travelling, but not make it go faster or slow it down. Indeed, a moving charged particle placed in a uniform magnetic field will turn around in a circle, because of the centripetal acceleration caused by the magnetic force.
More generally, we can write down the equation for the total electric + magnetic force that a charge feels. The combined force is called the Lorentz force, or electromagnetic force: \[ \vec{F}_{EM} = \underbrace{ q\vec{E} }_{\vec{F}_e} + \underbrace{ q (\vec{v}_q \times \vec{B}) }_{\vec{F}_b}. \]
Force on a current carrying conductor
Consider now a current $I$ flowing in a piece of wire of length $\ell$ placed in a magnetic field $\vec{B}$. The force on the piece of wire will be: \[ \vec{F}_b = \ell \vec{I} \times \vec{B}. \] Observe again that a cross product is used, so we need to use the second right-hand rule again to figure out the direction of the force.
Electromotive force
The two scenarios discussed above show how the magnetic field can produce a mechanical force on an object. Magnetic fields can also produce electromotive forces inside a given circuit, that is, the magnetic field can cause (we usually say induce to sound fancy) a voltage inside the circuit and made a current circulate. This phenomenon is called Faraday's law of induction and will be the subject of the next section.
Explanations
Some of you may feel cheated by this chapter. Here I am telling you to memorizing five formulas without telling you where they come from. Let's fix that.
Ampere's law
One of the most important laws for magnetism is Ampere's law. Like Gauss' law electromagnetism, it is not so much a law as a principle from which many laws can be derived.
The statement involves some area of space $A$ with a total current $I_{in}$ passing through that area. Let the closed path $\mathcal{C}$ correspond to the circumference of the area $A$ (the boundary). If you integrate the strength of the magnetic field along the path $\mathcal{C}$ (this is called the circulation), you will find that it is proportional to the total amount of current flowing inside the loop: \[ \oint_{\mathcal{C}} \vec{B} \cdot d\vec{s} = \mu_0 I_{in}. \] Like Gauss' law, Ampere's law simply tells us that we can do the accounting for magnetic phenomena in two different ways: either we calculate the circulation of the magnetic field along the boundary (the path $\mathcal{C}$) or we calculate the total current flowing inside.
The formula of for the strength of the $\vec{B}$ field around an infinitely long wire comes from Ampere's law. Let $\mathcal{C}$ be an imaginary circle of radius $r$ centred on the wire. The $\vec{B}$ field will be constant in magnitude and always pointing along the path of integration so we will get: \[ \oint_{\mathcal{C}} \vec{B} \cdot d\vec{s} = \int_{0}^{2\pi} |\vec{B}| \ r d\theta = |\vec{B}| 2\pi r = \mu_0 I_{in}. \] Solve for $|\vec{B}|$ to obtain the formula for the $\infty$-long wire.
The Biot–Savart law
More generally, to calculate the magnetic field produced by some arbitrarily shaped wire $\mathcal{L}$ that is carrying a current $I$ we use the following formula: \[ \vec{B}(\vec{r}) = \int_\mathcal{L}\frac{\mu_0}{4\pi} \frac{I}{|\vec{r}|^2} d\mathbf{l} \times {\hat r}, \] which tells you how strong the magnetic field $\vec{B}$ will be at a point $\vec{r}$. The cause of this field is the current $I$, that is flowing in the length of wire $\mathcal{L}$. The expression is an integral which tells us that we should split the entire length of the wire into little pieces of length $dl$ and add up all their magnetic contributions.
We need an integral because different parts of the wire may contribute to the magnetic field unevenly. This happens to be a vector integral, which you probably have not seen before, and I don't think you need to understand the whole machinery just yet. When you see integral think “adding up the pieces”.
Applications
Every time you have a moving charge, there will be a magnetic field $\vec{B}$. Here is a list of real-world phenomena that involve magnetic fields. In each case, when we analyze what is going on we see that some moving charge is causing the magnetic fields.
- light consists of little bundles of energy called photon.
A photon is a wave of EM energy produced by an excited
electron dropping to a lower energy level in some atom. * permanent magnets (like a fridge magnet) exhibit magnetic properties because of the many tiny loops of "electron flow" circling around Fe atoms. * The magnetic field of the earth is caused by the flow of charged magma in the earth's core.
And Mankind saw that magnetic field was good, and decided to make more of it. If moving charges create lots of magnetic field, then let's get lots of charge moving (a current $I$) and then we will have lots of magnetic field!
The following are some practical applications of the magnetic fields and the magnetic forces they produce:
- electromagnet = used to lift cars in the scrap yard, to lock the doors of buildings and to make particles spin around.
- magnetic field inside a motor = used to convert electric energy into mechanical work (think the motor of your elevator, or the one that drops the window down in your car).
- magnetic field inside a generator = used to convert mechanical work into electric energy (think you car's alternator).
- MRI = magnetic resonance imaging allows us to distinguish different molecules
in the human body by using carefully chosen oscillating magnetic fields.
Examples
Links
[ Nice pictures of magnetic fields ]
http://en.wikipedia.org/wiki/Magnetic_field
http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/magnetostatics/index.htm
[ An expandable summary of the magnetic field ]
http://www.telescopictext.org/text/pFjkqQY9bmfvQ
[ Good illustrations of the first right-hand rule ]
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html
Magnetic induction
In the previous section we learned about the magnetic field, how it is caused by current carrying wires and its effects on other current carrying wires. In this chapter we will learn how a changing magnetic fields can produce an electromotive force – how changing currents in one wire can induce a current in another wire.
Note that magnetic field has to be changing in order to produce induced voltages and an induced currents. A constant currents produces a constant magnetic field and a constant magnetic fields does not induce currents. This is a very important to keep in mind.
In this section we will study Faraday's law of induction. It states that any change in the total magnetic field flowing through some winding will cause an induced current to flow in the winding as a result. This is a special case of the more general Le Chatelier principle since the induced current will flow in such a direction as to produce a oppose magnetic field and counter act the external change.
Concepts
- $\mu_0$: the magnetic constant, or permeability of free space. It is equal to
$4\pi\times10^{-7}$ [Vs/Am] = $1.2566\times10^{-6}$ [H/m]=[N/A^2]
- $\vec{B}$: Magnetic field strength and direction.
- $\mathcal{E}\equiv V_{\mathcal{E}}$: Induced electric potential (induced voltage)
in the winding. It is also known as the electromotive force.
- $I_{\mathcal{E}}$: Induced electric current. The induced current in a winding of
resistance $R$[$\Omega$] will be $I_{\mathcal{E}}=\mathcal{E}/R$.
- $S$: some surface in space. ex: $S$=the area enclosed by a loop of wire.
- $\Phi_S$=The magnetic flux through $S$, i.e., how much magnetic
filed $B$ passes through the surface $S$. We have $\Phi_S = \vec{B} \cdot \vec{S}$,
where $\vec{S}$ is the oriented surface area.
* $N$: Number of loops in a winding. Each turn of wire in the winding produces and
reacts to the magnetic field. The induced voltage in a winding with $N$ turns
is $N$ times stronger than that induced in a single loop of wire.
Formulas
Magnetic flux
Consider the surface $S$ and let $\hat{n}$ be a vector that is perpendicular to the surface (the normal vector). The directed surface is given by $\vec{S}=S\hat{n}$.
The magnetic flux is given by: \[ \Phi_S = \vec{B} \cdot \vec{S} = |\vec{B}|S \cos \theta, \] where $\theta$ is the angle between the normal vector of the surface $S$ and the orientation of the magnetic field. The flux measures of how many magnetic field lines flow through the surface. If the magnetic field flows perpendicularly to the surface then $\theta=0$ and $\Phi_S = |\vec{B}|S$. On the other hand, if the magnetic field is parallel to the surface, then $\theta=90^\circ$ and there is zero magnetic flow through the surface.
Faraday's law of induction
Consider a loop of wire and let $S$ represent the area enclosed by this loop. Faraday's law states that any change in the magnetic flux through that loop will produce an induced voltage (an electromotive force) on all electrons in the wire. The magniture of this induced voltage is given by the formula: \[ \mathcal{E} = - \frac{d \Phi_S}{dt}. \] The negative sign is there to remind you that the induced voltage will always act in a opposite direction to the change in the flux.
Example: Changing B
Suppose you have a loop of wire with area $A=5$[m$^2$] in a place this loop in a location where an upward magnetic field exists, which is slowly increasing in time: \[ \vec{B}(t) = (0,0, 3t) = 3t \hat{k}. \] Every second the magnetic field will become stronger by $3$[T].
Faraday's law tells us that the changing magnetic field will induce a voltage (electromotive force) in the loop that is equal to \[ \mathcal{E} = - \frac{d \Phi_S}{dt} = - \frac{d}{dt} \left( \vec{B}(t)\cdot\vec{A} \right) = - \frac{d}{dt} \left( 3t \hat{k} \cdot A\hat{k} \right) = A \frac{d}{dt}\left( 3t \right) = 15 [V]. \] The effects of the induced voltage $\mathcal{E}$ in the loop is equivalent to connecting a $15$[V] battery somewhere in the loop.
If the electric resistance of the loop of wire is 10[$\Omega$], then the induced current will be 1.5[A]. This current will flow in the clockwise direction when looked from above. This is because the induced current is trying to counteract the increasing and upward pointing magnetic field by causing a downward magnetic field.
Observe that the value of the magnetic field was not important in this context: only the derivative of the field mattered. The answer would have been the same if we had $\vec{B}(t) = (3t + 3000)\hat{k}$, because the derivative of a constant is zero.
Generators
Consider now a constant magnetic field $\vec{B}$ and wire winding of area $A$[m$^2$] mounted on an axis so that it can rotate. Such a construction could serve as a rudimentary electric generators: a device which transforms rotational mechanical energy into electric energy.
The magnetic flux through the winding will be given by: \[ \Phi_S = N \vec{B} \cdot \vec{A} = NBA \cos(\theta), \] where $N$ is the number of turns in the winding and $\theta$ describes the orientation of the winding relative to the constant magnetic field.
If we use an external force to make the winding rotate at a constant speed $\omega$ then the magnetic flux as a function time will be: \[ \Phi_S(t) = NBA \cos(\omega t + \theta_0). \]
The induced voltage that we would be able to read if we were to put a voltmeter on the two ends of the turning winding would be: \[ \mathcal{E}(t) = - \frac{d \Phi_S(t) }{dt} = - \frac{d}{dt}\left( NBA \cos(\omega t + \theta_0) \right) = NBA\omega \sin(\omega t + \theta_0). \]
This is an alternating voltage, that keeps changing from positive to negative depending on the relative orientation of the loop in the magnetic field. This is how Hydro Quebec generates power. With big generators.
Electric motor
A generator can also be used backwards: the same device can also be used to convert electric energy into mechanical energy. Used in that direction, the rotating winding construction is called an electric motor.
A motor has two parts. The stator, which in our case is the constant background magnetic field $\vec{B}$ and a rotor, which is our rotating winding.
If we use electric energy to make a current flow in the winding, then the winding will produce its own magnetic field and the interaction between the two B-fields will cause the winding to turn.
Transformers
If you put two windings close to each other and put an make and alternating current flow in one of the windings, we will immediately see an induced alternating current in the second winding. This device is called a transformer. We will learn about these in more detail in the chapter on alternating currents.
Self inductance
Consider a solenoid of cross section area $A$ and winding density $n = N/L$ which has a current $i(t)$ flowing in the wire.
We learned in the last section that a current $i(t)$ flowing in the solenoid will produce a magnetic field inside the device and we know that the formula is given by: \[ |\vec{B}| = \mu_0 n i(t). \]
We learned in this section that any winding will react to a change in the magnetic flux through it by producing an induced voltage. Since a solenoid is a winding, so it will react to any changes in the magnetic field which would appear if the current were changing in time. The formula for the induced voltage is: \[ \mathcal{E} = - \frac{d \Phi_S(t) }{dt} = - \frac{d (AN|\vec{B}|) }{dt}, \] where we used the fact that the magnetic field everywhere inside an inductor is constant and that each of the $N$ windings contribute to the total induced voltage.
Combining these formulas we see that \[ \mathcal{E} \equiv v(t) = - \frac{d (AN|\vec{B}|) }{dt} = - \underbrace{AN\mu_0 n}_L \frac{d i(t)}{dt} = - L \frac{d i(t)}{dt}, \] where we have lumped together all the constants into a single one $L$.
This solenoid, and in general all windings, exhibit this phenomenon of self-inductance where the chaining current in the winding cause an induced voltage.
In circuits we call such devices inductors and they are in some sense the dual of the capacitor in which it was the changing voltage that caused a current. The constant $L$ is called the inductance or self-inductance of the device.
Examples
Example 1: Area changing
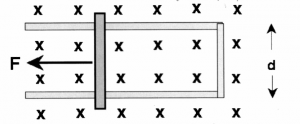 Consider the external force $\vec{F}$ that is dragging
the bar along with velocity $\vec{v}$. If the magnetic field
everywhere is given by $\vec{B}$ and points into the page.
Consider the external force $\vec{F}$ that is dragging
the bar along with velocity $\vec{v}$. If the magnetic field
everywhere is given by $\vec{B}$ and points into the page.
What is the change of flux $\frac{d \Phi_S(t) }{dt}$ ?
What is the induced voltage? Will the induced current flow in the clockwise or counter-clockwise direction when looked from above?
Example 2: Strength changing
If the magnet is moved away from the loop, what will be the induced current in the loop?
- none
- a
- b
explain
Discussion
Links
[ More on Faraday's law of from HyperPhysics ]
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/farlaw.html
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/fluxmg.html
[ Ilustrations of magnetic induction ]
http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/faraday/index.htm
physical element – self inductance derive
Inductors
\[ \int v(t) dt = Li(t), \qquad \Leftrightarrow \qquad \frac{d\Phi(t)}{dt} = v(t) = L \frac{di(t)}{dt} \]
Math review
AC currents are all about the sin function, its amplitude and its phase. This is a little question-based referesher course on the sin and cos funcitons. Q1. consider the funciton psi of x : ѱ(x) = sin(kx), where k is some constant (wavenumber) what is the wavelength of this wave? what is ѱ'(x) ? what is ѱ''(x) ? what is ѱ'''(x) ? see a pattern? bonus: what is the 1000 th derivative ѱ(x) ? Q2. sin(kx)+sin(kx + d) = 0 for what values of d is the above equation true? Q3. sin(kx)+sin(kx + c) = 2sin(kx) for what values of c is the above equation true? Q4. sin(x)+cos(x) = Asin(x+B) what are the values of A and B ? Q5. sin(x)+cos(x) = Ccos(x+D) what are the values of C and D ? Q6. sin(x+a) = Esin(x) + Fcos(x) What are the values of E and F (expressed in terms of a) ? Hint: the only thing you need to know to derive all of the above is the following three formulas: (1) sin^2 x + cos^2 x + 1 (2) sin(a+b) = sin(a)cos(b) + sin(b)cos(a) (3) cos(a+b) = cos(a)cos(b) - sin(a)sin(b) Eqns (2) and (3) come witha little mnemonic sin --> sico sico cos --> coco - sisi (the negative sign because it is not good to be a sissy) If you know (1), (2), (3) you kick ass !
Euler's formula
This is one of them crazy things in mathematics. Kind of thing make you want to change career and be a researcher.
If you input imaginary numbers (multiples of \sqrt{-1}) into the exponential function you get the cosine and the sine function: \[ \exp(ix) = \cos(x) + i\sin(x) \]
I mean I am sure you already had some doubts that sine and cosine were related, but the exponential function? Now that is mad!
Definitions
- $z\in \mathbb{C}$: A complex number
- $Re\{ z \}$: The real part of $z$.
- $Im\{ z \}$: The imaginary part of $z$.
- $\frac{d}{dx}$: Derivative with respect to $x$
What is this for?
Allows you to deal with derivatives simply in AC circuits.
Alternating current circuits
New kid on the block:
| + (~) | -
This is a source of alternating current. It may sound fancy, and soon you will see that it involves some trigonometric functions like sin and cos, but don't worry about that for now. Now I want you to tell me where you can see one of the above objects in your daily life?
I will give you a hint. It lives on walls. It often comes in pairs, and it has three holes.
 Yes. Your wall outlet. The mains. Hydro-Quebec, or whatever your
local electric company is called. They give you a two prong “voltage source”
that keeps changing. Sometimes the voltage on the + terminal is higher
than the - terminal and sometimes the polarity changes. If you were
to connect a voltmeter accross the two slots in the wall you would see
\[
v(t) = 150\sin\left( 120\pi t \right),
\]
where $\omega=2\pi f$ is the anglular frequency. I am assuming you
are in North America and the $f=60Hz$. The alternating current your
power company is sending you is changing polarity 60 times per second.
Yes. Your wall outlet. The mains. Hydro-Quebec, or whatever your
local electric company is called. They give you a two prong “voltage source”
that keeps changing. Sometimes the voltage on the + terminal is higher
than the - terminal and sometimes the polarity changes. If you were
to connect a voltmeter accross the two slots in the wall you would see
\[
v(t) = 150\sin\left( 120\pi t \right),
\]
where $\omega=2\pi f$ is the anglular frequency. I am assuming you
are in North America and the $f=60Hz$. The alternating current your
power company is sending you is changing polarity 60 times per second.
At first you might think, what's the point of having somethign oscillate like that? I mean, the average electricity user probably just wants to run his computer, or heat their house. What good is this wobbly electrycity that keeps alternating?
The reason while AC is better than DC, is that you can convert AC very easily using a transformer. If you have a 1.5V battery it is quite complicated to to make into a 300V battery, but if you have a 1.5V AC source you can turn it into a 300V AC source simply by using a transformer with 200 times more windings on the output side than the inputs side.
Concepts
- $i(t)$: Current as a function of time. Measured in Amperes $[A]$.
- $v(t)$: Voltate as a function of time. Measured in Volts [V].
- $R$: The resistance value of some resistor. Measured in Ohms [$\Omega$].
- $\omega=2\pi f$: Angular frequency = the coefficient in front ot $t$ inside $\sin$.
- $f$: Frequency of the AC current/voltages
- $p(t)$: power consumed/produced by some component. Measured in Watts [W].
I want to also give you some intuition about the units we normally see for circuit quantities. The voltage that is used for power transport over long distances is on the order of 50000$[V]$ – this is why they call them high-tension lines. The voltage amplitude of the wall outlets in North America is 150V, but the effective voltage as far as power is concerened is $\frac{1}{\sqrt{2}}$ of the maximum amplitude of the sine wave, which gives: \[ V_{rms}=110 \approx \frac{150}{\sqrt{2}}. \]
On a saftery note, note that it is not high voltage that kills, it is high current.
Circuit components
The basic building blocks of of circuits are called electic components.
The most basic are the following:
- Wire: Can carry any current and has no voltage drop accross it.
- Resistor: Can carry any current $I$, and has a voltage accross its terminals of $V=RI$ where $R$ is the resistance measured in Ohmns [$\Omega$]. The energy of the electrons (the voltage) right before netering the resistor is $IR$ [V] higher than when they leave the resistor. It is important to label the positive and negative terminals of the resistor. The positive temrinal is where the current enters, the negative where the current leaves.
- AC voltage source: Provides you with $v(t) = A\sin(2\pi f t)$ [V]
Then there are the energy storing ones:
- Capacitor:
\[ q(t) = \int i(t) dt = Cv(t), \qquad \Leftrightarrow \qquad \frac{dq(t)}{dt} = i(t) = C \frac{dv(t)}{dt} \]
- Inductors:
\[ \int v(t) dt = Li(t), \qquad \Leftrightarrow \qquad \frac{d\Phi(t)}{dt} = v(t) = L \frac{di(t)}{dt} \]
Formulas
Discussion
AC circuits
In North America the electric voltage of wall outlets looks like this: \[ v(t) = 150\cos\left( 120\pi t \right), \] where $\omega=2\pi f$ is the angular frequency.
Some smart people invented phasor notation because they found it annoying to always write down the cos part each time they had to solve calculate something in an AC circuit. In DC circuits, you could just write $150V$ next to a voltage source, but in AC circuits you need to write the whole function
In an AC circuit all quantities (voltages and currents) are oscillating at a frequency of 60Hz so we might as well skip the cos part! Instead of writing the whole expression for $v(t)$ we will write just: \[ \vec{V} = \vec{150}, \] where any quantity with an arrow is called a phasor. The oscillating part (cos term, possibly with some phase) is implicit in the phasor notation.
Concepts
First, let's introduce the main players. The objects of study.
- $i(t)$: Current the circuit as a function of time. Measured in Amperes $[A]$.
- $v(t)$: Voltage as a function of time. Measured in Volts [V].
- $v_{\mathcal{E}}(t)$: Voltage provided by some AC voltage source like the wall power outlet.
In North America and Japan $v_{\mathcal{E}}$ is 110 [V]rms.
The symbol $\mathcal{E}$ comes from the name //Electromotive force//.
This name has since decreased in usage. Do you see yourself asking your friend "Hey Jack, please plug in my laptop power supply into the electromotive force source"?
* $v_{R}(t)$: The voltage as a function of time across some //resistive load// $R$, like an electric heater.
Measured in Ohms [$\Omega$]s. The //current-voltage relationship// for a resistive element is
$v_{R}(t)=Ri(t)$, where $i(t)$ is the current flowing through the resistor.
* $P(t)=v(t)i(t)$: power consumed/produced by some component. Measured in Watts [W].
Every current and voltage in an AC circuit is oscillating. Current flows in one direction, then it stops, then it flows in the other direction, stops and turns around again, and does this 60 times per second. This is why we call it alternating.
- $f$: Frequency of the AC circuit. Measured in $[Hz]=[1/s]$.
- $\omega=2\pi f$: Angular frequency = the coefficient in front ot $t$ inside $\cos$.
We will use the phasor notation in order to deal with cos terms and sin terms in all our equations. The name phasor comes from the fact that this notation allows us to represent not only the magnitude but also the phase of the sinusoid. The examples below are shown correspond to a frequency of $f=60$ [Hz], which gives us an angular frequency of $\omega \equiv 2\pi f = 120 \pi$.
- $150 \equiv 150\angle 0$: The phasor notation for $150\cos\left( 120\pi t \right)$
- $150\angle 90$: The phasor notation for $150\sin\left( 120\pi t \right)=150\cos\left( 120\pi t -90 \right)$.
- $A\angle 0$: The phasor notation for $A\cos\left( 120\pi t - 0 \right)$
- $A\angle -90$: Is the negative sin function $-A\sin\left( 120\pi t \right)=A\cos\left( 120\pi t +90 \right)$
The following shorthands are very useful:
- $j \equiv 1\angle{90}$: The shorthand notation for $1\sin\left( \omega t \right)\equiv\cos\left( \omega t - 90 \right)$
- $-j\equiv 1\angle-90=-1\angle 90$: The shorthand notation for $-1\sin\left( \omega t \right)\equiv\cos\left( \omega t + 90 \right)\equiv-\cos\left( \omega t - 90 \right)$
- $150j\equiv 150\angle 90$: Equivalent to $150\sin\left( 120\pi t \right)=150\cos\left( 120\pi t -90 \right)$.
You can think of phasors as vector-like, and like vectors they have the component notation and the magnitude-direction notation.
- $\vec{A}$: Some phasor. Could be a voltage $\vec{V}$[V], a current$\vec{I}$[A], or the impedance $\vec{Z}$[$\Omega$] of an inductor, a capacitor or a resistor.
- $\vec{A}=(A_r,A_j)$: The phasor which corresponds to $A(t) = A_r+A_jj = A_r\cos(\omega t)+A_j\sin(\omega t)$.
- $A_r$: The resistive part of $\vec{A}$.
- $A_j$: The rective part of $\vec{A}$.
- $\vec{A}= A\angle \phi = |\vec{A}| \angle \phi_{A}$: The phasor $\vec{A}$ expressed in magnitude-direction notation.
- $|\vec{A}|=A$: The magnitude of the phasor $\vec{A}$. $|\vec{A}| = \sqrt{ A_r^2 + A_j^2}$. Sometimes we will simply refer to it as $A$, so that writing $\vec{A}=A \angle \phi_A$.
- $\phi_{A}=\tan^{-1}\left(A_j/A_r\right)$: The phase of $\vec{A}$
The circuit components which are commonly used in circuits are the following.
- $R$: Resistor. Measured in Ohms [$\Omega$]. We can think of resistance as a physical property of some device or as an operational interpretation: the voltage to current ratio of some device. Indeed, we have $R=V/I$.
- $\vec{Z}$: Impedance is a generalization of the concept of resistance that allows us to treat resistors, capacitors and inductors on the same footing.
The impedance of some device is defined as its voltage to current ratio
\[
\vec{Z}\equiv \frac{ \vec{V} }{ \vec{I} }.
\]
* $\vec{Z}=(Z_r,Z_j)=R+Xj$: Every impedance has a //resistive// part $R$ and a //reactive// part $X$. You can think of these as the two components of the vector $\vec{Z}$: $Z_r$ is the first component, $Z_j$ is the second component.
* $\vec{Z}=|\vec{Z}|\angle \theta=Z\angle \theta$: An can also impedance has a //resistive// part $R$ and a //reactive// part $X$. You can think of these as the two components of the vector $\vec{Z}$: $Z_r$ is the first component, $Z_j$ is the second component.
* $\vec{Z}_C=\frac{-j}{\omega C}$: The impedance of a capacito. $\vec{Z}_C=(0,X_C)=0-\frac{1}{\omega C}j$
* $\vec{Z}_{eq}$: The equivalent impedance of several circuit elements taken together. Similar to $R_{eq}$, but a little more complicated since we now have resistive and reactive parts. Adding p like vectors. more general n how difficult it is to get current through this device. Recall the The definition of impedance the type of resistance that a load circuit element to refits
impedance
For most purposes in AC circuits we will not talk about the amplitude of the voltage source but its power-average.
- $\vec{V}=150$: Amplitude phasor which corresponds to $v(t)=150\cos\left( 120\pi t \right)$
- $\vec{V}_{rms}=110$: Root-mean squared phasor which corresponds the voltage $v(t)=150\cos\left( 120\pi t \right)$
\[ V_{rms} \equiv \frac{V}{\sqrt{2}}. \]
sin and cos
They are brothers in arms. Every time sin is in the house, cos is there too.
I want to also give you some intuition about the units we normally see for circuit quantities.
Suppose the voltage source was actually source: Provides you with $v(t) = A\sin(2\pi f t)$ [V]
check for yourself if you don't trust me.
The derivative of $\sin(\omega t)$ is $\cos(\omega t)$ \[ \frac{d}{dt}\sin(\omega t) = \omega \cos(\omega t) \]
\[ \frac{d}{dt} \vec{j} = \omega 1 \]
Phasor arithmetic
adding
\[ (a + bj) + (c+dj) = (a+c) + (b+d)j \]
subtract
multiply \[ (aj)(bj) = ab(j^2) = -ab \]
divide \[ \frac{1}{j} = \frac{j}{j^2} = \frac{j}{-1} = -j \]
Types of impedance
Resistor
Resistor: Can carry any current $I$, and has a voltage accross its terminals of $V=RI$ where $R$ is the resistance measured in Ohmns [$\Omega$]. The energy of the electrons (the voltage) right before netering the resistor is $IR$ [V] higher than when they leave the resistor. It is important to label the positive and negative terminals of the resistor. The positive temrinal is where the current enters, the negative where the current leaves.
Then there are the energy storing ones:
Capacitor
Two plates
\[
\vec{Z}_C = 0 + X_Cj = \frac{-j}{\omega C}
\]
\[ q(t) = \int i(t) dt = Cv(t), \qquad \Leftrightarrow \qquad \frac{dq(t)}{dt} = i(t) = C \frac{dv(t)}{dt} \]
Inductor
The impedance of an inductor is
\[
\vec{Z}_L = 0 + X_Lj = j \omega L
\]
An inductor is given by the
\[
\int v(t) dt = Li(t), \qquad \Leftrightarrow \qquad \frac{d\Phi(t)}{dt} = v(t) = L \frac{di(t)}{dt}
\]
Formulas
There is only one really
\[ \vec{V} = \vec{Z} \vec{I}, \] where $Z$ is called the impedance.
It used to be $V=RI$, and actually it still is for resistors, but now we have also capacitors and inductors to deal with.
The way we defined $Z_C$ and $Z_L$ above, however, we can deal with them just as if they were resistors.
Impedances in series
\[ Z_{eq} = Z_1 + Z_2 \]
So for example if you have a resistor of 200[$\Omega$] in series with a capacitor of 60[$\mu F$] in an AC circuit at $f=60$[Hz], then the equivalent impedance will be:
\[ \vec{Z}_{eq} = Z_R + Z_C = Z_R + X_Cj = R + \frac{-1}{\omega C}j = 200 - 44.2j. \]
The magnitude of the impedance is: \[ Z = |\vec{Z}_{eq}| = \sqrt{200^2 + 44.2^2} = 204.83. \]
Thus, if I told you that the amplitude of the current is 1[A], and I asked you to find the maximum value of the voltage, then you could use:
\[ V_{max} = Z I_{max} \] and tell me that the amplitude of the voltage is 204.83[V].
Impedances in parallel
\[ Z_{eq} = \frac{Z_1Z_2}{Z_1 + Z_2} \]
Examples
LC circuit
RLC circuit
RMS Voltage and AC Power
Power is voltage times current \[ P=VI. \] For a resistive element, we can also write $P=VI=RI^2=V^2/R$.
In DC we were just muliplying numbers, but in AC circuits the current and the veoltage are oscillating funcitons, so the power will also be oscillating \[ p(t) = v(t)i(t) = V_{mac}\cos(\omega t) I_{max}\cos(\omega t) = V_{mac}I_{max}\cos^2(\omega t). \]
Two observations:
- The power is oscillating—humming. There is no clean continuous flow of electric energy, but a shaky 120Hz bumpy transfer. This shakyness in the power delivery would be a serious problem for devices that consume a lot of power. This is why Nicola Tesla had to follow up his invetion of alternating currents on two wires into an upgraded version: alternating currents on three wires or three-phase AC.
- The maximum power is $P_{max} = V_{mac}I_{max}$, but this is not what Hydro will charge you for. Hydro calculates the average power consmption over some time period. At $t=0,t=\pi,t=2\pi,\ldots$ the power consumption is maximum $P_{max}$, but at times $t=\frac{\pi}{2},t=\frac{3\pi}{2}$ the power consumption is zero. To calculate the average power consumption we need to integrate $\cos^2(x)$ over some representative interval, say $[0,2\pi]$:
\[ \frac{1}{2\pi}\int_0^{2\pi} |\cos(t)|^2 dt = \frac{1}{2}, \]
This means that \[ P_{avg} = \frac{P_{max}}{2 } = \frac{V_{max} I_{max}}{2} =\frac{V_{max}}{\sqrt{2}}\frac{I_{max}}{\sqrt{2} } \]
\[ V_{rms} \equiv \sqrt{ \mathop{avg}_t \{ |v(t)|^2 \} } \]
This is what Hydro charges you for.
The voltage amplitude of the wall outlets in North America is 150V, but the effective voltage as far as power is concerened is $\frac{1}{\sqrt{2}}$ of the maximum amplitude of the sine wave, which gives $V_{rms}=110 \approx \frac{150}{\sqrt{2}}$.
Note that it is not high voltage that kills, it is high current.
ELI ICE
E before I in L=inductor
I before E in C=capacitor
Discussion
Links
[ Alternating currents module in the US Navy Training Series ]
http://jacquesricher.com/NEETS/14174.pdf
Power
Formulas
Power in mechanics
TODO: symlink this section to Energy section of ../mechanics
[J]=[N][m]
heat produced by friction of brake on bike tire
power = F_f*v_rotation
Electric power
[W]=[V][I] how much powe is consumed by a light bulb, and a heater and a blow drier
WAVE PHENOMENA 2 coherence in phase/out of phase little circle with dash ala Feynman interference diffraction
Linear algebra
Introduction to linear algebra
Linear algebra is the math of vectors and matrices. A vector $\vec{v} \in \mathbb{R}^n$ is an array of $n$ numbers. For example, a three-dimensional vector is a triple of the form: \[ \vec{v} = (v_1,v_2,v_3) \ \in \ (\mathbb{R},\mathbb{R},\mathbb{R}) \equiv \mathbb{R}^3. \] To specify the vector $\vec{v}$, we need to specify the values for its three components $v_1$, $v_2$ and $v_3$.
A matrix $M \in \mathbb{R}^{m\times n}$ is an table of numbers with $m$ rows and $n$ columns. Consider as an example the following $3\times 3$ matrix: \[ A = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right] \ \in \ \left[\begin{array}{ccc} \mathbb{R} & \mathbb{R} & \mathbb{R} \nl \mathbb{R} & \mathbb{R} & \mathbb{R} \nl \mathbb{R} & \mathbb{R} & \mathbb{R} \end{array}\right] \equiv \mathbb{R}^{3\times 3}. \] To specify the matrix $A$ we need to specify the values of its nine components $a_{11}$, $a_{12}$, $\ldots$, $a_{33}$.
We will study the mathematical operations that we can performed on vectors and matrices and their applications. Many problems in science, business and technology are described naturally in terms of vectors and matrices so it is important for you to understand how to work with these things.
Context
To illustrate what is new about vectors and matrices, let us review the properties of something old and familiar: the real numbers $\mathbb{R}$. The basic operations on numbers are:
- addition (denoted $+$)
- subtraction, the inverse of addition (denoted $-$)
- multiplication (denoted $\times$ or implicit)
- division, the inverse of multiplication
(denoted $\div$ or as a fraction) You have been using these operations all your life, so you know how to use these operations when solving equations.
You also know about functions $f: \mathbb{R} \to \mathbb{R}$, which take real numbers as inputs and give real numbers as outputs. Recall that the inverse function of $f$ is defined as the function $f^{-1}$ which undoes the effect of $f$ to get back the original input variable: \[ f^{-1}\left( f(x) \right)=x. \] For example when $f(x)=\ln(x)$, $f^{-1}(x)=e^x$ and given $g(x)=\sqrt{x}$, the inverse is $g^{-1}(x)=x^2$.
Vectors $\vec{v}$ and matrices $A$ are the new objects of study, so our first step should be to similarly define the basic operations which we can perform on them.
For vectors we have the following operations:
- addition (denoted $+$)
- subtraction, the inverse of addition (denoted $-$)
- dot product (denoted $\cdot$)
- cross product (denoted $\times$)
For matrices we have the following operations:
- addition (denoted $+$)
- subtraction, the inverse of addition (denoted $-$)
- matrix product (implicitly denoted, e.g. $AB$).
The matrix-matrix product includes the matrix-vector products $A\vec{x}$ as a special case.
- matrix inverse (denoted $A^{-1}$)
- matrix trace (denoted $\textrm{Tr}(A)$)
- matrix determinant (denoted $\textrm{det}(A)$ or $|A|$)
Matrix-vector product
The matrix-vector product $A\vec{x}$ is a linear combination of the columns of the matrix $A$. For example, consider the product of a $3 \times 2$ matrix $A$ and $2 \times 1$ vector $\vec{x}$. The output of the product $A\vec{x}$ will be denoted $\vec{y}$ and is $3 \times 1$ vector given by: \[ \begin{align*} \vec{y} &= A \vec{x}, \nl \begin{bmatrix} y_1 \nl y_2 \nl y_3 \end{bmatrix} & = \begin{bmatrix} a_{11} & a_{12} \nl a_{21} & a_{22} \nl a_{31} & a_{32} \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = x_1\! \begin{bmatrix} a_{11} \nl a_{21} \nl a_{31} \end{bmatrix} + x_2\! \begin{bmatrix} a_{12} \nl a_{22} \nl a_{32} \end{bmatrix} = \begin{bmatrix} x_1a_{11} + x_2a_{12} \nl x_1a_{21} + x_2a_{22} \nl x_1a_{31} + x_2a_{32} \end{bmatrix}. \end{align*} \] The key thing to observe in the above formula is the new notion of product for matrices as linear combinations of their columns. We have $\vec{y}=A\vec{x}=x_1A_{[:,1]} + x_2A_{[:,2]}$ where $A_{[:,1]}$ and $A_{[:,2]}$ are the first and second columns of $A$.
Linear combinations as matrix products
Consider now some set of vectors $\{ \vec{e}_1, \vec{e}_2 \}$ and a third vector $\vec{y}$ which is a linear combination of the vectors $\vec{e}_1$ and $\vec{e}_2$: \[ \vec{y} = \alpha \vec{e}_1 \ + \ \beta \vec{e}_2. \] The numbers $\alpha, \beta \in \mathbb{R}$ are called coefficients of the linear combination.
The matrix-vector product is defined expressly for the purpose of studying linear combinations. We can describe the above linear combination as the following matrix-vector product: \[ \vec{y} = \begin{bmatrix} | & | \nl \vec{e}_1 & \vec{e}_2 \nl | & | \end{bmatrix} \begin{bmatrix} \alpha \nl \beta \end{bmatrix} = E\vec{x}. \] The matrix $E$ has $\vec{e}_1$ and $\vec{e}_2$ as columns. The dimensions of the matrix $E$ will be $d \times 2$, where $d$ is the dimension of the vectors $\vec{e}_1$, $\vec{e}_2$ and $\vec{y}$.
Matrices as vector functions
OK, my dear readers we have now reached the key notion in the study of linear algebra. One could even say the main idea.
I know you are ready to handle it because you are now familiar with functions of a real variable $f:\mathbb{R} \to \mathbb{R}$, and you just saw the definition of the matrix-vector product in which the variables were chosen to subliminally remind you of the standard convention for calling the function input $x$ and the function output $y=f(x)$. Without further ado, I present to you: the notion of a vector function, which is also known as a linear transformation.
Multiplication by a matrix $A \in \mathbb{R}^{m \times n}$ can be thought of as computing a vector function of the form: \[ T_A:\mathbb{R}^n \to \mathbb{R}^m, \] which take as input $n$-vectors and gives $m$-vectors as outputs. Instead of writing $T_A(\vec{x})=\vec{y}$ for the vector function $T_A$ applied to the vector $\vec{x}$ we can simply write $A\vec{x}=\vec{y}$ where the “application of function $T_A$” corresponds to the product of the matrix $A$ and the vector $\vec{x}$.
When the matrix $A\in \mathbb{R}^{n \times n}$ is invertible, there exists an inverse matrix $A^{-1}$ which undoes the effect of $A$ to give back the original input vector: \[ A^{-1}\!\left( A(\vec{x}) \right)=A^{-1}A\vec{x}=\vec{x}. \]
For example, the transformation which multiplies the first components of input vectors by $3$ and multiplies the second components by $5$ is described by the matrix \[ A = \begin{bmatrix} 3 & 0 \nl 0 & 5 \end{bmatrix}\!, \ \qquad A(\vec{x})= \begin{bmatrix} 3 & 0 \nl 0 & 5 \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} 3x_1 \nl 5x_2 \end{bmatrix}. \] Its inverse is \[ A^{-1} = \begin{bmatrix} \frac{1}{3} & 0 \nl 0 & \frac{1}{5} \end{bmatrix}, \ \qquad A^{-1}\!\left( A(\vec{x}) \right)= \begin{bmatrix} \frac{1}{3} & 0 \nl 0 & \frac{1}{5} \end{bmatrix} \begin{bmatrix} 3x_1 \nl 5x_2 \end{bmatrix} = \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} =\vec{x}. \] Note how the inverse matrix corresponds to the multiplication of the first component by $\frac{1}{3}$ and the second component by $\frac{1}{5}$, which has the effect of undoing the action of $A$.
Things get a little more complicated when matrices mix the different coefficients of the input vector as in the following example: \[ B = \begin{bmatrix} 1 & 2 \nl 0 & 3 \end{bmatrix}, \ \qquad \text{which acts as } \ \ B(\vec{x})= \begin{bmatrix} 1 & 2 \nl 0 & 3 \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} x_1 +2x_2 \nl 3x_2 \end{bmatrix}. \] To understand the output of the matrix $B$ on the vector $\vec{x}$, you must recall the definition of the matrix-vector product.
The inverse of the matrix $B$ is the matrix \[ B^{-1} = \begin{bmatrix} 1 & \frac{-2}{3} \nl 0 & \frac{1}{3} \end{bmatrix}. \] Multiplication by the matrix $B^{-1}$ is the “undo action” for the multiplication by $B$: \[ B^{-1}\!\left( B(\vec{x}) \right)= \begin{bmatrix} 1 & \frac{-2}{3} \nl 0 & \frac{1}{3} \end{bmatrix} \begin{bmatrix} 1 & 2 \nl 0 & 3 \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} 1 & \frac{-2}{3} \nl 0 & \frac{1}{3} \end{bmatrix} \begin{bmatrix} x_1 +2x_2 \nl 3x_2 \end{bmatrix} = \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} =\vec{x}. \]
We will discuss matrix inverses and how to compute them in more detail later, but for now it is important that you know that they exist and you know what they do. By definition, the inverse matrix $A^{-1}$ undoes the effects of the matrix $A$: \[ A^{-1}A\vec{x} =\mathbb{I}\vec{x} =\vec{x} \qquad \Rightarrow \qquad A^{-1}A = \begin{bmatrix} 1 & 0 \nl 0 & 1 \end{bmatrix}= \mathbb{I}. \] The cumulative effect of applying $A$ and $A^{-1}$ is an identity matrix, which has ones on the diagonal and zeros everywhere else.
An analogy
You can think of linear transformations as “vector functions” and describe their properties in analogy with the regular functions you are familiar with. The action of a function on a number is similar to the action of a matrix on a vector: \[ \begin{align*} \textrm{function } f:\mathbb{R}\to \mathbb{R} & \ \Leftrightarrow \! \begin{array}{l} \textrm{linear transformation } T_A:\mathbb{R}^{n}\! \to \mathbb{R}^{m} \end{array} \nl % \textrm{input } x\in \mathbb{R} & \ \Leftrightarrow \ \textrm{input } \vec{x} \in \mathbb{R}^n \nl %\textrm{compute } \textrm{output } f(x) & \ \Leftrightarrow \ % \textrm{compute matrix-vector product } \textrm{output } T_A(\vec{x})=A\vec{x} \in \mathbb{R}^m \nl %\textrm{function composition } g\circ f \! = \! g(f(x)) & \ \Leftrightarrow \ % \textrm{matrix product } T_B(T_A(\vec{x})) = BA \vec{x} \nl \textrm{function inverse } f^{-1} & \ \Leftrightarrow \ \textrm{matrix inverse } A^{-1} \nl \textrm{zeros of } f & \ \Leftrightarrow \ \mathcal{N}(A) \equiv \textrm{null space of } A \nl \textrm{range of } f & \ \Leftrightarrow \ \begin{array}{l} \mathcal{C}(A) \equiv \textrm{column space of } A =\textrm{range of } T_A \end{array} \end{align*} \]
The end goal of this book is to develop your intuition about vectors, matrices, and linear transformations. Our journey towards this goal will take us through many interesting new concepts along the way. We will develop new computational techniques and learn new ways of thinking that will open many doors for understanding science. Let us look in a little more detail at what lies ahead in the book.
Computational linear algebra
The first steps towards understanding linear algebra will be quite tedious. You have to develop the basic skills for manipulating vectors and matrices. Matrices and vectors have many entries and performing operations on them will involve a lot of arithmetic steps—there is no way to circumvent this complexity. Make sure you understand the basic algebra rules: how to add, subtract and multiply vectors and matrices, because they are a prerequisite for learning about the cool stuff later on.
The good news is that, except for the homework assignments and the problems on your final exam, you will not have to do matrix algebra by hand. In the real world, we use computers to take care of the tedious calculations, but that doesn't mean that you should not learn how to perform matrix algebra. The more you develop your matrix algebra intuition, the deeper you will be able to go into the advanced material.
Geometrical linear algebra
So far we described vectors and matrices as arrays of numbers. This is fine for the purpose of doing algebra on vectors and matrices, but it is not sufficient to understand their geometrical properties. The components of a vector $\vec{v} \in \mathbb{R}^n$ can be thought of as measuring distances along a coordinate system with $n$ axes. The vector $\vec{v}$ can therefore be said to “point” in a particular direction with respect to the coordinate system. The fun part of linear algebra starts when you learn about the geometrical interpretation of each of the algebraic operations on vectors and matrices.
Consider some unit length vector that specifies a direction of interest $\hat{r}$. Suppose we are given some other vector $\vec{v}$, and we are asked to find how much of $\vec{v}$ is in the $\hat{r}$ direction. The answer is computed using the dot product: $v_r = \vec{v} \cdot \hat{r} = \|\vec{v}\|\cos\theta$, where $\theta$ is the angle between $\vec{v}$ and $\hat{r}$. The technical term for the quantity $v_r$ is “the projection of $\vec{v}$ in the $\hat{r}$ direction.” By projection we mean that we ignore all parts of $\vec{v}$ that are not in the $\hat{r}$ direction. Projections are used in mechanics to calculate the $x$ and $y$ components of forces in force diagrams. In Chapter~\ref{chapter:geometrical_linear_algebra} we'll learn how to think intuitively about projections in terms of dot products.
TODO: check above reference is OK
As another example of the geometrical aspect of vector operations, consider the following situation. Suppose I give you two vectors $\vec{u}$ and $\vec{v}$ and I ask you to find a third vector $\vec{w}$ that is perpendicular to both $\vec{u}$ and $\vec{v}$. A priori this sounds like a complicated question to answer, but in fact the required vector $\vec{w}$ can easily be obtained by computing the cross product $\vec{w}=\vec{u}\times\vec{v}$.
You will also learn how to describe lines and planes in space using vectors. Given the equations of two lines (or planes), there is a procedure for finding their solution, that is, the point (or line) where they intercept.
The determinant of a matrix also carries geometrical interpretation. It tells you something about the relative orientation of the vectors that make up the rows of the matrix. If the determinant of a matrix is zero, it means that the rows are not linearly independent—at least one of the rows can be written in terms of the other rows. Linear independence, as we will learn shortly, is an important property for vectors to have and the determinant is a convenient way to test whether a set of vectors has this property.
It is really important that you try to visualize every new concept you learn about. You should always keep a picture in your head of what is going on. The relationships between two-dimensional vectors can easily be drawn on paper, while three-dimensional vectors can be visualized by pointing pens and pencils in different directions. Though our ability to draw and visualize only extends up to three dimensions, the notion of a vector does not stop there. We could have four-dimensional vectors $\mathbb{R}^4$ or even ten-dimensional vectors $\mathbb{R}^{10}$. All the intuition you build-up in two and three dimensions is still applicable to vectors with more dimensions.
Theoretical linear algebra
The most important aspects of linear algebra is that you will learn how to reason about vectors and matrices in a very abstract way. By thinking abstractly, you will be able to extend your geometrical intuition for two and three-dimensional problems to problems in higher dimensions. A lot of knowledge buzz awaits you as you learn about new concepts, pick up new computational skills and develop new ways of thinking.
You are probably familiar with the normal coordinate system made up of two orthogonal axes: the $x$ axis and the $y$ axis. A vector $\vec{v}$ can be specified in terms of their coordinates $(v_x,v_y)$ with respect to these axes, that is we can write down any vector $\vec{v} \in \mathbb{R}^2$ as $\vec{v} = v_x \hat{\imath} + v_y \hat{\jmath}$, where $\hat{\imath}$ and $\hat{\jmath}$ are unit vectors that point along the $x$ and $y$ axis respectively. It turns out that we can use many other kinds of coordinate systems in order to represent vectors. A basis for $\mathbb{R}^2$ is any set of two vectors $\{ \hat{e}_1, \hat{e}_2 \}$ that allows us to write all vectors $\vec{v} \in \mathbb{R}^2$ as a linear combination of the basis vectors $\vec{v} = v_1 \hat{e}_1 + v_2 \hat{e}_2$. The same vector $\vec{v}$ corresponds to two different coordinate pairs depending on which basis is used for the description: $\vec{v}=(v_x,v_y)$ in the basis $\{ \hat{\imath}, \hat{\jmath}\}$ and $\vec{v}=(v_1,v_2)$ in the $\{ \hat{e}_1, \hat{e}_2 \}$ basis. We will bases and their properties in great detail in the coming chapters.
The notions of eigenvalues and eigenvectors for matrices will allow you to describe their actions in the most natural way. The set of eigenvectors of a matrix is a special set of input vectors for which the action of the matrix is described as a scaling. When a matrix is multiplied by one of its eigenvectors the output is a vector in the same direction scaled by a constant, which we call an eigenvalue. Thinking of matrices in term of their eigenvalues and eigenvectors is a very powerful technique for describing their properties.
In the above text I explained that computing the product between a matrix and a vector $A\vec{x}=\vec{y}$ can be thought of as vector function, with input $\vec{x}$ and output $\vec{y}$. More specifically, we say that any linear transformation can be represented as a multiplication by a matrix $A$. Indeed, each $m\times n$ matrix $A \in \mathbb{R}^{m\times n}$ can be thought of as some linear transformation (vector function): $T_A \colon \mathbb{R}^n \to \mathbb{R}^m$. This relationship between matrices and linear transformations will allow us to identify certain matrix properties as properties of the corresponding linear transformations. For example, the column space of a matrix $A$ (the set of vectors that can be written as a combination of the columns of the matrix) corresponds to the image space $\textrm{Im}(T_A)$ (the set of possible outputs of the transformation $T_A$).
Part of what makes linear algebra so powerful is that linear algebra techniques can be applied to all kinds of “vector-like” objects. The abstract concept of a vector space captures precisely what it means for some class of mathematical objects to be “vector-like”. For example, the set of polynomials of degree at most two $P_2(x)$, which consists of all functions of the form $f(x)=a_0 + a_1x + a_2x^2$ is “vector like” because it is possible to describe each polynomial in terms of its coefficients $(a_0,a_1,a_2)$. Furthermore, the sum of two polynomials and the multiplication of a polynomial by a constant both correspond to vector-like calculations on their coefficients. This means that we can use concepts from linear algebra like linear independence, dimension and basis when dealing with polynomials.
Useful linear algebra
One of the most useful skills you will learn in linear algebra is the ability to solve systems of linear equations. Many real world problems can be expressed as linear relationships between multiple unknown quantities. To find these unknowns you will often have to solve $n$ equations in $n$ unknowns. You can use basic techniques such as substitution, elimination and subtraction to solve these equations, but the procedure will be very slow and tedious. If the system of equations is linear, then it can be expressed as an augmented matrix build from the coefficients in the equations. You can then use the Gauss-Jordan elimination algorithm to solve for the $n$ unknowns. The key benefit of this approach is that it allows you to focus on the coefficients and not worry about the variable names. This saves a lot of time when you have to solve many equations with many unknowns. Another approach for solving systems of equations is to express it as a matrix equation and then solve the matrix equation by computing the matrix inverse.
You will also learn how to decompose a matrix into a product of simpler matrices in various ways. Matrix decompositions are often performed for computational reasons: certain problems are easier to solve on a computer when the matrix is expressed in terms of its simpler constituents.
Other decompositions, like the decomposition of a matrix into its eigenvalues and eigenvectors,
give you valuable insights into the properties of the matrix.
Google's original PageRank algorithm for ranking webpages by importance
can be formalized as the search for an eigenvector of a matrix.
The matrix in question contains the information about all the hyperlinks that exist between webpages.
The eigenvector we are looking for corresponds to a vector which tells you the relative importance
of each page.
So when I say that learning about eigenvectors is valuable, I am not kidding:
a 300 billion dollar company was build starting from an eigenvector idea.
The techniques of linear algebra find application in many areas of science and technology. We will discuss applications such as finding approximate solutions (curve fitting), modelling of real-world problems, and constrained optimization problems using linear programming.
Discussion
In terms of difficulty of the content, I would say that you should get ready for some serious uphills. As your personal “mountain guide” to the “mountain” of linear algebra, it is my obligation to warn you about the difficulties that lie ahead so that you will be mentally prepared.
The computational aspects will be difficult in a boring and repetitive kind of way as you have to go through thousands of steps where you multiply things together and add up the results. The theoretical aspects will be difficult in a very different kind of way: you will learn about various theoretical properties of vectors, matrices and operations and how to use these properties to prove things. This is what real math is like, using axioms and basic facts about the mathematical objects in order to prove statements.
In summary, a lot of work and toil awaits you as you learn about the concepts from linear algebra, but the effort is definitely worth it. All the effort you put into understanding vectors and matrices will lead to mind-expanding insights. You will reap the benefits of your effort for the rest of your life; understanding linear algebra will open many doors for you.
Links
[ Wikibook on the subject (for additional reading) ]
http://en.wikibooks.org/wiki/Linear_Algebra
NOINDENT
[ Wikipedia overview on matrices ]
http://en.wikipedia.org/wiki/Matrix_(mathematics)
NOINDENT
[ List of applications of linear algebra ]
http://aix1.uottawa.ca/~jkhoury/app.htm
Linearity
What is linearity? What does a linear expression look like? Consider the following arbitrary function which contains terms with different powers of the input variable $x$: \[ f(x) = \frac{a}{x^3} \; + \; \frac{b}{x^2} \; + \; \frac{c}{x} \; + \; d \; + \; \underbrace{mx}_{\textrm{linear term}} \; + \; e x^2 \; + \; fx^3. \] The term $mx$ is the only linear term—it contains $x$ to the first power. All other terms are non-linear.
Introduction
A single-variable function takes as input a real number $x$ and outputs a real number $y$. The signature of this class of functions is \[ f \colon \mathbb{R} \to \mathbb{R}. \]
The most general linear function from $\mathbb{R}$ to $\mathbb{R}$ looks like this: \[ y \equiv f(x) = mx, \] where $m \in \mathbb{R}$ is some constant, which we call the coefficient of $x$. The action of a linear function is to multiply the input by a constant—this is not too complicated, right?
Example: composition of linear functions
Given the linear functions $f(x)=2x$ and $g(y)=3y$, what is the equation of the function $h(x) \equiv g\circ f \:(x) = g(f(x))$? The composition of the functions $f(x)=2x$ and $g(y)=3y$ is the function $h(x) =g(f(x))= 3(2x)=6x$. Note the composition of two linear functions is also a linear function whose coefficient is equal to the product of the coefficients of the two constituent functions.
Definition
A function is linear if, for any two inputs $x_1$ and $x_2$ and constants $\alpha$ and $\beta$, the following equation is true: \[ f(\alpha x_1 + \beta x_2) = \alpha f(x_1) + \beta f(x_2). \] A linear combination of inputs gets mapped to the same linear combination of outputs.
Lines are not linear functions!
Consider the equation of a line: \[ l(x) = mx+b, \] where the constant $m$ corresponds to the slope of the line and the constant $b =f(0)$ is the $y$-intercept of the line. A line $l(x)=mx+b$ with $b\neq 0$ is not a linear function. This is a bit weird, but if you don't trust me you just have to check: \[ l(\alpha x_1 + \beta x_2) = m(\alpha x_1 + \beta x_2)+b \neq m(\alpha x_1)+b + m(\beta x_2) + b = \alpha l(x_1) + \beta l(x_2). \] A function with a linear part plus some constant is called an affine transformation. These are cool too, but a bit off topic since the focus of our attention is on linear functions.
Multivariable functions
The study of linear algebra is the study of all things linear. In particular we will learn how to work with functions that take multiple variables as inputs. Consider the set of functions that take on as inputs two real numbers and give a real number as output: \[ f \colon \mathbb{R}\times\mathbb{R} \to \mathbb{R}. \] The most general linear function of two variables is \[ f(x,y) = m_xx + m_yy. \] You can think of $m_x$ as the $x$-slope and $m_y$ as the $y$-slope of the function. We say $m_x$ is the $x$-coefficient of and $m_y$ the $y$-coefficient in the linear expression $m_xx + m_yy$.
Linear expressions
A linear expression in the variables $x_1$, $x_2$, and $x_3$ has the form:
\[
a_1 x_1 + a_2 x_2 + a_3 x_3,
\]
where $a_1$, $a_2$, and $a_3$ are arbitrary constants.
Note the new terminology used ”expr is linear in $v$” to refer to the
expressions in which the variable $v$ appears only raised to the
first power in expr.
Linear equation
A linear equation in the variables $x_1$, $x_2$, and $x_3$ has the form \[ a_1 x_1 + a_2 x_2 + a_3 x_3 = c. \] This equation is linear because it contains no nonlinear terms in $x_i$. Note that the equation $\frac{1}{a_1} x_1 + a_2^6 x_2 + \sqrt{a_3} x_3 = c$, contains non-linear factors, but is still linear in $x_1$, $x_2$, and $x_3$.
Example
Linear equations are very versatile. Suppose you know that the following equation is an accurate model of some real-world phenomenon: \[ 4k -2m + 8p = 10, \] where the $k$, $m$, and $p$ correspond to three variables of interest. You can think of this equation as describing the variable $m$ as a function of the variables $k$ and $p$: \[ m(k,p) = 2k + 4p - 5. \] Using this function you can predict the value of $m$ given the knowledge of the quantities $k$ and $p$.
Another option would be to think of $k$ as a function of $m$ and $p$: $k(m,p) = 10 +\frac{m}{2} - 2p$. This model would be useful if you know the quantities $m$ and $p$ and you want to predict the value of the variable $k$.
Applications
Geometrical interpretation of linear equations
The most general linear equation in $x$ and $y$, \[ Ax + By = C \qquad B \neq 0, \] corresponds to the equation of a line $y=mx+b$ in the Cartesian plane. The slope of this line is $m=\frac{-A}{B}$ and its $y$-intercept is $\frac{C}{B}$. In the special case when $B=0$, the linear expression corresponds to a vertical line with equation $x=\frac{C}{A}$.
The most general linear equation in $x$, $y$, and $z$, \[ Ax + By + Cz = D, \] corresponds to the equation of a plane in a three-dimensional space. Assuming $C\neq 0$, we can rewrite this equation so that $z$ (the “height” of the plane) is a function of the coordinates $x$ and $y$: $z(x,y) = b + m_x x + m_y y$. The slope of the plane in the $x$-direction is $m_x= - \frac{A}{C}$ and $m_y = - \frac{B}{C}$ in the $y$-direction. The $z$-intercept of the plane is $b=\frac{D}{C}$.
First-order approximations
When we us a linear function as a mathematical model for a non-linear real-world phenomenon, we say the function represents a linear model or a first-order approximation. Let's analyze in a little more detail what that means.
In calculus, we learn that functions can be represented as infinite Taylor series: \[ f(x) = \textrm{taylor}(f(x)) = a_0 + a_1t + a_2t^2 + a_3t^3 + \cdots = \sum_{n=0}^\infty a_n x^n, \] where the coefficients $a_n$ depend on the $n$th derivative of the function $f(x)$. The Taylor series is only equal to the function $f(x)$ if infinitely many terms in the series are calculated. If we sum together only a finite terms of the series, we obtain a Taylor series approximation. The first-order Taylor series approximation to $f(x)$ is \[ f(x) \approx \textrm{taylor}_1(f(x)) = a_0 + a_1x = f(0) + f'(0)x. \] The above equation describes the best approximation to $f(x)$ near $x=0$, by a line of the form $l(x)=mx+b$. To build a linear model of a function $f(x)$, all you need to measure is its initial value $f(0)$, and its rate of change $f'(0)$.
For a function $F(x,y,z)$ that takes many variables as inputs, the first-order Taylor series approximation is \[ F(x,y,z) \approx b + m_x x + m_y y + m_z z. \] Except for the constant term, the function has the form of a linear expression. The “first order approximation” to a function of $n$ variables $F(x_1,x_2,\ldots, x_n)$ has the form $b + m_1x_1 + m_2x_2 + \cdots + m_nx_n$.
Discussion
In linear algebra, we learn about many new mathematical objects and define functions that operate on these objects. In all the different scenarios we will see, the notion of linearity $f(\alpha x_1 + \beta x_2) = \alpha f(x_1) + \beta f(x_2)$ play a key role.
We begin our journey of all things linear in the next section with the study of systems of linear equations.
Reduced row echelon form
In this section we'll learn how to solve systems of linear equations using the Gauss-Jordan elimination procedure. A system of equations can be represented as a matrix of coefficients. The Gauss-Jordan elimination procedure converts any matrix into its reduced row echelon form (RREF). We can easily read off the solution of the system of equations from the RREF.
This section requires your full-on caffeinated attention because the procedures you will learn is somewhat tedious. Gauss-Jordan elimination involves a lot of repetitive mathematical manipulations of arrays of numbers. It is important for you to suffer through the steps, and verify each step presented below on your own with pen and paper. You shouldn't trust me—always verify!
Solving equations
Suppose you are asked to solve the following system of equations: \[ \begin{eqnarray} 1x_1 + 2x_2 & = & 5, \nl 3x_1 + 9x_2 & = & 21. \end{eqnarray} \] The standard approach would be to use substitution, elimination, or subtraction tricks to combine these equations and find the values of the two unknowns $x_1$ and $x_2$.
The names of the two unknowns are irrelevant to the solution of these equations. Indeed, the solution $(x_1,x_2)$ to the above equations would be the same as the solution $(s,t)$ in the following system of equations: \[ \begin{align*} 1s + 2t & = 5, \nl 3s + 9t & = 21. \end{align*} \] What is important in this equation are the coefficients in front of the variables and the numbers in the column of constants on the right-hand side of each equation.
Augmented matrix
Any system of linear equations can be written down as a matrix of numbers: \[ \left[ \begin{array}{cccc} 1 & 2 &| & 5 \nl 3 & 9 &| & 21 \end{array} \right], \] where the first column corresponds to the coefficients of the first variable, the second column is for the second variable and the last column corresponds to the numbers of the right-hand side of the equation. It is customary to draw a vertical line where the equal sign in the equation would normally appear. This line helps us to distinguish the coefficients of the equations from the column of constants on the right-hand side of the equations.
Once you have the augmented matrix, we can start to use row operations on its entries to simplify it.
In the last step, we use the correspondence between the augmented matrix and the systems of linear equations to read off the solution.
After “simplification by row operations,” the above augmented matrix will be: \[ \left[ \begin{array}{cccc} 1 & 0 &| & 1 \nl 0 & 1 &| & 2 \end{array} \right]. \] This augmented matrix corresponds to the following system of linear equations: \[ \begin{eqnarray} x_1 & = & 1, \nl x_2 & = & 2, \end{eqnarray} \] in which there is not much left to solve. Right?
The augmented matrix approach to manipulating systems of linear equations is very convenient when we have to solve equations with many variables.
Row operations
We can manipulate each of the rows of the augmented matrix without chaining the solutions. We are allowed to perform the following three row operations:
- Add a multiple of one row to another row
- Swap two rows
- Multiply a row by a constant
Let's trace the sequence of row operations we would need to solve the system of linear equations which we described above.
- We start with the augmented matrix:
\[\left[ \begin{array}{cccc} 1 & 2 &| & 5 \nl 3 & 9 &| & 21 \end{array} \right]. \]
- As a first step we will eliminate the first variable in the second row.
We can do this by subtracting three times the first row from the second row:
\[\left[\begin{array}{cccc}1 & 2 & | &5\\0 & 3 & | &6\end{array}\right].\]
We can denote this row operation as $R_2 \gets R_2 - 3R_1$.
* Next, to simplify the second row we divide it by three: $R_2 \gets \frac{1}{3}R_2$:
\[\left[\begin{array}{cccc}1 & 2 & | &5\\0 & 1 & | &2\end{array}\right].\]
* The final step is to eliminate the second variable from the first row.
We do by subtracting two times the second row from the first row
$R_1 \gets R_1 - 2R_2$:
\[\left[\begin{array}{cccc}1 & 0 & | &1\\0 & 1 & | &2\end{array}\right].\]
From which we can read off the solution directly: $x_1 = 1$, $x_2=2$.
The procedure I used to find simplify the augmented matrix and get the solution were not random. I was following the Gauss-Jordan elimination algorithm brings the matrix into its the reduced row echelon form.
The reduced row echelon form is in some sense the simplest form for a matrix. Each row contains a leading one which is also sometimes called a pivot. The pivot of each column is used to eliminate all other numbers below and above in the same column until we obtain an augmented matrix of the form: \[ \left[ \begin{array}{cccc|c} 1 & 0 & * & 0 & * \nl 0 & 1 & * & 0 & * \nl 0 & 0 & 0 & 1 & * \end{array} \right] \]
Definitions
- The solution to a system of linear equations in the
variables $x_1,x_2$ is the set of values $\{ (x_1,x_2) \}$
that satisfy //all// the equations. * The //pivot// for row $j$ of a matrix is the left-most non-zero entry in the row $j$. Any //pivot// can be converted into a //leading one// by an appropriate scaling. * //Gaussian elimination// is the process of bringing a matrix into //row echelon form//. * A matrix is said to be in //row echelon form// (REF) if all the entries below the leading ones are zero. This can be obtained by adding or subtracting the row with the leading one from the rows below it. * //Gaussian-Jordan elimination// is the process of branding any matrix into the //reduced row echelon form//. * A matrix is said to be in //reduced row echelon form// (RREF) if all the entries below //and above// the leading ones are zero. Starting from the REF form, we can obtain the RREF form by subtracting the row which contains the leading one for that column from the rows above it.
Gauss-Jordan elimination algorithm
Forward phase (left to right):
- Get a pivot (leading one) in the left most column.
- Subtract this row from all rows below this one
to get zeros below in the entire column.
- Look for a leading one in the next column and repeat.
NOINDENT Backward phase (right to left):
- Find the rightmost pivot and use it to eliminate all the
numbers above it in the column.
- Move one step to the left and repeat
Example
We are asked to solve the following system of equations \[ \begin{align*} 1x + 2y +3 z = 14, \nl 2x + 5y +6 z = 30, \nl -1x +2y +3 z = 12. \end{align*} \]
Your first step is to write the corresponding augmented matrix \[\left[\begin{array}{ccccc}{\color{blue}1} & 2 & 3 & |& 14\\2 & 5 & 6 & |& 30\\-1 & 2 & 3 & |& 12\end{array}\right].\]
Conveniently, we already have a $1$ at the top of the first column.
- The first step is to clear the entire column below this leading one.
The two row operations are $R_2 \gets R_2 - 2R_1$ and
$R_3 \gets R_3 + R_1$ to obtain:
\[\left[\begin{array}{ccccc}1 & 2 & 3 & |& 14\\0 & {\color{blue}1} & 0 & |& 2\\0 & 4 & 6 & |& 26\end{array}\right].\]
We now shift our attention to the second column, second row.
* Using the leading one for the second column, we set the number in the column
below to zero: $R_3 \gets R_3 - 4R_2$.
\[\left[\begin{array}{ccccc}1 & 2 & 3 & |& 14\\0 & 1 & 0 & |& 2\\0 & 0 & {\color{red}6} & |& 18\end{array}\right].\]
We move to the third column now, and look for a leading one on the third row.
* There is a six there, which is we can turn into a leading one as follows: $R_3 \gets \frac{1}{6}R_3$
\[\left[\begin{array}{ccccc} 1 & 2 & 3 & |&14\\0 & 1 & 0 & |&2\\0 & 0 & {\color{blue}1} & |&3\end{array}\right].\]
The forward phase of the Gauss-Jordan elimination procedure is complete now. We have our three pivots and we used them to systematically set the entries below them to zero. The matrix is now in row echelon form.
We now start the backward phase, during which we work right to left and set all that numbers above the pivots to zero:
- The first step is $R_1 \gets R_1 -3R_3$, which leads to:
\[\left[\begin{array}{ccccc}1 & 2 & 0 & |& 5\\0 & 1 & 0 & |&2\\0 & 0 & 1 & |&3\end{array}\right].\]
- The final step is $R_1 \gets R_1 -2R_2$, which gives:
\[\left[\begin{array}{ccccc}1 & 0 & 0 & |& 1\\0 & 1 & 0 & |& 2\\0 & 0 & 1 & |& 3\end{array}\right].\]
From the reduced row echelon form we can read off the solution: $x=1$, $y=2$ and $z=3$.
Number of solutions
A system of $3$ linear equations in $3$ variables could have:
- One solution: If the RREF for of a matrix has a single $1$ in each
row, then we can read off the values of the solution by inspection:
\[
\left[ \begin{array}{ccc|c}
1 & 0 & 0 & c_1 \nl
0 & 1 & 0 & c_2 \nl
0 & 0 & 1 & c_3
\end{array}\right].
\]
The //unique// solution is $x_1=c_1$, $x_2=c_2$ and $x_3=c_3$.
* **Infinitely many solutions**: If one of the equations is redundant,
this will lead to a row of zeros when the matrix is brought to the RREF.
A row of zeros means that one of the original equations given was
a linear combination of the others. This means that we are really solving
//two// equations in three variables, which in turn means that we
won't be able to pin down one of the variables. It will be a free variable:
\[
\left[ \begin{array}{ccc|c}
1 & 0 & a_1 & c_1 \nl
0 & 1 & a_2 & c_2 \nl
0 & 0 & 0 & 0
\end{array}\right].
\]
The free variable is the one that doesn't have a //leading one// in its column.
To indicate that $x_3$ is free, we will give it a special name $x_3=t$
and we define $t$ which ranges from $-\infty$ to $+\infty$. In other words,
$t$ being free, means that $t$ could be //any// number $t \in \mathbb{R}$.
The first and second equation can now be used to obtain $x_1$ and $x_2$
in terms of the $c$-constants and $t$ so we get the final solution:
\[
\left\{
\begin{array}{rl}
x_1 & = c_1 -a_1\:t \nl
x_2 & = c_2 - a_2\:t \nl
x_3 & = t
\end{array}, \quad
\forall t \in \mathbb{R}
\right\}
=
\left\{
\begin{bmatrix} c_1 \nl c_2 \nl 0 \end{bmatrix}
+ t \!
\begin{bmatrix} -a_1 \nl -a_2 \nl 1 \end{bmatrix},\quad
\forall t \in \mathbb{R}
\right\},
\]
which corresponds to [[lines_and_planes|the equation of a line]] with direction
vector $(-a_1,-a_2,1)$ passing through the point $(c_1,c_2,0)$. \\ \\
Note that it is also possible to have a two-dimensional solution space,
if there is only a single leading one. This is the case in the following example:
\[
\left[ \begin{array}{ccc|c}
0 & 1 & a_2 & c_2 \nl
0 & 0 & 0 & 0 \nl
0 & 0 & 0 & 0
\end{array}\right].
\]
There are //two// free variables ($x_1$ and $x_3$) and therefore the solution
space is two-dimensional. The solution corresponds to the set
\[
\left\{
\begin{array}{rl}
x_1 & = s \nl
x_2 & = c_2 - a_2\:t \nl
x_3 & = t
\end{array}, \quad
\forall s,t \in \mathbb{R}
\right\}
=
\left\{
\begin{bmatrix} 0 \nl c_2 \nl 0 \end{bmatrix}
+ s\!
\begin{bmatrix} 1 \nl 0 \nl 0 \end{bmatrix}
+ t \!
\begin{bmatrix} 0 \nl -a_2 \nl 1 \end{bmatrix},\quad
\forall s,t \in \mathbb{R}
\right\}.
\]
This is the explicit parametrisation of the plane: $0x + 1y + a_2z = c_2$ in $\mathbb{R}^3$.
* **No solutions**: If there are no numbers $(x_1,x_2,x_3)$ that simultaneously
satisfy all three of the equations, then the system of equations has no solution.
An example of equations with no solution would be $x_1+x_2 = 4$, $x_1+x_2=44$.
There are no numbers $(x_1,x_2)$ that satisfy both of these equations.
You can recognize when this happens in an augmented matrix, by a row zero coefficients
with a non-zero constant in the right-hand side.
\[
\left[ \begin{array}{ccc|c}
1 & 0 & 0 & c_1 \nl
0 & 1 & 0 & c_2 \nl
0 & 0 & 0 & c_3
\end{array}\right].
\]
If $c_3 \neq 0$, then this system of equations is impossible to satisfy (has //no// solutions).
This is because there are no numbers $(x_1,x_2,x_3)$ such that $0x_1+0x_2+0x_3=c_3$.
Note that the notion of solution for a system of linear equations is more general than what you are used to. You are used to solutions being just sets of points in space, but in linear algebra the solutions could be entire spaces.
Geometric interpretation
Lines in two dimensions
Equations of the form $ax + by = c$ correspond to lines in $\mathbb{R}^2$. Thus, solving systems of equations of the form: \[ \begin{eqnarray} a_1 x + b_1 y & = & c_1, \nl a_2 x + b_2 y & = & c_2. \end{eqnarray} \] corresponds to finding the point $(x,y) \in \mathbb{R}^2$ where these lines intersect. There are three possibilities for the solution set:
- One solution if the two lines intersect at a point.
- Infinitely many solutions if the lines are superimposed.
- No solution: If the two lines are parallel,
then they will never intersect.
Planes in three dimensions
Equations of the form $Ax + By + Cz = D$ corresponds to planes in $\mathbb{R}^3$. When we are solving three such equations simultaneously: \[ \begin{eqnarray} a_1 x + b_1 y + c_1 z & = & c_1, \nl a_2 x + b_2 y + c_2 z & = & c_2, \nl a_3 x + b_3 y + c_3 z & = & c_3, \end{eqnarray} \] we are looking for the set of points $(x,y,z)$ that satisfy all three of the equations. There are four possibilities for the solution set:
- One solution: Three non-parallel planes in $\mathbb{R}^3$ intersect at a point.
- Infinitely many solutions 1: If one of the plane equations is redundant, then
we are looking for the intersection of two planes. Two non-parallel planes intersect on a line.
- Infinitely many solutions 2: If two of the equations are redundant, then
the solution space is a plane.
- No solution: If two (or more) of the planes are parallel,
then they will never intersect.
Computer power
The computer algebra system at http://live.sympy.org can be used to compute the reduced
row echelon form of any matrix. Here is an example of how to create a sympy Matrix object.
>>> from sympy.matrices import Matrix
>>> A = Matrix( [[2,-3,-8, 7],
[-2,-1,2,-7],
[1 ,0,-3, 6]])
>>> A
[ 2, -3, -8, 7]
[-2, -1, 2, -7]
[ 1, 0, -3, 6]
To compute the reduced row echelon form of a matrix,
call its rref method:
>>> A.rref() ([1, 0, 0, 0] # RREF of A [0, 1, 0, 3] # locations of pivots [0, 0, 1, -2], [0, 1, 2] )
In this case sympy returns a tuple containing the RREF of $A$
and an array that tells us the 0-based indices of the columns which contain the leading ones.
Since usually we just want to find the RREF of $A$, you can select the first (index zero) element of the tuple:
>>> Arref = A.rref()[0] >>> Arref [1, 0, 0, 0] [0, 1, 0, 3] [0, 0, 1, -2]
Discussion
The Gauss-Jordan elimination algorithm for simplifying matrices which you learned in this section is one of the most important computational tools of linear algebra. It is applicable not only to systems of linear equations but much more broadly in many contexts. We will discuss other applications of the Gauss-Jordan elimination algorithm the section Applications of Gauss-Jordan elimination.
Exercises
Verify that you can carry out the Gauss-Jordan elimination procedure by hand and obtain the RREF of the following matrix: \[ \left[\begin{array}{ccc|c} 2 & -3 & -8 & 7\nl -2 & -1 & 2 & -7\nl 1 & 0 & -3 & 6 \end{array}\right] \quad - \ \textrm{ G-J elimination} \to \quad \left[\begin{array}{ccc|c} 1 & 0 & 0 & 0\nl 0 & 1 & 0 & 3\nl 0 & 0 & 1 & -2 \end{array}\right]. \] If solution to the system of equations which corresponds to this augmented matrix is $(0,3,-2)$.
Vectors operations
In the chapter on vectors, we described the practical aspects of vectors. Also, people who have studied mechanics should be familiar with the force calculations which involved vectors.
In this section, we will describe vectors more abstractly—as mathematical objects. The first thing to do after one defines a new mathematical object is to specify its properties and the operations that we can perform on them. What can you do with numbers? I know how to add, subtract, multiply and divide numbers. The question, now, is to figure out the equivalent operations applied to vectors.
Formulas
Consider two vectors $\vec{u}=(u_1,u_2,u_3) $ and $\vec{v}=(v_1,v_2,v_3)$, and assume that $\alpha$ is some number. We have the following properties:
\[ \begin{align} \alpha \vec{u} &= (\alpha u_1,\alpha u_2,\alpha u_3) \nl \vec{u} + \vec{v} &= (u_1+v_1,u_2+v_2,u_3+v_3) \nl \vec{u} - \vec{v} &= (u_1-v_1,u_2-v_2,u_3-v_3) \nl ||\vec{u}|| &= \sqrt{u_1^2+u_2^2+u_3^2} \nl \vec{u} \cdot \vec{v} &= u_1v_1+u_2v_2+u_3v_3 \nl \vec{u} \times \vec{v} &= (u_2v_3-u_3v_2,\ u_3v_1-u_1v_3,\ u_1v_2-u_2v_1) \end{align} \]
In the sections that follow we will see what these operations can do for us and what they imply.
Notation
The set of real numbers is denoted $\mathbb{R}$, and vectors consists of $d$ numbers, slapped together in a bracket. The numbers in the bracket are called components. If $d=3$, we will denote the set of vectors as: \[ ( \mathbb{R}, \mathbb{R}, \mathbb{R} ) \equiv \mathbb{R}^3 = \mathbb{V}(3), \] and similarly for more dimensions.
The notation $\mathbb{V}(n)$ for the set of $n$-dimensional vectors is particular to this section. It will be useful here as an encapsulation method, when we want to describe function signatures: what parameters it takes as inputs, and what outputs it produces. This section lists all the operations that take one or more elements of $\mathbb{V}(n)$ as inputs.
Basic operations
Addition and subtraction
Addition and subtraction take two vectors as inputs and produce another vector as output. \[ +: \mathbb{V} \times \mathbb{V} \to \mathbb{V} \]
The addition and subtraction operations are performed component wise: \[ \vec{w}=\vec{u}+\vec{v} \qquad \Leftrightarrow \qquad w_{i} = u_i + v_i, \quad \forall i \in [1,\ldots,d]. \]
Scaling by a constant
The scaling of a vector by a constant is an operation that has the signature: \[ \textrm{scalar-mult}: \mathbb{R} \times \mathbb{V} \ \to \ \mathbb{V}. \] There is no symbol to denote scalar multiplication—we just write the scaling factor in front of the vector and it is implicit that we are multiplying the two.
The scaling factor $\alpha$ multiplying the vector $\vec{u}$ is equivalent to this scaling factor multiplying each component of the vector: \[ \vec{w}=\alpha\vec{u} \qquad \Leftrightarrow \qquad w_{i} = \alpha u_i, \quad \forall i \in [1,\ldots,d]. \] For example, choosing $\alpha=2$ we obtain the vector $\vec{w}=2\vec{u}$ which is two times longer than the vector $\vec{v}$: \[ \vec{w}=(w_1,w_2,w_3) = (2u_1,2u_2,2u_3) = 2(u_1,u_2,u_3) = 2\vec{u}. \]
TODO copy over images from vectors chapter, and import other good passages
Vector multiplication
There are two ways to multiply vectors. The dot product: \[ \cdot: \mathbb{V} \times \mathbb{V}\ \to \mathbb{R}, \] \[ c=\vec{u}\cdot\vec{v} \qquad \Leftrightarrow \qquad c = \sum_{i=1}^d u_iv_i, \] and the cross product: \[ \times: \mathbb{V}(3) \times \mathbb{V}(3) \ \to \mathbb{V}(3) \] \[ \vec{w} = \vec{u} \times \vec{v} \qquad \Leftrightarrow \qquad \begin{array}{rcl} w_1 &=& u_2v_3-u_3v_2, \nl w_2 &=& u_3v_1-u_1v_3, \nl w_3 &=& u_1v_2-u_2v_1. \end{array} \] The dot product is defined for any dimension $d$. So long as the two inputs are of the same length, we can “zip” down their length computing the sum of the products of the corresponding entries.
The dot product is the key tool for dealing with projections, decompositions, and calculating orthogonality. It is also known as the scalar product or the inner product. Intuitively, applying the dot product to two vectors produces a scalar number which carries information about how similar the two vectors are. Orthogonal vectors are not similar at all, since no part of one vector goes in the same direction as the other, so their dot product will be zero. For example: $\hat{\imath} \cdot \hat{\jmath} = 0$. Another notation for the inner product is $\langle u | v \rangle \equiv \vec{u} \cdot \vec{v}$.
The cross product or vector product as it is sometimes called, is an operator which returns a vector that is perpendicular to both of the input vectors. For example: $\hat{\imath} \times \hat{\jmath} = \hat{k}$. Note the cross product is only defined for $3$-dimensional vectors.
Length of a vector
The length of the vector $\vec{u} \in \mathbb{R}^d$ is computed as follows: \[ \|\vec{u}\| = \sqrt{u_1^2+u_2^2+ \cdots + u_d^2 } = \sqrt{ \vec{u} \cdot \vec{u} }. \] The length is number (always greater than zero) which describes the extent of the vector in space. The notion of length is a generalization of Pythagoras' formula for the length hypotenuse of a triangle given the lengths of the two sides (the components).
There exits more mathematically precise ways of talking about the intuitive notion of length. We could specify that we mean Euclidian length of the vector, or the ell-two norm $|\vec{u}|_2 \equiv ||u||$.
The first of these refers to the notion of a Euclidian space, which is the usual flat space that we are used to. Non-Euclidian geometries are possible. For example, the surface of the earth is spherical in shape and so when talking about lengths on the surface of the earth we will need to use spherical length, not Euclidian length. The name ell-two norm refers to the fact that we raise each coefficient to the second degree and then take the square root when computing the length. An example of another norm is the ell-four norm which is defined as the fourth root of the sum of the components raised to the fourth power: $|\vec{u}|_4 \equiv \sqrt[4]{u_1^4+u_2^4+u_3^4}$.
Often times in physics, we denote the length of a vector $\vec{r}$ simply as $r$. Another name for length is magnitude.
Note how the length of a vector can be computed by taking the dot product of the vector with itself and then taking the square root: \[ \|\vec{v}\| = \sqrt{ \vec{v} \cdot \vec{v} }. \]
Unit vector
Given a vector $\vec{v}$ of any length, we can build a unit vector in the same direction by dividing $\vec{v}$ by its length: \[ \hat{v} = \frac{\vec{v}}{ ||\vec{v}|| }. \]
Unit vectors are useful in many contexts. In general, when we want to specify a direction in space, we use a unit vector in that direction.
Projection
If I give you a direction $\hat{d}$ and some vector $\vec{v}$ and ask you how much of $\vec{v}$ is in the $\hat{d}$-direction, then the answer is computed using the dot product: \[ v_d = \hat{d} \cdot \vec{v} \equiv \| \hat{d} \| \|\vec{v} \| \cos\theta = 1\|\vec{v} \| \cos\theta, \] where $\theta$ is the angle between $\vec{v}$ and $\hat{d}$. We used this formula a lot in physics when we were computing the $x$-component of a force $F_x = \|\vec{F}\|\cos\theta$.
We define the projection of a vector $\vec{v}$ in the $\hat{d}$ direction as follows: \[ \Pi_{\hat{d}}(\vec{v}) = v_d \hat{d} = (\hat{d} \cdot \vec{v})\hat{d}. \]
If the direction is specified by a unit vector $\vec{d}$ which is not unit length, then the formula becomes: \[ \Pi_{\vec{d}}(\vec{v}) = \left(\frac{ \vec{d} \cdot \vec{v} }{ \|\vec{d}\|^2 } \right) \vec{d}. \] The division by the length squared is necessary in order to turn the vectors $\vec{d}$ into unit vectors $\hat{d}$ as required but the projection formula: \[ \Pi_{\vec{d}}(\vec{v}) = (\vec{v}\cdot\hat{d}) \:\hat{d} = \left(\vec{v}\cdot \frac{\vec{d}}{\|\vec{d}\|}\right) \frac{\vec{d}}{\|\vec{d}\|} = \left(\frac{\vec{v}\cdot\vec{d}}{\|\vec{d}\|^2}\right)\vec{d}. \]
Discussion
This section was a review of the properties of $d$-dimensional vectors. These are simply ordered tuples (lists) of $d$ coefficients. It is important to think of vectors as mathematical objects and not as coefficients. Sure, all the vector operations boil down to manipulations of the coefficients in the end, but vectors are most useful (and best understood) if you think of them as one thing that has components rather than focussing on the components.
In the next section we will learn about another mathematical object: the matrix, which is nothing more than a two-dimensional array (a table) of numbers. Again, you will see, that matrices are more useful when you think of their properties as mathematical objects rather than focussing on the individual numbers that make up their rows and columns.
Matrix operations
Consider the $m$ by $n$ matrix $A \in \mathbb{M}(m,n)\equiv \mathbb{R}^{m\times n}$. What operations can we do on it?
Notation
We denote the matrix as a whole $A$ and refer to its individual entries as $a_{ij}$, where $a_{ij}$ is the entry in the $i$-th row and the $j$-th column of $A$.
Addition and subtraction
The matrix addition and subtraction operations take two matrices as inputs (the matrices must have the same dimensions). \[ +: \mathbb{M}, \mathbb{M} \to \mathbb{M}, \qquad -: \mathbb{M}, \mathbb{M} \to \mathbb{M}. \]
The addition and subtraction operations are performed component wise. For two $m\times n$-matrices $A$ and $B$, their sum is the matrix $C$ with entries: \[ C = A + B \Leftrightarrow c_{ij} = a_{ij} + b_{ij}, \forall i \in [1,\ldots,m], j\in [1,\ldots,n]. \]
Or written out explicitly for $3\times3$ matrices: \[ \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right] + \left[\begin{array}{ccc} b_{11} & b_{12} & b_{13} \nl b_{21} & b_{22} & b_{23} \nl b_{31} & b_{32} & b_{33} \end{array}\right] = \left[\begin{array}{ccc} a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \nl a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \nl a_{31}+b_{31} & a_{32}+b_{32} & a_{33}+b_{33} \end{array}\right]. \]
Multiplication by a constant
Given a number $\alpha$ and a matrix $A$, we can scale $A$ by $\alpha$: \[ \alpha A = \alpha \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right] = \left[\begin{array}{ccc} \alpha a_{11} & \alpha a_{12} & \alpha a_{13} \nl \alpha a_{21} & \alpha a_{22} & \alpha a_{23} \nl \alpha a_{31} & \alpha a_{32} & \alpha a_{33} \end{array}\right] \]
Matrix-vector multiplication
The matrix-vector product of some matrix $A \in \mathbb{R}^{m\times n}$ and a vector $\vec{v} \in \mathbb{R}^n$ consists of computing the dot product between the vector $\vec{v}$ and each of the rows of $A$: \[ \textrm{matrix-vector product} : \mathbb{M}(m,n) \times \mathbb{V}(n) \to \mathbb{V}(m) \] \[ \vec{w} = A\vec{v} \Leftrightarrow w_{i} = \sum_{j=1}^n a_{ij}v_{j}, \forall i \in [1,\ldots,m]. \]
\[ A\vec{v} = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right] \left[\begin{array}{c} v_{1} \nl v_{2} \nl v_{3} \end{array}\right] = \left[\begin{array}{c} a_{11}v_{1} + a_{12}v_{2} + a_{13}v_{3} \nl a_{21}v_1 + a_{22}v_2 + a_{23}v_3 \nl a_{31}v_1 + a_{32}v_2 + a_{33}v_3 \end{array}\right] \quad \in \mathbb{R}^{3 \times 1}. \]
Matrix-matrix multiplication
The matrix multiplication $AB$ of matrices $A \in \mathbb{R}^{m\times n}$ and $B \in \mathbb{R}^{n\times \ell}$ consists of computing the dot product between each the rows of $A$ and each the columns of $B$. \[ \textrm{matrix-product} : \mathbb{M}(m,n) \times \mathbb{M}(n,\ell) \to \mathbb{M}(m,\ell) \] \[ C = AB \Leftrightarrow c_{ij} = \sum_{k=1}^n a_{ik}b_{kj}, \forall i \in [1,\ldots,m],j \in [1,\ldots,\ell]. \]
\[ \left[\begin{array}{ccc} a_{11} & a_{12} \nl a_{21} & a_{22} \nl a_{31} & a_{32} \end{array}\right] \left[\begin{array}{ccc} b_{11} & b_{12} \nl b_{21} & b_{22} \nl \end{array}\right] = \left[\begin{array}{ccc} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \nl a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} \nl a_{31}b_{11} + a_{32}b_{21} & a_{31}b_{12} + a_{32}b_{22} \end{array}\right] \qquad \in \mathbb{R}^{3 \times 2}. \]
Transpose
The transpose of a matrix $A$ is defined by: $a_{ij}^T=a_{ji}$, i.e., we just “flip” the matrix through the diagonal: \[ \textrm{T} : \mathbb{M}(m,n) \to \mathbb{M}(n,m), \] \[ \begin{bmatrix} \alpha_1 & \alpha_2 & \alpha_3 \nl \beta_1 & \beta_2 & \beta_3 \end{bmatrix}^T = \begin{bmatrix} \alpha_1 & \beta_1 \nl \alpha_2 & \beta_2 \nl \alpha_3 & \beta_3 \end{bmatrix}. \]
Note that the entries on the diagonal are not changed by the transpose operation.
Properties
\[ \begin{align*} (A+B)^T &= A^T + B^T \nl (AB)^T &= B^TA^T \nl (ABC)^T &= C^TB^TA^T \nl (A^T)^{-1} &= (A^{-1})^T \end{align*} \]
Vectors as matrices
You can think of vectors as a special kinds of matrices. You can think of a vector $\vec{v}$ either as a column vector (an $n\times 1$ matrix) or as a row vector (a $1 \times n$ matrix).
Inner product
Recall the definition of the dot product or inner product for vectors: \[ \textrm{inner-product} : \mathbb{V}(n) \times \mathbb{V}(n) \to \mathbb{R}. \] Given two $n$-dimensional vectors $\vec{u}$ and $\vec{v}$ with real coefficients, their dot product is computed as follows: $\vec{u}\cdot\vec{v} = \sum_{i=1}^n u_iv_i$.
If we think of these vectors as column vectors, i.e., think of them as $n\times1$ matrices, then we can write the dot product using the transpose operation $T$ and the standard rules of matrix multiplication: \[ \vec{u}\cdot \vec{v} = \vec{u}^T\vec{v} = \left[\begin{array}{ccc} u_{1} & u_{2} & u_{3} \end{array}\right] \left[\begin{array}{c} v_1 \nl v_2 \nl v_3 \end{array}\right] = u_1v_1 + u_2v_2 + u_3v_3. \]
You see that the dot product for vectors is really a special case of matrix multiplication. Alternately, you say that the matrix multiplication was defined in terms of the dot product.
Outer product
Consider again two column vectors ($n\times 1$ matrices) $\vec{u}$ and $\vec{v}$. We obtain the inner product if we put the transpose on the first vector $\vec{u}^T\vec{v}\equiv \vec{u}\cdot \vec{v}$. If instead we put the transpose on the second vector, we will obtain the outer product of $\vec{u}$ and $\vec{v}$: \[ \vec{u}\vec{v}^T = \left[\begin{array}{c} u_1 \nl u_2 \nl u_3 \end{array}\right] \left[\begin{array}{ccc} v_{1} & v_{2} & v_{3} \end{array}\right] = \begin{bmatrix} u_1v_1 & u_1v_2 & u_1v_3 \nl u_2v_1 & u_2v_2 & u_2v_3 \nl u_3v_1 & u_3v_2 & u_3v_3 \end{bmatrix} \qquad \in \mathbb{R}^{n \times n}. \] The result of this outer product is an $n \times n$ matrix. It is the result of a multiplication of an $n\times1$ matrix and a $1 \times n$ matrix. More specifically, the outer product is a map that takes two vectors as inputs and gives a matrix as output: \[ \textrm{outer-product} : \mathbb{V}(n) \times \mathbb{V}(n) \to \mathbb{M}(n,n). \] The outer product can be used to build projection matrices. For example, the matrix which corresponds to the projection onto the $x$-axis is given by $M_x = \hat{\imath}\hat{\imath}^T \in \mathbb{R}^{n \times n}$. The $x$-projection of any vector $\vec{v}$ can be computed as a matrix-vector product: $M_x\vec{v} = \hat{\imath}\hat{\imath}^T\vec{v} = \hat{\imath}(\hat{\imath}\cdot\vec{v}) = v_x \hat{\imath}$. The last equation follows dot-product formula for calculating the components of vectors.
Matrix inverse
The inverse matrix $A^{-1}$ has the property that $A A^{-1}=I = A^{-1}A$, where $I$ is the identity matrix which obeys $I\vec{v} = \vec{v}$ for all vectors $\vec{v}$. The inverse matrix $A^{-1}$ has the effect of undoing whatever $A$ did. The cumulative effect of multiplying by $A$ and $A^{-1}$ is equivalent to the identity transformation: \[ A^{-1}(A(\vec{v})) = (A^{-1}A)\vec{v} = I\vec{v} = \vec{v}. \]
We can think of “finding the inverse” $\textrm{inv}(A)=A^{-1}$ as an operation of the form: \[ \textrm{inv} : \mathbb{M}(n,n) \to \mathbb{M}(n,n). \] Note that only invertible matrices have an inverse.
Properties
\[ \begin{align*} (A+B)^{-1} &= A^{-1} + B^{-1} \nl (AB)^{-1} &= B^{-1}A^{-1} \nl (ABC)^{-1} &= C^{-1}B^{-1}A^{-1} \nl (A^T)^{-1} &= (A^{-1})^T \end{align*} \]
The matrix inverse plays the role of “division by the matrix A” in matrix equations. We will discuss the peculiarities of associated with matrix equations in the next section.
Trace
The trace of an $n\times n$ matrix, \[ \textrm{Tr} : \mathbb{M}(n,n) \to \mathbb{R}, \] is the sum of the $n$ values on the diagonal of the matrix: \[ \textrm{Tr}\!\left[ A \right] \equiv \sum_{i=1}^n a_{ii}. \]
Properties
\[ \begin{align*} \textrm{Tr}\!\left[ A + B\right] &= \textrm{Tr}\!\left[ A \right] + \textrm{Tr}\!\left[ B\right] \nl \textrm{Tr}\!\left[ AB \right] &= \textrm{Tr}\!\left[ BA \right] \nl \textrm{Tr}\!\left[ ABC \right] &= \textrm{Tr}\!\left[ CAB \right] = \textrm{Tr}\!\left[ BCA \right] \nl \textrm{Tr}\!\left[ A \right] &= \sum_{i=1}^{n} \lambda_i \qquad \textrm{ where } \{ \lambda_i\} = \textrm{eig}(A) \textrm{ are the eigenvalues } \nl \textrm{Tr}\!\left[ A^T \right] &= \textrm{Tr}\!\left[ A \right] \nl \end{align*} \]
Determinant
The determinant of a matrix is a calculation which involves all the coefficients of the matrix and the output of which a single real number: \[ \textrm{det} : \mathbb{M}(n,n) \to \mathbb{R}. \]
The determinant describes the relative geometry of the vectors that make up the matrix. More specifically, the determinant of a matrix $A$ tells you the volume of a box with sides given by rows of $A$.
For example, the determinant of a $2\times2$ matrix is \[ \det(A) = \det\left(\begin{array}{cc}a&b\nl c&d \end{array}\right) =\left|\begin{array}{cc}a&b\nl c&d \end{array}\right| =ad-cb, \] which corresponds to the area of the parallelogram formed by the vectors $(a,b)$ and $(c,d)$. Observe that if the rows of $A$ point in the same direction $(a,b) = \alpha(c,d)$ for some $\alpha \in \mathbb{R}$, then the area of the parallelogram will be zero. Conversely, if the determinant of a matrix is non-zero then the rows the matrix must be linearly independent.
Properties
\[ \begin{align*} \textrm{det}\!\left( AB\right) &= \textrm{det}\!\left( A \right)\textrm{det}\!\left( B\right) \nl \textrm{det}\!\left( A \right) &= \prod_{i=1}^{n} \lambda_i \qquad \textrm{ where } \{\lambda_i\} = \textrm{eig}(A) \textrm{ are the eigenvalues } \nl \textrm{det}\!\left( A^T \right) &= \textrm{det}\!\left( A \right) \nl \textrm{det}\!\left( A^{-1}\right) &= \frac{1}{\textrm{det}\!\left( A \right) } \end{align*} \]
Similarity transformation
For any invertible matrix $P$ we can define the similarity transformation: \[ \textrm{Sim}_P : \mathbb{M}(n,n) \to \mathbb{M}(n,n), \] which acts as follows: \[ \textrm{Sim}_P(A) = P A P^{-1}. \]
The similarity transformation $A^\prime = P A P^{-1}$ leaves many of the properties of the matrix unchanged:
- Trace: $\textrm{Tr}\!\left( A^\prime \right) = \textrm{Tr}\!\left( A \right)$.
- Determinant: $\textrm{det}\!\left( A^\prime \right) = \textrm{det}\!\left( A \right)$.
- Rank: $\textrm{rank}\!\left( A^\prime \right) = \textrm{rank}\!\left( A \right)$.
- Eigenvalues: $\textrm{eig}\!\left( A^\prime \right) = \textrm{eig}\!\left( A \right)$.
A similarity transformation can be interpreted as a change of basis in which case the matrix $P$ is called the change-of-basis matrix.
Discussion
In the remainder of this chapter we will learn about various algebraic and geometric interpretations for each of the matrix operations defined above. But first we must begin with an important discussion about matrix equations and how they differ from equations with numbers.
Matrix equations
If $a,b$ and $c$ were three numbers, and I told you to solve for $a$ in the equation \[ ab = c, \] then you would know to tell me that the answer is $a = c/b = c\frac{1}{b}=\frac{1}{b}c$, and that would be the end of it.
Now suppose that $A$, $B$ and $C$ are matrices and you want to solve for $A$ in the matrix equation \[ AB = C. \]
The naive answer $A=C/B$ is not allowed. So far, we have defined a matrix product and matrix inverse, but not matrix division. Instead of division, we must do a multiplication by $B^{-1}$, which plays the role of the “divide by $B$” operation since the product of $B$ and $B^{-1}$ gives the identity matrix: \[ BB^{-1} = I, \qquad B^{-1}B = I. \] When applying the inverse matrix $B^{-1}$ to the equation, we must specify whether we are multiplying from the left or from the right because the matrix product is not commutative. What do you think is the right answer for $A$ in the above equations? Is it this one $A = CB^{-1}$ or this one $A = B^{-1}C$?
Matrix equations
To solve a matrix equation we will employ the same technique as we used to solve equations in the first chapter of the book. Recall that doing the same thing to both sides of any equation gives us a new equation that is equally valid as the first. There are only two new things you need to keep in mind for matrix equations:
- The order in which the matrices are multiplied matters
because the matrix product is not a commutative operation $AB \neq BA$.
This means that the two expressions $ABC$ and $BAC$ are different, despite the fact that they are the product of the same matrices. * When performing operations on matrix equations you can act either from the //left// or from the //right// side of the equation.
The best way to get you used to the peculiarities of matrix equations is to look at some examples together. Don't worry there will be nothing too mathematically demanding. We will just explain what is going on with pictures.
In the following examples, the unknown (matrix) we are trying to solve is shaded in. Your task is to solve this equation for the unknown by isolating it on one side of the equation. Let us see what is going on.
Matrix times a matrix
Let us continue with the equation we were trying to solve in the introduction: $AB=C$. In order to solve for $A$ in
we will can multiply by $B^{-1}$ from the right on both sides of the equation:
This is good stuff because $B$ and $B^{-1}$ will cancel out ($BB^{-1}=I$) and give us the answer:
Matrix times a matrix variation
Okay, but what if we were trying to solve for $B$ in $AB=C$. How would we proceed then?
The answer is, again, to do the same to both sides of the equation. If we want to cancel $A$, then we have to multiply by $A^{-1}$ from the left:
The result will be:
Matrix times a vector
We start with the equation \[ A\vec{x}=\vec{b}, \] which shows some $n\times n$ matrix $A$, and the vectors $\vec{x}$ and $\vec{b}$, which are nothing more than tall and skinny matrices of dimensions $n \times 1$.
Assuming that $A$ is invertible, there is nothing special to do here and we proceed by multiplying by the inverse $A^{-1}$ on the left of both sides of the equation. We get:
By definition, $A^{-1}$ times its inverse $A$ is equal to the identity $I$, which is a diagonal matrix with ones on the diagonal and zeros everywhere else:
The product of anything with the identity is the thing itself:
which is our final answer.
Note however that the question “Solve for $\vec{x}$ in $A\vec{x} = \vec{b}$” can sometimes be asked in situations where the matrix $A$ is not invertible. If the system of equations is under-specified (A is wider than it is tall), then there will be a whole subspace of acceptable solutions $\vec{x}$. If the system is over-specified (A is taller than it is wide) then we might be interested in finding the best fit vector $\vec{x}$ such that $A\vec{x} \approx \vec{b}$. Such approximate solutions are of great practical importance in much of science.
\[ \ \]
This completes our lightning tour of matrix equations. There is nothing really new to learn here, I just had to make you aware of the fact that the order in which you apply do matrix operations matters and remind you the general principle of “doing the same thing to both sides of the equation”. Acting according to this principle is really important when manipulating matrices.
In the next section we look at matrix equations in more details as we analyze the properties of matrix multiplication. We will also discuss several algorithms for computing the matrix inverse.
Exercises
Solve for X
Solve for the matrix $X$ the following equations: (1) $XA = B$, (2) $ABCXD = E$, (3) $AC = XDC$. Assume the matrices $A,B,C$ and $D$ are all invertible.
Ans: (1) $X = BA^{-1}$, (2) $X = C^{-1}B^{-1}A^{-1}E D^{-1}$, (3) $X=AD^{-1}$.
Matrix multiplication
Suppose we are given two matrices \[ A = \left[ \begin{array}{cc} a&b \nl c&d \end{array} \right], \qquad B = \left[ \begin{array}{cc} e&f \nl g&h \end{array} \right], \] and we want to multiply them together.
Unlike matrix addition and subtraction, matrix products are not performed element-wise: \[ \left[ \begin{array}{cc} a&b \nl c&d \end{array} \right] \left[ \begin{array}{cc} e&f \nl g&h \end{array} \right] \neq \left[ \begin{array}{cc} ae&bf \nl cg&dh \end{array} \right]. \]
Instead, the matrix product is computed by taking the dot product of each row of the matrix on the left with each of the columns of the matrix on the right: \[ \begin{align*} \begin{array}{c} \begin{array}{c} \vec{r}_1 \nl \vec{r}_2 \end{array} \left[ \begin{array}{cc} a & b \nl c & d \end{array} \right] \nl \ \end{array} \begin{array}{c} \left[ \begin{array}{cc} e&f \nl g&h \end{array} \right] \nl {\vec{c}_1} \ \ {\vec{c}_2} \end{array} & \begin{array}{c} = \nl \ \end{array} \begin{array}{c} \left[ \begin{array}{cc} \vec{r}_1 \cdot \vec{c}_1 & \vec{r}_1 \cdot \vec{c}_2 \nl \vec{r}_2 \cdot \vec{c}_1 & \vec{r}_2 \cdot \vec{c}_2 \end{array} \right] \nl \ \end{array} \nl & = \left[ \begin{array}{cc} ae+ bg & af + bh \nl ce + dg & cf + dh \end{array} \right]. \end{align*} \] Recall that the dot product between to vectors $\vec{v}$ and $\vec{w}$ is given by $\vec{v}\cdot \vec{w} \equiv \sum_i v_iw_i$.
Let's now look at a picture which shows how to compute the product of a matrix with four rows and a matrix with five columns.
The top left entry of the product is computed by taking the dot product of the first row of the matrix on the left and the first column of the matrix on the right:
Similarly, the entry on the third row and fourth column of the product is computed by taking the dot product of the third row of the matrix on the left and the fourth column of the matrix on the right:
Note the size of the rows of the matrix on the left must equal the size of the columns of the matrix on the right for the product to be well defined.
Matrix multiplication rules
- Matrix multiplication is associative:
\[ (AB)C = A(BC) = ABC. \]
- The “touching” dimensions of the matrices must be the same.
For the triple product $ABC$ to exits, the number of rows of $A$ must
be equal to the number of columns of $B$ and the number of rows
of $B$ must equal the number of columns of $C$.
* Given two matrices $A \in \mathbb{R}^{m\times n}$ and $B \in \mathbb{R}^{n\times k}$,
the matrix product $AB$ will be a $m \times k$ matrix.
* The matrix product is //not commutative//:
{{:linear_algebra:linear_algebra--matrix_multiplication_not_commutative.png?300|Matrix multiplication is not commutative.}}
Explanations
Why is matrix multiplication defined like this? We will learn about this more in depth in the linear transformations section, but I don't want you to live in suspense until then, so I will tell you right now. You can think of multiplying some column vector $\vec{x} \in \mathbb{R}^n$ by a matrix $A \in \mathbb{R}^{m\times n}$ as analogous to applying the “vector function” $A$ on the vector input $\vec{x}$ to obtain a vector $\vec{y}$: \[ A: \mathbb{R}^n \to \mathbb{R}^m. \] Applying the vector function $A$ to the input $\vec{x}$ is the same as computing the matrix-vector product between $A\vec{x}$: \[ \textrm{for all } \vec{x} \in \mathbb{R}^n, \quad A\!\left(\vec{x}\right) \equiv A\vec{x}. \] Any linear function from $\mathbb{R}^n$ to $\mathbb{R}^m$ can be described as a matrix product by some matrix $A \in \mathbb{R}^{m\times n}$.
Okay, so what if you have some vector and you want to apply two linear operations on it. With functions, we call this function composition and we use a little circle to denote it: \[ z = g(f(x)) = g\circ f\:(x), \] where $g\circ f\;(x) $ means that you should apply $f$ to $x$ first to obtain some intermediary value $y$, and then you apply $g$ to $y$ to get the final output $z$. The notation $g \circ f$ is useful when you don't want to talk about the intermediary variable $y$ and you are interested in the overall functional relationship between $x$ and $z$. For example, we can define $h \equiv g\circ f$ and then talk about the properties of the function $h$.
With matrices, $B\circ A$ (applying $A$ then $B$) is equal to applying the product matrix $BA$: \[ \vec{z} = B\!\left( A(\vec{x}) \right) = (BA) \vec{x}. \] Similar to the case with functions, we can describe the overall map from $\vec{x}$'s to $\vec{z}$'s by a single entity $M\equiv BA$, and not only that, but we can even compute $M$ by taking the product of $B$ and $A$. So matrix multiplication turns out to be a very useful computational tool. You probably wouldn't have guessed this, given how tedious and boring the actual act of multiplying matrices is. But don't worry, you just have to multiply a couple of matrices by hand to learn how multiplication works. Most of the times, you will let computers multiply matrices for you. They are good at this kind of shit.
This perspective on matrices as linear transformations (functions on vectors) will also allow you to understand why matrix multiplication is not commutative. In general $BA \neq AB$ (non-commutativity of matrices), just the same way there is no reason to expect that $f \circ g$ will equal $g \circ f$ for two arbitrary functions.
Exercises
Basics
Compute the product \[ \left[ \begin{array}{cc} 1&2 \nl 3&4 \end{array} \right] \left[ \begin{array}{cc} 5&6 \nl 7&8 \end{array} \right] = \left[ \begin{array}{cc} \ \ \ & \ \ \ \nl \ \ \ & \ \ \ \end{array} \right] \]
Ans: $\left[ \begin{array}{cc}
19&22 \nl
43&50
\end{array}
\right]$
Determinants
The determinant of a matrix, denoted $\det(A)$ or $|A|$, is a particular way to multiply the entries of the matrix and produce a single number. The determinant operation takes a square matrix as input and produces a number as output: \[ \textrm{det}: \mathbb{R}^{n \times n} \to \mathbb{R}. \] We use determinants for all kinds of tasks: to compute areas and volumes, to solve systems of equations, to check whether a matrix is invertible or not, and many other tasks. The determinant calculation can be interpreted in several different ways.
The most intuitive interpretation of the determinant is the geometric one. Consider the geometric shape constructed using the rows of the matrix $A$ as the edges of the shape. The determinant is the “volume” of a this geometric shape. For $2\times 2$ matrices, the determinant corresponds to the area of a parallelogram. For $3 \times 3$ matrices, the determinant corresponds to the volume of a parallelepiped. For dimensions $d>3$ we say the determinant measures a $d$-dimensional hyper-volume of a $d$-dimensional parallele-something.
The determinant of the matrix $A$ is the scale factor associated with the linear transformation $T_A$ that is defined as the matrix-vector product with $A$: $T_A(\vec{x}) \equiv A\vec{x}$. The scale factor of the linear transformation $T_A$ describes how a unit cube (a cube with dimensions $1\times 1 \ldots \times 1$ in the input space will get transformed after going through $T_A$. The volume of the unit cube after passing through $T_A$ is $\det(A)$.
The determinant calculation can be used as a linear independence check for a set of vectors. The determinant of a matrix also tells us if the matrix is invertible or not. If $\det(A)=0$ then $A$ is not invertible. Otherwise, if $\det(A)\neq 0$, then $A$ is invertible.
The determinant has an important connection with the vector cross product and is also used in the definition of the eigenvalue equation. In this section we'll introduce all these aspects of determinants. I encourage you to try to connect the geometric, algebraic, and computational aspects of determinants as you read along. Don't worry if it doesn't all make sense right away—you can always come back and review this section once you have learned more about linear transformations, the geometry of the cross product, and the eigenvalue equation.
Formulas
For a $2\times2$ matrix, the determinant is \[ \det \!\left( \begin{bmatrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{bmatrix} \right) \equiv \begin{vmatrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{vmatrix} =a_{11}a_{22}-a_{12}a_{21}. \]
The formula for the determinants of larger matrices are defined recursively. For example, the $3 \times 3$ matrix is defined in terms of $2 \times 2$ determinants:
\[ \begin{align*} \ &\!\!\!\!\!\!\!\! \begin{vmatrix} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{vmatrix} = \nl &= a_{11} \begin{vmatrix} a_{22} & a_{23} \nl a_{32} & a_{33} \end{vmatrix} - a_{12} \begin{vmatrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \nl a_{31} & a_{32} \end{vmatrix} \nl &= a_{11}(a_{22}a_{33}-a_{23}a_{32}) - a_{12}(a_{21}a_{33} - a_{23}a_{31}) + a_{13}(a_{21}a_{32} - a_{22}a_{31}) \nl &= a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} -a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} +a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31}. \end{align*} \]
There is a neat computational trick for quickly computing $3 \times 3$ determinants which consists of extending the matrix $A$ into a $3\times 5$ array which contains the cyclic extension of the columns of $A$. The first column of $A$ is copied to in the fourth column of the array and the second column of $A$ is copied into the fifth column.
Computing the determinant is not the task of computing the sum of the three positive diagonals (solid lines) and subtracting the three negative diagonals (dashed lines).
The general formula for the determinant of an $n\times n$ matrix is \[ \det{A} = \sum_{j=1}^n \ (-1)^{1+j}a_{1j}\det(M_{1j}), \] where $M_{ij}$ is called the minor associated with the entry $a_{ij}$. The minor $M_{ij}$ is obtained by removing the $i$th row and the $j$th column of the matrix $A$. Note the “alternating term” $(-1)^{i+j}$ which switches between $1$ and $-1$ for the different terms in the formula.
In the case of $3 \times 3$ matrices, the determinant formula is \[ \begin{align*} \det{A} &= (1)a_{11}\det(M_{11}) + (-1)a_{12}\det(M_{12}) + (1)a_{13}\det(M_{13}) \nl &= a_{11} \begin{vmatrix} a_{22} & a_{23} \nl a_{32} & a_{33} \end{vmatrix} - a_{12} \begin{vmatrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \nl a_{31} & a_{32} \end{vmatrix} \end{align*} \]
The deteminant of a $4 \times 4$ matrix is \[ \det{A} = (1)a_{11}\det(M_{11}) + (-1)a_{12}\det(M_{12}) + (1)a_{13}\det(M_{13}) + (-1)a_{14}\det(M_{14}). \]
The general formula we gave above expands the determinant along the first row of the matrix. In fact, the formula for the determinant can be obtained by expanding along any row or column of the matrix. For example, expanding the determinant of a $3\times 3$ matrix along the second column corresponds to the following formula $\det{A} = (-1)a_{12}\det(M_{12}) + (1)a_{22}\det(M_{22}) + (-1)a_{32}\det(M_{32})$. The expand-along-any-row-or-column nature of determinants can be very handy sometimes: if you have to calculate the determinant of a matrix that has one row (or column) with many zero entries, then it makes sense to expand along that row because many of the terms in the formula will be zero. As an extreme case of this, if a matrix contains a row (or column) which consists entirely of zeros, its determinant is zero.
Geometrical interpretation
Area of a parallelogram
Suppose we are given two vectors $\vec{v} = (v_1, v_2)$ and $\vec{w} = (w_1, w_2)$ in $\mathbb{R}^2$ and we construct a parallelogram with corner points $(0,0), \vec{v}, \vec{w}, and \vec{v}+\vec{w}$.
The area of this parallelogram is equal to the determinant of the matrix which contains $(v_1, v_2)$ and $(w_1, w_2)$ as rows:
\[ \textrm{area} =\left|\begin{array}{cc} v_1 & v_2 \nl w_1 & w_2 \end{array}\right| = v_1w_2 - v_2w_1. \]
Volume of a parallelepiped
Suppose we are given three vectors $\vec{u} = (u_1, u_2, u_3)$, $\vec{v} = (v_1, v_2, v_3)$, and $\vec{w} = (w_1, w_2,w_3)$ in $\mathbb{R}^3$ and we construct the parallelepiped with corner points: $(0,0,0),\vec{v}, \vec{w}, \vec{v}+\vec{w}$, $\vec{u},\vec{u}+\vec{v}, \vec{u}+\vec{w}, and \vec{u}+\vec{v}+\vec{w}$.
The volume of this parallelepiped equal to the determinant of the matrix which contains the vectors $\vec{u}$, $\vec{v}$, and $\vec{w}$ as rows: \[ \begin{align*} \textrm{volume} &= \left|\begin{array}{ccc} u_1 & u_2 & u_3 \nl v_1 & v_2 & v_3 \nl w_1 & w_2 & w_3 \end{array}\right| \nl &= u_{1}(v_{2}w_{3} - v_{3}w_{2}) - u_{2}(v_{1}w_{3} - v_{3}w_{1}) + u_{3}(v_{1}w_{2} - v_{2}w_{1}). \end{align*} \]
Sign and absolute value of the determinant
The calculation of the area of a parallelogram and the volume of a parallelepiped using determinants can produce positive or negative numbers.
Consider the case of two dimensions. Given two vectors $\vec{v}=(v_1,v_2)$ and $\vec{w}=(w_1,w_2)$, we can construct the following determinant: \[ D \equiv \left|\begin{array}{cc} v_{1} & v_{2} \nl w_{1} & w_{2} \end{array}\right|. \] Let us denote the value of the determinant by $D$. The absolute value of the determinant is equal to the area of the parallelogram constructed by the vectors $\vec{v}$ and $\vec{w}$. The sign of the determinant (positive, negative or zero) tells us information about the relative orientation of the vectors $\vec{v}$ and $\vec{w}$. Let $\theta$ be the measure of the angle from $\vec{v}$ towards $\vec{w}$, then
- If $\theta$ is between $0$ and $\pi$[rad] ($180[^\circ]$),
the determinant will be positive $D>0$.
This is the case illustrated in {determinant-of-two-vectors} TODO FIX FIG REF.
* If $\theta$ is between
$\pi$ ($180[^\circ]$) and $2\pi$[rad] ($360[^\circ]$),
the determinant will be negative $D<0$.
* When $\theta=0$ (the vectors point in the same direction),
or when $\theta=\pi$ (the vectors point in opposite directions),
the determinant will be zero, $D=0$.
The formula for the area of a parallelogram is $A=b\times h$, where $b$ is the length of the base of a parallelogram and $h$ is the height of the parallelogram. In the case of the parallelogram in {determinant-of-two-vectors} TODO FIX FIG REF, the length of the base is $\|\vec{v}\|$ and the height is $\|\vec{w}\|\sin\theta$, where $\theta$ is the measure of the angle between $\vec{v}$ and $\vec{w}$. The geometrical interpretation of the $2\times 2$ determinant is describes by the following formula: \[ D \equiv \left|\begin{array}{cc} v_{1} & v_{2} \nl w_{1} & w_{2} \end{array}\right| \equiv v_1w_2 - v_2w_1 = \|\vec{v}\|\|\vec{w}\|\sin\theta. \] Observe the “height” of the parallelogram is negative when $\theta$ is between $\pi$ and $2\pi$.
Properties
Let $A$ and $B$ be two square matrices of the same dimension, then we have the following properties:
- $\det(AB) = \det(A)\det(B) = \det(B)\det(A) = \det(BA)$
- if $\det(A)\neq 0$ then the matrix is invertible, and
- $\det(A^{-1}) = \frac{1}{\det(A)}$
- $\det\!\left( A^T \right) = \det\!\left( A \right)$.
- $\det(\alpha A) = \alpha^n \det(A)$, for an $n \times n$ matrix $A$.
- $\textrm{det}\!\left( A \right) = \prod_{i=1}^{n} \lambda_i$,
where $\{\lambda_i\} = \textrm{eig}(A)$ are the eigenvalues of $A$.
TODO: More emphasis on detA = 0 or condition
The effects of row operations on determinants
Recall the three row operations that we used to produce the reduced row echelon form of a matrix as part of the Gauss-Jordan elimination procedure:
- Add a multiple of one row to another row.
- Swap two rows.
- Multiply a row by a constant.
The following figures describe the effects of row operations on the determinant of a matrix.
It is useful to think of the effects of the row operations in terms of the geometrical interpretation of the determinant. The first property follows from the fact that parallelograms with different slants have the same area. The second property is a consequence of the fact that we are measuring signed areas and that swapping two rows changes the relative orientation of the vectors. The third property follows from the fact that making one side of the parallelepiped $\alpha$ times longer, increases its volume of the parallelepiped by a factor of $\alpha$.
When the entire $n \times n$ matrix is multiplied by some constant $\alpha$, each of the rows is multiplied by $\alpha$ so the end result on the determinant is $\det(\alpha A) = \alpha^n \det(A)$, since $A$ has $n$ rows.
TODO: mention that isZero property of det is not affected by row operaitons
Applications
Apart from the geometric and invertibility-testing applications of determinants described above, determinants are used for many other tasks in linear algebra. We'll discuss some of these below.
Cross product as a determinant
We can compute the cross product of two vectors $\vec{v} = (v_1, v_2, v_3)$ and $\vec{w} = (w_1, w_2,w_3)$ in $\mathbb{R}^3$ by computing the determinant of a matrix. We place the vectors $\hat{\imath}$, $hat{\jmath}$, and $\hat{k}$ in the first row of the matrix, then write the vectors $\vec{v}$ and $\vec{w}$ in the second and third rows. After expanding the determinant along the first row, we obtain the cross product: \[ \begin{align*} \vec{v}\times\vec{w} & = \left|\begin{array}{ccc} \hat{\imath} & \hat{\jmath} & \hat{k} \nl v_1 & v_2 & v_3 \nl w_1 & w_2 & w_3 \end{array}\right| \nl & = \hat{\imath} \left|\begin{array}{cc} v_{2} & v_{3} \nl w_{2} & w_{3} \end{array}\right| \ - \hat{\jmath} \left|\begin{array}{cc} v_{1} & v_{3} \nl w_{1} & w_{3} \end{array}\right| \ + \hat{k} \left|\begin{array}{cc} v_{1} & v_{2} \nl w_{1} & w_{2} \end{array}\right| \nl &= (v_2w_3-v_3w_2)\hat{\imath} -(v_1w_3 - v_3w_1)\hat{\jmath} +(v_1w_2-v_2w_1)\hat{k} \nl & = (v_2w_3-v_3w_2,\ v_3w_1 - v_1w_3,\ v_1w_2-v_2w_1). \end{align*} \]
Observe that the anti-linear property of the vector cross product $\vec{v}\times\vec{w} = - \vec{w}\times\vec{v}$ corresponds to the swapping-rows-changes-the-sign property of determinants.
The extended-array trick for computing $3 \times 3$ determinants which we introduced earlier is a very useful approach for computing cross-products by hand.
Using the above correspondence between the cross-product and the determinant, we can write the determinant of a $3\times 3$ matrix in terms of the dot product and cross product: \[ \left|\begin{array}{ccc} u_1 & u_2 & u_3 \nl v_1 & v_2 & v_3 \nl w_1 & w_2 & w_3 \nl \end{array}\right| = \vec{u}\cdot(\vec{v}\times\vec{w}). \]
Cramer's rule
Cramer's rule is a way to solve systems of linear equations using determinant calculations. Consider the system of equations \[ \begin{align*} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 & = b_1, \nl a_{21}x_1 + a_{22}x_2 + a_{23}x_3 & = b_2, \nl a_{31}x_1 + a_{32}x_2 + a_{33}x_3 & = b_3. \end{align*} \] We are looking for the solution vector $\vec{x}=(x_1,x_2,x_3)$ that satisfies this system of equations.
Let's begin by rewriting the system of equations as an augment matrix: \[ \left[\begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \nl a_{21} & a_{22} & a_{23} & b_2 \nl a_{31} & a_{32} & a_{33} & b_3 \end{array}\right] \ \equiv \ \left[\begin{array}{ccc|c} | & | & | & | \nl \vec{a}_1 \ & \vec{a}_2 \ & \vec{a}_2 \ & \vec{b} \nl | & | & | & | \end{array}\right]. \] In the above equation I used the notation $\vec{a}_j$ to denote the $j^{th}$ column of coefficients in the augmented matrix and $\vec{b}$ is the column of constants.
Cramer's rule requires computing two determinants. To find $x_1$, the first component of the unknown vector $\vec{x}$, we compute the following ratio of determinants: \[ x_1= \frac{ \left|\begin{array}{ccc} | & | & | \nl \vec{b} & \vec{a}_2 & \vec{a}_2 \nl | & | & | \end{array}\right| }{ \left|\begin{array}{ccc} | & | & | \nl \vec{a}_1 & \vec{a}_2 & \vec{a}_2 \nl | & | & | \end{array}\right| } = \frac{ \left|\begin{array}{ccc} b_1 & a_{12} & a_{13} \nl b_2 & a_{22} & a_{23} \nl b_3 & a_{32} & a_{33} \end{array}\right| }{ \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right| }\;. \] Basically, we replace the column that corresponds to the unknown we want to solve for (in this case the first column) with the vector of constants $\vec{b}$ and compute the determinant.
To find $x_2$ we would compute the ratio of the determinants where $\vec{b}$ replaces the coefficients in the second column, and similarly to find $x_3$ we would replace the third column with $\vec{b}$. Cramer's rule is not a big deal, but it is neat computational trick to know that could come in handy if you ever want to solve for one particular coefficient in the unknown vector $\vec{x}$ and you don't care about the others.
Linear independence test
Suppose you are given a set of $n$, $n$-dimensional vectors $\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n \}$ and you asked to check whether these vectors are linearly independent.
We can use the Gauss–Jordan elimination procedure to accomplish this task. Write the vectors $\vec{v}_i$ as the rows of a matrix $M$. Next, use row operations to find the reduced row echelon form (RREF) of the matrix $M$. Row operations do not change the linear independence between the rows of the matrix so we use can the reduced row echelon form of the matrix $M$ to see if the rows are independent.
We can use the determinant test as direct way to check if the vectors are linearly independent. If $\det(M)$ is zero, the vectors that form the rows of $M$ are not linearly independent. On the other hand if $\det(M)\neq 0$, then the rows of $M$ and linearly independent.
Eigenvalues
The determinant operation is used to define the characteristic polynomial of a matrix and furthermore the determinant of $A$ is appears as the constant term in this polynomial:
\[ \begin{align*} p(\lambda) & \equiv \det( A - \lambda{11} ) \nl & = \begin{vmatrix} a_{11}-\lambda & a_{12} \nl a_{21} & a_{22}-\lambda \end{vmatrix} \nl & = (a_{11}-\lambda)(a_{22}-\lambda) - a_{12}a_{21} \nl & = \lambda^2 - \underbrace{(a_{11}+a_{22})}_{\textrm{Tr}(A)}\lambda + \underbrace{(a_{11}a_{22} - a_{12}a_{21})}_{\det{A}} \end{align*} \]
We don't want to get into a detailed discussion about the properties of the characteristic polynomial $p(\lambda)$ at this point. Still, I wanted to you to know that the characteristic polynomial is defined as the determinant of $A$ with $\lambda$s (the Greek letter lambda) subtracted from the diagonal. We will formally introduce the characteristic polynomial, eigenvalues, and eigenvectors in Section~\ref{eigenvalues and eigenvectors}. TODO check the above reference to eigenvals-section.
Exercises
Exercise 1: Find the determinant
\[ A = \left[\begin{array}{cc} 1&2\nl 3&4 \end{array} \right] \qquad \quad B = \left[\begin{array}{cc} 3&4\nl 1&2 \end{array} \right] \]
\[ C = \left[\begin{array}{ccc} 1 & 1 & 1 \nl 1 & 2 & 3 \nl 1 & 2 & 1 \end{array} \right] \qquad \quad D = \left[\begin{array}{ccc} 1 & 2 & 3 \nl 0 & 0 & 0 \nl 1 & 3 & 4 \end{array} \right] \]
Ans: $|A|=-2,\ |B|=2, \ |C|=-2, \ |D|=0$.
Observe that the matrix $B$ can be obtained from the matrix $A$ by swapping the first and second roes. The determinants of $A$ and $B$ have the same absolute value but different sign.
Exercise 2: Find the volume
Find the volume of the parallelepiped constructed by the vectors
$\vec{u}=(1, 2, 3)$, $\vec{v}= (2,-2,4)$, and $\vec{w}=(2,2,5)$.
Sol: http://bit.ly/181ugMm
Ans: $\textrm{volume}=2$.
Links
[ More information from wikipedia ]
http://en.wikipedia.org/wiki/Determinant
http://en.wikipedia.org/wiki/Minor_(linear_algebra)
Matrix inverse
Recall that the problem of solving a system of linear equations \[ \begin{align*} x_1 + 2x_2 & = 5, \nl 3x_2 + 9x_2 & = 21, \end{align*} \] can be written in the form of a matrix-times-vector product: \[ \begin{bmatrix} 1 & 2 \nl 3 & 9 \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} 5 \nl 21 \end{bmatrix}, \] or more compactly as \[ A\vec{x}=\vec{b}. \] Here $A$ is a $2 \times 2$ matrix, $\vec{x}$ is the vector of unknowns (a $2 \times 1$ matrix), and $\vec{b}$ is a vector of constants (a $2 \times 1$ matrix).
Consider now the matrix equation which corresponds the system of linear equations. We can solve this equation for $\vec{x}$ by multiplying (from the left) both sides of the equation by the inverse $A^{-1}$. We obtain: \[ A^{-1} A \vec{x} = I \vec{x} = \vec{x} = A^{-1}\vec{b}. \] Thus, solving a system of linear equations is equivalent to finding the inverse of the matrix of coefficients and then computing the product: \[ \vec{x} = \begin{bmatrix}x_1 \nl x_2 \end{bmatrix} = A^{-1} \vec{b} = \begin{bmatrix} 3 & -\frac{2}{3} \nl -1 & \frac{1}{3} \end{bmatrix} \begin{bmatrix}5 \nl 21 \end{bmatrix} = \begin{bmatrix}1 \nl 2 \end{bmatrix}. \]
As you can see computing the inverse of matrices is a pretty useful skill to have. In this section, we will learn about several approaches for computing the inverse of a matrix. Note that the matrix inverse is unique so no matter which method you use to find the inverse, you will always get the same answer. Knowing this is very useful because you can verify that your calculations are correct by computing the inverse in two different ways.
Existence of an inverse
Not all matrices can be inverted. Given any matrix $A \in \mathbb{R}^{n \times n }$ we can check whether $A$ is invertible or not by computing the determinant of $A$: \[ A^{-1} \ \textrm{ exists if and only if } \ \textrm{det}(A) \neq 0. \]
Adjugate matrix approach
The inverse of a $2\times2$ matrix can be computed as follows: \[ \left[ \begin{array}{cc} a&b\nl c&d\end{array} \right]^{-1}=\frac{1}{ad-bc} \left[ \begin{array}{cc} d&-b\nl -c&a \end{array}\right]. \]
This is the $2 \times 2$ version of a general formula for obtaining the inverse based on the adjugate matrix: \[ A^{-1} = \frac{1}{ \textrm{det}(A) } \textrm{adj}(A). \] What is the adjugate you ask? It is kind of complicated, so we need to go step by step. We need to define a few prerequisite concepts before we can get to the adjugate matrix.
In what follows we will work on a matrix $A \in \mathbb{R}^{n \times n}$ and refer to the its entries as $a_{ij}$, where $i$ is the row index and $j$ is the column index as usual. We will illustrate the steps in the $3 \times 3$ case: \[ A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{pmatrix}. \]
We first need to define two new terms for dealing with determinants:
- For each entry $a_{ij}$ we compute the minor $M_{ij}$,
which is the determinant of the matrix that remains when
we remove row $i$ and the column $j$ from the matrix $A$.
For example, the minor that corresponds to the entry $a_{12}$
is given by:
\[
M_{12} =
\left| \begin{matrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{matrix} \right|.
\]
- For each entry $a_{ij}$ de define the //sign// of the entry to be:
\[
\textrm{sign}(a_{ij}) = (-1)^{i+j}.
\]
- Define the //cofactor// $c_{ij}$ for each entry as
the product of its sign and its minor: $c_{ij} =\textrm{sign}(a_{ij})M_{ij}$.
The above concepts should be familiar to you from the section on determinants. Indeed, we can now write down a precise formula for computing the determinant. The most common way to take a determinant, it to expand along the top row which gives the following formula: \[ \textrm{det}(A) = \sum_{j=1}^n a_{1j} \textrm{sign}(a_{1j}) M_{1j} = \sum_{j=1}^n a_{1j} c_{1j}. \] Of course, we could have chosen any other row or column to expand along. Taking the determinant along the first column is given by: \[ \textrm{det}(A) = \sum_{i=1}^n a_{i1} \textrm{sign}(a_{i1}) M_{i1} = \sum_{i=1}^n a_{i1} c_{i1}. \] Perhaps now you can see where the name cofactor comes from: the cofactor $c_{ij}$ is what multiplies the entry $a_{ij}$ in the determinant formula.
OK, let us get back to our description of the adjugate matrix. The adjugate of a matrix is defined as the transpose of the matrix of cofactors $C$. The matrix of cofactors is a matrix of the same dimensions as the original matrix $A$, which is build by replacing each entry $a_{ij}$ by its cofactor $c_{ij}$: \[ C = \begin{pmatrix} c_{11} & c_{12} & c_{13} \nl c_{21} & c_{22} & c_{23} \nl c_{31} & c_{32} & c_{33} \end{pmatrix} = \begin{pmatrix} +\left| \begin{matrix} a_{22} & a_{23} \nl a_{32} & a_{33} \end{matrix} \right| & -\left| \begin{matrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{matrix} \right| & +\left| \begin{matrix} a_{21} & a_{22} \nl a_{31} & a_{32} \end{matrix} \right| \nl & & \nl -\left| \begin{matrix} a_{12} & a_{13} \nl a_{32} & a_{33} \end{matrix} \right| & +\left| \begin{matrix} a_{11} & a_{13} \nl a_{31} & a_{33} \end{matrix} \right| & -\left| \begin{matrix} a_{11} & a_{12} \nl a_{31} & a_{32} \end{matrix} \right| \nl & & \nl +\left| \begin{matrix} a_{12} & a_{13} \nl a_{22} & a_{23} \end{matrix} \right| & -\left| \begin{matrix} a_{11} & a_{13} \nl a_{21} & a_{23} \end{matrix} \right| & +\left| \begin{matrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{matrix} \right| \end{pmatrix}. \]
So to compute $\textrm{adj}(A)$ we simply take the transpose of $C$. Combining all of the above steps into the formula for the inverse $A^{-1} = \frac{1}{ \textrm{det}(A) } \textrm{adj}(A)= \frac{1}{ \textrm{det}(A) } C^T$ we obtain the final formula: \[ A^{-1} = \frac{1}{ \left|\begin{matrix} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{matrix} \right|} \begin{pmatrix} +\left| \begin{matrix} a_{22} & a_{23} \nl a_{32} & a_{33} \end{matrix} \right| & -\left| \begin{matrix} a_{12} & a_{13} \nl a_{32} & a_{33} \end{matrix} \right| & +\left| \begin{matrix} a_{12} & a_{13} \nl a_{22} & a_{23} \end{matrix} \right| \nl & & \nl -\left| \begin{matrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{matrix} \right| & +\left| \begin{matrix} a_{11} & a_{13} \nl a_{31} & a_{33} \end{matrix} \right| & -\left| \begin{matrix} a_{11} & a_{13} \nl a_{21} & a_{23} \end{matrix} \right| \nl & & \nl +\left| \begin{matrix} a_{21} & a_{22} \nl a_{31} & a_{32} \end{matrix} \right| & -\left| \begin{matrix} a_{11} & a_{12} \nl a_{31} & a_{32} \end{matrix} \right| & +\left| \begin{matrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{matrix} \right| \end{pmatrix}. \]
I know this is very complicated, but I had to show you. In practice you will rarely have to compute this by hand, and use a computer instead.
Reduced row echelon algorithm
Another way to obtain the inverse of a matrix is to record all the row operations $\mathcal{R}_1,\mathcal{R}_2,\ldots$ needed to transform the matrix $A$ into the identity matrix: \[ \mathcal{R}_k(\ldots \mathcal{R}_2( \mathcal{R}_1( A ) )\ldots) = I = A^{-1}A. \] Recall that the matrix $A$ can be thought of “doing” something to vectors. The identity operation corresponds to multiplication by the identity matrix $I\vec{v}=\vec{v}$. The above formula is an operational definition of the inverse $A^{-1}$ as the set of operations needed to “undo” the actions of $A$: \[ A^{-1}\vec{w} = \mathcal{R}_k(\ldots \mathcal{R}_2( \mathcal{R}_1( \vec{w} ) )\ldots). \]
This way of finding the inverse $A^{-1}$ may sound waaaaay too complicated to ever be useful. It would be if it weren't for the existence of a very neat trick for recording the row operations $\mathcal{R}_1$, $\mathcal{R}_2$,$\ldots$,$\mathcal{R}_k$.
We initialize an $n \times 2n$ array with the entries of the matrix $A$ on the left side and the identity matrix on the right-hand side: \[ [\;A\; | \ I\:\ ]. \] If you perform the RREF algorithm on this array (Gauss–Jordan elimination), you will end up with the inverse $A^{-1}$ on the right-hand side of the array: \[ [ \ \:I\ | \; A^{-1} ]. \]
Example
We now illustrate the procedure by computing the inverse the following matrix: \[ A = \begin{bmatrix} 1 & 2 \nl 3 & 9 \end{bmatrix}. \]
We start by writing the matrix $A$ next to the identity $I$ matrix: \[ \left[ \begin{array}{ccccc} 1 & 2 &|& 1 & 0 \nl 3 & 9 &|& 0 & 1 \end{array} \right]. \]
We now perform Gauss-Jordan elimination procedure on the resulting $2 \times 4$ matrix.
- The first step is to subtract three times the first row
from the second row, or written compactly $R_2 \gets R_2 -3R_1$ to obtain:
\[
\left[
\begin{array}{ccccc}
1 & 2 &|& 1 & 0 \nl
0 & 3 &|& -3 & 1
\end{array} \right].
\]
- Second we perform $R_2 \gets \frac{1}{3}R_2$ and get:
\[
\left[
\begin{array}{ccccc}
1 & 2 &|& 1 & 0 \nl
0 & 1 &|& -1 & \frac{1}{3}
\end{array} \right].
\]
- Finally we perform $R_1 \gets R_1 - 2R_2$ to obtain:
\[
\left[
\begin{array}{ccccc}
1 & 0 &|& 3 & -\frac{2}{3} \nl
0 & 1 &|& -1 & \frac{1}{3}
\end{array} \right].
\]
The inverse of $A$ can be found on the right-hand side of the above array: \[ A^{-1} = \begin{bmatrix} 3 & -\frac{2}{3} \nl -1 & \frac{1}{3} \end{bmatrix}. \]
The reason why this algorithm works is because we identify the sequence of row operations $\mathcal{R}_k(\ldots \mathcal{R}_2( \mathcal{R}_1( \ . \ ) )\ldots)$ with the inverse matrix $A^{-1}$ because for any vector $\vec{v}$ we have \[ \vec{w}=A\vec{v} \quad \Rightarrow \quad \mathcal{R}_k(\ldots \mathcal{R}_2( \mathcal{R}_1( \vec{w} ) )\ldots) = \vec{v}. \] The sequence of row operations has the same effect as the inverse operation $A^{-1}$. The right half in the above array is used to recorded the cumulative effect of all the row operations. In order to understand why this is possible we must learn a little more about the row operations and discuss their connection with elementary matrices.
Using elementary matrices
Each of the above row operations $\mathcal{R}_i$ can be represented as a matrix product with by an elementary matrix $E_{\mathcal{R}}$ from the left: \[ \vec{y} = \mathcal{R}_i(\vec{x}) \qquad \Leftrightarrow \qquad \vec{y} = E_{\mathcal{R}}\vec{x}. \] Applying all the operations $\mathcal{R}_1,\mathcal{R}_2,\ldots$ needed to transform the matrix $A$ into the identity matrix corresponds to a repeated product: \[ A^{-1}\vec{w} = \mathcal{R}_k(\ldots \mathcal{R}_2( \mathcal{R}_1( \vec{w} ) )\ldots) \quad \Leftrightarrow \quad \vec{w} = E_{k}\cdots E_{2}E_{1}\vec{w} = (E_{k}\cdots E_{2}E_{1})\vec{w}. \]
Thus we have obtained an expression for the inverse $A^{-1}$ as a product of elementary matrices: \[ A^{-1}\vec{w} = \mathcal{R}_k(\ldots \mathcal{R}_2( \mathcal{R}_1( \vec{w} ) )\ldots) = E_{k}\cdots E_{2}E_{1} \vec{w}. \]
There are three types of elementary matrices in correspondence with the three row operations we are allowed to use when transforming a matrix to its RREF form. We illustrate them here, with examples from the $2 \times 2$ case:
- Adding $m$ times row two to row one: $\mathcal{R}_\alpha:R_1 \gets R_1 +m R_2$
corresponds to the matrix:
\[
E_\alpha =
\begin{bmatrix}
1 & m \nl
0 & 1
\end{bmatrix}.
\]
* Swap rows one and two: $\mathcal{R}_\beta:R_1 \leftrightarrow R_2$
is the matrix:
\[
E_\beta =
\begin{bmatrix}
0 & 1 \nl
1 & 0
\end{bmatrix}.
\]
* Multiply row one by a constant $m$: $\mathcal{R}_\gamma:R_1 \gets m R_1$ is
\[
E_\gamma =
\begin{bmatrix}
m & 0 \nl
0 & 1
\end{bmatrix}.
\]
We will now illustrate the formula $A^{-1}=E_{k}\cdots E_{2}E_{1}$ on the matrix $A$ which we discussed above: \[ A = \begin{bmatrix} 1 & 2 \nl 3 & 9 \end{bmatrix}. \] Recall the row operations we had to apply in order to transform it to the identity were:
- $\mathcal{R}_1$: $R_2 \gets R_2 -3R_1$.
- $\mathcal{R}_2$: $R_2 \gets \frac{1}{3}R_2$.
- $\mathcal{R}_3$: $R_1 \gets R_1 - 2R_2$.
We now revisit the these steps performing each row operation using multiplication on the left by the elementary matrix:
- The first step, $R_2 \gets R_2 -3R_1$, corresponds to:
\[ \begin{bmatrix} 1 & 0 \nl -3 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 \nl 3 & 9 \end{bmatrix} = E_1 A = \begin{bmatrix} 1 & 2 \nl 0 & 3 \end{bmatrix} \]
- The second step is $R_2 \gets \frac{1}{3}R_2$:
\[ \begin{bmatrix} 1 & 0 \nl 0 & \frac{1}{3} \end{bmatrix} \begin{bmatrix} 1 & 2 \nl 0 & 3 \end{bmatrix} = E_2 E_1 A = \begin{bmatrix} 1 & 2 \nl 0 & 1 \end{bmatrix}. \]
- The final step is $R_1 \gets R_1 - 2R_2$:
\[ \begin{bmatrix} 1 & -2 \nl 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 \nl 0 & 1 \end{bmatrix} = E_3E_2E_1 A = \begin{bmatrix} 1 & 0 \nl 0 & 1 \end{bmatrix} = I \]
Therefore we have the formula: \[ A^{-1} = E_3E_2E_1 = \begin{bmatrix} 1 & -2 \nl 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \nl 0 & \frac{1}{3} \end{bmatrix} \begin{bmatrix} 1 & 0 \nl -3 & 1 \end{bmatrix} = \begin{bmatrix} 3 & -\frac{2}{3} \nl -1 & \frac{1}{3} \end{bmatrix}\!. \] Verify that this gives the correct $A^{-1}$ by carrying out the matrix products.
Note also that $A=(A^{-1})^{-1}=(E_3E_2E_1)^{-1}=E_1^{-1}E_2^{-1}E_3^{-1}$, which means that we can write $A$ as a product of elementary matrices: \[ A = E_1^{-1}E_2^{-1}E_3^{-1} = \begin{bmatrix} 1 & 0 \nl 3 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \nl 0 & 3 \end{bmatrix} \begin{bmatrix} 1 & 2 \nl 0 & 1 \end{bmatrix}. \] Note how the inverses of the elementary matrices are trivial to compute: they simply correspond to the opposite operations.
The elementary matrix approach teaches us that every invertible matrix $A$ can be decomposed as the product of elementary matrices. Furthermore, the inverse matrix $A^{-1}$ consists of the inverses of the elementary matrices that make up $A$ (in the reverse order).
By inspection
Sometimes it is possible to find the matrix inverse $A^{-1}$ by looking at the structure of the matrix $A$. For example, if we have the matrix $A = O\Lambda O^T$, where $\Lambda$ is a diagonal matrix, and $O$ is an orthogonal matrix ($O^{-1}=O^T$). Then $A^{-1} = O \Lambda^{-1} O^T$ and since $\Lambda$ is diagonal, it is easy to compute its inverse. One can verify that we have $AA^{-1} = O\Lambda O^T O \Lambda^{-1} O^T = O\Lambda \Lambda^{-1} O^T = O I O^T = I$ as required.
Using a computer
Every computer algebra system like Maple, MATLAB, Octave or Mathematica will provide
a way to specify matrices and a function for computing the matrix inverse.
In Python you can use the matrices from sympy.matrices.Matrix
or the matrices from numpy.mat to define the a matrix objects.
Let us illustrate the two approaches below.
You should sympy whenever you can are solving simple problems because
it will perform the calculations symbolically and tell you the exact fractions in the answer:
>>> from sympy.matrices import Matrix
>>> A = Matrix( [ [1,2], [3,4] ] ) # define a Matrix object
[1, 2]
[3, 4]
>>> A.inv() # call the inv method on A
[ -2, 1]
[3/2, -1/2]
Note how we defined the matrix as a list $[ ]$ of rows, each row also being represented as a list $[ ]$.
The notation for matrices as lists of lists is very tedious to use
for practical calculations. Imagine you had a matrix three columns
and ten rows – you would have to write a lot of square brackets!
There is another convention for specifying matrices which is more convenient.
If you have access to numpy on your computer, you can specify matrices
in the alternate notation
>>> import numpy
>>> M = numpy.mat('1 2; 3 9')
matrix([[1, 2],
[3, 4]])
The matrix is specified as a string in which the rows of the
matrix are separated by a semicolon ;.
Now that you have a numpy matrix object, you can
compute its inverse as follows:
>>> M.I
matrix([[ 3. , -0.66666667],
[-1. , 0.33333333]])
>>> # or equivalently using
>>> numpy.linalg.inv(M)
matrix([[ 3. , -0.66666667],
[-1. , 0.33333333]])
Note that the numpy inverse algorithm is based on
floating point numbers which have finite precision.
Floating point calculations can be very precise,
but they are not exact:
\[
0.\underbrace{33333333333 \ldots 33333}_{ n \textrm{ digits of precision} }
\neq
\frac{1}{3}.
\]
To represent $\frac{1}{3}$ exactly, you would need an infinitely long decimal expansion
which is not possible using floating point numbers.
We can build a sympy.matrices.Matrix by supplying a numpy.mat matrix
as an input:
>>> A = Matrix( numpy.mat('1 2; 3 9') )
>>> A.inv()
[ 3, -2/3]
[-1, 1/3]
We have combined the compact numpy.mat notation “1 2; 3 9” for specifying matrices
combined with the the symbolic (exact) inverse algorithm that sympy provides.
Thus, we have best of both worlds.
Discussion
In terms of finding the inverse of a matrix using pen and paper (like on a final exam, for example), I would recommend the $RREF$ algorithm the most: \[ [ \;A\; | \ I\: \ ] \qquad - \ \textrm{RREF} \to \qquad [ \ \:I\ | \; A^{-1} \;], \] unless of course you have a $2 \times 2$ matrix, in which case the formula is easier to use.
Exercises
Simple
Compute $A^{-1}$ where \[ A = \begin{bmatrix} 1 & 1 \nl 1 & 2 \end{bmatrix} \qquad \textrm{Ans: } A^{-1} = \begin{bmatrix} 2 & -1 \nl -1 & 1 \end{bmatrix}. \]
Determinant of the adjugate matrix
Show that for an $n \times n$ invertible matrix $A$, we have: $\left| \textrm{adj}(A) \right| = \left(\left| A \right|\right)^{n-1}$. Hint: Recall that $\left| \alpha A \right|=\alpha^n \left| A \right|$.
Lines and planes
We will now learn about points, lines and planes in $\mathbb{R}^3$. The purpose of this section is to help you understand the geometrical objets both in terms of the equations that describe them as well as to visualize what they look like.
Concepts
- $p=(p_x,p_y,p_z)$: a point in $\mathbb{R}^3$.
- $\vec{v}=(v_x,v_y,v_z)$: a vector in $\mathbb{R}^3$.
- $\hat{v}=\frac{ \vec{v} }{ |\vec{v}| }$: a unit vector in the direction of $\vec{v}$.
- $\ell: \{ p_o+t\:\vec{v}, t \in \mathbb{R} \}$:
the equation of a line with direction vector $\vec{v}$
passing through the point $p_o$.
* $ \ell: \left\{ \frac{x - p_{0x}}{v_x} = \frac{y - p_{0y}}{v_y} = \frac{z - p_{0z}}{v_z} \right\}$:
the symmetric equation of the line $\ell$.
* $P: \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=p_o+s\:\vec{v} + t\:\vec{w}, \ s,t \in \mathbb{R} \}$:
the //parametric// equation of a plane $P$.
* $P: \left\{ (x,y,z) \in \mathbb{R}^3 \ | \ \vec{n} \cdot [ (x,y,z) - p_o ] = 0 \right\}$.
the //geometric// equation of a plane
which contains $p_o$ and has normal vector $\hat{n}$.
* $P: \left\{ Ax+By+Cz=D \right\}$: the //general// equation of a plane.
* $d(a,b)$: the shortest //distance// between two objects $a$ and $b$.
Points
We can specify a point in $\mathbb{R}^3$ by its coordinates $p=(p_x,p_y,p_z)$, which is similar to how we specify vectors. In fact the two notions are equivalent: we can either talk about the destination point $p$ or the vector $\vec{p}$ that takes us from the origin to the point $p$. By this equivalence, it makes sense to add vectors and points.
We can also specify a point as the intersection of two lines. For example in $\mathbb{R}^2$ we can describe $p$ as the intersection of the lines $x + 2y = 5$ and $3x + 9y = 21$. To find the point, $p$ we would have to solve these equations in parallel. In other words, we are looking for a point which lies on both lines. The answer is the point $p=(1,2)$.
In three dimensions, a point can also be specified as the intersection of three planes. Indeed, this is precisely what is going on when we are solving equations of the form $A\vec{x}=\vec{b}$ with $A \in \mathbb{R}^{3 \times 3}$ and $\vec{b} \in \mathbb{R}^{3}$. We are looking for some $\vec{x}$ that is lies in all three planes.
Lines
A line $\ell$ is a one-dimensional space that is infinitely long. There are a number of ways to specify the equation of a line.
The parametric equation of a line is obtained as follows. Given a direction vector $\vec{v}$ and some point $p_o$ on the line, we can define the line as: \[ \ell: \ \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=p_o+t\:\vec{v}, t \in \mathbb{R} \}. \] We say the line is parametrized by the variable $t$. The line consists of all the points $(x,y,z)$ which can be obtained starting from the point $p_o$ and adding any multiple of the direction vector $\vec{v}$.
The symmetric equation is an equivalent way for describing a line that does not require an explicit parametrization. Consider the equation that corresponds to each of the coordinates in the equation of the line: \[ x = p_{0x} + t\:v_x, \quad y = p_{0y} + t\:v_y, \quad z = p_{0z} + t\:v_z. \] When we solve for $t$ in each of these equations and equate the results, we obtain the symmetric equation for a line: \[ \ell: \ \left\{ \ \frac{x - p_{0x}}{v_x} = \frac{y - p_{0y}}{v_y} = \frac{z - p_{0z}}{v_z} \right\}, \] in which the parameter $t$ does not appear at all. The symmetric equation specifies the line as the relationship between the $x$,$y$ and $z$ coordinates that holds for all the points on the line.
You are probably most familiar with this type of equation in the special case $\mathbb{R}^2$ when there is no $z$ variable. For non-vertical lines, we can think of $y$ as being a function of $x$ and write the line the equivalent form: \[ \frac{x - p_{0x}}{v_x} = \frac{y - p_{0y}}{v_y}, \qquad \Leftrightarrow \qquad y(x) = mx + b, \] where $m=\frac{v_y}{v_x}$ and $b=p_{oy}-\frac{v_y}{v_x}p_{ox}$, assuming $v_x \neq 0$. This makes sense intuitively, since we always thought of the slope $m$ as the “rise over run”, i.e., how much of the line goes in the $y$ direction divided by how much the line goes in the $x$ direction.
Another way to describe a line is to specify two points that are part of the line. The equation of a line that contains the points $p$ and $q$ can be obtained as follows: \[ \ell: \ \{ \vec{x}=p+t \: (p-q), \ t \in \mathbb{R} \}, \] where $(p-q)$ plays the role of the direction vector $\vec{v}$ of the line. We said any vector could be used in the definition so long as it is in the same direction as the line: $\vec{v}=p-q$ certainly can play that role since $p$ and $q$ are two points on the line.
In three dimensions, the intersection of two planes forms a line. The equation of the line corresponds to the solutions of the equation $A\vec{x}=\vec{b}$ with $A \in \mathbb{R}^{2 \times 3}$ and $\vec{b} \in \mathbb{R}^{2}$.
Planes
A plane $P$ in $\mathbb{R}^3$ is a two-dimensional space with infinite extent. The orientation of the plane is specified by a normal vector $\vec{n}$, which is perpendicular to the plane.
A plane is specified as the subspace that contains all the vectors that are orthogonal to the plane's normal vector $\vec{n}$ and contain the point $p_o$. The formula in compact notation is \[ P: \ \ \vec{n} \cdot [ (x,y,z) - p_o ] = 0. \] Recall that the dot product of two vectors is zero if and only if these vectors are orthogonal. In the above equation, the expression $[(x,y,z) - p_o]$ forms an arbitrary vector with one endpoint at $p_o$. From all these vectors we select only those that are perpendicular to the $\vec{n}$, and thus we obtain all the points of the plane.
If we expand the above formula, we obtain the general equation of the plane: \[ P: \ \ Ax + By + Cz = D, \] where $A = n_x, B=n_y, C=n_z$ and $D = \vec{n} \cdot p_o = n_xp_{0x} + n_yp_{0y} + n_yp_{oz}$.
We can also give a parametric description of a plane $P$, provided we have some point $p_o$ in the plane and two linearly independent vectors $\vec{v}$ and $\vec{w}$ which lie inside the plane: \[ P: \ \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=p_o+s\:\vec{v} + t\:\vec{w}, \ s,t \in \mathbb{R} \}. \] Note that since a plane is two-dimensional, we need two parameters $s$ and $t$ to describe it.
Suppose we're given three points $p$, $q$, and $r$ that lie in the plane. Can you find the equation for this plane in the form: $\vec{n} \cdot [ (x,y,z) - p_o ] = 0$? We can use the point $p$ as the point $p_o$, but how do we find the normal vector $\vec{n}$ for that plane. The trick is to use the cross product. First we build two vectors that lie in the plane $\vec{v} = q-p$ and $\vec{w} = r-p$ and then to find a vector that is perpendicular to them we compute: \[ \vec{n} = \vec{v} \times \vec{w} = (q - p) \times ( r - p ). \] We can then write down the equation of a plane $\vec{n} \cdot [ (x,y,z) - p ] = 0$ as usual. The key property we used was the fact that the cross product of two vectors results in a vector that is perpendicular to both vectors. The cross product is the perfect tool for finding the normal vector.
Distances
The distance between 2 points $p$ and $q$ is equal to the length of the vector that goes from $p$ to $q$: \[ d(p,q)=\| q - p \| = \sqrt{ (q_x-p_x)^2 + (q_y-p_y)^2 + (q_z-p_z)^2}. \]
The distance between the line $\ell: \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=p_o+t\:\vec{v}, t \in \mathbb{R} \}$ and the origin $O=(0,0,0)$ is given by the formula: \[ d(\ell,O) = \left\| p_o - \frac{ p_o \cdot \vec{v} }{ \| \vec{v} \|^2 } \vec{v} \right\|. \]
The interpretation of this formula is as follows. The first step is to identify a vector that starts at the origin and goes to any point $p_o$. The projection of $p_o$ onto line $\ell$ is given by the formula $\frac{ p_o \cdot \vec{v} }{ \| \vec{v} \|^2 } \vec{v}$. This is the part of the vector $p_o$ which is entirely in the direction of $\vec{v}$. The distance $d(\ell,O)$ is equal to the orthogonal complement of this vector.
The distance between a plane $P: \ \vec{n} \cdot [ (x,y,z) - p_o ] = 0$ and the origin $O$ is given by: \[ d(P,O)= \frac{| \vec{n}\cdot p_o |}{ \| \vec{n} \| }. \]
The above distance formulas are somewhat complicated expressions which involve computing dot products and taking the length of vectors a lot. In order to understand what is going on, we need to learn a bit about projective geometry which will help us measure distances between arbitrary points, lines and planes. As you can see from the formulas above, there will be no new math: just vector $+$, $-$, $\|.\|$ and dot products. The new stuff is actually all in picture-proofs (formally called vector diagrams). Projections play a key role in all of this and this is why we will learn about them in great detail in the next section.
Exercises
Find the plane which contains the line of intersection of the two planes $x+2y+z=1$ and $2x-y-z=2$ and is parallel to the line $x=1+2t$, $y=-2+t$, $z=-1-t$.
NOINDENT Sol: Find direction vector for the line of intersection $\vec{v}_1 = ( 1, 2,1 ) \times ( 2, -1, -1)$. We know that the plane is parallel to $\vec{v}_2=(2,1,-1)$. So the plane must be the $\textrm{span}\{\vec{v}_1, \vec{v}_2 \} + p_o$. To find a normal vector for the plane we do $\vec{n} = \vec{v}_1 \times \vec{v}_2$. Then choose a point that is on both of the above planes. Conveniently the point $(1,0,0)$ is in both of the above planes. So the anser is $\vec{n}\cdot[ (x,y,z) - (1,0,0) ]=0$.
Projections
In this section we will learn about the projections of vectors onto lines and planes. Given an arbitrary vector, your task will be to find how much of this vector is in a given direction (projection onto a line) or how much the vector lies within some plane. We will use the dot product a lot in this section.
For each of the formulas in this section, you must draw a picture. The picture will make projections and distances a lot easier to think about. In a certain sense, the pictures are much more important so be sure you understand them well. Don't worry about memorizing any of the formulas in this section: the formulas are nothing more than captions to go along with the pictures.
Concepts
- $S\subseteq \mathbb{R}^n$: a subspace of $\vec{R}^n$.
For the purposes of this chapter, we will use $S \subset \mathbb{R}^3$,
and $S$ will either be a line $\ell$ or a plane $P$ that **pass through the origin**.
* $S^\perp$: the orthogonal space to $S$.
We have $S^\perp = \{ \vec{w} \in \mathbb{R}^n \ | \ \vec{w} \cdot S = 0\}$.
* $\Pi_S$: the //projection// onto the space $S$.
* $\Pi_{S^\perp}$: the //projection// onto the orthogonal space $S^\perp$.
Projections
Let $S$ be a vector subspace of $\mathbb{R}^3$. We will define precisely what vector spaces are later on. For this section, our focus is on $\mathbb{R}^3$ which has as subspaces lines and planes through the origin.
The projection onto the space $S$ is a linear function of the form: \[ \Pi_S : \mathbb{R}^n \to \mathbb{R}^n, \] which cuts off all parts of the input that do not lie within $S$. More precisely we can describe $\Pi_S$ by its action on different inputs:
- If $\vec{v} \in S$, then $\Pi_S(\vec{v}) = \vec{v}$.
- If $\vec{w} \in S^\perp$, $\Pi_S(\vec{w}) = \vec{0}$.
- Linearity and the above two conditions imply that,
for any vector $\vec{u}=\alpha\vec{v}+ \beta \vec{w}$,
$\vec{v} \in S$ and $\vec{w} \in S^\perp$, we have:
\[
\Pi_S(\vec{u}) = \Pi_S(\alpha\vec{v}+ \beta \vec{w}) = \alpha\vec{v}.
\]
In the above we used the notion of an orthogonal space: \[ S^\perp = \{ \vec{w} \in \mathbb{R}^n \ | \ \vec{w} \cdot S = 0\}, \] where $\vec{w}\cdot S$ means that $\vec{w}$ is orthogonal to any vector $\vec{s} \in S$.
Projections project onto the space $S$ in the sense that, no matter which vector $\vec{u}$ you start from, applying the projection $\Pi_S$ will result in a vector that is part of $S$: \[ \Pi_S(\vec{u}) \in S. \] All parts of $\vec{u}$ that were in the perp space $S^\perp$ will get killed. Meet $\Pi_S$, the $S$-perp killer.
Being entirely inside $S$ or perpendicular to $S$ can be used to split the set vectors $\mathbb{R}^3$. We say that $\mathbb{R}^3$ decomposes into the direct sum of the subspaces $S$ and $S^\perp$: \[ \mathbb{R}^3 = S \oplus S^\perp, \] which means that any vector $\vec{u}\in \mathbb{R}^3$ can be split in terms of a $S$-part $\vec{v}=\Pi_S(\vec{u})$ and a non-$S$ part $\vec{w}=\Pi_{S^\perp}(\vec{u})$ such that: \[ \vec{u}=\vec{v} + \vec{w}. \]
Okay, that is enough theory for now. We now turn to the specific formulas for lines and planes. Let me just say one last fact. A defining property of projection operations is the fact that they are idempotent, which means that it doesn't matter if you project a vector once, twice or a million times: the result will always be the same. \[ \Pi_S( \vec{u} ) = \Pi_S( \Pi_S( \vec{u} )) = \Pi_S(\Pi_S(\Pi_S(\vec{u} ))) = \ldots. \] Once you project to the subspace $S$, any further projections onto $S$ don't do anything.
We will first derive formulas for projection onto lines and planes that pass through the origin.
Projection onto a line
Consider the one-dimensional subspace of the line $\ell$ with direction vector $\vec{v}$ that passes though the origin $\vec{0}$: \[ \ell: \ \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=\vec{0}+ t\:\vec{v}, t \in \mathbb{R} \}. \]
The projection onto $\ell$ for an arbitrary vector $\vec{u} \in \mathbb{R}^3$ is given by: \[ \Pi_\ell( \vec{u} ) = \frac{ \vec{v} \cdot \vec{u} }{ \| \vec{v} \|^2 } \vec{v}. \]
The orthogonal space to the line $\ell$ consists of all vectors that are perpendicular to the direction vector $\vec{v}$. Or mathematically speaking: \[ \ell^\perp: \ \ \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)\cdot \vec{v} = 0 \}. \] You should recognize the above equation is the definition of a plane. So the orthogonal space for a line $\ell$ with direction vector $\vec{v}$ is a plane with normal vector $\vec{v}$. Makes sense no?
From what we have above, we can get the projection onto $S^\perp$ very easily. Recall that any vector can be written as the sum of an $S$ part and a $S^\perp$ part: $\vec{u}=\vec{v} + \vec{w}$ where $\vec{v}=\Pi_\ell(\vec{u}) \in S$ and $\vec{w}=\Pi_{\ell^\perp}(\vec{u}) \in S^\perp$. This means that to obtain $\Pi_{\ell^\perp}(\vec{u})$ we can subtract the $\Pi_S$ part from the original vector $\vec{u}$: \[ \Pi_{\ell^\perp}(\vec{u}) = \vec{w} = \vec{u}-\vec{v} = \vec{u} - \Pi_{S}(\vec{u}) = \vec{u} - \frac{ \vec{v} \cdot \vec{u} }{ \| \vec{v} \|^2 } \vec{v}. \] Indeed, we can think of $\Pi_{\ell^\perp}(\vec{u}) = \vec{w}$ as what remains of $\vec{u}$ after we have removed all the $S$ part from it.
Projection onto a plane
Let $S$ now be the two-dimensional plane $P$ with normal vector $\vec{n}$ which passes through the origin: \[ P: \ \ \{ (x,y,z) \in \mathbb{R}^3 \ | \ \vec{n} \cdot (x,y,z) = 0 \}. \]
The perpendicular space $S^\perp$ is given by a line with direction vector $\vec{n}$: \[ P^\perp: \ \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=t\:\vec{n}, t \in \mathbb{R} \}, \] and we have again $\mathbb{R}^3 = S \oplus S^\perp$.
We are interested in finding $\Pi_P$, but it will actually be easier to find $\Pi_{P^\perp}$ first and then compute $\Pi_P(\vec{u}) = \vec{v} = \vec{u} - \vec{w}$, where $\vec{w}=\Pi_{P^\perp}(\vec{u})$.
Since $P^\perp$ is a line, we know how to project onto it: \[ \Pi_{P^\perp}( \vec{u} ) = \frac{ \vec{n} \cdot \vec{u} }{ \| \vec{n} \|^2 } \vec{n}. \] And we obtain the formula for $\Pi_P$ as follows \[ \Pi_P(\vec{u}) = \vec{v} = \vec{u}-\vec{w} = \vec{u} - \Pi_{P^\perp}(\vec{u}) = \vec{u} - \frac{ \vec{n} \cdot \vec{u} }{ \| \vec{n} \|^2 } \vec{n}. \]
Distances revisited
Suppose you have to find the distance between the line $\ell: \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=p_o+t\:\vec{v}, t \in \mathbb{R} \}$ and the origin $O=(0,0,0)$. This problem is equivalent to the problem of finding the distance from the line $\ell^\prime: \{ (x,y,z) \in \mathbb{R}^3 \ | \ (x,y,z)=\vec{0}+t\:\vec{v}, t \in \mathbb{R} \}$ and the point $p_o$. The answer to the latter question is the length of the projection $\Pi_{\ell^\perp}(p_o)$. \[ d(\ell^\prime,p_o) = \left\| \Pi_{\ell^\perp}(p_o) \right\| = \left\| p_o - \frac{ p_o \cdot \vec{v} }{ \| \vec{v} \|^2 } \vec{v} \right\|. \]
The distance between a plane $P: \ \vec{n} \cdot [ (x,y,z) - p_o ] = 0$ and the origin $O$ is the same as the distance between the plane $P^\prime: \vec{n} \cdot (x,y,z) = 0$ and the point $p_o$. We can obtain this distance by find the length of the projection of $p_o$ onto $P^{\prime\perp}$ using the formula above: \[ d(P^\prime,p_o)= \frac{| \vec{n}\cdot p_o |}{ \| \vec{n} \| }. \]
You should try to draw the picture for the above two scenarios and make sure that the formulas make sense to you.
Projections matrices
Because projections are a type of linear transformation, they can be expressed as a matrix product: \[ \vec{v} = \Pi(\vec{u}) \qquad \Leftrightarrow \qquad \vec{v} = M_{\Pi}\vec{u}. \] We will learn more about that later on, but for now I want to show you some simple examples of projection matrices. Let $\Pi$ be the projection onto the $xy$ plane. The matrix that corresponds to this projection is \[ \Pi(\vec{u}) = M_{\Pi}\vec{u} = \begin{pmatrix} 1 & 0 & 0 \nl 0 & 1 & 0 \nl 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} u_x \nl u_y \nl u_z \end{pmatrix} = \begin{pmatrix} u_x \nl u_y \nl 0 \end{pmatrix}. \] As you can see, multiplying by $M_{\Pi}$ has the effect of only selecting the $x$ and $y$ coordinates and killing the $z$ component.
Examples
Example: Color to greyscale
Consider a digital image where the colour of each pixel is specified as an RGB value.
Each color pixel is, in some sense, three-dimensional: the red, green and blue dimensions.
A pixel of a greyscale image is just one-dimensional and measures how bright the pixel needs to be.
When you tell your computer to convert an RGB image to greyscale,
what you are doing is applying the projection $\Pi_G$ of the form:
\[
P_G : \mathbb{R}^3 \to \mathbb{R},
\]
which is given by following equation:
\[
\begin{align*}
P_G(R,G,B)
&= 0.2989 \:R + 0.5870 \: G + 0.1140 \: B \nl
&= (0.2989, 0.5870, 0.1140)\cdot(R,G,B).
\end{align*}
\]
Discussion
In the next section we will talk about a particular set of projections known as the coordinate projections which we use to find the coordinates of a vector $\vec{v}$ with respect to a given coordinate system: \[ \begin{align*} v_x\hat{\imath} = (\vec{v} \cdot \hat{\imath})\hat{\imath} = \Pi_x(\vec{v}), \nl v_y\hat{\jmath} = (\vec{v} \cdot \hat{\jmath})\hat{\jmath} = \Pi_y(\vec{v}), \nl v_z\hat{k} = (\vec{v} \cdot \hat{k})\hat{k} = \Pi_z(\vec{v}). \end{align*} \] The linear transformation $\Pi_x$ is the projection onto the $x$ axis and similarly $\Pi_y$ and $\Pi_z$ project onto the $y$ and $z$ axes.
It is common in science to talk about vectors as triplets of numbers $(v_x,v_y,v_z)$ without making an explicit reference to the basis. Thinking of vectors as arrays of numbers is fine for computational purposes (to compute the sum of two vectors, you just need to manipulate the coefficients), but it masks one of the most important concepts: the basis or the coordinate system with respect to which the components of the vector are expressed. A lot of misconceptions students have about linear algebra stem from an incomplete understanding of this core concept.
Now since I want you to leave this chapter with a thorough understanding of linear algebra we will now review—in excruciating detail—the notion of a basis and how to compute vector coordinates with respect to this basis.
Vector coordinates
In the physics chapter we learned how to work with vectors in terms of their components. We can decompose the effects of a force $\vec{F}$ is terms of its $x$ and $y$ components: \[ F_x = \| \vec{F} \| \cos\theta, \qquad F_y = \| \vec{F} \| \sin\theta, \] where $\theta$ is the angle that the vector $\vec{F}$ makes with the $x$ axis. We can write the vector $\vec{F}$ in the following equivalent ways: \[ \vec{F} = F_x\hat{\imath} + F_y \hat{\jmath} = (F_x,F_y)_{\hat{\imath}\hat{\jmath}}, \] in which the vectors is expressed as components or coordinates with respect the basis $\{ \hat{\imath}, \hat{\jmath} \}$ (the $xy$ coordinate system).
The number $F_x$ (the first coordinate of $\vec{F}$) corresponds to the length of the projection of the vector $\vec{F}$ on the $x$ axis. In the last section we formalized the notion of projection and saw that the projection operation on a vector can be represented as a matrix product: \[ F_x\:\hat{\imath} = \Pi_x(\vec{v}) = (\vec{v} \cdot \hat{\imath})\hat{\imath} = \underbrace{\ \ \hat{\imath}\ \ \hat{\imath}^T}_{M_x} \ \vec{v}, \] where $M_x$ is called “the projection matrix onto the $x$ axis.”
In this section we will discuss in detail the relationship between vectors $\vec{v}$ (directions in space) and their representation in terms of coordinates with respect to a basis.
Definitions
We will discuss the three “quality grades” that exist for bases. For an $n$-dimensional vector space $V$, you could have a:
- A generic basis $B_f=\{ \hat{f}_1, \hat{f}_2, \ldots, \hat{f}_n \}$,
which consists of any set of linearly independent vectors in $V$.
- An orthogonal basis $B_{e}=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$,
which consists of $n$ mutually orthogonal vectors in $V$: $\vec{e}_i \cdot \vec{e}_j = \delta_{ij}$.
- An orthonormal basis $B_{\hat{e}}=\{ \hat{e}_1, \hat{e}_2, \ldots, \hat{e}_n \}$
which is an orthogonal basis of unit length vectors: $\| \vec{e}_i \|^2 =1, \ \forall i \in \{ 1,2,\ldots,n\}$.
The main idea is quite simple.
- Any vector can be expressed as coordinates with respect a basis:
\[ \vec{v} = v_1 \vec{e}_1 + v_2\vec{e}_2 + \cdots + v_n\vec{e}_n = (v_1, v_2, \ldots, v_n)_{B_e}. \]
However, things can get confusing when we use multiple bases:
- $\vec{v}$: a vector.
- $[\vec{v}]_{B_e}=(v_1, v_2, \ldots, v_n)_{B_e}$: the vector $\vec{v}$
expressed in terms of the basis $B_e$.
- $[\vec{v}]_{B_f}=(v^\prime_1, v^\prime_2, \ldots, v^\prime_n)_{B_f}$: the same vector $\vec{v}$
expressed in terms of the basis $B_f$.
- $_{B_f}[I]_{B_e}$: the change of basis matrix which converts the components of any vector
from the $B_e$ basis to the $B_f$ basis: $[\vec{v}]_{B_f} = _{B_f}[I]_{B_e}[\vec{v}]_{B_e}$.
Components with respect to a basis
The notion of “how much of a vector is in a given direction” is what we call the components of the vector $\vec{v}=(v_x,v_y,v_z)_{\hat{\imath}\hat{\jmath}\hat{k}}$, where we have indicated that the components are with respect to the standard orthonormal basis like $\{ \hat{\imath}, \hat{\jmath}, \hat{k} \}$. The dot product is used to calculate the components of the vector with respect to this basis: \[ v_x = \vec{v}\cdot \hat{\imath}, \quad v_y = \vec{v}\cdot \hat{\jmath}, \quad v_z = \vec{v} \cdot \hat{k}. \]
We can therefore write down the exact “prescription” for computing the components of a vector as follows: \[ (v_x,v_y,v_z)_{\hat{\imath}\hat{\jmath}\hat{k}} \ \Leftrightarrow \ (\vec{v}\cdot \hat{\imath})\: \hat{\imath} \ + \ (\vec{v}\cdot \hat{\jmath})\: \hat{\jmath} \ + \ (\vec{v} \cdot \hat{k})\: \hat{k}. \]
Let us consider now how this “prescription” can be applied more generally to compute the coordinates with respect to other bases. In particular we will think about an $n$-dimensional vector space $V$ and specify three different types of bases for that space: an orthonormal basis, an orthogonal basis and a generic basis. Recall that a basis for an $n$-dimensional space is any set of $n$ linearly independent vectors in that space.
Orthonormal basis
An orthonormal basis $B_{\hat{e}}=\{ \hat{e}_1, \hat{e}_2, \ldots, \hat{e}_n \}$ consists of a set of mutually orthogonal unit-length vectors: \[ \vec{e}_i \cdot \vec{e}_j = \delta_{ij}, \] The function $\delta_{ij}$ is equal to one whenever $i=j$ and equal to zero otherwise. For each $i$ we have: \[ \vec{e}_i \cdot \vec{e}_i = 1 \qquad \Rightarrow \qquad \| \vec{e}_i \|^2 =1. \]
To compute the components of the vector $\vec{a}$ with respect to an orthonormal basis $B_{\hat{e}}$ we use the standard “prescription” that we used for the $\{ \hat{\imath}, \hat{\jmath}, \hat{k} \}$ basis: \[ (a_1,a_2,\ldots,a_n)_{B_{\hat{e}}} \ \Leftrightarrow \ (\vec{a}\cdot \hat{e}_1)\: \hat{e}_1 \ + \ (\vec{a}\cdot \hat{e}_2)\: \hat{e}_2 \ + \ \cdots \ + \ (\vec{a}\cdot \hat{e}_n)\: \hat{e}_n. \]
Orthogonal basis
With appropriate normalization factors, you can use unnormalized vectors as a basis as well. Consider a basis which is orthogonal, but not orthonormal: $B_{e}=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$, then we have \[ (b_1,b_2,\ldots,b_n)_{B_{e}} \ \Leftrightarrow \ \left(\frac{\vec{v}\cdot\vec{e}_1}{\|\vec{e}_1\|^2}\right)\vec{e}_1 \ + \ \left(\frac{\vec{v}\cdot\vec{e}_2}{\|\vec{e}_2\|^2}\right)\vec{e}_2 \ + \ \cdots \ + \ \left(\frac{\vec{v}\cdot\vec{e}_n}{\|\vec{e}_n\|^2}\right)\vec{e}_n. \]
In order to find the coefficients of some vector $\vec{b}$ with respect to the basis $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ we proceed as follows: \[ b_1 = \frac{ \vec{b} \cdot \vec{e}_1 }{ \|\vec{e}_1\| }, \quad b_2 = \frac{ \vec{b} \cdot \vec{e}_2 }{ \|\vec{e}_2\| }, \quad \cdots, \quad b_n = \frac{ \vec{b} \cdot \vec{e}_n }{ \|\vec{e}_n\| }. \]
Observe that each of the coefficients can be computed independently of the coefficients for the other basis vectors. To compute $b_1$, all I need to know is $\vec{b}$ and $\vec{e}_1$ and I do not need to know what $\vec{e}_2$ and $\vec{e}_3$ are. This is because the computation of the coefficient corresponds to an orthogonal projection. The length $b_1$ corresponds to the length of $\vec{b}$ in the $\vec{e}_1$ dimension, and because we know that the basis is orthogonal, this means that the length $b_1\vec{e}_1$ is does not depend on the other dimensions.
Generic basis
What if we have a generic basis $\{ \vec{f}_1, \vec{f}_2, \vec{f}_3 \}$ for that space? To find the coordinates $(a_1,a_2,a_3)$ of some vector $\vec{a}$ with respect to this basis we need to solve the equation \[ a_1\vec{f}_1+ a_2\vec{f}_2+ a_3\vec{f}_3 = \vec{a}, \] for the three unknowns $a_1,a_2$ and $a_3$. Because the vectors $\{ \vec{v}_i \}$ are not orthogonal, the calculation of the coefficients $a_1,a_2,\ldots,a_n$ must be done simultaneously.
Example
Express the vector $\vec{v}=(5,6)_{\hat{\imath}\hat{\jmath}}$ in terms of the basis $B_f = \{ \vec{f}_1, \vec{f}_2 \}$ where $\vec{f}_1 = (1,1)_{\hat{\imath}\hat{\jmath}}$ and $\vec{f}_2 = (3,0)_{\hat{\imath}\hat{\jmath}}$.
We are looking for the coefficients $v_1$ and $v_2$ such that \[ v_1 \vec{f}_1 + v_2\vec{f}_2 = \vec{v} = (5,6)_{\hat{\imath}\hat{\jmath}}. \] To find the coefficients we need to solve the following system of equations simultaneously: \[ \begin{align*} 1v_1 + 3v_2 & = 5 \nl 1v_1 + 0 \ & = 6. \end{align*} \]
From the second equation we find that $v_1=6$ and substituting into the first equation we find that $v_2 = \frac{-1}{3}$. Thus, the vector $\vec{v}$ written with respect to the basis $\{ \vec{f}_1, \vec{f}_2 \}$ is \[ \vec{v} = 6\vec{f}_1 - \frac{1}{3}\vec{f}_2 = \left(6,\tfrac{-1}{3}\right)_{B_f}. \]
Change of basis
We often identify a vector $\vec{v}$ with its components in a certain basis $(v_x,v_y,v_z)$. This is fine for the most part, but it is important to always keep in mind the basis with respect to which the coefficients are taken, and if necessary specify the basis as a subscript $\vec{v}=(v_x,v_y,v_z)_{\hat{\imath}\hat{\jmath}\hat{k}}$.
When performing vector arithmetic operations like $\vec{u}+\vec{v}$, we don't really care what the basis the vectors are expressed in so long as the same basis is used for both $\vec{u}$ and $\vec{v}$.
We sometimes need to use two different bases. Consider for example the basis $B_e=\{ \hat{e}_1, \hat{e}_2, \ldots, \hat{e}_n \}$ and another basis $B_f=\{ \hat{f}_1, \hat{f}_2, \ldots, \hat{f}_n \}$. Suppose we are given the coordinates $v_1,v_2,v_3$ of some $\vec{v}$ in terms of the basis $B_e$: \[ \vec{v} = \left( v_1 , v_2 , v_3 \right)_{ B_e } = v_1 \hat{e}_1 + v_2 \hat{e}_2 + v_3 \hat{e}_3. \] How can we find the coefficients of $\vec{v}$ in terms of the basis $B_f$?
This is called a change-of-basis transformation and can be performed as a matrix multiplication: \[ \left[ \begin{array}{c} v_1^\prime \nl v_2^\prime \nl v_3^\prime \end{array} \right]_{ B_f } = \underbrace{ \left[ \begin{array}{ccc} \hat{f}_1 \cdot \hat{e}_1 & \hat{f}_1 \cdot \hat{e}_2 & \hat{f}_1 \cdot \hat{e}_3 \nl \hat{f}_2 \cdot \hat{e}_1 & \hat{f}_2 \cdot \hat{e}_2 & \hat{f}_2 \cdot \hat{e}_3 \nl \hat{f}_3 \cdot \hat{e}_1 & \hat{f}_3 \cdot \hat{e}_2 & \hat{f}_3 \cdot \hat{e}_3 \end{array} \right] }_{ _{B_f}[I]_{B_e} } \left[ \begin{array}{c} v_1 \nl v_2 \nl v_3 \end{array} \right]_{ B_e }. \] Each of the entries in the “change of basis matrix” describes how each of the $\hat{e}$ basis vectors transforms in terms of the $\hat{f}$ basis.
Note that the matrix doesn't actually do anything, since it doesn't move the vector. The change of basis acts like the identity transformation which is why we use the notation $_{B_f}[I]_{B_e}$. This matrix contains the information about how each of the vectors of the old basis ($B_e$) is expressed in terms of the new basis ($B_f$).
For example, the vector $\hat{e}_1$ will get mapped into: \[ \hat{e}_1 = (\hat{f}_1 \cdot \hat{e}_1)\:\hat{f}_1 + (\hat{f}_2 \cdot \hat{e}_1)\:\hat{f}_2 + (\hat{f}_3 \cdot \hat{e}_1)\:\hat{f}_3. \]
which is just the generic formula for expressing any vector in terms of the basis $B_f$.
The change of basis operation does not change the vector. The vector $\vec{v}$ stays the same, but we have now expressed it in terms of another basis: \[ \left( v_1^\prime , v_2^\prime , v_3^\prime \right)_{ B_f } = v_1^\prime \: \hat{f}_1 + v_2^\prime \: \hat{f}_2 + v_3^\prime \: \hat{f}_3 = \vec{v} = v_1 \:\hat{e}_1 + v_2 \: \hat{e}_2 + v_3 \: \hat{e}_3 = \left( v_1 , v_2 , v_3 \right)_{ B_e }. \]
Matrix components
So we have spoke in very mathematical terms about different representations of vectors. What about representations of linear transformations: \[ T_A : \mathbb{R}^n \to \mathbb{R}^n? \] Recall that each linear transformation can be represented as a matrix with respect to some basis. The matrix of $T_A$ with respect to the basis $B_{e}=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ is given by: \[ \ _{B_e}[A]_{B_e} = \begin{bmatrix} | & | & \mathbf{ } & | \nl T_A(\vec{e}_1) & T_A(\vec{e}_2) & \dots & T_A(\vec{e}_n) \nl | & | & \mathbf{ } & | \end{bmatrix}. \] where we assume that the outputs $T_A(\vec{e}_j)$ are given to us as column vectors with respect to $B_{e}$.
The action of $T_A$ on any vector $\vec{v}$ is the same as the matrix-vector multiplication by $\ _{B_e}[A]_{B_e}$ of the coefficients vector $(v_1,v_2,\ldots,v_n)_{B_{e}}$ expressed in the basis $B_e$.
A lot of mathematical buzz comes from this kind of parallel structure between worlds. The mathematical term used to describe a one-to-one correspondence between two mathematical objets is called an isomorphism. It's the same thing. Everything you know about matrices can be applied to linear transformation and everything you know about linear transformations can be applied to matrices.
In this case, we can say more precisely that the abstract concept of some linear transformation is represented as the concrete matrix of coefficients with respect to some basis. The matrix $\ _{B_{e}}[A]_{B_{e}}$ is the representation of $T_A$ with respect to the basis $B_{e}$.
What would be the representation of $T_A$ with respect to some other basis $B_{f}$?
Change of basis for matrices
Recall that the change of basis matrix $\ _{B_f}[I]_{B_e}$ which can be used to transform a coefficients $[\vec{v}]_{B_e}$ to a coefficient vector in a different basis $[\vec{v}]_{B_f}$: \[ [\vec{v}]_{B_f} = \ _{B_f}[I]_{B_e} \ [\vec{v}]_{B_e}. \]
Suppose now that you are given the representation $\ _{B_{e}}[A]_{B_{e}}$ of the linear transformation $T_A$ with respect to $B_e$ and you are asked to find the matrix $\ _{B_{f}}[A]_{B_{f}}$ which is the representation of $T_A$ with respect to the basis $B_f$.
The answer is very straightforward \[ \ _{B_f}[A]_{B_f} = \ _{B_f}[I]_{B_e} \ _{B_e}[A]_{B_e} \ _{B_e}[I]_{B_f}, \] where $\ _{B_e}[I]_{B_f}$ is the inverse matrix of $\ _{B_f}[I]_{B_e}$ and corresponds to the change of basis from the $B_f$ basis to the $B_e$ basis.
The interpretation of the above three-matrix sandwich is also straightforward. Imagine an input vector $[\vec{v}]_{B_f}$ multiplying the sandwich from the right. In the first step $\ _{B_e}[I]_{B_f}$ will convert it to the $B_e$ basis so that the $\ _{B_e}[A]_{B_e}$ matrix can be applied. In the last step the matrix $\ _{B_f}[I]_{B_e} $ converts the output of $T_A$ to the $B_f$ basis.
A transformation of the form: \[ A \to P A P^{-1}, \] where $P$ is any invertible matrix is called a similarity transformation.
The similarity transformation $A^\prime = P A P^{-1}$ leaves many of the properties of the matrix $A$ unchanged:
- Trace: $\textrm{Tr}\!\left( A^\prime \right) = \textrm{Tr}\!\left( A \right)$.
- Determinant: $\textrm{det}\!\left( A^\prime \right) = \textrm{det}\!\left( A \right)$.
- Rank: $\textrm{Tr}\!\left( A^\prime \right) = \textrm{Tr}\!\left( A \right)$.
- Eigenvalues: $\textrm{eig}\!\left( A^\prime \right) = \textrm{eig}\!\left( A \right)$.
In some sense, the basis invariant properties like the trace, the determinant, the rank and the eigenvalues are the only true properties of matrices. Everything else is maya—just one representation out of many.
Links
[ Change of basis explained. ]
http://planetmath.org/ChangeOfBases.html
NOINDENT
[ Change of basis example by Salman Khan. ]
http://www.youtube.com/watch?v=meibWcbGqt4
Vector spaces
We will now discuss no vector in particular, but rather the set of all possible vectors. In three dimensions this is the space $(\mathbb{R},\mathbb{R},\mathbb{R}) \equiv \mathbb{R}^3$. We will also discuss vector subspaces of $\mathbb{R}^3$ like lines and planes thought the origin.
In this section we develop the vocabulary needed to talk about vector spaces. Using this language will allow us to say some interesting things about matrices. We will formally define the fundamental subspaces for a matrix $A$: the column space $\mathcal{C}(A)$, the row space $\mathcal{R}(A)$, and the null space $\mathcal{N}(A)$.
Definitions
Vector space
A vector space $V \subseteq \mathbb{R}^n$ consists of a set of vectors and all possible linear combinations of these vectors. The notion of all possible linear combinations is very powerful. In particular it has the following two useful properties. We say that vector spaces are closed under addition, which means the sum of any two vectors taken from the vector space is a vector in the vector space. Mathematically, we write: \[ \vec{v}_1+\vec{v}_2 \in V, \qquad \forall \vec{v}_1, \vec{v}_2 \in V. \] A vector space is also closed under scalar multiplication: \[ \alpha \vec{v} \in V, \qquad \forall \alpha \in \mathbb{R},\ \vec{v} \in V. \]
Span
Given a vector $\vec{v}_1$, we can define the following vector space: \[ V_1 = \textrm{span}\{ \vec{v}_1 \} \equiv \{ \vec{v} \in V \ | \vec{v} = \alpha \vec{v}_1 \textrm{ for some } \alpha \in \mathbb{R} \}. \] We say $V_1$ is the space spanned by $\vec{v}_1$ which means that it is the set of all possible multiples of $\vec{v}_1$. The shape of $V_1$ is an infinite line.
Given two vectors $\vec{v}_1$ and $\vec{v}_2$ we can define a vector space: \[ V_{12} = \textrm{span}\{ \vec{v}_1, \vec{v}_2 \} \equiv \{ \vec{v} \in V \ | \vec{v} = \alpha \vec{v}_1 + \beta\vec{v}_2 \textrm{ for some } \alpha,\beta \in \mathbb{R} \}. \] The vector space $V_{12}$ contains all vectors that can be written as a linear combination of $\vec{v}_1$ and $\vec{v}_2$. This is a two-dimensional vector space which has the shape of an infinite plane.
Note that the same space $V_{12}$ can be obtained as the span of different vectors: $V_{12} = \textrm{span}\{ \vec{v}_1, \vec{v}_{2^\prime} \}$, where $\vec{v}_{2^\prime} = \vec{v}_2 + 30\vec{v}_1$. Indeed, $V_{12}$ can be written as the span of any two linearly independent vectors contained in $V_{12}$. This is precisely what is cool about vector spaces: you can talk about the space as a whole without necessarily having to talk about the vectors in it.
As a special case, consider the the situation when $\vec{v}_1 = \gamma\vec{v}_2$, for some $\gamma \in \mathbb{R}$. In this case, the vector space $V_{12} = \textrm{span}\{ \vec{v}_1, \vec{v}_2 \}=\textrm{span}\{ \vec{v}_1 \}$ is actually one-dimensional since $\vec{v}_2$ can be written as a multiple of $\vec{v}_1$.
Vector subspaces
A subset $W$ of the vector space $V$ is called a subspace if:
- It is closed under addition: $\vec{w}_1 + \vec{w}_2 \in W$, for all $\vec{w}_1,\vec{w}_2 \in W$.
- It is closed under scalar multiplication: $\alpha \vec{w} \in W$, for all $\vec{w} \in W$.
This means that if you take any linear combination of vectors in $W$, the result will also be a vector in $W$. We use the notation $W \subseteq V$ to indicate that $W$ is a subspace of $V$.
An important fact about subspaces is that they always contains the zero vector $\vec{0}$. This is implied by the second property, since any vector becomes the zero vector when multiplied by the scalar $\alpha=0$: $\alpha \vec{w} = \vec{0}$.
Constraints
One way to define a vector subspace $W$ is to start with a larger space $(x,y,z) \in V$ and describe the a set of constraints that must be satisfied by all points $(x,y,z)$ in the subspace $W$. For example, the $xy$-plane can be defined as the set points $(x,y,z) \in \mathbb{R}^3$ that satisfy \[ (0,0,1) \cdot (x,y,z) = 0. \] More formally, we define the $xy$-plane as follows: \[ P_{xy} = \{ (x,y,z) \in \mathbb{R}^3 \ | \ (0,0,1) \cdot (x,y,z) = 0 \}. \] The vector $\hat{k}\equiv(0,0,1)$ is perpendicular to all the vectors that lie in the $xy$-plane so another description for the $xy$-plane is “the set of all vectors perpendicular to the vector $\hat{k}$.” In this definition, the parent space is $V=\mathbb{R}^3$, and the subspace $P_{xy}$ is defined as the set of points that satisfy the constraint $(0,0,1) \cdot (x,y,z) = 0$.
Another way to represent the $xy$-plane would be to describe it as the span of two linearly independent vectors in the plane: \[ P_{xy} = \textrm{span}\{ (1,0,0), (1,1,0) \}, \] which is equivalent to saying: \[ P_{xy} = \{ \vec{v} \in \mathbb{R}^3 \ | \ \vec{v} = \alpha (1,0,0) + \beta(1,1,0), \forall \alpha,\beta \in \mathbb{R} \}. \] This last expression is called an explicit parametrization of the space $P_{xy}$ and $\alpha$ and $\beta$ are the two parameters. There corresponds a unique pair $(\alpha,\beta)$ for each point in the plane. The explicit parametrization of an $m$-dimensional vector space requires $m$ parameters.
Matrix subspaces
Consider the following subspaces which are associated with a matrix $M \in \mathbb{R}^{m\times n}$. These are sometiemes referred to as the fundamental subspaces of the matrix $M$.
- The row space $\mathcal{R}(M)$ is the span of the rows of the matrix.
Note that computing a given linear combination of the rows of a matrix can be
done by multiplying the matrix //on the left// with an $m$-vector:
\[
\mathcal{R}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \ | \ \vec{v} = \vec{w}^T M \textrm{ for some } \vec{w} \in \mathbb{R}^{m} \},
\]
where we used the transpose $T$ to make $\vec{w}$ into a row vector.
* The null space $\mathcal{N}(M)$ of a matrix $M \in \mathbb{R}^{m\times n}$
consists of all the vectors that the matrix $M$ sends to the zero vector:
\[
\mathcal{N}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \ | \ M\vec{v} = \vec{0} \}.
\]
The null space is also known as the //kernel// of the matrix.
* The column space $\mathcal{C}(M)$ is the span of the columns of the matrix.
The column space consist of all the possible output vectors that the matrix can produce
when multiplied by a vector on the right:
\[
\mathcal{C}(M) \equiv \{ \vec{w} \in \mathbb{R}^m
\ | \
\vec{w} = M\vec{v} \textrm{ for some } \vec{v} \in \mathbb{R}^{n} \}.
\]
* The left null space $\mathcal{N}(M^T)$ which is the null space of the matrix $M^T$.
We say //left// null space,
because this is the null space of vectors when multiplying the matrix by a vector on the left:
\[
\mathcal{N}(M^T) \equiv \{ \vec{w} \in \mathbb{R}^m \ | \ \vec{w}^T M = \vec{0}^T \}.
\]
The notation $\mathcal{N}(M^T)$ is suggestive of the fact that we can
rewrite the condition $\vec{w}^T M = \vec{0}^T$ as $M^T\vec{w} = \vec{0}^T$.
Hence the left null space of $A$ is equivalent to the null space of $A^T$.
The left null space consists of all the vectors $\vec{w} \in \mathbb{R}^m$
that are orthogonal to the columns of $A$.
The matrix-vector product $M \vec{x}$ can be thought of as the action of a vector function (a linear transformation $T_M:\mathbb{R}^n \to \mathbb{R}^m$) on an input vector $\vec{x}$. The columns space $\mathcal{C}(M)$ plays the role of the image of the linear transformation $T_M$, and the null space $\mathcal{N}(M)$ is the set of zeros (roots) of the function $T_M$. The row space $\mathcal{R}(M)$ is the pre-image of the column space $\mathcal{C}(M)$. To every point in $\mathcal{R}(M)$ (input vector) corresponds one point (output vector) in $\mathcal{C}(M)$. This means the column space and the rows space must have the same dimension. We call this dimension the rank of the matrix $M$: \[ \textrm{rank}(M) = \dim\left(\mathcal{R}(M) \right) = \dim\left(\mathcal{C}(M) \right). \] The rank is the number of linearly independent rows, which is also equal to the number of independent columns.
We can characterize the domain of $M$ (the space of $n$-vectors) as the orthogonal sum ($\oplus$) of the row space and the null space: \[ \mathbb{R}^n = \mathcal{R}(M) \oplus \mathcal{N}(M). \] Basically a vector either has non-zero product with at least one of the rows of $M$ or it has zero product with all of them. In the latter case, the output will be the zero vector – which means that the input vector was in the null space.
If we think of the dimensions involved in the above equation: \[ \dim(\mathbb{R}^n) = \dim(\mathcal{R}(M)) + \dim( \mathcal{N}(M)), \] we obtain an important fact: \[ n = \textrm{rank}(M) + \dim( \mathcal{N}(M)), \] where $\dim( \mathcal{N}(M))$ is called the nullity of $M$.
Linear independence
The set of vectors $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n \}$ is linear independent if the only solution to the equation \[ \sum\limits_i\lambda_i\vec{v}_i= \lambda_1\vec{v}_1 + \lambda_2\vec{v}_2 + \cdots + \lambda_n\vec{v}_n = \vec{0} \] is $\lambda_i=0$ for all $i$.
The above condition guarantees that none of the vectors can be written as a linear combination of the other vectors. To understand the importance of the “all zeros” solutions, let's consider an example where a non-zero solution exists. Suppose we have a set of three vectors $\{\vec{v}_1, \vec{v}_2, \vec{v}_3 \}$ which satisfy $\lambda_1\vec{v}_1 + \lambda_2\vec{v}_2 + \lambda_3\vec{v}_3 = 0$ with $\lambda_1=-1$, $\lambda_2=1$, and $\lambda_3=2$. This means that \[ \vec{v}_1 = 1\vec{v}_2 + 2\vec{v}_3, \] which shows that $\vec{v}_1$ can be written as a linear combination of $\vec{v}_2$ and $\vec{v}_3$, hence the vectors are not linearly independent.
Basis
In order to carry out calculations with vectors in a vector space $V$, we need to know a basis $B=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ for that space. A basis for an $n$-dimensional vector space $V$ is a set of $n$ linearly independent vectors in $V$. Intuitively, a basis is a set of vectors that can be used as a coordinate system for a vector space.
A basis $B=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ for the vector space $V$ has the following two properties:
- Spanning property.
Any vector $\vec{v} \in V$ can be expressed as a linear combination of the basis elements:
\[
\vec{v} = v_1\vec{e}_1 + v_2\vec{e}_2 + \cdots + v_n\vec{e}_n.
\]
This property guarantees that the vectors in the basis $B$ are //sufficient// to represent any vector in $V$.
* **Linear independence property**.
The vectors that form the basis $B = \{ \vec{e}_1,\vec{e}_2, \ldots, \vec{e}_n \}$ are linearly independent.
The linear independence of the vectors in the basis guarantees that none of the vectors $\vec{e}_i$ is redundant.
If a set of vectors $B=\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ satisfies both properties, we say $B$ is a basis for $V$. In other words $B$ can serve as a coordinate system for $V$. Using the basis $B$, we can represent any vector $\vec{v} \in V$ as a unique tuple of coordinates \[ \vec{v} = v_1\vec{e}_1 + v_2\vec{e}_2 + \cdots + v_n\vec{e}_n \qquad \Leftrightarrow \qquad (v_1,v_2, \ldots, v_n)_B. \] The coordinates of $\vec{v}$ are calculated with respect to the basis $B$.
The dimension of a vector space is defined as the number of vectors in a basis for that vector space. A basis for an $n$-dimensional vector space contains exactly $n$ vectors. Any set of less than $n$ vectors would not satisfy the spanning property. Any set of with more than $n$ vectors from $V$ cannot be linearly independent. To form a basis for a vector space, the set of vectors must be “just right”: it must contain a sufficient number of vectors but not too many so that the coefficients of each vector will be uniquely determined.
Distilling a basis
A basis for an $n$-dimensional vector space $V$ consist of exactly $n$ vectors. Any set of vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ can serve as a basis as long as they are linearly independent and there is exactly $n$ of them.
Sometimes an $n$-dimensional vector space $V$ will be specified as the span of more than $n$ vectors: \[ V = \textrm{span}\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}, \quad m > n. \] Since there are $m>n$ of the $\vec{v}$-vectors, they are too many to form a basis. We say this set of vectors is over-complete. They cannot all be linearly independent since there can be at most $n$ linearly independent vectors in an $n$-dimensional vector space.
If we want to have a basis for the space $V$, we'll have to reject some of the vectors. Given the set of vectors $\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}$, our task is to distill a set of $n$ linearly indecent vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ from them.
We can use the Gauss–Jordan elimination procedure to distil a set of linearly independent vectors. Actually, you know how to do this already! You can write the set of $m$ vectors as the rows of a matrix and then do row operations on this matrix until you find the reduced row echelon form. Since row operations do not change the row space of the matrix, there will be $n$ non-zero rows of the final RREF of the matrix which form a basis for $V$. We will learn more about this procedure in the next section.
Examples
Example 1
Describe the set of vectors which are perpendicular to the vector $(0,0,1)$ in $\mathbb{R}^3$.
Sol: We need to find all the vectors $(x,y,z)$ such that $(x,y,z)\cdot (0,0,1) = 0$.
By inspection we see that whatever choice of $x$ and $y$ components we choose will
work so we say that the set of vectors perpendicular to
$(0,0,1)$ is $\textrm{span}\{ (1,0,0), (0,1,0) \}$.
Applications of Gauss-Jordan elimination
In this section we'll learn about a practical algorithm for the characterization of vector spaces. Actually, the algorithm is not new: you already know about the Gauss-Jordan elimination procedure that uses row operations to transform any matrix into its reduced row echelon form. In this section we'll see how this procedure can be used to find bases for all kinds of vector spaces.
Finding a basis
Suppose we have a vector space $V$ defined as the span of some set of vectors $\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}$: \[ V = \textrm{span}\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}. \] Your task will be to find a basis for $V$.
Recall that a basis is the minimal set of linearly independent vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ which allow us to write any $\vec{v} \in V$ as $\vec{v} = v_1\:\vec{e}_1 + v_2\:\vec{e}_2 + \cdots +v_n\:\vec{e}_n$. In other words, we are looking for an alternate description of the vector space $V$ as \[ V = \textrm{span}\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}, \] such that the set $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ are all linearly independent.
One way to accomplish this task is to write the vectors $\vec{v}_i$ as the rows of a matrix $M$. By this construction, the space $V$ corresponds to $\mathcal{R}(M)$, the row space of the matrix $M$. We can now use the standard row operations to bring the matrix into the reduced row echelon form. Applying row operations to a matrix does not change its row space. By transforming the matrix into its RREF, we will be able to see which of the row were linearly independent and can serve as basis vectors $\vec{e}_j$:
\[ \left[\;\;\;\; \begin{array}{rcl} - & \vec{v}_1 & - \nl - & \vec{v}_2 & - \nl - & \vec{v}_3 & - \nl & \vdots & \nl - & \vec{v}_m & - \end{array} \;\;\;\;\right] \quad - \ \textrm{ G-J elim.} \to \quad \left[\;\;\;\;\begin{array}{rcl} - & \vec{e}_1 & - \nl & \vdots & \nl - & \vec{e}_n & - \nl 0 &\;\; 0 \;\; & 0 \nl 0 & \;\; 0 \;\; & 0 \end{array} \;\;\;\;\right]. \] The non-zero rows in the RREF of the matrix form a set of linearly independent vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ that span the vector space $V$. Any vectors that were not linearly independent have been reduced to rows of zeros.
The above process is called “finding a basis” and it is important to understand how to carry out the steps. Even more important is for you to understand why we are doing this. In the end we still have the same space $V$ just described in terms of some new vectors. Why is the description of the vector space $V$ in terms of the vectors $\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$ any better than the original description in terms of the vectors $\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_m \}$? The description of $V$ in terms of a basis of $n$ linearly independent vectors shows the space $V$ is $n$-dimensional.
TODO: say also unique coodinates w.r.t. B_e, not w.r.t. B_v
Definitions
- $B_S = \{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$: a basis for an $n$-dimensional
vector space $S$ is a set of $n$ linearly independent vectors in the space $S$.
Any vector is $\vec{v} \in S$ can be written as a linear combination of the basis elements:
\[ \vec{v} = v_1 \vec{e}_1 + v_2 \vec{e}_2 + \cdots + v_n \vec{e}_n. \]
The basis for an $n$-dimensional contains exactly $n$ vectors.
* $\textrm{dim}(S)$: the dimension of the space $S$ is equal to the number of elements
in a basis for $S$.
NOINDENT Recall the four fundamental spaces of a matrix $M \in \mathbb{R}^{m \times n}$ that we defined in the previous section:
- $\mathcal{R}(M)$: the row space of a matrix $M$, which consists of all possible linear
combinations of the rows of the matrix $M$.
- $\mathcal{C}(M)$: the column space of a matrix $M$, which
consists of all possible linear combinations of the columns of the matrix $M$.
- $\textrm{rank}(M)$: the rank of the matrix $M$. The ranks is equal to the number
of linearly independent columns and rows:
$\textrm{rank}(M)=\textrm{dim}(\mathcal{R}(M))=\textrm{dim}(\mathcal{C}(M))$.
* $\mathcal{N}(M)$: the //null space// a matrix $M$,
which is the set of vectors that the matrix $M$ sends to the zero vector:
\[
\mathcal{N}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \;\;| \;\;M\vec{v} = \vec{0} \}.
\]
* $\textrm{dim}(\mathcal{N}(M))$: the dimension of the null space,
also known as the //nullity// of $M$.
* $\mathcal{N}(M^T)$: the //left null space// a matrix $M$,
which is the set of vectors that the matrix $M$ sends to the zero vector
when multiplied on the left:
\[
\mathcal{N}(M^T) \equiv \{ \vec{w} \in \mathbb{R}^m \;\;| \;\;\vec{w}^T M = \vec{0} \}.
\]
Bases for fundamental spaces
The procedure we described in the beginning of this section can be used ``distill'' any set of vectors into a set of linearly independent vectors that form a basis. Indeed, the Gauss–Jordan elimination procedure allows us to find a simple basis for the row space $\mathcal{R}(M)$ of any matrix.
How do we find bases for the other fundamental spaces of a matrix? We'll now show how to use the RREF of a matrix $A$ to find bases for $\mathcal{C}(A)$ and $\mathcal{N}(A)$. Pay careful attention to the locations of the pivots (leading ones) in the RREF of $A$ because they play a crucial role in what follows.
Basis for the row space
The row space $\mathcal{R}(A)$ of a matrix $A$ is defined as the space of all vectors that can be written as a linear combinations of the rows of $A$. To find a basis for $\mathcal{R}(A)$, we use the Gauss–Jordan elimination procedure:
- Perform row operations to find the RREF of $A$.
- Read-off the non-zero rows.
Basis for the column space
To find a basis for the column space $\mathcal{C}(A)$ of a matrix $A$ you need to find which of the columns of $A$ are linearly independent. To find the linearly independent columns of $A$, use the following steps:
- Perform row operations to find the RREF of $A$.
- Identify the columns which contain the pivots (leading ones).
- The corresponding columns in the original matrix $A$
form a basis for the column space of $A$.
This procedure works because elementary row operations do not change the independence relations between the columns of the matrix. If two columns are independent in the reduced row echelon form, they were independent in the original matrix as well.
Note that the column space of the matrix $A$ corresponds to the row space of the matrix transposed $A^T$. Thus, another algorithm for finding the column space of a matrix $A$ would be to use the row space algorithm on $A^T$.
Basis for the null space
The null space $\mathcal{N}(A)$ of a matrix $A \in \mathbb{R}^{m \times n}$ is \[ \mathcal{N}(A) = \{ \vec{x}\in \mathbb{R}^n \ | \ A\vec{x} = \vec{0} \: \}. \] In words, the null space is the set of solutions of the equation $A\vec{x}=\vec{0}$.
The vectors in the null space are orthogonal to the row space of the matrix $A$. We can easily find the null space by working with the RREF of the matrix. The steps involved are as follows:
- Perform row operations to find the RREF of $A$.
- Identify the columns that do not contain a leading one.
These columns correspond to free variables of the solution.
For example, consider a matrix whose reduced row echelon form is
\[
\textrm{rref}(A) =
\begin{bmatrix}
\mathbf{1} & 2 & 0 & 0 \nl
0 & 0 & \mathbf{1} & -3 \nl
0 & 0 & 0 & 0
\end{bmatrix}.
\]
The second column and the fourth column do not contain leading ones (pivots),
so they correspond to free variables, which are customarily called $s$, $t$, $r$, etc.
We are looking for a vector with two free variables $(x_1,s,x_3,t)^T$.
- Rewrite the null space problem as a set of equations:
\[
\begin{bmatrix}
1 & 2 & 0 & 0 \nl
0 & 0 & 1 & -3 \nl
0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
x_1 \nl s \nl x_3 \nl t
\end{bmatrix}
=
\begin{bmatrix}
0 \nl 0 \nl 0
\end{bmatrix}
\qquad
\Rightarrow
\qquad
\begin{array}{rcl}
1x_1 + 2s &=&0 \nl
1x_3 - 3t &=&0 \nl
0 &=&0
\end{array}
\]
We can express the unknowns $x_1$ and $x_3$ in terms of the free variables $s$ and $t$
as follows $x_1 = -2s$ and $x_3=3t$.
We now have an expression for all vector in the null space: $(-2s,s,3t,t)^T$,
for any $s,t \in \mathbb{R}$.
We can rewrite the solution by splitting the $s$-part and the $t$-part:
\[
\begin{bmatrix}
x_1 \nl x_2 \nl x_3 \nl x_3
\end{bmatrix}
=
\begin{bmatrix}
-2s \nl s \nl 3t \nl t
\end{bmatrix}
=
\begin{bmatrix}
-2 \nl 1 \nl 0 \nl 0
\end{bmatrix}\!s
+
\begin{bmatrix}
0 \nl 0 \nl 3 \nl 1
\end{bmatrix}\!t.
\]
- The direction vectors associated with each free variable form a basis for the null space of the matrix:
\[
\mathcal{N}(A) =
\left\{ \begin{bmatrix}-2s \nl s \nl 3t \nl t \end{bmatrix}, \forall s,t \in \mathbb{R} \right\}
= \textrm{span}\left\{ \begin{bmatrix}-2\nl 1\nl0\nl0\end{bmatrix},
\begin{bmatrix}0\nl0\nl 3\nl1\end{bmatrix} \right\}.
\]
You can verify that the matrix $A$ times any vector in the null space produces a zero vector.
Examples
Example 1
Find a basis for the row space, the column space, and the null space of the matrix: \[ A = \left[\begin{array}{ccc}4 & -4 & 0\\1 & 1 & -2\\2 & -6 & 4\end{array}\right]. \] The first steps towards finding the row space, column space, and the null space of a matrix all require calculating the RREF of the matrix, so this is what we'll begin with.
- Let's focus on the first column.
To create a pivot in the top left corner, we divide the first row by four:
$R_1 \gets \frac{1}{4}R_1$:
\[\left[\begin{array}{ccc}1 & -1 & 0\\1 & 1 & -2\\2 & -6 & 4\end{array}\right].\]
* We use this pivot to clear the numbers on the second and third row below it
by performing $R_2 \gets R_2 -R_1$ and $R_3 \gets R_3 -2R_1$:
\[\left[\begin{array}{ccc}1 & -1 & 0\\0 & 2 & -2\\0 & -4 & 4\end{array}\right].\]
* We can create a pivot in the second row if we divide it by two
$R_2 \gets \frac{1}{2}R_2$:
\[\left[\begin{array}{ccc}1 & -1 & 0\\0 & 1 & -1\\0 & -4 & 4\end{array}\right].\]
* We now clear the column below it using $R_3 \gets R_3 +4R_2$:
\[\left[\begin{array}{ccc}1 & -1 & 0\\0 & 1 & -1\\0 & 0 & 0\end{array}\right].\]
* The final simplification is to clear the $-1$ above in the top of the second column
using: $R_1 \gets R_1 + R_2$:
\[\left[\begin{array}{ccc}1 & 0 & -1\\0 & 1 & -1\\0 & 0 & 0\end{array}\right].\]
Now that we have the RREF of the matrix, we can answer the questions.
Before we get to finding the bases for the fundamental spaces of $A$, let us first do some basic dimension-counting. Observe that the matrix has just two pivots. We say $\textrm{rank}(A)=2$. This means that both the row space and the column spaces are two-dimensional. Recall the equality: \[ n = \textrm{rank}( A ) \;\;+ \;\;\textrm{dim}( \mathcal{N}(A) ). \] The input space $\mathbb{R}^3$ splits into two types of vectors. Those that are in the row space of $A$ and those that are in the null space. Since we know that the row space is two-dimensional, we can deduce that the null space is going to be $\textrm{dim}( \mathcal{N}(A) ) = n - \textrm{dim}( \mathcal{R}(A) ) = 3 - 2 = 1$ dimensional.
We now proceed to answer the questions posed in the problem:
- The row space of $A$ consists of the two non-zero vectors in the RREF of $A$:
\[ \mathcal{R}(A) = \textrm{span}\{ (1,0,-1), (0,1,-1) \}. \]
- To find the column space of $A$, observe that it is the first and the second
columns that contain the pivots in the RREF of $A$. Therefore,
the first two columns of the original matrix $A$ form a basis for the column
space of $A$:
\[ \mathcal{C}(A) = \textrm{span}\left\{ \begin{bmatrix}4 \nl 1 \nl 2 \end{bmatrix},
\begin{bmatrix}-4\nl 1\nl -6 \end{bmatrix} \right\}. \]
* Let's now find an expression for the null space of $A$.
First observe that the third column does not contain a pivot.
This means that the third column corresponds to a free variable
and can take on any value $x_3= t, \;\;t \in \mathbb{R}$.
We want to give a description of all vectors $(x_1,x_2,t)^T$ such that:
\[\left[\begin{array}{ccc}1 & 0 & -1\nl 0 & 1 & -1\nl 0 & 0 & 0\end{array}\right]
\left[\begin{array}{c}x_1\nl x_2\nl t \end{array}\right]=
\left[\begin{array}{c}0\nl 0\nl 0 \end{array}\right]
\qquad
\Rightarrow
\qquad
\begin{array}{rcl}
1x_1 - 1t &=&0 \nl
1x_2 - 1t &=&0 \nl
0 &=&0 \;.
\end{array}
\]
We find $x_1=t$ and $x_2=t$ and obtain the following final expression for the null space:
\[ \mathcal{N}(A) = \left\{
\begin{bmatrix} t \nl t \nl t \end{bmatrix}, \;\;t \in \mathbb{R}\right\}
=
\textrm{span}\left\{ \begin{bmatrix}1\nl 1\nl 1\end{bmatrix} \right\}.
\]
The null space of $A$ is one dimensional and consists of all multiples of the vector $(1,1,1)^T$.
Example 2
Find a basis for the row space, column space and null space of the matrix: \[ B = \begin{bmatrix} 1 & 3 & 1 & 4 \nl 2 & 7 & 3 & 9 \nl 1 & 5 & 3 & 1 \nl 1 & 2 & 0 & 8 \end{bmatrix}. \]
First we find the reduced row echelon form of the matrix $B$: \[ \sim \begin{bmatrix} 1 & 3 & 1 & 4 \nl 0 & 1 & 1 & 1 \nl 0 & 2 & 2 & -3 \nl 0 & -1 & -1 & 4 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & -2 & 1 \nl 0 & 1 & 1 & 1 \nl 0 & 0 & 0 & -5 \nl 0 & 0 & 0 & 5 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & -2 & 0 \nl 0 & 1 & 1 & 0 \nl 0 & 0 & 0 & 1 \nl 0 & 0 & 0 & 0 \end{bmatrix}. \]
As in the previous example, we begin by calculating the dimensions of the subspaces. The rank of this matrix is $3$ so the column space and the row space will be $3$-dimensional. Since the input space is $\mathbb{R}^4$, this leaves one dimension for the null space. Let us proceed now to find the fundamental subspaces for the matrix $B$.
- The row space of $B$ consists of the three non-zero vectors in the RREF of $B$:
\[ \mathcal{R}(B) = \textrm{span}\{\; (1,0,-2,0), (0,1,1,0), (0,0,0,1) \}. \]
- The column space of $B$ is spanned by the first, second and fourth columns
of $B$ since these columns contain the leading ones in the RREF of $B$.
\[ \mathcal{C}(B) = \textrm{span}\left\{
\begin{bmatrix} 1 \nl 2 \nl 1 \nl 1\end{bmatrix},\;\;
\begin{bmatrix} 3 \nl 7 \nl 5 \nl 2\end{bmatrix},\;\;
\begin{bmatrix} 4 \nl 9 \nl 1 \nl 8\end{bmatrix}
\right\}. \]
* The third column lacks a leading one so it corresponds to a free variable $x_3= t,\;t \in \mathbb{R}$.
The null space of $B$ is the set of vectors $(x_1,x_2,t,x_4)^T$ such that:
\[\begin{bmatrix} 1 & 0 & -2 & 0 \nl 0 & 1 & 1 & 0 \nl 0 & 0 & 0 & 1 \nl 0 & 0 & 0 & 0 \end{bmatrix}
\left[\begin{array}{c}x_1\\x_2\\x_3\\x_4 \end{array}\right]=
\left[\begin{array}{c}0\\0\\0\\0 \end{array}\right]
\qquad
\Rightarrow
\qquad
\begin{array}{rcl}
1x_1 - 2t &=&0 \nl
1x_2 + 1t &=&0 \nl
x_4 &=&0 \nl
0 &=&0\;.
\end{array}
\]
We find the values of $x_1$, $x_2$, and $x_4$ in terms of $t$ and obtain
\[ \mathcal{N}(A) = \left\{ \begin{bmatrix} 2t \nl -t \nl t \nl 0 \end{bmatrix},
\;\;t \in \mathbb{R}\right\}
=
\textrm{span}\left\{ \begin{bmatrix}2\\-1\\1\\0 \end{bmatrix} \right\}.
\]
Discussion
Dimensions
Note that for an $m \times n$ matrix $M \in \mathbb{R}^{m \times n}$ the row space and the column space will consist of vectors with $n$ components, while the column space and the left null space will consist of vectors with $m$ components.
You shouldn't confuse the number of components or the number of rows in a matrix with the dimension of its row space. Suppose we are given a matrix with five rows and ten columns $M \in \mathbb{R}^{5 \times 10}$ and that the RREF of $M$ contains three non-zero rows. The row space of $M$ is therefore $3$-dimensional and a basis for it will consist of three vectors, each vector having ten components. The column space of the matrix will also be three-dimensional, but the basis for it will consist of vectors with five components. The null space of the matrix will be $10-3=7$-dimensional and also consist of $10$-vectors. Finally, the left null space will be $5-3=2$ dimensional and spanned by $5$-dimensional vectors.
Importance of bases
The procedures for identifying bases are somewhat technical and boring, but it is very important that you know how to find bases for vector spaces. To illustrate the importance of a basis consider a scenario in which you are given a description of the $xy$-plane $P_{xy}$ as the span of three vectors: \[ P_{xy}= \textrm{span}\{ (1,0,0), (0,1,0), (1,1,0) \}. \] The above definition of $P_{xy}$ says that any point $p \in P_{xy}$ can be written as a linear combination: \[ p = a (1,0,0) + b(0,1,0) + c(1,1,0) \] for some coefficients $(a,b,c)$. This representation of $P_{xy}$ is misleading. It might make us think (erroneously) that $P_{xy}$ is three-dimensional, since we need three coefficients $(a,b,c)$ to describe arbitrary vectors in $P_{xy}$.
Do we really need three coefficients to describe any $p \in P_{xy}$? No we don't. Two vectors are sufficient: $(1,0,0)$ and $(0,1,0)$ for example. The same point $p$ described above can be written in the form \[ p = \underbrace{(a+c)}_\alpha (1,0,0) + \underbrace{(b+c)}_\beta (0,1,0) = \alpha (1,0,0) + \beta (0,1,0), \] in terms of two coefficients $(\alpha, \beta)$. So the vector $(1,1,0)$ was not really necessary for the description of $P_{xy}$. It was redundant, because it can be expressed in terms of the other vectors. By getting rid of it, we obtain a description of $P_{xy}$ in terms of a basis: \[ P_{xy}= \textrm{span}\{ (1,0,0), (0,1,0) \}. \] Recall that the requirement for a basis $B$ for a space $V$ is that it be made of linearly independent vectors and that it span the space $V$. The vectors $\{ (1,0,0), (0,1,0) \}$ are sufficient to represent any vector in $P_{xy}$ and these vectors are linearly independent. We can conclude (this time correctly) that the space $P_{xy}$ is two-dimensional. If someone asks you “hod do you know that $P_{xy}$ is two dimensional?,” say “Because a basis for it contains two vectors.”
Exercises
Exercise 1
Consider the following matrix: \[ A= \begin{bmatrix} 1 & 3 & 3 & 3 \nl 2 & 6 & 7 & 6 \nl 3 & 9 & 9 & 10 \end{bmatrix} \] Find the RREF of $A$ and use it to find bases for $\mathcal{R}(A)$, $\mathcal{C}(A)$, and $\mathcal{N}(A)$.
NOINDENT Ans: $\mathcal{R}(A) = \textrm{span}\{ (1,3,0,0), (0,0,1,0), (0,0,0,1) \}$, $\mathcal{C}(A) = \textrm{span}\{ (1,2,3)^T, (3,7,9)^T, (3,6,10)^T \}$, and $\mathcal{N}(A)=\textrm{span}\{ (-3,1,0,0)^T \}$.
Invertible matrix theorem
In this section we will connect a number of results we learned about matrices and their properties. We know that matrices are useful in several different contexts. Originally we saw how matrices can be used to express and solve systems of linear equations. We also studied the properties of matrices like their row space, column space and null space. In the next chapter, we will also learn about how matrices can be used to represent linear transformations.
In each of these domains, invertible matrices play a particularly important role. The following theorem is a massive collection of facts about invertible matrices.
Invertible matrix theorem: For an $n \times n$ matrix $A$, the following statements are equivalent:
- $A$ is invertible.
- The determinant of $A$ is nonzero $\textrm{det}(A) \neq 0$.
- The equation $A\vec{x} = \vec{b}$ has exactly one solution for each $\vec{b} \in \mathbb{R}^n$.
- The equation $A\vec{x} = \vec{0}$ has only the trivial solution $\vec{x}=\vec{0}$.
- The RREF of $A$ is the $n \times n$ identity matrix.
- The rank of the matrix is $n$.
- The rows of $A$ are a basis for $\mathbb{R}^n$.
- The rows of $A$ are linearly independent.
- The rows of $A$ span $\mathbb{R}^n$. $\mathcal{R}(A)=\mathbb{R}^n$.
- The columns of $A$ are a basis for $\mathbb{R}^n$.
- The columns of $A$ are linearly independent.
- The columns of $A$ span $\mathbb{R}^n$. $\mathcal{C}(A)=\mathbb{R}^n$.
- The null space of $A$ contains only the zero vector $\mathcal{N}(A)=\{\vec{0}\}$.
- The transpose $A^T$ is also an invertible matrix.
This theorem states that for a given matrix $A$, the above statements are either all true or all false.
TODO: proof
[ See Section 2.3 of this page for a proof walkthrough ]
http://www.math.nyu.edu/~neylon/linalgfall04/project1/jja/group7.htm
Linear transformations
In this section we'll study functions that take vectors as inputs and produce vectors as outputs. In order to describe a function $T$ that takes $n$-dimensional vectors as inputs and produces $m$-dimensional vectors as outputs, we will use the notation: \[ T \colon \mathbb{R}^n \to \mathbb{R}^m. \] In particular, we'll restrict our attention to the class of linear transformations, which includes most of the useful transformations from analytic geometry: stretching, projections, reflections, and rotations. Linear transformations are used to describe and model many real-world phenomena in physics, chemistry, biology, and computer science.
Definitions
Linear transformation are mappings between vector inputs and vector outputs:
- $V =\mathbb{R}^n$: an $n$-dimensional vector space
$V$ is just a nickname we give to $\mathbb{R}^n$, which is the input vector space of $T$.
- $W = \mathbb{R}^m$: An $m$-dimensional vector space, which is the output space of $T$.
- ${\rm dim}(U)$: the dimension of the vector space $U$
- $T:V \to W$: a linear transformation that takes vectors $\vec{v} \in V$ as inputs
and produces outputs $\vec{w} \in W$. $T(\vec{v}) = \vec{w}$.
- $\textrm{Im}(T)$: the image space of the linear transformation $T$ is the
set of vectors that $T$ can output for some input $\vec{v}\in V$.
The mathematical definition of the image space is
\[
\textrm{Im}(T)
= \{ \vec{w} \in W \ | \ \vec{w}=T(\vec{v}), \textrm{ for some } \vec{v}\in V \}.
\]
The image space is the vector equivalent of the //image// of a function of a single variable
which you are familiar with $\{ y \in \mathbb{R} \ | \ y=f(x), \textrm{ for some } x \in \mathbb{R} \}$.
* $\textrm{Null}(T)$: The //null space// of the linear transformation $T$.
This is the set of vectors that get mapped to the zero vector by $T$.
Mathematically we write:
\[
\textrm{Null}(T) \equiv \{\vec{v}\in V \ | \ T(\vec{v}) = \vec{0} \},
\]
and we have $\textrm{Null}(T) \subseteq V$.
The null space is the vector equivalent of the set of //roots// of a function,
i.e., the values of $x$ where $f(x)=0$.
If we fix bases for the input and the output spaces, then a linear transformation can be represented as a matrix product:
- $B_V=\{ \vec{b}_1, \vec{b}_2, \ldots, \vec{b}_n\}$: A basis for the vector space $V$.
Any vector $\vec{v} \in V$ can be written as:
\[
\vec{v} = v_1 \vec{b}_1 + v_1 \vec{b}_1 + \cdots + v_n \vec{b}_n,
\]
where $v_1,v_2,\ldots,v_n$ are real numbers, which we call the
//coordinates of the vector $\vec{v}$ with respect to the basis $B_V$//.
* $B_W=\{\vec{c}_1, \vec{c}_2, \ldots, \vec{c}_m\}$: A basis for the output vector space $W$.
* $M_T \in \mathbb{R}^{m\times n}$: A matrix representation of the linear transformation $T$:
\[
\vec{w} = T(\vec{v}) \qquad \Leftrightarrow \qquad \vec{w} = M_T \vec{v}.
\]
Multiplication of the vector $\vec{v}$ by the matrix $M_T$ (from the left)
is //equivalent// to applying the linear transformation $T$.
Note that the matrix representation $M_T$ is //with respect to// the bases $B_{V}$ and $B_{W}$.
If we need to show the choice of input and output bases explicitly,
we will write them in subscripts $\;_{B_W}[M_T]_{B_V}$.
* $\mathcal{C}(M_T)$: The //column space// of a matrix $M_T$ consists of all possible linear
combinations of the columns of the matrix $M_T$.
Given $M_T$, the representation of some linear transformation $T$,
the column space of $M_T$ is equal to the image space of $T$:
$\mathcal{C}(M_T) = \textrm{Im}(T)$.
* $\mathcal{N}(M_T)$: The //null space// a matrix $M_T$ is the set of
vectors that the matrix $M_T$ sends to the zero vector:
\[
\mathcal{N}(M_T) \equiv \{ \vec{v} \in V \ | \ M_T\vec{v} = \vec{0} \}.
\]
The null space of $M_T$ is equal to the null space of $T$:
$\mathcal{N}(M_T) = \textrm{Null}(T)$.
Properties of linear transformation
Linearity
The fundamental property of a linear transformation is, you guessed it, its linearity. If $\vec{v}_1$ and $\vec{v}_2$ are two input vectors and $\alpha$ and $\beta$ are two constants, then: \[ T(\alpha\vec{v}_1+\beta\vec{v}_2)= \alpha T(\vec{v}_1)+\beta T(\vec{v}_2). \]
Transformations as black boxes
Suppose someone gives you a black box which implements the transformation $T$. You are not allowed to look inside the box and see how $T$ acts, but you are allowed to probe the transformation by choosing various input vectors and observing what comes out.
Suppose we have a linear transformation $T$ of the form $T \colon \mathbb{R}^n \to \mathbb{R}^m$. It turns out that probing this transformation with $n$ carefully chosen input vectors and observing the outputs is sufficient to characterize it completely!
To see why this is true, consider a basis $\{ \vec{v}_1, \vec{v}_2, \ldots , \vec{v}_n \}$ for the $n$-dimensional input space $V = \mathbb{R}^n$. Any input vector can be written as a linear combination of the basis vectors: \[ \vec{v} = \alpha_1 \vec{v}_1 + \alpha_2 \vec{v}_2 + \cdots + \alpha_n \vec{v}_n. \] In order to characterize $T$, all we have to do is input each of $n$ basis vectors $\vec{v}_i$ into the black box that implements $T$ and record the $T(\vec{v}_i)$ that comes out. Using these observations and the linearity of $T$ we can now predict the output of $T$ for arbitrary input vectors: \[ T(\vec{v}) = \alpha_1 T(\vec{v}_1) + \alpha_2 T(\vec{v}_2) + \cdots + \alpha_n T(\vec{v}_n). \]
This black box model can be used in many areas of science, and is perhaps one of the most important ideas in linear algebra. The transformation $T$ could be the description of a chemical process, an electrical circuit or some phenomenon in biology. So long as we know that $T$ is (or can be approximated by) a linear transformation, we can obtain a complete description by probing it with the a small number of inputs. This is in contrast to non-linear transformations which could correspond to arbitrarily complex input-output relationships and would require significantly more probing in order to characterize precisely.
Input and output spaces
We said that the transformation $T$ is a map from $n$-vectors to $m$-vectors: \[ T \colon \mathbb{R}^n \to \mathbb{R}^m. \] Mathematically, we say that the domain of the transformation $T$ is $\mathbb{R}^n$ and the codomain is $\mathbb{R}^m$. The image space $\textrm{Im}(T)$ consists of all the possible outputs that the transformation $T$ can have. In general $\textrm{Im}(T) \subseteq \mathbb{R}^m$. A transformation $T$ for which $\textrm{Im}(T)=\mathbb{R}^m$ is called onto or surjective.
Furthermore, we will identify the null space as the subspace of the domain $\mathbb{R}^n$ that gets mapped to the zero vector by $T$: $\textrm{Null}(T) \equiv \{\vec{v} \in \mathbb{R}^n \ | \ T(\vec{v}) = \vec{0} \}$.
Linear transformations as matrix multiplications
There is an important relationship between linear transformations and matrices. If you fix a basis for the input vector space and a basis for the output vector space, a linear transformation $T(\vec{v})=\vec{w}$ can be represented as matrix multiplication $M_T\vec{v}=\vec{w}$ for some matrix $M_T$.
We have the following equivalence: \[ \vec{w} = T(\vec{v}) \qquad \Leftrightarrow \qquad \vec{w} = M_T \vec{v}. \] Using this equivalence, we can re-interpret several of the fact we know about matrices as properties of linear transformations. The equivalence is useful in the other direction too since it allows us to use the language of linear transformations to talk about the properties of matrices.
The idea of representing the action of a linear transformation as a matrix product is extremely important since it allows us to transform the abstract description of what the transformation $T$ does into the practical description: “take the input vector $\vec{v}$ and multiply it on the left by a matrix $M_T$.”
We'll now illustrate the “linear transformation $\Leftrightarrow$ matrix” equivalence with an example. Define $T=\Pi_{P_{xy}}$ to be the orthogonal projection onto the $xy$-plane $P_{xy}$. In words, action of this projection is simply to “kill” the $z$-component of the input vector. The matrix that corresponds to this projection is \[ T(\:(v_x,v_y,v_z)\:) = (v_x,v_y,0) \qquad \Leftrightarrow \qquad M_{T}\vec{v} = \begin{bmatrix} 1 & 0 & 0 \nl 0 & 1 & 0 \nl 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} v_x \nl v_y \nl v_z \end{bmatrix} = \begin{bmatrix} v_x \nl v_y \nl 0 \end{bmatrix}. \]
Finding the matrix
In order to find the matrix representation of a the transformation $T \colon \mathbb{R}^n \to \mathbb{R}^m$, it is sufficient to “probe it” with the $n$ vectors in the standard basis for $\mathbb{R}^n$: \[ \hat{e}_1 \equiv \begin{bmatrix} 1 \nl 0 \nl \vdots \nl 0 \end{bmatrix} \!\!, \ \ \ \hat{e}_2 \equiv \begin{bmatrix} 0 \nl 1 \nl \vdots \nl 0 \end{bmatrix}\!\!, \ \ \ \ \ldots, \ \ \ \hat{e}_n \equiv \begin{bmatrix} 0 \nl \vdots \nl 0 \nl 1 \end{bmatrix}\!\!. \] To obtain $M_T$, we combine the outputs $T(\hat{e}_1)$, $T(\hat{e}_2)$, $\ldots$, $T(\hat{e}_n)$ as the columns of a matrix: \[ M_T = \begin{bmatrix} | & | & \mathbf{ } & | \nl T(\vec{e}_1) & T(\vec{e}_2) & \dots & T(\vec{e}_n) \nl | & | & \mathbf{ } & | \end{bmatrix}. \]
Observe that the matrix constructed in this way has the right dimensions: when multiplied by an $n$-vector on the left it will produce an $m$-vector. We have $M_T \in \mathbb{R}^{m \times n}$, since the outputs of $T$ are $m$-vectors and since we used $n$ “probe” vectors.
In order to help you visualize this new “column thing”, we can analyze the matrix product $M_T \hat{e}_2$. The probe vector $\hat{e}_2\equiv (0,1,0,\ldots,0)^T$ will “select” only the second column from $M_T$ and thus we will obtain the correct output: $M_T \hat{e}_2 = T(\hat{e}_2)$. Similarly, applying $M_T$ to the other basis vectors selects each of the columns of $M_T$.
Any input vector can be written as a linear combination of the standard basis vectors $\vec{v} = v_1 \hat{e}_1 + v_2 \hat{e}_2 + \cdots + v_n\hat{e}_n$. Therefore, by linearity, we can compute the output $T(\vec{v})$: \[ \begin{align*} T(\vec{v}) &= v_1 T(\hat{e}_1) + v_2 T(\hat{e}_2) + \cdots + v_n T(\hat{e}_n) \nl & = v_1\!\begin{bmatrix} | \nl T(\hat{e}_1) \nl | \end{bmatrix} + v_2\!\begin{bmatrix} | \nl T(\hat{e}_2) \nl | \end{bmatrix} + \cdots + v_n\!\begin{bmatrix} | \nl T(\hat{e}_n) \nl | \end{bmatrix} \nl & = \begin{bmatrix} | & | & \mathbf{ } & | \nl T(\vec{e}_1) & T(\vec{e}_2) & \dots & T(\vec{e}_n) \nl | & | & \mathbf{ } & | \end{bmatrix} \begin{bmatrix} | \nl \vec{v} \nl | \end{bmatrix} \nl & = M_T \vec{v}. \end{align*} \]
Input and output spaces
Observe that the outputs of $T$ consist of all possible linear combinations of the columns of the matrix $M_T$. Thus, we can identify the image space of the transformation $\textrm{Im}(T) = \{ \vec{w} \in W \ | \ \vec{w}=T(\vec{v}), \textrm{ for some } \vec{v}\in V \}$ and the column space $\mathcal{C}(M_T)$ of the matrix $M_T$.
Perhaps not surprisingly, there is also an equivalence between the null space of the transformation $T$ and the null space of the matrix $M_T$: \[ \textrm{Null}(T) \equiv \{\vec{v}\in \mathbb{R}^n | T(\vec{v}) = \vec{0} \} = \mathcal{N}(M_T) \equiv \{\vec{v}\in \mathbb{R}^n | M_T\vec{v} = \vec{0} \}. \]
The null space $\mathcal{N}(M_T)$ of a matrix consists of all vectors that are orthogonal to the rows of the matrix $M_T$. The vectors in the null space of $M_T$ have a zero dot product with each of the rows of $M_T$. This orthogonality can also be phrased in the opposite direction. Any vector in the row space $\mathcal{R}(M_T)$ of the matrix is orthogonal to the null space $\mathcal{N}(M_T)$ of the matrix.
These observation allows us identify the domain of the transformation $T$ as the orthogonal sum of the null space and the row space of the matrix $M_T$: \[ \mathbb{R}^n = \mathcal{N}(M_T) \oplus \mathcal{R}(M_T). \] This split implies the conservation of dimensions formula \[ {\rm dim}(\mathbb{R}^n) = n = {\rm dim}({\cal N}(M_T))+{\rm dim}({\cal R}(M_T)), \] which says that sum of the dimensions of the null space and the row space of a matrix $M_T$ must add up to the total dimensions of the input space.
We can summarize everything we know about the input-output relationship of the transformation $T$ as follows: \[ T \colon \mathcal{R}(M_T) \to \mathcal{C}(M_T), \qquad T \colon \mathcal{N}(M_T) \to \{ \vec{0} \}. \] Input vectors $\vec{v} \in \mathcal{R}(M_T)$ get mapped to output vectors $\vec{w} \in \mathcal{C}(M_T)$. Input vectors $\vec{v} \in \mathcal{N}(M_T)$ get mapped to the zero vector.
Composition
The consecutive application of two linear operations on an input vector $\vec{v}$ corresponds to the following matrix product: \[ S(T(\vec{v})) = M_S M_T \vec{v}. \] Note that the matrix $M_T$ “touches” the vector first, followed by the multiplication with $M_S$.
For such composition to be well defined, the dimension of the output space of $T$ must be the same as the dimension of the input space of $S$. In terms of the matrices, this corresponds to the condition that inner dimension in the matrix product $M_S M_T$ must be the same.
Choice of basis
In the above, we assumed that the standard bases were used both for the inputs and the outputs of the linear transformation. Thus, the coefficients in the matrix $M_T$ we obtained were with respect to the standard bases.
In particular, we assumed that the outputs of $T$ were given to us as column vectors in terms of the standard basis for $\mathbb{R}^m$. If the outputs were given to us in some other basis $B_W$, then the coefficients of the matrix $M_T$ would be in terms of $B_W$.
A non-standard basis $B_V$ could also be used for the input space $\mathbb{R}^n$, in which case to construct the matrix $M_T$ we would have to “probe” $T$ with each of the vectors $\vec{b}_i \in B_V$. Furthermore, in order to compute $T$ as “the matrix product with the matrix produced by $B_V$-probing,” we would have to express the input vectors $\vec{v}$ in terms of its coefficients with respect to $B_V$.
Because of this freedom regarding the choice of which basis to use, it would be wrong to say that a linear transformation is a matrix. Indeed, the same linear transformation $T$ would correspond to different matrices if different bases are used. We say that the linear transformation $T$ corresponds to a matrix $M$ for a given choice of input and output bases. We write $_{B_W}[M_T]_{B_V}$, in order to show the explicit dependence of the coefficients in the matrix $M_T$ on the choice of bases. With the exception of problems which involve the “change of basis,” you can always assume that the standard bases are used.
Invertible transformations
We will now revisit the properties of invertible matrices and connect it with the notion of an invertible transformation. We can think of the multiplication by a matrix $M$ as “doing” something to vectors, and thus the matrix $M^{-1}$ must be doing the opposite thing to put the vector back in its place again: \[ M^{-1} M \vec{v} = \vec{v}. \]
For simple $M$'s you can “see” what $M$ does. For example, the matrix \[ M = \begin{bmatrix}2 & 0 \nl 0 & 1 \end{bmatrix}, \] corresponds to a stretching of space by a factor of 2 in the $x$-direction, while the $y$-direction remains untouched. The inverse transformation corresponds to a shrinkage by a factor of 2 in the $x$-direction: \[ M^{-1} = \begin{bmatrix}\frac{1}{2} & 0 \nl 0 & 1 \end{bmatrix}. \] In general it is hard to see what the matrix $M$ does exactly since it is some arbitrary linear combination of the coefficients of the input vector.
The key thing to remember is that if $M$ is invertible, it is because when you get the output $\vec{w}$ from $\vec{w} = M\vec{v}$, the knowledge of $\vec{w}$ allows you to get back to the original $\vec{v}$ you started from, since $M^{-1}\vec{w} = \vec{v}$.
By the correspondence $\vec{w} = T(\vec{v}) \Leftrightarrow \vec{w} = M_T\vec{v}$, we can identify the class of invertible linear transformation $T$ for which there exists a $T^{-1}$ such that $T^{-1}(T(\vec{v}))=\vec{v}$. This gives us another interpretation for some of the equivalence statements in the invertible matrix theorem:
- $T\colon \mathbb{R}^n \to \mathbb{R}^n$ is invertible.
$\quad \Leftrightarrow \quad$
$M_T \in \mathbb{R}^{n \times n}$ is invertible.
- $T$ is //injective// (one-to-one function).
$\quad \Leftrightarrow \quad$
$M_T\vec{v}_1 \neq M_T\vec{v}_2$ for all $\vec{v}_1 \neq \vec{v}_2$.
- The linear transformation $T$ is //surjective// (onto).
$\quad \Leftrightarrow \quad$
$\mathcal{C}(M_T) = \mathbb{R}^n$.
- The linear transformation $T$ is //bijective// (one-to-one correspondence).
$\quad \Leftrightarrow \quad$
For each $\vec{w} \in \mathbb{R}^n$, there exists a unique $\vec{v} \in \mathbb{R}^n$,
such that $M_T\vec{v} = \vec{w}$.
- The null space of $T$ is zero-dimensional $\textrm{Null}(T) =\{ \vec{0} \}$
$\quad \Leftrightarrow \quad$
$\mathcal{N}(M_T) = \{ \vec{0} \}$.
When $M$ is not invertible, it means that it must send some vectors to the zero vector: $M\vec{v} = 0$. When this happens there is no way to get back the $\vec{v}$ you started from, i.e., there is no matrix $M^{-1}$ such that $M^{-1} \vec{0} = \vec{v}$, since $B \vec{0} = \vec{0}$ for all matrices $B$.
TODO: explain better the above par, and the par before the list…
Affine transformations
An affine transformation is a function $A:\mathbb{R}^n \to \mathbb{R}^m$ which is the combination of a linear transformation $T$ followed by a translation by a fixed vector $\vec{b}$: \[ \vec{y} = A(\vec{x}) = T(\vec{x}) + \vec{b}. \] By the $T \Leftrightarrow M_T$ equivalence we can write the formula for an affine transformation as \[ \vec{y} = A(\vec{x}) = M_T\vec{x} + \vec{b}, \] where the linear transformation is performed as a matrix product $M_T\vec{x}$ and then we add a vector $\vec{b}$. This is the vector generalization of the affine function equation $y=f(x)=mx+b$.
Discussion
The most general linear transformation
In this section we learned that a linear transformation can be represented as matrix multiplication. Are there other ways to represent linear transformations? To study this question, let's analyze from first principles the most general form that linear transformation $T\colon \mathbb{R}^n \to\mathbb{R}^m$ can take. We will use $V=\mathbb{R}^3$ and $W=\mathbb{R}^2$ to keep things simple.
Let us first consider the first coefficients $w_1$ of the output vector $\vec{w} = T(\vec{v})$, when the input vector is $\vec{v}$. The fact that $T$ is linear, means that $w_1$ can be an arbitrary mixture of the input vector coefficients $v_1,v_2,v_3$: \[ w_1 = \alpha_1 v_1 + \alpha_2 v_2 + \alpha_3 v_3. \] Similarly, the second component must be some other arbitrary linear combination of the input coefficients $w_2 = \beta_1 v_1 + \beta_2 v_2 + \beta_3 v_3$. Thus, we have that the most general linear transformation $T \colon V \to W$ can be written as: \[ \begin{align*} w_1 &= \alpha_1 v_1 + \alpha_2 v_2 + \alpha_3 v_3, \nl w_2 &= \beta_1 v_1 + \beta_2 v_2 + \beta_3 v_3. \end{align*} \]
This is precisely the kind of expression that can be expressed as a matrix product: \[ T(\vec{v}) = \begin{bmatrix} w_1 \nl w_2 \nl \end{bmatrix} = \begin{bmatrix} \alpha_1 & \alpha_2 & \alpha_3 \nl \beta_1 & \beta_2 & \beta_3 \end{bmatrix} \begin{bmatrix} v_1 \nl v_2 \nl v_3 \nl \end{bmatrix} = M_T \vec{v}. \]
In fact, the reason why the matrix product is defined the way it is because it allows us to express linear transformations so easily.
Links
[ Nice visual examples of 2D linear transformations ]
http://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors
NOINDENT
[ More on null space and range space and dimension counting ]
http://en.wikibooks.org/wiki/Linear_Algebra/Rangespace_and_Nullspace
NOINDENT
[ Rotations as three shear operations ]
http://datagenetics.com/blog/august32013/index.html
Finding matrix representations
Every linear transformation $T:\mathbb{R}^n \to \mathbb{R}^m$ can be represented as a matrix product with a matrix $M_T \in \mathbb{R}^{m \times n}$. Suppose that the transformation $T$ is defined in a word description like “Let $T$ be the counterclockwise rotation of all points in the $xy$-plane by $30^\circ$.” How do we find the matrix $M_T$ that corresponds to this transformation?
In this section we will discuss various useful linear transformations and derive their matrix representations. The goal of this section is to solidify the bridge in your understanding between the abstract specification of a transformation $T(\vec{v})$ and its specific implementation of this transformation as a matrix-vector product $M_T\vec{v}$.
Once you find the matrix representation of a given transformation you can “apply” that transformation to many vectors. For example, if you know the $(x,y)$ coordinates of each pixel of an image, and you replace these coordinates with the outcome of the matrix-vector product $M_T(x,y)^T$, you'll obtain a rotated version of the image. That is essentially what happens when you use the “rotate” tool inside an image editing program.
Concepts
In the previous section we learned about linear transformations and their matrix representations:
- $T:\mathbb{R}^{n} \to \mathbb{R}^{m}$:
A linear transformation, which takes inputs $\vec{v} \in \mathbb{R}^{n}$ and produces outputs vector $\vec{w} \in \mathbb{R}^{n}$: $T(\vec{v}) = \vec{w}$.
- $M_T \in \mathbb{R}^{m\times n}$:
A matrix representation of the linear transformation $T$.
The action of the linear transformation $T$ is equivalent to a multiplication by the matrix $M_T$: \[ \vec{w} = T(\vec{v}) \qquad \Leftrightarrow \qquad \vec{w} = M_T \vec{v}. \]
Theory
In order to find the matrix representation of the transformation $T \colon \mathbb{R}^n \to \mathbb{R}^m$ it is sufficient to “probe” $T$ with the $n$ vectors from the standard basis for the input space $\mathbb{R}^n$: \[ \hat{e}_1 \equiv \begin{bmatrix} 1 \nl 0 \nl \vdots \nl 0 \end{bmatrix} \!\!, \ \ \ \hat{e}_2 \equiv \begin{bmatrix} 0 \nl 1 \nl \vdots \nl 0 \end{bmatrix}\!\!, \ \ \ \ \ldots, \ \ \ \hat{e}_n \equiv \begin{bmatrix} 0 \nl \vdots \nl 0 \nl 1 \end{bmatrix}\!\!. \] The matrix $M_T$ which corresponds to the action of $T$ on the standard basis is \[ M_T = \begin{bmatrix} | & | & \mathbf{ } & | \nl T(\vec{e}_1) & T(\vec{e}_2) & \dots & T(\vec{e}_n) \nl | & | & \mathbf{ } & | \end{bmatrix}. \]
This is an $m\times n$ matrix that has as its columns the outputs of $T$ for the $n$ probes.
Projections
The first kind of linear transformation we will study is the projection.
X projection
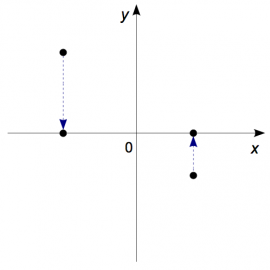 Consider the projection onto the $x$-axis $\Pi_{x}$.
The action of $\Pi_x$ on any vector or point is to leave the $x$-coordinate
unchanged and set the $y$-coordinate to zero.
Consider the projection onto the $x$-axis $\Pi_{x}$.
The action of $\Pi_x$ on any vector or point is to leave the $x$-coordinate
unchanged and set the $y$-coordinate to zero.
We can find the matrix associated with this projection by analyzing how it transforms the two vectors of the standard basis: \[ \begin{bmatrix} 1 \nl 0 \end{bmatrix} = \Pi_x\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right), \qquad \begin{bmatrix} 0 \nl 0 \end{bmatrix} = \Pi_x\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right). \] The matrix representation of $\Pi_x$ is therefore given by: \[ M_{\Pi_{x}}= \begin{bmatrix} \Pi_x\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) & \Pi_x\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) \end{bmatrix} = \left[\begin{array}{cc} 1 & 0 \nl 0 & 0 \end{array}\right]. \]
Y projection
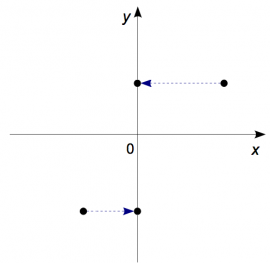 Can you guess what the matrix for the projection onto the $y$-axis will look like?
We use the standard approach to compute the matrix representation of $\Pi_y$:
\[
M_{\Pi_{y}}=
\begin{bmatrix}
\Pi_y\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) &
\Pi_y\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right)
\end{bmatrix}
=
\left[\begin{array}{cc}
0 & 0 \nl
0 & 1
\end{array}\right].
\]
Can you guess what the matrix for the projection onto the $y$-axis will look like?
We use the standard approach to compute the matrix representation of $\Pi_y$:
\[
M_{\Pi_{y}}=
\begin{bmatrix}
\Pi_y\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) &
\Pi_y\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right)
\end{bmatrix}
=
\left[\begin{array}{cc}
0 & 0 \nl
0 & 1
\end{array}\right].
\]
We can easily verify that the matrices $M_{\Pi_{x}}$ and $M_{\Pi_{y}}$ do indeed select the appropriate coordinate from a general input vector $\vec{v} = (v_x,v_y)^T$: \[ \begin{bmatrix} 1 & 0 \nl 0 & 0 \end{bmatrix} \begin{bmatrix} v_x \nl v_y \end{bmatrix} = \begin{bmatrix} v_x \nl 0 \end{bmatrix}, \qquad \begin{bmatrix} 0 & 0 \nl 0 & 1 \end{bmatrix} \begin{bmatrix} v_x \nl v_y \end{bmatrix} = \begin{bmatrix} 0 \nl v_y \end{bmatrix}. \]
Projection onto a vector
Recall that the general formula for the projection of a vector $\vec{v}$ onto another vector $\vec{a}$ is obtained as follows: \[ \Pi_{\vec{a}}(\vec{v})=\left(\frac{\vec{a} \cdot \vec{v} }{ \| \vec{a} \|^2 }\right)\vec{a}. \]
Thus, if we wanted to compute the projection onto an arbitrary direction $\vec{a}$, we would have to compute: \[ M_{\Pi_{\vec{a}}}= \begin{bmatrix} \Pi_{\vec{a}}\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) & \Pi_{\vec{a}}\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) \end{bmatrix}. \]
Projection onto a plane
We can also compute the projection of the vector $\vec{v} \in \mathbb{R}^3$ onto some plane $P: \ \vec{n}\cdot\vec{x}=n_xx+n_yy+n_zz=0$ as follows: \[ \Pi_{P}(\vec{v}) = \vec{v} - \Pi_{\vec{n}}(\vec{v}). \] The interpretation of the above formula is as follows. We compute the part of the vector $\vec{v}$ that is in the $\vec{n}$ direction, and then we subtract this part from $\vec{v}$ to obtain a point in the plane $P$.
To obtain the matrix representation of $\Pi_{P}$ we calculate what it does to the standard basis $\hat{\imath}=\hat{e}_1 = (1,0,0)^T$, $\hat{\jmath}=\hat{e}_2 = (0,1,0)^T$ and $\hat{k} =\hat{e}_3 = (0,0,1)^T$.
Projections as outer products
We can obtain a projection matrix onto any unit vector as an outer product of the vector with itself. Let us consider as an example how we could find the matrix for the projection onto the $x$-axis $\Pi_x(\vec{v}) = (\hat{\imath}\cdot \vec{v})\hat{\imath}=M_{\Pi_x}\vec{v}$. Recall that the inner product (dot product) between two column vectors $\vec{u}$ and $\vec{v}$ is equivalent to the matrix product $\vec{u}^T \vec{v}$, while their outer product is given by the matrix product $\vec{u}\vec{v}^T$. The inner product corresponds to a $1\times n$ matrix times a $n \times 1$ matrix, so the answer is $1 \times 1$ matrix, which is equivalent to a number: the value of the dot product. The outer product corresponds to $n\times 1$ matrix times a $1 \times n$ matrix so the answer is an $n \times n$ matrix. For example the projection matrix onto the $x$-axis is given by the matrix $M_{\Pi_x} = \hat{\imath}\hat{\imath}^T$.
What? Where did that equation come from? To derive this equation you simply have to rewrite the projection formula in terms of the matrix product and use the commutative law of scalar multiplication $\alpha \vec{v} = \vec{v}\alpha$ and the associative law of matrix multiplication $A(BC)=(AB)C$. Check it: \[ \begin{align*} \Pi_x(\vec{v}) = (\hat{\imath}\cdot\vec{v})\:\hat{\imath} = \hat{\imath} (\hat{\imath}\cdot\vec{v}) & = \hat{\imath} (\hat{\imath}^T \vec{v} ) = \left[\begin{array}{c} 1 \nl 0 \end{array}\right] \left( \left[\begin{array}{ccc} 1 & 0 \end{array}\right] \left[\begin{array}{c} v_x \nl v_y \end{array}\right] \right) \nl & = \left(\hat{\imath} \hat{\imath}^T\right) \vec{v} = \left( \left[\begin{array}{c} 1 \nl 0 \end{array}\right] \left[\begin{array}{ccc} 1 & 0 \end{array}\right] \right) \left[\begin{array}{c} v_x \nl v_y \end{array}\right] \nl & = \left(M \right) \vec{v} = \begin{bmatrix} 1 & 0 \nl 0 & 0 \end{bmatrix} \left[\begin{array}{c} v_x \nl v_y \end{array}\right] = \left[\begin{array}{c} v_x \nl 0 \end{array}\right]. \end{align*} \] We see that outer product $M\equiv\hat{\imath}\hat{\imath}^T$ corresponds to the projection matrix $M_{\Pi_x}$ which we were looking for.
More generally, the projection matrix onto a line with direction vector $\vec{a}$ is obtained by constructing a the unit vector $\hat{a}$ and then calculating the outer product: \[ \hat{a} \equiv \frac{ \vec{a} }{ \| \vec{a} \| }, \qquad M_{\Pi_{\vec{a}}}=\hat{a}\hat{a}^T. \]
Example
Find the projection matrix $M_d \in \mathbb{R}^{2 \times 2 }$ for the projection $\Pi_d$ onto the $45^\circ$ diagonal line, a.k.a. “the line with equation $y=x$”.
The line $y=x$ corresponds to the parametric equation $\{ (x,y) \in \mathbb{R}^2 | (x,y)=(0,0) + t(1,1), t\in \mathbb{R}\}$, so the direction vector is $\vec{a}=(1,1)$. We need to find the matrix which corresponds to $\Pi_d(\vec{v})=\left( \frac{(1,1) \cdot \vec{v} }{ 2 }\right)(1,1)^T$.
The projection matrix onto $\vec{a}=(1,1)$ is computed most easily using the outer product approach. First we compute a normalized direction vector $\hat{a}=(\tfrac{1}{\sqrt{2}},\tfrac{1}{\sqrt{2}})$ and then we compute the matrix product: \[ M_d = \hat{a}\hat{a}^T = \begin{bmatrix} \tfrac{1}{\sqrt{2}} \nl \tfrac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \tfrac{1}{\sqrt{2}} & \tfrac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \nl \frac{1}{2} & \frac{1}{2} \end{bmatrix}. \]
Note that the notion of an outer product is usually not covered in a first linear algebra class, so don't worry about outer products showing up on the exam. I just wanted to introduce you to this equivalence between projections onto $\hat{a}$ and the outer product $\hat{a}\hat{a}^T$, because it is one of the fundamental ideas of quantum mechanics.
The “probing with the standard basis approach” is the one you want to remember for the exam. We can verify that it gives the same answer: \[ M_{d}= \begin{bmatrix} \Pi_d\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) & \Pi_d\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) \end{bmatrix} = \begin{bmatrix} \left(\frac{\vec{a} \cdot \hat{\imath} }{ \| \vec{a} \|^2 }\right)\!\vec{a} & \left(\frac{\vec{a} \cdot \hat{\jmath} }{ \| \vec{a} \|^2 }\right)\!\vec{a} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \nl \frac{1}{2} & \frac{1}{2} \end{bmatrix}. \]
Projections are idempotent
Any projection matrix $M_{\Pi}$ satisfies $M_{\Pi}M_{\Pi}=M_{\Pi}$. This is one of the defining properties of projections, and the technical term for this is idempotence: the operation can be applied multiple times without changing the result beyond the initial application.
Subspaces
Note that a projection acts very differently on different sets of input vectors. Some input vectors are left unchanged and some input vectors are killed. Murder! Well, murder in a mathematical sense, which means being multiplied by zero.
Let $\Pi_S$ be the projection onto the space $S$, and $S^\perp$ be the orthogonal space to $S$ defined by $S^\perp = \{ \vec{w} \in \mathbb{R}^n \ | \ \vec{w} \cdot S = 0\}$. The action of $\Pi_S$ is completely different on the vectors from $S$ and $S^\perp$. All vectors $\vec{v} \in S$ comes out unchanged: \[ \Pi_S(\vec{v}) = \vec{v}, \] whereas vectors $\vec{w} \in S^\perp$ will be killed \[ \Pi_S(\vec{w}) = 0\vec{w} = \vec{0}. \] The action of $\Pi_S$ on any vector from $S^\perp$ is equivalent a multiplication by zero. This is why we call $S^\perp$ the null space of $M_{\Pi_S}$.
Reflections
We can easily compute the matrices for simple reflections in the standard two-dimensional space $\mathbb{R}^2$.
X reflection
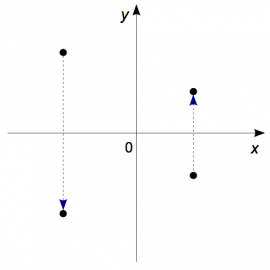 The reflection through the $x$-axis should leave the $x$-coordinate
unchanged and flip the sign of the $y$-coordinate.
The reflection through the $x$-axis should leave the $x$-coordinate
unchanged and flip the sign of the $y$-coordinate.
We obtain the matrix by probing as usual: \[ M_{R_x}= \begin{bmatrix} R_x\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) & R_x\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) \end{bmatrix} = \begin{bmatrix} 1 & 0 \nl 0 & -1 \end{bmatrix}. \]
Which correctly sends $(x,y)^T$ to $(x,-y)^T$ as required.
Y reflection
 The matrix associated with $R_y$, the reflection through the
$y$-axis is given by:
\[
M_{R_y}=
\left[\begin{array}{cc}
-1 & 0 \nl
0 & 1
\end{array}\right].
\]
The numbers in the above matrix tell you to change the sign
of the $x$-coordinate and leave the $y$-coordinate unchanged.
In other words, everything that was to the left of the
$y$-axis, now has to go to the right and vice versa.
The matrix associated with $R_y$, the reflection through the
$y$-axis is given by:
\[
M_{R_y}=
\left[\begin{array}{cc}
-1 & 0 \nl
0 & 1
\end{array}\right].
\]
The numbers in the above matrix tell you to change the sign
of the $x$-coordinate and leave the $y$-coordinate unchanged.
In other words, everything that was to the left of the
$y$-axis, now has to go to the right and vice versa.
Do you see how easy and powerful this matrix formalism is? You simply have to put in each column whatever you want the happen to the $\hat{e}_1$ vector and in the second column whatever you want to happen to the $\hat{e}_2$ vector.
Diagonal reflection
Suppose we want to find the formula for the reflection through the line $y=x$, which passes right through the middle of the first quadrant. We will call this reflection $R_{d}$ (this time, my dear reader the diagram is on you to draw). In words though, what we can say is that $R_d$ makes $x$ and $y$ “swap places”.
Starting from the description “$x$ and $y$ swap places” it is not difficult to see what the matrix should be: \[ M_{R_d}= \left[\begin{array}{cc} 0 & 1 \nl 1 & 0 \end{array}\right]. \]
I want to point out that an important property that all reflection have. We can always identify the action of a reflection by the fact that it does two very different things to two sets of points: (1) some points are left unchanged by the reflection and (2) some points become the exact negatives of themselves.
For example, the points that are invariant under $R_{y}$ are the points that lie on the $y$-axis, i.e., the multiples of $(0,1)^T$. The points that become the exact negative of themselves are those that only have an $x$-component, i.e, the multiples of $(1,0)^T$. The acton of $R_y$ on all other points can be obtained as a linear combination of the “leave unchanged” and the “multiply by $-1$” actions. We will discuss this line of reasoning more at the end of this section and we will sey generally how to describe the actions of $R_y$ on its different input subspaces.
Reflections through lines and planes
What about reflections through an arbitrary line? Consider the line $\ell: \{ \vec{0} + t\vec{a}, t\in\mathbb{R}\}$ that passes through the origin. We can write down a formula for the reflection through $\ell$ in terms of the projection formula: \[ R_{\vec{a}}(\vec{v})=2\Pi_{\vec{a}}(\vec{v})-\vec{v}. \] The reasoning behind the this formula is as follows. First we compute the projection of $\vec{v}$ onto the line $\Pi_{\vec{a}}(\vec{v})$, then take two steps in that direction and subtract $\vec{v}$ once. Use a pencil to annotate the figure to convince yourself the formula works.
Similarly, we can also derive and expression for the reflection through an arbitrary plane $P: \ \vec{n}\cdot\vec{x}=0$: \[ R_{P}(\vec{v}) =2\Pi_{P}(\vec{v})-\vec{v} =\vec{v}-2\Pi_{\vec{n}}(\vec{v}). \]
The first form of the formula uses a reasoning similar to the formula for the reflection through a line.
The second form of the formula can be understood as computing the shortest vector from the plane to $\vec{v}$, subtracting that vector once from $\vec{v}$ to get to a point in the plane, and subtracting it a second time to move to the point $R_{P}(\vec{v})$ on the other side of the plane.
Rotations
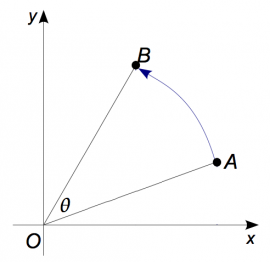 We now want to find the matrix which corresponds to the
counterclockwise rotation by the angle $\theta$.
An input point $A$ in the plane will get rotated around the origin
by an angle $\theta$ to obtain a new point $B$.
We now want to find the matrix which corresponds to the
counterclockwise rotation by the angle $\theta$.
An input point $A$ in the plane will get rotated around the origin
by an angle $\theta$ to obtain a new point $B$.
By now you know the drill. Probe with the standard basis: \[ M_{R_\theta}= \begin{bmatrix} R_\theta\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) & R_\theta\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) \end{bmatrix}. \] To compute the values in the first column, observe that the point $(1,0)=1\angle 0=(1\cos0,1\sin0)$ will be moved to the point $1\angle \theta=(\cos \theta, \sin\theta)$. The second input $\hat{e}_2=(0,1)$ will get rotated to $(-\sin\theta,\cos \theta)$. We therefore get the matrix: \[ M_{R_\theta} = \begin{bmatrix} \cos\theta &-\sin\theta \nl \sin\theta &\cos\theta \end{bmatrix}. \]
Finding the matrix representation of a linear transformation is like a colouring-book activity for mathematicians—you just have to fill in the columns.
Inverses
Can you tell me what the inverse matrix of $M_{R_\theta}$ is?
You could use the formula for finding the inverse of a $2 \times 2$ matrix or you could use the $[ \: A \: |\; I \;]$-and-RREF algorithm for finding the inverse, but both of these approaches would be waaaaay too much work for nothing. I want you to try to guess the formula intuitively. If $R_\theta$ rotates stuff by $+\theta$ degrees, what do you think the inverse operation will be?
Yep! You got it. The inverse operation is $R_{-\theta}$ which rotates stuff by $-\theta$ degrees and corresponds to the matrix \[ M_{R_{-\theta}} = \begin{bmatrix} \cos\theta &\sin\theta \nl -\sin\theta &\cos\theta \end{bmatrix}. \] For any vector $\vec{v}\in \mathbb{R}^2$ we have $R_{-\theta}\left(R_{\theta}(\vec{v})\right)=\vec{v}=R_{\theta}\left(R_{-\theta}(\vec{v})\right)$ or in terms of matrices: \[ M_{R_{-\theta}}M_{R_{\theta}} = I = M_{R_{\theta}}M_{R_{-\theta}}. \] Cool no? That is what representation really means, the abstract notion of composition of linear transformations is represented by the matrix product.
What is the inverse operation to the reflection through the $x$-axis $R_x$? Reflect again!
What is the inverse matrix for some projection $\Pi_S$? Good luck finding that one. The whole point of projections is to send some part of the input vectors to zero (the orthogonal part) so a projection is inherently many to one and therefore not invertible. You can also see this from its matrix representation: if a matrix does not have full rank then it is not invertible.
Non-standard basis probing
At this point I am sure that you feel confident to face any linear transformation $T:\mathbb{R}^2\to\mathbb{R}^2$ and find its matrix $M_T \in \mathbb{R}^{2\times 2}$ by probing with the standard basis. But what if you are not allowed to probe $T$ with the standard basis? What if you are given the outputs of $T$ for some other basis $\{ \vec{v}_1, \vec{v}_2 \}$: \[ \begin{bmatrix} t_{1x} \nl t_{1y} \end{bmatrix} = T\!\!\left( \begin{bmatrix} v_{1x} \nl v_{1y} \end{bmatrix} \right), \qquad \begin{bmatrix} t_{2x} \nl t_{2y} \end{bmatrix} = T\!\!\left( \begin{bmatrix} v_{2x} \nl v_{2y} \end{bmatrix} \right). \] Can we find the matrix for $M_T$ given this data?
Yes we can. Because the vectors form a basis, we can reconstruct the information about the matrix $M_T$ from the input-output data provided. We are looking for four unknowns $m_{11}$, $m_{12}$, $m_{21}$, and $m_{22}$ that make up the matrix $M_T$: \[ M_T = \begin{bmatrix} m_{11} & m_{12} \nl m_{21} & m_{22} \end{bmatrix}. \] Luckily, the input-output data allows us to write four equations: \[ \begin{align} m_{11}v_{1x} + m_{12} v_{1y} & = t_{1x}, \nl m_{21}v_{1x} + m_{22} v_{1y} & = t_{1y}, \nl m_{11}v_{2x} + m_{12} v_{2y} & = t_{2x}, \nl m_{21}v_{2x} + m_{22} v_{2y} & = t_{2y}. \end{align} \] We can solve this system of equations using the usual techniques and find the coefficients $m_{11}$, $m_{12}$, $m_{21}$, and $m_{22}$.
Let's see how to do this in more detail. We can think of the entries of $M_T$ as a $4\times 1$ vector of unknowns $\vec{x}=(m_{11}, m_{12}, m_{21}, m_{22})^T$ and then rewrite the four equations as a matrix equation: \[ A\vec{x} = \vec{b} \qquad \Leftrightarrow \qquad \begin{bmatrix} v_{1x} & v_{1y} & 0 & 0 \nl 0 & 0 & v_{1x} & v_{1y} \nl v_{2x} & v_{2y} & 0 & 0 \nl 0 & 0 & v_{2x} & v_{2y} \end{bmatrix} \begin{bmatrix} m_{11} \nl m_{12} \nl m_{21} \nl m_{22} \end{bmatrix} = \begin{bmatrix} t_{1x} \nl t_{1y} \nl t_{2x} \nl t_{2y} \end{bmatrix}. \] We can then solve for $\vec{x}$ by finding $\vec{x}=A^{-1}\vec{b}$. As you can see, it is a little more work than probing with the standard basis, but it is still doable.
Eigenspaces
Probing the transformation $T$ with any basis should give us sufficient information to determine its matrix with respect to the standard basis using the above procedure. Given the freedom we have for choosing the “probing basis”, is there a natural basis for probing each transformation $T$? The standard basis is good for computing the matrix representation, but perhaps there is another choice of basis which would make the abstract description of $T$ simpler.
Indeed, this is the case. For many linear transformations there exists a basis $\{ \vec{e}_1, \vec{e}_2, \ldots \}$ such that the action of $T$ on the basis vector $\vec{e}_i$ is equivalent to the scaling of $\vec{e}_i$ by a constant $\lambda_i$: \[ T(\vec{e}_i) = \lambda_i \vec{e}_i. \]
Recall for example how projections leave some vectors unchanged (multiply by $1$) and send some vectors to zero (multiply by $0$). These subspaces of the input space are specific to each transformation and are called the eigenspaces (own spaces) of the transformation $T$.
As another example, consider the reflection $R_x$ which has two eigenspaces.
- The space of vectors that are left unchanged
(the eigenspace correspondence to $\lambda=1$),
which is spanned by the vector $(1,0)$:
\[
R_x\!\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right)
= 1 \begin{bmatrix} 1 \nl 0 \end{bmatrix}.
\]
- The space of vectors which become the exact negatives of themselves
(the eigenspace correspondence to $\lambda=-1$),
which is spanned by $(0,1)$:
\[
R_x\!\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right)
= -1 \begin{bmatrix} 0 \nl 1 \end{bmatrix}.
\]
From the theoretical point of view, describing the action of $T$ in its natural basis is the best way to understand what it does. For each of the eigenvectors in the various eigenspaces of $T$, the action of $T$ is a simple scalar multiplication!
In the next section we will study the notions of eigenvalues and eigenvectors in more detail. Note, however, that you are already familiar with the special case of the “zero eigenspace”, which we call the null space. The action of $T$ on the vectors in its null space is equivalent to a multiplication by the scalar $0$.
Eigenvalues and eigenvectors
The set of eigenvectors of a matrix is a special set of input vectors for which the action of the matrix is described as a scaling. Decomposing a matrix in terms of its eigenvalues and its eigenvectors gives valuable insights into the properties of the matrix.
Certain matrix calculations like computing the power of the matrix become much easier when we use the eigendecomposition of the matrix. For example, suppose you are given a square matrix $A$ and you want to compute $A^5$. To make this example more concrete, let's use the matrix \[ A = \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix}. \]
We want to compute \[ A^5 = \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix}. \] That is a lot of matrix multiplications. You'll have to multiply and add entries for a while! Imagine how many times you would have to multiply the matrix if I had asked for $A^{55}$ instead?
Let's be smart about this. Every matrix corresponds to some linear operation. This means that it is a legitimate question to ask “what does the matrix $A$ do?” and once we figure out what it does, we can compute $A^{55}$ by simply doing what $A$ does $55$ times.
The best way to see what a matrix does is to look inside of it and see what it is made of. What is its natural basis (own basis) and what are its values (own values).
Deep down inside, the matrix $A$ is really a product of three matrices: \[ \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} = \underbrace{\begin{bmatrix} 0.850.. & -0.525.. \nl 0.525.. & 0.850.. \end{bmatrix} }_Q \ \underbrace{\! \begin{bmatrix} 1.618.. & 0 \nl 0 &-0.618.. \end{bmatrix} }_{\Lambda} \underbrace{ \begin{bmatrix} 0.850.. & 0.525.. \nl -0.525.. & 0.850.. \end{bmatrix} }_{Q^{-1}}. \] \[ A = Q\Lambda Q^{-1} \] I am serious. You can multiply these three matrices together and you will get $A$. Notice that the “middle matrix” $\Lambda$ (the capital Greek letter lambda) has entries only on the diagonal, the matrix $\Lambda$ is sandwiched between between the matrix $Q$ on the left and $Q^{-1}$ (the inverse of $Q$) on the right. This way of writing $A$ will allow us to compute $A^5$ in a civilized manner: \[ \begin{eqnarray} A^5 & = & A A A A A \nl & = & Q\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda \underbrace{Q^{-1}Q}_{I}\Lambda Q^{-1} \nl & = & Q\Lambda I \Lambda I \Lambda I \Lambda I \Lambda Q^{-1} \nl & = & Q\Lambda \Lambda \Lambda \Lambda \Lambda Q^{-1} \nl & = & Q\Lambda^5 Q^{-1}. \end{eqnarray} \]
Since the matrix $\Lambda$ is diagonal, it is really easy to compute its fifth power $\Lambda^5$: \[ \begin{bmatrix} 1.618.. & 0 \nl 0 &-0.618.. \end{bmatrix}^5 = \begin{bmatrix} (1.618..)^5 & 0 \nl 0 &(-0.618..)^5 \end{bmatrix} = \begin{bmatrix} 11.090.. & 0 \nl 0 &-0.090.. \end{bmatrix}\!. \]
Thus we have \[ \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix}^5 \! = \underbrace{\begin{bmatrix} 0.850..\! & -0.525.. \nl 0.525..\! & 0.850.. \end{bmatrix} }_Q \! \begin{bmatrix} 11.090.. \! & 0 \nl 0 \! &-0.090.. \end{bmatrix} \! \underbrace{ \begin{bmatrix} 0.850.. & 0.525.. \nl -0.525.. & 0.850.. \end{bmatrix} }_{Q^{-1}}\!. \] We still have to multiply these three matrices together, but we have brought down the work from $4$ matrix multiplications down to just two.
The answer is \[ A^5 = Q\Lambda^5 Q^{-1} = \begin{bmatrix} 8 & 5 \nl 5 & 3 \end{bmatrix}. \]
Using the same technique, we can just as easily compute $A^{55}$: \[ A^{55} = Q\Lambda^{55} Q^{-1} = \begin{bmatrix} 225851433717 & 139583862445 \nl 139583862445 & 86267571272 \end{bmatrix}. \]
We could even compute $A^{5555}$ if we wanted to, but you get the point. If you look at $A$ in the right basis, repeated multiplication only involves computing the powers of its eigenvalues.
Definitions
- $A$: an $n\times n$ square matrix.
When necessary, we will denote the individual entries of $A$ as $a_{ij}$.
- $\textrm{eig}(A)\equiv(\lambda_1, \lambda_2, \ldots, \lambda_n )$:
the list of eigenvalues of $A$. Usually denoted with the greek letter lambda.
Note that some eigenvalues could be repeated.
* $p(\lambda)=\det(A - \lambda I)$:
the //characteristic polynomial// for the matrix $A$. The eigenvalues are the roots of this polynomial.
* $\{ \vec{e}_{\lambda_1}, \vec{e}_{\lambda_2}, \ldots, \vec{e}_{\lambda_n} \}$:
the set of //eigenvectors// of $A$. Each eigenvector is associated with a corresponding eigenvalue.
* $\Lambda \equiv {\rm diag}(\lambda_1, \lambda_2, \ldots, \lambda_n)$:
the diagonal version of $A$. The matrix $\Lambda$ contains the eigenvalues of $A$ on the diagonal:
\[
\Lambda =
\begin{bmatrix}
\lambda_1 & \cdots & 0 \nl
\vdots & \ddots & 0 \nl
0 & 0 & \lambda_n
\end{bmatrix}.
\]
The matrix $\Lambda$ corresponds to the matrix representation of $A$ with respect to its eigenbasis.
* $Q$: a matrix whose columns are the eigenvectors of $A$:
\[
Q
\equiv
\begin{bmatrix}
| & & | \nl
\vec{e}_{\lambda_1} & \cdots & \vec{e}_{\lambda_n} \nl
| & & |
\end{bmatrix}
= \
_{B_s}\![I]_{B_\lambda}.
\]
The matrix $Q$ corresponds to the //change of basis matrix//
from the eigenbasis $B_\lambda = \{ \vec{e}_{\lambda_1}, \vec{e}_{\lambda_2}, \vec{e}_{\lambda_3}, \ldots \}$
to the standard basis $B_s = \{\hat{\imath}, \hat{\jmath}, \hat{k}, \ldots \}$.
* $A=Q\Lambda Q^{-1}$: the //eigendecomposition// of the matrix $A$.
* $\Lambda = Q^{-1}AQ$: the //diagonalization// of the matrix $A$.
TODO: fix/tensorify indices above and use \ mathbbm{1} instead of I
Eigenvalues
The eigenvalue equation is \[ A\vec{e}_\lambda =\lambda\vec{e}_\lambda, \] where $\lambda$ is an eigenvalue and $\vec{e}_\lambda$ is an eigenvector of the matrix $A$. If we multiply $A$ by an eigenvector $\vec{e}_\lambda$, we get back the same vector scaled by the constant $\lambda$.
To find the eigenvalue of a matrix we start from the eigenvalue equation $A\vec{e}_\lambda =\lambda\vec{e}_\lambda$, insert the identity ${11}$, and rewrite it as a null-space problem: \[ A\vec{e}_\lambda =\lambda{11}\vec{e}_\lambda \qquad \Rightarrow \qquad \left(A - \lambda{11}\right)\vec{e}_\lambda = \vec{0}. \] This equation will have a solution whenever $|A - \lambda{11}|=0$. The eigenvalues of $A \in \mathbb{R}^{n \times n}$, denoted $(\lambda_1, \lambda_2, \ldots, \lambda_n )$, are the roots of the characteristic polynomial: \[ p(\lambda)=\det(A - \lambda I) \equiv |A-\lambda I|=0. \] When we calculate this determinant, we'll obtain an expression involving the coefficients $a_{ij}$ and the variable $\lambda$. If $A$ is an $n \times n $ matrix, the characteristic polynomial is of degree $n$ in the variable $\lambda$.
We denote the list of eigenvalues as $\textrm{eig}(A)=( \lambda_1, \lambda_2, \ldots, \lambda_n )$. If a $\lambda_i$ is a repeated root of the characteristic polynomial $p(\lambda)$, we say that it is a degenerate eigenvalue. For example the identity matrix $I \in \mathbb{R}^{2\times 2}$ has the characteristic polynomial $p_I(\lambda)=(\lambda-1)^2$ which has a repeated root at $\lambda=1$. We say the eigenvalue $\lambda=1$ has algebraic multiplicity $2$. It is important to keep track of degenerate eigenvalues, so we'll specify the multiplicity of an eigenvalue by repeatedly including it in the list of eigenvalues $\textrm{eig}(I)=(\lambda_1, \lambda_2) = (1,1)$.
Eigenvectors
The eigenvectors associated with eigenvalue $\lambda_i$ of matrix $A$ are the vectors in the null space of the matrix $(A-\lambda_i I )$.
To find the eigenvectors associated with the eigenvalue $\lambda_i$, you have to solve for the components $e_{\lambda,x}$ and $e_{\lambda,y}$ of the vector $\vec{e}_\lambda=(e_{\lambda,x},e_{\lambda,y})$ that satisfies the equation: \[ A\vec{e}_\lambda =\lambda\vec{e}_\lambda, \] or equivalently \[ (A-\lambda I ) \vec{e}_\lambda = 0\qquad \Rightarrow \qquad \begin{bmatrix} a_{11}-\lambda & a_{12} \nl a_{21} & a_{22}-\lambda \end{bmatrix} \begin{bmatrix} e_{\lambda,x} \nl e_{\lambda,y} \end{bmatrix} = \begin{bmatrix} 0 \nl 0 \end{bmatrix}. \]
If $\lambda_i$ is a repeated root (degenerate eigenvalue), the null space $(A-\lambda_i I )$ could contain multiple eigenvectors. The dimension of the null space of $(A-\lambda_i I )$ is called the geometric multiplicity of the eigenvalue $\lambda_i$.
Eigendecomposition
If an $n \times n$ matrix $A$ is diagonalizable, this means that we can find $n$ eigenvectors for that matrix. The eigenvectors that come from different eigenspaces are guaranteed to be linearly independent (see exercises). We can also pick a set of linearly independent vectors within each of the degenerate eigenspaces. Combining the eigenvectors from all the eigenspaces we get a set of $n$ linearly independent eigenvectors, which form a basis for $\mathbb{R}^n$. We call this the eigenbasis.
Let's put the $n$ eigenvectors next to each other as the columns of a matrix: \[ Q = \begin{bmatrix} | & & | \nl \vec{e}_{\lambda_1} & \cdots & \vec{e}_{\lambda_n} \nl | & & | \end{bmatrix}. \]
We can decompose $A$ into its eigenvalues and its eigenvectors: \[ A = Q \Lambda Q^{-1} = \begin{bmatrix} | & & | \nl \vec{e}_{\lambda_1} & \cdots & \vec{e}_{\lambda_n} \nl | & & | \end{bmatrix} \begin{bmatrix} \lambda_1 & \cdots & 0 \nl \vdots & \ddots & 0 \nl 0 & 0 & \lambda_n \end{bmatrix} \begin{bmatrix} \ \nl \ \ \ \ \ \ Q^{-1} \ \ \ \ \ \ \nl \ \end{bmatrix}. \] The matrix $\Lambda$ is a diagonal matrix of eigenvalues and the matrix $Q$ is the “change of basis” matrix which contains the corresponding eigenvectors as columns.
Note that only the direction of each eigenvector is important and not the length. Indeed if $\vec{e}_\lambda$ is an eigenvector (with value $\lambda$), then so is any $\alpha \vec{e}_\lambda$ for all $\alpha \in \mathbb{R}$. Thus we are free to use any multiple of the vectors $\vec{e}_{\lambda_i}$ as the columns of the matrix $Q$.
Example
Find the eigenvalues, the eigenvectors and the diagonalization of the matrix: \[ A=\begin{bmatrix} 1 & 2 & 0 \nl 0 & 3 & 0 \nl 2 & -4 & 2 \end{bmatrix}. \]
The eigenvalues of the matrix are (in decreasing order) \[ \lambda_1 = 3, \quad \lambda_2 = 2, \quad \lambda_3= 1. \] When an $n \times n$ matrix has $n$ distinct eigenvalues, it is diagonalizable since it will have $n$ linearly independent eigenvectors. Since the matrix $A$ has has $3$ different eigenvalues it is diagonalizable.
The eigenvalues of $A$ are the values that will appear in the diagonal of $\Lambda$, so by finding the eigenvalues of $A$ we already know its diagonalization. We could stop here, but instead, let's continue and find the eigenvectors of $A$.
The eigenvectors of $A$ are found by solving for the null space of the matrices $(A-3I)$, $(A-2I)$, and $(A-I)$ respectively: \[ \vec{e}_{\lambda_1} = \begin{bmatrix} -1 \nl -1 \nl 2 \end{bmatrix}, \quad \vec{e}_{\lambda_2} = \begin{bmatrix} 0 \nl 0 \nl 1 \end{bmatrix}, \quad \vec{e}_{\lambda_3} = \begin{bmatrix} -1 \nl 0 \nl 2 \end{bmatrix}. \] Check that $A \vec{e}_{\lambda_k} = \lambda_k \vec{e}_{\lambda_k}$ for each of the above vectors. Let $Q$ be the matrix with these eigenvectors as its columns: \[ Q= \begin{bmatrix} -1 & 0 & -1 \nl -1 & 0 & 0 \nl 2 & 1 & 2 \end{bmatrix}, \qquad \textrm{and} \qquad Q^{-1} = \begin{bmatrix} 0 & -1 & 0 \nl 2 & 0 & 1 \nl -1 & 1 & 0 \end{bmatrix}. \] These matrices form the eigendecomposition of the matrix $A$: \[ A = Q\Lambda Q^{-1} = \begin{bmatrix} 1 & 2 & 0 \nl 0 & 3 & 0 \nl 2 & -4 & 2 \end{bmatrix} = \begin{bmatrix} -1 & 0 & -1 \nl -1 & 0 & 0 \nl 2 & 1 & 2 \end{bmatrix} \!\! \begin{bmatrix} 3 & 0 & 0 \nl 0 & 2 & 0 \nl 0 & 0 & 1\end{bmatrix} \!\! \begin{bmatrix} 0 & -1 & 0 \nl 2 & 0 & 1 \nl -1 & 1 & 0 \end{bmatrix}\!. \]
To find the diagonalization of $A$, we must move $Q$ and $Q^{-1}$ to the other side of the equation. More specifically, we multiply the equation $A=Q\Lambda Q^{-1}$ by $Q^{-1}$ on the left and by $Q$ on the right to obtain the diagonal matrix: \[ \Lambda = Q^{-1}AQ = \begin{bmatrix} 0 & -1 & 0 \nl 2 & 0 & 1 \nl -1 & 1 & 0 \end{bmatrix} \!\! \begin{bmatrix} 1 & 2 & 0 \nl 0 & 3 & 0 \nl 2 & -4 & 2 \end{bmatrix} \!\! \begin{bmatrix} -1 & 0 & -1 \nl -1 & 0 & 0 \nl 2 & 1 & 2 \end{bmatrix} = \begin{bmatrix} 3 & 0 & 0 \nl 0 & 2 & 0 \nl 0 & 0 & 1\end{bmatrix}\!. \]
Explanations
Eigenspaces
Recall the definition of the null space of a matrix $M$: \[ \mathcal{N}(M) \equiv \{ \vec{v} \in \mathbb{R}^n \ | \ M\vec{v} = 0 \}. \] The dimension of the null space is the number of linearly independent vectors you can find in the null space. If $M$ sends exactly two linearly independent vectors $\vec{v}$ and $\vec{w}$ to the zero vector: \[ M\vec{v} = 0, \qquad M\vec{w} = 0, \] then the null space is two-dimensional. We can always choose the vectors $\vec{v}$ and $\vec{w}$ to be orthogonal $\vec{v}\cdot\vec{w}=0$ and thus obtain an orthogonal basis for the null space.
Each eigenvalue $\lambda_i$ has an eigenspace associated with it. The eigenspace is the null space of the matrix $(A-\lambda_i I)$: \[ E_{\lambda_i} \equiv \mathcal{N}\left( A-\lambda_i I \right) = \{ \vec{v} \in \mathbb{R}^n \ | \ \left( A-\lambda_i I \right)\vec{v} = 0 \}. \] For degenerate eigenvalues (repeated roots of the characteristic polynomial) the null space of $\left( A-\lambda_i I \right)$ could contain multiple eigenvectors.
Change of basis
The matrix $Q$ can be interpreted as a change of basis matrix. Given a vector written in terms of the eigenbasis $[\vec{v}]_{B_{\lambda}}=(v^\prime_1,v^\prime_2,v^\prime_3)_{B_{\lambda}} = v^\prime_1\vec{e}_{\lambda_1}+ v^\prime_2\vec{e}_{\lambda_3}+v^\prime_3\vec{e}_{\lambda_3}$, we can use the matrix $Q$ to convert it to the standard basis $[\vec{v}]_{B_{s}} = (v_1, v_2,v_3) = v_1\hat{\imath} + v_2\hat{\jmath}+v_3\hat{k}$ as follows: \[ [\vec{v}]_{B_{s}} = \ Q [\vec{v}]_{B_{\lambda}} = \ _{B_{s}\!}[{11}]_{B_{\lambda}} [\vec{v}]_{B_{\lambda}}. \]
The change of basis in the other direction is given by the inverse matrix: \[ [\vec{v}]_{B_{\lambda}} = \ Q^{-1} [\vec{v}]_{B_{s}} = _{B_{\lambda}\!}\left[{11}\right]_{B_{s}} [\vec{v}]_{B_{s}}. \]
Interpretations
The eigendecomposition $A = Q \Lambda Q^{-1}$ allows us to interpret the action of $A$ on an arbitrary input vector $\vec{v}$ as the following three steps: \[ [\vec{w}]_{B_{s}} = \ _{B_{s}\!}[A]_{B_{s}} [\vec{v}]_{B_{s}} = Q\Lambda Q^{-1} [\vec{v}]_{B_{s}} = \ \underbrace{\!\!\ _{B_{s}\!}[{11}]_{B_{\lambda}} \ \underbrace{\!\!\ _{B_{\lambda}\!}[\Lambda]_{B_{\lambda}} \underbrace{\ _{B_{\lambda}\!}[{11}]_{B_{s}} [\vec{v}]_{B_{s}} }_1 }_2 }_3. \]
- In the first step we convert the vector $\vec{v}$ from the standard basis
to the eigenabasis.
- In the second step the action of $A$ on vectors expressed with respect to its eigenbasis
corresponds to a multiplication by the diagonal matrix $\Lambda$.
- In the third step we convert the output $\vec{w}$ from the eigenbasis
back to the standard basis.
Another way of interpreting the above steps is to say that, deep down inside, the matrix $A$ is actually the diagonal matrix $\Lambda$. To see the diagonal form of the matrix, we have to express the input vectors with respect to the eigenabasis: \[ [\vec{w}]_{B_{\lambda}} = \ _{B_{\lambda}\!}[\Lambda]_{B_{\lambda}} [\vec{v}]_{B_{\lambda}}. \]
It is extremely important that you understand the the equation $A=Q\Lambda Q^{-1}$ intuitively in terms of the three step procedure. To help you understand, we'll analyze in detail what happens when we multiply $A$ by one of its eigenvectors. Let's pick $\vec{e}_{\lambda_1}$ and verify the equation $A\vec{e}_{\lambda_1} = Q\Lambda Q^{-1}\vec{e}_{\lambda_1} \lambda_1\vec{e}_{\lambda_1}$ by follow the vector through the three steps: \[ \ _{B_{s}\!}[A]_{B_{s}} [\vec{e}_{\lambda_1}]_{B_{s}} = Q\Lambda Q^{-1} [\vec{e}_{\lambda_1}]_{B_{s}} = \ \underbrace{\!\!\ _{B_{s}\!}[{11}]_{B_{\lambda}} \ \underbrace{\!\!\ _{B_{\lambda}\!}[\Lambda]_{B_{\lambda}} \underbrace{\ _{B_{\lambda}\!}[{11}]_{B_{s}} [\vec{e}_{\lambda_1}]_{B_{s}} }_{ (1,0,\ldots)^T_{B_\lambda} } }_{ (\lambda_1,0,\ldots)^T_{B_\lambda} } }_{ \lambda_1 [\vec{e}_{\lambda_1}]_{B_{s}} } = \lambda_1 [\vec{e}_{\lambda_1}]_{B_{s}} \] In the first step, we convert the vector $[\vec{e}_{\lambda_1}]_{B_{s}}$ to the eigenbasis and obtain $(1,0,\ldots,0)^T_{B_\lambda}$. The result of the second step is $(\lambda_1,0,\ldots,0)^T_{B_\lambda}$ because multiplying $\Lambda$ by the vector $(1,0,\ldots,0)^T_{B_\lambda}$ “selects only the first column of $\Lambda$. In the third step we convert $(\lambda_1,0,\ldots,0)^T_{B_\lambda}=\lambda_1(1,0,\ldots,0)^T_{B_\lambda}$ back to the standard basis to obtain $\lambda_1[\vec{e}_{\lambda_1}]_{B_{s}}$.
Invariant properties of matrices
The determinant and the trace of a matrix are strictly functions of the eigenvalues. The determinant of $A$ is the product of its eigenvalues: \[ \det(A) \equiv |A| =\prod_i \lambda_i = \lambda_1\lambda_2\cdots\lambda_n, \] and the trace is their sum: \[ {\rm Tr}(A)=\sum_i a_{ii}=\sum_i \lambda_i = \lambda_1 + \lambda_2 + \cdots \lambda_n. \]
Here are the steps we followed to obtain these equations: \[ |A|=|Q\Lambda Q^{-1}| =|Q||\Lambda| |Q^{-1}| =|Q||Q^{-1}||\Lambda| =|Q| \frac{1}{|Q|}|\Lambda| =|\Lambda| =\prod_i \lambda_i, \] \[ {\rm Tr}(A)={\rm Tr}(Q\Lambda Q^{-1}) ={\rm Tr}(\Lambda Q^{-1}Q) ={\rm Tr}(\Lambda)=\sum_i \lambda_i. \]
In fact the above calculations remain valid when the matrix undergoes any similarity transformation. A similarity transformation is essentially a “change of basis”-type of calculation: the matrix $A$ gets multiplied by an invertible matrix $P$ from the left and by the inverse of $P$ on the right: $A \to PA P^{-1}$. Therefore, the determinant and the trace of a matrix are two properties that do not depend on the choice of basis used to represent the matrix! We say the determinant and the trace are invariant properties of the matrix.
Relation to invertibility
Let us briefly revisit three of the equivalent conditions we stated in the invertible matrix theorem. For a matrix $A \in \mathbb{R}^{n \times n}$, the following statements are equivalent:
- $A$ is invertible
- $|A|\neq 0$
- The null space contains only the zero vector $\mathcal{N}(A)=\vec{0}$
Using the formula $|A|=\prod_{i=1}^n \lambda_i$, it is easy to see why the last two statements are equivalent. If $|A|\neq 0$ then none of the $\lambda_i$s is zero, otherwise the product of the eigenvalues would be zero. We know that $\lambda=0$ is not and eigenvalues of $A$ which means that there is no vector $\vec{v}$ such that $A\vec{v} = 0\vec{v}=\vec{0}$. Therefore there are no vectors in the null space: $\mathcal{N}(A)=\{ \vec{0} \}$.
We can also follow the reasoning in the other direction. If the null space of $A$ is empty, then there is no non-zero vector $\vec{v}$ such that $A\vec{v} = \vec{0}$, which means $\lambda=0$ is not an eigenvalue of $A$, and hence the product $\lambda_1\lambda_2\cdots \lambda_n \neq 0$.
However, if there exists a non-zero vector $\vec{v}$ such that $A\vec{v} = \vec{0}$, then $A$ has a non-empty null space and $\lambda=0$ is an eigenvalue of $A$ and thus $|A|=0$.
Normal matrices
A matrix $A$ is normal if it satisfies the equation $A^TA = A A^T$. All normal matrices are diagonalizable and furthermore the diagonalization matrix $Q$ can be chosen to be an orthogonal matrix $O$.
The eigenvectors corresponding to different eigenvalues of a normal matrix are orthogonal. Furthermore we can always choose the eigenvectors within the same eigenspace to be orthogonal. By collecting the eigenvectors from all of the eigenspaces of the matrix $A \in \mathbb{R}^{n \times n}$, it is possible to obtain a complete basis $\{\vec{e}_1,\vec{e}_2,\ldots, \vec{e}_n\}$ of orthogonal eigenvectors: \[ \vec{e}_{i} \cdot \vec{e}_{j} = \left\{ \begin{array}{ll} \|\vec{e}_i\|^2 & \text{ if } i =j, \nl 0 & \text{ if } i \neq j. \end{array}\right. \] By normalizing each of these vectors we can find a set of eigenvectors $\{\hat{e}_1,\hat{e}_2,\ldots, \hat{e}_n \}$ which is an orthonormal basis for the space $\mathbb{R}^n$: \[ \hat{e}_{i} \cdot \hat{e}_{j} = \left\{ \begin{array}{ll} 1 & \text{ if } i =j, \nl 0 & \text{ if } i \neq j. \end{array}\right. \]
Consider now the matrix $O$ constructed by using these orthonormal vectors as the columns: \[ O= \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix}. \]
The matrix $O$ is an orthogonal matrix, which means that it satisfies $OO^T=I=O^TO$. In other words, the inverse of $O$ is obtained by taking the transpose $O^T$. To see that this is true consider the following product: \[ O^T O = \begin{bmatrix} - & \hat{e}_{1} & - \nl & \vdots & \nl - & \hat{e}_{n} & - \end{bmatrix} \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \nl 0 & \ddots & 0 \nl 0 & 0 & 1 \end{bmatrix} ={11}. \] Each of the ones on the diagonal arises from the dot product of a unit-length eigenvector with itself. The off-diagonal entries are zero because the vectors are orthogonal. By definition, the inverse $O^{-1}$ is the matrix which when multiplied by $O$ gives $I$, so we have $O^{-1} = O^T$.
Using the orthogonal matrix $O$ and its inverse $O^T$, we can write the eigendecomposition of a matrix $A$ as follows: \[ A = O \Lambda O^{-1} = O \Lambda O^T = \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix} \begin{bmatrix} \lambda_1 & \cdots & 0 \nl \vdots & \ddots & 0 \nl 0 & 0 & \lambda_n \end{bmatrix} \begin{bmatrix} - & \hat{e}_{1} & - \nl & \vdots & \nl - & \hat{e}_{n} & - \end{bmatrix}\!. \]
The key advantage of using a diagonalization procedure with an orthogonal matrix $O$ is that computing the inverse is simplified significantly since $O^{-1}=O^T$.
Discussion
Non-diagonalizable matrices
Not all matrices are diagonalizable. For example, the matrix \[ B= \begin{bmatrix} 3 & 1 \nl 0 & 3 \end{bmatrix}, \] has $\lambda = 3$ as a repeated eigenvalue, but the null space of $(B-3{11})$ contains only one vector $(1,0)^T$. The matrix $B$ has a single eigenvector in the eigenspace $\lambda=3$. We're one eigenvector short, and it is not possible to obtain a complete basis of eigenvectors. Therefore we cannot build the diagonalizing change of basis matrix $Q$. We say $B$ is not diagonalizable.
Matrix power series
One of the most useful concepts of calculus is the idea that functions can be represented as Taylor series. The Taylor series of the exponential function $f(x) =e^x$ is \[ e^x = \sum_{k=0}^\infty \frac{x^k}{n!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots. \] Nothing stops us from using the same Taylor series expression to define the exponential function of a matrix: \[ e^A = \sum_{k=0}^\infty \frac{A^k}{n!} = 1 + A + \frac{A^2}{2} + \frac{A^3}{3!} + \frac{A^4}{4!} + \frac{A^5}{5!} + \ldots . \] Okay, there is one thing stopping us, and that is having to compute an infinite sum of progressively longer matrix products! But wait, remember how we used the diagonalization of $A=Q\Lambda Q^{-1}$ to easily compute $A^{55}=Q\Lambda^{55} Q^{-1}$? We can use that trick here too and obtain the exponential of a matrix in a much simpler form: \[ \begin{align*} e^A & = \sum_{k=0}^\infty \frac{A^k}{n!} = \sum_{k=0}^\infty \frac{(Q\Lambda Q^{-1})^k}{n!} \nl & = \sum_{k=0}^\infty \frac{Q\:\Lambda^k\:Q^{-1} }{n!} \nl & = Q\left[ \sum_{k=0}^\infty \frac{ \Lambda^k }{n!}\right]Q^{-1} \nl & = Q\left( 1 + \Lambda + \frac{\Lambda^2}{2} + \frac{\Lambda^3}{3!} + \frac{\Lambda^4}{4!} + \ldots \right)Q^{-1} \nl & = Qe^\Lambda Q^{-1} = \begin{bmatrix} \ \nl \ \ \ \ \ \ Q \ \ \ \ \ \ \ \nl \ \end{bmatrix} \begin{bmatrix} e^{\lambda_1} & \cdots & 0 \nl \vdots & \ddots & 0 \nl 0 & 0 & e^{\lambda_n} \end{bmatrix} \begin{bmatrix} \ \nl \ \ \ \ \ \ Q^{-1} \ \ \ \ \ \ \nl \ \end{bmatrix}\!. \end{align*} \]
We can use this approach to talk about “matrix functions” of the form: \[ F: \mathbb{M}(n,n) \to \mathbb{M}(n,n), \] simply by defining them as Taylor series of matrices. Computing the matrix function $F(M)$ on an input matrix $M=Q\Lambda Q^{-1}$ is equivalent to computing the function $f$ to the eigenvalues of $M$ as follows: $F(M)=Q\:f(\Lambda)\:Q^{-1}$.
Review
In this section we learned how to decompose matrices in terms of their eigenvalues and eigenvectors. Let's briefly review everything that we discussed. The fundamental equation is $A\vec{e}_{\lambda_i} = \lambda_i\vec{e}_{\lambda_i}$, where the vector $\vec{e}_{\lambda_i}$ is an eigenvector of the matrix $A$ and the number $\lambda_i$ is an eigenvalue of $A$. The word eigen is the German word for self.
The characteristic polynomial comes about from a simple manipulations of the eigenvalue equation: \[ \begin{eqnarray} A\vec{e}_{\lambda_i} & = &\lambda_i\vec{e}_{\lambda_i} \nl A\vec{e}_{\lambda_i} - \lambda \vec{e}_{\lambda_i} & = & 0 \nl (A-{\lambda_i} I)\vec{e}_{\lambda_i} & = & 0. \end{eqnarray} \]
There are two ways we can get a zero, either the vector $\vec{e}_\lambda$ is the zero vector or it lies in the null space of $(A-\lambda I)$. The problem of finding the eigenvalues therefore reduces to finding the values of $\lambda$ for which the matrix $(A-\lambda I)$ is not invertible, i.e., it has a null space. The easiest way to check if a matrix is invertible is to compute the determinant: $|A-\lambda I| = 0$.
There will be multiple eigenvalues and eigenvector that satisfy this equation, so we keep a whole list of eigenvalues $(\lambda_1, \lambda_2, \ldots, \lambda_n )$, and corresponding eigenvectors $\{ \vec{e}_{\lambda_1}, \vec{e}_{\lambda_2}, \ldots \}$.
Applications
Many scientific applications use the eigen-decomposition of a matrix as a building block.
We'll mention a few of these applications without going into too much detail.
- Principal component analysis
- PageRank
- quantum mechanics energy, and info-theory
TODO, finish the above points
Analyzing a matrix in terms of its eigenvalues and its eigenvectors is a very powerful way to “see inside the matrix” and understand what the matrix does. In the next section we'll analyze several different types of matrices and discuss their properties in terms of their eigenvalues.
Links
[ Good visual examples from wikipedia ]
http://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors
Exercises
Q1
Prove that a collection of nonzero eigenvectors corresponding to distinct eigenvalues is linearly independent.
Hint: Proof by contradiction. Assume that we have $n$ distinct eigenvalues $\lambda_i$ and eigenvectors $\{ \vec{e}_i \}$ which are linearly dependent: $\sum_{i=1}^n \alpha_i \vec{e}_i = \vec{0}$ with some $\alpha_i \neq 0$. If a non-zero combination of $\alpha_i$ really could give the zero vector as a linear combination then this equation would be true: $(A-\lambda_n I )\left(\sum \alpha_i\vec{e}_i\right) = (A-\lambda_n I )\vec{0}=\vec{0}$, but if you expand the expression on the left you will see that it is not equal to zero.
Q2
Show that an $n \times n$ matrix has at most $n$ distinct eigenvalues.
Q3
Check out Problems 1 through 5 in the following book
http://en.wikibooks.org/wiki/Linear_Algebra/Eigenvalues_and_Eigenvectors
http://en.wikibooks.org/wiki/Linear_Algebra/Eigenvalues_and_Eigenvectors/Solutions
Special types of matrices
Mathematicians like to categorize things. There are some types of matrices to which mathematicians give specific names so that they can refer to them quickly without having to explain what they do in words:
I have this matrix A whose rows are perpendicular vectors and then when you multiply any vector by this matrix it doesn't change the length of the vector but just kind of rotates it and stuff...
It is much simpler just to say:
Let A be an orthogonal matrix.
Most advanced science textbooks and research papers will use terminology like “diagonal matrix”, “symmetric matrix”, and “orthogonal matrix”, so I want you to become familiar with these concepts.
This section also serves to review and reinforce what we learned about linear transformations. Recall that we can think of the matrix-vector product $A\vec{x}$ as applying a linear transformations $T_A$ to the input vector $\vec{x}$. Therefore, each of the special matrices which we will discuss here also corresponds to a special type of linear transformation. Keep this dual-picture in mind because the same terminology can be used to describe matrices and linear transformations.
Notation
- $\mathbb{R}^{m \times n}$: the set of $m \times n$ matrices
- $A,B,O,P,\ldots$: typical variable names for matrices
- $a_{ij}$: the entry in the $i$th row and $j$th column of the matrix $A$
- $A^T$: the transpose of the matrix $A$
- $A^{-1}$: the inverse of the matrix $A$. The inverse obeys $AA^{-1}=A^{-1}A=I$.
- $\lambda_1, \lambda_2, \ldots$: the eigenvalues of the matrix $A$.
For each eigenvalue $\lambda_i$ there is at least one associated eigenvector $\vec{e}_{\lambda_i}$ such that the following equation holds:
\[
A\vec{e}_{\lambda_i} = \lambda_i \vec{e}_{\lambda_i}.
\]
Multiplying the matrix $A$ by its eigenvectors $\vec{e}_{\lambda_i}$
is the same scaling $\vec{e}_{\lambda_i}$ by the number $\lambda_i$.
Diagonal matrices
These are matrices that only have entries on the diagonal and are zero everywhere else. For example: \[ \left(\begin{array}{ccc} a_{11} & 0 & 0 \nl 0 & a_{22}& 0 \nl 0 & 0 & a_{33} \end{array}\right). \] More generally we say that a diagonal matrix $A$ satisfies, \[ a_{ij}=0, \quad \text{if } i\neq j. \]
The eigenvalues of a diagonal matrix are $\lambda_i = a_{ii}$.
Symmetric matrices
A matrix $A$ is symmetric if and only if \[ A^T = A, \qquad a_{ij} = a_{ji}, \quad \text{ for all } i,j. \] All eigenvalues of a symmetric transformation are real numbers, and the its eigenvectors can be chosen to be mutually orthogonal. Given any matrix $B\in\mathbb{M}(m,n)$, the product of $B$ with its transpose $B^TB$ is always a symmetric matrix.
Upper triangular matrices
Upper triangular matrices have zero entries below the main diagonal: \[ \left(\begin{array}{ccc} a_{11} & a_{12}& a_{13} \nl 0 & a_{22}& a_{23} \nl 0 & 0 & a_{33} \end{array}\right), \qquad a_{ij}=0, \quad \text{if } i > j. \]
A lower triangular matrix is one for which all the entries above the diagonal are zeros: $a_{ij}=0, \quad \text{if } i < j$.
Identity matrix
The identity matrix is denoted as $I$ or $I_n \in \mathbb{M}(n,n)$ and plays the role of the number $1$ for matrices: $IA=AI=A$. The identity matrix is diagonal with ones on the diagonal: \[ I_3 = \left(\begin{array}{ccc} 1 & 0 & 0 \nl 0 & 1 & 0 \nl 0 & 0 & 1 \end{array}\right). \]
Any vector $\vec{v} \in \mathbb{R}^3$ is an eigenvector of the identity matrix with eigenvalue $\lambda = 1$.
Orthogonal matrices
A matrix $O \in \mathbb{M}(n,n)$ is orthogonal if it satisfies $OO^T=I=O^TO$. The inverse of an orthogonal matrix $O$ is obtained by taking its transpose: $O^{-1} = O^T$.
The best way to think of orthogonal matrices is to think of them as linear transformations $T_O(\vec{v})=\vec{w}$ which preserve the length of vectors. The length of a vector before applying the linear transformation is given by: $\|\vec{v}\|=\sqrt{ \vec{v} \cdot \vec{v} }$. The length of a vector after the transformation is \[ \|\vec{w}\| =\sqrt{ \vec{w} \cdot \vec{w} } =\sqrt{ T_O(\vec{v}) \cdot T_O(\vec{v}) } = (O\vec{v})^T(O\vec{v}) = \vec{v}^TO^TO\vec{v}. \] When $O$ is an orthogonal matrix, we can substitute $O^TO=I$ in the above expression to establish $\|\vec{w}\|=\vec{v}^TI\vec{v}=\|\vec{v}\|$, which shows that orthogonal transformations are length preserving.
The eigenvalues of an orthogonal matrix have unit length, but can in general be complex numbers $\lambda_i=\exp(i\theta) \in \mathbb{C}$. The determinant of an orthogonal matrix is either one or minus one $|O|\in\{-1,1\}$.
A good way to think about orthogonal matrices is to imagine that their columns form an orthonormal basis for $\mathbb{R}^n$: \[ \{ \hat{e}_1,\hat{e}_2,\ldots, \hat{e}_n \}, \quad \hat{e}_{i} \cdot \hat{e}_{j} = \left\{ \begin{array}{ll} 1 & \text{ if } i =j, \nl 0 & \text{ if } i \neq j. \end{array}\right. \] The resulting matrix \[ O= \begin{bmatrix} | & & | \nl \hat{e}_{1} & \cdots & \hat{e}_{n} \nl | & & | \end{bmatrix} \] is going to be an orthogonal matrix. You can verify this by showing that $O^TO=I$. We can interpret the matrix $O$ as a change of basis from the stander basis to the $\{ \hat{e}_1,\hat{e}_2,\ldots, \hat{e}_n \}$ basis.
The set of orthogonal matrices contains as special cases the following important classes of matrices: rotation matrices, refection matrices, and permutation matrices. We'll now discuss each of these in turn.
Rotation matrices
A rotation matrix takes the standard basis $\{ \hat{\imath}, \hat{\jmath}, \hat{k} \}$ to a rotated basis $\{ \hat{e}_1,\hat{e}_2,\hat{e}_3 \}$.
Consider first an example in $\mathbb{R}^2$. The counterclockwise rotation by the angle $\theta$ is given by the matrix \[ R_\theta = \begin{bmatrix} \cos\theta &-\sin\theta \nl \sin\theta &\cos\theta \end{bmatrix}. \] The matrix $R_\theta$ takes $\hat{\imath}=(1,0)$ to $(\cos\theta,\sin\theta)$ and $\hat{\jmath}=(0,1)$ to $(-\sin\theta,\cos\theta)$.
As a second example, consider the rotation by the angle $\theta$ around the $x$-axis in $\mathbb{R}^3$: \[ \begin{bmatrix} 1&0&0\nl 0&\cos\theta&-\sin\theta\nl 0&\sin\theta&\cos\theta \end{bmatrix}. \] Note this is a rotation entirely in the $yz$-plane: the $x$-component of a vector multiplying this matrix would remain unchanged.
The determinant of a rotation matrix is equal to one. The eigenvalues of rotation matrices are complex numbers with magnitude one.
Reflections
If the determinant of an orthogonal matrix $O$ is equal to negative one, then we say that it is mirrored orthogonal. For example, the reflection through the line with direction vector $(\cos\theta, \sin\theta)$ is given by: \[ R= \begin{bmatrix} \cos(2\theta) &\sin(2\theta)\nl \sin(2\theta) &-\cos(2\theta) \end{bmatrix}. \]
A reflection matrix will always have at least one eigenvalue equal to minus one, which corresponds to the direction perpendicular to the axis of reflection.
Permutation matrices
Another important class of orthogonal matrices is the class permutation matrices. The action of a permutation matrix is simply to change the order of the coefficients of a vector. For example, the permutation $\hat{e}_1 \to \hat{e}_1$, $\hat{e}_2 \to \hat{e}_3$, $\hat{e}_3 \to \hat{e}_2$ can be represented as the following matrix: \[ M_\pi = \begin{bmatrix} 1 & 0 & 0 \nl 0 & 0 & 1 \nl 0 & 1 & 0 \end{bmatrix}. \] An $n \times n$ permutation contains $n$ ones in $n$ different columns and zeros everywhere else.
The sign of a permutation corresponds to the determinant $\det(M_\pi)$. We say that a permutation $\pi$ is even if $\det(M_\pi) = +1$ and odd if $\det(M_\pi) = -1$.
Positive matrices
A matrix $P \in \mathbb{M}(n,n)$ is positive semidefinite if \[ \vec{v}^T P \vec{v} \geq 0, \] for all $\vec{v} \in \mathbb{R}^n$. The eigenvalues of a positive semidefinite matrix are all non-negative $\lambda_i \geq 0$.
If we have $\vec{v}^T P \vec{v} > 0$, for all $\vec{v} \in \mathbb{R}^n$, we say that the matrix is positive definite. These matrices have eigenvalues strictly greater than zero.
Projection matrices
The defining property of a projection matrix is that it can be applied multiple times without changing the result: \[ \Pi = \Pi^2= \Pi^3= \Pi^4= \Pi^5 = \cdots. \]
A projection has two eigenvalues: one and zero. The space $S$ which is left invariant by the projection $\Pi_S$ corresponds to the eigenvalue $\lambda=1$. The space $S^\perp$ of vectors that get completely annihilated by $\Pi_S$ corresponds to the eigenvalue $\lambda=0$, which is also the null space of $\Pi_S$.
Normal matrices
The matrix $A = \mathbb{M}(n,n)$ is normal if $A^TA=AA^T$. If $A$ is normal we have the following properties:
- The matrix $A$ has a full set of linearly independent eigenvectors.
Eigenvectors corresponding to distinct eigenvalues are orthogonal
and eigenvectors from the same eigenspace can be chosen to be mutually orthogonal.
- For all vectors $\vec{v}$ and $\vec{w}$ and a normal transformation $A$ we have:
\[
(A\vec{v}) \cdot (A\vec{w})
= (A^TA\vec{v})\cdot \vec{w}
=(AA^T\vec{v})\cdot \vec{w}.
\]
- $\vec{v}$ is an eigenvector of $A$ if and only if $\vec{v}$ is an eigenvector of $A^T$.
Every normal matrix is diagonalizable by an orthogonal matrix $O$. The eigendecomposition of a normal matrix can be written as $A = O\Lambda O^T$, where $O$ is orthogonal and $\Lambda$ is a diagonal matrix. Note that orthogonal ($O^TO=I$) and symmetric ($A^T=A$) matrices are special types of normal matrices since $O^TO=I=OO^T$ and $A^TA=A^2=AA^T$.
Discussion
In this section we defined several types of matrices and stated their properties. You're now equipped with some very precise terminology for describing the different types of matrices.
TODO: add a mini concept map here More importantly, we discussed the relations. It might be a good idea to summarize these relationships as a concept map…
Abstract vector spaces
The math we learned for dealing with vectors can be applied more generally to vector-like things. We will see that several mathematical objects like matrices and polynomials behave similarly to vectors. For example, the addition of two polynomials $P$ and $Q$ is done by adding the coefficients for each power of $x$ component-wise, the same way the addition of vectors happens component-wise.
In this section, we'll learn how to use the terminology and concepts associated with regular vector spaces to study other mathematical objects. In particular we'll see that notions such as linear independence, basis, and dimension can be applied to pretty much all mathematical objects that have components.
Definitions
To specify an abstract vector space $(V,F,+,\cdot)$, we must specify four things:
- A set of vector-like objects $V=\{\mathbf{u},\mathbf{v},\ldots \}$.
- A field $F$ of scalar numbers, usually $F=\mathbb{R}$ or $F=\mathbb{C}$.
In this section $F=\mathbb{R}$.
- An addition operation “$+$” for the elements of $V$ that dictates
how to add vectors $\mathbf{u} + \mathbf{v}$.
- A scalar multiplication operation “$\cdot$” for scaling a vector
by an element of the field. Scalar multiplication is usually denoted
implicitly $\alpha \mathbf{u}$ (without the dot).
NOINDENT A vector space satisfies the following eight axioms, for all scalars $\alpha, \beta \in F$ and all $\mathbf{u}, \mathbf{v}, \mathbf{w} \in V$:
- $\mathbf{u} + (\mathbf{v}+ \mathbf{w}) = (\mathbf{u}+ \mathbf{v}) + \mathbf{w}$. (associativity of addition)
- $\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}$. (commutativity of addition)
- There exists zero vector $\mathbf{0} \in V$,
such that $\mathbf{u} + \mathbf{0} = \mathbf{0} +\mathbf{u} = \mathbf{u}$ for all $\mathbf{u} \in V$.
- For every $\mathbf{u} \in V$, there exists an inverse element
$-\mathbf{u}$ such that $\mathbf{u} + (-\mathbf{u}) = \mathbf{u} -\mathbf{u} = \mathbf{0}$.
- $\alpha (\mathbf{u} + \mathbf{v}) = \alpha \mathbf{u} + \alpha \mathbf{v}$. (distributivity I)
- $(\alpha + \beta)\mathbf{u}= \alpha\mathbf{u} + \beta\mathbf{u}$. (distributivity II)
- $\alpha (\beta \mathbf{u})= (\alpha\beta) \mathbf{u}$
(associativity of scalar multiplication).
- There exists a unit scalar $1$ such that $1 \mathbf{u}= \mathbf{u}$.
If you know anything about vectors, then the above properties should be familiar to you. Indeed, these are standard properties for the vector space $\mathbb{R}^n$ (and its subsets), where the field $F$ is $\mathbb{R}$ and we use the standard vector addition and scalar multiplication operations.
In this section, we'll see that the many of the things we learned about $\mathbb{R}^n$ vectors apply to other mathematical objects which are vector like.
Examples
Matrices
Consider the vector space of $m\times n$ matrices over the real numbers $\mathbb{R}^{m \times n}$. The addition operation for two matrices $A,B \in \mathbb{R}^{m \times n}$ is the usual rule matrix addition: $(A+B)_{ij} = a_{ij}+b_{ij}$.
This vector space is $mn$-dimensional. This can be seen by explicitly constructing a basis for this space. The standard basis for this space consists of matrices with zero entries everywhere except for a single one in the $i$th row and the $j$th column. This set is a basis because any matrix $A \in \mathbb{R}^{m \times n}$ can be written as a linear combination of the standard basis and since each of them is manifestly independent from the others.
Symmetric 2x2 matrices
Consider now the set of $2\times2$ symmetric matrices: \[ \mathbb{S}(2,2) \equiv \{ A \in \mathbb{R}^{2 \times 2} \ | \ A = A^T \}, \] in combination with the usual laws for matrix addition an scalar multiplication.
An explicit basis for this space is obtained as follows: \[ \mathbf{v}_1 = \begin{bmatrix} 1 & 0 \nl 0 & 0 \end{bmatrix}, \ \ \mathbf{v}_1 = \begin{bmatrix} 0 & 1 \nl 1 & 0 \end{bmatrix}, \ \ \mathbf{v}_3 = \begin{bmatrix} 0 & 0 \nl 0 & 1 \end{bmatrix}. \]
Observe how any symmetric matrix $\mathbf{s} \in \mathbb{S}(2,2)$ can be written as a linear combination: \[ \mathbf{s} = \begin{bmatrix} a & b \nl b & c \end{bmatrix} = a \begin{bmatrix} 1 & 0 \nl 0 & 0 \end{bmatrix} + b \begin{bmatrix} 0 & 1 \nl 1 & 0 \end{bmatrix} + c \begin{bmatrix} 0 & 0 \nl 0 & 1 \end{bmatrix}. \]
Since there are three vectors in the basis, the vector space of symmetric matrices $\mathbb{S}(2,2)$ is three-dimensional.
Polynomials of degree n
Define the vector space $P_n(t)$ of polynomials with real coefficients and degree less than or equal to $n$. The “vectors” in this space are polynomials of the form: \[ \mathbf{p} = a_0 + a_1x + a_2x^2 + \cdots + a_n x^n, \] where $a_0,a_1,\ldots,a_n$ are the coefficients of the polynomial $\mathbf{p}$.
The addition of vectors $\mathbf{p}, \mathbf{q} \in P_n(t)$ is performed component-wise: \[ \begin{align*} \mathbf{p} + \mathbf{q} & = (a_0+a_1x+\cdots+a_nx^n)+(b_0+b_1x+\cdots+b_nx^n) \nl & =(a_0+b_0)+(a_1+b_1)x+\cdots +(a_n+b_n)x^n. \end{align*} \] Similarly, scalar multiplication acts as you would expect: \[ \alpha \mathbf{p} = \alpha\cdot (a_0+a_1x+\ldots a_nx^n)=(\alpha a_0)+(\alpha a_1)x+\ldots (\alpha a_n)x^n. \]
The space $P_n(x)$ is $n+1$-dimensional since each “vector” in that space has $n+1$ coefficients.
Functions
Another interesting vector space is the set of all functions $f:\mathbb{R} \to \mathbb{R}$ in combination with the point-wise addition and scaler multiplication operations: \[ \mathbf{f}+\mathbf{g}=(f+g)(x) = f(x) + g(x), \qquad \alpha\mathbf{f} = (\alpha f)(x) = \alpha f(x). \]
The space of functions is infinite-dimensional.
Discussion
In this section we saw that we can talk about linear independence and bases for more abstract vector spaces. Indeed, these notions are well defined for any vector-like object.
In the next section we will generalize the concept of orthogonality for abstract vector spaces. In order to do this, we have to define an abstract inner product operation.
Links
[ More examples of vector spaces ]
http://en.wikibooks.org/wiki/Linear_Algebra/Definition_and_Examples_of_Vector_Spaces
Inner product spaces
An inner product space is an abstract vector space $(V,\mathbb{R},+,\cdot)$ for which we define an abstract inner product operation: \[ \langle \cdot, \cdot \rangle : V \times V \to \mathbb{R}. \]
Any inner product operation can used, so long as it satisfies the following properties for all $\mathbf{u}, \mathbf{v}, \mathbf{v}_1,\mathbf{v}_2\in V$ and $\alpha,\beta \in \mathbb{R}$.
- Symmetric: $\langle \mathbf{u},\mathbf{v}\rangle =\langle \mathbf{v},\mathbf{u}\rangle$.
- Linear: $\langle \mathbf{u},\alpha\mathbf{v}_1+\beta\mathbf{v}_2\rangle =\alpha\langle \mathbf{u},\mathbf{v}_1\rangle +\beta\langle \mathbf{u},\mathbf{v}_2\rangle $
- Positive semi-definite: $\langle \mathbf{u},\mathbf{u}\rangle \geq0$ for all $\mathbf{u}\in V$, $\langle \mathbf{u},\mathbf{u}\rangle =0$ if and only if $\mathbf{u}=\mathbf{0}$.
The above properties are inspired by the properties of the standard inner product (dot product) for vectors in $\mathbb{R}^n$: \[ \langle \vec{u}, \vec{v}\rangle \equiv \vec{u} \cdot \vec{v} = \sum_{i=1}^n u_i v_i = \vec{u}^T \vec{v}. \] In this section, we generalize the idea of dot product to abstract vectors $\mathbf{u}, \mathbf{v} \in V$ by defining an inner product operation $\langle \mathbf{u},\mathbf{v}\rangle$ appropriate for the elements of $V$. We will define a product for matrices $\langle M,N\rangle$, polynomials $\langle \mathbf{p},\mathbf{q}\rangle$ and functions $\langle f,g \rangle$. This inner product will in turn allow us to talk about orthogonality between abstract vectors, \[ \mathbf{u} \textrm{ and } \mathbf{v} \textrm{ are orthogonal } \quad \Leftrightarrow \quad \langle \mathbf{u},\mathbf{v}\rangle = 0, \] the length of an abstract vector, \[ \| \mathbf{u} \| \equiv \sqrt{ \langle \mathbf{u},\mathbf{u}\rangle }, \] and the distance between two abstract vectors: \[ d(\mathbf{u},\mathbf{v}) \equiv \| \mathbf{u}-\mathbf{v} \| =\sqrt{ \langle (\mathbf{u}-\mathbf{v}),(\mathbf{u}-\mathbf{v})\rangle }. \]
Let's get started.
Definitions
We will be dealing with vectors from an abstract vector space $(V,\mathbb{R},+,\cdot)$ where:
- $V$ is the set of vectors in the vector space.
- $\mathbb{R}=F$ is the field of real numbers.
The coefficients of the generalized vectors are taken from that field.
- $+$ is the addition operation defined for elements of $V$.
- $\cdot$ is the scalar multiplication operation between an
element of the field $\alpha \in \mathbb{R}$ and vector $\mathbf{u} \in V$.
Scalar multiplication is usually denoted implicitly $\alpha \mathbf{u}$
so as not to be confused with the dot product.
We define a new operation called inner product for that space: \[ \langle \cdot, \cdot \rangle : V \times V \to \mathbb{R}, \] which takes as inputs two abstract vectors $\mathbf{u}, \mathbf{v} \in V$ and returns a real number $\langle \mathbf{u},\mathbf{v}\rangle$.
We define the following related quantities in term so the inner product operation:
- $\| \mathbf{u} \| \equiv \sqrt{ \langle \mathbf{u},\mathbf{u}\rangle }$:
the norm or length of an abstract vector $\mathbf{u} \in V$.
- $d(\mathbf{u},\mathbf{v}) \equiv \| \mathbf{u}-\mathbf{v} \|$:
the distance between two abstract vector $\mathbf{u},\mathbf{v} \in V$.
Orthogonality
Recall that two vectors $\vec{u}, \vec{v} \in \mathbb{R}^n$ are said to be orthogonal if their dot product is zero. This follows from the geometric interpretation of the dot product: \[ \vec{u}\cdot \vec{v} = \|\vec{u}\| \|\vec{v}\| \cos\theta, \] where $\theta$ is the angle between $\vec{u}$ and $\vec{v}$. Orthogonal means “at right angle with.” Indeed, the angle between $\vec{u}$ and $\vec{v}$ must be $90^\circ$ or $270^\circ$ if we have $\vec{u}\cdot \vec{v}=0$ since $\cos\theta = 0$ only for those angles.
In analogy with the above reasoning, we now define the notion of orthogonality between abstract vectors in terms of the inner product: \[ \mathbf{u} \textrm{ and } \mathbf{v} \textrm{ are orthogonal } \quad \Leftrightarrow \quad \langle \mathbf{u},\mathbf{v}\rangle = 0. \]
Norm
Every definition of an inner product for an abstract vector space $(V,\mathbb{R},+,\cdot)$ induces a norm on that vector space: \[ \| . \| : V \to \mathbb{R}. \] The norm is defined in terms of the inner product: \[ \|\mathbf{u}\|=\sqrt{\langle \mathbf{u},\mathbf{u}\rangle }. \] The norm $\|\mathbf{u}\|$ of a vector $\mathbf{u}$ corresponds, in some sense, to the “length” of the vector.
NOINDENT Important properties of norms:
- $\|\mathbf{v}\| \geq 0$ with equality only if $v = 0$
- $\| k\mathbf{v} \| = k \|\mathbf{v}\|$
- The triangle inequality:
\[ \|\mathbf{u}+\mathbf{v}\|\leq\|\mathbf{u}\|+\|\mathbf{v}\| \]
- Cauchy-Schwarz inequality
\[ | \langle \mathbf{x} , \mathbf{y} \rangle | \leq \|\mathbf{x} \|\: \| \mathbf{y} \|. \]
The equality holds if and only if $\mathbf{x}$ and $\mathbf{y} $ are linearly dependent.
Distance
The distance between two points $p$ and $q$ in $\mathbb{R}^n$ is equal to the length of the vector that goes from $p$ to $q$: $d(p,q)=\| q - p \|$. We can similarly define a distance function between pairs of vectors in an abstract vector space $V$: \[ d : V \times V \to \mathbb{R}. \] The distance between two abstract vectors is the norm of their difference: \[ d(\mathbf{u},\mathbf{v}) \equiv \| \mathbf{u}-\mathbf{v} \| =\sqrt{ \langle (\mathbf{u}-\mathbf{v}),(\mathbf{u}-\mathbf{v})\rangle }. \]
NOINDENT Important properties of distances:
- $d(\mathbf{u},\mathbf{v}) = d(\mathbf{v},\mathbf{u})$
- $d(\mathbf{u},\mathbf{v}) \geq 0$ with equality only if $\mathbf{u}=\mathbf{v}$.
Examples
Matrix inner product
The Hilbert-Schmidt inner product for real matrices is \[ \langle A, B \rangle_{\textrm{HS}} = \textrm{Tr}\!\left[ A^T B \right]. \]
We can use this inner product to talk about orthogonality properties of matrices. In the last section we defined the set of $2\times2$ symmetric matrices \[ \mathbb{S}(2,2) = \{ A \in \mathbb{M}(2,2) \ | \ A = A^T \}, \] and gave an explicit basis for this space: \[ \mathbf{v}_1 = \begin{bmatrix} 1 & 0 \nl 0 & 0 \end{bmatrix}, \ \ \mathbf{v}_1 = \begin{bmatrix} 0 & 1 \nl 1 & 0 \end{bmatrix}, \ \ \mathbf{v}_3 = \begin{bmatrix} 0 & 0 \nl 0 & 1 \end{bmatrix}. \]
It is easy to show that these vectors are all mutually orthogonal with respect to the Hilbert-Schmidt inner product $\langle \cdot , \cdot \rangle_{\textrm{HS}}$: \[ \langle \mathbf{v}_1 , \mathbf{v}_2 \rangle_{\textrm{HS}}=0, \quad \langle \mathbf{v}_1 , \mathbf{v}_3 \rangle_{\textrm{HS}}=0, \quad \langle \mathbf{v}_2 , \mathbf{v}_3 \rangle_{\textrm{HS}}=0. \] Verify each of these by hand on a piece of paper right now. The above equations certify that the set $\{ \mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3 \}$ is an orthogonal basis for the vector space $\mathbb{S}(2,2)$.
Hilbert-Schmidt norm
The Hilbert-Schmidt inner product induces the Hilbert-Schmidt norm: \[ ||A||_{\textrm{HS}} \equiv \sqrt{ \langle A, A \rangle_{\textrm{HS}} } = \sqrt{ \textrm{Tr}\!\left[ A^T A \right] } = \left[ \sum_{i,j=1}^{n} |a_{ij}|^2 \right]^{\frac{1}{2}}. \]
We can therefore talk about the norm or length of a matrix. To continue with the above example, we can obtain an orthonormal basis $\{ \hat{\mathbf{v}}_1, \hat{\mathbf{v}}_2, \hat{\mathbf{v}_3} \}$ for $\mathbb{S}(2,2)$ as follows: \[ \hat{\mathbf{v}}_1 = \mathbf{v}_1, \quad \hat{\mathbf{v}}_2 = \frac{ \mathbf{v}_2 }{ \|\mathbf{v}_2\|_{\textrm{HS}} } = \frac{1}{\sqrt{2}}\mathbf{v}_2, \quad \hat{\mathbf{v}}_3 = \mathbf{v}_3. \] Verify that $\|\hat{\mathbf{v}}_2\|_{\textrm{HS}}=1$.
Function inner product
Consider two functions $\mathbf{f}=f(t)$ and $\mathbf{g}=g(t)$ and define their inner product as follows: \[ \langle f,g\rangle =\int_{-\infty}^\infty f(t)g(t)\; dt. \] The above formula is the continuous-variable version of the inner product formula for vectors $\vec{u}\cdot\vec{v}=\sum_i u_i v_i$. Instead of a summation we have an integral, but otherwise the idea is again to measure how strong the overlap between the $\mathbf{f}$ and $\mathbf{g}$ is.
Example
Consider the function inner product on the interval $[-1,1]$ as defined by the formula: \[ \langle f,g\rangle =\int_{-1}^1 f(t)g(t)\; dt. \]
Verify that the following polynomials, known as the Legendre polynomials $P_n(x)$, are mutually orthogonal with respect to the above inner product. \[ P_0(x)=1, \quad P_1(x)=x, \quad P_2(x)=\frac{1}{2}(3x^2-1), \quad P_3(x)=\frac{1}{2}(5x^3-3x), \] \[ \quad P_4(x)=\frac{1}{8}(35x^4-30x^2+3), \quad P_5(x)=\frac{1}{8}(63x^5-70x^3+15x). \]
TODO: Maybe add to math section on polynomials with intuitive expl: the product of any two of these: half above x axis, half below
Generalized dot product
We can think of the regular dot product for vectors as the following matrix product: \[ \vec{u} \cdot \vec{v} = \vec{u}^T \vec{v}= \vec{u}^T I \vec{v}. \]
In fact we can insert any symmetric and positive semidefinite matrix $M$ in between the vectors to obtain the generalized inner product: \[ \langle \vec{x}, \vec{y} \rangle_M \equiv \vec{x}^T M \vec{y}. \] The matrix $M$ is called the metric for this inner product and it encodes the relative contributions of the different components of the vectors to the length.
The requirement that $M$ be a symmetric matrix stems from the symmetric requirement of the inner product: $\langle \mathbf{u},\mathbf{v}\rangle =\langle \mathbf{v},\mathbf{u}\rangle$. The requirement that the matrix be positive semidefinite comes from the positive semi-definite requirement of the inner product: $\langle \mathbf{u},\mathbf{u}\rangle = \vec{u}^T M \vec{u} \geq 0$ for all $\mathbf{u}\in V$.
We can always obtain a symmetric and positive semidefinite matrix $M$ by setting $M = A^TA$ for some matrix $A$. To understand why we might want to construct $M$ in this way you need to recall that we can think of the matrix $A$ as performing some linear transformation $T_A(\vec{u})=A\vec{u}$. An inner product $\langle \vec{u},\vec{v}\rangle_M$ can be interpreted as the inner product in the image space of $T_A$: \[ \langle \vec{u}, \vec{v} \rangle_M = \vec{u}^T M \vec{v}= \vec{u}^T A^T A \vec{v}= (A\vec{u})^T (A \vec{v})= T_A(\vec{u}) \cdot T_A(\vec{v}). \]
Standard inner product
Why is the standard inner product for vectors $\langle \vec{u}, \vec{v} \rangle = \vec{u} \cdot \vec{v} = \sum_i u_i v_i$ called the “standard” inner product? If we are free to define ….
TODO: copy from paper… maybe move below next par
To be a inner product space
A standard question that profs like to ask on exams is to make you check whether some weird definition of an inner product forms an inner product space. Recall that any operation can be used as the inner product so long as it satisfies the symmetry, linearity, and positive semidefinitness requirements. Thus, what you are supposed to do is check whether the weird definition of an inner product which you will be given satisfies the three axioms. Alternately, you can show that the vector space $(V,\mathbb{R},+,\cdot)$ with inner product $\langle \mathbf{u}, \mathbf{v} \rangle$ is not an inner product space if you find an example of one of more $\mathbf{u},\mathbf{v} \in V$ which do not satisfy one of the axioms.
Discussion
This has been another one of those sections where we learn no new linear algebra but simply generalize what we already know about standard vectors $\vec{v} \in \mathbb{R}^n$ to more general vector-like things $\textbf{v} \in V$. You can now talk about inner products, orthogonality, and norms of matrices, polynomials, and other functions.
Gram-Schmidt orthogonalization
Suppose you are given a set of $n$ linearly independent vectors $\{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n \}$ taken from an $n$-dimensional space $V$ and you are asked to transform them into an orthonormal basis $\{\hat{\mathbf{e}}_1,\hat{\mathbf{e}}_2,\ldots,\hat{\mathbf{e}}_n \}$ for which: \[ \langle \hat{\mathbf{e}}_i, \hat{\mathbf{e}}_j \rangle =\left\{ \begin{array}{ll} 1 & \textrm{ if } i = j, \nl 0 & \textrm{ if } i \neq j. \end{array}\right. \] This procedure is known as orthogonalization. In this section, we'll learn an intuitive algorithm for converting any set of vectors into a set of orthonormal vectors. The algorithm is called Gram-Schmidt orthogonalization and it uses repeated projection and subtraction operations.
Definitions
- $V$: An $n$-dimensional vector space.
- $\{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n \}$: A generic basis for the space $V$.
- $\{ \mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n \}$: An orthogonal basis for $V$,
is one which satisfies $\mathbf{e}_i \cdot \mathbf{e}_j=0$ if $i\neq j$.
- $\{ \hat{\mathbf{e}}_1, \hat{\mathbf{e}}_2, \ldots, \hat{\mathbf{e}}_n \}$: An orthonormal basis for $V$
is an orthogonal basis of unit length vectors.
We assume that the vector space $V$ is equipped with an inner product operation: \[ \langle \cdot, \cdot \rangle : V \times V \to \mathbb{R}. \]
The following operations are defined in terms of the inner product:
- The length of a vector $\|\mathbf{v}\| = \langle \mathbf{v}, \mathbf{v} \rangle$.
- The projection operation. The projection of the vector $\mathbf{u}$ onto the subspace
spanned by $\mathbf{v}$ is given by:
\[
\Pi_{\mathbf{v}}(\mathbf{u}) = \frac{ \langle \mathbf{u}, \mathbf{v} \rangle }{ \|\mathbf{v}\|^2 } \mathbf{v}.
\]
* The //projection complement// of the projection $\Pi_{\mathbf{v}}(\mathbf{u})$ is the vector
$\mathbf{w}$ that we need to add to $\Pi_{\mathbf{v}}(\mathbf{u})$
to get back the //complete// original vector $\mathbf{u}$:
\[
\Pi_{\mathbf{v}}(\mathbf{u}) + \mathbf{w} = \mathbf{u}
\qquad
\textrm{or}
\qquad
\mathbf{w} = \mathbf{u} - \Pi_{\mathbf{v}}(\mathbf{u}).
\]
Observe that the vector $\mathbf{w}$ is, by construction, //orthogonal// to the vector $\mathbf{v}$:
$\langle \mathbf{u} - \Pi_{\mathbf{v}}(\mathbf{u}), \mathbf{v} \rangle = 0$.
The discussion in this section is in terms of abstract vectors denoted in bold $\mathbf{u}$ and the operations are performed in an abstract inner product space. Thus, the algorithm described below can be used with vectors $\vec{v} \in \mathbb{R}^n$, matrices $M \in \mathbb{R}^{m\times n}$, and polynomials $\mathbf{p} \in P_n(x)$. Indeed, we can talk about orthogonality for any vector space for which we can define an inner product operation.
Orthonormal bases are nice
Recall that a basis for an $n$-dimensional vector space $V$ is any set of $n$ linearly independent vectors in $V$. The choice of basis is a big deal because it is with respect to that basis that we write down the coordinates of vectors and matrices. From the theoretical point of view, all bases are equally good, but from a practical point of view orthogonal and orthonormal bases are much easier to work with.
An orthonormal basis is the most useful kind of basis because the coefficients $(c_1,c_2,c_3)$ of a vector $\mathbf{c}$ can be obtained simply using the inner product: \[ c_1 = \langle \mathbf{c}, \hat{\mathbf{e}}_1 \rangle, \quad c_2 = \langle \mathbf{c}, \hat{\mathbf{e}}_2 \rangle, \quad c_3 = \langle \mathbf{c}, \hat{\mathbf{e}}_3 \rangle. \]
Indeed we can write down any vector $\mathbf{v}$ as \[ \mathbf{v} = \langle \mathbf{v}, \hat{\mathbf{e}}_1 \rangle \hat{\mathbf{e}}_1 + \langle \mathbf{v}, \hat{\mathbf{e}}_2 \rangle \hat{\mathbf{e}}_2 + \langle \mathbf{v}, \hat{\mathbf{e}}_3 \rangle \hat{\mathbf{e}}_3. \] This formula is a generalization of the usual formula for coefficients with respect to the standard basis $\{ \hat{\imath}, \hat{\jmath},\hat{k} \}$: \[ \vec{v} = (\vec{v}\cdot\hat{\imath})\hat{\imath} + (\vec{v}\cdot\hat{\jmath})\hat{\jmath} + (\vec{v}\cdot\hat{k}) \hat{k}. \]
Orthogonalization
As we said earlier, the “best” kind of basis for computational purposes is an orthonormal one like $\{ \hat{\mathbf{e}}_1, \hat{\mathbf{e}}_2, \ldots, \hat{\mathbf{e}}_n \}$. A common task in linear algebra is to upgrade some general set of $n$ linearly independent vectors $\{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n \}$ into an orthonormal basis $\{ \hat{\mathbf{e}}_1, \hat{\mathbf{e}}_2, \ldots, \hat{\mathbf{e}}_n \}$, where the vectors $\{\hat{\mathbf{e}}_i\}$ are all formed as linear combinations of the vectors $\{\mathbf{v}_i\}$. Note that the vector space spanned by both these sets of vectors is the same: \[ V \equiv \textrm{span}\{\mathbf{v}_1,\mathbf{v}_2,\ldots,\mathbf{v}_n \} = \textrm{span}\{\hat{\mathbf{e}}_1,\hat{\mathbf{e}}_2,\ldots,\hat{\mathbf{e}}_n \}, \] but the basis $\{\hat{\mathbf{e}}_1,\hat{\mathbf{e}}_2,\ldots,\hat{\mathbf{e}}_m \}$ is easier to work with since we can compute the vector coefficients using the inner product $u_i = \langle \mathbf{u}, \hat{\mathbf{e}}_i \rangle$.
The technical term for distilling a high quality basis from a low quality basis is called orthogonalization. Note that it is not called orthonormalization, which would be 1) way too long for a word (in German it would be Okay I guess) and 2) over-complicated for nothing. You see, the actual work is in getting the set of vectors $\{ \mathbf{e}_i\}$ which are orthogonal to each other: \[ \mathbf{e}_i \cdot \mathbf{e}_j=0, \quad \textrm{ for all } i \neq j. \] Converting these into an orthonormal basis is then done simply by dividing each vector by its length: $\hat{\mathbf{e}}_i = \frac{\mathbf{e}_i}{ \| \mathbf{e}_i \| }$.
Let's now see how this is done.
Gram-Schmidt orthogonalization
The Gram-Schmidt orthogonalization procedure converts a set of arbitrary vectors $\{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n \}$ into an orthonormal set of vectors $\{ \hat{\mathbf{e}}_1, \hat{\mathbf{e}}_2, \ldots, \hat{\mathbf{e}}_n \}$. The main idea is to take the directions of the vectors $\{ \mathbf{v}_i \}$ one at a time and each time define a new vector $\mathbf{e}_i$ as the orthogonal complement to all the previously chosen vectors $\mathbf{e}_1$, $\mathbf{e}_2$, $\ldots$, $\mathbf{e}_{i-1}$. The orthogonalization algorithm consists of $n$ steps: \[ \begin{align*} \mathbf{e}_1 &= \mathbf{v}_1 & \hat{\mathbf{e}}_1 &= {\mathbf{v}_1 \over \|\mathbf{v}_1\|}, \nl \mathbf{e}_2 &= \mathbf{v}_2-\Pi_{\hat{\mathbf{e}}_1}\!(\mathbf{v}_2), & \hat{\mathbf{e}}_2 &= {\mathbf{e}_2 \over \|\mathbf{e}_2\|}, \nl \mathbf{e}_3 &= \mathbf{v}_3-\Pi_{\hat{\mathbf{e}}_1}\!(\mathbf{v}_3)-\Pi_{\hat{\mathbf{e}}_2}\!(\mathbf{v}_3), & \hat{\mathbf{e}}_3 &= {\mathbf{e}_3 \over \|\mathbf{e}_3\|}, \nl \mathbf{e}_4 &= \mathbf{v}_4-\Pi_{\hat{\mathbf{e}}_1}\!(\mathbf{v}_4)-\Pi_{\hat{\mathbf{e}}_2}\!(\mathbf{v}_4), -\Pi_{\hat{\mathbf{e}}_3}\!(\mathbf{v}_4), & \hat{\mathbf{e}}_4 &= {\mathbf{e}_4 \over \|\mathbf{e}_4\|}, \nl & \vdots &&\vdots \nl \mathbf{e}_n &= \mathbf{v}_n-\sum_{i=1}^{n-1}\Pi_{\hat{\mathbf{e}}_i}\!(\mathbf{v}_n), &\hat{\mathbf{e}}_n &= {\mathbf{e}_n\over\|\mathbf{e}_n\|}. \end{align*} \] In the $j$th step of the procedure, we compute a vector $\mathbf{e}_j$ by starting from $\mathbf{v}_j$ and subtracting all the projections onto the previous vectors $\mathbf{e}_i$ for all $i<j$. In other words, $\mathbf{e}_j$ is the part of $\mathbf{v}_j$ that is orthogonal to all the vectors $\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_{j-1}$.
The above procedure is known as orthogonalization because it splits the vector space $V$ into orthogonal subspaces $V_1, V_2, \ldots, V_n$: \[ W_j = \textrm{span}\{ \mathbf{v} \in V \ | \ \mathbf{v}= \sum_{i=1}^j \alpha_i \mathbf{v}_i \} \setminus \textrm{span}\{ \mathbf{v} \in V \ | \ \mathbf{v}= \sum_{i=1}^{j-1} \alpha_i \mathbf{v}_i \}. \] Recall that the symbol $\setminus$ denotes the set minus operation. The set $A \setminus B$ consists of all elements that are in $A$ but not in $B$.
Observe that the subspaces $V_1, V_2, \ldots, V_n$ are, by construction, mutually orthogonal. Given any vector $\mathbf{u} \in V_i$ and another vector $\mathbf{v} \in V_j, j\neq i$ then $\mathbf{u} \cdot \mathbf{v} = 0$.
The vector space $V$ is sum of these subspaces: \[ V = V_1 \oplus V_2 \oplus V_3 \oplus \cdots \oplus V_n. \] The notation $\oplus$ means orthogonal sum.
Discussion
The main point about orthogonalization that I want you to know is that it can be done. Any “low quality” basis (a set of $n$ linearly independent vectors $\{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n \}$ in an $n$-dimensional space) can be converted into a “high quality” orthonormal basis $\{ \hat{\mathbf{e}}_1, \hat{\mathbf{e}}_2, \ldots, \hat{\mathbf{e}}_n \}$ by using the Gram-Schmidt procedure.
In the next section we will learn how to think about this orthogonalization procedure in terms of matrices, where the Gram-Schmidt procedure is known as the $QR$ decomposition.
Matrix Decompositions
It is often useful to express a given matrix $M$ as the product of different, simpler, matrices. These matrix decompositions (factorizations) can help us understand the structure of matrices by looking at their constituents. In this section we'll discuss various matrix factorizations and specify what types of matrices they are applicable to.
Most of the material covered here is not usually part of a first-year course on linear algebra. Nevertheless, I want you to know about the different matrix decompositions because many linear algebra applications depend on these techniques.
Eigendecomposition
The eigenvalue decomposition is a way to break-up a matrix into its natural basis. In its natural basis, a diagonalizable matrix can be written as: \[ M = Q \Lambda Q^{-1}, \] where $Q$ is a matrix of eigenvectors $Q=[\vec{e}_1,\vec{e}_2,\ldots,\vec{e}_n]$ and $\Lambda$ is a diagonal matrix $\Lambda_{ii} = \lambda_i$, where $\lambda_1,\lambda_2,\ldots,\lambda_n$ are the eigenvalues the matrix $M$.
When the matrix $M$ is normal ($MM^T = M^T M$), we can choose $Q$ to be an orthogonal matrix $O$ which satisfies $O^T O = I$. Calculating the inverse of an orthogonal matrix is easy: $O^{-1}=O^T$, so the diagonalization for normal matrices becomes: \[ M = O \Lambda O^T. \]
If the matrix $M$ is symmetric, then all its eigenvalues will be real numbers.
Similarity transformation
Consider the matrix $N \in \mathbb{R}^{n\times n}$ and an invertible matrix $P \in \mathbb{R}^{n\times n}$. In a similarity transformation the matrix $N$ is multiplied by $P$ from the left and by the inverse of $P$ on the right: \[ M = P N P^{-1}. \]
Because $P$ is an invertible matrix, its columns form a basis for the space $\mathbb{R}^n$. Thus we can interpret $P$ as a change of basis from the standard basis to the basis of the columns of $P$. The matrix $P^{-1}$ corresponds to the inverse change of basis.
The matrices $M$ and $N$ correspond to the same linear transformation but with respect to different bases. We say matrix $N$ is similar to the matrix $M$. Similar matrices have the same eigenvalues $\textrm{eig}(N)=\textrm{eig}(M)$, and therefore have the same trace $\textrm{Tr}(M)=\textrm{Tr}(N)=\sum_i \lambda_i$ and the same determinant $|M|=|N|=\prod_i \lambda_i$.
Note that the eigendecomposition of a matrix is a type of similarity transformation where the change of basis matrix is constructed from the set of eigenvectors.
Singular value decomposition
We can generalize the concept of eigenvalues to non-square matrices. Consider an $m \times n$ matrix $M$. We can always write it as a diagonal matrix $\Sigma$ surrounded by matrices of left eigenvectors and right eigenvectors: \[ M = U\Sigma V, \] where
- $\Sigma \in \mathbb{R}^{m\times n}$ is a diagonal matrix containing the square roots $\sigma_i$
of the eigenvalues $\lambda_i$ of the matrix $MM^T$ (or the matrix $M^TM$,
since $M^TM$ and $MM^T$ have the same eigenvalues):
\[
\sigma_i = \sqrt{ \lambda_i },
\textrm{ where } \{ \lambda_i \} = \textrm{eig}(MM^T) = \textrm{eig}(M^T M).
\]
* $U$ is an orthogonal matrix who's columns are the $m$-dimensional eigenvectors
of $MM^T$.
\[
U=
\begin{bmatrix}
| & & | \nl
\hat{u}_{\lambda_1} & \cdots & \hat{u}_{\lambda_m} \nl
| & & |
\end{bmatrix},
\textrm{ where } \{ (\lambda_i,\hat{u}_i) \} = \textrm{eigv}(MM^T).
\]
* $V$ is a orthogonal matrix whose //rows// are the $n$-dimensional
eigenvectors of $M^T M$.
\[
V=
\begin{bmatrix}
- & \hat{v}_{1} & - \nl
& \vdots & \nl
- & \hat{v}_{n} & -
\end{bmatrix},
\textrm{ where } \{ (\lambda_i,\hat{v}_i) \} = \textrm{eigv}(M^T M).
\]
Written more explicitly, the singular value decomposition of the matrix $M$ is \[ M= \underbrace{ \begin{bmatrix} | & & | \nl \hat{u}_{\lambda_1} & \cdots & \hat{u}_{\lambda_m} \nl | & & | \end{bmatrix} }_U \underbrace{ \begin{bmatrix} \sigma_1 & 0 & \cdots \nl 0 & \sigma_2 & \cdots \nl 0 & 0 & \cdots \end{bmatrix} }_\Sigma \underbrace{ \begin{bmatrix} \ \ - & \hat{v}_{1} & - \ \ \nl & \vdots & \nl - & \hat{v}_{n} & - \end{bmatrix} }_V. \] The above formula allows us to see the structure of the matrix $M$. We can interpret the operation $\vec{y} = M\vec{x}$ as a three step process:
- Convert the input vector $\vec{x}$ from the standard basis to the basis $\{ \vec{v}_i \}$
- Scale each component by the corresponding singular value $\sigma_i$
- Convert the output from the $\{ \vec{u}_i \}$ basis
back to the standard basis
LU decomposition
It is much easier to compute the inverse of a triangular matrix than it is for a general matrix. Thus, it is useful to write a matrix as the product of two triangular matrices for computational purposes. We call this the $LU$ decomposition: \[ A = LU, \] where $U$ is an upper triangular matrix and $L$ is a lower triangular matrix.
The main application of this decomposition is to obtain more efficient solutions to equations of the form $A\vec{x}=\vec{b}$. Because $A=LU$, we can solve this equation in two steps. Starting from $L^{-1}LU\vec{x}=U\vec{x}=L^{-1}\vec{b}$ and then $U^{-1}U\vec{x}=\vec{x}=U^{-1}L^{-1}\vec{b}$. We have split the work of finding the inverse $A^{-1}$ into two simpler subtasks: finding $L^{-1}$ and $U^{-1}$.
The $LU$ decomposition is mainly used in computer algorithms, but it is also possible to find the $LU$ decomposition of a matrix by hand. Recall the algorithm for finding the inverse of a matrix in which you start from the array $[A|I]$ and do row operations until you get the array into the reduced row echelon form $[I|A^{-1}]$. Consider the midpoint of the algorithm, when the left-hand side of the array is the row echelon form (REF). Since the matrix $A$ in its REF is upper triangular, the array will contain $[U|L^{-1}]$. The $U$ part of the decomposition is on the left-hand side, and the $L$ part is obtained by finding the inverse of the right hand side of the array.
Cholesky decomposition
For a symmetric and positive semidefinite matrix $A$, the $LU$ decomposition takes the simpler form. Such matrices can be written as the product of a triangular matrix with its transpose: \[ A = LL^T, \quad \textrm{or} \quad A=U^TU, \] where $U$ is an upper triangular matrix and L is a lower triangular matrix.
QR decomposition
Any real square matrix $A \in \mathbb{R}^{n\times n}$ can be decomposed as a product of an orthogonal matrix $O$ and an upper triangular matrix $U$: \[ A = OU. \] For historical reasons, the orthogonal matrix is usually denoted $Q$ instead of $O$ and the upper triangular matrix is $R$ instead (think “right-triangular” since it has entries only to the right of main diagonal). The decomposition then becomes: \[ A = QR, \] and this is why it is known as the QR decomposition.
The $QR$ decomposition is equivalent to the Gram-Schmidt orthogonalization procedure.
Example
Consider the decomposition of \[ A = \begin{bmatrix} 12 & -51 & 4 \nl 6 & 167 & -68 \nl -4 & 24 & -41 \end{bmatrix} = OR. \]
We are looking for the orthogonal matrix $O$, i.e., a matrix $O$ which obeys $O^{T}\,O = I$ and an upper triangular matrix $R$. We can obtain an orthogonal matrix by making its columns orthonormal vectors (Gram–Schmidt procedure) and recording the Gram–Schmidt coefficients in the matrix $R$.
Let us now illustrate the procedure can be used to compute the factorization $A=OR$. The first step is to change the second column in $A$ so that it becomes orthogonal to the first (by subtracting a multiple of the first column). Next we change the third column in $A$ so that it is orthogonal to both of the first columns (by subtracting multiples of the first two columns). In doing so we obtain a matrix which has the same column space as $A$ but which has orthogonal columns: \[ \begin{bmatrix} | & | & | \nl \mathbf u_1 & \mathbf u_2 & \mathbf u_3 \nl | & | & | \end{bmatrix} = \begin{bmatrix} 12 & -69 & -58/5 \nl 6 & 158 & 6/5 \nl -4 & 30 & -33 \end{bmatrix}. \] To obtain an orthogonal matrix we must normalize each column to be of unit length: \[ O = \begin{bmatrix} | & | & | \nl \frac{\mathbf u_1}{\|\mathbf u_1\|} & \frac{\mathbf u_2}{\|\mathbf u_2\|} & \frac{\mathbf u_3}{\|\mathbf u_3\|} \nl | & | & | \end{bmatrix} = \begin{bmatrix} 6/7 & -69/175 & -58/175 \nl 3/7 & 158/175 & 6/175 \nl -2/7 & 6/35 & -33/35 \end{bmatrix}. \]
We can find the matrix $R$ as follows: \[ \begin{matrix} O^{T} A = O^{T}Q\,R = R \end{matrix}, \qquad \begin{matrix} R = O^{T}A = \end{matrix} \begin{bmatrix} 14 & 21 & -14 \nl 0 & 175 & -70 \nl 0 & 0 & 35 \end{bmatrix}. \] The columns of $R$ contain the mixture coefficients required to obtain the columns of $A$ from the columns of $O$. For example, the second column of $A$ is equal to $21\frac{\mathbf u_1}{\|\mathbf u_1\|}+175\frac{\mathbf u_2}{\|\mathbf u_2\|}$.
Discussion
You will no doubt agree with me that spending time on learning about these different decompositions was educational. If you are interested in pursuing the subject matrix factorization (decomposition) you will find that there we have only scratched the subject. I encourage you to research this subject on your own. There are countless areas of application for matrix methods. I will just mention three topics from machine learning: nonnegative matrix factorization, latent semantic indexing, and latent Dirichlet allocation.
Links
[ Retro movie showing steps in SVD ]
http://www.youtube.com/watch?v=R9UoFyqJca8
NOINDENT
[ More info from wikipedia ]
http://en.wikipedia.org/wiki/Matrix_decomposition
http://en.wikipedia.org/wiki/Singular_value_decomposition
NOINDENT
[ A detailed example of the QR factorization of a matrix ]
http://www.math.ucla.edu/~yanovsky/Teaching/Math151B/handouts/GramSchmidt.pdf
NOINDENT
[ Cholesky decomposition ]
http://en.wikipedia.org/wiki/Cholesky_decomposition
Linear algebra with complex numbers
So far we have discussed the math of vectors with real entries, i.e., vectors $(v_1,v_2,v_3)$ where $v_1,v_2,v_3 \in \mathbb{R}$. In fact we can do linear algebra over any field. The term field applies to any mathematical object (think different types of numbers) for which we have defined the operations of addition, subtraction, multiplication and division.
The complex numbers $\mathbb{C}$ are a field. Therefore we can do linear algebra over the complex numbers. We can define complex vectors $\mathbb{C}^n$ and complex matrices $\mathbb{C}^{m \times n}$ which behave similarly to their real counterparts. You will see that complex linear algebra is no more complex than real linear algebra. It is the same, in fact, except for one small difference: instead of matrix transpose $A^T$ we have to use the Hermitian transpose $A^\dagger$ which is the combination of the transpose and an entry-wise complex conjugate operation.
Complex vectors are not just an esoteric mathematical concept intended for specialists. Complex vectors can arise as answers for problems involving ordinary real matrices. For example, the rotation matrix \[ R_\theta = \begin{bmatrix} \cos\theta &-\sin\theta \nl \sin\theta &\cos\theta \end{bmatrix} \] has complex eigenvalues $\lambda_1 = e^{i\theta}$ and $\lambda_2 = e^{-i\theta}$ and eigenvectors with complex coefficients. Thus, if you want to know how to calculate the eigenvalues and eigenvectors of rotation matrices, you need to understand how to do linear algebra calculations with $\mathbb{C}$.
This section will also serve as a review of many of the important concepts in linear algebra so I recommend that you read it even if your class doesn't require you to know about complex matrices. As your linear algebra teacher, I want you to know about linear algebra over the field of complex numbers because I have a hidden agenda, which I'll tell you about at the end of this section.
Definitions
Recall the basic notions of complex numbers:
- $i$: the unit imaginary number $i \equiv \sqrt{-1}$ or $i^2 = -1$
- $z=a+bi$: a complex number that has both real part and imaginary part
- $\mathbb{C}$: the set of complex numbers $\mathbb{C} = \{ a + bi \ | \ a,b \in \mathbb{R} \}$
- $\textrm{Re}\{ z \}=a$: the real part of $z=a+bi$
- $\textrm{Im}\{ z \}=b$: the imaginary part of $z=a+bi$
- $\bar{z}$: the complex conjugate of $z$. If $z=a+bi$, then $\bar{z}=a-bi$.
- $|z|=\sqrt{ \bar{z}z }=\sqrt{a^2+b^2}$: the magnitude or length of $z=a+bi$
Complex vectors
A complex vector $\vec{v} \in \mathbb{C}^n$ is an array of $n$ complex numbers. \[ \vec{v} = (v_1,v_2,v_3) \ \in \ (\mathbb{C},\mathbb{C},\mathbb{C}) \equiv \mathbb{C}^3. \]
Complex matrices
A complex matrix $A \in \mathbb{C}^{m\times n}$ is a two-dimensional array of numbers: \[ A = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right] \ \in \ \left[\begin{array}{ccc} \mathbb{C} & \mathbb{C} & \mathbb{C} \nl \mathbb{C} & \mathbb{C} & \mathbb{C} \nl \mathbb{C} & \mathbb{C} & \mathbb{C} \end{array}\right] \equiv \mathbb{C}^{3\times 3}. \]
Hermitian transpose
The Hermitian transpose operation, complex transpose or “dagger”($\dagger$) operation consists of the combination of the regular transpose ($A \to A^T$) and the complex conjugation of each entry in the matrix ($a_{ij} \to \overline{a_{ij}}$): \[ A^\dagger \equiv \overline{(A^T)}=(\overline{A})^T. \] Expressed in terms of the entries of the matrix $a_{ij}$, the Hermitian transpose corresponds to the transformation $a_{ij} \to \overline{ a_{ji} }$.
For example, the Hermitian conjugation operation applied to a $3\times3$ matrix is \[ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{bmatrix}, \qquad A^\dagger = \begin{bmatrix} \overline{a_{11}} & \overline{a_{21}} & \overline{a_{31}} \nl \overline{a_{12}} & \overline{a_{22}} & \overline{a_{32}} \nl \overline{a_{13}} & \overline{a_{23}} & \overline{a_{33}} \end{bmatrix}. \]
Recall that a vector is a special case of a matrix: you can identify a vector $\vec{v} \in \mathbb{C}^n$ with a column matrix $\vec{v} \in \mathbb{C}^{n \times 1}$. We can therefore apply the complex conjugation operation on vectors: \[ \vec{v}^\dagger \equiv \overline{(\vec{v}^T)}=(\overline{\vec{v}})^T \] The complex conjugate of a column vector is a row vector in which each of the coefficients have been conjugated: \[ \vec{v} = \begin{bmatrix} \alpha \nl \beta \nl \gamma \end{bmatrix}, \qquad \vec{v}^\dagger = \begin{bmatrix} \alpha \nl \beta \nl \gamma \end{bmatrix}^\dagger = \begin{bmatrix} \overline{\alpha} & \overline{\beta} & \overline{\gamma} \end{bmatrix}. \]
The complex conjugation of vectors is important to understand because it allows us to define an inner product operation for complex vectors.
Complex inner product
Recall that the inner product for vectors with complex coefficients ($\vec{u}, \vec{v} \in \mathbb{C}^n$) is defined as the operation: \[ \langle \vec{u}, \vec{v} \rangle \equiv \sum_{i=1}^n \overline{u_i} v_i \equiv \vec{u}^\dagger \vec{v}. \] Note that the complex conjugation is applied to each of the first vector's components in the expression. This corresponds naturally to the notion of applying the Hermitian transpose on the first vector to turn it into a row vector of complex conjugates and then following the general rule for matrix multiplication of a $1 \times n$ matrix $\vec{u}^\dagger$ by an $n \times 1$ matrix $\vec{v}$.
Linear algebra over the complex field
Let us jump right into the heart of the matter. One of the fundamental ideas we learned in this chapter has been how to model linear systems, that is, input-output phenomena in which one vector $\vec{v}$ is related to another vector $\vec{w}$ in a linear way. We can think of this input-output relation as a linear transformation $T:\mathbb{R}^m \to \mathbb{R}^n$. Furthermore, we learned that any linear transformation can be represented as a $m\times n$ matrix with real coefficients with respect to some choice of input basis and output basis.
Linear algebra thinking can also be applied for complex vectors. For example, a linear transformation from $\mathbb{C}^2$ to $\mathbb{C}^2$ can be represented in terms of the matrix product \[ \begin{bmatrix} w_1 \nl w_2 \end{bmatrix} = \begin{bmatrix} \alpha & \beta \nl \gamma & \delta \end{bmatrix} \begin{bmatrix} v_1 \nl v_2 \end{bmatrix}, \] for some $2 \times 2$ matrix $\begin{bmatrix} \alpha & \beta \nl \gamma & \delta \end{bmatrix}$ where $\alpha,\beta, \gamma,\delta \in \mathbb{C}$.
This change from the real numbers to the complex numbers has the effect of doubling the dimensions of the transformation. Indeed, a $2 \times 2$ complex matrix has eight “parameters” not four. Where did you see the eight? Here: \[ \begin{bmatrix} \alpha & \beta \nl \gamma & \delta \end{bmatrix} = \begin{bmatrix} \textrm{Re}\{\alpha\} & \textrm{Re}\{\beta\} \nl \textrm{Re}\{\gamma\} & \textrm{Re}\{\delta\} \end{bmatrix} + \begin{bmatrix} \textrm{Im}\{\alpha\} & \textrm{Im}\{\beta\} \nl \textrm{Im}\{\gamma\} & \textrm{Im}\{\delta\} \end{bmatrix}i \] Each of the four coefficients of the matrix has a real part and an imaginary part $z =\textrm{Re}\{ z \}+\textrm{Im}\{ z \}i$ so there is a total of eight parameters to “pick” when specifying the matrix.
Similarly, to specify a vector $\vec{v}=\mathbb{C}^2$ you need to specify four parameters \[ \begin{bmatrix} v_1 \nl v_2 \end{bmatrix} = \begin{bmatrix} \textrm{Re}\{v_1\} \nl \textrm{Re}\{v_2\} \end{bmatrix} + \begin{bmatrix} \textrm{Im}\{v_1\} \nl \textrm{Im}\{v_2\} \end{bmatrix}i. \]
Example 1: Solving systems of equations
Suppose you are solving a problem which involves complex numbers and system of two linear equations in two unknowns: \[ \begin{align*} x_1 + 2x_2 & = 3+i, \nl 3x_2 + (9+i)x_2 & = 6+2i. \end{align*} \] You are asked to solve this system, i.e., to find the values of the unknowns $x_1$ and $x_2$.
The solutions $x_1$ and $x_2$ will be complex numbers, but apart from that there is nothing special about this problem: linear algebra with complex numbers is the same as linear algebra with the real numbers. To illustrate this point, we'll now go through the steps we need to solve this system of equations. You will see that all the linear algebra techniques you learned also work for complex numbers.
First observe that the system of equations can be written as a matrix-vector product: \[ \begin{bmatrix} 1 & 2 \nl 3 & 9+i \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} 3+i \nl 6+2i \end{bmatrix}, \] or more compactly as $A\vec{x}=\vec{b}$. Here $A$ is a $2 \times 2$ matrix and $\vec{x}$ is the vector of unknowns (a $2 \times 1$ matrix) and $\vec{b}$ is a vector of constants (a $2 \times 1$ matrix).
The solution can easily be obtained if by first finding the inverse matrix $A^{-1}$. We have $\vec{x}=A^{-1}\vec{b}$.
For the above matrix $A$, the inverse matrix $A^{-1}$ is \[ A^{-1} = \begin{bmatrix} 1 + \frac{6}{3 + i} & - \frac{2}{3 + i}\nl - \frac{3}{3 + i} & \frac{1}{3 + i} \end{bmatrix} \] We can now compute the answer $\vec{x}$ using the matrix inverse and the equation $\vec{x}=A^{-1}\vec{b}$. We obtain \[ \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} 1 + \frac{6}{3 + i} & - \frac{2}{3 + i}\nl - \frac{3}{3 + i} & \frac{1}{3 + i} \end{bmatrix} \begin{bmatrix} 3+i\nl 6 + 2i \end{bmatrix} = \begin{bmatrix} 3+i + 6 - 4 \nl -3 + 2 \end{bmatrix} = \begin{bmatrix} 5+i \nl -1 \end{bmatrix}. \]
Example 2: Finding the inverse
Recall that we learned several different approaches for computing the matrix inverse. Here we will review the general procedure for computing the inverse of a matrix by using row operations.
Given the matrix \[ A = \begin{bmatrix} 1 & 2 \nl 3 & 9+i \end{bmatrix}, \] the first step is to build an augmented array which contains the matrix $A$ and the identity $I$ matrix. \[ \left[ \begin{array}{ccccc} 1 & 2 &|& 1 & 0 \nl 3 & 9+i &|& 0 & 1 \end{array} \right]. \]
We now perform Gauss-Jordan elimination procedure on the resulting $2 \times 4$ matrix.
- The first step is to subtract three times the first row
from the second row, or written compactly $R_2 \gets R_2 -3R_1$ to obtain:
\[
\left[
\begin{array}{ccccc}
1 & 2 &|& 1 & 0 \nl
0 & 3+i &|& -3 & 1
\end{array} \right].
\]
- Second we perform $R_2 \gets \frac{1}{3+i}R_2$ and get:
\[
\left[
\begin{array}{ccccc}
1 & 2 &|& 1 & 0 \nl
0 & 1 &|& \frac{-3}{3+i} & \frac{1}{3+i}
\end{array} \right].
\]
- Finally we perform $R_1 \gets R_1 - 2R_2$ to obtain:
\[
\left[
\begin{array}{ccccc}
1 & 0 &|& 1 + \frac{6}{3+i} & - \frac{2}{3+i} \nl
0 & 1 &|& \frac{-3}{3+i} & \frac{1}{3+i}
\end{array} \right].
\]
The inverse of $A$ can be found on the right-hand side of the above array: \[ A^{-1} = \begin{bmatrix} 1 + \frac{6}{3 + i} & - \frac{2}{3 + i}\nl - \frac{3}{3 + i} & \frac{1}{3 + i} \end{bmatrix}. \]
Example 3: Linear transformations as matrices
The effects of multiplying a vector $\vec{v} \in \mathbb{C}^n$ by a matrix $M \in \mathbb{C}^{m\times n}$ has the same effect as a linear transformation $T_M:\mathbb{C}^n \to \mathbb{C}^m$: \[ \vec{w} = M \vec{v} \qquad \Leftrightarrow \qquad \vec{w} = T(\vec{v}). \] The opposite is also true—any linear transformation $T$ can be represented as a matrix product: \[ \vec{w} = T(\vec{v}) \qquad \Leftrightarrow \qquad \vec{w} = M_T \vec{v}, \] for some matrix $M_T$. We will now illustrate the procedure for finding the matrix representation of a linear transformation with a simple example.
Consider the linear transformation $T:\mathbb{C}^2 \to \mathbb{C}^2$ which produces the following input-output pairs: \[ T\!\left( \begin{bmatrix} 1 \nl 0 \end{bmatrix} \right) = \begin{bmatrix} 3 \nl 2i \end{bmatrix}, \quad \textrm{and} \quad T\!\left( \begin{bmatrix} 0 \nl 2 \end{bmatrix} \right) = \begin{bmatrix} 2 \nl 4+4i \end{bmatrix}. \] Do you remember how you can use the information provided above to find the matrix representation $M_T$ of the linear transformation $T$ with respect to the standard basis?
To obtain the matrix representation of $T$ with respect to a given basis we have to combine, as columns, the outputs $T$ for the different elements of the basis: \[ M_T = \begin{bmatrix} | & | & \mathbf{ } & | \nl T(\vec{e}_1) & T(\vec{e}_2) & \dots & T(\vec{e}_n) \nl | & | & \mathbf{ } & | \end{bmatrix}, \] where $\{ \hat{e}_1,\hat{e}_2,\ldots, \hat{e}_n\}$ are the elements of the basis for the input space $\mathbb{R}^n$.
We know the value for the first column $T(\hat{e}_1)$ but we are not given the output of $T$ for the $\hat{e}_2$. This is OK though since we can use the fact that $T$ is a linear transformation ($T(\alpha \vec{v}) = \alpha T(\vec{v})$ which means that \[ T\!\left( 2 \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) = 2 \begin{bmatrix} 1 \nl 2+2i \end{bmatrix} \quad \Rightarrow \quad T\!\left( \begin{bmatrix} 0 \nl 1 \end{bmatrix} \right) = \begin{bmatrix} 1 \nl 2+2i \end{bmatrix}. \]
Thus we find the final answer \[ M_T= \begin{bmatrix} 3 & 1 \nl 2i & 2+2i \end{bmatrix}. \]
Complex eigenvalues
The main reason why I want you, my dear students, to learn about linear algebra with complex vectors is so that we can complete the important task of classifying the basic types of linear transformations in term of their eigenvalues. Recall that
- projections obey $\Pi=\Pi^2$ and have eigenvalues zero or one
- reflections have at least one eigenvalue equal to negative one
What kind of eigenvalues do rotations matrices have? The eigenvalues of a matrix $M$ are the roots of its characteristic polynomial $p_M(\lambda)=\textrm{det}(M - \lambda I)$. Thus, to find the eigenvalues of the rotation matrix $R_\theta$ we must solve the following equaiton \[ p_{R_\theta}(\lambda) =\textrm{det}(R_\theta - \lambda I) =\textrm{det}\left( \begin{bmatrix} \cos\theta -\lambda &-\sin\theta \nl \sin\theta &\cos\theta -\lambda \end{bmatrix} \right) =(\cos\theta - \lambda)^2+\sin^2\theta = 0. \]
To solve for $\lambda$ we first move $\sin^2\theta$ to the other side of the equation and then take the square root \[ \cos\theta-\lambda = \pm \sqrt{ - \sin^2 \theta } = \pm \sqrt{ - 1} \sin \theta = \pm i\sin\theta. \] The eigenvalues are $\lambda_1 = \cos\theta + i \sin\theta$ and $\lambda_2 = \cos\theta - i \sin\theta$. Note that by using Euler's equation we can also write the eigenvalues as $\lambda_1 = e^{i\theta}$ and $\lambda_2 =e^{-i\theta}$. All of a sudden, complex numbers show up out of nowhere! This is not a coincidence: complex exponentials are in many ways the natural way to talk about rotations, periodic motion, and waves.
If you pursue a career in math, physics or engineering you will no doubt run into complex numbers and Euler's equation many more times. In this case what is interesting is that complex numbers come out as answers to a problem that was stated strictly in terms of real variables.
Special types of matrices
We now define some special types of matrices which describe matrices with complex coefficients.
Unitary matrices
Let $V$ be a complex space on which an inner product is defined. Than a linear transformation $U$ is unitary if $U^\dagger U={11}$. It has determinant $|\det(U)|=1$.
For a $n\times n$ matrix $U$ the following statements are equivalent:
- $U$ is unitary
- The columns of $U$ are an orthonormal set
- The rows of $U$ are an orthonormal set
- The inverse of $U$ is $U^\dagger$
Unitary matrices are the complex analogues of the orthogonal matrices. Indeed, if a unitary matrix $U$ has real coefficients then $U^\dagger = U^T$ and we have $U^TU={11}$, which is the definition of an orthogonal matrix.
Hermitian matrices
A Hermitian matrix $H$ is the complex analogue of the symmetric matrix: \[ H^T = H, \qquad h_{ij} = \overline{ h_{ji}}, \quad \text{ for all } i,j. \] The eigenvalues of a Hermitian matrix are all real.
A Hermitian matrix $H$ can be freely moved from one side to the other in a dot product calculation: \[ \langle H\vec{x},\vec{y}\rangle =(H\vec{x})^\dagger\vec{y} =\vec{x}^\dagger H^\dagger \vec{y} =\vec{x}^\dagger \: (H\vec{y}) =\langle\vec{x},H\vec{y}\rangle. \]
Normal matrices
We defined the set of real normal matrices to be matrices that satisfy $A^TA=AA^T$. For matrices with complex coefficients, the definition of a normal matrix uses the dagger operation instead: $AA^\dagger = A^\dagger A$.
Inner product for complex vectors
The inner product is defined in terms of the matrix product of the vector $\vec{u}^T$ (a row vector) and the column vector $\vec{v}$. We saw that extending the notion of inner product to work with complex vectors, required that we modify the formula for the inner product slightly. The complex inner product is an operation of the form: \[ \langle \cdot, \cdot \rangle : \mathbb{C}^n \times \mathbb{C}^n \to \mathbb{C}. \] The inner product for vectors $\vec{u},\vec{v} \in \mathbb{C}^n$ is defined by \[ \langle \vec{u},\vec{v}\rangle \equiv \sum_{i=1}^n \overline{u_i} v_i \equiv \vec{u}^\dagger \vec{v}. \] The formula is similar, but we use the Hermitian transpose $\dagger$ on the first vector instead of the regular transpose $^T$.
This dagger thing is very important actually. It is an operation that is close to my heart as it pertains to quantum mechanics, Hilbert space, and probabilities computed as dot products. If we want to preserve the connection between length and dot product we need to use the complex conjugation. For column vectors $\vec{u},\vec{v} \in \mathbb{C}^n$, we have: \[ \vec{u}\cdot \vec{v} = \bar{u}_1v_1 + \bar{u}_2v_2 + \bar{u}_3v_3 = \left[\begin{array}{ccc} \bar{u}_{1} & \bar{u}_{2} & \bar{u}_{3} \nl \end{array}\right] \left[\begin{array}{c} v_1 \nl v_2 \nl v_3 \end{array}\right] = \vec{u}^\dagger\vec{v} \]
Using this definition of the dot product, for $\vec{v} \in \mathbb{R}^n$, we get $|\vec{v}| \equiv \sqrt{\vec{v}\cdot\vec{v}} =\sqrt{ |v_1|^2 + |v_2|^2 + |v_3|^2}$, where $|v_i|^2 = \bar{v}_iv_i$ is the magnitude of the complex coefficient $v_i \in \mathbb{C}$.
Length of a complex vector
The inner product of input vectors induces the following norm for complex vectors: \[ \|\vec{v}\| = \sqrt{ \vec{v}^\dagger\vec{v} } = \sqrt{ \sum_{i=1}^n |v_i|^2 } = \sqrt{ \sum_{i=1}^n \overline{v_i}v_i }. \]
Inner product example
TODO: add an example
Complex inner product space
Recall that an inner product space is some vector space $V$ for which we have defined an inner product operation $\langle \mathbf{u} , \mathbf{v} \rangle$ which has (1) a symmetric property, (2) a linearity property and (3) a non negativity property.
linear linearity The complex inner product on a complex vector space is defined as follows: for all $\mathbf{u}, \mathbf{v}, \mathbf{v}_1,\mathbf{v}_2\in V$ and $\alpha,\beta \in\mathbb{C}$.
- $\langle \mathbf{u},\mathbf{v}\rangle =\overline{\langle \mathbf{v},\mathbf{u}\rangle }$,
- $\langle \mathbf{u},\alpha\mathbf{v}_1+\beta\mathbf{v}_2\rangle =\alpha\langle \mathbf{u},\mathbf{v}_1\rangle +\beta\langle \mathbf{u},\mathbf{v}_2\rangle $
- $\langle \mathbf{u},\mathbf{u}\rangle \geq0$ for all $\mathbf{u}\in V$, $\langle \mathbf{u},\mathbf{u}\rangle =0$ if and only if $\mathbf{u}=\mathbf{0}$.
Note that, because of the conjugate symmetric property $\langle \mathbf{u},\mathbf{v}\rangle =\overline{\langle \mathbf{v},\mathbf{u}\rangle }$, the inner product of a vector with itself must be a real number: $\langle \mathbf{u},\mathbf{u}\rangle = \overline{\langle \mathbf{u},\mathbf{u}\rangle } \in\mathbb{R}$.
Example
The Hilbert-Schmidt inner product \[ \langle A, B \rangle_{\textrm{HS}} = \textrm{Tr}\!\left[ A^\dagger B \right]. \]
Hilbert-Schmidt norm \[ ||A||_{\textrm{HS}} \equiv \sqrt{ \langle A, A \rangle } = \sqrt{ \textrm{Tr}\!\left[ A^\dagger A \right] } = \left[ \sum_{i,j=1}^{n} |a_{ij}|^2 \right]^2. \]
Matrix decompositions
The matrix decompositions we leaned about in Section~\ref{sec:matrix_decompositions} can be applied to matrices with complex entries. Below we give a
TODO: check others
Singular value decomposition
The singular value decomposition of an $m \times n$ complex matrix $M$ is a way to write $M$ as a diagonal matrix $\Sigma$ surrounded by matrices of left eigenvectors and right eigenvectors: \[ M = U\Sigma V^\dagger. \] where
TODO: copy details from paper, check for consistency with Section~\ref{sec:matrix_decompositions}
Explanations
Complex eigenvectors
The characteristic polynomial of the rotation matrix $R_\theta$ is $p(\lambda)=(\cos\theta - \lambda)^2+\sin^2\theta=0$. The eigenvalues are $\lambda_1 = \cos\theta + i \sin\theta = e^{i\theta}$ and $\lambda_2 = \cos\theta - i \sin\theta=e^{-i\theta}$. What are its eigenvectors?
Before we go into the calculation I want to show you a useful trick for rewriting $\cos$ and $\sin$ expressions in terms of the complex exponential function. Recall Euler's equation $e^{i\theta} = \cos\theta + i \sin\theta$. Using this equation and the analogous expression for $e^{-i\theta}$, we can obtain the following expressions for $\cos\theta$ and $\sin\theta$: \[ \cos\theta = \frac{1}{2}\left( e^{i\theta} + e^{-i\theta} \right), \qquad \sin\theta = \frac{1}{2i}\left( e^{i\theta} - e^{-i\theta} \right). \] Try calculating the right-hand side in each case to verify the accuracy of each expression. These formulas are useful because they allow us to rewrite expression of the form $e^{i\theta}\cos\phi$ as $e^{i\theta}\frac{1}{2}\left( e^{i\phi} + e^{-i\phi} \right) = \frac{1}{2}\left( e^{i(\theta+\phi)} + e^{i(\theta-\phi)} \right)$.
Let us now see how to calculate the eigenvector $\vec{e}_{1}$ which corresponds to the eigenvalue $\lambda_1 = e^{i\theta}$. The eigenvalue equation for the eigenvalue $\lambda_1 = e^{i\theta}$ is \[ R_\theta \vec{e}_1 = e^{i\theta} \vec{e}_1, \qquad \begin{bmatrix} \cos\theta &-\sin\theta \nl \sin\theta &\cos\theta \end{bmatrix} \begin{bmatrix} \alpha \nl \beta \end{bmatrix} = e^{i\theta} \begin{bmatrix} \alpha \nl \beta \end{bmatrix}. \] We are looking for the coefficients $\alpha, \beta$ of the eigenvector $\vec{e}_1$.
Do you remember how to go about finding these coefficients? Wasn't there some sort of algorithm for finding the eigenvector(s) which correspond to a given eigenvalue? Don't worry if you have forgotten. This is why we are having this review chapter. We will go over the problem in details.
The “finding the eigenvector(s) of $M$ for the eigenvalue $\lambda_1$” problem is solved by calculating the null space of the matrix $(M-\lambda_1 I)$. Indeed, we can rewrite the eigenvalue equation stated above as: \[ (R_\theta - e^{i\theta}I) \vec{e}_1 = 0, \qquad \begin{bmatrix} \cos\theta - e^{i\theta} &-\sin\theta \nl \sin\theta &\cos\theta - e^{i\theta} \end{bmatrix} \begin{bmatrix} \alpha \nl \beta \end{bmatrix} = \begin{bmatrix} 0 \nl 0 \end{bmatrix}, \] in which it is clear the finding-the-eigenvectors procedure corresponds to a null space calculation.
We can now use the trick described above and rewrite the expression which appears twice on the main diagonal of the matrix as: \[ \begin{align*} \cos\theta - e^{i\theta} &= \frac{1}{2}\left(e^{i\theta} + e^{-i\theta} \right) \ - e^{i\theta} \nl & = \frac{1}{2}e^{i\theta} + \frac{1}{2}e^{-i\theta} - e^{i\theta} = \frac{-1}{2}e^{i\theta} + \frac{1}{2}e^{-i\theta} = \frac{-1}{2}\left(e^{i\theta} - e^{-i\theta} \right) \nl &= -i \frac{1}{2i}\left(e^{i\theta} - e^{-i\theta} \right) = -i\sin\theta. \end{align*} \]
TODO: finish steps
Hermitian transpose operation
For matrices with complex entries we define the Hermitian transpose (denoted $\dagger$ by physicists, and $*$ by mathematicians) which, in addition to taking the transpose of a matrix, also takes the complex conjugate of each entry: $a_{ij}^\dagger=\bar{a}_{ji}$.
The Hermitian transpose has the following properties: \[ \begin{align} (A+B)^\dagger &= A^\dagger + B^\dagger \nl (AB)^\dagger &= B^\dagger A^\dagger \nl (ABC)^\dagger &= C^\dagger B^\dagger A^\dagger \nl (A^\dagger)^{-1} &= (A^{-1})^\dagger \end{align} \]
Note that these are the same properties as the regular transpose operation, we just have an extra
Conjugate linearity in the first input
We defined the complex inner product as linear in the second component and conjugate-linear in the first component: \[ \begin{align*} \langle\vec{v}, \alpha\vec{a}+ \beta\vec{b} \rangle &= \alpha\langle\vec{v},\vec{a}\rangle+ \beta\langle\vec{v}, \vec{b}\rangle, \nl \langle\alpha\vec{a}+\beta\vec{b}, \vec{w} \rangle &= \overline{\alpha}\langle\vec{a}, \vec{w}\rangle + \overline{\beta}\langle\vec{b}, \vec{w}\rangle. \end{align*} \] You will want to keep that in mind every time you deal with complex inner products. The inner complex inner product is not symmetric since it requires that the complex conjugation be perfumed on the first input. Remember that $\langle\vec{v}, \vec{w} \rangle \neq \langle \vec{w}, \vec{v}\rangle$, instead we have $\langle\vec{v}, \vec{w} \rangle = \overline{ \langle \vec{w}, \vec{v}\rangle}$.
Note that the choice of complex conjugation in the first entry is a matter of convention. In this text we defined the inner product $\langle \cdot, \cdot \rangle$ with the $\dagger$ operation on the first entry, which is known as the physics convention. Some mathematics texts define the inner product of complex vectors using the complex conjugation on the second entry, which would make the inner product linear in the first entry and conjugate-linear in the second entry. That is fine too. The choice of convention doesn't matter so long as one of the entries is conjugated in order to ensure $\langle \vec{u}, \vec{u} \rangle \in \mathbb{R}$.
Function inner product
In the section on inner product spaces we discussed the notion of the vector space of all functions of a real variable $f:\mathbb{R} \to \mathbb{R}$ and the product between two functions was defined as \[ \langle \mathbf{f},\mathbf{g}\rangle =\int_{-\infty}^\infty f(t) g(t)\; dt. \]
We can Given two complex functions $\mathbf{f}=f(t)$ and $\mathbf{g}=g(t)$: \[ f\colon \mathbb{R} \to \mathbb{C}, \qquad g\colon \mathbb{R} \to \mathbb{C}, \] and define their inner product as follows: \[ \langle \mathbf{f},\mathbf{g}\rangle =\int_{-\infty}^\infty \overline{f(t)} g(t)\; dt \] This formula is the complex valued version of the function inner product. The conjugation on one of the entries in the product ensures that the inner product always results in a real number. The function inner product measures the overlap between $\mathbf{f}$ and $\mathbf{g}$.
Linear algebra over other fields
We can carry out linear algebra calculations over any field. A field is a set of numbers for which an addition, subtraction, multiplication, and division operation are defined. The addition and multiplication operations we define must be and associative and commutative, and multiplication is distributive over addition. Furthermore a field must contain an additive identity element (denoted $0$) and a multiplicative identity element (denoted $1$). The properties of a field are essentially all the properties of the numbers you are familiar.
The focus of our discussion in this section was to show that the linear algebra techniques we learned for manipulating real coefficients work equally well with the complex numbers. This shouldn't be too surprising since, after all, linear algebra manipulations boil down to arithmetic manipulations of the coefficients of vectors and matrices. Since both real numbers and complex numbers can be added, subtracted, multiplied, and divided, we can do linear algebra over both fields.
We can also do linear algebra over finite fields. A finite field is a set $F_q \equiv \{ 0,1,2, \ldots, q-1\}$, where $q$ is prime number or the power of a prime number. All the arithmetic operations in this field are performed modulo the number $q$. If the result of operation is outside the field, you either add or subtract $q$ until the number falls in the range $[0,1,2, \ldots, q-1]$. Consider the finite field $F_5 =\{0,1,2,3,4\}$. To add two numbers in $F_5$ we proceed as follows: $3 + 3 \ \bmod \ 5 = 6 \ \bmod \ 5 = 1 \ \bmod \ 5 = 1$. Similarly for subtraction $1-4 \ \bmod \ 5 = (-3) \ \bmod \ 5 = 2 \ \bmod \ 5 = 2$.
The field of binary numbers $F_2 \equiv \{ 0,1 \}$ of an important finite field which is used in many areas of communication engineering and cryptography. Each data packet that your cellular phone sends over the airwaves is first encoded using an error correcting code. The encoding operation essentially consists of a matrix-vector product where the calculation is carried out over $F_2$.
The field of rational numbers $\mathbb{Q}$ is another example of a field which is often used in practice. Solving systems of equations over using the rational numbers on computers is interesting because the answers obtained are exact—we can avoid many of the numerical accuracy problems associated with floating point arithmetic.
Discussion
The hidden agenda I had in mind is the following: understanding linear algebra over the complex field means you understand quantum mechanics. Quantum mechanics unfolds in a complex inner product space (Hilbert space) and the “mysterious” quantum effects are not mysterious at all: quantum operations are represented as matrices and quantum measurements are projection operators. Thus, if you understood the material in this section, you should be able to pick up any book on quantum mechanics and you will feel right at home!
Exercises
Calculate $(2+5i)-(3+4i)$, $(2+5i)(3+4i)$ and $(2+5i)/(3+4i)$.
further reading