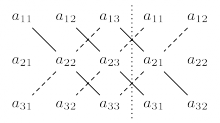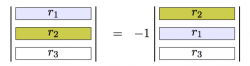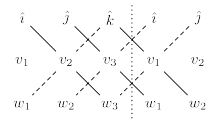The determinant of a matrix, denoted $\det(A)$ or $|A|$, is a particular way to multiply the entries of the matrix and produce a single number. The determinant operation takes a square matrix as input and produces a number as output: \[ \textrm{det}: \mathbb{R}^{n \times n} \to \mathbb{R}. \] We use determinants for all kinds of tasks: to compute areas and volumes, to solve systems of equations, to check whether a matrix is invertible or not, and many other tasks. The determinant calculation can be interpreted in several different ways.

The most intuitive interpretation of the determinant is the geometric one. Consider the geometric shape constructed using the rows of the matrix $A$ as the edges of the shape. The determinant is the “volume” of a this geometric shape. For $2\times 2$ matrices, the determinant corresponds to the area of a parallelogram. For $3 \times 3$ matrices, the determinant corresponds to the volume of a parallelepiped. For dimensions $d>3$ we say the determinant measures a $d$-dimensional hyper-volume of a $d$-dimensional parallele-something.

The determinant of the matrix $A$ is the scale factor associated with the linear transformation $T_A$ that is defined as the matrix-vector product with $A$: $T_A(\vec{x}) \equiv A\vec{x}$. The scale factor of the linear transformation $T_A$ describes how a unit cube (a cube with dimensions $1\times 1 \ldots \times 1$ in the input space will get transformed after going through $T_A$. The volume of the unit cube after passing through $T_A$ is $\det(A)$.

The determinant calculation can be used as a linear independence check for a set of vectors. The determinant of a matrix also tells us if the matrix is invertible or not. If $\det(A)=0$ then $A$ is not invertible. Otherwise, if $\det(A)\neq 0$, then $A$ is invertible.

The determinant has an important connection with the vector cross product and is also used in the definition of the eigenvalue equation. In this section we'll introduce all these aspects of determinants. I encourage you to try to connect the geometric, algebraic, and computational aspects of determinants as you read along. Don't worry if it doesn't all make sense right away—you can always come back and review this section once you have learned more about linear transformations, the geometry of the cross product, and the eigenvalue equation.

For a $2\times2$ matrix, the determinant is \[ \det \!\left( \begin{bmatrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{bmatrix} \right) \equiv \begin{vmatrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{vmatrix} =a_{11}a_{22}-a_{12}a_{21}. \]

The formula for the determinants of larger matrices are defined recursively. For example, the $3 \times 3$ matrix is defined in terms of $2 \times 2$ determinants:

\[ \begin{align*} \ &\!\!\!\!\!\!\!\! \begin{vmatrix} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{vmatrix} = \nl &= a_{11} \begin{vmatrix} a_{22} & a_{23} \nl a_{32} & a_{33} \end{vmatrix} - a_{12} \begin{vmatrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \nl a_{31} & a_{32} \end{vmatrix} \nl &= a_{11}(a_{22}a_{33}-a_{23}a_{32}) - a_{12}(a_{21}a_{33} - a_{23}a_{31}) + a_{13}(a_{21}a_{32} - a_{22}a_{31}) \nl &= a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} -a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} +a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31}. \end{align*} \]

There is a neat computational trick for quickly computing $3 \times 3$ determinants which consists of extending the matrix $A$ into a $3\times 5$ array which contains the cyclic extension of the columns of $A$. The first column of $A$ is copied to in the fourth column of the array and the second column of $A$ is copied into the fifth column.

Computing the determinant is not the task of computing the sum of the three positive diagonals (solid lines) and subtracting the three negative diagonals (dashed lines).

The general formula for the determinant of an $n\times n$ matrix is \[ \det{A} = \sum_{j=1}^n \ (-1)^{1+j}a_{1j}\det(M_{1j}), \] where $M_{ij}$ is called the minor associated with the entry $a_{ij}$. The minor $M_{ij}$ is obtained by removing the $i$th row and the $j$th column of the matrix $A$. Note the “alternating term” $(-1)^{i+j}$ which switches between $1$ and $-1$ for the different terms in the formula.

In the case of $3 \times 3$ matrices, the determinant formula is \[ \begin{align*} \det{A} &= (1)a_{11}\det(M_{11}) + (-1)a_{12}\det(M_{12}) + (1)a_{13}\det(M_{13}) \nl &= a_{11} \begin{vmatrix} a_{22} & a_{23} \nl a_{32} & a_{33} \end{vmatrix} - a_{12} \begin{vmatrix} a_{21} & a_{23} \nl a_{31} & a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \nl a_{31} & a_{32} \end{vmatrix} \end{align*} \]

The deteminant of a $4 \times 4$ matrix is \[ \det{A} = (1)a_{11}\det(M_{11}) + (-1)a_{12}\det(M_{12}) + (1)a_{13}\det(M_{13}) + (-1)a_{14}\det(M_{14}). \]

The general formula we gave above expands the determinant along the first row of the matrix. In fact, the formula for the determinant can be obtained by expanding along any row or column of the matrix. For example, expanding the determinant of a $3\times 3$ matrix along the second column corresponds to the following formula $\det{A} = (-1)a_{12}\det(M_{12}) + (1)a_{22}\det(M_{22}) + (-1)a_{32}\det(M_{32})$. The expand-along-any-row-or-column nature of determinants can be very handy sometimes: if you have to calculate the determinant of a matrix that has one row (or column) with many zero entries, then it makes sense to expand along that row because many of the terms in the formula will be zero. As an extreme case of this, if a matrix contains a row (or column) which consists entirely of zeros, its determinant is zero.

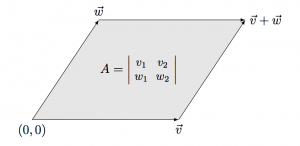
Suppose we are given two vectors $\vec{v} = (v_1, v_2)$ and $\vec{w} = (w_1, w_2)$ in $\mathbb{R}^2$ and we construct a parallelogram with corner points $(0,0), \vec{v}, \vec{w}, and \vec{v}+\vec{w}$.

The area of this parallelogram is equal to the determinant of the matrix which contains $(v_1, v_2)$ and $(w_1, w_2)$ as rows:

\[ \textrm{area} =\left|\begin{array}{cc} v_1 & v_2 \nl w_1 & w_2 \end{array}\right| = v_1w_2 - v_2w_1. \]

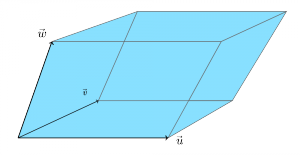
Suppose we are given three vectors $\vec{u} = (u_1, u_2, u_3)$, $\vec{v} = (v_1, v_2, v_3)$, and $\vec{w} = (w_1, w_2,w_3)$ in $\mathbb{R}^3$ and we construct the parallelepiped with corner points: $(0,0,0),\vec{v}, \vec{w}, \vec{v}+\vec{w}$, $\vec{u},\vec{u}+\vec{v}, \vec{u}+\vec{w}, and \vec{u}+\vec{v}+\vec{w}$.

The volume of this parallelepiped equal to the determinant of the matrix which contains the vectors $\vec{u}$, $\vec{v}$, and $\vec{w}$ as rows: \[ \begin{align*} \textrm{volume} &= \left|\begin{array}{ccc} u_1 & u_2 & u_3 \nl v_1 & v_2 & v_3 \nl w_1 & w_2 & w_3 \end{array}\right| \nl &= u_{1}(v_{2}w_{3} - v_{3}w_{2}) - u_{2}(v_{1}w_{3} - v_{3}w_{1}) + u_{3}(v_{1}w_{2} - v_{2}w_{1}). \end{align*} \]

The calculation of the area of a parallelogram and the volume of a parallelepiped using determinants can produce positive or negative numbers.

Consider the case of two dimensions. Given two vectors $\vec{v}=(v_1,v_2)$ and $\vec{w}=(w_1,w_2)$, we can construct the following determinant: \[ D \equiv \left|\begin{array}{cc} v_{1} & v_{2} \nl w_{1} & w_{2} \end{array}\right|. \] Let us denote the value of the determinant by $D$. The absolute value of the determinant is equal to the area of the parallelogram constructed by the vectors $\vec{v}$ and $\vec{w}$. The sign of the determinant (positive, negative or zero) tells us information about the relative orientation of the vectors $\vec{v}$ and $\vec{w}$. Let $\theta$ be the measure of the angle from $\vec{v}$ towards $\vec{w}$, then

• If $\theta$ is between $0$ and $\pi$[rad] ($180[^\circ]$),

the determinant will be positive $D>0$.

  This is the case illustrated in {determinant-of-two-vectors} TODO FIX FIG REF.
* If $\theta$ is between 
  $\pi$ ($180[^\circ]$) and $2\pi$[rad] ($360[^\circ]$), 
  the determinant will be negative $D<0$.
* When $\theta=0$ (the vectors  point in the same direction),
  or when $\theta=\pi$ (the vectors point in opposite directions),
  the determinant will be zero, $D=0$. 

The formula for the area of a parallelogram is $A=b\times h$, where $b$ is the length of the base of a parallelogram and $h$ is the height of the parallelogram. In the case of the parallelogram in {determinant-of-two-vectors} TODO FIX FIG REF, the length of the base is $\|\vec{v}\|$ and the height is $\|\vec{w}\|\sin\theta$, where $\theta$ is the measure of the angle between $\vec{v}$ and $\vec{w}$. The geometrical interpretation of the $2\times 2$ determinant is describes by the following formula: \[ D \equiv \left|\begin{array}{cc} v_{1} & v_{2} \nl w_{1} & w_{2} \end{array}\right| \equiv v_1w_2 - v_2w_1 = \|\vec{v}\|\|\vec{w}\|\sin\theta. \] Observe the “height” of the parallelogram is negative when $\theta$ is between $\pi$ and $2\pi$.

Let $A$ and $B$ be two square matrices of the same dimension, then we have the following properties:

• $\det(AB) = \det(A)\det(B) = \det(B)\det(A) = \det(BA)$
• if $\det(A)\neq 0$ then the matrix is invertible, and
  • $\det(A^{-1}) = \frac{1}{\det(A)}$
• $\det\!\left( A^T \right) = \det\!\left( A \right)$.
• $\det(\alpha A) = \alpha^n \det(A)$, for an $n \times n$ matrix $A$.
• $\textrm{det}\!\left( A \right) = \prod_{i=1}^{n} \lambda_i$,

where $\{\lambda_i\} = \textrm{eig}(A)$ are the eigenvalues of $A$.

TODO: More emphasis on detA = 0 or condition

Recall the three row operations that we used to produce the reduced row echelon form of a matrix as part of the Gauss-Jordan elimination procedure:

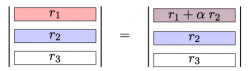
1. Add a multiple of one row to another row.
2. Swap two rows.
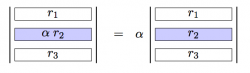
3. Multiply a row by a constant.

The following figures describe the effects of row operations on the determinant of a matrix.

It is useful to think of the effects of the row operations in terms of the geometrical interpretation of the determinant. The first property follows from the fact that parallelograms with different slants have the same area. The second property is a consequence of the fact that we are measuring signed areas and that swapping two rows changes the relative orientation of the vectors. The third property follows from the fact that making one side of the parallelepiped $\alpha$ times longer, increases its volume of the parallelepiped by a factor of $\alpha$.

When the entire $n \times n$ matrix is multiplied by some constant $\alpha$, each of the rows is multiplied by $\alpha$ so the end result on the determinant is $\det(\alpha A) = \alpha^n \det(A)$, since $A$ has $n$ rows.

TODO: mention that isZero property of det is not affected by row operaitons

Apart from the geometric and invertibility-testing applications of determinants described above, determinants are used for many other tasks in linear algebra. We'll discuss some of these below.

We can compute the cross product of two vectors $\vec{v} = (v_1, v_2, v_3)$ and $\vec{w} = (w_1, w_2,w_3)$ in $\mathbb{R}^3$ by computing the determinant of a matrix. We place the vectors $\hat{\imath}$, $hat{\jmath}$, and $\hat{k}$ in the first row of the matrix, then write the vectors $\vec{v}$ and $\vec{w}$ in the second and third rows. After expanding the determinant along the first row, we obtain the cross product: \[ \begin{align*} \vec{v}\times\vec{w} & = \left|\begin{array}{ccc} \hat{\imath} & \hat{\jmath} & \hat{k} \nl v_1 & v_2 & v_3 \nl w_1 & w_2 & w_3 \end{array}\right| \nl & = \hat{\imath} \left|\begin{array}{cc} v_{2} & v_{3} \nl w_{2} & w_{3} \end{array}\right| \ - \hat{\jmath} \left|\begin{array}{cc} v_{1} & v_{3} \nl w_{1} & w_{3} \end{array}\right| \ + \hat{k} \left|\begin{array}{cc} v_{1} & v_{2} \nl w_{1} & w_{2} \end{array}\right| \nl &= (v_2w_3-v_3w_2)\hat{\imath} -(v_1w_3 - v_3w_1)\hat{\jmath} +(v_1w_2-v_2w_1)\hat{k} \nl & = (v_2w_3-v_3w_2,\ v_3w_1 - v_1w_3,\ v_1w_2-v_2w_1). \end{align*} \]

Observe that the anti-linear property of the vector cross product $\vec{v}\times\vec{w} = - \vec{w}\times\vec{v}$ corresponds to the swapping-rows-changes-the-sign property of determinants.

The extended-array trick for computing $3 \times 3$ determinants which we introduced earlier is a very useful approach for computing cross-products by hand.

Using the above correspondence between the cross-product and the determinant, we can write the determinant of a $3\times 3$ matrix in terms of the dot product and cross product: \[ \left|\begin{array}{ccc} u_1 & u_2 & u_3 \nl v_1 & v_2 & v_3 \nl w_1 & w_2 & w_3 \nl \end{array}\right| = \vec{u}\cdot(\vec{v}\times\vec{w}). \]

Cramer's rule is a way to solve systems of linear equations using determinant calculations. Consider the system of equations \[ \begin{align*} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 & = b_1, \nl a_{21}x_1 + a_{22}x_2 + a_{23}x_3 & = b_2, \nl a_{31}x_1 + a_{32}x_2 + a_{33}x_3 & = b_3. \end{align*} \] We are looking for the solution vector $\vec{x}=(x_1,x_2,x_3)$ that satisfies this system of equations.

Let's begin by rewriting the system of equations as an augment matrix: \[ \left[\begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \nl a_{21} & a_{22} & a_{23} & b_2 \nl a_{31} & a_{32} & a_{33} & b_3 \end{array}\right] \ \equiv \ \left[\begin{array}{ccc|c} | & | & | & | \nl \vec{a}_1 \ & \vec{a}_2 \ & \vec{a}_2 \ & \vec{b} \nl | & | & | & | \end{array}\right]. \] In the above equation I used the notation $\vec{a}_j$ to denote the $j^{th}$ column of coefficients in the augmented matrix and $\vec{b}$ is the column of constants.

Cramer's rule requires computing two determinants. To find $x_1$, the first component of the unknown vector $\vec{x}$, we compute the following ratio of determinants: \[ x_1= \frac{ \left|\begin{array}{ccc} | & | & | \nl \vec{b} & \vec{a}_2 & \vec{a}_2 \nl | & | & | \end{array}\right| }{ \left|\begin{array}{ccc} | & | & | \nl \vec{a}_1 & \vec{a}_2 & \vec{a}_2 \nl | & | & | \end{array}\right| } = \frac{ \left|\begin{array}{ccc} b_1 & a_{12} & a_{13} \nl b_2 & a_{22} & a_{23} \nl b_3 & a_{32} & a_{33} \end{array}\right| }{ \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \nl a_{21} & a_{22} & a_{23} \nl a_{31} & a_{32} & a_{33} \end{array}\right| }\;. \] Basically, we replace the column that corresponds to the unknown we want to solve for (in this case the first column) with the vector of constants $\vec{b}$ and compute the determinant.

To find $x_2$ we would compute the ratio of the determinants where $\vec{b}$ replaces the coefficients in the second column, and similarly to find $x_3$ we would replace the third column with $\vec{b}$. Cramer's rule is not a big deal, but it is neat computational trick to know that could come in handy if you ever want to solve for one particular coefficient in the unknown vector $\vec{x}$ and you don't care about the others.

Suppose you are given a set of $n$, $n$-dimensional vectors $\{ \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n \}$ and you asked to check whether these vectors are linearly independent.

We can use the Gauss–Jordan elimination procedure to accomplish this task. Write the vectors $\vec{v}_i$ as the rows of a matrix $M$. Next, use row operations to find the reduced row echelon form (RREF) of the matrix $M$. Row operations do not change the linear independence between the rows of the matrix so we use can the reduced row echelon form of the matrix $M$ to see if the rows are independent.

We can use the determinant test as direct way to check if the vectors are linearly independent. If $\det(M)$ is zero, the vectors that form the rows of $M$ are not linearly independent. On the other hand if $\det(M)\neq 0$, then the rows of $M$ and linearly independent.

The determinant operation is used to define the characteristic polynomial of a matrix and furthermore the determinant of $A$ is appears as the constant term in this polynomial:

\[ \begin{align*} p(\lambda) & \equiv \det( A - \lambda{11} ) \nl & = \begin{vmatrix} a_{11}-\lambda & a_{12} \nl a_{21} & a_{22}-\lambda \end{vmatrix} \nl & = (a_{11}-\lambda)(a_{22}-\lambda) - a_{12}a_{21} \nl & = \lambda^2 - \underbrace{(a_{11}+a_{22})}_{\textrm{Tr}(A)}\lambda + \underbrace{(a_{11}a_{22} - a_{12}a_{21})}_{\det{A}} \end{align*} \]

We don't want to get into a detailed discussion about the properties of the characteristic polynomial $p(\lambda)$ at this point. Still, I wanted to you to know that the characteristic polynomial is defined as the determinant of $A$ with $\lambda$s (the Greek letter lambda) subtracted from the diagonal. We will formally introduce the characteristic polynomial, eigenvalues, and eigenvectors in Section~\ref{eigenvalues and eigenvectors}. TODO check the above reference to eigenvals-section.

\[ A = \left[\begin{array}{cc} 1&2\nl 3&4 \end{array} \right] \qquad \quad B = \left[\begin{array}{cc} 3&4\nl 1&2 \end{array} \right] \]

\[ C = \left[\begin{array}{ccc} 1 & 1 & 1 \nl 1 & 2 & 3 \nl 1 & 2 & 1 \end{array} \right] \qquad \quad D = \left[\begin{array}{ccc} 1 & 2 & 3 \nl 0 & 0 & 0 \nl 1 & 3 & 4 \end{array} \right] \]

Ans: $|A|=-2,\ |B|=2, \ |C|=-2, \ |D|=0$.

Observe that the matrix $B$ can be obtained from the matrix $A$ by swapping the first and second roes. The determinants of $A$ and $B$ have the same absolute value but different sign.

Find the volume of the parallelepiped constructed by the vectors $\vec{u}=(1, 2, 3)$, $\vec{v}= (2,-2,4)$, and $\vec{w}=(2,2,5)$.
Sol: http://bit.ly/181ugMm
Ans: $\textrm{volume}=2$.

[ More information from wikipedia ]
http://en.wikipedia.org/wiki/Determinant
http://en.wikipedia.org/wiki/Minor_(linear_algebra)