Vectors are mathematical objects that have multiple components. The vector $\vec{v}$ is equivalent to a pair of numbers \[ \vec{v} \equiv (v_x, v_y), \] where $v_x$ is the $x$ component of $\vec{v}$ and $v_y$ is the $y$ component.

Just like numbers, you can add vectors \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y), \] subtract them \[ \vec{v}-\vec{w} = (v_x, v_y) - (w_x, w_y) = (v_x-w_x, v_y-w_y), \] and solve all kinds of equations where the unknown variable is a vector.

This might sound like a formidably complicated new development in mathematics, but it is not. Doing arithmetic calculations on vectors is simply doing arithmetic operations on their components.

Thus, if I told you that $\vec{v}=(4,2)$ and $\vec{w}=(3,7)$, then \[ \vec{v}-\vec{w} = (4, 2) - (3, 7) = (1, -5). \]

Vectors are extremely useful in all areas of life. In physics, for example, to describe phenomena in the three-dimensional world we use vectors with three components: $x,y$ and $z$. It is of no use to say that we have a force of 20[N] pushing on a block unless we specify in which direction the force acts. Indeed, both of these vectors have length 20 \[ \vec{F}_1 = (20,0,0), \qquad \vec{F}_2=(0,20,0), \] but one points along the $x$ axis, and the other along the $y$ axis, so they are completely different vectors.

• $\hat{x},\hat{y},\hat{z}$: the usual coordinate system. Every vector is implicitly defined in terms of this coordinate system. When you and I talk about the point $P=(3,4,2)$,

we are really saying “start from the origin, $(0,0,0)$, move 3 units in the $x$ direction, then move 4 units in the $y$ direction, and finally move 2 units in the $z$ direction.” Obviously it is simpler to just say $(3,4,2)$, but keep in mind that these numbers are relative to the coordinate system $\hat{x}\hat{y}\hat{z}$.

• $\hat{\imath},\hat{\jmath},\hat{k}$: is an alternate way of describing the $xyz$-coordinate system

in terms of three unit length vectors:

  \[\hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1).\]
  Any number multiplied by $\hat{\imath}$ corresponds to a vector
  with that number in the first coordinate. For example, $\vec{v}=3\hat{\imath}\equiv(3,0,0)$.
* $\vec{v}=(v_x,v_y,v_z)=v_x\hat{\imath} + v_y \hat{\jmath}+v_z\hat{k}$:
  A //vector// expressed in terms of components and in terms of $\hat{\imath}$, $\hat{\jmath}$ and $\hat{k}$.

In two dimensions there are two equivalent ways to denote vectors:

• In component notation $\vec{v} =(v_x, v_y)$,

which describes the vector as seen from the $x$ axis and the $y$ axis.

• As a length and direction $\vec{v}=\|\vec{v}\|\angle \theta$, where $\|\vec{v}\|$

is the length of the vector and $\theta$ is the angle that the vector

  makes with the $x$ axis. 

The most common types of vectors are $2$-dimensional vectors (like the ones in the Cartesian plane), and $3$-dimensional vectors (directions in 3D space). These kinds of vectors are easier to work with since we can visualize them and draw them in diagrams. Vectors in general can exist in any number of dimensions. An example of a $n$-dimensional vector is \[ \vec{v} = (v_1, v_2, \ldots, v_n) \in \mathbb{R}^n. \]

Addition of vectors is done component wise \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y). \] Vector subtraction works the same way: component by component.

The length of a vector is obtained from Pythagoras theorem. Imagine a triangle with one side of length $v_x$ and the other side of length $v_y$. The length of the vector is equal to the length of the hypotenuse: \[ \|\vec{v}\| = \sqrt{ v_x^2 + v_y^2 }. \]

We can also scale a vector by any number $\alpha \in \mathbb{R}$: \[ \alpha \vec{v} = (\alpha v_x, \alpha v_y), \] where we see that each component gets multiplied by the scaling factor $\alpha$. If $\alpha>1$ the vector will get longer, if $0\leq \alpha <1 $ then the vector will shrink. If $\alpha$ is a negative number, then the resulting vector will point in the opposite direction.

A particularly useful scaling is to divide a vector $\vec{v}$ by its length $\|\vec{v}\|$ to obtain a unit length vector that points in the same direction as $\vec{v}$: \[ \hat{v} = \frac{\vec{v}}{ \|\vec{v}\| }. \] Unit-length vectors (denoted with a hat instead of an arrow) are useful when you want to describe a direction in space.

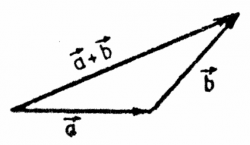You can think of a vectors as arrows, and addition as putting together of vectors head-to-tail as shown in the diagram.

The negative of a vector—a vector multiplied by $\alpha=-1$—is a vector of same length but in the opposite direction. So the graphical subtraction of vectors is also possible.

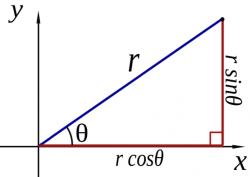We have seen so far how to represent vectors as coefficients. There is also another way of expressing vectors: we can specify their length $||\vec{v}||$ and their orientation—the angle they make with the $x$ axis. For example, the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$. It is useful to represent vectors in the magnitude and direction notation because their physical size becomes easier to see.

There are formulas for converting between the two notations. To convert the length-and-direction vector $\|\vec{r}\|\angle\theta$ to components $(r_x,r_y)$ use: \[ r_x=\|\vec{r}\|\cos\theta, \qquad\qquad r_y=\|\vec{r}\|\sin\theta. \] To convert from component notation $(r_x,r_y)$ to length-and-direction $\|\vec{r}\|\angle\theta$ use \[ r=\|\vec{r}\|=\sqrt{r_x^2+r_y^2}, \qquad\quad \theta=\tan^{-1}\!\left(\frac{r_y}{r_x}\right). \]

Note that the second part of the equation involves the arctangent (or inverse tan) function which by convention returns values between $\pi/2$ and $\mbox{-}\pi/2$ and must be used carefully for vectors that have direction outside of this range.

A vector $\vec{v}=(v_x, v_y, v_z)$ is really a prescription to “go a distance $v_x$ in the $x$-direction, then a distance $v_y$ in the $y$-direction and $v_z$ in the $z$-direction.”

A more explicit notation for denoting vectors is as multiples of the basis vectors $\hat{\imath}, \hat{\jmath}$ and $\hat{k}$, which are unit length vectors pointing in the $x$, $y$ and $z$ direction respectively: \[ \hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1). \]

People who do a lot of numerical calculations with vectors often prefer to use the following alternate notation: \[ v_x \hat{\imath} + v_y\hat{\jmath} + v_z \hat{k} \qquad \Leftrightarrow \qquad \vec{v} \qquad \Leftrightarrow \qquad (v_x, v_y, v_z) . \]

The addition rule looks as follows in the new notation: \[ \underbrace{2\hat{\imath}+ 3\hat{\jmath}}_{\vec{v}} \ \ + \ \ \underbrace{ 5\hat{\imath} - 2\hat{\jmath}}_{\vec{w}} \ = \ \underbrace{ 7\hat{\imath} + 1\hat{\jmath} }_{\vec{v}+\vec{w}}. \] It is the same story repeating: adding $\hat{\imath}$s with $\hat{\imath}$s and $\hat{\jmath}$s with $\hat{\jmath}$s.

You are heading to your physics class after a safety meeting with a friend and looking forward to two hours of amazement and absolute awe of the laws of Mother nature. As it turns out, there is no enlightenment to be had that day because there is going to be an in-class midterm. The first question you have to solve involves a block sliding down an incline. You look at it, draw a little diagram and then wonder how the hell you are going to find the net force acting on the block (this is what they are asking you to find). The three forces acting on the block are $\vec{W} = 30 \angle -90^{\circ} $, $\vec{N} = 200 \angle -290^{\circ} $ and $\vec{F}_f = 50 \angle 60^{\circ} $.

You happen to remember the formula: \[ \sum \vec{F} = \vec{F}_{net} = m\vec{a}. \qquad \text{[ Newton's \ 2nd law ]} \]

You get the feeling that this is the answer to all your troublems. You know that because the keyword “net force” that appeared in the question appears in this equation also.

The net force is simply the sum of all the forces acting on the block: \[ \vec{F}_{net} = \sum \vec{F} = \vec{W} + \vec{N} + \vec{F}_f. \]

All that separates you from the answer is the addition of these vectors. Vectors right. Vectors have components, and there is the whole sin cos thing for decomposing length and direction vectors in terms of their components. But can't you just add them together as arrows too? It is just a sum, of things right, should be simple.

OK, chill. Let's do this one step at a time. The net force must have and $x$-component which, according to the equation, must be equal to the sum of the $x$ components of all the forces: \[ \begin{align*} F_{net,x} & = W_x + N_x + F_{f,x} \nl & = 30\cos(-90^{\circ}) + 200\cos(-290^{\circ})+ 50\cos(60^{\circ}) \nl & = 93.4[\textrm{N}]. \end{align*} \] You find the $y$ component of the net force using the $\sin$ of the angles: \[ \begin{align*} F_{net,y} & = W_y + N_y + F_{f,y} \nl & = 30\sin(-90) + 200\sin(-290)+ 50\sin(60) \nl & = 201.2[\textrm{N}]. \end{align*} \]

Combining the two components of the victor, we get the final answer: \[ \vec{F}_{net} = (F_{net,x},F_{net,y}) =(93.4,201.2) =93.4 \hat{\imath} + 201.2 \hat{\jmath}. \] Bam! Just like that you are done because you overstand them mathematics. Nuh problem. What-a-di next question fi me?

A boat can reach a top speed of 12 knots in calm seas. Instead of being in a calm sea, however, it is trying to sail up the St-Laurence river. The speed of the current is 5 knots.

If the boat goes directly upstream at full throttle 12$\vec{\imath}$, then the speed of the boat relative to the shore will be \[ 12\hat{\imath} - 5 \hat{\imath} = 7\hat{\imath}, \] since we have to “deduct” the speed of the current from the speed of the boat relative to the water.

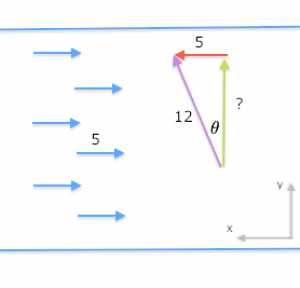If the boat wants to cross the river perpendicular to the current flow, then it can use some of its thrust to counterbalance the current, and the other part to push across. What direction should the boat sail in so that it moves in the across-the-river direction? We are looking for the direction of $\vec{v}$ the boat should take such that, after adding the current component, the boat moves in a straight line between the two banks (the $\hat{\jmath}$ direction).

The geometrical picture is necessary so draw a river and a triangle in the river with the long side perpendicular to the current flow. Make the short side of length $5$ and the hypotenuse of length $12$. We will take the up-the-river component of the speed $\vec{v}$ to be equal to $5\hat{\imath}$ so that it cancels exactly the $-5\hat{\imath}$ flow of the river. We have also labeled the hypotenuse as 12 since this is the ultimate speed that the boat can have relative to the water.

From all of this we can answer the questions like professionals. You want the angle? OK, well we have that $12\sin(\theta)=5$, where $\theta$ is the angle of the boat's course relative to the straight line between the two banks. We can use the inverse-sin function to solve for the angle: \[ \theta = \sin^{-1}\!\left(\frac{5}{12} \right) = 24.62^\circ. \] The accross-the-river component speed can be calculated from $v_y = 12\cos(\theta)$, or from Pythagoras Theorem if you prefer $v_y = \sqrt{ \|\vec{v}\|^2 - v_x^2 } = \sqrt{ 12^2 - 5^2 }=10.91$.

Throughout this section we have used the $x$, $y$ and $z$ axes and described vectors as components along each of these directions. It is very convenient to have perpendicular axes like this, and a set of unit vectors pointing in each of the three directions like the vectors $\{\hat{\imath},\hat{\jmath},\hat{k}\}$.

More generally, we can express vectors in terms of any basis $\{ \hat{e}_1, \hat{e}_2, \hat{e}_3 \}$ for the space of three-dimensional vectors $\mathbb{R}^3$. What is a basis you ask? I am glad you asked, because it is a very important concept.