The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Electric field
We will now discuss a new language for dealing with electrostatic problems.
So far we saw that the electric force, $\vec{F}_e$, exists between two charges $Q$ and $q$, and that the formula is given by Coulomb's law $\vec{F}_e=\frac{k_eQq}{r^2}\hat{r}$. How exactly this force is produced, we don't know. We just know from experience that it exists.
The electric field is an intuitive way to explain how the electric force works. We imagine that the charge $Q$ creates an electric field everywhere in space described by the formula $\vec{E} = \frac{k_eQ}{r^2}\hat{r}$ $[N/C]$. We further say that any charge placed in an electric field will feel an electric force proportional to the strength of the electric field. A charge $q$ placed in an electric field of strength $\vec{E}$ will feel an electric force $\vec{F}_e = q \vec{E}=\frac{k_eQq}{r^2}\hat{r}$.
This entire chapter is about this change of narrative when explaining electrostatic phenomena. There is no new physics. The electric field is just a nice way of thinking in terms of cause and effect. The charge $Q$ caused the electric field $\vec{E}$ and the electric field $\vec{E}$ caused the force $\vec{F}_e$ on the charge $q$.
You have to admit that this new narrative is nicer, than just saying that somehow the electric force “happens”.
Concepts
Recall the concepts from electrostatics:
- $q,Q,q_1,q_2$: The electric charge of some particle or object. It is measured in Coulombs $[C]$.
- $\vec{F}$: Electic force strength and direction, measured in Newtons $[N]$
- $U$: Potential energy (electrical), measured in Joules $[J]=[N*m]$
- $\vec{r}$: The vector-distance between two charges.
- $r \equiv |\vec{r}|$: Distance between two charges, measured in meters $[m]$
- $\hat{r}$: A direction vector (unit length vector) in the $\vec{r}$ direction.
In this section we will introduce a new language to talk about the same ideas.
- $\vec{E}$: Electric field strength and direction, measured in $[V/m]$ or Gauss
- $V$: Electric potential, measured in Volts $[V]$
Formulas
Electric field
The electric field caused by a charge $Q$ at a distance $r$ is given by \[ \vec{E}({r}) = \frac{kQ}{r^2}\hat{r} \qquad \text{[N/C]=[V/m]}. \]
Electric force
When asked to calculate the force between two particles we simply have to multiply the electric field times the charge \[ \vec{F}_e({r}) = q\vec{E}({r}) = q\frac{kQ}{r^2}\hat{r} = \frac{kQq}{r^2}\hat{r} \qquad \text{[N]}. \]
Electric potential
The electric potential $V$ (not to be confused with the electric potential energy $U_e$) of a charge $Q$ is given by \[ V({r})= \frac{kQ}{r} \qquad \text{[V]} \equiv \text{[J/C]} \]
Electric potential energy
The electric potential energy necessary to bring charge $q$ to point where an electric potential $V({r})$ exists is given by \[ U_e({r}) = q V({r}) = q\frac{kQ}{r} = \frac{kQq}{r} \qquad \text{[J]}. \]
Relations between the above four quantities
We can think of the electric field $\vec{E}$ as an electric force per unit charge. Indeed the dimensions of the electric field is $\text{[N/C]}$, so the electric field tells us the amount of force that a test charge of $q=1$[C] would feel at that point. Similarly, the electric potential is $V$ is the electric potential energy per unit charge, as can be seen from the dimensions: $\text{[V]}=\text{[J/C]}$.
In the electrostatics chapter we saw that, \[ U_e({R}) = - W_{done} = - \int_{\infty}^R \vec{F}_e({r}) \cdot d\vec{s}, \qquad \qquad \vec{F}_e({r}) = - \frac{dU({r}) }{dr}. \]
An analogous relation exists between the per unit charge quantities. \[ V({R}) = - \int_{\infty}^R \vec{E}({r}) \cdot d\vec{s}, \qquad \qquad \qquad \qquad \ \ \vec{E}({r}) = - \frac{dV({r}) }{dr}. \]
Explanations
Electric potential
A major issue in understanding the ideas of electromagnetism is to get an intuitive understanding of the concept of electric potential $V$. First, there is the naming problem. There are at least four other terms for the concept: voltage, potential difference, electromotive force and even electromotance! Next, we have the possible source of confusion with the concept of electric potential energy, which doesn't help the situation. Perhaps the biggest problem with the concept of electric potential is that it doesn't exist in the real world: like the electric field to which it is related, it is simply a construct of the mind, which we use to solve problems and do calculations.
Despite the seemingly unsurmountable difficulty of describing the nature of something which doesn't exist, I will persist in this endeavour. I want to give you a proper intuition about voltage, because this concept will play an extremely important role in circuits. While it is true that voltage doesn't exist, energy does exist and energy is just $U=qV$. Voltage, therefore, is electric potential energy per unit charge, and we can talk about the voltage in the language of energy.
Every time you need to think about some electric potential, just imagine what would happen to a unit test charge: q=1[C], and then think in terms of energy. If the potential difference between point (a) and point (b) is $V_{ab}=16$[V], this means that a charge of 1[C] that goes from (a) to (b) will gain 16[J] of energy. If you have some circuit with a 3[V] battery in it, then each Coulomb of charge that is pumped through the battery gains $3$[J] of energy. This is the kind of reasoning we used in the opening example in the beginning of electrostatics, in which we calculated the kinetic energy of the electrons inside an old-school TV.
Field lines
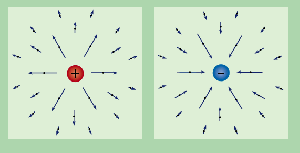 We can visualize the electric field caused by some charge as
electric field lines everywhere around it.
For a positive charge ($Q>0$), the field lines will be leaving it
in all directions towards negative charges or expanding to infinity.
We say that a positive charge is a source of electric field lines
and that a negative charge ($Q<0$) is a sink for electric field lines,
i.e., it will have electric field lines going into it
The diagram on the right illustrates the field lines for two isolated
charges. If these charges were placed next to each other, then
the field lines leaving the (+) charge would all curve around and go into the (-) charge.
We can visualize the electric field caused by some charge as
electric field lines everywhere around it.
For a positive charge ($Q>0$), the field lines will be leaving it
in all directions towards negative charges or expanding to infinity.
We say that a positive charge is a source of electric field lines
and that a negative charge ($Q<0$) is a sink for electric field lines,
i.e., it will have electric field lines going into it
The diagram on the right illustrates the field lines for two isolated
charges. If these charges were placed next to each other, then
the field lines leaving the (+) charge would all curve around and go into the (-) charge.
Links
[ A guided tour of the electie vield lines ]
http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/electrostatics/index.htm
