The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Electricity & magnetism
This course is about all things electrical and magnetic. Every object which has a mass $m$ will be affected by gravity. Similarly, every object which has a charge $q$ will feel the electric force $\vec{F}_e$. Furthermore, if a charge is moving then it will also be affected by the magnetic force $\vec{F}_b$. The formula for the electric force between objects is very similar to the formula for the gravitational force, but the magnetism stuff is totally new. Get read for some mind expansion!
Understanding the laws of electricity and magnetism will make you very powerful. Have you heard of Nikola Tesla? He is a pretty cool guy, and he was a student of electricity and magnetism just like you:
This course requires a good understanding of vector and basic calculus techniques. If you are feel a little rusty on these subjects, I highly recommend that you review the general ideas of vectors and integration before you start reading the material.
Below is a short overview of the topics which we will discuss.
Electricity
We start of with a review of Newton's formula for the gravitation force ($F_g=\frac{GMm}{r^2}$), then learn about electrostatics ($F_e=\frac{kQq}{r^2}$) and discuss three related concepts: the electric potential energy $U_e=\frac{kQq}{r}$, the electric field ($E=\frac{GQ}{r^2}$, $F_e=qE$) and the electric potential ($V=\int E\;dx$, $\vec{E}=\frac{dV}{dx}$).
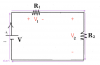
Circuits
Electrostatic interactions between two points in space A and B take on a whole new nature if a charge-conducting wire is used to connect the two points. Charge will be able to flow from one point to the other along the wire. This flow of charge is called electric current. Current is denoted as $I$[A] and measured in Amperes.
The flow of current is a abstract way of describing moving charges. If you understand that well, you can start to visualize stuff and it will be all simple. The current $I$[A] is the “total number of electrons” passing in the wire in one second.
Electric current can be “accumulated” in charge containers called capacitors.
Magnetism
Understanding current is very important because each electron by virtue of its motion through
space is creating a magnetic field around it.
The strength of the magnetic field created by each electron is tiny—we could just ignore it.
However if there is a current of 1[A] flowing through the wire, you know how many electrons that makes? It means there is a flow of $6.242 \times 10^{18}$ electrons per second in that wire. This is something we can't ignore. The magnetic field created by this wire will be quite powerful. You can use the magnetic field to build electromagnets (to lift cars in junk yards, or for magnetic locks—when you are fighting the front doors of McConnell to get into Blues Pub after 9PM—you are fighting with the magnetic force). You can also have two magnets push on each other while turning an engine forward—this is called an electric motor (think electric cars).
But hey, you don't have time to learn all of this now. Read a couple of pages and then go practice on the exams from previous years! If you have any problems come ask here: http://bit.ly/XYOhE1 (only on April 21st, 22nd, and 23rd)