The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Applications of integration
Integration is used in many areas of science.
Applications to mechanics
Calculus was kind of invented for mechanics, so it is not surprising that there will be many links between the two subjects.
Kinematics
Suppose that an object of mass $m$ has a constant force $F_{net}$ applied to it. Newton's second law tells us that the acceleration of the object will be $a =\frac{F_{net}}{m}$.
If the net force is constant, then the acceleration will also be constant. We can find the equations of motion of the object $x(t)$ by integrating $a(t)$ twice since $a(t)=x^{\prime\prime}(t)$.
We start with the acceleration function $a(t) = a$ and integrate once to obtain: \[ v(\tau) = \int_0^\tau a(t) \; dt = a t + v_i, \] where $v_i=v(0)$ is the initial velocity of the object at $t=0$. We obtain the position function by integrating the velocity function and adding the initial position $x_i=x(0)$: \[ x(\tau) = \int v(t) \; dt = \int ( a t + v_i )\; dt = \frac{1}{2}a\tau^2 + v_i\tau + x_i. \]
Non-constant acceleration
If net force on the object is not constant then the acceleration will not be constant either. In general both the force and the mass could change over time so the acceleration will also change over time $a(t)=\frac{F_{net}(t)}{m(t)}$. This sort of problem is usually not covered in the first mechanics course because the establishment assume that it would be too complicated for you to handle.
Now that you know more about integrals, you can learn how to predict the motion of the object with an arbitrary acceleration function $a(t)$. To find the velocity at time $t=\tau$, we need sum up all acceleration felt by the object between $t=0$ and $t=\tau$: \[ v(\tau) = v_i + \int_0^\tau a(t)\; dt. \] The equation of motion $x(t)$ is obtained by integrating the velocity $v(t)$: \[ x(s) = x_i + \int_0^s v(\tau) \; d\tau = \int_0^s \left[ v_i + \int_0^\tau a(t)\; dt \right] \; d\tau. \] The above expression looks quite intense, but in fact it is nothing more complicated than the simple integrals used in UAM. The expression just looks complicated because we have three different variables which are used to represent the time and two consecutive integration steps. Computer games often include a “physics engine” to simulates the motion of objects in the real world using the equation described above.
Gravitational potential
By definition, the integral of a conservative force over some distance $d$ gives you the potential energy of that force. Since gravity $\vec{F}_g$ is a conservative force, we can integrate it to obtain the gravitational potential energy $U_g$.
On the surface of the earth we have $\vec{F}_g = -gm \hat{\jmath}$, where the negative sign means that it acts in the opposite direction to “upwards” as represented by the $\hat{\jmath}$ unit vector, which points in the positive $y$-direciton (towards the sky). In particular the gravitational force as a function of height $\vec{F}_g(y)$ is a constant $\vec{F}_g(y)=\vec{F}_g$. By definition, the gravitational potential energy is the negative of the integral of the force over some distance, say from height $y_i=0$ to height $y_f=h$: \[ \Delta U_{g} = U_{gf} - U_{gi} = - \int_{y_i}^{y_f} \vec{F}_g \cdot \hat{\jmath} \ dy = - \int_{0}^{h} - mg \ dy = \left[ mg y \right]_{0}^{h} = mgh. \]
More generally, i.e., not on the surface of the earth, the gravitational force acting on an object of mass $m$ due to another object of mass $M$ is given by Newton's famous one-over-$r$-squared law: \[ \vec{F}_g = \frac{GMm}{r^2} \hat{r}, \] where $r$ is the distance between the objects and $\hat{r}$ points towards the other object. The general formula for gravitational potential is obtained, again, by taking the integral of the gravitational force over some distance. We will start the object of mass $m$ from a distance $r=r_i$ and move it away until it is infinitely far away. The change in the gravitational potential from $r=r_i$ to $r=\infty$ is: \[ \begin{align} \Delta U_g & = \int_{r=r_i}^{r=\infty} \frac{GMm}{r^2} \ dr \nl & = GMm \int_{r_i}^{\infty} \frac{1}{r^2} \ dr \nl & = GMm \left[ \frac{-1}{r} \right]_{r_i}^{\infty} \nl & = GMm \left[ \frac{-1}{\infty} - \frac{-1}{r_i} \right] \nl & = \frac{GMm}{r_i}. \end{align} \]
Integrals over circular objects
Consider the circular region $S = \{x,y \in \mathbb{R} : x^2 + y^2 \leq R^2\}$. In polar coordinates we would describe this region as $r \leq R$, where it is implicit that the angle $\theta$ varies between $0$ and $2 \pi$. Because this region is two dimensional, in order to integrate it, we would need a double integral.
Even before you learn about double integrals, you can still integrate over the circular region if you brake it up into little pieces of circle $dS$. In fact, this is the whole point of this subsection.
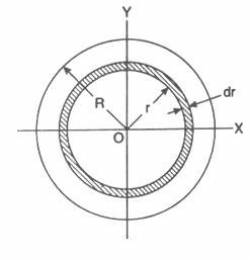 A natural way to break up the circular region is in
terms of thin
circular strips at a different radius and with width $dr$.
Each circular strip will have an area of:
\[
dS = 2\pi r dr,
\]
where $2\pi r$ is the circumference of a circle with radius $r$.
A natural way to break up the circular region is in
terms of thin
circular strips at a different radius and with width $dr$.
Each circular strip will have an area of:
\[
dS = 2\pi r dr,
\]
where $2\pi r$ is the circumference of a circle with radius $r$.
Using this way of braking up the circle, we can check that indeed we get a total area of $\pi R^2$ when we add up all the pieces $dS$: \[ A_{circle} = \int_S \ dS = \int_{r=0}^{r=R} 2\pi r \ dr = 2\pi \int_{0}^{R} r \ dr = \pi R^2. \]
The following sections discuss different extensions of this idea. We use the circular symmetry of various objects to integrate over them by breaking them into thin circular strips of thickness $dr$.
In all circular integrals, you can think of the object as being described by a rotation, or revolution of some function around one of the axes, thus, this kind of integrals are called integrals of revolution.
Total mass of a disk
Suppose you have a disk of total mass $m$ and radius $R$. You can think of the disk as being made of parts, each of mass $\Delta m$, such that when you add them all up you get the total mass: \[ \int_{disk} \Delta m = m. \]
The mass density is defined as the total mass divided by the area of the disk: $\sigma = \frac{m}{A_{disk}} = \frac{m}{\pi R^2}$. The mass density corresponds to the amount of mass per unit area. Let's split the disk into concentric circular strips of width $dr$. The mass contribution of a strip as a function of the radius will be $\Delta m({r}) = \sigma 2\pi r dr $, since the stip at radius $r$ has circumference $2\pi r$ and width $dr$. Let's check that when we add up the pieces we get the total mass: \[ m = \int_0^R \Delta m ({r}) = \int_0^R \sigma 2 \pi r \ dr = 2\pi\sigma \left[ \frac{r^2}{2} \right]_0^R = 2\pi \frac{m}{\pi R^2} \frac{R^2-0}{2} = m. \]
Moment of inertia of a disk
The moment of inertia of an object is a measure of how difficult it is to make it turn. It appears in the rotational version of $F=ma$, in place of the inertial mass $m$: \[ \mathcal{T} = I \alpha. \]
To compute the moment of inertia of an object you need to add up all the mass contributions $\Delta m$ and weight them by $r^2$, where $r$ is the distance of the piece $\Delta m$ from the centre: \[ I = \int_{disk} r^2 \Delta m. \]
We can perform the integral over the whole disk, by adding up the contributions of all the strips: \[ I_{disk} = \int_0^R r^2 \Delta m ({r}) = \int_0^R r^2 \sigma 2 \pi r \ dr = \int_0^R r^2 \frac{m}{\pi R^2} 2 \pi r \ dr = \] \[ \qquad = \frac{2m}{R^2} \int_0^R r^3 \ dr = \frac{2m}{R^2} \left[ \frac{r^4}{4} \right]_0^R = \frac{2m}{R^2} \frac{R^4}{4} = \frac{1}{2}mR^2. \]
Arc lengths of a curve
Given a function $y=f(x)$ and an interval $x \in [x_i, x_f]$, how can you calculate the total length $\ell$ of the curve $f(x)$ between these two points?
If the curve were a straight line, then we would simply take the hypotenuse of the change in $x$ and the change in $y$: $\sqrt{ \text{run}^2 + \text{rise}^2 }=$ $\sqrt{ (x_f-x_i)^2 + (f(x_f)-f(x_i))^2}$.
If the function is not a straight line, however, we have to do this hypotenuse thing on each piece of the curve $d\ell = \sqrt{ dx^2 + dy^2}$, and add up all the contributions as an integral.
The arc length $\ell$ of a curve $y = f(x)$ is given by: \[ \ell=\int d\ell = \int_{x_i}^{x_f} \sqrt{1+\left(\frac{df(x)}{dx}\right)^2} \ dx. \]
Surface of revolution
We can use the above formula for arc-length to ask how much surface area $A$ a solid of revolution with boundary $f(x)$ would have.
Each piece of length $d\ell$, must be multiplied by $2 \pi f(x)$ since it is being rotated around the $x$-axis in a circle of radius $f(x)$. The area of the surface of revolution traced out by $f(x)$ rotated around the $x$-axis is given by the following integral: \[ A= \int 2\pi f(x) d\ell = \int_{x_i}^{x_f} 2\pi f(x)\ \sqrt{1+\left(\frac{df(x)}{dx}\right)^2} \ dx. \]
Volumes of revolution
Next we raise the stakes. We already showed that we can express two dimensional integrals with circular symmetry as one dimensional integrals. Now we move on to three dimensional integrals: integrals over volumes. We will use the circular symmetry to calculate the volume using a single integral again.
Washer method
We can split any volume into a number of disks of thickness $dx$ and with radius proportional to the function $f(x)$.
 The volume $V$ of a solid of traced out by
some $f(x)$ as revolution is:
\[
V
= \int A_{disk}(x) \times h_{disk}
= \int \pi f^2(x) \ dx.
\]
The volume $V$ of a solid of traced out by
some $f(x)$ as revolution is:
\[
V
= \int A_{disk}(x) \times h_{disk}
= \int \pi f^2(x) \ dx.
\]
If we want the volume of revolution in between two functions $g(x)$ and $f(x)$, then we have to imagine splitting the volume into washers: disks of inner radius $f(x)$, outer radius $g(x)$ and thickness $dx$: \[ V = \int A_{washer}(x) \; dx = \int \pi [f^2(x)-g^2(x)] \; dx. \] Each washer consist of a disk of are $\pi f^2(x)$ from which a circular piece of area $\pi g^2(x)$ has been cut out.
Example
Let's calculate the volume of a sphere of radius $r$ using the disk method. Our generating region will be the region bounded by the curve $f(x)=\sqrt{r^2-x^2}$ and the line $y=0$. Our limits of integration will be the $x$-values where the curve intersects the line $y=0$, namely, $x=\pm r$. We have: \[ \begin{align} V_{sphere}&=\int_{-r}^r \pi(r^2-x^2)dx \nl &=\pi(\int_{-r}^r r^2 dx-\int_{-r}^r x^2 dx)\nl &=\pi(r^2 x\bigr|_{-r}^r - \frac{x^3}{3}\biggr|_{-r}^r)\nl &=\pi(r^2 (r-(-r)) - (\frac{r^3}{3}-\frac{(-r)^3}{3})\nl &=\pi(2r^3-\frac{2r^3}{3})\nl &=\pi\frac{6r^3-2r^3}{3}\nl &=\frac{4\pi r^3}{3}. \end{align} \]
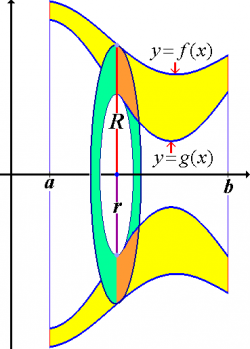
Cylindrical shell method
Alternately we can split any circularly symmetric volume into thin cylindrical shells of thickness $dr$. If the volume has a circular symmetry and is bounded from above by $F(r )$ and from below by $G(r )$, then the integral over the volume will be: \[ \begin{align*} V & = \int C_{shell}(r ) \: h_{shell}(r ) \; dr \nl & = \int_a^b 2\pi r | F(r ) - G(r ) | \; dr, \end{align*} \] where $2\pi r$ is the circumference of each cylindrical shell and $|F(r )-G(r )|$ is its height.
Example
 Calculate the volume of a sphere of radius $R$ using the cylindrical
shell method. We are talking about the region enclosed by the
surface $x^2 + y^2 + z^2 = R^2$.
Calculate the volume of a sphere of radius $R$ using the cylindrical
shell method. We are talking about the region enclosed by the
surface $x^2 + y^2 + z^2 = R^2$.
The shell at radius $r=\sqrt{x^2+y^2}$ will have a roof of $z=F(r)=2\sqrt{R^2-r^2}$, a floor of $z=G(r)=-2\sqrt{R^2-r^2}$, circumference $2\pi r$ and a width of $dr$. The integral will proceed as follows: \[ \begin{align*} V &= \int_0^R 2\pi r | F(r ) - G(r ) | \; dr \nl &= \int_0^R 2 \pi r 2\sqrt{R^2-r^2} \ dr \nl &= - 2\pi \int_{R^2}^0 \sqrt{u} \ du \nl &= - 2\pi \frac{2}{3} u^{3/2}\bigg|_{R^2}^0 \nl &= - 2\pi [ 0 - \frac{2}{3}R^3] \nl &= \frac{4\pi R^3}{3}, \end{align*} \] where in the second line we carried out the substitution $u=R^2-r^2, du = -2r dr$.
Exercises
Exercise 1
Calculate the volume of the cone with radius $R$ and height $h$ which is generated by the revolution of the region bounded by $y=R-\frac{R}{h}x$ and the lines $y=0$ and $x=0$ around the $x$-axis. Answer: $\frac{\pi R^2 h}{3}$.
Exercise 2
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curve $y=x^2$ and the lines $x=1$ and $y=0$ around the $x$-axis. Answer:$\frac{\pi}{5}$.
Exercise 3
Use the washer method to find the volume of a cone containing a central hole formed by revolving the region bounded by $y=R-\frac{R}{h}x$ and the lines $y=r$ and $x=0$ around the $x$-axis. Answer:$\pi h\left(\frac{R^2}{3}-r^2\right)$.
Exercise 4
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curves $y=x^2$ and $y=x^3$ and the lines $x=1$ and $y=0$ around the $x$-axis. Answer: $\frac{2\pi}{35}$.
Exercise 5
Find the volume of a cone with radius $R$ and height $h$ by using the shell method on the appropriate region which, when rotated around the $y$-axis, produces a cone with the given characteristics. Answer:$\frac{\pi r^2 h}{3}$.
Exercise 6
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curve $y=x^2$ and the lines $x=1$ and $y=0$ around the $y$-axis. Answer:$\frac{\pi}{2}$.
