There exists an unspoken rule in mathematics which states that if the word theorem appears in your writing, it has to be followed by the word proof. We therefore have to look into the proof of the Fundamental Theorem of Calculus (FTC). It is not that important that you understand the details of the proof, but I still recommend that you read this section for your general math culture. If you are in a rush though, feel free to skip it.

Before we get to the proof of the FTC, let me first introduce the squeezing principle, which will be used in the proof. Suppose you have three functions $f, \ell$, and $u$, such that: \[ \ell(x) \leq f(x) \leq u(x) \qquad \text{ for all } x. \] We say that $\ell(x)$ is a lower bound on $f(x)$ since its graph is always below that of $f(x)$. Similarly $u(x)$ is an upper bound on $f(x)$. Whatever the value of $f(x)$ is, we know that it is in between that of $\ell(x)$ and $u(x)$.

Suppose that $u(x)$ and $\ell(x)$ both converge to the same limit $L$: \[ \lim_{x\to a} \ell(x) = L, \quad \text{and} \quad \lim_{x\to a} u(x) = L, \] then it must be true that $f(x)$ also converges to the same limit: \[ \lim_{x\to a} f(x) = L. \] This is true because the function $f$ is squeezed between $\ell$ and $u$; it has no other choice than to converge to the same limit.

The formula for the derivative of $F(x)$ looks like this: \[ F'(x) = \lim_{\epsilon \to 0} \frac{ F(x+\epsilon) - F(x) }{ \epsilon }. \] Let us look more closely at the term in the numerator, and express it in terms of the definition of $F(x)$: \[ \begin{align*} {\color{red} F(x+\epsilon) - F(x) } &= \int_a^{x+\epsilon} f(t) \ dt - \int_a^x f(t) \; dt \nl &= {\color{red} \int_x^{x+\epsilon} f(t) \;dt }. \end{align*} \] 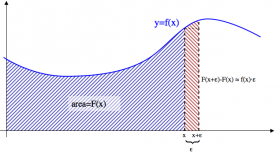Thus the difference of $F(x+\epsilon)$ and $F(x)$ is just the integral of $f(x)$ between $x$ and $x+\epsilon$. The region which corresponds to this difference looks like a long narrow strip of width $\epsilon$ and height varying according to $f(x)$: \[ {\color{red} \int_x^{x+\epsilon} f(t) \ dt} \approx \underbrace{\text{width}}_{\epsilon}\times \underbrace{\text{height}}_?. \]

Let us define the maximum and minimum values of the height of the function $f(x)$ on that interval: \[ M \equiv \max_{t\in[x,x+\epsilon]} f(t), \qquad \qquad m \equiv \min_{t\in[x,x+\epsilon]} f(t). \] By definition, the quantities $m$ and $M$ provide a lower and an upper bound on the quantity we are trying to study: \[ \epsilon m \leq {\color{red} \int_x^{x+\epsilon} f(t) \ dt } \leq \epsilon M. \]

Recall that we said that $f$ is continuous in the theorem statement. If $f$ is continuous then as $\epsilon \to 0$ we will have: \[ \lim_{\epsilon \to 0} f(x+\epsilon ) = f(x). \]

In fact, as $\epsilon \to 0$ all the values of $f$ on the shortening interval $[x, x+\epsilon]$ will approach $f(x)$. In particular, both the minimum value $m$ and the maximum value $M$ will approach $f(x)$: \[ \lim_{\epsilon \to 0} f(x+\epsilon ) = f(x) = \lim_{\epsilon \to 0} m = \lim_{\epsilon \to 0} M. \]

So starting from the inequality, \[ \epsilon m \leq \int_x^{x+\epsilon} f(t) \ dt \leq \epsilon M, \] and taking the limit as $\epsilon \to 0$ we get: \[ \begin{align} \lim_{\epsilon \to 0} \epsilon m \leq & \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt \leq \lim_{\epsilon \to 0} \epsilon M, \nl \lim_{\epsilon \to 0} \epsilon f(x) \leq & \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt \leq \lim_{\epsilon \to 0} \epsilon f(x), \end{align} \]

Using the squeezing principle, we can affirm that \[ \qquad \qquad \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt = \lim_{\epsilon \to 0} \epsilon f(x). \qquad \qquad \qquad \qquad (\dagger) \]

To complete the proof, we substitute this expression into the derivative formula: \[ \begin{align} F'(x) & = \lim_{\epsilon \to 0} \frac{ F(x+\epsilon) - F(x) }{ \epsilon } \nl & = \lim_{\epsilon \to 0} \frac{\int_x^{x+\epsilon} f(t) \ dt }{\epsilon} \qquad \qquad \text{( by the definition of } F) \nl & = \lim_{\epsilon \to 0} \frac{ \epsilon f(t) }{\epsilon} \qquad \qquad \qquad \ \ \ ( \text{ by using equation } (\dagger)\ ) \nl & = f(x) \lim_{\epsilon \to 0} \frac{ \epsilon }{\epsilon} \nl & = f(x). \end{align} \]

We have thus proved that, for all continuous functions $f(x)$, we have: \[ \left(\frac{d}{dx} \circ \int dx \right) f(x) \equiv \frac{d}{dx} \int_a^x f(t) dt = f(x). \]

Integrals look at the “accumulation” of some quantity, whereas derivatives look at the incremental changes. In words, the Fundamental theorem says that the change in the accumulation of $f$ is just $f$ itself. Taking the derivative after taking an integral is as if someone asked you to add up a long list of numbers, and in each step state by how much the sum has changed. You don't need to add or subtract anything, just read out loud all the values in the list.

[ Another proof of the FTC ]
http://archives.math.utk.edu/visual.calculus/4/ftc.9/int1.html
http://archives.math.utk.edu/visual.calculus/4/ftc.9/int2.html