The reason why you need to learn about derivatives is that this skill will allow you to optimize any function. Suppose you have control over the input of the function $f(x)$ and you want to pick the best value of $x$. Best usually means maximum (if the function measures something good like profits) or minimum (if the function describes something bad like costs).

The drug boss for the whole of lower Chicago area has recently had a lot of problems with the police intercepting his people on the street. It is clear that the more drugs he sells the more, money he will make, but if he starts to sell too much, the police arrests start to become more frequent and he loses money.

Fed up with this situation, he decides he needs to find the optimal amount of drugs to put out on the streets: as much as possible, but not too much for the police raids to kick in. So one day he tells his brothers and sisters in crime to leave the room and picks up a pencil and a piece of paper to do some calculus.

If $x$ is the amount of drugs he puts out on the street every day, then the amount of money he makes is given by the function: \[ f(x) = 3000x e^{-0.25x}, \] where the linear part $3000x$ represents his profits if there is no police and the $e^{-0.25x}$ represents the effects of the police stepping up their actions when more drugs is pumped on the street.

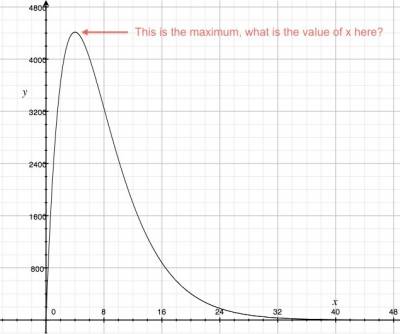
Looking at the function he asks “What is the value of $x$ which will give me the most profits from my criminal dealings?” Stated mathematically, he is asking for \[ \mathop{\text{argmax}}_x \ 3000x e^{-0.25x} \ = \ ?, \] which is read “find the value of the argument $x$ that gives the maximum value of $f(x)$.”

He remembers the steps required to find the maximum of a function from a conversation with a crooked stock trader he met in prison. First he must take the derivative of the function. Because the function is a product of two functions, he has to use the product rule $(fg)' = f'g+fg'$. When he takes the derivative of $f(x)$ he gets: \[ f'(x) = 3000e^{-0.25x} + 3000x(-0.25)e^{-0.25x}. \]

Whenever $f'(x)=0$ this means the function $f(x)$ has zero slope. A maximum is just the kind of place where there is zero slope: think of the peak of a mountain that has steep slopes to the left and to right, but right at the peak it is momentarily horizontal.

So when is the derivative zero? \[ f'(x) = 3000e^{-0.25x} + 3000x(-0.25)e^{-0.25x} = 0. \] We can factor out the $3000$ and the exponential function to get \[ 3000e^{-0.25x}( 1 -0.25x) = 0. \] Now $3000\neq0$ and the exponential function $e^{-0.25x}$ is never equal to zero either so it must be the term in the bracket which is equal to zero: \[ (1 -0.25x) = 0, \] or $x=4$. The slope of $f(x)$ is equal to zero when $x=4$. This correspond to the peak of the curve.

Right then and there the crime boss called his posse back into the room and proudly announced that from now on his organization will put out exactly four kilograms of drugs on the street per day.
“Boss, how much will we make per day if we sell four kilograms?”, asks one of the gangsters in sweatpants.
“We will make the maximum possible!”, replies the boss.
“Yes I know Boss, but how much money is the maximum?”
The dude in sweatpants is asking a good question. It is one thing to know where the maximum occurs and it is another to know the value of the function at this point. He is asking the following mathematical question: \[ \max_x \ 3000x e^{-0.25x} \ = \ ?. \] Since we already know the value $x^*=4$ where the maximum occurs, we simply have to plug it into the function $f(x)$ to get: \[ \max_x f(x) = f(4) = 3000(4)e^{-0.25(4)} = \frac{12000}{e} \approx 4414.55. \] After that conversation, everyone, including the boss, started to question their choice of occupation in life. Is crime really worth it when you do the numbers?

As you may know, the system is obsessed with this whole optimization thing. Optimize to make more profits, optimize to minimize costs, optimize stealing of natural resources from Third World countries, optimize anything that moves basically. Therefore, the system wants you, the young and powerful generation of the future, to learn this important skill and become faithful employees in the corporations. They want you to know so that you can help them optimize things, so that the whole enterprise will continue to run smoothly.

Mathematics makes no value judgments about what should and should not be optimized; this part is up to you. If, like me, you don't want to use optimization for system shit, you can use calculus for science. It doesn't matter whether it will be physics or medicine or building your own business, it is all good. Just stay away from the system. Please do this for me.