The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Quick guide to vectors
Vectors
Vectors are mathematical objects that have multiple components. The vector $\vec{v}$ is equivalent to a pair of numbers \[ \vec{v} \equiv (v_x, v_y), \] where $v_x$ is the $x$ component of $\vec{v}$ and $v_y$ is the $y$ component.
Just like numbers, you can add vectors \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y), \] subtract them \[ \vec{v}-\vec{w} = (v_x, v_y) - (w_x, w_y) = (v_x-w_x, v_y-w_y), \] and solve all kinds of equations where the unknown variable is a vector.
This might sound like a formidably complicated new development in mathematics, but it is not. Doing arithmetic calculations on vectors is simply doing arithmetic operations on their components.
Thus, if I told you that $\vec{v}=(4,2)$ and $\vec{w}=(3,7)$, then \[ \vec{v}-\vec{w} = (4, 2) - (3, 7) = (1, -5). \]
Vectors are extremely useful in all areas of life. In physics, for example, to describe phenomena in the three-dimensional world we use vectors with three components: $x,y$ and $z$. It is of no use to say that we have a force of 20[N] pushing on a block unless we specify in which direction the force acts. Indeed, both of these vectors have length 20 \[ \vec{F}_1 = (20,0,0), \qquad \vec{F}_2=(0,20,0), \] but one points along the $x$ axis, and the other along the $y$ axis, so they are completely different vectors.
Definitions
- $\hat{x},\hat{y},\hat{z}$: the usual coordinate system. Every vector is implicitly defined in terms of this coordinate system. When you and I talk about the point $P=(3,4,2)$,
we are really saying “start from the origin, $(0,0,0)$, move 3 units in the $x$ direction, then move 4 units in the $y$ direction, and finally move 2 units in the $z$ direction.” Obviously it is simpler to just say $(3,4,2)$, but keep in mind that these numbers are relative to the coordinate system $\hat{x}\hat{y}\hat{z}$.
- $\hat{\imath},\hat{\jmath},\hat{k}$: is an alternate way of describing the $xyz$-coordinate system
in terms of three unit length vectors:
\[\hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1).\]
Any number multiplied by $\hat{\imath}$ corresponds to a vector
with that number in the first coordinate. For example, $\vec{v}=3\hat{\imath}\equiv(3,0,0)$.
* $\vec{v}=(v_x,v_y,v_z)=v_x\hat{\imath} + v_y \hat{\jmath}+v_z\hat{k}$:
A //vector// expressed in terms of components and in terms of $\hat{\imath}$, $\hat{\jmath}$ and $\hat{k}$.
In two dimensions there are two equivalent ways to denote vectors:
- In component notation $\vec{v} =(v_x, v_y)$,
which describes the vector as seen from the $x$ axis and the $y$ axis.
- As a length and direction $\vec{v}=\|\vec{v}\|\angle \theta$, where $\|\vec{v}\|$
is the length of the vector and $\theta$ is the angle that the vector
makes with the $x$ axis.
Vector dimension
The most common types of vectors are $2$-dimensional vectors (like the ones in the Cartesian plane), and $3$-dimensional vectors (directions in 3D space). These kinds of vectors are easier to work with since we can visualize them and draw them in diagrams. Vectors in general can exist in any number of dimensions. An example of a $n$-dimensional vector is \[ \vec{v} = (v_1, v_2, \ldots, v_n) \in \mathbb{R}^n. \]
Vector arithmetic
Addition of vectors is done component wise \[ \vec{v}+\vec{w} = (v_x, v_y) + (w_x, w_y) = (v_x+w_x, v_y+w_y). \] Vector subtraction works the same way: component by component.
The length of a vector is obtained from Pythagoras theorem. Imagine a triangle with one side of length $v_x$ and the other side of length $v_y$. The length of the vector is equal to the length of the hypotenuse: \[ \|\vec{v}\| = \sqrt{ v_x^2 + v_y^2 }. \]
We can also scale a vector by any number $\alpha \in \mathbb{R}$: \[ \alpha \vec{v} = (\alpha v_x, \alpha v_y), \] where we see that each component gets multiplied by the scaling factor $\alpha$. If $\alpha>1$ the vector will get longer, if $0\leq \alpha <1 $ then the vector will shrink. If $\alpha$ is a negative number, then the resulting vector will point in the opposite direction.
A particularly useful scaling is to divide a vector $\vec{v}$ by its length $\|\vec{v}\|$ to obtain a unit length vector that points in the same direction as $\vec{v}$: \[ \hat{v} = \frac{\vec{v}}{ \|\vec{v}\| }. \] Unit-length vectors (denoted with a hat instead of an arrow) are useful when you want to describe a direction in space.
Vector geometry
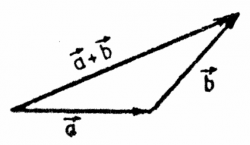 You can think of a vectors as arrows, and addition
as putting together of vectors head-to-tail
as shown in the diagram.
You can think of a vectors as arrows, and addition
as putting together of vectors head-to-tail
as shown in the diagram.
The negative of a vector—a vector multiplied by $\alpha=-1$—is a vector of same length but in the opposite direction. So the graphical subtraction of vectors is also possible.
Length and direction of vectors
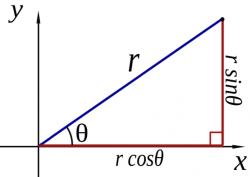 We have seen so far how to represent vectors as coefficients.
There is also another way of expressing vectors: we can
specify their length $||\vec{v}||$ and their orientation—the angle they
make with the $x$ axis.
For example,
the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$.
It is useful to represent vectors in the
magnitude and direction notation because their physical
size becomes easier to see.
We have seen so far how to represent vectors as coefficients.
There is also another way of expressing vectors: we can
specify their length $||\vec{v}||$ and their orientation—the angle they
make with the $x$ axis.
For example,
the vector $(1,1)$ can also be written as $\sqrt{2}\angle45\,^{\circ}$.
It is useful to represent vectors in the
magnitude and direction notation because their physical
size becomes easier to see.
There are formulas for converting between the two notations. To convert the length-and-direction vector $\|\vec{r}\|\angle\theta$ to components $(r_x,r_y)$ use: \[ r_x=\|\vec{r}\|\cos\theta, \qquad\qquad r_y=\|\vec{r}\|\sin\theta. \] To convert from component notation $(r_x,r_y)$ to length-and-direction $\|\vec{r}\|\angle\theta$ use \[ r=\|\vec{r}\|=\sqrt{r_x^2+r_y^2}, \qquad\quad \theta=\tan^{-1}\!\left(\frac{r_y}{r_x}\right). \]
Note that the second part of the equation involves the arctangent (or inverse tan) function which by convention returns values between $\pi/2$ and $\mbox{-}\pi/2$ and must be used carefully for vectors that have direction outside of this range.
Alternate notation
A vector $\vec{v}=(v_x, v_y, v_z)$ is really a prescription to “go a distance $v_x$ in the $x$-direction, then a distance $v_y$ in the $y$-direction and $v_z$ in the $z$-direction.”
A more explicit notation for denoting vectors is as multiples of the basis vectors $\hat{\imath}, \hat{\jmath}$ and $\hat{k}$, which are unit length vectors pointing in the $x$, $y$ and $z$ direction respectively: \[ \hat{\imath} = (1,0,0), \quad \hat{\jmath} = (0,1,0), \quad \hat{k} = (0,0,1). \]
People who do a lot of numerical calculations with vectors often prefer to use the following alternate notation: \[ v_x \hat{\imath} + v_y\hat{\jmath} + v_z \hat{k} \qquad \Leftrightarrow \qquad \vec{v} \qquad \Leftrightarrow \qquad (v_x, v_y, v_z) . \]
The addition rule looks as follows in the new notation: \[ \underbrace{2\hat{\imath}+ 3\hat{\jmath}}_{\vec{v}} \ \ + \ \ \underbrace{ 5\hat{\imath} - 2\hat{\jmath}}_{\vec{w}} \ = \ \underbrace{ 7\hat{\imath} + 1\hat{\jmath} }_{\vec{v}+\vec{w}}. \] It is the same story repeating: adding $\hat{\imath}$s with $\hat{\imath}$s and $\hat{\jmath}$s with $\hat{\jmath}$s.
Examples
Vector addition example
You are heading to your physics class after a safety meeting with a friend and looking forward to two hours of amazement and absolute awe of the laws of Mother nature. As it turns out, there is no enlightenment to be had that day because there is going to be an in-class midterm. The first question you have to solve involves a block sliding down an incline. You look at it, draw a little diagram and then wonder how the hell you are going to find the net force acting on the block (this is what they are asking you to find). The three forces acting on the block are $\vec{W} = 30 \angle -90^{\circ} $, $\vec{N} = 200 \angle -290^{\circ} $ and $\vec{F}_f = 50 \angle 60^{\circ} $.
You happen to remember the formula: \[ \sum \vec{F} = \vec{F}_{net} = m\vec{a}. \qquad \text{[ Newton's \ 2nd law ]} \]
You get the feeling that this is the answer to all your troublems. You know that because the keyword “net force” that appeared in the question appears in this equation also.
The net force is simply the sum of all the forces acting on the block: \[ \vec{F}_{net} = \sum \vec{F} = \vec{W} + \vec{N} + \vec{F}_f. \]
All that separates you from the answer is the addition of these vectors. Vectors right. Vectors have components, and there is the whole sin cos thing for decomposing length and direction vectors in terms of their components. But can't you just add them together as arrows too? It is just a sum, of things right, should be simple.
OK, chill. Let's do this one step at a time. The net force must have and $x$-component which, according to the equation, must be equal to the sum of the $x$ components of all the forces: \[ \begin{align*} F_{net,x} & = W_x + N_x + F_{f,x} \nl & = 30\cos(-90^{\circ}) + 200\cos(-290^{\circ})+ 50\cos(60^{\circ}) \nl & = 93.4[\textrm{N}]. \end{align*} \] You find the $y$ component of the net force using the $\sin$ of the angles: \[ \begin{align*} F_{net,y} & = W_y + N_y + F_{f,y} \nl & = 30\sin(-90) + 200\sin(-290)+ 50\sin(60) \nl & = 201.2[\textrm{N}]. \end{align*} \]
Combining the two components of the victor, we get the final answer: \[ \vec{F}_{net} = (F_{net,x},F_{net,y}) =(93.4,201.2) =93.4 \hat{\imath} + 201.2 \hat{\jmath}. \] Bam! Just like that you are done because you overstand them mathematics. Nuh problem. What-a-di next question fi me?
Relative motion example
A boat can reach a top speed of 12 knots in calm seas. Instead of being in a calm sea, however, it is trying to sail up the St-Laurence river. The speed of the current is 5 knots.
If the boat goes directly upstream at full throttle 12$\vec{\imath}$, then the speed of the boat relative to the shore will be \[ 12\hat{\imath} - 5 \hat{\imath} = 7\hat{\imath}, \] since we have to “deduct” the speed of the current from the speed of the boat relative to the water.
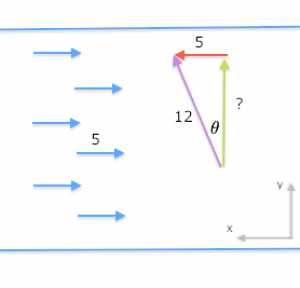 If the boat wants to cross the river perpendicular to
the current flow, then it can use some
of its thrust to counterbalance the current, and the other
part to push across.
What direction should the boat sail in so that it moves
in the across-the-river direction?
We are looking for the direction of $\vec{v}$ the boat
should take such that, after adding the current
component, the boat moves in a straight line
between the two banks (the $\hat{\jmath}$ direction).
If the boat wants to cross the river perpendicular to
the current flow, then it can use some
of its thrust to counterbalance the current, and the other
part to push across.
What direction should the boat sail in so that it moves
in the across-the-river direction?
We are looking for the direction of $\vec{v}$ the boat
should take such that, after adding the current
component, the boat moves in a straight line
between the two banks (the $\hat{\jmath}$ direction).
The geometrical picture is necessary so draw a river and a triangle in the river with the long side perpendicular to the current flow. Make the short side of length $5$ and the hypotenuse of length $12$. We will take the up-the-river component of the speed $\vec{v}$ to be equal to $5\hat{\imath}$ so that it cancels exactly the $-5\hat{\imath}$ flow of the river. We have also labeled the hypotenuse as 12 since this is the ultimate speed that the boat can have relative to the water.
From all of this we can answer the questions like professionals. You want the angle? OK, well we have that $12\sin(\theta)=5$, where $\theta$ is the angle of the boat's course relative to the straight line between the two banks. We can use the inverse-sin function to solve for the angle: \[ \theta = \sin^{-1}\!\left(\frac{5}{12} \right) = 24.62^\circ. \] The accross-the-river component speed can be calculated from $v_y = 12\cos(\theta)$, or from Pythagoras Theorem if you prefer $v_y = \sqrt{ \|\vec{v}\|^2 - v_x^2 } = \sqrt{ 12^2 - 5^2 }=10.91$.
Throughout this section we have used the $x$, $y$ and $z$ axes and described vectors as components along each of these directions. It is very convenient to have perpendicular axes like this, and a set of unit vectors pointing in each of the three directions like the vectors $\{\hat{\imath},\hat{\jmath},\hat{k}\}$.
More generally, we can express vectors in terms of any basis $\{ \hat{e}_1, \hat{e}_2, \hat{e}_3 \}$ for the space of three-dimensional vectors $\mathbb{R}^3$. What is a basis you ask? I am glad you asked, because it is a very important concept.
Basis
One of the most important concepts in the study of vectors is the concept of a basis. In the English language, the word basis carries the meaning of criterion. Thus, in the sentence “The students were selected on the basis of their results in the MEQ exams” means that the numerical results of some stupid test were used in order to classify the worth of the candidates. Sadly, this type of thing happens a lot and people often disregard the complex characteristics of a person and focus on a single criterion. The meaning of basis in mathematics is more holistic. A basis is a set of criteria that collectively capture all the information about an object.
Let's start with a simple example. If one looks at the HTML code behind the average
web-page there will certainly be at least one mention of a colour like
background-color:#336699; which should be read as a triplet of values $(33,66,99)$,
each one describing how much red, green and blue is needed to create the given colour.
The triple $(33,66,99)$ describes the colour “hotmail blue.”
This convention for colour representation is called
the RGB scale or something I would like to call this the RGB basis. A basis is a
set of elements which can be used together to express something more
complicated. In our case we have the R, G and B elements which are pure colours
and when mixed appropriately they can create any colour. Schematically we can
write this as:
\[
{\rm RGB\_color}(33,66,99)=33{\mathbf R}+66{\mathbf G}+99{\mathbf B},
\]
where we are using the coefficients to determine the strength of each
colour component.
To create the colour, we combine its components and
the $+$ operation symbolizes the mixing of the colours.
The reason why we are going into such detail is to illustrate that the
coefficients by themselves do not mean much. In fact they do not mean
anything unless we know the basis that is being used.
Another colour scheme that is commonly used is the cyan, magenta and yellow (CMY) colour basis. We would get a completely different colour if we were to interpret the same triplet of coordinates $(33,66,99)$ with respect to the CMY basis. To express the “hotmail blue” colour in the CMY basis you would need the following coefficients: \[ {\rm Hotmail Blue} = (33,66,99)_{RGB} = (222,189,156)_{CMY}. \]
A basis is a mapping which converts mathematical objects like the triple $(a,b,c)$ into real world ideas like colours. If there is ever an ambiguity about which basis is being used for a given vector, we can indicate the basis as a subscript after the bracket as we did above.
The ijk Basis
Look at the bottom left corner of the room you are in. Let's call “the $x$ axis” the edge between the wall that is to your left and the floor. The right wall and the floor meet at the $y$ axis. Finally, the vertical line where the two walls meet will be called the $z$ axis. This is a right-handed $xyz$ coordinate system. It is used by everyone in math and physics. It has three very nice axes. They are nice because they are orthogonal (perpendicular, i.e., at 90$^\circ$ with each other) and orthoginal is good for your life. We will see why that is shortly.
Now take an object of fixed definite length, say the size of your foot. We will call this the unit length. Measure a unit length along the $x$ axis. This is the $\hat{\imath}$ vector. Repeat the same procedure with the $y$ axis and you will have the $\hat{\jmath}$ vector. Using these two vectors and the property of addition, we can build new vectors. For example, I can describe a vector pointing at 45$^\circ$ with both the $x$ axis and the $y$ axis by the following expression: \[ \vec{v}=1\:\hat{\imath}+ 1\:\hat{\jmath}, \] which means measure one step out on the $x$ axis, one step out on the $y$ axis. Using our two basis vectors we can express any vector in the plane of the floor by a linear combination like \[ \vec{v}_{\mathrm{spoint\ on\ the\ floor}}=a\:\hat{\imath}+b\:\hat{\jmath}. \] The precise mathematical statement that describtes this situation is that the basis formed by the pair $\hat{\imath}$,$\hat{\jmath}$ span the two dimensional space of the floor. We can extend this idea to three dimensions by specifying the coordinates of any point in room as a weighted sum of the three basis vectors: \[ \vec{v}_{\mathrm{point\ in\ the\ room}}=a\:\hat{\imath}+b\:\hat{\jmath}+c\:\hat{k}, \] where $\hat{k}$ is the unit length vector along the $z$ axis.
Choice of basis
In the case where it is clear which coordinate system we are using in a particular situation, we can take the liberty to omit the explicit mention of the basis vectors and simply write $(a,b,c)$ as an ordered triplet which contains only the coefficients. When there is more than one basis in some context (like in problems where you have to change basis, then for every tuple of numbers we should be explicit about which basis it refers to. We can do this by putting a subscript after the tuple. For example, the vector $\vec{v}=a\:\hat{\imath} + b\:\hat{\jmath}+c\:\hat{k}$ in the standard basis is referred to as $(a,b,c)_{\hat{\imath}\hat{\jmath}\hat{k}}$.
Discussion
It is hard to over-emphasize the importance of the notion of a basis. Every time you solve a problem with vectors, you need to be consistent in your choice of basis, because all the numbers and variables in your equations will depend on it. The basis is the bridge between real world vector quantities and their mathematical representation in terms of components.
Vector products
If addition of two vectors $\vec{v}$ and $\vec{w}$ is given by the equation $(v_x+w_x, v_y+w_y,v_z+w_z)$, you might think that the product of two vectors is $(v_xw_x, v_yw_y,v_zw_z)$, but you would be wrong. This way of multiplying vectors is not used in practice. We will define two other useful ways to multiply vectors in this section.
The dot product tells you how similar two vectors are to each other: \[ \vec{v}\cdot\vec{w}\equiv v_xw_x+v_yw_y+v_zw_z \equiv \|\vec{v}\|\|\vec{w}\|\cos(\varphi) \quad \in \mathbb{R}, \] where $\varphi$ is the angle between the two vectors. The factor $\cos(\varphi)$ is largest when the two vectors point in the same direction.
The formula for the cross product is more complicated so I will not show it to you just yet. What is important is that the cross product of two vectors is another vector: \[ \vec{v}\times\vec{w} = \{ \text{ a vector perpendicular to both } \vec{v} \text{ and } \vec{w} \ \} \quad \in \mathbb{R}^3. \] If you take the $\times$ product of one vector that points in the $x$ direction with another vector in the $y$ direction, you will get a vector in the $z$ direction.
Dot product
The dot product between two vectors is given by the formula: \[ \vec{v}\cdot\vec{w}\equiv v_xw_x+v_yw_y+v_zw_z \equiv \|\vec{v}\|\|\vec{w}\|\cos(\varphi) \in \mathbb{R}, \] where $\varphi$ is the angle between the two vectors. This operation is also known as the inner product or scalar product. The name scalar comes from the fact that the result of the dot product is a scalar number: a number that does not change when the basis changes.
The signature for the dot product operation is \[ \cdot : \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}. \] The dot product takes two vectors as inputs and outputs a real number.
The geometric factor $\cos(\varphi)$ depends on the relative orientation of the two vectors:
- If the vectors point in the same direction, then
$\cos(\varphi)=\cos(0^\circ) = 1$ and so
$\vec{v}\cdot\vec{w}=\|\vec{v}\|\|\vec{w}\|$.
* If the vectors are perpendicular to each other,
$\cos(\varphi)=\cos(90^\circ) = 0$ and so
$\vec{v}\cdot\vec{w}=\|\vec{v}\|\|\vec{w}\|(0)=0$.
* If the vectors point in exactly opposite directions, then
$\cos(\varphi)=\cos(180^\circ) = -1$ and so
$\vec{v}\cdot\vec{w}=-\|\vec{v}\|\|\vec{w}\|$.
Cross product
The cross product takes as inputs two vectors and returns another vector: \[ \times : \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}^3. \] The fact that the output of this operation is a vector is why we sometimes refer to the cross product as the vector product.
The cross products of the individual basis elements is defined as follows: \[ \hat{\imath}\times\hat{\jmath} =\hat{k}, \ \ \ \hat{\jmath}\times\hat{k} =\hat{\imath}, \ \ \ \hat{k}\times \hat{\imath}= \hat{\jmath}. \]
The cross product is anti-symmetric in its inputs, which means that swapping the order of the inputs introduces a negative sign in the output: \[ \hat{\jmath}\times \hat{\imath} =-\hat{k}, \ \ \ \hat{k}\times\hat{\jmath} =-\hat{\imath}, \ \ \ \hat{\imath}\times \hat{k} = -\hat{\jmath}. \] I bet you had not seen an anti-symmetric product before. Most products you have seen so far in math are commutative, which means that the order of the inputs doesn't matter. The product of two numbers is commutative $ab=ba$, the dot product is commutative $\vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$, but the cross product of two vectors is non commutative $\hat{\imath}\times \hat{\jmath} \neq \hat{\jmath}\times \hat{\imath}$.
For two arbitrary vectors $\vec{a}=(a_x,a_y,a_z)$ and $\vec{b}=(b_x,b_y,b_z)$, the cross product is calculated as follows: \[ \vec{a}\times\vec{b}=\left( a_yb_z-a_zb_y, \ a_zb_x-a_xb_z, \ a_xb_y-a_yb_x \right). \]
The length of the output of the cross product is proportional to the $\sin$ of the angle between the vectors: \[ \|\vec{a}\times\vec{b}\|=\|\vec{a}\|\|\vec{b}\|\sin(\varphi). \] The direction of the vector $\vec{a}\times\vec{b}$ is perpendicular to both $\vec{a}$ and $\vec{b}$.
Vectors operations
In the chapter on vectors, we described the practical aspects of vectors. Also, people who have studied mechanics should be familiar with the force calculations which involved vectors.
In this section, we will describe vectors more abstractly—as mathematical objects. The first thing to do after one defines a new mathematical object is to specify its properties and the operations that we can perform on them. What can you do with numbers? I know how to add, subtract, multiply and divide numbers. The question, now, is to figure out the equivalent operations applied to vectors.
Formulas
Consider two vectors $\vec{u}=(u_1,u_2,u_3) $ and $\vec{v}=(v_1,v_2,v_3)$, and assume that $\alpha$ is some number. We have the following properties:
\[ \begin{align} \alpha \vec{u} &= (\alpha u_1,\alpha u_2,\alpha u_3) \nl \vec{u} + \vec{v} &= (u_1+v_1,u_2+v_2,u_3+v_3) \nl \vec{u} - \vec{v} &= (u_1-v_1,u_2-v_2,u_3-v_3) \nl ||\vec{u}|| &= \sqrt{u_1^2+u_2^2+u_3^2} \nl \vec{u} \cdot \vec{v} &= u_1v_1+u_2v_2+u_3v_3 \nl \vec{u} \times \vec{v} &= (u_2v_3-u_3v_2,\ u_3v_1-u_1v_3,\ u_1v_2-u_2v_1) \end{align} \]
In the sections that follow we will see what these operations can do for us and what they imply.
Notation
The set of real numbers is denoted $\mathbb{R}$, and vectors consists of $d$ numbers, slapped together in a bracket. The numbers in the bracket are called components. If $d=3$, we will denote the set of vectors as: \[ ( \mathbb{R}, \mathbb{R}, \mathbb{R} ) \equiv \mathbb{R}^3 = \mathbb{V}(3), \] and similarly for more dimensions.
The notation $\mathbb{V}(n)$ for the set of $n$-dimensional vectors is particular to this section. It will be useful here as an encapsulation method, when we want to describe function signatures: what parameters it takes as inputs, and what outputs it produces. This section lists all the operations that take one or more elements of $\mathbb{V}(n)$ as inputs.
Basic operations
Addition and subtraction
Addition and subtraction take two vectors as inputs and produce another vector as output. \[ +: \mathbb{V} \times \mathbb{V} \to \mathbb{V} \]
The addition and subtraction operations are performed component wise: \[ \vec{w}=\vec{u}+\vec{v} \qquad \Leftrightarrow \qquad w_{i} = u_i + v_i, \quad \forall i \in [1,\ldots,d]. \]
Scaling by a constant
The scaling of a vector by a constant is an operation that has the signature: \[ \textrm{scalar-mult}: \mathbb{R} \times \mathbb{V} \ \to \ \mathbb{V}. \] There is no symbol to denote scalar multiplication—we just write the scaling factor in front of the vector and it is implicit that we are multiplying the two.
The scaling factor $\alpha$ multiplying the vector $\vec{u}$ is equivalent to this scaling factor multiplying each component of the vector: \[ \vec{w}=\alpha\vec{u} \qquad \Leftrightarrow \qquad w_{i} = \alpha u_i, \quad \forall i \in [1,\ldots,d]. \] For example, choosing $\alpha=2$ we obtain the vector $\vec{w}=2\vec{u}$ which is two times longer than the vector $\vec{v}$: \[ \vec{w}=(w_1,w_2,w_3) = (2u_1,2u_2,2u_3) = 2(u_1,u_2,u_3) = 2\vec{u}. \]
TODO copy over images from vectors chapter, and import other good passages
Vector multiplication
There are two ways to multiply vectors. The dot product: \[ \cdot: \mathbb{V} \times \mathbb{V}\ \to \mathbb{R}, \] \[ c=\vec{u}\cdot\vec{v} \qquad \Leftrightarrow \qquad c = \sum_{i=1}^d u_iv_i, \] and the cross product: \[ \times: \mathbb{V}(3) \times \mathbb{V}(3) \ \to \mathbb{V}(3) \] \[ \vec{w} = \vec{u} \times \vec{v} \qquad \Leftrightarrow \qquad \begin{array}{rcl} w_1 &=& u_2v_3-u_3v_2, \nl w_2 &=& u_3v_1-u_1v_3, \nl w_3 &=& u_1v_2-u_2v_1. \end{array} \] The dot product is defined for any dimension $d$. So long as the two inputs are of the same length, we can “zip” down their length computing the sum of the products of the corresponding entries.
The dot product is the key tool for dealing with projections, decompositions, and calculating orthogonality. It is also known as the scalar product or the inner product. Intuitively, applying the dot product to two vectors produces a scalar number which carries information about how similar the two vectors are. Orthogonal vectors are not similar at all, since no part of one vector goes in the same direction as the other, so their dot product will be zero. For example: $\hat{\imath} \cdot \hat{\jmath} = 0$. Another notation for the inner product is $\langle u | v \rangle \equiv \vec{u} \cdot \vec{v}$.
The cross product or vector product as it is sometimes called, is an operator which returns a vector that is perpendicular to both of the input vectors. For example: $\hat{\imath} \times \hat{\jmath} = \hat{k}$. Note the cross product is only defined for $3$-dimensional vectors.
Length of a vector
The length of the vector $\vec{u} \in \mathbb{R}^d$ is computed as follows: \[ \|\vec{u}\| = \sqrt{u_1^2+u_2^2+ \cdots + u_d^2 } = \sqrt{ \vec{u} \cdot \vec{u} }. \] The length is number (always greater than zero) which describes the extent of the vector in space. The notion of length is a generalization of Pythagoras' formula for the length hypotenuse of a triangle given the lengths of the two sides (the components).
There exits more mathematically precise ways of talking about the intuitive notion of length. We could specify that we mean Euclidian length of the vector, or the ell-two norm $|\vec{u}|_2 \equiv ||u||$.
The first of these refers to the notion of a Euclidian space, which is the usual flat space that we are used to. Non-Euclidian geometries are possible. For example, the surface of the earth is spherical in shape and so when talking about lengths on the surface of the earth we will need to use spherical length, not Euclidian length. The name ell-two norm refers to the fact that we raise each coefficient to the second degree and then take the square root when computing the length. An example of another norm is the ell-four norm which is defined as the fourth root of the sum of the components raised to the fourth power: $|\vec{u}|_4 \equiv \sqrt[4]{u_1^4+u_2^4+u_3^4}$.
Often times in physics, we denote the length of a vector $\vec{r}$ simply as $r$. Another name for length is magnitude.
Note how the length of a vector can be computed by taking the dot product of the vector with itself and then taking the square root: \[ \|\vec{v}\| = \sqrt{ \vec{v} \cdot \vec{v} }. \]
Unit vector
Given a vector $\vec{v}$ of any length, we can build a unit vector in the same direction by dividing $\vec{v}$ by its length: \[ \hat{v} = \frac{\vec{v}}{ ||\vec{v}|| }. \]
Unit vectors are useful in many contexts. In general, when we want to specify a direction in space, we use a unit vector in that direction.
Projection
If I give you a direction $\hat{d}$ and some vector $\vec{v}$ and ask you how much of $\vec{v}$ is in the $\hat{d}$-direction, then the answer is computed using the dot product: \[ v_d = \hat{d} \cdot \vec{v} \equiv \| \hat{d} \| \|\vec{v} \| \cos\theta = 1\|\vec{v} \| \cos\theta, \] where $\theta$ is the angle between $\vec{v}$ and $\hat{d}$. We used this formula a lot in physics when we were computing the $x$-component of a force $F_x = \|\vec{F}\|\cos\theta$.
We define the projection of a vector $\vec{v}$ in the $\hat{d}$ direction as follows: \[ \Pi_{\hat{d}}(\vec{v}) = v_d \hat{d} = (\hat{d} \cdot \vec{v})\hat{d}. \]
If the direction is specified by a unit vector $\vec{d}$ which is not unit length, then the formula becomes: \[ \Pi_{\vec{d}}(\vec{v}) = \left(\frac{ \vec{d} \cdot \vec{v} }{ \|\vec{d}\|^2 } \right) \vec{d}. \] The division by the length squared is necessary in order to turn the vectors $\vec{d}$ into unit vectors $\hat{d}$ as required but the projection formula: \[ \Pi_{\vec{d}}(\vec{v}) = (\vec{v}\cdot\hat{d}) \:\hat{d} = \left(\vec{v}\cdot \frac{\vec{d}}{\|\vec{d}\|}\right) \frac{\vec{d}}{\|\vec{d}\|} = \left(\frac{\vec{v}\cdot\vec{d}}{\|\vec{d}\|^2}\right)\vec{d}. \]
Discussion
This section was a review of the properties of $d$-dimensional vectors. These are simply ordered tuples (lists) of $d$ coefficients. It is important to think of vectors as mathematical objects and not as coefficients. Sure, all the vector operations boil down to manipulations of the coefficients in the end, but vectors are most useful (and best understood) if you think of them as one thing that has components rather than focussing on the components.
In the next section we will learn about another mathematical object: the matrix, which is nothing more than a two-dimensional array (a table) of numbers. Again, you will see, that matrices are more useful when you think of their properties as mathematical objects rather than focussing on the individual numbers that make up their rows and columns.
Solving systems of linear equations
You know that to solve equations with one unknown like $2x + 4 = 7x$, you have to manipulate both sides of the equation until you isolate the unknown variable on one side. For the above equation we would subtract $2x$ from both sides to obtain: $4 = 5x$, which means that $x=\frac{4}{5}$.
What if you have two equations and two unknowns? For example: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \] Can you find values of $x$ and $y$ that satisfy these equations?
Concepts
- $x,y$: the two unknowns in the equations.
- $eq1, eq2$: a system of two equations that need to be solved simultaneously.
These equations will look like:
\[
\begin{align*}
a_1x + b_1y & = c_1, \nl
a_2x + b_2y & = c_2,
\end{align*}
\]
where the $a$s, $b$s and $c$s are given constants.
Principles
If you have $n$ equations and $n$ unknowns you can solve the equations simultaneously and find the values of the unknowns. There are different tricks which you can use to solve these equations simultaneously. We learn about three such tricks in this section.
Solution techniques
Solving by equating
We want to solve the following system of equations: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \]
We can isolate $x$ in both equations by moving all other variables and constants to the right sides of the equations: \[ \begin{align*} x & = 5 -2y, \nl x & = \frac{1}{3}(21 - 9y) = 7 - 3y. \end{align*} \]
The variable $x$ is still unknown, but we know two facts about it. We know that $x$ is equal to $5 - 2y$ and also that $x$ is equal to $7 - 3y$. So it must be that: \[ 5 - 2y = 7 -3y. \]
We can now solve for $y$ by adding $3y$ to both sides and subtracting $5$ from both sides to get $y = 2$.
We got $y=2$, but what is $x$? That is easy, we can plug in the value of $y$ that we found into any of the above equations. Say I pick the first one: \[ x = 5 - 2y = 5 - 2(2) = 1. \]
We are done, and $x=1,y=2$ is our solution.
Substitution
Let us go back to our set of equations: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \]
Looking at the first equation we can isolate $x$ to obtain: \[ \begin{align*} x & = 5 - 2y, \nl 3x + 9y & = 21. \end{align*} \]
If we substitute the top equation for $x$ into the bottom equation we will obtain: \[ 3(5-2y) + 9y = 21. \] We have just eliminated one of the unknowns by substitution. Let's do some massaging of this equation now. Expanding the bracket we get: \[ 15 - 6y +9y = 21, \] or \[ 3y = 6, \] which means that $y=2$. To get $x$, we use the original substitution $x = (5-2y)$ to get $x = (5-2(2)) = 1$.
Subtraction
There is a third way to solve the equations: \[ \begin{align*} x + 2y & = 5, \nl 3x + 9y & = 21. \end{align*} \]
Observe that we would not change the truth of any equation if we were to multiply it by some constant. For example, we can multiply the first equation by $3$ to obtain an equivalent set of equations: \[ \begin{align*} 3x + 6y & = 15, \nl 3x + 9y & = 21. \end{align*} \]
Why did I pick three as the multiplier? I chose this constant so that the first term (the $x$ term) now has the same coefficient in both equations.
If we subtract two true equations from each other we obtain another true equation. Let's do that. Let's subtract the top equation from the bottom one. We get: \[ 3x - 3x + 9y - 6y = 21 - 15 \quad \Rightarrow \quad 3y = 6. \] Did you see how the $3x$'s cancelled? That is why I originally chose to multiply the first equation by three. Now it is obvious that $y=2$, and substituting back into one of the original equations we have \[ x + 2(2) = 5, \] or moving the $2(2)=4$ to the other side we get $x=1$.
Discussion
These techniques can be extended to as many unknowns as you want. When we get to the chapter on linear algebra, we will learn a much more systematic way of solving this type of equations.
