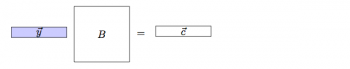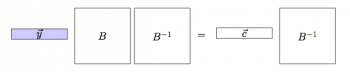Given an unknown function $f()$ which takes as inputs $\mathbb{e}$ objects

The main focus of this book is to highlight the intricate connections between the concepts of

Seeing the similarities and parallels between the concepts is the key to understanding.

There was no way I was going to let learning experience of these beautiful subjects for the next generation.

The first book in the series, “No bullshit guide to math and physics,” covered concepts from high school math, mechanics, and calculus.

The current book on linear algebra is the second book followup

A lot of knowledge buzz awaits you if you choose to follow the path of understanding, instead of trying to memorize a bunch of formulas.

\[ \begin{align*} \textrm{number } x\in \mathbb{R} & \ \Leftrightarrow \ \textrm{vector } \vec{v} \in \mathbb{R}^n, \nl \textrm{function } f:\mathbb{R}\to \mathbb{R} & \ \Leftrightarrow \ \textrm{matrix } A:\mathbb{R}^{n} \to \mathbb{R}^{n}, \nl \textrm{compute } f(x) & \ \Leftrightarrow \ \textrm{compute matrix-vector product } A\vec{x}, \nl \textrm{function composition } g\circ f = g(f(x)) & \ \Leftrightarrow \ \textrm{matrix product } BA = B(A(\vec{x})), \nl \textrm{function inverse } f^{-1} & \ \Leftrightarrow \ \textrm{matrix inverse } A^{-1}. \end{align*} \]

You'll soon see that the matrix-vector product formula which we have been using until now is actually quite useful

where the vector coefficients are the raw data bits you want to transmit and the matrix is called an encoding matrix.

Each isometric transformation in a finite-dimensional complex vector space is unitary.

isometirc?

\[ \sum_{i=0}^{d-1} \overline{a_i} b_i \equiv \langle\vec{a}, \vec{b}) \equiv \vec{a}^\dagger \vec{b} \]

The author himself only discovered the relationship between the $QR$ factorization and the Gram-Schmidt orthogonalization procedure recently.

People love to categorize people. Categorize based on physical appearance, way of speaking, clothes, shoes, accents, etc.

Of particular interest for many applications is the class of symmetric matrices $S$, which satisfy $S=S^T$. All symmetric matrices are normal since $S^TS=S^2=SS^T$.

In this section we learned about the diagonalization procedure for writing a matrix in terms of its eigenvectors and its eigenvalues: \[ A = Q \Lambda Q^{-1}. \] Deep down inside, we see that the matrix $A$ corresponds to a simple diagonal matrix $\Lambda$, but the true nature of the matrix $A$ is only revealed if we write it in the basis of eigenvectors.

and we defined the eigenspace of $\lambda_i$ to be the span of all the eigenvectors associated with the eigenvalue $\lambda_i$.

Using this way of thinking, we can interpret the matrix $Q^{-1}$ on the right as the pre-transformation needed to convert the input vector $\vec{v}$ to the eigenbasis and the multiplication by $Q$ on the left as the post-transformation needed to convert the output vector $\vec{w}$ back to the standard basis.

from invertible_matrix_theorem.txt

[ More discussion on http://www.math.nyu.edu/~neylon/linalgfall04/project1/jja/group7.htm [ temporarily offiline http://tutorial.math.lamar.edu/Classes/LinAlg/FindingInverseMatrices.aspx

Bases for eigenspaces. It is worth mentioning here that the steps used to find the null space of a matrix also have applications for finding bases for what are called the eigenspaces of a matrix. For any $\lambda$, which we will call the eigenvalue, we define the $\lambda$-eigenspace as the null space of the matrix $A$ with the value $\lambda$ subtracted from each of the diagonal entries: \[ E_\lambda(A) = \mathcal{N}(A - \lambda I). \] We will learn more about this in the section on eigenvalues and eigenvectors.

The number of linearly independent columns of a matrix is equal to the number of linearly independent rows and is called the $\textrm{rank}$ of the matrix.

When this is the case, we say the basis spans the vector space $V = \textrm{span}\{ \vec{e}_1, \vec{e}_2, \ldots, \vec{e}_n \}$.

The distance between a line and a plane (assuming they don't intersect).

$ = \lambda^2 - T\lambda + D.$

Consider two row vectors $\vec{v}, \vec{w} \in \mathbb{R}^2$ in two dimensions places written $\vec{v}$ above $\vec{w}$ so that they form a $2\times 2$ matrix. The determinant of that matrix is equal to the area of

The determinant we can also say check whether the system of equations $A\vec{x}=\vec{b}$ has unique solution.

Define the linear transformation $T_A:\mathbb{R}^2 \to \mathbb{R}^2$ which corresponds to the multiplication by the matrix $A$: \[ T_A(\vec{x}) = \vec{y} \qquad \Leftrightarrow \qquad A\vec{x} = \begin{bmatrix} a_{11} & a_{12} \nl a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} x_1 \nl x_2 \end{bmatrix} = \begin{bmatrix} y_1 \nl y_2 \end{bmatrix} = \vec{y}. \]

A unit square in the input space has corners with coordinates $(0,0)$, $(1,0)$, $(1,1)$, and $(0,1)$. After passing the square through $T_A$ the square will look like a parallelogram with corners $(0,0)$, $(a_{11}, a_{21})$, $(a_{11}+a_{12}, a_{21} +a_{22})$, and $(a_{12}, a_{22})$.

There are two ways to denote the determinant of a matrix $A$: either we write $\det(A)$ or $|A|$. We'll use both these notations interchangeably.

Finally recall that for any invertible matrix A (invertible $\Leftrightarrow \ |A| \neq 0$), there exists an inverse matrix $A^{-1}$ such that the product of $A$ with $A^{-1}$ gives the identity matrix $1$:

Recall that when we write $AB$, what we mean is another matrix in which we put the results of the dot products of the each of the rows of $A$ with each of the columns of $B$.

For completeness, let us also analyze the case when a vector is multiplied by a matrix from the right.

.

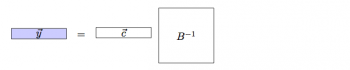
Asked to solve for $\vec{y}$ and assuming $B^{-1}$ exists, we would simply multiply by $B^{-1}$ from the right to obtain:

,

which leads to the final answer:

Rather than go on and on about the theory of vectors and their abstract meaning, which is ALSO very important, I will just give you some condensed examples. This is like a kung fu master beating up some little bad guys in order to impress his students. Once you have seen me slap these vector questions around like 14 year olds, you will not be afraid to take on similar problems of their kind. \[ (1,2) + (5,6)= (6,8) \] TODO: more examples

We can think of vectors as $1\times d$ matrices (row vectors) or as $d \times 1$ matrices (column vectors): \[ \mathbb{V} \qquad \Leftrightarrow \qquad ( \mathbb{R}, \mathbb{R}, \mathbb{R} )^T \equiv \begin{pmatrix} \mathbb{R} \nl \mathbb{R} \nl \mathbb{R} \end{pmatrix}. \] The distinction is largely unimportant when you are dealing with vectors on their own, but it will become important when we study the connections between vectors and matrices. To transform from a row vector to a column vector and vice versa, we use the “transpose” operation $^{T}$.

the cross product is calculated as follows: \[ \vec{a}\times\vec{b}=\left( a_yb_z-a_zb_y, \ a_zb_x-a_xb_z, \ a_xb_y-a_yb_x \right) = \left|\begin{array}{ccc} \hat{\imath}&\hat{\jmath}&\hat{k}\nl a_x&a_y&a_z \nl b_x&b_y&b_z\end{array}\right|. \]

The equation of a plane in $\mathbb{R}^3$ which has normal vector $\vec{n}$ and passes through the point $P=(p_x, p_y, p_z)$ is given by \[ \vec{n}\cdot(x,y,z) - d = 0, \] where $d= \vec{n}\cdot (p_x,p_y,p_z)$.

This subsection contains some facts and definition about the number of basis elements and the dimensions of the space of objects. These are good to know.

For all intents and purposes, when a basis is not specified you should assume that we are using the standard basis: $\{ \hat{\imath}, \hat{\jmath}, \hat{k} \}$ which is orthonormal.

$\vec{u}^T M \vec{v}==\vec{v}^T M \vec{u}$.

  and with $\varphi$ the angle between $\mathbf{u}$ and $\mathbf{v}$ holds: 
  $\langle \mathbf{u},\mathbf{v}    \rangle =\|\mathbf{u}\|\cdot\|\mathbf{v}\|\cos(\varphi)$. 

Let $\{\mathbf{u}_1,...,\mathbf{u}_n\}$ be a set of vectors in an inner product space $V$. Than the {Gramian G} of this set is given by: $G_{ij}=\langle \mathbf{u}_i,\mathbf{u}_j\rangle $.

The set of vectors is independent if and only if $\det(G)=0$.

A set is {orthonormal} if $\langle \mathbf{u}_i,\mathbf{u}_j\rangle =\delta_{ij}$. If $\mathbf{e}_1,\mathbf{e}_2,...$ form an orthonormal row in an infinite-dimensional vector space Bessel’s inequality holds: \[ \|\mathbf{x}\|^2\geq\sum_{i=1}^\infty|\langle \mathbf{e}_i,\mathbf{x}\rangle |^2 \]

The equal sign holds if and only if $\lim\limits_{n\rightarrow\infty}\|\mathbf{x}_n-\mathbf{x}\|=0$. The inner product space $\ell^2$ is defined in $\mathbb{R}^\infty$ by: \[ \ell^2=\left\{\mathbf{u}=(a_1,a_2,...)~|~\sum_{n=1}^\infty|a_n|^2<\infty\right\} \] A space is called a {Hilbert space} if it is $\ell^2$ and if also holds: $\lim\limits_{n\rightarrow\infty}|a_{n+1}-a_n|=0$.

* Cauchy-Schwarz inequality \[ | \langle \mathbf{x} , \mathbf{y} \rangle | \leq \|\mathbf{x} \|\: \| \mathbf{y} \|. \] with equality only if $\mathbf{x} $ and $\mathbf{y} $ are linearly independent. Proof: Observe that $\| \mathbf{x} - t\mathbf{y} \|^2 \geq 0$ for all $t\in \mathbb{R}$

$\cos\theta = 0 \ \Rightarrow \ \theta = \{ \theta = \frac{\pi}{2}+k\pi, k\in \mathbb{Z} \}$.

: <math>A = \begin{pmatrix} 12 & -51 & 4
6 & 167 & -68
-4 & 24 & -41 \end{pmatrix} .</math>

Recall that an orthogonal matrix <math>Q</math> has the property : <math> \begin{matrix} Q^{T}\,Q = I. \end{matrix} </math>

Then, we can calculate <math>Q</math> by means of Gram–Schmidt as follows: : <math> U = \begin{pmatrix} \mathbf u_1 & \mathbf u_2 & \mathbf u_3 \end{pmatrix} = \begin{pmatrix} 12 & -69 & -58/5
6 & 158 & 6/5
-4 & 30 & -33 \end{pmatrix}; </math> : <math> Q = \begin{pmatrix} \frac{\mathbf u_1}{\|\mathbf u_1\|} & \frac{\mathbf u_2}{\|\mathbf u_2\|} & \frac{\mathbf u_3}{\|\mathbf u_3\|} \end{pmatrix} = \begin{pmatrix}

   6/7    &    -69/175   &   -58/175   \\
   3/7    &    158/175   &     6/175   \\
  -2/7    &      6/35    &   -33/35    

\end{pmatrix}. </math>

Thus, we have : <math> \begin{matrix} Q^{T} A = Q^{T}Q\,R = R; \end{matrix} </math> : <math> \begin{matrix} R = Q^{T}A = \end{matrix} \begin{pmatrix}

  14  &  21          &            -14 \\
   0  & 175          &           -70 \\
   0  &   0          &          35

\end{pmatrix}. </math>

\[ \begin{bmatrix}1 & 1 & -2 & 5\\2 & -6 & 4 & 6\\4 & -2 & 0 & 9\end{bmatrix} = \begin{bmatrix}-0.29328253999295 & -0.61822518807978 & -0.729234508617772\\-0.629653584621234 & 0.698883524966229 & -0.339261229592195\\-0.719389821382617 & -0.359665727244755 & 0.594238041138892\end{bmatrix} \begin{bmatrix}13.5989101458191 & 0 & 0 & 0\\0 & 6.16399538618487 & 0 & 0\\0 & 0 & 1.03672741114992 & 0\end{bmatrix} \begin{bmatrix}-0.325772355818374 & 0.362045087268509 & -0.142073830754227 & -0.861748660332062\\-0.106930814484968 & -0.663886753153536 & 0.654118671967409 & -0.346336459074744\\0.934860201755825 & 0.11368155736028 & 0.0978310188155117 & -0.321779425145112\\-0.0920574617898327 & 0.644402232528826 & 0.736459694318659 & 0.184114923579665\end{bmatrix}. \]

If a matrix is positive semidefinite $\lambda_i \geq 0,\ \forall i$. If a matrix is positive definite $\lambda_i > 0,\ \forall i$.

Another good reason to learn about complex vectors is because they are used to represent quantum states. Thus, if you understand how to manipulate

A matrix $A$ is positive semi-definite if $\vec{v}^T A \vec{v} \geq 0$, for all vectors $\vec{v}$. A real matrix $A$ is symmetric if $A^T=A$. A complex matrix $A$ is Hermitian if $A^\dagger=A$.

Let $\lambda_1$ and $\lambda_2$ be the roots of the characteristic polynomial, than also holds: $\Re(\lambda_1)=\Re(\lambda_2)=\cos(\theta)$, and $\lambda_1=\exp(i\theta)$, $\lambda_2=\exp(-i\theta)$. In $\mathbb{R}^3$ holds: $\lambda_1=1$, $\lambda_2=\lambda_3^*=\exp(i\theta)$. Mirrored orthogonal transformations in $\mathbb{R}^3$ are rotational mirrorings: rotations of axis $<\vec{a}_1>$ through angle $\theta$ and mirror plane $<\vec{a}_1>^\perp$. The matrix of such a transformation is given by: \[ \left(\begin{array}{ccc} -1&0&0\nl 0&\cos(\theta)&-\sin(\theta)\nl 0&\sin(\theta)&\cos(\theta) \end{array}\right) \]

A transformation $A$ on $\mathbb{R}^n$ is {symmetric} if $(A\vec{x},\vec{y})=(\vec{x},A\vec{y})$. A matrix $A\in\mathbb{M}(n)$ is symmetric if $A=A^T$. A linear operator is only symmetric if its matrix w.r.t. an arbitrary basis is symmetric. If $A$ is symmetric, than $A^T=A=A^H$ on an orthogonal basis.

Let the different roots of the characteristic polynomial of $A$ be $\beta_i$ with multiplicities $n_i$. Than the dimension of each eigenspace $V_i$ equals $n_i$. These eigenspaces are mutually perpendicular and each vector $\vec{x}\in V$ can be written in exactly one way as \[ \vec{x}=\sum_i\vec{x}_i~~~\mbox{with}~~~\vec{x}_i\in V_i \] This can also be written as: $\vec{x}_i=P_i\vec{x}$ where $P_i$ is a projection on $V_i$. This leads to the {spectral mapping theorem}: let $A$ be a normal transformation in a complex vector space $V$ with dim$(V)=n$. Than: There exist projection transformations $P_i$, $1\leq i\leq p$, with the properties

1. $P_i\cdot P_j=0$ for $i\neq j$,
2. $P_1+...+P_p=I$,
3. ${\rm dim}P_1(V)+...+{\rm dim}P_p(V)=n$ and complex numbers $\alpha_1,...,\alpha_p$ so that $A=\alpha_1P_1+...+\alpha_pP_p$.
4. If $A$ is unitary than holds $|\alpha_i|=1~\forall i$.
5. If $A$ is Hermitian than $\alpha_i\in\mathbb{R}~\forall i$.
6. All Hermitian matrices are normal but have real eigenvalues,

whereas a general normal matrix has no such restriction on its eigenvalues.

1. All normal matrices are diagonalizable, but not all diagonalizable matrices are normal.

A matrix is isometric when it preserves the lengths of vectors \[ \|A\vec{x}\|=\|\vec{x}\|. \]. The name comes from the Greek root iso, which means same and meter which means length.

Isometric matches when acting on vectors preserve the angles between them. If you have two vectors $\vec{x}$ and $\vec{y}$ with an an angle $\theta$ between them, then the angle between $A\vec{x}$ and $A\vec{y}$ will also be $\theta$.

Since the inner product (dot product) between two vectors is proportional to cosine of the angle between them we can restate the angle preserving property as follows \[ A\vec{x} \cdot A\vec{y} = \vec{x} \cdot \vec{y}. \]

The rotation matrices we saw above are a type of isometric transformation, and so are reflections and translations.

For all orthogonal transformations $O$ in $\mathbb{R}^3$ holds that $O(\vec{x})\times O(\vec{y})=O(\vec{x}\times\vec{y})$. $\mathbb{R}^n$ $(n<\infty)$ can be decomposed in invariant subspaces with dimension 1 or 2 for each orthogonal transformation.

Let's multiply this equation by $Q$ on the right \[ AQ = Q \Lambda Q^{-1}Q, \] and now multiply by $Q^{-1}$ on the left \[ Q^{-1}AQ = \underbrace{Q^{-1}Q}_{I} \Lambda \underbrace{Q^{-1}Q}_{I} = \Lambda. \] Thus, we see that the matrix $A$ corresponds to the diagonal matrix $\Lambda$ We see that this which is the final expression If we want to obtain the diagonal matrix $\Lambda$ we can compute: \[ \Lambda = Q^{-1}AQ. \]

Cayley–Hamilton theorem

$p(\lambda) = 0$

$p(A) = 0$

[ Matrix exponential ]
http://en.wikipedia.org/wiki/Matrix_exponential

\[ \Lambda = \begin{bmatrix} 1.61803399 & 0 \nl 0 &-0.61803399 \end{bmatrix} \]

\[ Q = \begin{bmatrix} 0.85065081 & -0.52573111 \nl 0.52573111 & 0.85065081 \end{bmatrix} \]

\[ Q \Lambda Q^T = \begin{bmatrix} 1 & 1 \nl 1 & 0 \nl \end{bmatrix} \]

\[ Q^T A Q = \begin{bmatrix} 1.618\ldots & 0 \nl 0 & -0.6180 \end{bmatrix} = \Lambda \]

i.e., it corresponds to a linear operator: something that takes a vector $(x,y)$ and gives a vector $(x',y')$.

\[ \begin{bmatrix} x' \nl y' \end{bmatrix} = \begin{bmatrix} 1 & 1 \nl 1 & 0 \end{bmatrix} \begin{bmatrix} x \nl y \end{bmatrix} \]

Basis? Nullspace? I hear what you're saying: “Whoa, chill with the theory! Do I really need to know all this stuff?” Yes, actually the whole point of linear algebra is to get you to start imagining these vector spaces: spaces with vectors in them and understanding their properties. We just defined a very important vector space based on the property that $M\vec{v}=0$, for all the vectors $\vec{v}$ that it contains.

Now onto the question why you need to know what a basis is. Without a basis vectors are meaningless. If I tell you that the vectors $\{ \vec{v}, \vec{w} \}$ are a basis for the null space of $M$, then this means that you can write any vector $\vec{n} \in \mathcal{N}(M)$ as a linear combination of the basis vectors: \[ \vec{n} = n_v\vec{v} + n_w\vec{w} = (n_v, n_w)_{\vec{v}\vec{w}}. \] Once we fix the basis, we can compute stuff in terms of the coefficients $n_v, n_w$. At all times though, you have to keep in mind that your computations are with respect to the basis $\vec{v}\vec{w}$, which forms the bridge from the abstract space, to the computation.

When doing calculations, it is really good if your vectors are expressed with respect to an orthonormal basis like the $\hat{\imath}\hat{\jmath}\hat{k}$ basis. The ortho part says that \[ \hat{\imath}\cdot\hat{\jmath}=0, \quad \hat{\imath}\cdot\hat{k}=0, \quad \hat{\jmath}\cdot\hat{k}=0 \] and the normal part says that \[ \hat{\imath}\cdot\hat{\imath}=1, \quad \hat{\jmath}\cdot\hat{\jmath}=1, \quad \hat{k}\cdot\hat{k}=1. \] Starting from any set of linearly independent vectors you can obtain an orthonormal basis by using the Gram-Schmidt orthogonalization algorithm. Look it up if you are taking a linear algebra class.

can be solved with . The eigenvalues follow from this characteristic polynomial.

The eigenvalues $\lambda_i$ are independent of the chosen basis.

Perhaps a more descriptive name would be “the space of vectors that get mapped to the zero vector by M”.

This is actually exactly what happens when we have some function $(x,y=f(x))$ of some function and think of it as a mapping $x \to f(x)$ you would say The inverse of function has the graph $y = f^{-1}(x)$ Therefore the $R_d( plot(f(x),x) ) = plot( f^{-1}(y),y ) $

When the input is $(1,0)^T\equiv\hat{i}$ should come out as $(0,1)^T\equiv\hat{j}$, so the first column will look like \[ M_{R_{inv}}= \left[\begin{array}{cc} 0 & ? \nl 1 & ? \end{array}\right]. \]

Now we also want that when we input $\hat{j}$ to we should get $\hat{i}$ out. This tells us how to fill out the second column: \[ M_{R_{inv}}= \left[\begin{array}{cc} 0 & 1 \nl 1 & 0 \end{array}\right]. \]

Let's verify that that $x$ and $y$ really get swapped by this matrix. I know you all trust me, but in math there should be no things taken on fate. \[ \left[\begin{array}{cc} 0 & 1 \nl 1 & 0 \end{array}\right] \left[\begin{array}{c} v_x \nl v_y \end{array}\right] = \left[\begin{array}{c} v_y \nl v_x \end{array}\right]. \]

The $x$ becomes the $y$ and the $y$ becomes the $x$. reflection you can use if you want to plot the inverse of some function.

ORTHOGONAL For a projection holds: $\vec{x}-P_W(\vec{x})\perp P_W(\vec{x})$ and $P_W(\vec{x})\in W$.

What about reflections through an arbitrary line? Let $l(t) = \vec{r}_0 + t\vec{a}$ be the equation of a line, then \[ R_{\vec{a}}(\vec{x})=2P_{\vec{a}}(\vec{x})-\vec{x} \]

Given the plane $\vec{n}\cdot\vec{x})=d$. \[ R_{\vec{n},d}(\vec{x}) =2P_{\vec{n},d}(\vec{x})-\vec{x} =\vec{x}-2P_{\vec{n}}(\vec{x}) \]

Observe that $P_{\vec{a}}$ satisfies the projector requirement: \[ P_{\vec{a}}\left( P_{\vec{a}}(\vec{x}) \right) = P_{\vec{a}}(\vec{x}), \] since $P_{\vec{a}}(\vec{a}) = \vec{a}$.

When you learn about QM and run into an expression like $|\hat{a}\rangle \langle \hat{a} |$ (the projector onto $\hat{a}$) you will know that they are really talking about $\hat{a}\hat{a}^T$.

Recall that “a functions of a real variable $f$” has the signature: \[ f:\mathbb{R} \to \mathbb{R}, \] and a series $a_n$ has a signature: \[ a:\mathbb{N} \to \mathbb{R}. \] A discrete function is one that measures things that are quantized (how many sheep you have, how many electrons there are in an atom). It has the form: \[ d: \mathbb{R} \to \mathbb{N}. \]

The dot product is important because we use it to define the length of a vector: $|\vec{v}| \equiv \sqrt{\vec{v}\cdot\vec{v}}$.

A matrix that is not invertible is called singular. If you want to decide whether a matrix is invertible or singular, you can choose any one of the properties (i)-(v) and see whether it holds. And if you know that a matrix has one of the five properties (i)-(v), then you are free to use any of the other properties. For example, if in the particular problem you are working on it happens to be easy to show that the determinant of is zero, you could slip over to (i) and say, “Let us choose such that .”

I would like to close this section by highlighting an important property of the abstract definition of a linear transformation $\vec{w} = T(\vec{v})$.

An definition Note also that the equation on the left above does not depend on the basis is really nice, does not depend on There is a one to one equivalence between the set of all linear transformations and the set of all matrices:

\[ \Pi_{P_{xy}}(\:(v_x,v_y,v_z)\:) = (v_x,v_y,0) \qquad \Leftrightarrow \qquad M_{\Pi_{P_{xy}}}\vec{v} = \begin{pmatrix} 1 & 0 & 0 \nl 0 & 1 & 0 \nl 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} v_x \nl v_y \nl v_z \end{pmatrix} = \begin{pmatrix} v_x \nl v_y \nl 0 \end{pmatrix}. \]

TODO: REWRITE THIS change of basis ########### ########################

The linear transformation $A$ from $\mathbb{K}^n\rightarrow\mathbb{K}^m$ is given by ($\mathbb{K}=\mathbb{R}$ of $\mathbb{C}$): \[ \vec{y}=A^{m\times n}\vec{x} \] where a column of $A$ is the image of a base vector in the original. The matrix $A_\alpha^\beta$ transforms a vector given w.r.t. a basis $\alpha$ into a vector w.r.t. a basis $\beta$. It is given by: \[ A_\alpha^\beta=\left(\beta(A\vec{a}_1),...,\beta(A\vec{a}_n)\right) \] where $\beta(\vec{x})$ is the representation of the vector $\vec{x}$ w.r.t. basis $\beta$. The {transformation matrix} $S_\alpha^\beta$ transforms vectors from coordinate system $\alpha$ into coordinate system $\beta$: \[ S_\alpha^\beta:=I_\alpha^\beta=\left(\beta(\vec{a}_1),...,\beta(\vec{a}_n)\right) \] and $S_\alpha^\beta\cdot S_\beta^\alpha=I$ The matrix of a transformation $A$ is than given by: \[ A_\alpha^\beta=\left(A_\alpha^\beta\vec{e}_1,...,A_\alpha^\beta\vec{e}_n\right) \] For the transformation of matrix operators to another coordinate system holds: $A_\alpha^\delta=S_\lambda^\delta A_\beta^\lambda S_\alpha^\beta$, $A_\alpha^\alpha=S_\beta^\alpha A_\beta^\beta S_\alpha^\beta$ and $(AB)_\alpha^\lambda=A_\beta^\lambda B_\alpha^\beta$. Further is $A_\alpha^\beta=S_\alpha^\beta A_\alpha^\alpha$, $A_\beta^\alpha=A_\alpha^\alpha S_\beta^\alpha$. A vector is transformed via $X_\alpha=S_\alpha^\beta X_\beta$.

Thus, we could pick as our basis for $P_{xy}$ any two vectors that are linearly independent. For example: \[ P_{xy}= \textrm{span}\{ (100,1,0), (200,1,0) \}. \] Since $(100,1,0) \neq k (200,1,0)$ for no $k \in \mathbb{R}$ this means that these two vectors are linearly independent and can therefore serve as a basis for $P_{xy}$. For computational reasons however, we prefer to use simple bases, that is ones whose basis vectors are maid up of mainly zeros and a single leading one.

The usual way to get a basis is to start with some set of vectors that span the space and then remove from this set any linear combinations.

Consider the vector subspace $V_3 \subset \mathbb{R}^4$ defined as the span of three vectors $\vec{v}_1$, $\vec{v}_2$ and $\vec{v}_3$: \[ V_3 = \textrm{span}\{ \vec{v}_1, \vec{v}_2, \vec{v}_3 \}. \] in a four-dimensional space $\mathbb{R}^4$, can you give me three vectors $\vec{e}_1, \vec{e}_2, \vec{e}_3 \in \mathbb{R}^4$ which are as orthogonal with a leading one in each direction.

This algorithm is best phrased in term of matrices. Starting from an arbitrary matrix

\[ \left[ \begin{array}{cccc} v_{11} & v_{12} & v_{13} & v_{14} \nl v_{21} & v_{22} & v_{23} & v_{14} \nl v_{31} & v_{32} & v_{33} & v_{34} \end{array} \right] \] give this \[ \left[ \begin{array}{cccc} 1 & 0 & 1/2 & 0 \nl 0 & 1 & -1/3 & 0 \nl 0 & 0 & 0 & 1 \end{array} \right] \]

Consider a systems of linear equations where the constants on the right hand side are all zero: \[ \begin{eqnarray} a_{11}x_1 + a_{12} x_2 & = & 0, \nl a_{21}x_1 + a_{22}x_2 & = & 0. \end{eqnarray} \] Such a system of equations is called homogenous.

In two dimensions homogenous equations correspond to the equation of lines through the origin. The origin is $(0,0)$ is therefore always a solution. The the second equation is redundant ($a_{11}/a_{12} = a_{21}/a_{22}$) then the solution solution is the entire line.

In three dimensions, equation of the form $Ax + By + Cz=0$ correspond to planes through the origin. Again, $(0,0,0)$ is always a solution.

\[ \left\{ \begin{array}{rl} x_1 & = s \nl x_2 & = c_2 - a_2\:t \nl x_3 & = t \end{array}, \quad s \in \mathbb{R}, t \in \mathbb{R}, \right\} = \begin{bmatrix} 0 \nl c_2 \nl 0 \end{bmatrix} + \textrm{span}\!\!\left\{ \begin{bmatrix} 1 \nl 0 \nl 0 \end{bmatrix}, \ \begin{bmatrix} 0 \nl -a_2 \nl 1 \end{bmatrix} \right\} \] space solution space consists

Recall that any linear system of equations can be written in the form $A\vec{x}=\vec{b}$ where $\vec{x}$ are the unknowns you want to solve for, $A$ is some matrix and $\vec{b}$ is a column vector of constants.

In this section we will learn an algorithm for solving such equations using simple row operations performed simultaneously on the matrix $A$ and the vector $\vec{b}$.

Our coal will be to get the matrix into a form where there is a single $1$ in each row, so that we can simply read off the answer by inspection:

\[ \left[ \begin{array}{cccc|c} 1 & 0 & 1/2 & 0 & b_1 \nl 0 & 1 & -1/3 & 0 & b_2 \nl 0 & 0 & 0 & 1 & b_3 \end{array} \right] \]

instead define a convention for the product of two matrices so that we can write instead In fact you might as well skip mentioning This turns out to be a pretty good \[ A\vec{x}=\vec{b}, \] In doing so we will learn of the ways this Of course it will be good to know how to find the inverse right? reduced row echelon form elementary matrices adjoint Solve matrix equations

given a vector space spanned Once we fix the basis, we can further simplify Another problem in math

In other words take any three real numbers and slap a bracket around them and you have a vector.

We will discuss this technique in more details after when we learn about the meaning of row operations, but since this is the section on matrix inverses we need to make a not of this method here and

the subject of the next section.

The general equation of a plane corresponds to an affine function \[ f(x,y) = ax + by + c, \] which is essentially a linear function plus an additive constant. The constant $c$ is equal to $f(0,0)$ – the initial value of the function.

This is really powerful stuff. If you want to compute $ABC\vec{x}_i$ for many $\vec{x}_i$'s, then instead of computing six matrix-times-vector products for each $\vec{x}_i$, you could compute the matrix product up front $M=ABC$, and then apply the equivalent transformation $M$ to each $\vec{x}_i$. You don't have such “pre-computation” power for functions. For general functions $f$, $g$ and $h$, there is not such way to precompute $f\circ g \circ h$. Given a long list of numbers $x_i$, if you are asked to compute $f(g(h(x_i)))$, you will have compute $h$, $g$ and $f$ in turn for each input.

“So what-a-dem linear transformations?” shouts the audience, “Stop beating about the bush with this single variable shit which we know. Let's have it!” Ok, I will tell you dear readers.

When the function has only one input variable, there is only one term $x$ that is linear. So the most general linear function you can write would be \[ f(x) = ax + 0, \] where $a$ is some constant (previously called $m$) and $b$, the initial value, is set to $0$. This is necessary in order to satisfy $f( x + y ) = f(x) + f(y)$. If $f$ contained an additive constant term, then it would appear once on the left-hand side, and twice on the right-hand side. Thus, the equality can't be true unless $b=0$.

Consider this weird function of two variables: \[ f(x,y) = \frac{1}{xy^2} + \frac{1}{xy} + \frac{1}{x} + 1 + {\mathbf x} + {\mathbf y} + xy + x^2 + y^2 + xy^7. \] The linear terms are shown in bold again. Note that $xy$ is not in a linear term despite the fact that technically it is “linear” in both $x$ and $y$.

think of equations as a row of numbers. \[ f = [a \ b ] \] The first column represents the number that multiplies $x$ in the formula for $f(x,y)$, the second number is the number multiplying $y$ and the third is the constant.

This is why they are making you do all those excruciating operations on those matrices.

Fact Sets of linear equations
$f_1(x,y)=a_1x+b_1y$
$f_2(x,y)=a_2x+b_2y$
correspond to matrices of the form

$ \left[ \array{ f_1(x,y) \nl f_2(x,y) } \right] \ = \ \left[\array{ a_1 & b_1 \nl a_2 & b_2 } \right] \left[\array{ x \nl y } \right] $

Minstream textbooks are like organized tour guides that take try to cater to the masses. but no matter where you go you will find solid steps build by really smart people.

Below to paragraphs are trying to say “you will see – the smart people who came before us and figure things out, figured out how to think about these complicated concepts – how to make them simple.

The fundamental thing I want you to realize is that everytime something compicated arises, you are in good company.

This book is about complicated things. I am not going to lie to you and say it will be easy. I promise simple not necessarily easy. Mathematics is like a stairway up an ancient mountain. There are many heights to see and many steps to climb. I am your personal guide to the mountain. We will take a fairly intensive route up.

The MATLAB command diag can be used to convert a vector into a diagonal matrix or alternatively to extract the entries on the diagonal of a matrix.

For each linear transformation $A$ in a complex vector space $V$ there exists exactly one linear transformation $B$ so that $(A\vec{x},\vec{y})=(\vec{x},B\vec{y})$. This $B$ is called the {adjungated transformation} of $A$. Notation: $B=A^*$. The following holds: $(CD)^*=D^*C^*$. $A^*=A^{-1}$ if $A$ is unitary and $A^*=A$ if $A$ is Hermitian. {Definition}:

We are staying abstract here because we want to discuss the math of vector spaces in general, but if you want to think about something concrete you should think of the field as being the set of real numbers $F=\mathbb{R}$ and the vector space $V$ being the set of $3$-vectors, i.e., the vector space will be the ordinary 3D space around you $\mathbb{R}^3$.

nice way to word it:

Even though we are going from , the column basis could be different from the row basis. Fortunately for our purposes, we are not going to consider what basis is appropriate to choose. All that matters is that fixing a basis, the matrix representation of a linear map is unique, and so we may interchange the notation freely. Even so, the truly interesting things about matrices are those properties which are true no matter which basis we prefer to use.

2. basis is important $\hat{N}$ and $\hat{E}$

  could have $\hat{W}$ and $\hat{N}$.
  also magnitude orientation...
  so same POINT different instructions depending on the basis

Route A: 3km N, 4km E Route B: 4km E, 3km N Route C: 5km at 37 degrees North of East (on standard compas degrees, N=0 degrees, so this will be 90-37 = 53 degrees)

Together these instructions describe a displacement tell us how to go from the point

vectors = nice way to specify directions

Another really useful basis is the eigen-basis of a matrix $A$. The set of eigenvectors $\{\vec{e}_i\}$ of $A$ satisfy: $A\vec{e}_i = \lambda_i \vec{e}_i$, where $\lambda_i$ are the eigenvalues.

This is called the projection of $\vec{v}$ onto $\hat{d}$. and is sometimes denoted as $P_{\hat{d}}(\vec{v})$.

$\cal G$ is a group for the operation $\otimes$ if:

1. $\forall a,b\in{\cal G}\Rightarrow a\otimes b\in\cal G$: a group is {closed}.
2. $(a\otimes b)\otimes c = a\otimes (b\otimes c)$: a group is {associative}.
3. $\exists e\in{\cal G}$ so that $a\otimes e=e\otimes a=a$: there exists a {unit element}.
4. $\forall a\in{\cal G}\exists \overline{a}\in{\cal G}$ so that $a\otimes\overline{a}=e$: each element has an {inverse}.

If {4.5mm}5. $a\otimes b=b\otimes a$ the group is called {Abelian} or {commutative}. Vector spaces form an Abelian group for addition and multiplication: $1\cdot\vec{a}=\vec{a}$, $\lambda(\mu\vec{a})=(\lambda\mu)\vec{a}$, $(\lambda+\mu)(\vec{a}+\vec{b})=\lambda\vec{a}+\lambda\vec{b}+\mu\vec{a}+\mu\vec{b}$. $W$ is a {linear subspace} if $\forall \vec{w}_1,\vec{w}_2\in W$ holds: $\lambda\vec{w}_1+\mu\vec{w}_2\in W$. $W$ is an {invariant subspace} of $V$ for the operator $A$ if $\forall\vec{w}\in W$ holds: $A\vec{w}\in W$.

Geometry spaces the $xy$ place is a subspace of $\mathbb{R}^3$ that is spanned by the vectors $\hat{\imath}$ and $\hat{\jmath}$ and that the vector $\hat{k}$ is orthogonal to that subspace.

But

lead in what is new for matrices:

For the purpose of this section, we just need to review the following important properties of addition and multiplication:

• Associative property: $a+b+c=(a+b)+c=a+(b+c)$ and $abc=(ab)c=a(bc)$,
• Commutative property: $a+b=b+a$ and $ab=ba$,
• Distributive property: $a(b+c)=ab+ac$.

The derivative of a matrix is a matrix with the derivatives of the coefficients: \[ \frac{dA}{dt}=\frac{da_{ij}}{dt}~~~\mbox{and}~~~\frac{dAB}{dt}=B\frac{dA}{dt}+A\frac{dB}{dt} \]

When the rows of a matrix are considered as vectors the {row rank} of a matrix is the number of independent vectors in this set. Similar for the {column rank}. The row rank equals the column rank for each matrix. Let $\tilde{A}:\tilde{V}\rightarrow\tilde{V}$ be the complex extension of the real linear operator $A:V\rightarrow V$ in a finite-dimensional $V$. Then $A$ and $\tilde{A}$ have the same caracteristic equation. When $A_{ij}\in\mathbb{R}$ and $\vec{v}_1+i\vec{v_2}$ is an eigenvector of $A$ at eigenvalue $\lambda=\lambda_1+i\lambda_2$, than holds:

1. $A\vec{v}_1=\lambda_1\vec{v}_1-\lambda_2\vec{v}_2$ and $A\vec{v}_2=\lambda_2\vec{v}_1+\lambda_1\vec{v}_2$.
2. $\vec{v}^{~*}=\vec{v}_1-i\vec{v}_2$ is an eigenvalue at $\lambda^*=\lambda_1-i\lambda_2$.
3. The linear span $<\vec{v}_1,\vec{v}_2>$ is an invariant subspace of $A$.

If $\vec{k}_n$ are the columns of $A$, than the transformed space of $A$ is given by: \[ R(A)=<A\vec{e}_1,...,A\vec{e}_n>=<\vec{k}_1,...,\vec{k}_n> \] If the columns $\vec{k}_n$ of a $n\times m$ matrix $A$ are independent, than the nullspace ${\cal N}(A)=\{\vec{0}\}$.

The {determinant function} $D=\det(A)$ is defined by: \[ \det(A)=D(\vec{a}_{*1},\vec{a}_{*2},...,\vec{a}_{*n}) \]

The derivative of the determinant is given by: \[ \frac{d\det(A)}{dt}=D(\frac{d\vec{a}_1}{dt},...,\vec{a}_n)+ D(\vec{a}_1,\frac{d\vec{a}_2}{dt},...,\vec{a}_n)+...+D(\vec{a}_1,...,\frac{d\vec{a}_n}{dt}) \]

REDUCED ROW ECHELON

\[ B=\left[\begin{array}{cccccc} 1 &0 &\ast & 0 &\ast &\ast \nl cline{1-1} temp & 1&\ast & 0 &\ast &\ast \nl cline{2-3} 0&0&. &1&\ast &\ast \nl cline{4-6} 0 & 0& 0& 0& 0&0 \end{array}\right] \]

Vectors can in general have as coefficients any kind of number. For the most part we deal with real vectors $(\mathbb{R}, \mathbb{R})$

2-dimensional space of complex numbers $\mathbb{C}$ used to describe spin-states in Quantum Mechanics and the codewords used in ECC codes to store information reliably. An example of a case where the coefficients of vector are chosen from a finite set is the previously discussed RGB triplets, which takes its coefficients in the set of integers between 0 and 255 also known as $\mathbb {Z}_{256}$.

If the speed of the current was 12 knots, then even when doing full steam up-the river, the boat would be standing still relative to the shore!

In this section we will give a birds eye view of all the mathematical objects and operations which are part of a standard linear algebra course. It is expected of you to know these inside out by the end of the course, but our purpose here is only to expose you to them so you know what is waiting for you in the next chapters.

Both of these consist of numbers arranged into a structure. We will learn how to do math with these “structures”: how to add and subtract them, how to multiply them and how to solve for them in equations.

By doing simple manipulations on these objects we can achieve amazingly powerful algebraic, geometrical and computational feats. Indeed, a lot of what is actually known in science relates to linear system and so the natural language to study it is through vector and matrices.

Vectors have components

Vectors also have a magnitude and a direction.

The best example of a vector from everyday life is velocity. When I say: “I am doing 120km/h” this is a statement about the speed at which I am going. Speed is not a vector - it is just a number or a scalar. Now if I say I am flying at “500 km/h northwards” then we have a vector quantity. This is because I am also telling you an exact reference about which way I am going. Graphically we can represent this statement by an arrow pointing northward (or up on a regularly oriented map) like so:

The length of the arrow is proportional to how fast I am going: if I was flying at 250mi/h then the arrow would have to be twice smaller.

Representations of a Vectors To bring this concept of objects-with-magnitude-and-direction (vectors) into the realm of mathematics we need to find some sort of convention about how to represent these objects. We have several choices that will be useful in different situations. We are going to treat vectors as arrow-like objects on the mathematical space and we can move them around as we please because an arrow pointing northwards is still an arrow pointing northwards no matter how we translate it around. Second we will introduce the cartesian coordinate system

… INSERT DRAWING HERE &ndash; cartesian coordinate system … and use the tick-marks as units.

Starting from the origin, you throw a ball at a speed of 20[m/s] at an angle of $40$ degrees with the horizontal. How far from you will it fall?

The equation of motion, tells us the $x$ and the $y$ coordinate of the ball as a function of time: \[ \left[\begin{array}{c} x(t) \nl y(t) \end{array}\right] = \left[\begin{array}{c} x_i + v_{xi}t \nl y_i + v_{yi}t + \frac{1}{2}a_yt^2 \end{array}\right]. \]

The motion starts from the origin, so the initial position is $(x_i,y_i) = (0,0)$. The initial velocity is $\vec{v}_i=20\angle 40$, which can be expressed as \[ \vec{v}_i=20\angle 40 = (20\cos 40, 20\sin 40) = (v_{xi}, v_{yi} ), \] and the acceleration in the $y$-direction is $a_y = -g$, due to the gravitational pull of the earth.

The problem sakes for the final $x$-position when the ball falls back to earth $y=0$. In other words we are looking for a point $(x(t), y(t))=(x_f, 0)$. Let's plug that into the general equation and substitute all the known parameters: \[ \left[\begin{array}{c} x_f \nl 0 \end{array}\right] = \left[\begin{array}{c} 0 + 20\cos40 t \nl 0 + 20\sin40 t + \frac{1}{2}(-9.8)t^2 \end{array}\right]. \] In the bottom of the equation we have just one unknown: $t$, so we can solve for it: \[ 20\sin40 t + \frac{1}{2}(-9.8)t^2 = 0 = t (20\sin40 + \frac{1}{2}(-9.8)t), \] where clearly $t_i=0$ is one of the solutions, and $t_f=\frac{(2)(20)\sin40}{9.8}$ is the other solution.

We plug this value in the top row, to obtain the answer \[ x_f = 20\cos40 t_f = 20\cos40 \frac{(2)(20)\sin40}{9.8} = . \]