The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Definitions
Calculus is the study of functions $f(x)$ over the real numbers $\mathbb{R}$: \[ f: \mathbb{R} \to \mathbb{R}. \] The function $f$ takes as input some number, usually called $x$ and gives as output another number $f(x)=y$. You are familiar with many functions and have used them in many problems.
In this chapter we will learn about different operations that can be performed on functions. It worth understanding these operations because of the numerous applications which they have.
Differential calculus
Differential calculus is all about derivatives:
- $f'(x)$: the derivative of $f(x)$ is the rate of change of $f$ at $x$.
The derivative is also a function of the form
\[
f': \mathbb{R} \to \mathbb{R},
\]
The output of $f'(x)$ represents the //slope// of
a line parallel (tangent) to $f$ at the point $(x,f(x))$.
Integral calculus
Integral calculus is all about integration:
- $\int_a^b f(x)\:dx$: the integral of $f(x)$ from $x=a$ to $x=b$
corresponds to the area under $f(x)$ between $a$ and $b$:
\[
A(a,b) = \int_a^b f(x) \: dx.
\]
The $\int$ sign is a mnemonic for //sum//.
The integral is the "sum" of $f(x)$ over that interval.
* $F(x)=\int f(x)\:dx$: the anti-derivative of the function $f(x)$
contains the information about the area under the curve for
//all// limits of integration.
The area under $f(x)$ between $a$ and $b$ is computed as the
difference between $F(b)$ and $F(a)$:
\[
A(a,b) = \int_a^b f(x)\;dx = F(b)-F(a).
\]
Sequences and series
Functions are usually defined for continuous inputs $x\in \mathbb{R}$, but there are also functions which are defined only for natural numbers $n \in \mathbb{N}$. Sequences are the discrete analogue functions.
- $a_n$: sequence of numbers $\{ a_0, a_1, a_2, a_3, a_4, \ldots \}$.
You can think about each sequence as a function
\[
a: \mathbb{N} \to \mathbb{R},
\]
where the input $n$ is an integer (index into the sequence) and
the output is $a_n$ which could be any number.
NOINDENT The integral of a sequence is called a series.
- $\sum$: sum.
The summation sign is the short way to express
the sum of several objects:
\[
a_3 + a_4 + a_5 + a_6 + a_7
\equiv \sum_{3 \leq i \leq 7} a_i
\equiv \sum_{i=3}^{7} a_i.
\]
Note that summations could go up to infinity.
* $\sum a_i$: the series corresponds to the running total of a sequence until $n$:
\[
S_n = \sum_{i=1}^{n} a_i = a_1 + a_2 + \cdots + a_{n-1} + a_n.
\]
* $f(x)=\sum_{i=0}^\infty a_i x^i$: a //power series// is a series
which contains powers of some variable $x$.
Power series give us a way to express any function $f(x)$ as
an infinitely long polynomial.
For example, the power series of $\sin(x)$ is
\[
\sin(x)
= x - \frac{x^3}{3!} + \frac{x^5}{5!}
- \frac{x^7}{7!} + \frac{x^9}{9!}+ \ldots.
\]
Don't worry if you don't understand all the notions and the new notation in the above paragraphs. I just wanted to present all the calculus actors in the first scene. We will talk about each of them in more detail in the following sections.
Limits
Actually, we have not mentioned the main actor yet: the limit. In calculus, we do a lot of limit arguments in which we take some positive number $\epsilon>0$ and we make it progressively smaller and smaller:
- $\displaystyle\lim_{\epsilon \to 0}$: the mathematically rigorous
way of saying that the number $\epsilon$ becomes smaller and smaller. We can also take limits to infinity, that is, we imagine some number $N$ and we make that number bigger and bigger:
- $\displaystyle\lim_{N \to \infty}$: the mathematical
way of saying that the number $N$ will get larger and larger.
Indeed, it wouldn't be wrong to say that calculus is the study of the infinitely small and the infinitely many. Working with infinitely small quantities an infinitely large numbers can be tricky business but it is extremely important that you become comfortable with the concept of a limit which is the rigorous way of talking about infinity. Before we learn about derivatives, integrals and series we will spend some time learning about limits.
Infinity
Let's say you have a length $\ell$ and you want to divide it into infinitely many, infinitely short segments. There are infinitely many of them, but they are infinitely short so they add up to the total length $\ell$.
OK, that sounds complicated. Let's start from something simpler. We have a piece of length $\ell$ and we want to divide this length into $N$ pieces. Each piece will have length: \[ \delta = \frac{\ell}{N}. \] Let's check that, together, the $N$ pieces of length $\delta$ add up to the total length of the string: \[ N \delta = N \frac{\ell}{N} = \ell. \] Good.
Now imagine that $N$ is a very large number. In fact it can take on any value, but always larger and larger. The larger $N$ gets, the more fine grained the notion of “small piece of string” becomes. In this case we would have: \[ \lim_{N\to \infty} \delta = \lim_{N\to \infty} \frac{\ell}{N} = 0, \] so effectively the pieces of string are infinitely small. However, when you add them up you will still get: \[ \lim_{N\to \infty} \left( N \delta \right) = \lim_{N\to \infty} \left( N \frac{\ell}{N} \right) = \ell. \]
The lesson to learn here is that, if you keep things well defined you can use the notion of infinity in your equations. This is the central idea of this course.
Infinitely large
The number $\infty$ is really large. How large? Larger than any number you can think of! Say you think of a number $n$, then it is true that $\infty > n$. But no, you say, actually I thought of a different number $N > n$, well still it will be true that $\infty > N$. In fact any finite number you can think of, no matter how large will always be strictly smaller than $\infty$.
Infinitely small
If instead of a really large number, we want to have a really small number $\epsilon$, we can simply define it as the reciprocal of (one over) a really large number $N$: \[ \epsilon = \lim_{N \to \infty \atop N \neq \infty} \frac{1}{N}. \] However small $\epsilon$ must get, it remains strictly greater than zero $\epsilon > 0$. This is ensured by the condition $N\neq \infty$, otherwise if we would have $\lim_{N \to \infty} \frac{1}{N} = 0$.
The infinitely small $\epsilon>0$ is a new beast like nothing you have seen before. It is a non-zero number that is smaller than any number you can think of. Say you think $0.00001$ is pretty small, well it is true that $0.00001 > \epsilon > 0$. Then you say, no actually I was thinking about $10^{-16}$, a number with 15 zeros after the decimal point. It will still be true that $10^{-16} > \epsilon$, or even $10^{-123} > \epsilon > 0$. Like I said, I can make $\epsilon$ smaller than any number you can think of simply by choosing $N$ to be larger and larger, yet $\epsilon$ always remains non-zero.
Infinity for limits
When evaluating a limit, we often make the variable $x$ go to infinity. This is useful information, for example if we want to know what the function $f(x)$ looks like for very large values of $x$. Does it get closer and closer to some finite number, or does it blow up? For example the negative-power exponential function tends to zero for large values of $x$: \[ \lim_{x \to \infty} e^{-x} = 0. \] In the above examples we also saw that the inverse-$x$ function also tends to zero: \[ \lim_{x \to \infty} \frac{1}{x} = 0. \]
Note that in both cases, the functions will never actually reach zero. They get closer and closer to zero but never actually reach it. This is why the limit is a useful quantity, because it says that the functions get arbitrarily close to 0.
Sometimes infinity might come out as an answer to a limit question: \[ \lim_{x\to 3^-} \frac{1}{3-x} = \infty, \] because as $x$ gets closer to $3$ from below, i.e., $x$ will take on values like $2.9$, $2.99$, $2.999$, and so on and so forth, the number in the denominator will get smaller and smaller, thus the fraction will get larger and larger.
Infinity for derivatives
The derivative of a function is its slope, defined as the “rise over run” for an infinitesimally short run: \[ f'(x) = \lim_{\epsilon \to 0} \frac{\text{rise}}{\text{run}} = \lim_{\epsilon \to 0} \frac{f(x+\epsilon)\ - \ f(x)}{x+\epsilon \ - \ x}. \]
Infinity for integrals
The area under the curve $f(x)$ for values of $x$ between $a$ and $b$, can be though of as consisting of many little rectangles of width $\epsilon$ and height $f(x)$: \[ \epsilon f(a) + \epsilon f(a+\epsilon) + \epsilon f(a+2\epsilon) + \cdots + \epsilon f(b-\epsilon). \] In the limit where we take infinitesimally small rectangles, we obtain the exact value of the integral \[ \int_a^b f(x) \ dx= A(a,b) = \lim_{\epsilon \to 0}\left[ \epsilon f(a) + \epsilon f(a+\epsilon) + \epsilon f(a+2\epsilon) + \cdots + \epsilon f(b-\epsilon) \right], \]
Infinity for series
For a given $|r|<1$, what is the sum \[ S = 1 + r + r^2 + r^3 + r^4 + \ldots = \sum_{k=0}^\infty r^k \ \ ? \] Obviously, taking your calculator and performing the summation is not practical since there are infinitely many terms to add.
For several such infinite series, there is actually a closed form formula for their sum. The above series is called the geometric series and its sum is $S=\frac{1}{1-r}$. How were we able to tame the infinite? In this case, we used the fact that $S$ is similar to a shifted version of itself $S=1+rS$, and then solved for $S$.
Limits
To understand the ideas behind derivatives and integrals, you need to understand what a limit is and how to deal with the infinitely small, infinitely large and the infinitely many. In practice, using calculus doesn't actually involve taking limits since we will learn direct formulas and algebraic rules that are more convenient than doing limits. Do not skip this section though just because it is “not on the exam”. If you do so, you will not know what I mean when I write things like $0,\infty$ and $\lim$ in later sections.
Introduction in three acts
Zeno's paradox
The ancient greek philosopher Zeno once came up with the following argument. Suppose an archer shoots an arrow and sends it flying towards a target. After some time it will have travelled half the distance, and then at some later time it will have travelled the half of the remaining distance and so on always getting closer to the target. Zeno observed that no matter how little distance remains to the target, there will always be some later instant when the arrow will have travelled half of that distance. Thus, he reasoned, the arrow must keep getting closer and closer to the target, but never reaches it.
Zeno, my brothers and sisters, was making some sort of limit argument, but he didn't do it right. We have to commend him for thinking about such things centuries before calculus was invented (17th century), but shouldn't repeat his mistake. We better learn how to take limits, because limits are important. I mean a wrong argument about limits could get you killed for God's sake! Imagine if Zeno tried to verify experimentally his theory about the arrow by placing himself in front of one such arrow!
Two monks
Two young monks were sitting in silence in a Zen garden one autumn afternoon.
“Can something be so small as to become nothing?” asked one of the monks, braking the silence.
“No,” replied the second monk, “if it is something then it is not nothing.”
“Yes, but what if no matter how close you look you cannot see it, yet you know it is not nothing?”, asked the first monk, desiring to see his reasoning to the end.
The second monk didn't know what to say, but then he found a counterargument. “What if, though I cannot see it with my naked eye,
I could see it using a magnifying glass?”.
The first monk was happy to hear this question, because he had already prepared a response for it. “If I know that you will be looking with a magnifying glass, then I will make it so small that you cannot see with you magnifying glass.”
“What if I use a microscope then?”
“I can make the thing so small that even with a microscope you cannot see it.”
“What about an electron microscope?”
“Even then, I can make it smaller, yet still not zero.” said the first monk victoriously and then proceeded to add “In fact, for any magnifying device you can come up with, you just tell me the resolution and I can make the thing smaller than can be seen”.
They went back to concentrating on their breathing.
Epsilon and delta
The monks have the right reasoning but didn't have the right language to express what they mean. Zeno has the right language, the wonderful Greek language with letters like $\epsilon$ and $\delta$, but he didn't have the right reasoning. We need to combine aspects of both of the above stories to understand limits.
Let's analyze first Zeno's paradox. The poor brother didn't know about physics and the uniform velocity equation of motion. If an object is moving with constant speed $v$ (we ignore the effects of air friction on the arrow), then its position $x$ as a function of time is given by \[ x(t) = vt+x_i, \] where $x_i$ is the initial location where the object starts from at $t=0$. Suppose that the archer who fired the arrow was at the origin $x_i=0$ and that the target is at $x=L$ metres. The arrow will hit the target exactly at $t=L/v$ seconds. Shlook!
It is true that there are times when the arrow will be $\frac{1}{2}$, $\frac{1}{4}$, $\frac{1}{8}$th, $\frac{1}{16}$th, and so forth distance from the target. In fact there infinitely many of those fractional time instants before the arrow hits, but that is beside the point. Zeno's misconception is that he thought that these infinitely many timestamps couldn't all fit in the timeline since it is finite. No such problem exists though. Any non-zero interval on the number line contains infinitely many numbers ($\mathbb{Q}$ or $\mathbb{R}$).
Now let's get to the monks conversation. The first monk was talking about the function $f(x)=\frac{1}{x}$. This function becomes smaller and smaller but it never actually becomes zero: \[ \frac{1}{x} \neq 0, \textrm{ even for very large values of } x, \] which is what the monk told us.
Remember that the monk also claimed that the function $f(x)$ can be made arbitrarily small. He wants to show that, in the limit of large values of $x$, the function $f(x)$ goes to zero. Written in math this becomes \[ \lim_{x\to \infty}\frac{1}{x}=0. \]
To convince the second monk that he can really make $f(x)$ arbitrarily small, he invents the following game. The second monk announces a precision $\epsilon$ at which he will be convinced. The first monk then has to choose an $S_\epsilon$ such that for all $x > S_\epsilon$ we will have \[ \left| \frac{1}{x} - 0 \right| < \epsilon. \] The above expression indicates that $\frac{1}{x}\approx 0$ at least up to a precision of $\epsilon$.
The second monk will have no choice but to agree that indeed $\frac{1}{x}$ goes to 0 since the argument can be repeated for any required precision $\epsilon >0$. By showing that the function $f(x)$ approaches $0$ arbitrary closely for large values of $x$, we have proven that $\lim_{x\to \infty}f(x)=0$.
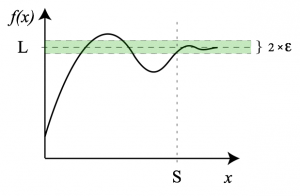 More generally, the function $f(x)$ can converge to any number $L$
for as $x$ takes on larger and larger values:
\[
\lim_{x \to \infty} f(x) = L.
\]
The above expressions means that, for any precision $\epsilon>0$,
there exists a starting point $S_\epsilon$,
after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision:
\[
\left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon.
\]
More generally, the function $f(x)$ can converge to any number $L$
for as $x$ takes on larger and larger values:
\[
\lim_{x \to \infty} f(x) = L.
\]
The above expressions means that, for any precision $\epsilon>0$,
there exists a starting point $S_\epsilon$,
after which $f(x)$ equals its limit $L$ to within $\epsilon$ precision:
\[
\left|f(x) - L\right| <\epsilon, \qquad \forall x \geq S_\epsilon.
\]
Example
You are asked to calculate $\lim_{x\to \infty} \frac{2x+1}{x}$, that is you are given the function $f(x)=\frac{2x+1}{x}$ and you have to figure out what the function looks like for very large values of $x$. Note that we can rewrite the function as $\frac{2x+1}{x}=2+\frac{1}{x}$ which will make it easier to see what is going on: \[ \lim_{x\to \infty} \frac{2x+1}{x} = \lim_{x\to \infty}\left( 2 + \frac{1}{x} \right) = 2 + \lim_{x\to \infty}\left( \frac{1}{x} \right) = 2 + 0, \] since $\frac{1}{x}$ tends to zero for large values of $x$.
In a first calculus course you are not required to prove statements like $\lim_{x\to \infty}\frac{1}{x}=0$, you can just assume that the result is obvious. As the denominator $x$ becomes larger and larger, the fraction $\frac{1}{x}$ becomes smaller and smaller.
Types of limits
Limits to infinity
\[ \lim_{x\to \infty} f(x) \] what happens to $f(x)$ for very large values of $x$.
Limits to a number
The limit of $f(x)$ approaching $x=a$ from above (from the right) is denoted: \[ \lim_{x\to a^+} f(x) \] Similarly, the expression \[ \lim_{x\to a^-} f(x) \] describes what happens to $f(x)$ as $x$ approaches $a$ from below (from the left), i.e., with values like $x=a-\delta$, with $\delta>0, \delta \to 0$. If both limits from the left and from the right of some number are equal, then we can talk about the limit as $x\to a$ without specifying the direction: \[ \lim_{x\to a} f(x) = \lim_{x\to a^+} f(x) = \lim_{x\to a^-} f(x). \]
Example 2
You now asked to calculate $\lim_{x\to 5} \frac{2x+1}{x}$. \[ \lim_{x\to 5} \frac{2x+1}{x} = \frac{2(5)+1}{5} = \frac{11}{5}. \]
Example 3
Find $\lim_{x\to 0} \frac{2x+1}{x}$. If we just plug $x=0$ into the fraction we get an error divide by zero $\frac{2(0)+1}{0}$ so a more careful treatment will be required.
Consider first the limit from the right $\lim_{x\to 0+} \frac{2x+1}{x}$. We want to approach the value $x=0$ with small positive numbers. The best way to carry out the calculation is to define some small positive number $\delta>0$, to choose $x=\delta$, and to compute the limit: \[ \lim_{\delta\to 0} \frac{2(\delta)+1}{\delta} = 2 + \lim_{\delta\to 0} \frac{1}{\delta} = 2 + \infty = \infty. \] We took it for granted that $\lim_{\delta\to 0} \frac{1}{\delta}=\infty$. Intuitively, we can imagine how we get closer and closer to $x=0$ in the limit. When $\delta=10^{-3}$ the function value will be $\frac{1}{\delta}=10^3$. When $\delta=10^{-6}$, $\frac{1}{\delta}=10^6$. As $\delta \to 0$ the function will blow up—$f(x)$ will go up all the way to infinity.
If we take the limit from the left (small negative values of $x$) we get \[ \lim_{\delta\to 0} f(-\delta) =\frac{2(-\delta)+1}{-\delta}= -\infty. \] Therefore, since $\lim_{x\to 0^+}f(x)$ does not equal $\lim_{x\to 0^-} f(x)$, we say that $\lim_{x\to 0} f(x)$ does not exist.
Continuity
A function $f(x)$ is continuous at $a$ if the limit of $f$ as $x\to a$ converges to $f(a)$: \[ \lim_{x \to a} f(x) = f(a). \]
Most functions we will study in calculus are continuous, but not all functions are. For example, functions which make sudden jumps are not continuous. Another examples is the function $f(x)=\frac{2x+1}{x}$ which is discontinuous at $x=0$ (because the limit $\lim_{x \to 0} f(x)$ doesn't exist and $f(0)$ is not defined). Note that $f(x)$ is continuous everywhere else on the real line.
Formulas
We now switch gears into reference mode, as I will state a whole bunch known formulas for limits of various kinds of functions. You are not meant to know why these limit formulas are true, but simply understand what they mean.
The following statements tell you about the relative sizes of functions. If the limit of the ratio of two functions is equal to $1$, then these functions must behave similarly in the limit. If the limit of the ratio goes to zero, then one function must be much larger than the other in the limit.
Limits of trigonometric functions: \[ \lim_{x\rightarrow0}\frac{\sin(x)}{x}=1,\quad \lim_{x\rightarrow0} \cos(x)=1,\quad \lim_{x\rightarrow 0}\frac{1-\cos x }{x}=0, \quad \lim_{x\rightarrow0}\frac{\tan(x)}{x}=1. \]
The number $e$ is defined as one of the following limits: \[ e \equiv \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n = \lim_{\epsilon\to 0 }(1+\epsilon)^{1/\epsilon}. \] The first limit corresponds to a compound interest calculation, with annual interest rate of $100\%$ and compounding performed infinitely often.
For future reference, we state some other limits involving the exponential function: \[ \lim_{x\rightarrow0}\frac{{\rm e}^x-1}{x}=1,\qquad \quad \lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n={\rm e}^x. \]
These are some limits involving logarithms: \[ \lim_{x\rightarrow 0^+}x^a\ln(x)=0,\qquad \lim_{x\rightarrow\infty}\frac{\ln^p(x)}{x^a}=0, \ \forall p < \infty \] \[ \lim_{x\rightarrow0}\frac{\ln(x+a)}{x}=a,\qquad \lim_{x\rightarrow0}\left(a^{1/x}-1\right)=\ln(a). \]
A polynomial of degree $p$ and the exponential function base $a$ with $a > 1$ both go to infinity as $x$ goes to infinity: \[ \lim_{x\rightarrow\infty} x^p= \infty, \qquad \qquad \lim_{x\rightarrow\infty} a^x= \infty. \] Though both functions go to infinity, the exponential function does so much faster, so their relative ratio goes to zero: \[ \lim_{x\rightarrow\infty}\frac{x^p}{a^x}=0, \qquad \mbox{for all } p \in \mathbb{R}, |a|>1. \] In computer science, people make a big deal of this distinction when comparing the running time of algorithms. We say that a function is computable if the number of steps it takes to compute that function is polynomial in the size of the input. If the algorithm takes an exponential number of steps, then for all intents and purposes it is useless, because if you give it a large enough input the function will take longer than the age of the universe to finish.
Other limits: \[ \lim_{x\rightarrow0}\frac{\arcsin(x)}{x}=1,\qquad \lim_{x\rightarrow\infty}\sqrt[x]{x}=1. \]
Limit rules
If you are taking the limit of a fraction $\frac{f(x)}{g(x)}$, and you have $\lim_{x\to\infty}f(x)=0$ and $\lim_{x\to\infty}g(x)=\infty$, then we can informally write: \[ \lim_{x\to \infty} \frac{f(x)}{g(x)} = \frac{\lim_{x\to \infty} f(x)}{ \lim_{x\to \infty} g(x)} = \frac{0}{\infty} = 0, \] since both functions are helping to drive the fraction to zero.
Alternately if you ever get a fraction of the form $\frac{\infty}{0}$ as a limit, then both functions are helping to make the fraction grow to infinity so we have $\frac{\infty}{0} = \infty$.
L'Hopital's rule
Sometimes when evaluating limits of fractions $\frac{f(x)}{g(x)}$, you might end up with a fraction like \[ \frac{0}{0}, \qquad \text{or} \qquad \frac{\infty}{\infty}. \] These are undecidable conditions. Is the effect of the numerator stronger or the effect of the denominator stronger?
One way to find out, is to compare the ratio of their derivatives. This is called L'Hopital's rule: \[ \lim_{x\rightarrow a}\frac{f(x)}{g(x)} \ \ \ \overset{\textrm{H.R.}}{=} \ \ \ \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}. \]
Derivatives
The derivative of a function $f(x)$ is another function, which we will call $f'(x)$ that tells you the slope of $f(x)$. For example, the constant function $f(x)=c$ has slope $f'(x)=0$, since a constant function is flat. What is the derivative of a line $f(x)=mx+b$? The derivative is the slope right, so we must have $f'(x)=m$. What about more complicated functions?
Definition
The derivative of a function is defined as: \[ f'(x) \equiv \lim_{ \epsilon \rightarrow 0}\frac{f(x+\epsilon)-f(x)}{\epsilon}. \] You can think of $\epsilon$ as a really small number. I mean really small. The above formula is nothing more than the rise-over-run rule for calculating the slope of a line, \[ \frac{ rise } { run } = \frac{ \Delta y } { \Delta x } = \frac{y_f - y_i}{x_f - x_i} = \frac{f(x+\epsilon)\ - \ f(x)}{x + \epsilon \ -\ x}, \] but by taking $\epsilon$ to be really small, we will get the slope at the point $x$.
Derivatives occur so often in math that people have come up with many different notations for them. Don't be fooled by that. All of them mean the same thing $Df(x) = f'(x)=\frac{df}{dx}=\dot{f}=\nabla f$.
Applications
Knowing how to take derivatives is very useful in life. Given some phenomenon described by $f(x)$ you can say how it changes over time. Many times we don't actually care about the value of $f'(x)$, just its sign. If the derivative is positive $f'(x) > 0$, then the function is increasing. If $f'(x) < 0$ then the function is decreasing.
When the function is flat at a certain $x$ then $f'(x)=0$. The points where $f'(x)=0$ (the roots of $f'(x)$) are very important for finding the maximum and minimum values of $f(x)$. Recall how we calculated the maximum height $h$ that projectile reaches by first finding the time $t_{top}$ when its velocity in the $y$ direction was zero $y^\prime(t_{top})=v(t_{top})=0$ and then substituting this time in $y(t)$ to obtain $h=\max\{ y(t) \} =y(t_{top})$.
Example
Now let's take a derivative of $f(x)=2x^2 + 3$ to see how that complicated-looking formula works: \[ f'(x)=\lim_{\epsilon \rightarrow 0} \frac{f(x+\epsilon)-f(x)}{\epsilon} = \lim_{\epsilon \rightarrow 0} \frac{2(x+\epsilon)^2+3 \ \ - \ \ 2x^2 + 3}{\epsilon}. \] Let's simplify the right-hand side a bit \[ \frac{2x^2+ 4x\epsilon +\epsilon^2 - 2x^2}{\epsilon} = \frac{4x\epsilon +\epsilon^2}{\epsilon}= \frac{4x\epsilon}{\epsilon} + \frac{\epsilon^2}{\epsilon}. \] Now when we take the limit, the second term disappears: \[ f'(x) = \lim_{\epsilon \rightarrow 0} \left( \frac{4x\epsilon}{\epsilon} + \frac{\epsilon^2}{\epsilon} \right) = 4x + 0. \] Congratulations, you have just taken your first derivative! The calculations were not that complicated, but it was pretty long and tedious. The good news is that you only need to calculate the derivative from first principles only once. Once you find a derivative formula for a particular function, you can use the formula every time you see a function of that form.
A derivative formula
\[ f(x) = x^n \qquad \Rightarrow \qquad f'(x) = n x^{n-1}. \]
Example
Use the above formula to find the derivatives of the following three functions: \[ f(x) = x^{10}, \quad g(x) = \sqrt{x^3}, \qquad h(x) = \frac{1}{x^3}. \] In the first case, we use the formula directly to find the derivative $f'(x)=10x^9$. In the second case, we first use the fact that square root is equivalent to an exponent of $\frac{1}{2}$ to rewrite the function as $g(x)=x^{\frac{3}{2} }$, then using the formula we find that $g'(x)=\frac{3}{2}x^{\frac{1}{2} } =\frac{3}{2}\sqrt{x}$. We can also rewrite the third function as $h(x)=x^{-3}$ and then compute the derivative $h'(x)=-3x^{-4}=\frac{-3}{x^4}$ using the formula.
Discussion
In the next section we will develop derivative formulas for other functions.
Formulas to memorize
\[ \begin{align*} F(x) & \ - \textrm{ diff. } \to \quad F'(x) \nl \int f(x)\;dx & \ \ \leftarrow \textrm{ int. } - \quad f(x) \nl a &\qquad\qquad\qquad 0 \nl x &\qquad\qquad\qquad 1 \nl af(x) &\qquad\qquad\qquad af'(x) \nl f(x)+g(x) &\qquad\qquad\qquad f'(x)+g'(x) \nl x^n &\qquad\qquad\qquad nx^{n-1} \nl 1/x=x^{-1} &\qquad\qquad\qquad -x^{-2} \nl \sqrt{x}=x^{\frac{1}{2}} &\qquad\qquad\qquad \frac{1}{2}x^{-\frac{1}{2}} \nl {\rm e}^x &\qquad\qquad\qquad {\rm e}^x \nl a^x &\qquad\qquad\qquad a^x\ln(a) \nl \ln(x) &\qquad\qquad\qquad 1/x \nl \log_a(x) &\qquad\qquad\qquad (x\ln(a))^{-1} \nl \sin(x) &\qquad\qquad\qquad \cos(x) \nl \cos(x) &\qquad\qquad\qquad -\sin(x) \nl \tan(x) &\qquad\qquad\qquad \sec^2(x)\equiv\cos^{-2}(x) \nl \csc(x) \equiv \frac{1}{\sin(x)} &\qquad\qquad\qquad -\sin^{-2}(x)\cos(x) \nl \sec(x) \equiv \frac{1}{\cos(x)} &\qquad\qquad\qquad \tan(x)\sec(x) \nl \cot(x) \equiv \frac{1}{\tan(x)} &\qquad\qquad\qquad -\csc^2(x) \nl \sinh(x) &\qquad\qquad\qquad \cosh(x) \nl \cosh(x) &\qquad\qquad\qquad \sinh(x) \nl \sin^{-1}(x) &\qquad\qquad\qquad \frac{1}{\sqrt{1-x^2}} \nl \cos^{-1}(x) &\qquad\qquad\qquad \frac{-1}{\sqrt{1-x^2}} \nl \tan^{-1}(x) &\qquad\qquad\qquad \frac{1}{1+x^2} \end{align*} \]
Derivative rules
Taking derivatives is a simple task: you just have to lookup the appropriate formula in the table of derivative formulas. However the tables of derivatives usually don't have the formulas for composite functions. In this section, we will learn about some important rules for derivatives, so that you will know how to handle derivatives of composite functions.
Formulas
Linearity
The derivative of a sum of two functions is the sum of the derivatives: \[ \left[f(x) + g(x)\right]^\prime= f^\prime(x) + g^\prime(x), \] and for any constant $a$, we have \[ \left[a f(x)\right]^\prime= a f^\prime(x). \] The fact that the derivative operation obeys these two conditions means that derivatives are linear operations.
Product rule
The derivative of a product of two functions is obtained as follows: \[ \left[ f(x)g(x) \right]^\prime = f^\prime(x)g(x) + f(x)g^\prime(x). \]
Quotient rule
As a special case the product rule, we obtain the derivative rule for a fraction of two functions: \[ \frac{d}{dx}\left[ \frac{f(x)}{g(x)}\right]^\prime=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}. \]
Chain rule
If you have a situation with an inner function and outer function like $f(g(x))$, then the derivative is obtained in a two step process: \[ \left[ f(g(x)) \right]^\prime = f^\prime(g(x))g^\prime(x). \] In the first step you leave $g(x)$ alone and focus on taking the derivative of the outer function. Just copy over whatever $g(x)$ is inside the $f'$ expression. The second step is to multiply the resulting expression by the derivative of the inner function $g'(x)$.
In words, the chain rule tells us that the rate of change of a composite function can be calculated as the product of the rate of change of the components.
Example
\[ \frac{d}{dx}\left[ \sin(x^2)) \right] = \cos(x^2)[x^2]' = \cos(x^2)2x. \]
More complicated example
The chain rule also applies to functions of functions of functions $f(g(h(x)))$. To take the derivative, just start from the outermost function and then work your way towards $x$. \[ \left[ f(g(h(x))) \right]' = f'(g(h(x))) g'(h(x)) h'(x). \] Now let's try this \[ \frac{d}{dx} \left[ \sin( \ln( x^3) ) \right] = \cos( \ln(x^3) ) \frac{1}{x^3} 3x^2 = \cos( \ln(x^3) ) \frac{3}{x}. \] Simple right?
Examples
The above rules are all that you need to take the derivative of any function no matter how complicated. To convince you of this, I will now show you some examples of really hairy functions. Don't be scared by complexity: as long as you follow the rules, you will get the right answer in the end.
Example
Calculate the derivative of \[ f(x) = e^{x^2}. \] We just need the chain rule for this one: \[ \begin{align} f'(x) & = e^{x^2}[x^2]' \nl & = e^{x^2}2x. \end{align} \]
Example 2
\[ f(x) = \sin(x)e^{x^2}. \] We will need the product rule for this one: \[ \begin{align} f'(x) & = \cos(x)e^{x^2} + \sin(x)2xe^{x^2}. \end{align} \]
Example 3
\[ f(x) = \sin(x)e^{x^2}\ln(x). \] This is still the product rule, but now we will have three terms. In each term, we take the derivative of one of the functions and multiply by the other two: \[ \begin{align} f'(x) & = \cos(x)e^{x^2}\ln(x) + \sin(x)2xe^{x^2}\ln(x) + \sin(x)e^{x^2}\frac{1}{x}. \end{align} \]
Example 4
Ok let's go crazy now: \[ f(x) = \sin\!\left( \cos\!\left( \tan(x) \right) \right). \] We need a triple chain rule for this one: \[ \begin{align} f'(x) & = \cos\!\left( \cos\!\left( \tan(x) \right) \right) \left[ \cos\!\left( \tan(x) \right) \right]^\prime \nl & = -\cos\!\left( \cos\!\left( \tan(x) \right) \right) \sin\!\left( \tan(x) \right)\left[ \tan(x) \right]^\prime \nl & = -\cos\!\left( \cos\!\left( \tan(x) \right) \right) \sin\!\left( \tan(x) \right)\sec^2(x). \end{align} \]
Explanations
Proof of the product rule
By definition, the derivative of $f(x)g(x)$ is \[ \left( f(x)g(x) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(x+\epsilon)g(x+\epsilon)-f(x)g(x)}{\epsilon}. \] Consider the numerator of the fraction. If we add and subtract $f(x)g(x+\epsilon)$, we can factor the expression into two terms like this: \[ \begin{align} & f(x+\epsilon)g(x+\epsilon) \ \overbrace{-f(x)g(x+\epsilon) +f(x)g(x+\epsilon)}^{=0} \ - f(x)g(x) \nl & \ \ \ = [f(x+\epsilon)-f(x) ]g(x+\epsilon) + f(x)[ g(x+\epsilon)- g(x)], \end{align} \] thus the expression for the derivative of the product becomes \[ \left( f(x)g(x) \right)' = \left\{ \lim_{\epsilon \rightarrow 0} \frac{[f(x+\epsilon)-f(x) ]}{\epsilon}g(x+\epsilon) + f(x) \frac{[ g(x+\epsilon)- g(x)]}{\epsilon} \right\}. \] This looks almost exactly like the product rule formula, except that we have $g(x+\epsilon)$ instead of $g(x)$. This is not a problem, though, since we assumed that $f(x)$ and $g(x)$ are differentiable functions, which implies that they are continuous functions. For continuous functions, we have $\lim_{\epsilon \rightarrow 0}g(x+\epsilon) = g(x)$ and we obtain the final form of the product rule: \[ \left( f(x)g(x) \right)' = f'(x)g(x) + f(x)g'(x). \]
Proof of the chain rule
Before we begin the proof, I want to make a remark on the notation used in the definition of the derivative. I like the greek letter epsilon $\epsilon$ so I defined the derivative of $f(x)$ as \[ f'(x)=\lim_{\epsilon \rightarrow 0} \frac{f(x+\epsilon)-f(x)}{\epsilon}, \] but I could have used any other variable instead: \[ f'(x) \equiv \lim_{\delta \rightarrow 0} \frac{f(x+\delta)-f(x)}{\delta} \equiv \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}. \] All that matters is that we divide by the same quantity that is added to $x$ in the numerator, and that this quantity goes to zero.
The derivative of $f(g(x))$ is \[ \left( f(g(x)) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(g(x+\epsilon))-f(g(x))}{\epsilon}. \] The trick is to define a new quantity \[ \delta = g(x+\epsilon)-g(x), \] and then substitute $g(x+\epsilon) = g(x) + \delta$ into the expression for the derivative as follows \[ \left( f(g(x)) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\epsilon}. \] This is starting to look more like a derivative formula, but the quantity added in the input is different from the quantity by which we divide. To fix this we will multiply and divide by $\delta$ to obtain \[ \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\epsilon}\frac{\delta}{\delta} = \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\delta}\frac{\delta}{\epsilon}. \] We now use the definition of the quantity $\delta$ and rearrange the fraction as follows: \[ \left( f(g(x)) \right)' = \lim_{\epsilon \rightarrow 0} \frac{f(g(x) + \delta)-f(g(x))}{\delta}\frac{g(x+\epsilon)-g(x)}{\epsilon}. \] This is starting to look a lot like $f'(g(x))g'(x)$, and in fact it is: taking the limit $\epsilon \to 0$ implies that the quantity $\delta(\epsilon) \to 0$. This is because the function $g(x)$ is continuous: $\lim_{\epsilon \rightarrow 0} g(x+\epsilon)-g(x)=0$. And so the quantity $\delta$ is just as good as $\epsilon$ for taking a derivative. Thus, we have proved that: \[ \left( f(g(x)) \right)' = f'(g(x))g'(x). \]
Alternate notation
The presence of so much primes and brackets in the above expressions can make them difficult to read. This is why we sometimes use a different notation for derivatives. The three rules of derivatives in the alternate notation are as follows:
Linearity: \[ \frac{d}{dx}(\alpha f(x) + \beta g(x))= \alpha\frac{df}{dx} + \beta\frac{dg}{dx}. \] Product rule: \[ \frac{d}{dx}(f(x)g(x)) = \frac{df}{dx}g(x) + f(x)\frac{dg}{dx}. \] Chain rule: \[ \frac{d}{dx}\left( f(g(x)) \right) = \frac{df}{dg}\frac{dg}{dx}. \]
Optimization: calculus' killer app
The reason why you need to learn about derivatives is that this skill will allow you to optimize any function. Suppose you have control over the input of the function $f(x)$ and you want to pick the best value of $x$. Best usually means maximum (if the function measures something good like profits) or minimum (if the function describes something bad like costs).
Example
The drug boss for the whole of lower Chicago area has recently had a lot of problems with the police intercepting his people on the street. It is clear that the more drugs he sells the more, money he will make, but if he starts to sell too much, the police arrests start to become more frequent and he loses money.
Fed up with this situation, he decides he needs to find the optimal amount of drugs to put out on the streets: as much as possible, but not too much for the police raids to kick in. So one day he tells his brothers and sisters in crime to leave the room and picks up a pencil and a piece of paper to do some calculus.
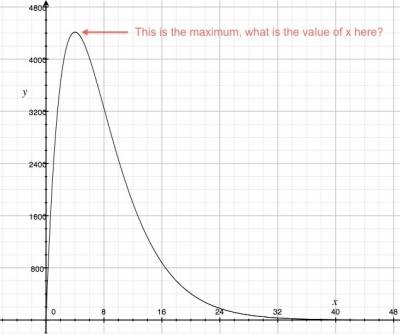
If $x$ is the amount of drugs he puts out on the street every day, then the amount of money he makes is given by the function: \[ f(x) = 3000x e^{-0.25x}, \] where the linear part $3000x$ represents his profits if there is no police and the $e^{-0.25x}$ represents the effects of the police stepping up their actions when more drugs is pumped on the street.
Looking at the function he asks “What is the value of $x$ which will give me the most profits from my criminal dealings?” Stated mathematically, he is asking for \[ \mathop{\text{argmax}}_x \ 3000x e^{-0.25x} \ = \ ?, \] which is read “find the value of the argument $x$ that gives the maximum value of $f(x)$.”
He remembers the steps required to find the maximum of a function from a conversation with a crooked stock trader he met in prison. First he must take the derivative of the function. Because the function is a product of two functions, he has to use the product rule $(fg)' = f'g+fg'$. When he takes the derivative of $f(x)$ he gets: \[ f'(x) = 3000e^{-0.25x} + 3000x(-0.25)e^{-0.25x}. \]
Whenever $f'(x)=0$ this means the function $f(x)$ has zero slope. A maximum is just the kind of place where there is zero slope: think of the peak of a mountain that has steep slopes to the left and to right, but right at the peak it is momentarily horizontal.
So when is the derivative zero? \[ f'(x) = 3000e^{-0.25x} + 3000x(-0.25)e^{-0.25x} = 0. \] We can factor out the $3000$ and the exponential function to get \[ 3000e^{-0.25x}( 1 -0.25x) = 0. \] Now $3000\neq0$ and the exponential function $e^{-0.25x}$ is never equal to zero either so it must be the term in the bracket which is equal to zero: \[ (1 -0.25x) = 0, \] or $x=4$. The slope of $f(x)$ is equal to zero when $x=4$. This correspond to the peak of the curve.
Right then and there the crime boss called his posse back
into the room and proudly announced that from now on his
organization will put out exactly four kilograms of drugs
on the street per day.
“Boss, how much will we make per day if we sell four kilograms?”, asks
one of the gangsters in sweatpants.
“We will make the maximum possible!”, replies the boss.
“Yes I know Boss, but how much money is the maximum?”
The dude in sweatpants is asking a good question.
It is one thing to know where the maximum occurs and it is another to know
the value of the function at this point.
He is asking the following mathematical question:
\[
\max_x \ 3000x e^{-0.25x} \ = \ ?.
\]
Since we already know the value $x^*=4$ where the maximum occurs,
we simply have to plug it into the function $f(x)$ to get:
\[
\max_x f(x) = f(4) = 3000(4)e^{-0.25(4)} = \frac{12000}{e} \approx 4414.55.
\]
After that conversation, everyone, including the boss, started to question
their choice of occupation in life.
Is crime really worth it when you do the numbers?
As you may know, the system is obsessed with this whole optimization thing. Optimize to make more profits, optimize to minimize costs, optimize stealing of natural resources from Third World countries, optimize anything that moves basically. Therefore, the system wants you, the young and powerful generation of the future, to learn this important skill and become faithful employees in the corporations. They want you to know so that you can help them optimize things, so that the whole enterprise will continue to run smoothly.
Mathematics makes no value judgments about what should and should not be optimized; this part is up to you. If, like me, you don't want to use optimization for system shit, you can use calculus for science. It doesn't matter whether it will be physics or medicine or building your own business, it is all good. Just stay away from the system. Please do this for me.
Optimization algorithm
In this section we show and explain the details of the algorithm for finding the maximum of a function. This is called optimization, as in finding the optimal value(s).
Say you have the function $f(x)$ that represents a real world phenomenon. For example, $f(x)$ could represent how much fun you have as a function of alcohol consumed during one evening. We all know that too much $x$ and the fun stops and you find yourself, like the Irish say, “talking to God on the big white phone.” Too little $x$ and you might not have enough Dutch courage to chat up that girl/guy from the table across the room. To have as much fun as possible, you want to find the alcohol consumption $x^*$ where $f$ takes on its maximum value.
This is one of the prominent applications of calculus (optimization not alcohol consumption). This is why you have been learning about all those limits, derivative formulas and differentiation rules in the previous sections.
Definitions
- $x$: the variable we have control over.
- $[x_i,x_f]$: some interval of values where $x$ can be chosen from, i.e., $x_i \leq x \leq x_f$. These are the constraints on the optimization problem. (For the drinking optimization problem $x\geq 0$ since you can't drink negative alcohol, and probably $x<2$ (in litres of hard booze) because roughly around there you will die from alcohol poisoning. So we can say we are searching for the optimal amount of alcohol $x$ in the interval $[0,2]$.)
- $f(x)$: the function we want to optimize. This function has to be differentiable, meaning that we can take its derivative.
- $f'(x)$: The derivative of $f(x)$. The derivative contains the information about the slope of $f(x)$.
- maximum: A place where the function reaches a peak. Furthermore, when there are multiple peaks, we call the highest of them the global maximum, while all others are called local maxima.
- minimum: A place where the function reaches a low point: the bottom of a valley. The global minimum is the lowest point overall, whereas a local minimum is only the minimum in some neighbourhood.
- extremum: An extremum is a general term that includes maximum and minimum.
- saddle point: A place where $f'(x)=0$ but that point is neither a max nor a min. Ex: $f(x)=x^5$ when $x=0$.
Suppose some function $f(x)$ has a global maximum at $x^*$ and the value of that maximum is $f(x^*)=M$. The following mathematical notations apply:
- $\mathop{\text{argmax}}_x \ f(x)=x^*$, to refer the location (the argument) where the maximum occurs.
- $\max_x \ f(x) = M$, to refer to the maximum value.
Algorithm for finding extrema
Input: Some function $f(x)$ and a constraint region $C=[x_i,x_f]$.
Output: The location and value of all maxima and minima of $f(x)$.
You should proceed as follows to find the extrema of a function:
- First look at $f(x)$. If you can, plot it. If not, just try to imagine it.
- Find the derivative $f'(x)$.
- Solve the equation $f'(x)=0$. There will usually be multiple solutions. Make a list of them. We will call this the list of candidates.
- For each candidate $x^*$ in the list check if is a max, a min or a saddle point.
- If $f'(x^*-0.1)$ is positive and $f'(x^*+0.1)$ is negative, then the point $x^*$ is a max.
The function was going up, then flattens at $x^*$ then goes down after $x^*$. Therefore $x^*$ must be a peak.
- If $f'(x^*-0.1)$ is negative and $f'(x^*+0.1)$ is positive, then the point $x^*$ is a min.
The function goes down, flattens then goes up, so the point must be a minimum.
- If $f'(x^*-0.1)$ and $f'(x^*+0.1)$ have the same sign, then the point $x^*$ is a saddle point. Remove it from the list of candidates.
- Now go through the list one more time and reject all candidates $x^*$ that do not satisfy the constraints C. In other words if $x\in [x_i,x_f]$ it stays, but if $x \not\in [x_i,x_f]$, we remove it since it is not feasible. For example, if you have a candidate solution in the alcohol consumption problem that says you should drink 5[L] of booze, you have to reject it, because otherwise you would die.
- Add $x_i$ and $x_f$ to the list of candidates. These are the boundaries of the constraint region and should also be considered. If no constrain was specified use the default constraint $x \in \mathbb{R}\equiv[-\infty,\infty]$ and add $-\infty$ and $\infty$ to the list.
- For each candidate $x^*$, calculate the function value $f(x^*)$.
The resulting list is a list of local extrema: maxima, minima and endpoints. The global maximum is the largest value from the list of local maxima. The global minimum is the smallest of the local minima.
Note that in dealing with points at infinity like $x^*=\infty$, you are not actually calculating a value but the limit $\lim_{x\to\infty}f(x)$. Usually the function either blows up $f(\infty)=\infty$ (like $x$, $x^2$, $e^x$, $\ldots$), drops down indefinitely $f(\infty)=-\infty$ (like $-x$, $-x^2$, $-e^x$, $\ldots$), or reaches some value (like $\lim_{x\to\infty} \frac{1}{x}=0, \ \lim_{x\to\infty} e^{-x}=0$). If a function goes to positive $\infty$ it doesn't have a global maximum: it simply keeps growing indefinitely. Similarly, functions that go towards negative $\infty$ don't have a global minimum.
Example 1
Find all the maxima and minima of the function \[ f(x)=x^4-8x^2+356. \]
Since no interval is specified we will use the default interval $x \in \mathbb{R}= -\infty,\infty$. Let's go through the steps of the algorithm.
- We don't know how a $x^4$ function looks like, but it is probably similar to the $x^2$ – it goes up to infinity on the far left and the far right.
- Taking the derivative is simple for polynomials:
\[ f'(x)=4x^3-16x. \]
- Now we have to solve
\[ 4x^3-16x=0, \]
which is the same as
\[
4x(x^2-4)=0,
\]
which is the same as
\[
4x(x-2)(x+2)=0.
\]
So our list of candidates is $\{ x=-2, x=0, x=2 \}$.
- For each of these we have to check if it is a max, a min or a saddle point.
- For $x=-2$, we check $f'(-2.1)=4(-2.1)(-2.1-2)(-2.1+2) < 0$ and
$f'(-1.9)=4(-1.9)(-1.9-2)(-1.9+2) > 0$ so $x=-2$ must be minimum.
- For $x=0$ we try $f'(-0.1)=4(-0.1)(-0.1-2)(-0.1+2) > 0$ and
$f'(0.1)=4(0.1)(0.1-2)(0.1+2) < 0$ so we have a maximum.
- For $x=2$, we check $f'(1.9)=4(1.9)(1.9-2)(1.9+2) < 0$
and $f'(2.1)=4(2.1)(2.1-2)(2.1+2) > 0$ so $x=2$ must be a minimum.
- We don't have any constraints so all of the above candidates make the cut.
- We add the two constraint boundaries $-\infty$ and $\infty$ to the list of candidates. At this point our final shortlist of candidates contains $\{ x=-\infty, x=-2, x=0, x=2, x=\infty \}$.
- We now evaluate the function $f(x)$ for each of the values to
get location-value pairs $(x,f(x))$ like so: $\{ (-\infty,\infty),$ $(-2,340),$ $(0,356),$ $(2,340),$ $(\infty,\infty) \}$.
Note that $f(\infty)=\lim_{x\to\infty} f(x) =$ $\infty^4 - 8\infty^2+356$ $= \infty$ and same for $f(-\infty)=\infty$.
We are done now. The function has no global maximum since it goes up to infinity. It has a local maximum at $x=0$ with value $356$ and two global minima at $x=-2$ and $x=2$ both of which have value $340$. Thank you, come again.
Alternate algorithm
Instead of checking nearby points to the left and to the right of each critical point, we can use an alternate Step 4 of the algorithm known as the second derivative test. Recall that the second derivative tells you the curvature of the function: if the second derivative is positive at a critical point $x^*$, then the point $x^*$ must be a minimum. If on the other hand the second derivative at a critical point is negative, then the function must be a maximum at $x^*$. If the second derivative is zero, the test is inconclusive.
Alternate Step 4
- For each candidate $x^*$ in the list check if is a max, a min or a saddle point.
- If $f^{\prime\prime}(x^*) < 0$ then $x^*$ is a max.
- If $f^{\prime\prime}(x^*) > 0$ then $x^*$ is a min.
- If $f^{\prime\prime}(x^*) = 0$ then, revert back to checking nearby values: $f'(x^*-\epsilon)$ and $f'(x^*+\epsilon)$,
to determine if $x^*$ is max, min or saddle point.
Limitations
The above optimization algorithm applies to differentiable functions of a single variable. It just happens to be that most functions you will face in life are of this kind, so what you have learned is very general. Not all functions are differentiable however. Functions with sharp corners like the absolute value function $|x|$ are not differentiable everywhere and therefore we cannot use the algorithms above. Functions with jumps in them (like the Heaviside step function) are not continuous and therefore not differentiable either so the algorithm cannot be used on them either.
There are also more general kinds of functions and optimization scenarios. We can optimize functions of multiple variables $f(x,y)$. You will learn how to do this in multivariable calculus. The techniques will be very similar to the above, but with more variables and intricate constraint regions.
At last, I want to comment on the fact that you can only maximize one function. Say the Chicago crime boss in the example above wanted to maximize his funds $f(x)$ and his gangster street cred $g(x)$. This is not a well posed problem, either you maximize $f(x)$ or you maximize $g(x)$, but you can't do both. There is no reason why a single $x$ will give the highest value for $f(x)$ and $g(x)$. If both functions are important to you, you can make a new function that combines the other two $F(x)=f(x)+g(x)$ and maximize $F(x)$. If gangster street cred is three times more important to you than funds, you could optimize $F(x)=f(x)+3g(x)$, but it is mathematically and logically impossible to maximize two things at the same time.
Exercises
The function $f(x)=x^3-2x^2+x$ has a local maximum on the interval $x \in [0,1]$. Find where this maximum occurs and the value of $f$ at that point. ANS:$\left(\frac{1}{3},\frac{4}{27}\right)$.
Integrals
We now begin our discussion of integrals, which is the second topic in calculus. Integrals are a fancy way to add up the value of a function to get “the whole” or the sum of its values over some interval. Normally integral calculus is taught as a separate course after differential calculus, but this separation is not necessary and can be even counter-productive.
The derivative $f'(x)$ measures the change in $f(x)$, i.e., the derivative measures the differences in $f$ for an $\epsilon$-small change in the input variable $x$: \[ \text{derivative } \ \propto \ \ f(x+\epsilon)-f(x). \] Integrals, on the other hand, measure the sum of the values of $f$, between $a$ and $b$ at regular intervals of $\epsilon$: \[ \text{integral } \propto \ \ \ f(a) + f(a+\epsilon) + f(a+2\epsilon) + \ldots + f(b-2\epsilon) + f(b-\epsilon). \] The best way to understand integration is to think of it as the opposite operation of differentiation: adding up all the changes in function gives you the function value.
In Calculus I we learned how to take a function $f(x)$ and find its derivative $f'(x)$. In integral calculus, we will be given a function $f(x)$ and we will be asked to find its integral on various intervals.
Definitions
These are some concepts that you should already be familiar with:
- $\mathbb{R}$: The set of real numbers.
- $f(x)$: A function:
\[ f: \mathbb{R} \to \mathbb{R}, \]
which means that $f$ takes as input some number (usually we call that number $x$)
and it produces as an output another number $f(x)$ (sometimes we also give an alias for the output $y=f(x)$).
* $\lim_{\epsilon \to 0}$: limits are the mathematically rigorous
way of speaking about very small numbers.
* $f'(x)$: the derivative of $f(x)$ is the rate of change of $f$ at $x$:
\[
f'(x) = \lim_{\epsilon \to 0} \frac{f(x+\epsilon)\ - \ f(x)}{\epsilon}.
\]
The derivative is also a function of the form
\[
f': \mathbb{R} \to \mathbb{R}.
\]
The function $f'(x)$ represents the //slope// of
the function $f(x)$ at the point $(x,f(x))$.
NOINDENT These are the new concepts:
- $x_i=a$: where the integral starts, i.e., some given point on the $x$ axis.
- $x_f=b$: where the integral stops.
- $A(x_i,x_f)$: The value of the area under the curve $f(x)$ from $x=x_i$ to $x=x_f$.
- $\int f(x)\; dx$: the integral of $f(x)$.
More precisely we can define the antiderivative of $f(x)$ as follows:
\[
F(b) = \int_0^b f(x) dx \ \ + \ \ F(0).
\]
The area $A$ of the region under $f(x)$ from $x=a$ to $x=b$ is given by:
\[
\int_a^b f(x) dx = F(b) - F(a) = A(a,b).
\]
The $\int$ sign is a mnemonic for //sum//.
Indeed the integral is nothing more than the "sum" of $f(x)$ for all values of $x$ between $a$ and $b$:
\[
A(a,b) = \lim_{\epsilon \to 0}\left[ \epsilon f(a) + \epsilon f(a+\epsilon) + \ldots + \epsilon f(b-2\epsilon) + \epsilon f(b-\epsilon) \right],
\]
where we imagine the total area broken-up into thin rectangular
strips of width $\epsilon$ and height $f(x)$.
* The name antiderivative comes from the fact that
\[
F'(x) = f(x),
\]
so we have:
\[
F(x) \!= \text{int}\!\left( \text{diff}( F(x) ) \right)= \int_0^x \left( \frac{d}{dt} F(t) \right) \ dt = \int_0^x \! f'(t) \ dt = F(x).
\]
Indeed, the //fundamental theorem of calculus//,
tells us that the derivative and integral are //inverse operations//,
so we also have:
\[
f(x) \!= \text{diff}\!\left( \text{int}( f(x) ) \right)
= \frac{d}{dx}\left[\int_0^x f(t) dt\right]
= \frac{d}{dx}\left[ F(x) - F(0) \right]
= f(x).
\]
Formulas
Riemann Sum
The Riemann sum is a good way to define the integral from first principles. We will brake up the area under the curve into many little strips of height varying according to $f(x)$. To obtain the total area, we sum-up all the areas of the rectangles. We will discuss Riemann sums in the next section, but first we look at the properties of integrals.
Area under the curve
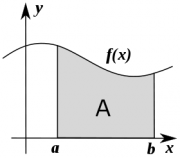 The value of an integral corresponds to the area $A$,
under the curve $f(x)$ between $x=a$ and $x=b$:
\[
A(a,b) = \int_a^b f(x) \; dx.
\]
The value of an integral corresponds to the area $A$,
under the curve $f(x)$ between $x=a$ and $x=b$:
\[
A(a,b) = \int_a^b f(x) \; dx.
\]
For certain functions it is possible to find an anti-derivative function $F(\tau)$, which describes the “running total” of the area under the curve starting from some arbitrary left endpoint and going all the way until $t=\tau$. We can compute the area under $f(t)$ between $a$ and $b$ by looking at the change in $F(\tau)$ between $a$ and $b$. \[ A(a,b) = F(b) - F(a). \]
We can illustrate the reasoning behind the above formula graphically:
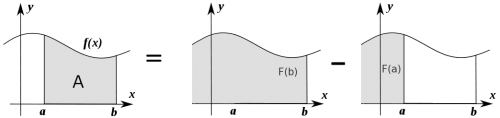 The area $A(a,b)$ is equal to the “running total” until $x=b$
minus the running total until $x=a$.
The area $A(a,b)$ is equal to the “running total” until $x=b$
minus the running total until $x=a$.
Indefinite integral
The problem of finding the anti-derivative is also called integration. We say that we are finding an indefinite integral, because we haven't defined the limits $x_i$ and $x_f$.
So an integration problem is one in which you are given the $f(x)$, and you have to find the function $F(x)$. For example, if $f(x)=3x^2$, then $F(x)=x^3$. This is called “finding the integral of $f(x)$”.
Definite integrals
A definite integral specifies the function to integrate as well as the limits of integration $x_i$ and $x_f$: \[ \int_{x_i=a}^{x_f=b} f(x) \; dx = \int_{a}^{b} f(x) \; dx. \]
To find the value of the definite integral first calculate the indefinite integral (the antiderivative): \[ F(x) = \int f(x)\; dx, \] and then use it to compute the area as the difference of $F(x)$ at the two endpoints: \[ A(a,b) = \int_{x=a}^{x=b} f(x) \; dx = F(b) - F(a) \equiv F(x)\bigg|_{x=a}^{x=b}. \]
Note the new “vertical bar” notation: $g(x)\big\vert_{\alpha}^\beta=g(\beta)-g(\alpha)$, which is shorthand notation to denote the expression to the left evaluated at the top limit minus the same expression evaluated at the bottom limit.
Example
What is the value of the integral $\int_a^b x^2 \ dx$? We have \[ \int_a^b x^2 dx = \frac{1}{3}x^3\bigg|_{x=a}^{x=b} = \frac{1}{3}(b^3-a^3). \]
Signed area
If $a < b$ and $f(x) > 0$, then the area \[ A(a,b) = \int_{a}^{b} f(x) \ dx, \] will be positive.
However if we swap the limits of integration, in other words we start at $x=b$ and integrate backwards all the way to $x=a$, then the area under the curve will be negative! This is because $dx$ will always consist of tiny negative steps. Thus we have that: \[ A(b,a) = \int_{b}^{a} f(x) \ dx = - \int_{a}^{b} f(x) \ dx = - A(a,b). \] In all expressions involving integrals, if you want to swap the limits of integration, you have to add a negative sign in front of the integral.
The area could also come out negative if we integrate a negative function from $a$ to $b$. In general, if $f(x)$ is above the $x$ axis in some places these will be positive contributions to the total area under the curve, and places where $f(x)$ is below the $x$ axis will count as negative contributions to the total area $A(a,b)$.
Additivity
The integral from $a$ to $b$ plus the integral from $b$ to $c$ is equal to the integral from $a$ to $c$: \[ A(a,b) + A(b,c) = \int_a^b f(x) \; dx + \int_b^c f(x) \; dx = \int_a^c f(x) \; dx = A(a,c). \]
Linearity
Integration is a linear operation: \[ \int [\alpha f(x) + \beta g(x)]\; dx = \alpha \int f(x)\; dx + \beta \int g(x)\; dx, \] for arbitrary constants $\alpha, \beta$.
Recall that this was true for differentiation: \[ [\alpha f(x) + \beta g(x)]' = \alpha f'(x) + \beta g'(x), \] so we can say that the operations of calculus as a whole are linear operations.
The integral as a function
So far we have looked only at definite integrals where the limits of integration were constants $x_i=a$ and $x_f=b$, and so the integral was a number $A(a,b)$.
More generally, we can have one (or more) variable integration limits. For example we can have $x_i=a$ and $x_f=x$. Recall that area under the curve $f(x)$ is, by definition, computed as a difference of the anti-derivative function $F(x)$ evaluated at the limits: \[ A(x_i,x_f) = A(a,x) = F(x) - F(a). \]
The expression $A(a,x)$ is a bit misleading as a function name since it looks like both $a$ and $x$ are variable when in fact $a$ is a constant parameter, and only $x$ is the variable. Let's call it $A_a(x)$ instead. \[ A_a(x) = \int_a^x f(t) \; dt = F(x) - F(a). \]
Two observations. First, note that $A_a(x)$ and $F(x)$ differ only by a constant, so in fact the anti-derivative is the integral up to a constant which is usually not important. Second, note that because the variable $x$ appears in the upper limit of the expression, I had to use a dummy variable $t$ inside the integral. If we don't use a different variable, we could confuse the running variable inside the integral, with the limit of integration.
Fundamental theorem of calculus
Let $f(x)$ be a continuous function, and let $F(x)$ be its antiderivative on the interval $[a,b]$: \[ F(x) = \int_a^x f(t) \; dt, \] then, the derivative of $F(x)$ is equal to $f(x)$: \[ F'(x) = f(x), \] for any $x \in (a,b)$.
We see that differentiation and integration are inverse operations: \[ F(x) \!= \text{int}\left( \text{diff}( F(x) ) \right)= \int_0^x \left( \frac{d}{dt} F(t) \right) \; dt = \int_0^x f(t) \; dt = F(x) + C, \] \[ f(x) \!= \text{diff}\left( \text{int}( f(x) ) \right) = \frac{d}{dx}\left[\int_0^x f(t) dt\right] = \frac{d}{dx}\left[ F(x) - F(0) \right] = f(x). \]
We can think of the inverse operators $\frac{d}{dt}$ and $\int\cdot dt$ symbolically on the same footing as the other mathematical operations that you know about. The usual equation solving techniques can then be applied to solve equations which involve derivatives. For example, suppose that you want to solve for $f(t)$ in the equation \[ \frac{d}{dt} \; f(t) = 100. \] To get to $f(t)$ we must undo the $\frac{d}{dt}$ operation. We apply the integration operation to both sides of the equation: \[ \int \left(\frac{d}{dt}\; f(t)\right) dt = f(t) = \int 100\;dt = 100t + C. \] The solution to the equation $f'(t)=100$ is $f(t)=100t+C$ where $C$ is called the integration constant.
Gimme some of that
OK, enough theory. Let's do some anti-derivatives. But how does one do anti-derivatives? It's in the name, really. Derivative and anti. Whatever the derivative does, the integral must do the opposite. If you have: \[ F(x)=x^4 \qquad \overset{\frac{d}{dx} }{\longrightarrow} \qquad F'(x)=4x^3 \equiv f(x), \] then it must be that: \[ f(x)=4x^3 \qquad \overset{\ \int\!dx }{\longrightarrow} \qquad F(x)=x^4 + C. \] Each time you integrate, you will always get the answer up to an arbitrary additive constant $C$, which will always appear in your answers.
Let us look at some more examples:
- The integral of $\cos\theta$ is:
\[ \int \cos\theta \ d\theta = \sin\theta + C, \]
since $\frac{d}{d\theta}\sin\theta = \cos\theta$,
and similarly the integral for $\sin\theta$ is:
\[
\int \sin\theta \ d\theta = - \cos\theta + C,
\]
since $\frac{d}{d\theta}\cos\theta = - \sin\theta$.
* The integral of $x^n$ for any number $n \neq -1$ is:
\[
\int x^n \ dx = \frac{1}{n+1}x^{n+1} + C,
\]
since $\frac{d}{d\theta}x^n = nx^{n-1}$.
* The integral of $x^{-1}=\frac{1}{x}$ is
\[
\int \frac{1}{x} \ dx = \ln x + C,
\]
since $\frac{d}{dx}\ln x = \frac{1}{x}$.
I could go on but I think you get the point: all the derivative formulas you learned can be used in the opposite direction as an integral formula.
With limits now
What is the area under the curve $f(x)=\sin(x)$, between $x=0$ and $x=\pi$? First we take the anti derivative \[ F(x) = \int \sin(x) \ dx = - \cos(x) + C. \] Now we calculate the difference between $F(x)$ at the end-point minus $F(x)$ at the start-point: \[ \begin{align} A(0,\pi) & = \int_{x=0}^{x=\pi} \sin(x) \ dx \nl & = \underbrace{\left[ - \cos(x) + C \right]}_{F(x)} \bigg\vert_0^\pi \nl & = [- \cos\pi + C] - [- \cos(0) + C] \nl & = \cos(0) - \cos\pi \ \ = \ \ 1 - (-1) = 2. \end{align} \]
The constant $C$ does not appear in the answer, because it is in both the upper and the lower limits.
What next
If integration is nothing more than backwards differentiation and you already know differentiation inside out from differential calculus, you might be wondering what you are going to do during an entire semester of integral calculus. For all intents and purposes, if you understood the conceptual material in this section, then you understand integral calculus. Give yourself a tap on the back—you are done.
The establishment, however, doesn't just want you to know the concepts of integral calculus, but also wants you to know how to apply them in the real world. Thus, you need not only understand, but also practice the techniques of integration. There are a bunch of techniques, which allow you to integrate complicated functions. For example, if I asked you to integrate $f(x)=\sin^2(x) = (\sin(x))^2$ from $0$ to $\pi$ and you look in the formula sheet you won't find a function $F(x)$ who's derivative equals $f(x)$. So how do we solve: \[ \int_0^\pi \sin^2(x) \ dx = ?. \] One way to approach this problem is to use the trigonometric identity which says that $\sin^2(x)=\frac{1-\cos(2x)}{2}$ so we will have \[ \int_0^\pi \! \sin^2(x) dx = \int_0^\pi \left[ \frac{1}{2} - \frac{1}{2}\cos(2x) \right] dx = \underbrace{ \frac{1}{2} \int_0^\pi 1 \ dx}_{T_1} - \underbrace{ \frac{1}{2} \int_0^\pi \cos(2x) \ dx }_{T_2}. \] The fact that we can split the integral into two parts, and factor out the constant $\frac{1}{2}$ comes from the fact that integration is linear.
Let's continue the calculation of our integral, where we left off: \[ \int_0^\pi \sin^2(x) \ dx = T_1 - T_2. \] The value of the integral in the first term is: \[ T_1 = \frac{1}{2} \int_0^\pi 1 \ dx = \frac{1}{2} x \bigg\vert_0^\pi = \frac{\pi-0}{2} =\frac{\pi}{2}. \] The value of the second term is \[ T_2 =\frac{1}{2} \int_0^\pi \cos(2x) \ dx = \frac{1}{4} \sin(2x) \bigg\vert_0^\pi = \frac{\sin(2\pi) - \sin(0) }{4} = \frac{0 - 0 }{4} = 0. \] Thus we find the final answer for the integral to be: \[ \int_0^\pi \sin^2(x) \ dx = T_1 - T_2 = \frac{\pi}{2} - 0 = \frac{\pi}{2}. \]
Do you see how integration can quickly get tricky? You need to learn all kinds of tricks to solve integrals. I will teach you all the necessary tricks, but to become proficient you can't just read: you have to practice the techniques. Promise me you will practice! As my student, I expect nothing less than a total ass kicking of the questions you will face on the final exam.
Riemann sum
We defined the integral operation $\int f(x)\;dx$ as the inverse operation of $\frac{d}{dx}$, but it is important to know how to think of the integral operation on its own. No course on calculus would be complete without a telling of the classical “rectangles story” of integral calculus.
Definitions
- $x$: $\in \mathbb{R}$, the argument of the function.
- $f(x)$: a function $f \colon \mathbb{R} \to \mathbb{R}$.
- $x_i$: where the sum starts, i.e., some given point on the $x$ axis.
- $x_f$: where the sum stops.
- $A(x_i,x_f)$: Exact value of the area under the curve $f(x)$ from $x=x_i$ to $x=x_f$.
- $S_n(x_i,x_f)$: An approximation to the area $A$ in terms of
$n$ rectangles.
- $s_k$: Area of $k$-th rectangle when counting from the left.
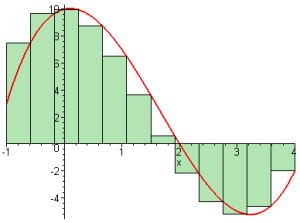 In the picture on the right, we are approximating the function $f(x)=x^3-5x^2+x+10$ between $x_i=-1$ and $x_f=4$ using $n=12$ rectangles.
The sum of the areas of the 12 rectangles is what we call $S_{12}(-1,4)$.
We say that $S_{12}(-1,4) \approx A(-1,4)$.
In the picture on the right, we are approximating the function $f(x)=x^3-5x^2+x+10$ between $x_i=-1$ and $x_f=4$ using $n=12$ rectangles.
The sum of the areas of the 12 rectangles is what we call $S_{12}(-1,4)$.
We say that $S_{12}(-1,4) \approx A(-1,4)$.
Formulas
The main formula you need to know is that the combined area approximation is given by the sum of the areas of the little rectangles: \[ S_n = \sum_{k=1}^{n} s_k. \]
Each of the little rectangles has an area $s_k$ given by its height multiplied by its width. The height of each rectangle will vary, but the width is constant. Why constant? Riemann figured that having each rectangle with a constant width $\Delta x$ would make it very easy to calculate the approximation. The total length of the interval from $x_i$ to $x_f$ is $(x_f-x_i)$. If we divide this length into $n$ equally spaced segments, each of width $\Delta x$ given by: \[ \Delta x = \frac{x_f - x_i}{n}. \]
OK, we have the formula for the width figured out, let's see what the height will be for the $k$-th rectangle, where $k$ is our counter from left to right in the sequence of rectangles. The height of the function varies as we move along the $x$ axis. For the rectangles, we pick isolated “samples” of $f(x)$ for the following values \[ x_k = x_i + k\Delta x, \textrm{ for } k \in \{ 1, 2, 3, \ldots, n \}, \] all of them equally spaced $\Delta x$ apart.
The area of each rectangle is height times width: \[ s_k = f(x_i + k\Delta x)\Delta x. \]
Now, my dear students, I want you to stare at the above equation and do some simple calculations to check that you understand. There is no point in continuing if you are just taking my word for it. Verify that when $k=1$, the formula gives the area of the first little rectangle. Verify also that when $k=n$, the formula for the $x_n$ gives the right value ($x_f$).
Ok let's put our formula for $s_k$ in the sum where it belongs. The Riemann sum approximation using $n$ rectangles is given by \[ S_n = \sum_{k=1}^{n} f(x_i + k\Delta x)\Delta x, \] where $\Delta x =\frac{|x_f - x_i|}{n}$.
Let us get back to the picture where we try to approximate the area under the curve $f(x)=x^3-5x^2+x+10$ by using 12 pieces.
For this scenario the value we would get for the 12-rectangle
approximation to the area under the curve with
\[
S_{12} = \sum_{k=1}^{12} f(x_i + k\Delta x)\Delta x = 11.802662.
\]
You shouldn't trust me though, but always check for yourself using
live.sympy.org by typing in the following expressions:
>>> n=12.0; xk = -1 + k*5/n; sk = (xk**3-5*xk**2+xk+10)*(5/n);
>>> summation( sk, (k,1,n) )
11.802662...
More is better
Who cares though? This is such a crappy approximation! You can clearly see that some rectangles lie outside of the curve (overestimates), and some are too far inside (underestimates). You might be wondering why I wasted so much of your time to achieve such a lousy approximation. We have not been wasting our time. You see, the Riemann sum formula $S_n$ gets better and better as you cut the region into smaller and smaller rectangles.
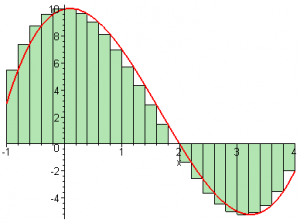
With $n=25$, we get a more fine grained approximation
in which the sum of the rectangles is given by:
\[
S_{25} = \sum_{k=1}^{25} f(x_i + k\Delta x)\Delta x = 12.4.
\]
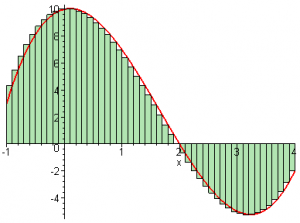 Then for $n=50$ we get:
\[
S_{50} = 12.6625.
\]
Then for $n=50$ we get:
\[
S_{50} = 12.6625.
\]
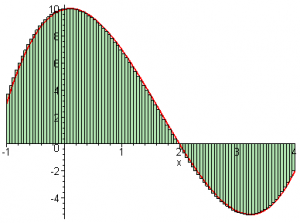 For $n=100$ the sum of the rectangles areas is starting to look pretttttty much like the function.
The calculation gives us $S_{100} = 12.790625$.
For $n=100$ the sum of the rectangles areas is starting to look pretttttty much like the function.
The calculation gives us $S_{100} = 12.790625$.
For $n=1000$ we get $S_{1000} = 12.9041562$ which is very close to the actual value of the area under the curve: \[ A(-1,4) = 12.91666\ldots \]
You see in the long run, when $n$ gets really large the rectangle approximation (Riemann sum) can be made arbitrarily good. Imagine you cut the region into $n=10000$ rectangles, wouldn't $S_{10000}(-1,4)$ be a pretty accurate approximation of the actual area $A(-1,4)$?
Integral
The fact that you can approximate the area under the curve with a bunch of rectangles is what integral calculus is all about. Instead of mucking about with bigger and bigger values of $n$, mathematicians go right away for the kill and make $n$ go to infinity.
In the limit of $n \to \infty$, you can get arbitrarily close approximations to the area under the curve. All this time, that which we were calling $A(-1,4)$ was actually the “integral” of $f(x)$ between $x=-1$ and $x=4$, or written mathematically: \[ A(-1,4) \equiv \int_{-1}^4 f(x)\;dx \equiv \lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \sum_{k=1}^{n} f(x_i + k\Delta x)\Delta x. \]
While it is not computationally practical to make $n \to \infty$,
we can convince ourselves that the approximation becomes better and
better as $n$ becomes larger. For example the approximation using $n=1$M rectangles is accurate up to the fourth decimal place as
can be verified using the following commands on live.sympy.org:
>>> n=1000000.0; xk = -1 + k*5/n; sk = (xk**3-5*xk**2+xk+10)*(5/n);
>>> summation( sk, (k,1,n) )
12.9166541666563
>>> integrate( x**3-5*x**2+x+10, (x,-1,4) ).evalf()
12.9166666666667
In practice, when we want to compute the area under the curve, we don't use Riemann sums. There are formulas for directly calculating the integrals of functions. In fact, you already know the integration formulas: they are simply the derivative formulas used in the opposite direction. In the next section we will discuss the derivative-integral inverse relationship in more details.
Links
[ Riemann sum wizard ]
http://mathworld.wolfram.com/RiemannSum.html
Fundamental theorem of calculus
Though it may not be apparent at first, the study of derivatives (Calculus I) and integrals (Calculus II) are intimately related. Differentiation and integration are inverse operations.
You have previously studied the inverse relationship for functions. Recall that for any bijective function $f$ (a one-to-one relationship) there exists an inverse functions $f^{-1}$ which undoes the effects of $f$: \[ (f^{-1}\!\circ f) (x) \equiv f^{-1}(f(x)) = x. \] and \[ (f \circ f^{-1}) (y) \equiv f(f^{-1}(y)) = y. \] The circle $\circ$ stands for composition of functions, i.e., first you apply one function and then you apply the second function. When you apply a function followed by its inverse to some input you get back the original input.
The integral is the “inverse operation” to the derivative. If perform the integral operation followed by the derivative operation on some function, you will get back the same function. This is stated more formally as the Fundamental Theorem of Calculus.
Statement
Let $f(x)$ be a continuous function and let $F(x)$ be its antiderivative on the interval $[a,b]$: \[ F(x) = \int_a^x f(t) \; dt, \] then, the derivative of $F(x)$ is equal to $f(x)$: \[ F'(x) = f(x), \] for any $x \in (a,b)$.
Thus, we see that differentiation is the inverse operation of integration. We obtained $F(x)$ by integrating $f(x)$. If we then take the derivative of $F(x)$ we get back to $f(x)$. It works the other way too. If you integrate a function and then take its derivative, you get back to the original function. Differential calculus and integral calculus are two sides of the same coin. If you understand this fact, then you understand something very deep about calculus.
Note that $F(x)$ is not a unique anti-derivative. We can add an arbitrary constant $C$ to $F(x)$ and it will still satisfy the above conditions since the derivative of a constant is zero.
Formulas
If you are given some function $f(x)$, you take its integral and then take the derivative of the result, you will get back the same function: \[ \left(\frac{d}{dx} \circ \int dx \right) f(x) \equiv \frac{d}{dx} \int_a^x f(t) dt = f(x). \] Alternately, you can first take the derivative, and then take the integral, and you will get back the function (up to a constant): \[ \left( \int dx \circ \frac{d}{dx}\right) f(x) \equiv \int_a^x f'(t) dt = f(x) - f(a). \]
Note that we had to use a dummy variable $t$ inside the integral since $x$ is used in the limit. Indeed, all integrals are functions of their limits and the inner variable is not important: we could write $\int_a^x f(y)\;dy$ or $\int_a^x f(z)\;dz$ or even $\int_a^x f(\xi)\;d\xi$ and the answer for all of these will be $F(x)-F(a)$.
Discussion
As a consequence of the Fundamental theorem, you can reuse all your knowledge of differential calculus to solve integrals.
Example: Reverse engineering
Suppose you are asked find this integral: \[ \int x^2 dx. \] Using the Fundamental theorem, we can rephrase this question as the search for some function $F(x)$ such that \[ F'(x) = x^2. \] Now since you remember your derivative formulas well, you will guess right away that $F(x)$ must contain a $x^3$ term. This is because you get back quadratic term when you take the derivative of cubic term. So we must have $F(x)=cx^3$, for some constant $c$. We must pick the constant that makes this work out: \[ F'(x) = 3cx^2 = x^2, \] therefore $c=\frac{1}{3}$ and the integral is: \[ \int x^2 dx = \frac{1}{3}x^3 + C. \] Did you see what just happened? We were able to take an integral using only derivative formulas and “reverse engineering”. You can check that, indeed, $\frac{d}{dx}\left[\frac{1}{3}x^3\right] = x^2$.
You can also use the Fundamental theorem to check your answers.
Example: Integral verification
Suppose a friend tells you that
\[
\int \ln(x) dx = x\ln(x) - x + C,
\]
but he is a shady character and you don't trust him.
How can you check his answer?
If you had a smartphone handy, you can check on live.sympy.org,
but what if you just have pen and paper?
If $x\ln(x) - x$ is really the antiderivative of $\ln(x)$, then
by the Fundamental theorem of calculus, if we take the derivative
we should get back $\ln(x)$. Let's check:
\[
\frac{d}{dx}\!\left[ x\ln(x) - x \right] = \underbrace{\frac{d}{dx}\!\left[x\right]\ln(x)+ x \left[\frac{d}{dx} \ln(x) \right]}_{\text{product rule} } - \frac{d}{dx}\left[ x \right] = 1\ln(x) + x\frac{1}{x} - 1 = \ln(x).
\]
OK, so your friend is correct.
Proof of the Fundamental theorem
There exists an unspoken rule in mathematics which states that if the word theorem appears in your writing, it has to be followed by the word proof. We therefore have to look into the proof of the Fundamental Theorem of Calculus (FTC). It is not that important that you understand the details of the proof, but I still recommend that you read this section for your general math culture. If you are in a rush though, feel free to skip it.
Before we get to the proof of the FTC, let me first introduce the squeezing principle, which will be used in the proof. Suppose you have three functions $f, \ell$, and $u$, such that: \[ \ell(x) \leq f(x) \leq u(x) \qquad \text{ for all } x. \] We say that $\ell(x)$ is a lower bound on $f(x)$ since its graph is always below that of $f(x)$. Similarly $u(x)$ is an upper bound on $f(x)$. Whatever the value of $f(x)$ is, we know that it is in between that of $\ell(x)$ and $u(x)$.
Suppose that $u(x)$ and $\ell(x)$ both converge to the same limit $L$: \[ \lim_{x\to a} \ell(x) = L, \quad \text{and} \quad \lim_{x\to a} u(x) = L, \] then it must be true that $f(x)$ also converges to the same limit: \[ \lim_{x\to a} f(x) = L. \] This is true because the function $f$ is squeezed between $\ell$ and $u$; it has no other choice than to converge to the same limit.
Proof
The formula for the derivative of $F(x)$ looks like this:
\[
F'(x) = \lim_{\epsilon \to 0} \frac{ F(x+\epsilon) - F(x) }{ \epsilon }.
\]
Let us look more closely at the term in the numerator, and express it in
terms of the definition of $F(x)$:
\[
\begin{align*}
{\color{red} F(x+\epsilon) - F(x) }
&= \int_a^{x+\epsilon} f(t) \ dt - \int_a^x f(t) \; dt \nl
&= {\color{red} \int_x^{x+\epsilon} f(t) \;dt }.
\end{align*}
\]
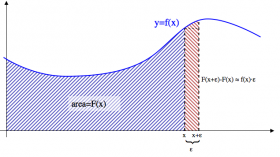 Thus the difference of $F(x+\epsilon)$ and $F(x)$ is just the integral of $f(x)$ between
$x$ and $x+\epsilon$.
The region which corresponds to this difference looks like a long narrow strip
of width $\epsilon$ and height varying according to $f(x)$:
\[
{\color{red} \int_x^{x+\epsilon} f(t) \ dt} \approx \underbrace{\text{width}}_{\epsilon}\times \underbrace{\text{height}}_?.
\]
Thus the difference of $F(x+\epsilon)$ and $F(x)$ is just the integral of $f(x)$ between
$x$ and $x+\epsilon$.
The region which corresponds to this difference looks like a long narrow strip
of width $\epsilon$ and height varying according to $f(x)$:
\[
{\color{red} \int_x^{x+\epsilon} f(t) \ dt} \approx \underbrace{\text{width}}_{\epsilon}\times \underbrace{\text{height}}_?.
\]
Let us define the maximum and minimum values of the height of the function $f(x)$ on that interval: \[ M \equiv \max_{t\in[x,x+\epsilon]} f(t), \qquad \qquad m \equiv \min_{t\in[x,x+\epsilon]} f(t). \] By definition, the quantities $m$ and $M$ provide a lower and an upper bound on the quantity we are trying to study: \[ \epsilon m \leq {\color{red} \int_x^{x+\epsilon} f(t) \ dt } \leq \epsilon M. \]
Recall that we said that $f$ is continuous in the theorem statement. If $f$ is continuous then as $\epsilon \to 0$ we will have: \[ \lim_{\epsilon \to 0} f(x+\epsilon ) = f(x). \]
In fact, as $\epsilon \to 0$ all the values of $f$ on the shortening interval $[x, x+\epsilon]$ will approach $f(x)$. In particular, both the minimum value $m$ and the maximum value $M$ will approach $f(x)$: \[ \lim_{\epsilon \to 0} f(x+\epsilon ) = f(x) = \lim_{\epsilon \to 0} m = \lim_{\epsilon \to 0} M. \]
So starting from the inequality, \[ \epsilon m \leq \int_x^{x+\epsilon} f(t) \ dt \leq \epsilon M, \] and taking the limit as $\epsilon \to 0$ we get: \[ \begin{align} \lim_{\epsilon \to 0} \epsilon m \leq & \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt \leq \lim_{\epsilon \to 0} \epsilon M, \nl \lim_{\epsilon \to 0} \epsilon f(x) \leq & \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt \leq \lim_{\epsilon \to 0} \epsilon f(x), \end{align} \]
Using the squeezing principle, we can affirm that \[ \qquad \qquad \lim_{\epsilon \to 0} \int_x^{x+\epsilon} f(t) \ dt = \lim_{\epsilon \to 0} \epsilon f(x). \qquad \qquad \qquad \qquad (\dagger) \]
To complete the proof, we substitute this expression into the derivative formula: \[ \begin{align} F'(x) & = \lim_{\epsilon \to 0} \frac{ F(x+\epsilon) - F(x) }{ \epsilon } \nl & = \lim_{\epsilon \to 0} \frac{\int_x^{x+\epsilon} f(t) \ dt }{\epsilon} \qquad \qquad \text{( by the definition of } F) \nl & = \lim_{\epsilon \to 0} \frac{ \epsilon f(t) }{\epsilon} \qquad \qquad \qquad \ \ \ ( \text{ by using equation } (\dagger)\ ) \nl & = f(x) \lim_{\epsilon \to 0} \frac{ \epsilon }{\epsilon} \nl & = f(x). \end{align} \]
We have thus proved that, for all continuous functions $f(x)$, we have: \[ \left(\frac{d}{dx} \circ \int dx \right) f(x) \equiv \frac{d}{dx} \int_a^x f(t) dt = f(x). \]
Integrals look at the “accumulation” of some quantity, whereas derivatives look at the incremental changes. In words, the Fundamental theorem says that the change in the accumulation of $f$ is just $f$ itself. Taking the derivative after taking an integral is as if someone asked you to add up a long list of numbers, and in each step state by how much the sum has changed. You don't need to add or subtract anything, just read out loud all the values in the list.
Links
Techniques of integration
The operation of “taking the integral” of some function is usually much more complicated than that of taking the derivative. In fact, you can take the derivative of any function – no matter how complex – simply by using the product rule, the chain rule and the derivative formulas. The same is not true for integrals.
There are plenty of integrals for which there is no closed form solution, which means that the function doesn't have an anti-derivative. There simply doesn't exist a simple procedure to follow, such that you input a function and you “turn the crank” until the integral comes out. Integration is a bit of an art.
What can we integrate then and how? Back in the day, scientists used to collect big tables with integral formulas for various complicated functions. That is what you can lookup-integrate.
There are also some integration techniques which can help you make complicated integrals simpler. Think of the techniques below, as adapters you need to use for cases when the function you are trying to integrate doesn't appear in your table of integrals, but a similar one is in the table.
The intended audience for this chapter are Calculus II students. This is exactly the kind of skills which you will be asked to show on the final. Instead of using the table of integrals to lookup some complicated integral, you have know how to make your own table.
For people interested in learning physics, I will honestly tell
you that if you skip this section you won't miss much.
You should just read the section on substitution which is the important one,
but don't bother reading the details of all the recipes for
integrating things.
For most intents and purposes, once you understand
what an integral is, you can use a computer to calculate it.
A good tool for this is the computer algebra system at live.sympy.org.
>>> integrate( sin(x) )
-cos(x)
>>> integrate( x**2*exp(x) )
x**2*exp(x) - 2*x*exp(x) + 2*exp(x)
You can use sympy for all your integration needs.
For those of you reading this book for general culture and who want to understand what calculus is without having to write a final exam on it, consider the next couple of pages as an ethnographic survol of the academic realities in which bright first year students are forced to integrate things they don't want to integrate and this for many long hours. Just picture some unlucky science student locked up in her room doing calculus and hundreds of dangling integrals grabbing at her with their hooks, keeping her away from her friends.
Actually, it is not that bad. There are, like, four tricks to learn and if you practice you can learn all of them in a week or so. Mastering these four tricks is essentially the entire Calculus II class. If you understand the material in this section, you will be done with integral calculus and you will have two months to chill.
Substitution
Say you are integrating some complicated function which contains a square root $\sqrt{x}$. You are wondering how to go about computing this integral: \[ \int \frac{1}{x - \sqrt{x}} \; dx \ = \ ? \]
Sometimes you can simplify the integral by substituting a new variable in the expression. Let $u=\sqrt{x}$. Substitution is like search-and-replace in a word processor. Every time you see the expression $\sqrt{x}$, you have to replace it with $u$: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{1}{u^2 - u} \; dx. \] Note that we also replaced $x=(\sqrt{x})^2$ with $u^2$.
We are not done yet. When you change from the $x$ variable to the $u$ variable, you have to be thorough. You have to change the $dx$ to a $du$ also. Can we just replace $dx$ with $du$? Unfortunately no, otherwise it would be like saying that the “short step” $du$ is equal in length to the “short step” $dx$, which is only true for the trivial substitution $u=x$.
To find the relation between the infinitesimals we take the derivative: \[ u(x) = \sqrt{x} \quad \Rightarrow \quad u'(x) = \frac{du}{dx} = \frac{1}{2\sqrt{x}}. \] For the next step, I need you to stop thinking about the expression $\frac{du}{dx}$ as a whole, but think about it as a rise-over-run fraction which can be split. Lets take the run $dx$ to the other side of the equation: \[ du = \frac{1}{2\sqrt{x}} \; dx, \] and to isolate $dx$, we multiply both sides by $2\sqrt{x}$: \[ dx = 2\sqrt{x} \; du = 2u \; du, \] where in the last step we used the fact that $u=\sqrt{x}$ again.
Now we have an expression for $dx$ entirely in terms of $u$'s. Let's see what that gives: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{1}{u^2 - u} 2u \; du = \int \frac{2}{u - 1} \; du. \]
We can now recognize the general form $\frac{1}{x}$ which has integral $\ln(x)$, but we have to account for the $-1$ shift inside the function. The integral therefore is: \[ \int \frac{1}{x - \sqrt{x}} \; dx = \int \frac{2}{u - 1} \; du = 2\ln(u-1) = 2\ln(\sqrt{x}-1). \] Note that in the last step we changed back to the $x$ variable, to give the final answer. The variable $u$ exists only in our calculation. We invented it out of thin air, when we said “Let $u=\sqrt{x}$” in the beginning. It is only natural to convert back to the original variable $x$ in the last step.
Notice what happened thanks to the substitution? The integral got simpler since we got rid of the square roots. On the outside we had just an extra $u$ appearing, which ends up cancelling with the $u$ in the denominator making things even simpler. In practice, substituting inside $f$ is the easy part. The hard part is making sure that our choice of substitution leads to a replacement for $dx$ which helps to make the integral simpler.
For definite integrals, i.e., integrals that have explicit limits, there is an extra step that we need to take when changing variables: we have to change the $x$ limits of integration to $u$ limits. In our expression, when changing to the $u$ variable, we would have to write: \[ \int_a^b \frac{1}{x - \sqrt{x}} \; dx = \int_{u(a)}^{u(b)} \frac{2}{u - 1} \; du. \] If the integral had asked for the integral between $x_i=4$ and $x_f=9$, then the new limits will be $u_i=\sqrt{4}=2$ and $u_f=\sqrt{9}=3$, so we will have: \[ \int_4^9 \frac{1}{x - \sqrt{x}} \; dx = \int_{2}^{3} \frac{2}{u - 1} \; du = 2\ln(u-1)\bigg|_2^3 = 2(\ln(2) - \ln(1)) = 2\ln(2). \]
OK, so let's recap. Substitution involves three steps:
- Replace all occurrences of $u(x)$ with $u$.
- Replace $dx$ with $\frac{1}{u'(x)}du$.
- If there are limits, replace the $x$ limits with $u$ limits.
If the resulting integral is simpler to solve then good for you!
Example
We are asked to find $\int \tan(x)\; dx$. We know that $\tan(x)=\frac{\sin(x)}{\cos(x)}$, so we can use the substitution $u=\cos(x)$, $du=-\sin(x)dx$ as follows: \[ \begin{eqnarray} \int \tan(x)dx &=& \int \frac{\sin(x)}{\cos(x)} dx \nl &=& \int \frac{-1}{u} du \nl &=& -\ln |u| + C \nl &=& -\ln |\cos(x) | + C. \end{eqnarray} \]
Integrals of trig functions
Because $\sin$, $\cos$, $\tan$ and the other trig functions are related, we can often express one function in terms of another in order to simplify integrals.
Recall the trigonometric identity: \[ \cos^2(x) + \sin^2(x) = 1, \] which is the statement of Pythagoras theorem.
If we choose to make the substitution $u=\sin(x)$, then we can replace all kinds of trigonometric terms with the new variable $u$: \[ \begin{align*} \sin^2(x) &= u^2, \nl \cos^2(x) &= 1 - \sin^2(x) = 1 - u^2, \nl \tan^2(x) &= \frac{\sin^2(x)}{\cos^2(x)} = \frac{u^2}{1-u^2}. \end{align*} \]
Of course the change of variable $u=\sin(x)$ means that you have to change the $du=u'(x) dx= \cos(x) dx$ so there better be something to cancel this $\cos(x)$ term in the integral.
Let me show you one example when things work out perfectly. Suppose $m$ is some arbitrary number, and you have to integrate: \[ \int \left(\sin(x)\right)^{m}\cos^{3}(x) \; dx \equiv \int \sin^{m}(x)\cos^{3}(x) \; dx. \] This integral contains $m$ powers of the $\sin$ function and a three powers of the $\cos$ function. Let us split the $\cos$ term into two parts: \[ \int \sin^{m}(x)\cos^{3}(x) \; dx = \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx. \]
Making the change of variable $u=\sin(x)$, $du=\cos(x)dx$ means that we can replace $\sin^m(x)$ by $u^m$, and $\cos^2(x)=1-u^2$ in the above expression to get: \[ \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx = \int u^{m} \left(1-u^2\right) \cos(x) \; dx. \]
Conveniently we happen to have $du= \cos(x)dx$ so the complete change of variable step is: \[ \begin{align*} \int \sin^{m}(x) \cos^{2}(x) \cos(x) \; dx & = \int u^{m} \left(1-u^2\right) \; du. \end{align*} \] This is what I was talking about earlier about “having an extra $\cos(x)$” to cancel the one that will appear from the $dx \to du$ change.
What is the answer then? It is a simple integral of a polynomial: \[ \begin{align*} \int u^{m} \left(1-u^2\right) \; du & = \int \left( u^{m} - u^{m+2} \right) \; du \nl & = \frac{1}{m+1}u^{m+1} - \frac{1}{m+3}u^{m+3} \nl & = \frac{1}{m+1}\sin^{m+1}(x) - \frac{1}{m+3}\sin^{m+3}(x). \end{align*} \]
You might be wondering how useful this substitution technique really is. I mean, how often do you have to integrate such a particular combinations of $\sin$ and $\cos$ powers so that the substitution works out perfectly. You would surprised! Sins and cos functions are used a lot in this thing called the Fourier transform, which is a way of expressing a sound wave $f(t)$ in terms of the frequencies it contains. Also on exams, they love to test this kinds of things. Teachers often want to check if you can do integrals and substitutions and they check if you remember all the trigonometric identities, which you are supposed to have learned in high school.
What other trigonometric functions should you know how to integrate? On an exam you should try any possible substitution you can think of, combined with any trigonometric identity that seems to simplify things. Some common ones are described below.
Cos
Just as we can substitute $\sin$, we can also substitute $u=\cos(x)$ and use $\sin^2(x)=1-u^2$. Again, this substitution only makes sense if you have a $\sin$ left over somewhere in the integral to cancel with the $du = -\sin(x)dx$.
Tan and sec
We can get some more mileage out of $\cos^2(x) + \sin^2(x) = 1$. If we divide both sides by $\cos^2(x)$ we get: \[ 1 + \tan^2(x) = \sec^2(x) \equiv \frac{1}{\cos^2(x)}, \] which is useful because $u=\tan(x)$ gives $du=\sec^2(x)dx$ so you can often “kill off” even powers of $\sec^2(x)$ in integrals of the form \[ \int\tan^m(x)\sec^n(x)\,dx. \]
Even powers of sin and cos
There are other trigonometric identities called half-angle and double-angle formulas which give you formulas like: \[ \sin^2(x)=\frac{1}{2}(1-\cos(2x)), \qquad \cos^2(x)=\frac{1}{2}(1+\cos(2x)). \]
These are useful if you have to integrate even powers of $\sin$ and $\cos$.
Example
Let's see how we would find $I=\int\sin^2(x)\cos^4(x)\,dx$: \[ \begin{eqnarray} I &=& \int\sin^2(x)\cos^4(x)\;dx \nl &=& \int \left( {1 \over 2}(1 - \cos(2x)) \right) \left( {1 \over 2}(1 + \cos(2x)) \right)^2 \;dx, \nl &=& \frac{1}{8} \int \left( 1 - \cos^2(2x) + \cos(2x)- \cos^3(2x) \right) \;dx. \nl & = & \frac{1}{8} \int \left( 1 - \cos^2(2x) + \cos(2x) -\cos^2(2x) \cos(2x) \right)\; dx \nl & = & \frac{1}{8} \int \left( 1 - \frac{1}{2} (1 + \cos(4x)) + \underline{\cos(2x)} - (\underline{1}-\sin^2(2x))\underline{\cos(2x)} \right) \; dx \nl & = & \frac{1}{8} \int \left( \frac{1}{2} - \frac{1}{2} \cos(4x) + \underbrace{\sin^2(2x)}_{u^2}\cos(2x) \right) \;dx \nl & = & \frac{1}{8} \left( \frac{x}{2} - \frac{\sin(4x)}{8} + \frac{\sin^3(2x)}{6} \right) \nl &=& \frac{x}{16}-\frac{\sin(4x)}{64} + \frac{\sin^3(2x)}{48}+C. \end{eqnarray} \]
There is no limit to the number of combinations of simplification steps you can try. On a homework question or an exam, the teacher will ask for something simple. You just have to find the right substitution.
Sneaky example
Sometime, the substitution is not obvious at all, as in the case of $\int \sec(x)dx$. To find the integral you need to know the following trick: multiply and divide by $\tan(x) +\sec(x) $.
What we get is \[ \begin{eqnarray} \int \sec(x) \, dx &=& \int \sec(x)\ 1 \, dx \nl &=& \int \sec(x)\frac{\tan(x) +\sec(x)}{\tan(x) +\sec(x)} \; dx \nl &=& \int \frac{\sec^2(x) + \sec(x) \tan(x)}{\tan(x) +\sec(x)} \; dx\nl &=& \int \frac{1}{u} du \nl &=& \ln |u| + C \nl &=& \ln |\tan(x) + \sec(x) | + C, \end{eqnarray} \] where in the fourth line we used the substitution $u=\tan(x)+\sec(x)$ and $du = (\sec^2(x) + \tan(x)\sec(x))dx$.
I highly recommend you view and practice all the examples you can get your hands on. Don't bother memorizing any recipes though, you will do just as well with trial and error.
Trig substitution
Often times when doing integrals for physics we get terms of the form $\sqrt{a^2-x^2}$, $\sqrt{a^2+x^2}$ or $\sqrt{x^2-a^2}$ which are not easy to handle. In each of the above three cases, we can do a trig substitution, in which we substitute $x$ with one of the trigonometric functions $a\sin(\theta)$, $a\tan(\theta)$ or $a\sec(\theta)$, and the resulting integral becomes much simpler.
Sine substitution
Consider an integral which contains an expression of the form $\sqrt{a^2-x^2}$. If we use the substitution $x=a\sin \theta$, the complicated square-root expression will get simpler: \[ \sqrt{a^2-x^2} = \sqrt{a^2-a^2\sin^2\theta} = a\sqrt{1-\sin^2\theta} = a\cos\theta, \] because we have $\cos^2\theta = 1 - \sin^2\theta$. The transformed integral now involves a trigonometric function which we know how to integrate.
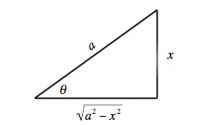 Once we find the integral in terms of $\theta$, we have to convert
the various $\theta$ expressions in the answer back
to the original variables $x$ and $a$:
\[
\sin\theta = \frac{x}{a}, \ \
\cos\theta = \frac{\sqrt{a^2-x^2}}{a}, \ \
\tan\theta = \frac{x}{\sqrt{a^2-x^2}}, \ \
\]
\[
\csc\theta = \frac{a}{x}, \ \
\sec\theta = \frac{a}{\sqrt{a^2-x^2}}, \ \
\cot\theta = \frac{\sqrt{a^2-x^2}}{x}. \ \
\]
Once we find the integral in terms of $\theta$, we have to convert
the various $\theta$ expressions in the answer back
to the original variables $x$ and $a$:
\[
\sin\theta = \frac{x}{a}, \ \
\cos\theta = \frac{\sqrt{a^2-x^2}}{a}, \ \
\tan\theta = \frac{x}{\sqrt{a^2-x^2}}, \ \
\]
\[
\csc\theta = \frac{a}{x}, \ \
\sec\theta = \frac{a}{\sqrt{a^2-x^2}}, \ \
\cot\theta = \frac{\sqrt{a^2-x^2}}{x}. \ \
\]
Example 1
Suppose you are asked to calculate $\int \sqrt{1-x^2}\; dx$.
We will approach the problem by making the substitution \[ x=\sin \theta, \qquad dx=\cos \theta \; d\theta, \] which is the simplest case of the sine substitution with $a=1$.
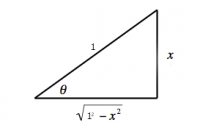 We proceed as follows:
\[
\begin{eqnarray}
\int \sqrt{1-x^2} \; dx
& = & \int \sqrt{1-\sin^2 \theta} \cos \theta \; d\theta \nl
& = & \int \cos^2 \theta \; d\theta \nl
& = & \frac{1}{2} \int \left[ 1+ \cos 2\theta \right] \; d\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{4}\sin2\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{2}\sin\theta\cos\theta \nl
& = & \frac{1}{2}\sin^{-1}\!\left(x \right)
+\frac{1}{2}\frac{x}{1}\frac{\sqrt{1-x^2}}{1}.
\end{eqnarray}
\]
We proceed as follows:
\[
\begin{eqnarray}
\int \sqrt{1-x^2} \; dx
& = & \int \sqrt{1-\sin^2 \theta} \cos \theta \; d\theta \nl
& = & \int \cos^2 \theta \; d\theta \nl
& = & \frac{1}{2} \int \left[ 1+ \cos 2\theta \right] \; d\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{4}\sin2\theta \nl
& = & \frac{1}{2}\theta +\frac{1}{2}\sin\theta\cos\theta \nl
& = & \frac{1}{2}\sin^{-1}\!\left(x \right)
+\frac{1}{2}\frac{x}{1}\frac{\sqrt{1-x^2}}{1}.
\end{eqnarray}
\]
Note how in the last step we used the triangle diagram to “read off” the values of $\theta$, $\sin\theta$ and $\cos\theta$ from the triangle. The substitution $x = \sin\theta$ means the hypotenuse in the diagram should be of length 1, and the opposite side is of length $x$.
Example 2
We want to compute $\int \sqrt{ \frac{a+x}{a-x}} \; dx$. We can rewrite this fraction as follows: \[ \sqrt{\frac{a+x}{a-x}} = \sqrt{\frac{a+x}{a-x} \frac{1}{1}} = \sqrt{\frac{a+x}{a-x} \frac{a+x}{a+x}} =\frac{a+x}{\sqrt{a^2-x^2}}. \]
Next we can make the substitution \[ x=a \sin \theta, \qquad dx=a\cos \theta d\theta, \]
 \[
\begin{eqnarray}
\int \frac{a+x}{\sqrt{a^2-x^2}} dx
& = & \int \frac{a+a\sin \theta}{a\cos \theta} a \cos \theta \, d\theta \nl
& = & a \int \left[ 1+ \sin \theta \right] d\theta \nl
& = & a \left[ \theta - \cos \theta \right] \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - a\frac{\sqrt{a^2-x^2}}{a} \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - \sqrt{a^2-x^2}.
\end{eqnarray}
\]
\[
\begin{eqnarray}
\int \frac{a+x}{\sqrt{a^2-x^2}} dx
& = & \int \frac{a+a\sin \theta}{a\cos \theta} a \cos \theta \, d\theta \nl
& = & a \int \left[ 1+ \sin \theta \right] d\theta \nl
& = & a \left[ \theta - \cos \theta \right] \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - a\frac{\sqrt{a^2-x^2}}{a} \nl
& = & a\sin^{-1}\left(\frac{x}{a}\right) - \sqrt{a^2-x^2}.
\end{eqnarray}
\]
Tan substitution
When an integral contains $\sqrt{a^2+x^2}$, we use the substitution: \[ x = a \tan \theta, \qquad dx = a \sec^2 \theta d\theta. \]
Because of the identity $1+\tan^2\theta=\sec^2\theta$, the square root expression will simplify drastically: \[ \sqrt{a^2+x^2} = \sqrt{a^2+a^2 \tan^2 \theta} = a\sqrt{1+\tan^2 \theta} = a \sec \theta. \] Simplification is a good thing. You are much more likely to be able to find the integral in terms of $\theta$, using trig identities, than in terms of $\sqrt{a^2+x^2}$.
Once you calculate the integral in terms of $\theta$, you will want to convert the answer back into $x$ coordinates. To do this, you need to use a triangle labeled according to our substitution: \[ \tan\theta = \frac{x}{a} = \frac{\text{opp}}{\text{adj}}. \] The equivalent of $\sin\theta$ in terms of $x$ is going to be $\sin\theta \equiv \frac{\text{opp}}{\text{hyp}} = \frac{x}{\sqrt{a^2+x^2}}$. Similarly, the other trigonometric functions are defined as various ratios of $a$, $x$ and $\sqrt{a^2+x^2}$.
Example
Calculate $\int\frac{1}{x^2+1}\,dx$.
The denominator of this function is equal to $\left(\sqrt{1+x^2}\right)^2$. This suggests that we try to substitute $\displaystyle x=\tan \theta\,$ and use the identity $\displaystyle 1 + \tan^2 \theta =\sec^2 \theta\,$. With this substitution, we obtain that $\displaystyle dx= \sec^2 \theta\, d\theta$ and thus: \[ \begin{align} \int\frac{1}{x^2+1}\,dx & =\int\frac{1}{\tan^2 \theta+1} \sec^2 \theta\,d\theta \nl & =\int\frac{1}{\sec^2 \theta} \sec^2 \theta\,d\theta \nl & =\int 1\;d\theta \nl &=\theta \nl &=\tan^{-1}(x) + C. \end{align} \]
Obfuscated example
What if we don't have $x^2 + 1$ in the denominator (a second degree polynomial with a missing linear term), but a full second degree polynomial like: \[ \frac{1}{y^2 - 6y + 10}. \] How would you integrate something like this? If there were no $-2y$, you would be able to use the tan substitution as above – or perhaps you can lookup the formula $\int \frac{1}{x^2+1}dx = \tan^{-1}(x)$ in the table of integrals. But there is no formula for \[ \int \frac{1}{y^2 - 6y + 10} \; dy, \] in the table so how should you proceed.
We will use the good old substitution technique $u=\ldots$ and a high-school algebra trick called “completing the square” in order to rewrite the fraction inside the integral so that it looks like $(y-h)^2 + k$, i.e., with no middle term.
The first step is to find “by inspection” the values of $h$ and $k$: \[ \frac{1}{y^2 - 6y + 10} = \frac{1}{(y-h)^2+k} = \frac{1}{(y-3)^2+1}. \] The “square completed” quadratic expression has no linear term, which is what we wanted. We can now use the substitution $x=y-3$ and $dx=dy$ to obtain an integral which we know how to solve: \[ \!\int \!\! \frac{1}{y^2 - 6y + 10}\; dy \!= \!\int \!\! \frac{1}{(y-3)^2+1}\; dy \!= \!\int \!\!\frac{1}{x^2+1}\; dx = \tan^{-1}(x) = \tan^{-1}(y-3). \]
Sec substitution
In the last two sections we learned how to deal with $\sqrt{a^2-x^2}$, $\sqrt{x^2+a^2}$ and so only the last option remains: $\sqrt{x^2-a^2}$.
Recall the trigonometric identity $1+\tan^2\theta=\sec^2\theta$, or rewritten differently we get \[ \sec^2\theta - 1 = \tan^2\theta. \]
The appropriate substitution for terms like $\sqrt{x^2-a^2}$, is the following: \[ x = a \sec \theta, \qquad dx = a \tan \theta \sec \theta \; d\theta. \]
The substitution method and procedure is the same as in both previous cases, so we will not get into the details. We label the sides of the triangle in the appropriate fashion, namely: \[ \sec\theta = \frac{x}{a} = \frac{\text{hyp}}{\text{opp}}, \] and use this triangle when we are converting back from $\theta$ to $x$ in the final steps.
Interlude
By now, things are starting to get pretty tight for your Calculus teacher. You are starting to know how to “handle” any kind of integral he can throw at you: polynomials, fractions with $x^2$ plus or minus $a^2$ and square roots. He can't even use the dirty old trigonometric tricks, with the $\sin$, the $\cos$ and the $\tan$ since you know that too. What options are there left for him to come up with an integral that you wouldn't know how to solve?
OK, I am exaggerating, but you should at least feel, by now, that you know how to do some integrals that you didn't know before. Just remember to come back to this section when you are hit with some complicated integral. When this happens, check to see which of the examples in this section looks the most similar and use the same approach. Don't bother memorizing the steps in each problem. The substitution $u=\ldots$ may be different from any problem that you have seen so far. You should think of “integration techniques” like general recipe ideas which you must adapt depending on the ingredients that you have to work with.
The most important integration techniques is substation. Recall the steps involved: (1) the change of variable $u=\ldots$, (2) the associated $dx$ to $du$ change and (3) the change in the limits of integration required for definite integrals. With medium to advanced substitution skills you will get at least an 80% on your Calculus II final.
Where is the remaining 20% of the exam going to come from? There are two more recipes to go. I know all these tricks that I have been throwing at you during the last ten pages may seem arduous and difficult to understand, but this is what you got yourself into when you signed-up for the course “Integral Calculus”: there are integrals and you calculate them.
The good news is that we are almost done. There is just one more “trick” to go, and finally I will tell you about “integration by parts”, which is kind of the analogue of the product rule for derivatives $(fg)'=f'g + fg'$.
Partial fractions
Suppose you have to integrate a rational function $\frac{P(x)}{Q(x)}$, where $P$ and $Q$ are polynomials.
For example, you could be asked to integrate \[ \frac{P(x)}{Q(x)} = \frac{Dx+E}{Fx^2 + G x + H}, \] where $D$, $E$, $F$, $G$ and $H$ are arbitrary constants. To get even more specific, let's say you are asked to calculate: \[ \int {3x+ 1 \over x^2+x} \; dx. \]
By magical powers, I can transform the function in this integral into two partial fractions as follows: \[ \int {3x+ 1 \over x^2+x} \; dx = \int \left( \frac{1}{x} + \frac{2}{x+1} \right) \; dx = \int \frac{1}{x} \; dx \ + \ \int \frac{2}{x+1} \; dx, \] in which both terms will give something $\ln$-like when integrated (since $\frac{d}{dx}\ln(x)=\frac{1}{x}$). The final answer is: \[ \int {3x+ 1 \over x^2+x} \; dx = \ln \left| x \right| + 2 \ln \left| x+1 \right| + C. \]
How did I split the problem into partial fractions? Is it really magic or is there a method? There is a little bit of both. The method part is that I assumed that there exist constants $A$ and $B$ such that \[ {3x+ 1 \over x^2+x}={3x+ 1 \over x(x+1)}= {A \over x}+ {B \over x+1}, \] and then I solved the above equation for $A$ and $B$, by computing the sum of the two fractions: \[ {3x+1 \over x(x+1)} = {{A(x+1) + Bx} \over {x(x+1)}}. \]
The magic part is the fact that you can solve for two unknowns in one equation. The relevant part of the equation is just the numerator because both sides have the same denominator. To find $A$ and $B$ we have to solve \[ 3x+1 = (3)x + (1)1 = A(x+1)+Bx = (A+B)x + (A)1. \] To solve this you just have to group the unknown constants into bunches and then read off their value from the equation. The bunch of numbers in front of the constant 1 on the left-hand side is (1) and the coefficient of 1 on the right-hand side is $A$, so $A=1$. Similarly you can deduce that $B=2$ from $A+B=3$ having found that $A=1$ in the first step.
Another way of looking at this, is that the equation \[ 3x+1 = A(x+1)+Bx \] must hold for all values of the variable $x$. If we put in $x=0$ we get $1 = A$ and putting $x=-1$ gives $-2=-B$ so $B=2$.
The above problem highlights the power of the partial fractions method for attacking integrals of polynomial fractions $\frac{P(x)}{Q(x)}$. Most of the work goes into some high-school math (factoring and finding unknowns) and then you do some simple calculus steps once you have split the problem into partial fractions. Some people call this method separation of quotients, but whatever you call it, it is clear that having a way to split a fraction into multiple parts is a good thing: \[ \frac{3x+ 1}{x^2+x} = \frac{A}{x} + \frac{B}{x+1}. \]
How many parts are there going to be for a fraction $\frac{P(x)}{Q(x)}$? What will each part look like? The answer is that there will be as many as the degree of the polynomial $Q(x)$, which is in the denominator of the fraction. Each part will consist of one of the factors of $Q(x)$.
Here is the general procedure:
- Split the denominator $Q(x)$ into the product of parts (factorize),
and for each part assume an appropriate partial fraction term
on the right.
You will get three types of fractions:
* Simple factors like $(x-\alpha)^1$. For each of these
you should //assume// a partial fraction of the form:
\[
\frac{A}{x-\alpha},
\]
as in the above example.
* Repeated factors like $(x-\beta)^n$ for which we have to
assume $n$ different terms on the right-hand side:
\[
\frac{B}{x-\beta} + \frac{C}{(x-\beta)^2} + \cdots + \frac{F}{(x-\beta)^n}.
\]
* If the denominator contains a portion $ax^2+bx+c$ that cannot be factored, like
$x^2+1$ for example, we have to keep it as whole
and assume that a term of the form:
\[
\frac{Gx + H}{ax^2+bx+c}
\]
exists on the right-hand side. A polynomial $ax^2+bx+c$ cannot be factored
if $b^2 < 4ac$, which means it has no real roots $r_1$, $r_2$
such that $ax^2+bx+c=(x-r_1)(x-r_2)$.
- Add together all the parts on the right-hand side by first
cross multiplying them to set all the fractions to a
common denominator. If you followed the steps
correctly in Part 1, the //least common denominator// (LCD) will turn
out to be $Q(x)$,
so both sides will have the same denominator.
Solve for the unknown coefficients $A, B, C, \ldots$
in the numerators. Find the coefficients
of each power of $x$ on the right-hand side and set them
equal to the corresponding coefficient in the numerator $P(x)$ of the left-hand side.
- Use the appropriate integral formula for each kind of term:
* For simple factors we have
\[
\int \frac{1}{x-\alpha} \; dx= A \ln|x-\alpha| + C.
\]
* For higher powers in the denominator we have
\[
\int \frac{1}{(x-\beta)^m} \; dx= \frac{1-m}{(x-\beta)^{m-1}} + C.
\]
* For the quadratic denominator terms with "matching" numerator
terms we can obtain:
\[
\int \frac{2ax+b}{ax^2+bx+c} \; dx= \ln|ax^2+bx+c| + C.
\]
For quadratic terms with just a constant on top we use
a two step substitution process.
First we change to a complete-the-square variable $y=x-h$:
\[
\int \frac{1}{ax^2+bx+c} \; dx
=
\int \frac{1/a}{(x-h)^2+k} \; dx
=
\frac{1}{a}\int \frac{1}{y^2+k} \; dy,
\]
and then we use a trig substitution $y = \sqrt{k}\tan\theta$ to get
\[
\frac{1}{a} \int \frac{1}{y^2+k} \; dy =
\frac{\sqrt{k}}{a}\tan^{-1}\!\!\left(\frac{y}{\sqrt{k}} \right) =
\frac{\sqrt{k}}{a}\tan^{-1}\!\!\left(\frac{x-h}{\sqrt{k}} \right).
\]
Example
Find $\int {1 \over (x+1)(x+2)^2}dx$?
Here $P(x)=1$ and $Q(x)=(x+1)(x+2)^2$. If I wanted to be sneaky, I could have asked for $\int {1 \over x^3+5x^2+8x+4}dx$, instead – which is actually the same question, but you have to do the factoring yourself.
According to the recipe outlined above, we have to look for a split fraction of the form: \[ \frac{1}{(x+1)(x+2)^2}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}. \] To make the equation more explicit, let us add the fractions on the right. We set all of them to a the least common denominator and add up: \[ \begin{align} \frac{1}{(x+1)(x+2)^2} & =\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2} \nl &= \frac{A(x+2)^2}{(x+1)(x+2)^2}+\frac{B(x+1)(x+2)}{(x+1)(x+2)^2}+\frac{C(x+1)}{(x+1)(x+2)^2} \nl & = \frac{A(x+2)^2+B(x+1)(x+2)+C(x+1)}{(x+1)(x+2)^2}. \end{align} \]
The denominators are the same on both sides in the above equation, so we can focus our attention on the numerator: \[ A(x+2)^2+B(x+1)(x+2)+C(x+1) = 1. \] We choose three different values of $x$ in order to find the values of $A$, $B$ and $C$: \[ \begin{matrix} x=0 & 1= 2^2A +2B+C \nl x=-1 & 1=A \nl x=-2 & 1= -C \end{matrix} \] so $A=1$, $B=-1$, $C=-1$, and thus \[ \frac{1}{(x+1)(x+2)^2}=\frac{1}{x+1}-\frac{1}{x+2}-\frac{1}{(x+2)^2}. \]
We can now calculate the integral by integrating each of the terms: \[ \int \frac{1}{(x+1)(x+2)^2} dx= \ln(x+1) - \ln({x+2}) + \frac{1}{x+2} +C. \]
Integration by parts
Suppose you have to integrate the product of two functions. If one of the functions happens to look like the derivative of a function that you recognize, then you can do the following trick: \[ \int f(x) g'(x) \; dx \ \ = \ \ f(x) g(x) \ \ \ \ - \int f'(x)g(x) \; dx. \]
This means that you can shift the work to evaluating a different integral where one function is replaced by its derivative and another is replaced by its integral.
Derivatives tend to simplify functions whereas integrals make functions more complicated, so such shifting of work can be quite beneficial: you will save yourself some work on integrating the $f$ part, but you will do more work on the $g$ part.
It is easier to remember the integration by parts formula in the shorthand notation: \[ \int u\; dv = uv - \int v\; du. \] In fact, you can think of integration by parts as a form of “double substitution”, where you replace $u$ and $dv$ at the same time. To be sure of what is going on, I recommend you always make a little table like this: \[ \begin{align} u &= & \qquad dv &= \nl du &= & \qquad v &= \end{align} \] and fill in the blanks. The first row consists of the two parts that you see in your original problem. Then you differentiate in the left column, and integrate in the right column. If you do this, using the integration by parts formula will be really easy since you have all your expressions ready.
For definite integrals the integration by parts rule needs to take into account the evaluation at the limits: \[ \int_a^b u\; dv = \left(uv\right)\Big|_a^b \ \ - \ \ \int_a^b v \; du, \] which tells us to evaluate the difference of the value of $uv$ at the two endpoints and then subtract the switched integral with the same endpoints.
Example 1
Find $\int x e^x \, dx$. We identify the good candidates for $u$ and $dv$ in the original expression, and perform all the work necessary for the substitution: \[ \begin{align} u &=x & \qquad dv &= e^x \; dx, \nl du &=dx & \qquad v &= e^x. \end{align} \] Next we apply the integration by parts formula \[ \int u\; dv = uv - \int v\; du, \] to get the following: \[ \begin{align} \int xe^x \, dx &= x e^x - \int e^x \; dx \nl &= x e^x - e^x + C. \end{align} \]
Example 2
Find $\int x \sin x \; dx$. We choose $u=x$ and $dv=\sin x dx$. With these choices, we have $du=dx$ and $v=-\cos x$, and integrating by parts we get: \[ \begin{align} \int x \sin x \, dx &= -x \cos x - \int \left(-\cos x\right) \; dx \nl &= -x \cos x + \int \cos x \; dx \nl &= -x \cos x + \sin x + C. \end{align} \]
Example 3
Often times, you have to integrate by parts multiple times. To calculate $\int x^2 e^x \, dx$, we start by choosing: \[ \begin{align} u &=x^2 & \qquad dv &= e^x \; dx \nl du &= 2x \; dx & \qquad v &= e^x, \end{align} \] which gives the following after integration by parts: \[ \int x^2 e^x \; dx = x^2 e^x \ - \ 2 \int x e^x \; dx. \] We apply integration by parts again on the remaining integral this time using $u=x$ and $dv=e^x\; dx$, which gives $du = dx$ and $v=e^x$.
\[ \begin{align} \int x^2 e^x \; dx &= x^2 e^x - 2 \int x e^x \; dx \nl &= x^2 e^x - 2\left(x e^x - \int e^x \; dx \right) \nl &= x^2 e^x - 2x e^x + 2e^x + C. \end{align} \]
By now I hope you are starting to see that this integration by parts thing is good. If you always write down the substitutions clearly (who is who in $\int u dv$), and use the formula correctly ($=uv-\int v du$) you can do damage to any integral. Sometimes the choice of $u$ and $dv$ you make might not be good: if the integral $\int v du$ is not simpler than the original $\int u dv$ then what is the point of integrating by parts?
Sometimes, however, you can get into a weird self-referential loop when doing integration by parts. After a couple of integration-by-parts steps you might end up back with an integral you started with! The way out of this loop is best shown by example.
Example 4
Evaluate the integral $ \int \sin(x) e^x\; dx$. First we let $u = \sin(x) $ and $dv=e^x \; dx$, which gives $dv=\cos(x)dx$ and $v=e^x$. Using integration by parts gives \[ \int \sin(x) e^x\, dx = e^x\sin(x)- \int \cos(x)e^x\, dx. \]
We integrate by parts again. This time we set $u = \cos(x)$, $dv=e^x dx$ and $du=-\sin(x)dx$, $v=e^x$. We obtain \[ \underbrace{ \int \sin(x) e^x\, dx}_I \ = \ e^x\sin(x) - e^x\cos(x)\ \ -\ \ \underbrace{\int e^x \sin(x)\, dx}_I. \] Do you see the Ouroboros? We could continue integrating by parts indefinitely like that.
Let us define clearly what we are doing here. The question asked us to find $I$ where \[ I = \int \sin(x) e^x\, dx, \] and after doing two integration by parts steps we obtain the following equation: \[ I = e^x\sin(x) - e^x\cos(x) - I. \] OK, good. Now just move all the I's to one side: \[ 2I = e^x\sin(x) - e^x\cos(x), \] or finally \[ \int \sin(x) e^x\, dx = I = \frac{1}{2} e^x\left(\sin(x) - \cos(x) \right) +C. \]
Derivation of the Integration by parts formula
Remember the product rule for derivatives? \[ \frac{d}{dx}(f(x)g(x)) = \frac{df}{dx}g(x) + f(x)\frac{dg}{dx}. \] We can rewrite this as: \[ f(x)\frac{dg}{dx} = \frac{d}{dx}(f(x)g(x)) \ -\ \frac{df}{dx}g(x) . \] Now we take the integral on both sides \[ \int f(x)\frac{dg}{dx} \ dx \ = \ \int \left[ \frac{d}{dx}(f(x)g(x)) \; dx - \frac{df}{dx}g(x) \; dx \right]. \]
At this point, you need to recall the Fundamental Theorem of Calculus, which says that taking the derivative and taking an integral are inverse operations \[ \int \frac{d}{dx} h(x) \; dx = h(x). \] We use this to simplify the product rule equation as follows: \[ \int f(x)\frac{dg}{dx} \; dx \ = \ f(x)g(x) \ \ - \ \ \int \frac{df}{dx}g(x) \; dx. \]
Outro
We are done. Now you know all the integration techniques. I know it took a while, but we had to go through a lot of tricks. In any case, I must say I am glad to be done writing this section. My job of teaching you is done. Now your job begins. Do all the examples you can find. Do all the exercises. Practice the tricks.
Here is a suggestion for you. Make your own formula-sheet-slash-trophy-case where you record any complex integral that you have personally calculated from first principles in homework assignments. If by the end of the class you trophy case has 50 integrals which you calculated yourself, then you will get $100\%$ on your final. Another thing to try is to go over the integral formulas in the back of the book and see how many of them you can derive.
Links
[ More examples of integration techniques ]
http://en.wikibooks.org/wiki/Calculus/Integration_techniques/
Applications of integration
Integration is used in many areas of science.
Applications to mechanics
Calculus was kind of invented for mechanics, so it is not surprising that there will be many links between the two subjects.
Kinematics
Suppose that an object of mass $m$ has a constant force $F_{net}$ applied to it. Newton's second law tells us that the acceleration of the object will be $a =\frac{F_{net}}{m}$.
If the net force is constant, then the acceleration will also be constant. We can find the equations of motion of the object $x(t)$ by integrating $a(t)$ twice since $a(t)=x^{\prime\prime}(t)$.
We start with the acceleration function $a(t) = a$ and integrate once to obtain: \[ v(\tau) = \int_0^\tau a(t) \; dt = a t + v_i, \] where $v_i=v(0)$ is the initial velocity of the object at $t=0$. We obtain the position function by integrating the velocity function and adding the initial position $x_i=x(0)$: \[ x(\tau) = \int v(t) \; dt = \int ( a t + v_i )\; dt = \frac{1}{2}a\tau^2 + v_i\tau + x_i. \]
Non-constant acceleration
If net force on the object is not constant then the acceleration will not be constant either. In general both the force and the mass could change over time so the acceleration will also change over time $a(t)=\frac{F_{net}(t)}{m(t)}$. This sort of problem is usually not covered in the first mechanics course because the establishment assume that it would be too complicated for you to handle.
Now that you know more about integrals, you can learn how to predict the motion of the object with an arbitrary acceleration function $a(t)$. To find the velocity at time $t=\tau$, we need sum up all acceleration felt by the object between $t=0$ and $t=\tau$: \[ v(\tau) = v_i + \int_0^\tau a(t)\; dt. \] The equation of motion $x(t)$ is obtained by integrating the velocity $v(t)$: \[ x(s) = x_i + \int_0^s v(\tau) \; d\tau = \int_0^s \left[ v_i + \int_0^\tau a(t)\; dt \right] \; d\tau. \] The above expression looks quite intense, but in fact it is nothing more complicated than the simple integrals used in UAM. The expression just looks complicated because we have three different variables which are used to represent the time and two consecutive integration steps. Computer games often include a “physics engine” to simulates the motion of objects in the real world using the equation described above.
Gravitational potential
By definition, the integral of a conservative force over some distance $d$ gives you the potential energy of that force. Since gravity $\vec{F}_g$ is a conservative force, we can integrate it to obtain the gravitational potential energy $U_g$.
On the surface of the earth we have $\vec{F}_g = -gm \hat{\jmath}$, where the negative sign means that it acts in the opposite direction to “upwards” as represented by the $\hat{\jmath}$ unit vector, which points in the positive $y$-direciton (towards the sky). In particular the gravitational force as a function of height $\vec{F}_g(y)$ is a constant $\vec{F}_g(y)=\vec{F}_g$. By definition, the gravitational potential energy is the negative of the integral of the force over some distance, say from height $y_i=0$ to height $y_f=h$: \[ \Delta U_{g} = U_{gf} - U_{gi} = - \int_{y_i}^{y_f} \vec{F}_g \cdot \hat{\jmath} \ dy = - \int_{0}^{h} - mg \ dy = \left[ mg y \right]_{0}^{h} = mgh. \]
More generally, i.e., not on the surface of the earth, the gravitational force acting on an object of mass $m$ due to another object of mass $M$ is given by Newton's famous one-over-$r$-squared law: \[ \vec{F}_g = \frac{GMm}{r^2} \hat{r}, \] where $r$ is the distance between the objects and $\hat{r}$ points towards the other object. The general formula for gravitational potential is obtained, again, by taking the integral of the gravitational force over some distance. We will start the object of mass $m$ from a distance $r=r_i$ and move it away until it is infinitely far away. The change in the gravitational potential from $r=r_i$ to $r=\infty$ is: \[ \begin{align} \Delta U_g & = \int_{r=r_i}^{r=\infty} \frac{GMm}{r^2} \ dr \nl & = GMm \int_{r_i}^{\infty} \frac{1}{r^2} \ dr \nl & = GMm \left[ \frac{-1}{r} \right]_{r_i}^{\infty} \nl & = GMm \left[ \frac{-1}{\infty} - \frac{-1}{r_i} \right] \nl & = \frac{GMm}{r_i}. \end{align} \]
Integrals over circular objects
Consider the circular region $S = \{x,y \in \mathbb{R} : x^2 + y^2 \leq R^2\}$. In polar coordinates we would describe this region as $r \leq R$, where it is implicit that the angle $\theta$ varies between $0$ and $2 \pi$. Because this region is two dimensional, in order to integrate it, we would need a double integral.
Even before you learn about double integrals, you can still integrate over the circular region if you brake it up into little pieces of circle $dS$. In fact, this is the whole point of this subsection.
 A natural way to break up the circular region is in
terms of thin
circular strips at a different radius and with width $dr$.
Each circular strip will have an area of:
\[
dS = 2\pi r dr,
\]
where $2\pi r$ is the circumference of a circle with radius $r$.
A natural way to break up the circular region is in
terms of thin
circular strips at a different radius and with width $dr$.
Each circular strip will have an area of:
\[
dS = 2\pi r dr,
\]
where $2\pi r$ is the circumference of a circle with radius $r$.
Using this way of braking up the circle, we can check that indeed we get a total area of $\pi R^2$ when we add up all the pieces $dS$: \[ A_{circle} = \int_S \ dS = \int_{r=0}^{r=R} 2\pi r \ dr = 2\pi \int_{0}^{R} r \ dr = \pi R^2. \]
The following sections discuss different extensions of this idea. We use the circular symmetry of various objects to integrate over them by breaking them into thin circular strips of thickness $dr$.
In all circular integrals, you can think of the object as being described by a rotation, or revolution of some function around one of the axes, thus, this kind of integrals are called integrals of revolution.
Total mass of a disk
Suppose you have a disk of total mass $m$ and radius $R$. You can think of the disk as being made of parts, each of mass $\Delta m$, such that when you add them all up you get the total mass: \[ \int_{disk} \Delta m = m. \]
The mass density is defined as the total mass divided by the area of the disk: $\sigma = \frac{m}{A_{disk}} = \frac{m}{\pi R^2}$. The mass density corresponds to the amount of mass per unit area. Let's split the disk into concentric circular strips of width $dr$. The mass contribution of a strip as a function of the radius will be $\Delta m({r}) = \sigma 2\pi r dr $, since the stip at radius $r$ has circumference $2\pi r$ and width $dr$. Let's check that when we add up the pieces we get the total mass: \[ m = \int_0^R \Delta m ({r}) = \int_0^R \sigma 2 \pi r \ dr = 2\pi\sigma \left[ \frac{r^2}{2} \right]_0^R = 2\pi \frac{m}{\pi R^2} \frac{R^2-0}{2} = m. \]
Moment of inertia of a disk
The moment of inertia of an object is a measure of how difficult it is to make it turn. It appears in the rotational version of $F=ma$, in place of the inertial mass $m$: \[ \mathcal{T} = I \alpha. \]
To compute the moment of inertia of an object you need to add up all the mass contributions $\Delta m$ and weight them by $r^2$, where $r$ is the distance of the piece $\Delta m$ from the centre: \[ I = \int_{disk} r^2 \Delta m. \]
We can perform the integral over the whole disk, by adding up the contributions of all the strips: \[ I_{disk} = \int_0^R r^2 \Delta m ({r}) = \int_0^R r^2 \sigma 2 \pi r \ dr = \int_0^R r^2 \frac{m}{\pi R^2} 2 \pi r \ dr = \] \[ \qquad = \frac{2m}{R^2} \int_0^R r^3 \ dr = \frac{2m}{R^2} \left[ \frac{r^4}{4} \right]_0^R = \frac{2m}{R^2} \frac{R^4}{4} = \frac{1}{2}mR^2. \]
Arc lengths of a curve
Given a function $y=f(x)$ and an interval $x \in [x_i, x_f]$, how can you calculate the total length $\ell$ of the curve $f(x)$ between these two points?
If the curve were a straight line, then we would simply take the hypotenuse of the change in $x$ and the change in $y$: $\sqrt{ \text{run}^2 + \text{rise}^2 }=$ $\sqrt{ (x_f-x_i)^2 + (f(x_f)-f(x_i))^2}$.
If the function is not a straight line, however, we have to do this hypotenuse thing on each piece of the curve $d\ell = \sqrt{ dx^2 + dy^2}$, and add up all the contributions as an integral.
The arc length $\ell$ of a curve $y = f(x)$ is given by: \[ \ell=\int d\ell = \int_{x_i}^{x_f} \sqrt{1+\left(\frac{df(x)}{dx}\right)^2} \ dx. \]
Surface of revolution
We can use the above formula for arc-length to ask how much surface area $A$ a solid of revolution with boundary $f(x)$ would have.
Each piece of length $d\ell$, must be multiplied by $2 \pi f(x)$ since it is being rotated around the $x$-axis in a circle of radius $f(x)$. The area of the surface of revolution traced out by $f(x)$ rotated around the $x$-axis is given by the following integral: \[ A= \int 2\pi f(x) d\ell = \int_{x_i}^{x_f} 2\pi f(x)\ \sqrt{1+\left(\frac{df(x)}{dx}\right)^2} \ dx. \]
Volumes of revolution
Next we raise the stakes. We already showed that we can express two dimensional integrals with circular symmetry as one dimensional integrals. Now we move on to three dimensional integrals: integrals over volumes. We will use the circular symmetry to calculate the volume using a single integral again.
Washer method
We can split any volume into a number of disks of thickness $dx$ and with radius proportional to the function $f(x)$.
 The volume $V$ of a solid of traced out by
some $f(x)$ as revolution is:
\[
V
= \int A_{disk}(x) \times h_{disk}
= \int \pi f^2(x) \ dx.
\]
The volume $V$ of a solid of traced out by
some $f(x)$ as revolution is:
\[
V
= \int A_{disk}(x) \times h_{disk}
= \int \pi f^2(x) \ dx.
\]
If we want the volume of revolution in between two functions $g(x)$ and $f(x)$, then we have to imagine splitting the volume into washers: disks of inner radius $f(x)$, outer radius $g(x)$ and thickness $dx$: \[ V = \int A_{washer}(x) \; dx = \int \pi [f^2(x)-g^2(x)] \; dx. \] Each washer consist of a disk of are $\pi f^2(x)$ from which a circular piece of area $\pi g^2(x)$ has been cut out.
Example
Let's calculate the volume of a sphere of radius $r$ using the disk method. Our generating region will be the region bounded by the curve $f(x)=\sqrt{r^2-x^2}$ and the line $y=0$. Our limits of integration will be the $x$-values where the curve intersects the line $y=0$, namely, $x=\pm r$. We have: \[ \begin{align} V_{sphere}&=\int_{-r}^r \pi(r^2-x^2)dx \nl &=\pi(\int_{-r}^r r^2 dx-\int_{-r}^r x^2 dx)\nl &=\pi(r^2 x\bigr|_{-r}^r - \frac{x^3}{3}\biggr|_{-r}^r)\nl &=\pi(r^2 (r-(-r)) - (\frac{r^3}{3}-\frac{(-r)^3}{3})\nl &=\pi(2r^3-\frac{2r^3}{3})\nl &=\pi\frac{6r^3-2r^3}{3}\nl &=\frac{4\pi r^3}{3}. \end{align} \]
Cylindrical shell method
Alternately we can split any circularly symmetric volume into thin cylindrical shells of thickness $dr$. If the volume has a circular symmetry and is bounded from above by $F(r )$ and from below by $G(r )$, then the integral over the volume will be: \[ \begin{align*} V & = \int C_{shell}(r ) \: h_{shell}(r ) \; dr \nl & = \int_a^b 2\pi r | F(r ) - G(r ) | \; dr, \end{align*} \] where $2\pi r$ is the circumference of each cylindrical shell and $|F(r )-G(r )|$ is its height.
Example
 Calculate the volume of a sphere of radius $R$ using the cylindrical
shell method. We are talking about the region enclosed by the
surface $x^2 + y^2 + z^2 = R^2$.
Calculate the volume of a sphere of radius $R$ using the cylindrical
shell method. We are talking about the region enclosed by the
surface $x^2 + y^2 + z^2 = R^2$.
The shell at radius $r=\sqrt{x^2+y^2}$ will have a roof of $z=F(r)=2\sqrt{R^2-r^2}$, a floor of $z=G(r)=-2\sqrt{R^2-r^2}$, circumference $2\pi r$ and a width of $dr$. The integral will proceed as follows: \[ \begin{align*} V &= \int_0^R 2\pi r | F(r ) - G(r ) | \; dr \nl &= \int_0^R 2 \pi r 2\sqrt{R^2-r^2} \ dr \nl &= - 2\pi \int_{R^2}^0 \sqrt{u} \ du \nl &= - 2\pi \frac{2}{3} u^{3/2}\bigg|_{R^2}^0 \nl &= - 2\pi [ 0 - \frac{2}{3}R^3] \nl &= \frac{4\pi R^3}{3}, \end{align*} \] where in the second line we carried out the substitution $u=R^2-r^2, du = -2r dr$.
Exercises
Exercise 1
Calculate the volume of the cone with radius $R$ and height $h$ which is generated by the revolution of the region bounded by $y=R-\frac{R}{h}x$ and the lines $y=0$ and $x=0$ around the $x$-axis. Answer: $\frac{\pi R^2 h}{3}$.
Exercise 2
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curve $y=x^2$ and the lines $x=1$ and $y=0$ around the $x$-axis. Answer:$\frac{\pi}{5}$.
Exercise 3
Use the washer method to find the volume of a cone containing a central hole formed by revolving the region bounded by $y=R-\frac{R}{h}x$ and the lines $y=r$ and $x=0$ around the $x$-axis. Answer:$\pi h\left(\frac{R^2}{3}-r^2\right)$.
Exercise 4
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curves $y=x^2$ and $y=x^3$ and the lines $x=1$ and $y=0$ around the $x$-axis. Answer: $\frac{2\pi}{35}$.
Exercise 5
Find the volume of a cone with radius $R$ and height $h$ by using the shell method on the appropriate region which, when rotated around the $y$-axis, produces a cone with the given characteristics. Answer:$\frac{\pi r^2 h}{3}$.
Exercise 6
Calculate the volume of the solid of revolution generated by revolving the region bounded by the curve $y=x^2$ and the lines $x=1$ and $y=0$ around the $y$-axis. Answer:$\frac{\pi}{2}$.
Sequences
A sequence is and ordered list of numbers, usually following some pattern like the “find the pattern” questions on IQ tests. We will study the properties of these sequences. For example, we can check whether the sequence converges to some limit.
Understanding sequences is also a prerequisite for understanding series, which is an important topic we will discuss in the next section.
Definitions
- $\mathbb{N}$: The set of natural numbers $\{0, 1, 2, 3, \ldots \}$.
- $\mathbb{N}^*=\mathbb{N} \setminus \{0\}$:
The set of strictly positive natural numbers $\{1, 2, 3, \ldots \}$,
which is the same as the above, but we skip zero.
* $a_n$: sequence of numbers $a_0, a_1, a_2, a_3, a_4, \ldots$.
You can also think about each sequence as a function
\[
a: \mathbb{N} \to \mathbb{R},
\]
where the input is $n$ an integer (the //index// into the sequence) and
the output is some number $a_n \in \mathbb{R}$.
Examples
Consider the following common sequences.
Arithmetic progression
Consider a sequence in which successive terms differ by one: \[ 1, \ 2,\ 3, \ 4, \ 5, \ 6, \ \ldots \] which is described by the formula: \[ a_n = n, \qquad n \in \mathbb{N}^*. \]
More generally, an arithmetic sequence can start at any value $a_0$ and make jumps of size $d$ at each step: \[ a_n = a_0 + nd, \qquad n \in \mathbb{N}. \]
Harmonic sequence
If we choose to make the sequence elements inversely proportional to the index $n$ we obtain the harmonic sequence: \[ 1, \ \frac{1}{2},\ \frac{1}{3}, \ \frac{1}{4}, \ \frac{1}{5}, \ \frac{1}{6}, \ \ldots \] \[ a_n = \frac{1}{n}, \qquad n \in \mathbb{N}^*. \]
More generally, we can define a $p$-sequence in which the index $n$ appears in the denominator raised to the power $p$: \[ a_n = \frac{1}{n^p}, \qquad n \in \mathbb{N}^*. \]
For example, when $p=2$ we get the sequence of inverse squares of the integers: \[ 1, \ \frac{1}{4}, \ \frac{1}{9}, \ \frac{1}{16}, \ \frac{1}{25}, \ \frac{1}{36}, \ \ldots. \]
Geometric sequence
If we use the index as an exponent to a fixed number $r$ we obtain the geometric series: \[ a_n = r^n, \ \ n \in \mathbb{N}, \] which is a sequence of the form \[ 1, r, r^2, r^3, r^4, r^5, r^6, \ldots. \]
Suppose we choose $r=\frac{1}{2}$, then the geometric series with this ratio will be: \[ 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}, \frac{1}{128}, \ldots. \]
Fibonacci
\[ a_0 =1, a_1 = 1, \qquad \ a_n = a_{n-1} + a_{n-2}, \ \ n > 1. \] \[ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \ldots. \]
Convergence
We say a sequence $a_n$ converges to a limit $L$, or written mathematically: \[ \lim_{n \to \infty} a_n \ = \ L, \] if for large $n$ the sequence values get arbitrarily close to the value $L$.
More precisely, the limit notation means that for any choice of precisions $\epsilon>0$, we can pick a number $N_\epsilon$ such that: \[ | a_n - L | < \epsilon, \qquad \forall n \geq N_\epsilon. \]
The notion of a limit of a sequence is the same as that of a limit of a function. The same way we learned how to calculate which number the function $f(x)$ tends to for large $x$, we can study which number the sequence $a_n$ tends to for large $n$. Indeed, sequences are functions that are defined only at integer values of $x$.
Ratio convergence
The numbers in the Fibonacci sequence grow indefinitely large ($\lim_{n \to \infty} a_n = \infty$), but the ratio of $\frac{a_n}{a_{n-1}}$ converges to a constant: \[ \lim_{n \to \infty}\frac{a_n}{a_{n-1}} = \phi = \frac{1+\sqrt{5}}{2} \approx 1.618033\ldots, \] which is known as the golden ratio.
Calculus on sequences
If a sequence $a_n$ is like a function $f(x)$, then we should be able to do calculus on it. We already saw we can take limits of sequences, but can we also compute derivatives and integrals of sequences? Derivatives are a no-go, because they depend on the function $f(x)$ being continuous and sequences are only defined for integer values. We can take integrals of sequences, however, and this is the subject of the next section.
Series
Can you compute $\ln(2)$ using only a basic
calculator with four operations: [+], [-], [$\times$], [$\div$]?
I can tell you one way. Simply compute the following sum:
\[
1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} + \ldots.
\]
We can compute the above sum for large values of $n$ using live.sympy.org:
>>> def axn_ln2(n): return 1.0*(-1)**(n+1)/n
>>> sum([ axn_ln2(n) for n in range(1,100) ])
0.69(817217931)
>>> sum([ axn_ln2(n) for n in range(1,1000) ])
0.693(64743056)
>>> sum([ axn_ln2(n) for n in range(1,1000000) ])
0.693147(68056)
>>> ln(2).evalf()
0.693147180559945
As you can see, the more terms you add in this series, the more accurate the series approximation of $\ln(2)$ becomes. A lot of practical mathematical computations are done in this iterative fashion. The notion of series is a powerful way to calculate quantities to arbitrary precision by summing together more and more terms.
Definitions
- $\mathbb{N}$: $ = \{0, 1, 2, 3, 4, 5, 6, \ldots \}$.
- $\mathbb{N}^*=\mathbb{N} \setminus \{0\}$: = $\{1, 2, 3, 4, 5, 6, \ldots \}$.
- $a_n$: sequence of numbers $a_0, a_1, a_2, a_3, a_4, \ldots$.
- $\sum$: sum. Means to take the sum of several objects
put together. The summation sign is the short way to express
certain long expressions:
\[
a_3 + a_4 + a_5 + a_6 + a_7 = \sum_{3 \leq i \leq 7} a_i = \sum_{i=3}^7 a_i.
\]
* $\sum a_i$: series. The running total of a sequence until $n$:
\[
S_n = \sum_{i=1}^n a_i = a_1 + a_2 + \ldots + a_{n-1} + a_n.
\]
Most often, we take the sum of all the terms in the sequence:
\[
S_\infty = \sum_{i=1}^\infty = a_1 + a_2 + a_{3} + a_4 + \ldots.
\]
* $n!$: the //factorial// function: $n!=n(n-1)(n-2)\cdots 3\cdot2\cdot1$.
* $f(x)=\sum_{n=0}^\infty a_n x^n$: //Taylor series// approximation
of the function $f(x)$. It has the form of an infinitely long polynomial
$a_0 + a_1x + a_2x^2 + a_3x^3 + \ldots$ where the coefficients $a_n$ are
chosen so as to encode the properties of the function $f(x)$.
Exact sums
There exist formulas for calculating the exact sum of certain series. Sometimes even infinite series can be calculated exactly.
The sum of the geometric series of length $n$ is: \[ \sum_{k=0}^n r^k = 1 + r + r^2 + \cdots + r^n =\frac{1-r^{n+1}}{1-r}. \]
If $|r|<1$, we can take the limit as $n\to \infty$ in the above expression to obtain: \[ \sum_{k=0}^\infty r^k=\frac{1}{1-r}. \]
Example
Consider the geometric series with $r=\frac{1}{2}$. If we apply the above formula formula we obtain \[ \sum_{k=0}^\infty \left(\frac{1}{2}\right)^k=\frac{1}{1-\frac{1}{2}} = 2. \]
You can also visualize this infinite summation graphically. Imagine you start with a piece of paper of size one-by-one and then you add next to it a second piece of paper with half the size of the first, and a third piece with half the size of the second, etc. The total area that this sequence of pieces of papers will occupy is:
\[ \ \]
The sum of the first $N+1$ terms in arithmetic progression is given by: \[ \sum_{n=0}^N (a_0+nd)= a_0(N+1)+\frac{N(N+1)}{2}d. \]
We have the following closed form expression involving the first $N$ integers: \[ \sum_{k=1}^N k = \frac{N(N+1)}{2}, \qquad \quad \sum_{k=1}^N k^2=\frac{N(N+1)(2N+1)}{6}. \]
Other series which have exact formulas for their sum are the $p$-series with even values of $p$: \[ \sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}, \quad \sum_{n=1}^\infty\frac{1}{n^4}=\frac{\pi^4}{90}, \quad \sum_{n=1}^\infty\frac{1}{n^6}=\frac{\pi^6}{945}. \] These series are computed by Euler's method.
Other closed form sums: \[ \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n^2}=\frac{\pi^2}{12}, \qquad \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{n}=\ln(2), \] \[ \sum_{n=1}^\infty\frac{1}{4n^2-1}=\frac{1}{2}, \] \[ \sum_{n=1}^\infty\frac{1}{(2n-1)^2}=\frac{\pi^2}{8}, \quad \sum_{n=1}^\infty\frac{(-1)^{n+1}}{(2n-1)^3}=\frac{\pi^3}{32}, \quad \sum_{n=1}^\infty\frac{1}{(2n-1)^4}=\frac{\pi^4}{96}. \]
Convergence and divergence of series
Even when we cannot compute an exact expression for the sum of a series it is very important to distinguish series that converge from series that do not converge. A great deal of what you need to know about series is different tests you can perform on a series in order to check whether it converges or diverges.
Note that convergence of a series is not the same as convergence of the underlying sequence $a_i$. Consider the sequence of partial sums $S_n = \sum_{i=0}^n a_i$: \[ S_0, S_1, S_2, S_3, \ldots , \] where each of these corresponds to \[ a_0, \ \ a_0 + a_1, \ \ a_0 + a_1 + a_2, \ \ a_0 + a_1 + a_2 + a_3, \ldots. \]
We say that the series $\sum a_i$ converges if the sequence of partial sums $S_n$ converges to some limit $L$: \[ \lim_{n \to \infty} S_n = L. \]
As with all limits, the above statement means that for any precision $\epsilon>0$, there exists an appropriate number of terms to take in the series $N_\epsilon$, such that \[ |S_n - L | < \epsilon,\qquad \text{ for all } n \geq N_\epsilon. \]
Sequence convergence test
The only way the partial sums will converge is if the entries in the sequences $a_n$ tend to zero for large $n$. This observation gives us a simple series divergence test. If $\lim\limits_{n\rightarrow\infty}a_n\neq0$ then $\sum\limits_n a_n$ diverges. How could an infinite sum of non-zero quantities add up to a finite number?
Absolute convergence
If $\sum\limits_n|a_n|$ converges, $\sum\limits_n a_n$ also converges. The opposite is not necessarily true, since the convergence of $a_n$ might be due to some negative terms cancelling with the positive ones.
A sequence $a_n$ for which $\sum_n |a_n|$ converges is called absolutely convergent. A sequence $b_n$ for which $\sum_n b_n$ converges, but $\sum_n |b_n|$ diverges is called conditionally convergent.
Decreasing alternating sequences
An alternating series of which the absolute values of the terms are decreasing and go to zero converges.
p-series
The series $\displaystyle\sum_{n=1}^\infty \frac{1}{n^p}$ converges if $p>1$ and diverges if $p\leq1$.
Limit comparison test
Suppose $\displaystyle\lim_{n\rightarrow\infty}\frac{a_n}{b_n}=p$, then the following is true:
- if $p>0$ then $\sum\limits_{n}a_n$ and $\sum\limits_{n}b_n$ either both converge or both diverge.
- if $p=0$ holds: if $\sum\limits_{n}b_n$ converges, then $\sum\limits_{n}a_n$ also converges.
n-th root test
If $L$ is defined by $\displaystyle L=\lim_{n\rightarrow\infty}\sqrt[n]{|a_n|}$ then $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Ratio test
$\displaystyle L=\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|$, then is $\sum\limits_{n}a_n$ diverges if $L>1$ and converges if $L<1$. If $L=1$ the test is inconclusive.
Radius of convergence for power series
In a power series $a_n=c_nx^n$, the $n$th term is multiplied by the $n$th power of $x$. For such series, the convergence or divergence of the series depends on the choice of the variable $x$.
The radius of convergence $\rho$ of $\sum\limits_n c_n$ is given by: $\displaystyle\frac{1}{\rho}=\lim_{n\rightarrow\infty}\sqrt[n]{|c_n|}= \lim_{n\rightarrow\infty}\left|\frac{c_{n+1}}{c_n}\right|$. For all $-\rho < x < \rho$ the series $a_n$ converges.
Integral test
If $\int_a^{\infty}f(x)dx<\infty$, then $\sum\limits_n f(n)$ converges.
Taylor series
The Taylor series approximation to the function $\sin(x)$ to the 9th power of $x$ is given by \[ \sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!}. \] If we want to get rid of the approximate sign, we have to take infinitely many terms in the series: \[ \sin(x) = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \frac{x^{11}}{11!} + \ldots . \]
This kind of formula is known as a Taylor series approximation. The Taylor series of a function $f(x)$ around the point $a$ is given by: \[ \begin{align*} f(x) & =f(a)+f'(a)(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3+\cdots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n. \end{align*} \]
The McLaurin series of $f(x)$ is the Taylor series expanded at $a=0$: \[ \begin{align*} f(x) & =f(0)+f'(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3 + \ldots \nl & = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n . \end{align*} \]
Taylor series of some common functions: \[ \begin{align*} \cos(x) &= 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} + \ldots \nl e^x &= 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots \nl \ln(x+1) &= x - \frac{x^2}2 + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} - \frac{x^6}{6} + \ldots \nl \cosh(x) &= 1 + \frac{x^2}{2} + \frac{x^4}{4!} + \frac{x^6}{6!} + \frac{x^8}{8!} + \frac{x^{10} }{10!} + \ldots \nl \sinh(x) &= x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!} + \frac{x^9}{9!} + \frac{x^{11} }{11!} + \ldots \end{align*} \] Note the similarity in the Taylor series of $\sin$, $\cos$ and $\sinh$ and $\cosh$. The formulas are the same, but the hyperbolic version do not alternate.
Explanations
Taylor series
The names Taylor series and McLaurin series are used interchangeably. Another synonym for the same concept is a power series. Indeed, we are talking about a polynomial approximation with coefficients $a_n=\frac{f^{(n)}(0)}{n!}$ in front of different powers of $x$.
If you remember your derivative rules correctly, you can calculate the McLaurin series of any function simply by writing down a power series $a_0 + a_1x + a_2x^2 + \ldots$ taking as the coefficients $a_n$ the value of the n'th derivative divided by the appropriate factorial. The more terms in the series you compute, the more accurate your approximation is going to get.
The zeroth order approximation to a function is \[ f(x) \approx f(0). \] It is not very accurate in general, but at least it is correct at $x=0$.
The best linear approximation to $f(x)$ is its tangent $T(x)$, which is a line that passes through the point $(0, f(0))$ and has slope equal to $f'(0)$. Indeed, this is exactly what the first order Taylor series formula tells us to compute. The coefficient in front of $x$ in the Taylor series is obtained by first calculating $f'(x)$ and then evaluating it at $x=0$: \[ f(x) \approx f(0) + f'(0)x = T(x). \]
To find the best quadratic approximation to $f(x)$, we find the second derivative $f^{\prime\prime}(x)$. The coefficient in front of the $x^2$ term will be $f^{\prime\prime}(0)$ divided by $2!=2$: \[ f(x) \approx f(0) + f'(0)x + \frac{f^{\prime\prime}(0)}{2!}x^2. \]
If we continue like this we will get the whole Taylor series of the function $f(x)$. At step $n$, the coefficient will be proportional to the $n$th derivative of $f(x)$ and the resulting $n$th degree approximation is going to imitate the function in its behaviour up the $n$th derivative.
Proof of the sum of the geometric series
We are looking for the sum $S$ given by: \[ S = \sum_{k=0}^n r^k = 1 + r + r^2 + r^3 + \cdots + r^n. \] Observe that there is a self similar pattern in the expanded summation $S$ where each term to the right has an additional power of $r$. The effects of multiplying by $r$ will therefore to “shift” all the terms of the series: \[ rS = r\sum_{k=0}^n r^k = r + r^2 + r^3 + \cdots + r^n + r^{n+1}, \] we can further add one to both sides to obtain \[ 1 + rS = \underbrace{1 + r + r^2 + r^3 + \cdots + r^n}_S + r^{n+1} = S + r^{n+1}. \] Note how the sum $S$ appears as the first part of the expression on the right-hand side. The resulting equation is quite simple: $1 + rS = S + r^{n+1}$. Since we wanted to find $S$, we just isolate all the $S$ terms to one side: \[ 1 - r^{n+1} = S - rS = S(1-r), \] and then solve for $S$ to obtain $S=\frac{1-r^{n+1}}{1-r}$. Neat no? This is what math is all about, when you see some structure you can exploit to solve complicated things in just a few lines.
Examples
An infinite series
Compute the sum of the infinite series \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n. \] This may appear complicated, but only until you recognize that this is a type of geometric series $\sum ar^n$, where $a=\frac{1}{N+1}$ and $r=\frac{N}{N+1}$: \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n = \sum_{n=0}^\infty a r^n = \frac{a}{1-r} = \frac{1}{N+1}\frac{1}{1-\frac{N}{N+1}} = 1. \]
Calculator
How does a calculator compute $\sin(40^\circ)=0.6427876097$ to ten decimal places? Clearly it must be something simple with addition and multiplication, since even the cheapest scientific calculators can calculate that number for you.
The trick is to use the Taylor series approximation of $\sin(x)$: \[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} + \ldots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}. \]
To calculate sin of 40 degrees we just compute the sum of the series on the right with $x$ replaced by 40 degrees (expressed in radians). In theory, we need to sum infinitely many terms to satisfy the equality, but in practice you calculator will only have to sum the first seven terms in the series in order to get an accuracy of 10 digits after the decimal. In other words, the series converges very quickly.
Let me show you how this is done in Python.
First we define the function for the $n^{\text{th}}$ term:
\[
a_n(x) = \frac{(-1)^nx^{2n+1}}{(2n+1)!}
\]
>>> def axn_sin(x,n): return (-1.0)**n * x**(2*n+1) / factorial(2*n+1)
Next we convert $40^\circ$ to radians:
>>> forti = (40*pi/180).evalf()
0.698131700797732 # 40 degrees in radians
NOINDENT These are the first 10 coefficients in the series:
>>> [ axn_sin( forti ,n) for n in range(0,10) ] [(0, 0.69813170079773179), # the values of a_n for Taylor(sin(40)) (1, -0.056710153964883062), (2, 0.0013819920621191727), (3, -1.6037289757274478e-05), (4, 1.0856084058295026e-07), (5, -4.8101124579279279e-10), (6, 1.5028144059670851e-12), (7, -3.4878738801065803e-15), (8, 6.2498067170560129e-18), (9, -8.9066666494280343e-21)]
NOINDENT To compute $\sin(40^\circ)$ we sum together all the terms:
>>> sum( [ axn_sin( forti ,n) for n in range(0,10) ] )
0.642787609686539 # the Taylor approximation value
>>> sin(forti).evalf()
0.642787609686539 # the true value of sin(40)
Discussion
You can think of the Taylor series as “similarity coefficients” between $f(x)$ and the different powers of $x$. By choosing the coefficients as we have $a_n = \frac{f^{(n)}(?)}{n!}$, we guarantee that Taylor series approximation and the real function $f(x)$ will have identical derivatives. For a McLaurin series the similarity between $f(x)$ and its power series representation is measured at the origin where $x=0$, so the coefficients are chosen as $a_n = \frac{f^{(n)}(0)}{n!}$. The more general Taylor series allow us to build an approximation to $f(x)$ around any point $x_o$, so the similarity coefficients are calcualted to match the derivatives at that point: $a_n = \frac{f^{(n)}(x_o)}{n!}$.
Another way of looking at the Taylor series is to imagine that it is a kind of X-ray picture for each function $f(x)$. The zeroth coefficient $a_0$ in the power series tells you how much of the constant function there is in $f(x)$. The first coefficient, $a_1$, tells you how much of the linear function $x$ there is in $f$, the coefficient $a_2$ tells you about the $x^2$ contents of $f$, and so on and so forth.
Now get ready for some crazy shit. Using your new found X-ray vision for functions, I want you to go and take a careful look at the power series for $\sin(x)$, $\cos(x)$ and $e^x$. As you will observe, it is as if $e^x$ contains both $\sin(x)$ and $\cos(x)$, except for the alternating negative signs. How about that? This is a sign that these three functions are somehow related in a deeper mathematical sense: recall Euler's formula.
Exercises
Derivative of a series
Show that \[ \sum_{n=0}^\infty \frac{1}{N+1} \left( \frac{ N }{ N +1 } \right)^n n = N. \] Hint: take the derivative with respect to $r$ on both sides of the formula for the geometric series.