The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Introduction to calculus
Calculus is the study of functions. We use calculus in order to describe how quantities change over time (derivatives $\frac{d}{dt}$) or to find the total amount of quantities that vary over time (integration $\int\cdot\;dt$).
Derivatives
The derivative function $f'(t)$ is a description of how the function $f(t)$ changes over time. The derivative encodes the information about rate of change or the slope of the function $f(t)$: \[ f'(t) \equiv \text{slope}_f(t) = \frac{ \text{change in} \ f(t) }{ \text{change in}\ t } = \frac{ f(t+\Delta t) - f(t) }{ \Delta t }. \] If the slope of $f(t)$ is big at some value of $t$, this means that the function changes very quickly at that time. At the other extreme we have the points where $f'(t)=0$ which correspond to locations where the function is flat—it is neither increasing nor decreasing.
Derivatives are used widely in many areas of science, so there are many names and symbols used to denote this operation: $Df(t) = f'(t)=\frac{df}{dt}=\frac{d}{dt}\!\left\{ f(t) \right\}=\dot{f}$. You shouldn't think of $f'(t)$ as a separate entity from $f(t)$, but as a property of the function $f(t)$. Indeed, it is best to think of the derivative as an operator $\frac{d}{dt}$ which can be applied to any function in order to obtain the slope information.
Integrals
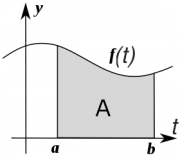 An integral corresponds to the computation of an area
under a curve $f(t)$ between two points:
\[
A(a,b) \equiv \int_{t=a}^{t=b} f(t)\;dt.
\]
The symbol $\int$ is a mnemonic for sum,
since the area under the curve corresponds in some
sense to the sum of the values of the function $f(t)$
between $t=a$ and $t=b$.
The integral is the total amount of $f$ between $a$ and $b$.
An integral corresponds to the computation of an area
under a curve $f(t)$ between two points:
\[
A(a,b) \equiv \int_{t=a}^{t=b} f(t)\;dt.
\]
The symbol $\int$ is a mnemonic for sum,
since the area under the curve corresponds in some
sense to the sum of the values of the function $f(t)$
between $t=a$ and $t=b$.
The integral is the total amount of $f$ between $a$ and $b$.
Example 1
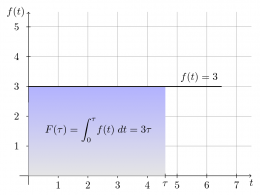 We can easily find the area under the constant function $f(t) = 3$
between any two points because the region under the curve is rectangular.
We choose to use $t=0$ as the reference point and compute
the indefinite integral $F(\tau)$ which corresponds to the
area under $f(t)$ starting from $t=0$ and going until $t=\tau$:
\[
F(\tau) \equiv A(0,\tau) = \! \int_0^\tau \!\! f(t)\;dt = 3 \tau.
\]
Indeed the area is equal to the height times the length of the rectangle.
We can easily find the area under the constant function $f(t) = 3$
between any two points because the region under the curve is rectangular.
We choose to use $t=0$ as the reference point and compute
the indefinite integral $F(\tau)$ which corresponds to the
area under $f(t)$ starting from $t=0$ and going until $t=\tau$:
\[
F(\tau) \equiv A(0,\tau) = \! \int_0^\tau \!\! f(t)\;dt = 3 \tau.
\]
Indeed the area is equal to the height times the length of the rectangle.
Example 2
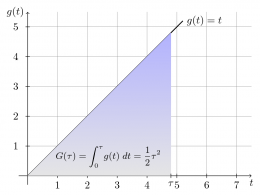 We can also easily compute the area under the line $g(t)=t$
since the region under the curve is triangular.
Recall that the area of a triangle is given by the length of
the base times the height divided by two.
We can also easily compute the area under the line $g(t)=t$
since the region under the curve is triangular.
Recall that the area of a triangle is given by the length of
the base times the height divided by two.
We choose $t=0$ as our starting point again and find the area: \[ G(\tau) \equiv A(0,\tau) = \int_0^\tau g(t) \; dt = \frac{\tau\times\tau}{2} = \frac{1}{2}\tau^2. \]
We were able to compute the above integrals thanks to the simple geometry of the areas under the curves. Later on in this book we will develop techniques for finding integrals of more complicated functions. In fact, there is an entire course, Calculus II, which is dedicated to the task of finding integrals.
What I need you to remember for now is that the integral of a function gives you the area under the curve, which is in some sense the total amount of the function accumulated during that period.
You should also remember the following two formulas: \[ \int_0^\tau a \;dt = a\tau, \qquad \int_0^\tau at \;dt = \frac{1}{2}a\tau^2. \] The second formula is a generalization of the formula we saw in Example 2.
Using the above formulas in combination, you can now compute the integral under an arbitrary line $h(t)=mt+b$ as follows: \[ H(\tau)= \int_0^\tau h(t)\;dt = \int_0^\tau (mt + b)\;dt = \int_0^\tau \!mt\;dt\ + \int_0^\tau \!b\;dt = \frac{1}{2}m\tau^2 + b \tau. \]
Why do we need integrals? How often do you need to compute the area below a function $f(t)$ in the real life?
Inverse operations
The integral is the inverse operation of the derivative. You are already familiar with the inverse relationship between functions. When solving equations, we use inverse functions to undo the effects of functions that stand in the way. Similarly, we use the integral operation to undo the effects of the derivative operation. For example, if you want to find the function $f(t)$ in an equation of the form \[ \frac{d}{dt} \left\{ f(t) \right\} = g(t), \] you have to apply the integration operation on both sides of the equation. The integral operation will undo the derivative operation on the left so we will obtain: \[ \int \frac{d}{dt} \left\{ f(t) \right\} \;dt = f(t) = \int g(t) \; dt. \]
From now on, every time you want to undo a derivative, you can apply the integral operation: \[ \text{int}\!\left( \text{diff}( f(x) ) \right) = \int_0^x \left( \frac{d}{dt} f(t) \right) \; dt = \int_0^x \! f'(t) \; dt = f(x) + C. \] Note that integration always introduces an additive constant term $+C$. This is because the derivative operation destroys the information about the initial value of the function. The functions $f(x)+1$ and $f(x)+2$ have same derivative $f'(x)$ so when we solve the inverse problem of finding $f(x)$ from $f'(x)$, we must state our answer as $f(x)+C$ for some constant $C$.
Banking example
In order to illustrate how derivative and integral operations can be used in the real world, we will draw an analogy with a scenario that every student is familiar with. Consider the function $\textrm{ba}(t)$ which represents your bank account balance at time $t$, and the function $\textrm{tr}(t)$ which corresponds to the transactions (deposits and withdraws) on your account.
The function $\textrm{tr}(t)$ is the derivative of the function $\textrm{ba}(t)$. Indeed, if you ask “how does my balance change over time”, the answer will be the function $\textrm{tr}(t)$. Using the mathematical symbols, we can represent this relationship as follows: \[ \textrm{tr}(t) = \frac{d}{dt} \left\{ \textrm{ba}(t) \right\}. \] If the derivative is big (and negative), your account balance will be depleted quickly.
Suppose now, that you have the record of all the transactions on your account $\textrm{tr}(t)$ and you want to compute the final account balance at the end of the month. Since $\textrm{tr}(t)$ is the derivative of $\textrm{ba}(t)$, you can use an integral (the inverse operation to the derivative) in order to obtain $\textrm{ba}(t)$. Knowing the balance of your account at the beginning of the month, you can calculate the balance at the end of the month by calculating the following integral: \[ \textrm{ba}(30)=\textrm{ba}(0)+\int_0^{30} \textrm{tr}(t)\:dt. \] This calculation makes sense intuitively since $\textrm{tr}(t)$ represents the instantaneous change in $\textrm{ba}(t)$. If you want to find the overall change from day 0 until day 30, you need to compute the total of all the changes on the account. More generally, the integrals are used every time you need to calculate the total of some quantity over a time period.
In the next section we will see how the integration techniques learned in this section can be applied to the subject of kinematics. We will see how the equations of motion for UAM are derived from first principles.
