We will now study the physics of objects in rotation. A simple example of this kind of motion is a rotating disk. Other examples include rotating bicycle wheels, spinning footballs and spinning figure skaters.

As you will see shortly, the basic concepts used to describe angular motion are directly analogous to the concepts for linear motion: position, velocity, acceleration, force, momentum and energy.

It is instructive to begin our discussion with a brief review of the concepts and formulas used to describe the linear motion of objects.

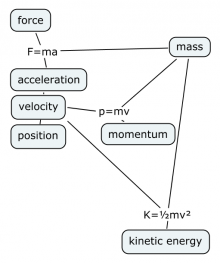The linear motion of an object is described by its position $x(t)$, velocity $v(t)$ and acceleration $a(t)$ as functions of time. The position function tells you where the object is, the velocity tells you how fast it is moving and the acceleration measures the change in the velocity of the object.

The motion of objects is governed by Newton's first and second laws. In the absence of external forces, objects will maintain a uniform velocity (UVM) which corresponds to the equations of motion: $x(t)=x_i+v_it$, $v(t)=v_i$. If there is a net force $\vec{F}$ acting on the object, the force will cause the object to accelerate and the magnitude of the acceleration is obtained using the formula $F=ma$. A constant force acting on an object will produce a constant acceleration (UAM), which corresponds to the equations of motion: $x(t)=x_i+v_it+\frac{1}{2}at^2$, $v(t)=v_i + at$.

We also learned how to quantify the momentum $\vec{p}=m\vec{v}$ and the kinetic energy $K=\frac{1}{2}mv^2$ of moving objects. The momentum vector is the natural measure of the “quantity of motion,” which plays a key role in collisions. The kinetic energy measures how much energy the object has by virtue of its motion.

The mass of the object $m$ is an important factor in many of the equations of physics. In the equation $F=ma$, the mass $m$ measures the objects inertia, i.e., how much resistance the object offers to being accelerated. The mass of the object also appears in the formulas for momentum and kinetic energy: the heavier the object is, the larger its momentum and its kinetic energy will be.

We now introduce the new concepts used to describe the angular motion of objects.

• The kinematics of rotating objects is described in terms of angular quantities:
  • $\theta(t)$[rad]: The angular position.
  • $\omega(t)$[rad/s]: The angular velocity.
  • $\alpha(t)$[rad/s$^2$]: The angular acceleration.
• $I$[kg m$^2$]: The moment of inertia of an object tells you how difficult it is to make it turn.

The quantity $I$ plays the same role in angular motion as the mass $m$ plays in linear motion.

• $\mathcal{T}$[N$\:$m]: The torque is a measures angular force.

Torque is the cause of angular acceleration.

  The angular equivalent of Newton's second law $\sum F=ma$ is given by the equation
  $\sum\mathcal{T}=I\alpha$. 
  In words, this law states that applying an angular force (torque) $\mathcal{T}$
  will produce an amount of angular acceleration $\alpha$ which is
  inversely proportional to the moment of inertia $I$ of the object.
* $L=I\omega$[kg$\:$m$^2$/s]: The //angular momentum// of a rotating object describes
  the "quantity of spinning stuff."
* $K_r=\frac{1}{2}I\omega^2$[J]: The //angular// or //rotational// kinetic energy 
  quantifies the amount of energy an object has by virtue of its rotational motion.

Instead of talking about position $x$, velocity $v$ and acceleration $a$, we will now talk about the angular position $\theta$, angular velocity $\omega$ and angular acceleration $\alpha$. Except for this change of ingredients, the recipe for fining the equations of motion remains the same: \[ \alpha(t) \ \ \overset{\omega_i + \int\!dt}{\longrightarrow} \ \ \omega(t) \ \ \overset{\theta_i+ \int\!dt }{\longrightarrow} \ \ \theta(t). \] Given the knowledge of the angular acceleration $\alpha(t)$, the initial velocity $\omega_i$ and the initial position $\theta_i$, we can use integration in order to find the equation of motion $\theta(t)$ which describes the angular position of the rotating object at all times.

Though this recipe can be applied to any form of angular acceleration function, you are only required to know the equations of motion for two special cases: the case of constant angular acceleration $\alpha(t)=\alpha$ and the case of zero angular acceleration $\alpha(t)=0$. These are the angular analogues of uniform acceleration motion and uniform velocity motion which we studied in the kinematics section.

The equations which describe uniformly accelerated angular motion are: \[ \begin{align*} \alpha(t) &= \alpha, \nl \omega(t) &= \alpha t + \omega_i, \nl \theta(t) &= \frac{1}{2}\alpha t^2 + \omega_it + \theta_i, \nl \omega_f^2 &= \omega_i^2 + 2\alpha(\theta_f - \theta_i). \end{align*} \] Note how the form of the equations is identical to the UAM equations. This should come as no surprise since the both sets of equations are obtained from the same integrals.

The equations of motion for uniform velocity angular motion are: \[ \begin{align*} \alpha(t) &= 0, \nl \omega(t) &= \omega_i, \nl \theta(t) &= \omega_it + \theta_i. \end{align*} \]

The angular quantities $\theta$, $\omega$ and $\alpha$ are the natural parameters for describing the motion of rotating objects. In certain situations, however, we may want to relate the angular quantities to linear quantities like distance, velocity and linear acceleration. This can be accomplished by multiplying the angular quantity by the radius of motion: \[ d = R\theta, \quad v = R\omega, \quad a = R\alpha. \]

For example, suppose you have a spool of network cable with radius 20[cm] and you need to measure out a length of 20[m] so as to connect your computer to your neighbours' computer. How many turns from the spool will you need? To find out, we can solve for $\theta$ in the formula $d=R\theta$ and obtain $\theta = 20/0.2=100$[rad] which corresponds to 15.9 turns.

Torque is angular force. In order to make an object rotate, you must exert a torque on it. Torque is measured in Newton metres [N$\:$m].

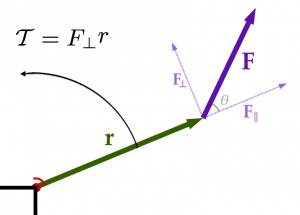The torque produced by a force depends on how far from the centre of rotation it is applied: \[ \mathcal{T} = F_{\!\perp}\: r = \|\vec{F}\|\sin\theta\; r, \] where $r$ is called the leverage. Note that only the $F_{\perp}$ component of the force creates a torque.

To understand the meaning of the torque equation, you should stop reading right now and go experiment with a door. If you push the door close to the hinges, it will take a lot more force to make it move than if you push far from the hinges. The more leverage $r$ you have, the more torque you will produce. Also, if you pull on the door handle away from the hinges, your force will have only a $F_{||}$ component so no matter how hard you pull, you will not cause the door to move.

The standard convention is to call torques that produce counter-clockwise motion positive and torques that cause clockwise rotation negative.

The relationship between torque and force can also be used in the other direction. If an electric motor produces a torque of $\mathcal{T}$[N$\:$m] and is attached to a chain wheel of radius $R$ then the tension in the chain will be: \[ T = F_{\perp} = \mathcal{T}/R \qquad [\text{N}]. \] Using this equation, you could compute the maximum pulling force produced by your car. You will have to lookup the value of the maximum torque produced by your car's engine and then divide by the radius of your wheels.

The momentum of inertia of an object describes how difficult it is to make the object rotate: \[ I = \{ \text{ how difficult it is to make an object turn } \}. \]

The calculation of the moment of inertia takes into account the mass distribution of the object. An object which has most of its mass close to the centre will have a smaller moment of inertia, whereas objects which have their mass far from the centre will have a large moment of inertia.

The formula for calculating the moment of inertia is: \[ I = \sum m_i r_i^2 = \int_{obj} r^2 \; dm \qquad [\text{kg}\:\text{m}^2]. \] The above equation indicates that we need to weight each part of the object by the squared distance of that part from the centre, hence the units $[\text{kg}\:\text{m}^2]$.

We rarely calculate the moment of inertia of objects using the above formula. Most of the physics problems you will have to solve will involve geometrical shapes for which the moment of inertia is given by simple formulas: \[ I_{disk} = \frac{1}{2}mR^2, \quad I_{ring}=mR^2, \] \[ I_{sphere} = \frac{2}{5} mR^2, \quad I_{sph. shell} = \frac{2}{3} mR^2. \] When you learn more about calculus, you will be able to derive each of the above formulas on your own. For now, just try to remember the formulas for the inertia of the disk and the ring as they are likely to come up in problems.

The quantity $I$ plays the same role in the equations of angular motion as the mass $m$ plays in the equations of linear motion.

Recall Newton's second law $F=ma$ which describes the amount of acceleration produced by a given force acting on an object. The angular analogue of Newton's second law is the following equation: \[ \mathcal{T} = I \alpha. \] This equation indicates that the angular acceleration produced by the a toque $\mathcal{T}$ is inversely proportional to the object's moment of inertia. Torque is the cause of angular acceleration.

The angular momentum of a spinning object measures the “amount of rotational motion” that the object has. The formula for the angular momentum of a an object with moment of inertia $I$ rotating at an angular velocity $\omega$ is: \[ L = I \omega \qquad [\text{kg}\:\text{m}^2/\text{s}]. \]

The angular momentum of an object is a conserved quantity in the absence of external torques: \[ L_{in} = L_{out}. \] This is similar to the way momentum $\vec{p}$ is a conserved quantity in the absence of external forces.

The kinetic energy of a rotating object is calculated as follows: \[ K_r = \frac{1}{2} I \omega^2 \qquad [\text{J}]. \] This is the rotational analogue to the linear kinetic energy $\frac{1}{2}mv^2$.

The amount of work produced by a torque $\mathcal{T}$ which is applied during an angular displacement of $\theta$ is given by: \[ W = \mathcal{T}\theta \qquad [\text{J}]. \]

Using the above equations, we can now include the energy and work associated with rotational motion into conservation of energy calculations.

A disk is spinning at a constant angular velocity of $12$[rad/s]. How many turns will the disk complete in one minute?

Since the angular velocity is constant, we can use the equation $\theta(t) = \omega t + \theta_i$ to find the total angular displacement after one minute. We obtain $\theta(60)=12\times 60=720$[rad]. To obtain the number of turns, we divide this number by $2\pi$ and obtain 114.6[turns].

A solid disk of mass $20$[kg] and radius $30$[cm] is initially spinning with an angular velocity of $20$[rad/s]. A brake pad applied to the edge of the disk produces a friction force of 60[N]. How long before the disk stops?

To solve the kinematics problem, we need to find the angular acceleration produced by the brake. We can do this using the equation $\mathcal{T}=I\alpha$. We must find $\mathcal{T}$ and $I_{disk}$ and solve for $\alpha$. The torque produced by the brake is calculated using the force-times-leverage formula: $\mathcal{T}=F_{\perp}r= 60\times 0.3=18$[N$\:$m]. The moment of inertia of a disk is given by $I_{disk} = \frac{1}{2}mR^2=\frac{1}{2}(20)(0.3)^2=0.9$[kg m$^2$]. Thus we have $\alpha=20$[rad/s$^2$]. We can now use the UAM formula for the angular velocity $\omega(t) = \alpha t + \omega_i$ and solve for the time when the motion will stop: $0 = \alpha t + \omega_i$. The disk will come to a stop after $t=\omega_i/\alpha = 1$[s].

A pulley of radius $R$ and moment of inertia $I$ has a rope wound around it and a mass $m$ attached at the end of the rope. What will be the angular acceleration of the disk if we let the mass drop to the ground while unwinding the rope.

A force diagram on the mass tells us that $mg-T=ma_y$ (where $\hat{y}$ points downwards). The torque diagram on the disk tells us that $TR = I \alpha$. Adding $R$ times the first equation to the second we get: \[ R({mg - T}) + T R = R m a_y + I \alpha, \] or after simplification we get: \[ R m g = R m a_y + I \alpha. \] But we know that the rope forms a solid connection between the disk and the mass block, so we must also have $R \alpha = a_y$, so if we substitute for $a_y$ we get: \[ R m g = R m R \alpha + I \alpha = (R^2 m + I) \alpha. \] Solving for $\alpha$ we obtain: \[ \alpha = \frac{ R m g }{ R^2 m + I }. \] This answer makes sense intuitively. The numerator is the “cause” of the motion while the denominator is the effective moment of inertia of the mass-pulley system as a whole.

A spinning figure skater starts from an initial angular velocity of $\omega_i=12$[rad/s] with her arms far away from her body. The moment of inertia of her body in this configuration is $I_i=3$[kg$\:$m$^2$]. She then brings her arms close to her body and in the process her moment of inertia changes to $I_f=0.5$[kg$\:$m$^2$]. What will be her new angular velocity?

We will solve this problem using the law of conservation of angular momentum: \[ L_i = L_f \qquad \Rightarrow \qquad I_i\omega_i = I_f \omega_f, \] which we can solve for the final angular velocity $\omega_f$. The answer is $\omega_f = I_i\omega_i/I_f= 3\times 12/0.5=72$[rad/s], which corresponds to 11.46 turns per second.

A 14[in] bicycle wheel with mass $m=4$[kg] with all its mass concentrated near the rim is set in rolling motion at a velocity of 20[m/s] up an incline. How far up the incline will the wheel reach before it stops?

We will solve this problem using the principle of conservation of energy $\sum E_i = \sum E_f$. We must take into account both the linear and rotational kinetic energies of the wheel: \[ \begin{align*} K_i \ \ + \ \ K_{ri} \ + U_i & = K_f + K_{rf} + U_f \nl \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2 + 0 \ & = \ 0 \ + \ 0 \ + mgh. \end{align*} \]

The first step is to calculate $I_{wheel}$ using the formula $I_{wheel} = mR^2 = 4 \times (0.355)^2=0.5$[kg m$^2$]. If the linear velocity of the wheel is 20[m/s], then its angular velocity is $\omega=v_t/R=20/0.355=56.34$[rad/s]. We can now use these values in the energy equation: \[ \frac{1}{2}(4)(20)^2 + \frac{1}{2}(0.5)(56.34)^2 + 0 = 800.0 + 793.55 = (4)(9.81)h. \] The maximum height reached will be $h=40.61$[m].

Note that roughly half of the kinetic energy of the wheel was stored in the rotational motion. This shows that it is important to take into account $K_r$ when solving problems using energy principles.

We say that a system is in equilibrium when all the forces and torques acting on the system balance each other out. Since there is no net force on the system, it will just sit there motionless.

Conversely, if you see an object that is not moving, then the forces on it must be in equilibrium: \[ \sum F_x = 0, \quad \sum F_y = 0, \quad \sum \mathcal{T} = 0. \] There must be zero net force in the $x$ direction, zero net force in the $y$ direction and zero net torque on the object.

A heavy wooden plank is placed so that one third of its length protrudes from the side of a pirate ship. The plank has a length of 12[m] and total weight 120[kg]: this means that 40[kg] of its weight is suspended above the ocean, while 80[kg] is lying on the ship's deck. How far out on the plank can a 80[kg] person walk before the plank tips over?

We will use the torque equilibrium equation $\sum \mathcal{T}_E = 0$ where we calculate the torques relative to the edge of the ship. The torque produced by person when he has walked a distance of $x$[m] from the edge of ship is $\mathcal{T}_1 = -80x$. The torque produced by the weight of the plank is given by $\mathcal{T}_2=120\times 2=240$[N$\:$m] since the weight acts in the centre of gravity of the plank, which is located $2$[m] from the edge. The maximum distance that can be walked before the plank tips over is therefore $x=240/80=3$[m]. After that it is all sharks.

Our coverage of the ideas of rotational motion has been very brief. The reason for this, is that there was no new physics to be learned. In this section we used the techniques and ideas developed in the context of linear motion to describe the rotational motion of objects.

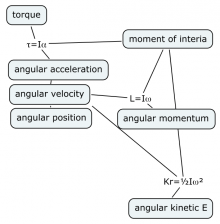It is really important that you see the parallels between the new rotational concepts and their linear counterparts. To help you see the connections, you can compare the diagram shown on the right with the diagram from the beginning of this section.

Let us summarize. If you know the torque acting on an object, then you can calculate its angular acceleration $\alpha$. Knowing the angular acceleration $\alpha(t)$ and the initial conditions $\theta_i$ and $\omega_i$, you can then calculate the equations of motion $\omega(t)$ and $\theta(t)$ at all times.

Furthermore, the angular velocity $\omega$ is related to the angular momentum $L=I\omega$ and the rotational kinetic energy $K_r=\frac{1}{2}I \omega^2$ of the rotating object. The angular momentum measures the “quantity of rotational motion”, while the rotational kinetic energy measures how much energy the object has by virtue of its rotational motion.

The moment of inertia $I$ plays the role of the mass $m$ in the rotational equations. In the equation $\mathcal{T}=I\alpha$, the moment of inertia $I$ measures how difficult it is to make the object turn. The moment of inertia also appears in the formulas for the angular momentum and rotational kinetic energy.