The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Uniform circular motion
In this section we will learn about the circular motion of objects. Circular motion is different from linear motion and we will have to develop new techniques and concepts which are better suited for the description of circular motion.
Imagine a rock of mass $m$ is swinging around in a horizontal circle attached at the end of a rope. The rock is flying through the air at a constant (uniform) speed of $v_t$[m/s] along a circular path of radius $R$[m] at a height $h$[m] above the ground. What is the tension $T$ in the rope?
Consider a coordinate system which has the $x$ and $y$ axis placed on the ground level at the centre of the circle of motion are the $z$ axis measuring the height above the ground. In that coordinate system, the trajectory of the rock is described by the equation \[ \vec{r}(t) =(x(t),y(t),z(t)) = \left(R\cos\!\left(\frac{v_t}{R}\:t\right),\ R\sin\!\left(\frac{v_t}{R}\:t\right), \ h\right). \] You will agree with me that this expression looks somewhat complicated. This complexity stems from the fact that the $(x,y,z)$ coordinate system is not very well adapted for the description of circular paths.
A new coordinate system
Instead of the usual coordinate system $\hat{x},\hat{y},\hat{z}$ which is static, we can use a new coordinate system $\hat{t},\hat{r},\hat{z}$ that is “attached” to the rotating object.
Three important directions can be identified:
- $\hat{t}$: the tangential direction in the instantaneous direction of motion of the object.
The name comes from the Greek word for “touch” (imagine a straight line “touching” the circle).
- $\hat{r}$: the radial direction always points towards the centre of the circle of rotation.
- $\hat{z}$: the usual $\hat{z}$ direction, which is perpendicular to the plane of rotation.
From the point of view of a static observer, the tangential and radial directions constantly change their orientation as the object rotates around in a circle. From the point of view of the rotating object, the tangential and radial directions are fixed. The tangential direction is always “forward” and the radial direction is always to the side.
We can use the new coordinate system to describe the position, velocity and acceleration of the object undergoing circular motion:
- $\vec{v}=(v_r,v_t)_{\hat{r}\hat{t}}$: the velocity of object expressed with respect to
the $\hat{r}\hat{t}$ coordinates.
- $\vec{a}=(a_r,a_t)_{\hat{r}\hat{t}}$: The acceleration of the object in the $\hat{r}\hat{t}$ coordinates.
The most important parameters of motion are the tangential velocity $v_t$, the radial acceleration $a_r$ and the radius of the circle of motion $R$. We have $v_r=0$ since the motion is entirely in the $\hat{t}$ direction, and $a_t=0$ because we assumed that the tangential velocity $v_t$ remains constant (uniform circular motion).
In the next section we will learn how to calculate the radial acceleration $a_r$.
Radial acceleration
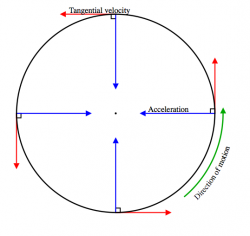 The defining feature of circular motion is the presence of an acceleration
that acts perpendicularly to direction of motion.
At each instant, the object wants to continue moving along the tangential direction,
but the radial acceleration causes the velocity to change direction.
The result of this constant inward acceleration is that the object will
follow a circular path.
The defining feature of circular motion is the presence of an acceleration
that acts perpendicularly to direction of motion.
At each instant, the object wants to continue moving along the tangential direction,
but the radial acceleration causes the velocity to change direction.
The result of this constant inward acceleration is that the object will
follow a circular path.
The radial acceleration $a_r$ of an object moving in a circle of radius $R$ with a tangential velocity $v_t$ is given by: \[ a_r = \frac{v^2_t}{ R }. \] This is an important equation which relates the three key parameters of circular motion.
According to Newton's second law $\vec{F}=m\vec{a}$, the radial acceleration of the object must be caused by a radial force. We can calculate the magnitude of this radial force $F_r$ as follows: \[ F_{r} = ma_r = m \frac{v^2_t}{ R }. \] The above formula allows us to connect the observable aspects of the circular motion $v_t$ and $R$ with its cause: the force $F_r$ which always acts towards the centre of rotation.
To put it differently, we can say that circular motion requires a radial force. From now on, every time you see an object undergoing circular motion, you should try to visualize the radial force which is causing the circular motion.
In the rock-on-a-rope example described in the beginning of this section, the circular motion was caused by the tension of the rope which always acts in the radial direction (towards the centre of rotation). We are now in a position to calculate the value of the tension $T$ in the rope using the equation: \[ F_{r} = T = ma_r, \qquad \Rightarrow \qquad T=m \frac{v^2_t}{ R }. \]
Example
During a student protest, a young activist called David is stationed on the rooftop of a building of height $12$[m]. A mob of blood-thirsty neoconservatives is slowly approaching his position determined to lynch him because of his leftist views. David has put together a make-shift weapon by attaching a 0.3[kg] rock to the end of a shoelace of length $1.5$[m]. The maximum tension that the shoelace can support is 500[N]. What is the maximum tangential velocity $\max\{v_t\}$ that the shoelace can support? What is the maximum range for this projectile when it is launched from the roof?
The first part of the question is answered easily using the $T=m \frac{v^2_t}{ R }$ formula: $\max\{v_t\} = \sqrt{ \frac{R T}{m} }= \sqrt{ \frac{1.5\times 500}{0.3} }=50$[m/s]. To answer the second question, we must solve for the distance travelled by a projectile with initial velocity $\vec{v}_i=(v_{ix},v_{iy})=(50,0)$[m/s] launched from $\vec{r}_i=(x_i,y_i)=(0,12)$[m]. First we solve for the total time of flight $t_f=\sqrt{2\times 12/9.81}=1.56$[s]. Then we find the range by multiplying this time by the horizontal speed $x(t_f)=0+v_{ix} t_f = 50\times 1.56=78.20$[m].
After carrying out these calculations on a piece of paper, David starts to spin-up the rock and waits for the neocons to come into range.
Circular motion parameters
We now introduce some further terminology used to describe circular motion:
- $C=2\pi R$[m]: The circumference of the circle of motion.
- $T$: The period of the motion is how long it takes for the object to complete one full circle.
The period is measured in seconds [s].
- $f=\frac{1}{T}$: The frequency of rotation. How many times per second does the object pass by
some reference point on the circle. Frequency is measured in Hertz [Hz]=[1/s].
We sometimes describe the frequency of rotation in //revolutions per minute// (RPM).
* $\omega\equiv\frac{v_t}{R}=2\pi f$: The //angular velocity// describes how fast the
object is rotating. Angular velocity is measured in [rad/s].
Recall that a circle of radius $R$ has circumference $C = 2 \pi R$. The period $T$ is defined as how long it will take the object to complete one full turn around the circle: \[ T = \frac{\text{distance}}{\text{speed}} = \frac{C}{v_t} = \frac{2\pi R}{v_t}, \] where $C=2\pi R$ is total distance that must be travelled to compete one turn and $v_t$ is the velocity of the object along the curve. The object will complete one full turn every $T$ seconds.
Another way of describing the motion is to talk about the frequency: \[ f=\frac{1}{T} = \text{[Hz]}. \] The frequency tells you how many turns the object completes in one second. If the object competes one turn in $T=0.2$[s], then the motion has frequency $f=5$[Hz], or $f=60\times 5 = 300$[RPM].
The most natural parameter for describing rotation is in terms of the angular velocity $\omega$[rad/s]. We know that one full turn corresponds to an angle of rotation of $2\pi$[rad], so the angular velocity is obtained by dividing $2\pi$ by the time it takes to complete one turn: \[ \omega = \frac{2\pi}{T} = 2\pi f = \frac{v_t}{R}. \]
The angular velocity $\omega$ is very useful because it describes the speed of the circular motion without any reference to the radius. If we know that the angular velocity of an object is $\omega$, we can obtain the tangential velocity by multiplying times the radius: $v_t=R\omega$[m/s].
Let us now look at some examples in which we are asked to compute some angular velocities.
Bicycle odometer
Imagine that you place a small speed detector gadget on one of the spokes of the front wheel of your bicycle. Your bike's wheels have a radius $R=14$[in] and the gadget is attached at a distance of $\frac{3}{4}R$[m] from the centre of the wheel. Find the angular velocity $\omega$, period $T$, and frequency $f$ of rotation for the wheel when the speed of the bicycle relative to the ground is $40$[km/h]. What is the tangential velocity $v_t$ of the detector gadget?
The velocity of the bicycle relative to the ground $v_{bike}=40$[km/h] is equal to the tangential velocity of the rim of the wheel: \[ v_{bike} = v_{rim} = 40 [\text{km/h}] \times \frac{ 1000 [\text{m}] }{ 1 [\text{km}]} \times \frac{ 1 [\text{h}] }{ 3600 [\text{s}]} = 11.11 [\text{m/s}]. \] We can find the angular velocity using $\omega = \frac{v_{rim}}{R}$ and the radius of the wheel $R=14[\text{in}]=0.355$[m]. We obtain $\omega = \frac{11.11}{0.355}= 31.24[\text{rad/s}]$. From this we can easily calculate $T=\frac{2\pi}{\omega}=0.20$[s] and $f=\frac{1}{0.20}=5$[Hz]. Finally, to compute the tangential velocity of the gadget we multiply the angular velocity $\omega$ by its radius of rotation to obtain $v_{det}= \omega \times \frac{3}{4}R = 8.333$[m/s].
Rotation of the Earth
It takes exactly 23 hours, 56 minutes and 4.09 seconds for the Earth to compete one full turn ($2\pi$ radians) around its axis of rotation. What is its angular velocity? What is the tangential speed at a latitude of $45^\circ$ (Montreal)?
We can find $\omega$ by carrying out a simple conversion: \[ \frac{2\pi \text{ [rad]}}{ 1 \text{ [day]} } \cdot \frac{1 \text{ [day]}}{ 23.93447 \text{ [h]} } \cdot \frac{1 \text{ [h]}}{ 3600 \text{ [s]} } = 7.2921\times 10^{-5} \text{ [rad/s]}. \]
The radius of the trajectory traced out by someone at a latitude of $45^\circ$ (Montreal) is given by $r=R\cos(45^\circ)=4.5025\times 10^6$[m], where $R=6.3675×10^6$[m] is the radius of the Earth. Thus, though it may seem that you are not moving right now, in reality you are hurtling through space at a speed of \[ v_t = r \omega = 4.5025\times 10^6 \times 7.2921\times 10^{-5} = 464.32 \text{ [m/s]}. \] Which is $1671.56$[km/h]. Just try to imagine that for a second. You can try to use this fact if you get stopped by the cops one day for a speeding infraction: “Yes officer, I was doing 130[km/h], but this is really a negligible speed relative to the 1671[km/h] that the Earth is doing around the sun.”
Three dimensions
For some problems involving circular motion, it will be necessary to consider the $z$ direction in the force diagram. The best approach in this case is to draw the force diagram as a cross section, which is perpendicular to the tangential direction. The diagram will show the $\hat{r}$ and $\hat{z}$ axes.
Using the force diagram, you should be able to find all the forces in the radial and vertical directions and solve for accelerations $a_r$, $a_z$. Remember that you can always use the relation $a_r=\frac{v_t^2}{R}$ which connects the value of $a_r$ with the tangential velocity $v_t$ and the radius of rotation $R$.
Example
Japanese people of the future want to design a giant racetrack for retired superconducting speed trains. The shape of the race track is a big circle with radius $R=3$[km]. Because the trains are magnetically levitated, there is no friction between the track and the train $\mu_s=0, \mu_k=0$. What is the bank angle required for the race track so that trains moving at a speed of exactly $400$[km/h] will stay on the track without moving laterally?
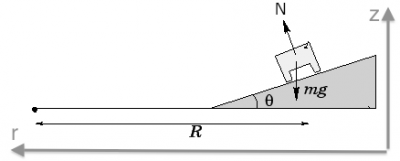 We begin by drawing a force diagram which shows a cross-cut of the
train in the $\hat{r}$ and $\hat{z}$ directions.
The bank angle of the racetrack is $\theta$. This is the unknown we are looking for.
Because of the frictionless-ness of levitated superconducting suspension
there cannot be any force of friction $F_f$ so the only forces on the
train will be it weight $\vec{W}$ and the normal force $\vec{N}$.
We begin by drawing a force diagram which shows a cross-cut of the
train in the $\hat{r}$ and $\hat{z}$ directions.
The bank angle of the racetrack is $\theta$. This is the unknown we are looking for.
Because of the frictionless-ness of levitated superconducting suspension
there cannot be any force of friction $F_f$ so the only forces on the
train will be it weight $\vec{W}$ and the normal force $\vec{N}$.
The next step is to write down the force equations for the two directions: \[ \begin{align*} \sum F_r &= N\sin\theta = m a_r = m \frac{v_t^2}{R} \quad \Rightarrow \quad N\sin\theta = m \frac{v_t^2}{R}, \nl \sum F_z &= N\cos\theta - mg = 0 \ \ \quad \quad \Rightarrow \quad N\cos\theta = mg. \end{align*} \] Note how the normal force $\vec{N}$ is split into two parts: the vertical component counter balances the weight of the train, while the component in the $\hat{r}$ direction is the force that is responsible for causing the rotational motion of the train around the track.
We want to solve for $\theta$ in the above equations. A commonly used trick for solving equations containing multiple trigonometric functions is to divide one equation by the other. We obtain: \[ \frac{ N \sin\theta }{ N\cos\theta } =\frac{ m \frac{v_t^2}{R} }{ mg} \quad \Rightarrow \quad \tan\theta = \frac{ v_t^2 }{ Rg }. \] The final answer is $\theta = \tan^{-1}\!\!\left(\frac{v_t^2}{gR} \right) = \tan^{-1}\!\!\left(\frac{(400\times\frac{1000}{3600})^2}{9.81 \times 3000} \right) = 22.76^\circ$. If the angle were any steeper, the trains would fall towards the centre. If the bank angle were any shallower, the trains would fly off to the side. The angle $22.76^\circ$ is just right.
Discussion
Radial acceleration
In the kinematics section we studied problems involving linear acceleration: in which an acceleration $a$ was acting in the same direction as the velocity and was thus causing a change the magnitude of the velocity $v$.
Circular motion deals with a different situation in which the speed $\|\vec{v}\|$ of the object remains constant but the velocity $\vec{v}$ changes direction. At each point along the circle, the velocity of the object points along the tangential direction and during each instant the radial acceleration pulls the object inwards and causes it to rotate.
Another term for radial acceleration is centripetal acceleration, which literally means “tending towards the centre”.
Centrifugal force
When a car makes a left turn, the passenger riding shotgun will feel pushed towards the right: into the passenger door. Some people erroneously attribute this effect to a centrifugal force, which acts away from the centre of rotation. During a sharp turn, these people feel as though they are being flung out of the car and therefore they conclude that there must be some force which is responsible for this.
The reason why we feel as though we are being thrown out of the car is due to Newton's first law which says that, in the absence of external forces, an object will continue moving in a straight line. Since your initial motion is in the $\hat{t}$ direction, your body will naturally continue moving in that direction because of Newton's first law. The force of the car door pushes you inwards and keeps you in the circular trajectory. If it weren't for the door, you would fly straight on.
Radial forces do no work
An interesting property of radial forces is that they do zero work. Recall that the work done by a force $\vec{F}$ during a displacement $\vec{d}$ is computed using the dot product $W=\vec{F}\cdot \vec{d}$. For circular motion, the displacement is always in the $\hat{t}$ direction, whereas the radial force is in the $\hat{r}$ direction so the dot product of the two is zero.
This is why it is possible for the speed of the object undergoing circular motion to remain constant despite the fact that it is being accelerated. The effects of the radial acceleration do not increase the speed: they only act to change the direction of the velocity.
Exercises
Staying in touch
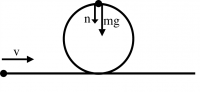 A vertical loop of radius 5[m] is placed on a racetrack.
What is the minimum speed $v$ for a motorcyclist to come into
the loop and make it around? The motorcyclist will “lose contact” with the top of the ramp if the magnitude of the normal force becomes zero.
A vertical loop of radius 5[m] is placed on a racetrack.
What is the minimum speed $v$ for a motorcyclist to come into
the loop and make it around? The motorcyclist will “lose contact” with the top of the ramp if the magnitude of the normal force becomes zero.
Solution. Find $v_{top}$ when $\vec{N}=0$ and then use conservation of energy to find $v$ in terms of $v_{top}$. Ans: $v=\sqrt{5g+20g}=5\sqrt{g}$.
Links
[ Banked curve exercise ]
http://www.chaostoy.com/cd/html/banked_e.htm
