The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Energy
Instead of thinking about velocities $v(t)$ and motion trajectories $x(t)$, we can solve physics problems using energy calculations. In this section, we will define precisely the different kinds of energies that exist and then learn the rules of converting one energy into another. The key idea in this section is the principle of total energy conservation, which tells us that, in any physical process, the sum of the initial energies is equal to the sum of the final energies.
Example
Say you drop a ball from a height $h$[m] and you want to predict its speed right before it hits the ground. Using the kinematics approach, you would go for the general equation of motion: \[ v_f^2 = v_i^2 + 2a(y_f-y_i), \] and substitute $y_i=h$, $y_f=0$, $v_i=0$ and $a=-g$ to obtain the answer $v_f = \sqrt{2gh}$ for the final velocity at impact.
Alternately, you could use an energy calculation. Initially the ball starts from a height $h$, which means it has $U_i=mgh$[J] of potential energy. As the ball falls, the potential energy is converted into kinetic energy. Right before the ball hits the ground, it will have a final kinetic energy equal to the initial potential enegy: $K_f=U_i$ [J]. Since the formula for kinetic energy is $K=\frac{1}{2}mv^2$, we have $\frac{1}{2}mv_f^2 = mgh$. After cancelling the mass on both sides of the equation and solving for $v_f$ we obtain $v_f=\sqrt{2gh}$.
Both methods of solving the example problem come to the same conclusion, but the energy reasoning is arguably more intuitive than plugging values into a formula. In science, it is really important to know different ways for arriving at some answer. Knowing about these alternate routes will allow you to check your answers and to understand concepts better.
Concepts
Energy is measured in Joules [J] and it arises in several different contexts:
- $K =$ kinetic energy.
This is the type of energy that objects have by virtue of their motion.
- $W$ = work.
This is the amount of energy that an external
force adds or subtracts from a system. Positive work corresponds to energy being added to the system while negative work corresponds to energy being withdrawn from the system. * $U_g=$ **gravitational potential energy**. This is the energy that an object has by virtue of its position above the ground. We say this energy is //potential// because it is a form of //stored work//. The potential energy corresponds to the amount of work that the force of gravity will add to an object when you let the object fall to the ground. * $U_s= $ **spring potential energy.** This is the energy stored in a spring when it is displaced from its relaxed position. * There are many kinds other kinds of energy: electrical energy, magnetic energy, sound energy, thermal energy, etc. In this section, however, we limit out focus only on the //mechanical// energy concepts described above.
Formulas
Kinetic energy
An object of mass $m$ moving at velocity $\vec{v}$ has a kinetic energy of \[ K=\frac{1}{2}m\|\vec{v}\|^2 \qquad \text{[J]}. \] Note that the kinetic energy only depends on the speed $\|\vec{v}\|$ of the object and not the direction of motion.
Work
If an external force $\vec{F}$ acts on a object as it moves through a distance $\vec{d}$, the work done by this force is \[ W=\vec{F}\cdot \vec{d} = \|\vec{F}\| \|\vec{d}\|\cos \theta \qquad \text{[J]}, \] where the second equality follows from the geometrical interpretation of the dot product: $\vec{u}\cdot \vec{v} = \|\vec{u}\| \|\vec{v}\|\cos \theta$, with $\theta$ is the angle between $\vec{u}$ and $\vec{v}$.
If the force $\vec{F}$ acts in the same direction as the displacement $\vec{d}$, then it will do positive work ($\cos(180^\circ)=+1$)—the force will be adding energy to the system. If the force acts in the direction opposite to the displacement, then the work done will be negative ($\cos(180^\circ)=-1$), which means that energy is being withdrawn from the system.
Gravitational potential energy
An object raised to a height $h$ above the ground has a gravitational potential energy given by: \[ U_g(h) = mgh \qquad \text{[J]}, \] where $m$ is the mass of the object and $g=9.81$[m/s$^2$] is the gravitational acceleration on the surface of Earth.
Spring potential energy
The potential energy stored in a spring when it is displaced by $\vec{x}$[m] from its relaxed position is given by \[ U_{s} = \frac{1}{2}k\|\vec{x}\|^2 \qquad \text{[J]}, \] where $k$[N/m] is the spring constant.
Note that it doesn't matter whether the spring is stretched or compressed by a certain length: only the magnitude of the displacement matters $\|\vec{x}\|$.
Conservation of energy
Consider a system which starts from an initial state (i), undergoes some motion and arrives at a final state (f). The law of conservation of energy states that energy cannot be created or destroyed in any physical process. This means that the initial energy of the system plus the work that was input into the system must equal the final energy of the system plus any work that the was output: \[ \sum E_{i} \ \ + W_{in} \ \ \ = \ \ \ \sum E_{f} \ \ + W_{out}. \] The expression $\sum E_{(a)}$ corresponds to the sum of the different types of energy the system has in state (a). If we write down the equation in full we have: \[ K_i + U_{gi} + U_{si} \ \ \ + W_{in} \ \ \ = \ \ \ K_f + U_{gf} + U_{sf} \ \ \ + W_{out}. \] Usually, some of the terms in the above expression can be dropped. For example, we do not need to consider the spring potential energy $U_s$ in physics problems that do not involve springs.
Explanations
Work and energy are measured in Joules [J]. Joules can be expressed in terms of the fundamental units as follows: \[ [\text{J}] = [\text{N}\:\text{m}] = [\text{kg}\:\text{m}^2/\text{s}^{2}]. \] The first equality follows from the definition of work as force times displacement. The second equality comes from definition of the Newton [N]$=[\text{kg}\:\text{m}/\text{s}^2]$ via $F=ma$.
Kinetic energy
A moving object has energy $K=\frac{1}{2}m\|\vec{v}\|^2$[J], which we call kinetic energy from the Greek word for motion kinema.
Note that velocity $\vec{v}$ and speed $\|\vec{v}\|$ are not the same as energy. Suppose you have two objects of the same mass and one is moving twice faster than the other. The faster object will have twice the velocity, but four times more kinetic energy.
Work
When hiring someone to help you move, you have to pay them for the work they do. Work is the product of how much force is necessary for the move and the distance of the move. The more force, the more work there will be for a fixed displacement. The more displacement (think moving to the South Shore versus moving next door) the more money the movers will ask for.
The amount of work done by a force $\vec{F}$ on an object which moves along some path $p$ is given by: \[ W = \int_p \vec{F}(x) \cdot d\vec{x}, \] where we account for the fact that the magnitude and direction of the force might change throughout the motion.
If the force is constant and the displacement path is a straight line, the formula for work simplifies to: \[ W = \int_0^d \vec{F}\cdot d\vec{x} = \vec{F}\cdot\int_0^d d\vec{x} = \vec{F}\cdot \vec{d} = \|\vec{F}\|\|\vec{d}\|\cos\theta. \] Note the use of the dot product to obtain only the part of $\vec{F}$ that is pushing in the direction of the displacement $\vec{d}$. A force which acts perpendicular to the displacement produces no work, since it neither speeds up or slows down the motion.
Potential energy is stored work
Some kinds of work are just a waste of your time, like working in a bank for example. You work and you get your paycheque, but nothing remains with you at the end of the day. Other kinds of work leave you with some resource at the end of the work day. Maybe you learn something, or you network with a lot of good people.
In physics, we make a similar distinction. Some types of work, like work against friction, are called dissipative since they just waste energy. Other kinds of work are called conservative since the work you do is not lost: it is converted into potential energy.
The gravitational force and the spring force are conservative forces. Any work you do while lifting an object up into the air against the force of gravity is not lost but stored in the height of the object. You can get all the work/energy back if you let go of the object. The energy will come back in the form of kinetic energy since the object will pick up speed during the fall.
The negative of the work done against a conservative force is called potential energy. For any conservative force $\vec{F}_?$, we can define the associated potential energy $U_?$ through the formula: \[ U_?(d) = -W_{done} = - \int_0^d \vec{F}_? \cdot d\vec{x}. \] We will discuss two specific examples of this general formula below: the gravitational and spring potential energies. Being high in the air means you have a lot of potential to fall, and compressing a spring by a certain distance means it has the potential to spring back to its normal position. Let us look now at the exact formulas for these two cases.
Gravitational potential energy
The force of gravity is given by: \[ \vec{F}_g = -mg \hat{\jmath}. \] The direction of the gravitational force is downwards, towards the centre of the Earth.
The gravitational potential energy of lifting an object from a height of $y=0$ to a height of $y=h$ is given by: \[ \begin{align*} U_g(h) &\equiv - W_{done} \nl &= - \!\int_0^h \! \vec{F}_g \cdot d\vec{y} = - \!\int_0^h \!\!(-mg \hat{\jmath})\cdot \hat{\jmath} \; dy = mg \!\int_0^h \!\!\! 1\:dy = mg y\big\vert_{y=0}^{y=h} = mgh. \end{align*} \]
Spring energy
The force of a spring when stretched a distance $\vec{x}$[m] form its natural position is given by: \[ \vec{F}_s(\vec{x}) = - k\vec{x}. \]
The potential energy stored in a spring as it is compressed from $y=0$ to $y=x$[m] is given by: \[ \begin{align*} U_s(x) &= -W_{done} \nl &=-\!\int_0^x \!\vec{F}_{s}(y) \cdot d\vec{y} = \int_0^x \!\! ky dy = k\int_0^x \!\! y dy = k\frac{1}{2}y^2\big\vert_{y=0}^{y=x} = \frac{1}{2}kx^2. \end{align*} \]
Conservation of energy
Energy cannot be created or destroyed. It can only be transforms from one form to another. If there are no external forces acting on the system, then we have conservation of energy: \[ \sum E_i \ \ = \ \ \sum E_f. \]
If there are external forces like friction that do work on the system, we must take their energy contributions into account as well: \[ \sum E_i \ +\ W_{in} = \sum E_f, \quad \text{or} \quad \sum E_i = \sum E_f \ +\ W_{out}. \]
This is one of the most important equations you will find in this book, because it will allow you to solve very complicated problems simply by accounting for all the different kinds of energy involved in the problem.
Examples
Banker dropped
An investment banker is dropped (from rest) from a 100[m] tall building. What is his speed when he hits the ground?
We start from: \[ \begin{align*} \sum E_i \ \ &= \ \ \sum E_f, \nl K_i + U_i \ \ & = \ \ K_f + U_f, \end{align*} \] and plugging in the numbers we get: \[ 0 + m \times9.81 \times100 = \frac{1}{2}mv^2 + 0. \] After cancelling the mass $m$ from both sides of the equation we are left with \[ 9.81\times 100 = \frac{1}{2}v_f^2. \] Solving for $v_f$ in the above equation, we find that the banker will be going at $v_f =\sqrt{ 2\times 9.81\times 100}=44.2945$[m/s] when he hits the ground. This is like $160$[km/h]. Ouch! That will definitely hurt.
Bullet speedometer
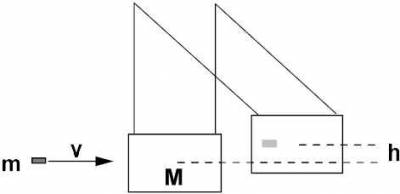 An incoming bullet at speed $v$ hits a mass $M$ suspended on two strings.
Use conservation of momentum and conservation of energy principles to
find the speed $v$ of the bullet if the block rises to a height $h$ after
it is hit by the bullet.
An incoming bullet at speed $v$ hits a mass $M$ suspended on two strings.
Use conservation of momentum and conservation of energy principles to
find the speed $v$ of the bullet if the block rises to a height $h$ after
it is hit by the bullet.
First we use the conservation of momentum principle to find the (horizontal) speed of the block and mass right after the bullet hits: \[ \vec{p}_{in,m} + \vec{p}_{in,M} = \vec{p}_{out}, \] \[ m v + 0 = (m+M) v_{out}, \] so the velocity of the block with the bullet embedded in it is $v_{out}= \frac{mv}{M+m}$ right after collision.
Next we use the conservation of energy principle to relate the initial kinetic energy of the block-plus-bullet and the height $h$ by which it rises: \[ K_i + U_i = K_f + U_f, \] \[ \frac{1}{2}(M+m)v_{out}^2 + 0 = 0 + (m+M)gh. \] Isolating $v_{out}$ in the above equation and setting it equal to the $v_{out}$ we got from the momentum calculation we get: \[ v_{out} = \frac{mv}{M+m} = \sqrt{2gh} = v_{out}. \] We can use this equation to find the speed of the incoming bullet: \[ v = \frac{M+m}{m}\sqrt{2gh}. \]
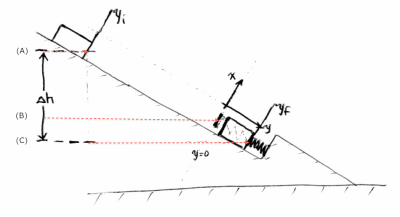
Incline and spring
A block of mass $m$ is released from rest at point (A) on the top of an incline at a coordinate $y=y_i$. It slides down the frictionless incline to the point (B) $y=0$. The coordinate $y=0$ corresponds to the relaxed length of a spring of spring constant $k$. The block then compresses the spring all the way to point (C ), corresponding to $y=y_f$, when the block comes to rest again. The angle of the slope is $\theta$.
What is the speed of the block at $y=0$? How far does the spring get compressed $y_f$? Bonus points if you can express your answer for $y_f$ in terms of $\Delta h$, the difference in height between $y_i$ and $y_f$.
We have essentially two problems: the motion from (A) to (B) in which the gravitational potential energy of the block is converted into kinetic energy and the motion from (B) to (C ) in which the all the energy of the block gets converted into spring potential energy.
In both cases, there is no friction so we can use the conservation of energy formula: \[ \sum E_i \ \ = \ \ \sum E_f. \]
For the motion from (A) to (B) we have: \[ K_i + U_i = K_f + U_f. \] The block starts from rest so $K_i=0$. The difference in potential energy is equal to $mgh$ and in this case the block is $|y_i|\sin\theta$ [m] higher at (A) than it is at (B), so we can write: \[ 0 + mg|y_i|\sin\theta = \frac{1}{2}mv_B^2 + 0. \] The above formula uses the point (B) at $y=0$ as reference for the gravitational potential energy. The potential at point (A) is $U_i=mgh=mg|y_i-0|\sin\theta$ relative to point (B) since the point (A) is $h=|y_i-0|\sin\theta$ metres higher than the point (B).
Solving for $v_B$ in this equation gives us the answer to the first part of the question: \[ v_{B} = \sqrt{ 2 g|y_i|\sin\theta }. \]
Now for the second part of the motion. The law of conservation of energy dictates that: \[ K_i + U_{gi} + U_{si} = K_f + U_{gf} + U_{sf}, \] where now $i$ refers to the moment (B) and $f$ refers to the moment (C ). Initially the spring is uncompressed so $U_{si}=0$, and by the end of the motion the spring is compressed by a total of $\Delta y=|y_f-0|$[m], so its spring potential energy is $U_{sf}=\frac{1}{2}k|y_f|^2$. We choose the height of (C ) as the reference potential energy and thus $U_{gf}=0$. Since the difference in gravitational potential energy is $U_{gi} - U_{gf}=mgh=|y_f-0|\sin\theta$, we can fill-in the entire energy equation: \[ \frac{1}{2}m v_B^2 + mg|y_f|\sin\theta + 0 = 0 + 0 + \frac{1}{2}k|y_f|^2. \] Since $k$ and $m$ are given and we know $v_B$ from the first part of the question, we can solve for $|y_f|$ (a quadratic equation).
To obtain the answer $|y_f|$ in terms of $\Delta h$ we can use $\sum E_i = \sum E_f$ again, but this time $i$ will refer moment (A) and $f$ refers to the moment (C ). The energy equation becomes $mg\Delta h = \frac{1}{2}k|y_f|$ from which we obtain $|y_f|=\frac{ 2 mg\Delta h}{k}$.
Energy lost to friction
You have a block of mass 50[kg] on an incline. The force of friction between the block and the incline is 30N. The block slides for 200[m] down the incline. The incline is at a slope $\theta=30^\circ$ so the total vertical displacement of the block is $200\sin30=100$[m]. What is its speed as it reaches the bottom of the incline?
This is a problem in which initial energies are converted into final energies and some lost work: \[ \sum E_i = \sum E_f + W_{lost}. \] The term $W_{lost}$ represents the energy lost due to the friction.
Another (better) way of describing the situation is that the block had a negative amount of word done on it \[ \sum E_i + \underbrace{W_{done}}_{ \textrm{negative} } = \sum E_f. \] The quantity $W_{done}$ is negative because during the entire motion the friction force on the object was acting in the opposite direction to the motion: \[ W_{done} = \vec{F}\cdot \vec{d} = \|\vec{F}_f\|\|\vec{d}\|\cos(180^\circ) = - F_f\|\vec{d}\|, \] where $\vec{d}$ is the $200$[m] of sliding distance during which the friction acts. Since we are told that $F_f = 30$[N], we can calculate $W_{done} = W_{friction} = -30[\text{N}]\times 200[\text{m}] = -6000$[J].
We can now substitute this value into the conservation of energy equation: \[ \begin{align*} K_i + U_i + W_{done} &= K_f + U_f, \nl 0 + mgh + (-F_f|d|) &= \frac{1}{2}mv_f^2 + 0, \end{align*} \] where we have used the formula $mgh= U_i- U_f$ for the difference in gravitational potential energy. Substituting all the values we know we get \[ 0 + 50 \times 9.81 \times 100 - 6000 = \frac{1}{2}(50)v_f^2 + 0, \] which can be solved for $v_f$.
Discussion
In this section we saw that describing physical situation in terms of the energies involved is a useful way of thinking. The law of conservation of energy allows us to do simple “energy accounting” and calculate the values of unknown quantities.