The page you are reading is part of a draft (v2.0) of the "No bullshit guide to math and physics."
The text has since gone through many edits and is now available in print and electronic format. The current edition of the book is v4.0, which is a substantial improvement in terms of content and language (I hired a professional editor) from the draft version.
I'm leaving the old wiki content up for the time being, but I highly engourage you to check out the finished book. You can check out an extended preview here (PDF, 106 pages, 5MB).
Simple harmonic motion
Vibrations and oscillations are all around us. White light is made up of many oscillations of the electromagnetic field at different frequencies (colors). Sounds are made up of a combination of many air vibrations with different frequencies and strengths. In this section we will learn about simple harmonic motion, which describes the oscillation of a mechanical system at a fixed frequency and with a constant amplitude. By studying oscillations in their simplest form, you will pick up important intuition which you can apply to all other types of oscillations.
 The canonical example of simple harmonic motion is the motion of a mass-spring system
illustrated in the figure on the right. The block is free to slide along
the horizontal frictionless surface. If the system is disturbed from its
equilibrium position, it will start to oscillate back and forth at
a certain natural frequency, which depends on the mass of the block and the stiffness of the spring.
The canonical example of simple harmonic motion is the motion of a mass-spring system
illustrated in the figure on the right. The block is free to slide along
the horizontal frictionless surface. If the system is disturbed from its
equilibrium position, it will start to oscillate back and forth at
a certain natural frequency, which depends on the mass of the block and the stiffness of the spring.
In this section we will focus our attention on two mechanical systems: the mass-spring system and the simple pendulum. We will follow the usual approach and describe the positions, velocities, accelerations and energies associated with this type of motion. The notion of simple harmonic motion (SHM) is far more important than just these two systems. The equations and intuition developed for the analysis of the oscillation of these simple mechanical systems can be applied much more generally to sound oscillations, electric current oscillations and even quantum oscillations. Pay attention, that is all I am saying.
Concepts
- $A$: The amplitude of the movement, how far the object goes back and forth relative to the centre position.
- $x(t)$[m], $v(t)$[m/s], $a(t)$[m/s$^2$]: The position, velocity and acceleration of the object as functions of time.
- $T$[s]: The period of the motion, i.e., how long it takes for the motion to repeat.
- $f$[Hz]: The frequency of the motion.
- $\omega$[rad/s]: The angular frequency of the simple harmonic motion.
- $\phi$[rad]: The phase constant. The Greek letter $\phi$ is pronounced “phee”.
Simple harmonic motion
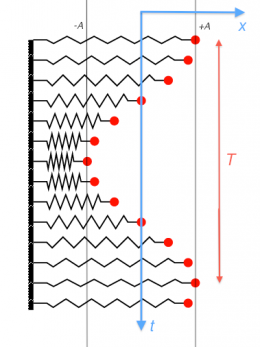 The figure on the right illustrates a mass-spring system undergoing simple harmonic motion.
Observe that the position of the mass as a function of time behaves like the cosine function.
From the diagram, we can also identify two important parameters of the motion: the amplitude $A$,
which describes the maximum displacement of the mass from the centre position,
and the period $T$, which describes how long it takes for the mass to come back to its initial position.
The figure on the right illustrates a mass-spring system undergoing simple harmonic motion.
Observe that the position of the mass as a function of time behaves like the cosine function.
From the diagram, we can also identify two important parameters of the motion: the amplitude $A$,
which describes the maximum displacement of the mass from the centre position,
and the period $T$, which describes how long it takes for the mass to come back to its initial position.
The equation which describes the position of the object as a function of time is the following: \[ x(t)=A\cos(\omega t + \phi). \] The constant $\omega$ (omega) is called the angular frequency of the motion. It is related to the period $T$ by the equation $\omega = \frac{2\pi}{T}$. The additive constant $\phi$ (phee) is called the phase constant or phase shift and its value depends on the initial condition for the motion $x_i\equiv x(0)$.
I don't want you to be scared by the formula for simple harmonic motion. I know there are a lot of Greek letters that appear in it, but it is actually pretty simple. In order to understand the purpose of the three parameters $A$, $\omega$ and $\phi$, we will do a brief review of the properties of the $\cos$ function.
Review of sin and cos functions
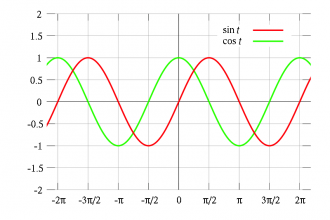 The functions $f(t)=\sin(t)$ and $f(t)=\cos(t)$ are periodic functions
which oscillate between $-1$ and $1$ with a period of $2\pi$.
Previously we used the functions $\cos$ and $\sin$ in order to find the horizontal and vertical components of vectors,
and called the input variable $\theta$ (theta).
However, in this section the input variable is the time $t$ measured in seconds.
Look carefully at the plot of the function $\cos(t)$.
As $t$ goes from $t=0$ to $t=2\pi$, the function $\cos(t)$ completes one full cycle.
The period of $\cos(t)$ is $T=2\pi$ because this is how long it takes
(in radians) for a point to go around the unit circle.
The functions $f(t)=\sin(t)$ and $f(t)=\cos(t)$ are periodic functions
which oscillate between $-1$ and $1$ with a period of $2\pi$.
Previously we used the functions $\cos$ and $\sin$ in order to find the horizontal and vertical components of vectors,
and called the input variable $\theta$ (theta).
However, in this section the input variable is the time $t$ measured in seconds.
Look carefully at the plot of the function $\cos(t)$.
As $t$ goes from $t=0$ to $t=2\pi$, the function $\cos(t)$ completes one full cycle.
The period of $\cos(t)$ is $T=2\pi$ because this is how long it takes
(in radians) for a point to go around the unit circle.
Time-scaling
To describe periodic motion with a different period, we can still use the $\cos$ function but we must add a multiplier in front of the variable $t$ inside the $\cos$ function. This multiplier is called the angular frequency and is usually denoted $\omega$ (omega). The input-scaled $\cos$ function: \[ f(t) = \cos(\omega t ), \] has a period of $T=\frac{2\pi}{\omega}$.
If you want to have a periodic function with period $T$, you should use the multiplier constant $\omega = \frac{2\pi}{T}$ inside the $\cos$ function. When you vary $t$ from $0$ to $T$, the function $\cos(\omega t )$ will go through one cycle because the quantity $\omega t$ goes from $0$ to $2\pi$. You shouldn't just take my word for this: try this for yourself by building a cos function with a period of 3 units.
The frequency of periodic motion describes how many times per second the motion repeats. The frequency is equal to the inverse of the period: \[ f=\frac{1}{T}=\frac{\omega}{2\pi} \text{ [Hz].} \] The relation between $f$ (frequency) and $\omega$ (angular frequency) is a factor of $2\pi$. This multiplier is needed since the natural cycle length of the $\cos$ function is $2\pi$ radians.
Output-scaling
If we want to have oscillations that go between $-A$ and $+A$ instead of between $-1$ and $+1$, we can multiply the $\cos$ function by the appropriate amplitude: \[ f(t)=A\cos(\omega t). \] The above function has period $T=\frac{2\pi}{\omega}$ and oscillates between $-A$ and $A$ on the $y$ axis.
Time-shifting
The function $A\cos(\omega t)$ starts from its maximum value at $t=0$. In the case of the mass-spring system, this corresponds to the case when the motion begins with the spring maximally stretched $x_i\equiv x(0)=A$.
In order to describe other starting positions for the motion, it may be necessary to introduce a phase shift inside the $\cos$ function: \[ f(t)=A\cos(\omega t + \phi). \] The constant $\phi$ must be chosen so that at $t=0$, the function $f(t)$ correctly describes the initial position of the system.
For example, if the harmonic motion starts from the centre $x_i \equiv x(0)=0$ and is initially going in the positive direction, then the equation of motion is described by the function $A\sin(\omega t)$. However, since $\sin(\theta)=\cos(\theta - \frac{\pi}{2})$ we can equally well describe the motion in terms of a shifted $\cos$ function: \[ x(t) = A\cos\!\left(\omega t - \frac{\pi}{2}\right) = A\sin(\omega t). \] Note that the function $x(t)$ correctly describes the initial position: $x(0)=0$.
By now, the meaning of all the parameters in the simple harmonic motion equation should be clear to you. The constant in front of the $\cos$ tells us the amplitude $A$ of the motion, the multiplicative constant $\omega$ inside the $\cos$ is related to the period/frequency of the motion $\omega = \frac{2\pi}{T} = 2\pi f$. Finally, the additive constant $\phi$ is chosen depending on the initial conditions.
Mass and spring
OK, enough math. It is time to learn about the first physical system which exhibits simple harmonic motion: the mass-spring system.
An object of mass $m$ is attached to a spring with spring constant $k$. If disturbed from rest, this mass-spring system will undergo simple harmonic motion with angular frequency: \[ \omega = \sqrt{ \frac{k}{m} }. \] A stiff spring attached to a small mass will result in very rapid oscillations. A weak spring or a large mass will result in slow oscillations.
A typical exam question will tell you $k$ and $m$ and ask about the period $T$. If you remember the definition of $T$, you can easily calculate the answer: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{ \frac{m}{k} }. \]
Equations of motion
The general equations of motion for the mass-spring system are as follows: \[ \begin{align} x(t) &= A\cos(\omega t + \phi), \nl v(t) &= -A\omega \sin(\omega t + \phi), \nl a(t) &= -A\omega^2\cos(\omega t + \phi). \end{align} \]
The general shape of the function $x(t)$ is $\cos$-like. The angular frequency $\omega$ parameter is governed by the physical properties of the system. The parameters $A$ and $\phi$ describe the specifics of the motion, namely, the size of the oscillation and where it starts from.
The function $v(t)$ is obtained, as usual, by taking the derivative of $x(t)$. The function $a(t)$ is obtained by taking the derivative of $v(t)$, which corresponds to the second derivative of $x(t)$.
Motion parameters
The velocity and the acceleration of the object are also periodic functions.
We can find the maximum values of the velocity and the acceleration by reading off the coefficient in front of the $\sin$ and $\cos$ in the functions $v(t)$ and $a(t)$.
- The maximum velocity of the object is
\[ v_{max} = A \omega. \]
- The maximum acceleration is
\[ a_{max} = A \omega^2. \] The velocity is maximum as the object passes through the centre, while the acceleration is maximum when the spring is maximally stretched (compressed).
You will often be asked to solve for the quantities $v_{max}$ and $a_{max}$ in exercises and exams. This is an easy task if you remember the above formulas and you know the values of the amplitude $A$ and the angular frequency $\omega$.
Energy
The potential energy stored in a spring which is stretched (compressed) by a length $x$ is given by the formula $U_s=\frac{1}{2}k x^2$. Since we know $x(t)$, we can obtain the potential energy of the mass-spring system as a function of time: \[ U_s(t)= \frac{1}{2} kx(t)^2 =\frac{1}{2}kA^2\cos^2(\omega t +\phi). \] The potential energy reaches its maximum value $U_{s,max}=\frac{1}{2}kA^2$ when the spring is fully stretched or fully compressed.
The kinetic energy of the mass as a function of time is given by: \[ K(t)= \frac{1}{2} mv(t)^2 = \frac {1}{2}m\omega^2A^2\sin^2(\omega t +\phi). \] The kinetic energy is maximum when the mass passes through the centre position. The maximum kinetic energy is given by $K_{max} = \frac{1}{2} mv_{max}^2= \frac{1}{2}mA^2\omega^2$.
Conservation of energy
The conservation of energy equation tells us that the total energy of the mass-spring system is conserved. The sum of the potential energy and the kinetic energy at any two instants $t_1$ and $t_2$ is the same: \[ U_{s1} + K_2 = U_{s2} + K_2. \]
It is also useful to calculate the total energy of the system $E_T = U_s(t) + K(t) = \text{const}$. This means that even if $U_s(t)$ and $K(t)$ change over time, the total energy of the system always remains constant.
We can use the identity $\cos^2\theta + \sin^2\theta =1$ to verify that the total energy is indeed a constant and that it is equal $U_{s,max}$ and $K_{max}$: \[ \begin{align} E_{T} &= U_s(t) + K(t) \nl &= \frac{1}{2}kA^2\cos^2(\omega t) + \frac {1}{2}m\omega^2A^2\sin^2(\omega t) \nl &= \frac{1}{2}m\omega^2A^2\cos^2(\omega t ) + \frac {1}{2}m\omega^2A^2\sin^2(\omega t ) \ \ \ (\text{since } k = m\omega^2 )\nl &= \frac{1}{2}m\underbrace{\omega^2A^2}_{v_{max}^2}\underbrace{\left[ \cos^2(\omega t) + \sin^2(\omega t)\right]}_{=1} = \frac{1}{2}mv_{max}^2 = K_{max} \nl & =\frac{1}{2}m(\omega A)^2 = \frac{1}{2}(m \omega^2) A^2 =\frac{1}{2}kA^2 = U_{s,max}. \end{align} \]
The best way to understand SHM is to visualize how the energy of the system shifts between the potential energy of the spring and the kinetic energy of the moving mass. When the spring is maximally stretched $x=\pm A$, the mass will have zero velocity and hence zero kinetic energy $K=0$. At this moment all the energy of the system is stored in the spring $E_T= U_{s,max}$. The other important moment is when the mass has zero displacement but maximal velocity $x=0, U_s=0, v=\pm A\omega, E_T=K_{max}$, which corresponds to all the energy being stored as kinetic energy.
Pendulum motion
We now turn our attention to another simple mechanical system whose motion is also described by the simple harmonic motion equations.
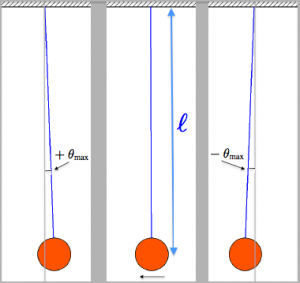 Consider a mass suspended at the end of a long string of length $\ell$ in a gravitational field of strength $g$.
If we start the pendulum from a certain angle $\theta_{max}$ away from the vertical position and then release it,
the pendulum will swing back and forth undergoing simple harmonic motion.
Consider a mass suspended at the end of a long string of length $\ell$ in a gravitational field of strength $g$.
If we start the pendulum from a certain angle $\theta_{max}$ away from the vertical position and then release it,
the pendulum will swing back and forth undergoing simple harmonic motion.
The period of oscillation is given by the following formula: \[ T = 2\pi \sqrt{ \frac{\ell}{g} }. \] Note that the period does not depend on the amplitude of the oscillation (how far the pendulum swings) nor the mass of the pendulum. The only factor that plays a role is the length of the string $\ell$. The angular frequency for a pendulum of length $\ell$ is going to be: \[ \omega \equiv \frac{2\pi}{T} = \sqrt{ \frac{g}{\ell} }. \]
We describe the position of the pendulum in terms of the angle $\theta$ that it makes with the vertical. The equations of motion are described in terms of angular variables: the angular position $\theta$, the angular velocity $\omega_\theta$ and the angular acceleration $\alpha_\theta$: \[ \begin{align} \theta(t) &= \theta_{max} \: \cos\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right), \nl \omega_\theta(t) &= -\theta_{max}\sqrt{ \frac{g}{\ell} } \: \sin\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right), \nl \alpha_\theta(t) &= -\theta_{max}\frac{g}{\ell} \: \cos\!\left( \sqrt{ \frac{g}{\ell} } t + \phi\right). \end{align} \] The angle $\theta_{max}$ describes the maximum angle that the pendulum swings to. Note how we had to use a new variable name $\omega_\theta$ for the angular velocity of the pendulum $\omega_\theta(t)=\frac{d}{dt}\!\left(\theta(t)\right)$, so as not to confuse it with the constant $\omega=\sqrt{ \frac{g}{\ell} }$ inside the $\cos$ function, which describes angular frequency of the periodic motion.
Energy
The motion of the pendulum is best understood by imagining how the energy of the system shifts between the gravitational potential energy of the mass and its kinetic energy.
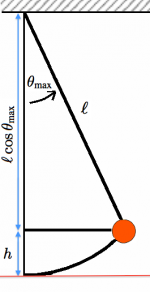 The pendulum will have a maximum potential energy when it swings to the side by the angle $\theta_{max}$.
At that angle, the vertical position of the mass will be increased by a height $h$ above the lowest point.
We can calculate $h$ as follows:
\[
h = \ell - \ell \cos \theta_{max}.
\]
Thus the maximum gravitational potential energy of the mass is therefore:
\[
U_{g,max}= mgh= mg\ell(1-\cos\theta_{max}).
\]
The pendulum will have a maximum potential energy when it swings to the side by the angle $\theta_{max}$.
At that angle, the vertical position of the mass will be increased by a height $h$ above the lowest point.
We can calculate $h$ as follows:
\[
h = \ell - \ell \cos \theta_{max}.
\]
Thus the maximum gravitational potential energy of the mass is therefore:
\[
U_{g,max}= mgh= mg\ell(1-\cos\theta_{max}).
\]
By the conservation of energy principle, the maximum kinetic energy of the pendulum must be equal to the maximum of the gravitational potential energy: \[ mg\ell(1-\cos\theta_{max}) = U_{g,max} = K_{max} = \frac{1}{2} mv_{max}^2, \] where $v_{max}=\ell \omega_\theta$ is the linear velocity of the mass as it swings through the centre.
Explanations
It is worthwhile to understand how the equations of simple harmonic motion come about. In this subsection, we will discuss how the equations are derived from Newton's second law $F=ma$.
Trigonometric derivatives
The slope (derivative) of the function $\sin(t)$ varies between $-1$ and $1$. The slope is largest when $\sin$ passes through the $x$ axis and the slope is zero when it reaches its maximum and minimum values. A careful examination of the graphs of the bare functions $\sin$ and $\cos$ reveals that the derivative of the function $\sin(t)$ is described by the function $\cos(t)$ and vice versa: \[ f(t) = \sin(t) \:\qquad \Rightarrow \qquad f'(t) = \cos(t), \] \[ f(t) = \cos(t) \qquad \Rightarrow \qquad f'(t) = -\sin(t). \] When you learn more about calculus you will know how to find the derivative of any function you want, but for now just take my word that the above two formulas are true.
The chain rule for derivatives tells us that the derivative of a composite function $f(g(x))$ is given by $f'(g(x))\cdot g'(x)$, i.e., you must take the derivative of the outer function and then multiply by the derivative of the inner function. We can use the chain rule to the find derivative of the simple harmonic motion position function: \[ x(t)=A\cos(\omega t +\phi) \ \ \Rightarrow \ \ v(t) \equiv x^{\prime}(t)=-A\sin(\omega t +\phi)(\omega) = -A\omega\sin(\omega t +\phi), \] where the outer function is $f(x)=A\cos(x)$ with derivative $f'(x)=-A\sin(x)$ and the inner function is $g(x)=\omega x +\phi$ with derivative $g'(x)=\omega$.
The same reasoning is used to obtain the second derivative: \[ a(t)\equiv \frac{d}{dt}\!\left\{ v(t) \right\} =-A\omega^2 \cos(\omega t +\phi) = -\omega^2 x(t). \] Note that $a(t)=x^{\prime\prime}(t)$ has the same form as $x(t)$, but always acts in the opposite direction.
I hope this clarifies for you how we obtained the functions $v(t)$ and $a(t)$: we simply took the derivative of the function $x(t)$.
Derivation of the mass-spring SHM equation
You may be wondering where the equation $x(t)=A\cos(\omega t + \phi)$ comes from. This formula looks very different from the kinematics equations for linear motion $x(t) = x_i + v_it + \frac{1}{2}at^2$, which we obtained starting from Newton's second law $F=ma$ after two integration steps.
In this section, we pulled the $x(t)=A\cos(\omega t + \phi)$ formula out of thin air, as if by revelation. Why did we suddenly start talking about $\cos$ functions and Greek letters with dubious names like phase. Are you phased by all of this? When I was first learning about simple harmonic motion, I was totally phased because I didn't see where the $\sin$ and $\cos$ came from.
The $\cos$ also comes from $F=ma$, but the story is a little more complicated this time. The force exerted by a spring is $F_{s} = -kx$. If you draw a force diagram on the mass, you will see that the force of the spring is the only force acting on it so we have: \[ \sum F = F_s =ma \qquad \Rightarrow \qquad -kx = ma. \] Recall that the acceleration is the second derivative of the position: \[ a=\frac{dv(t)}{dt} = \frac{d^2x(t)}{dt^2} = x^{\prime\prime}(t). \]
We now rewrite the equation $-kx = ma$ in terms of the function $x(t)$ and its second derivative: \[ \begin{align*} -kx(t) &= m\frac{d^2x(t)}{dt^2} \nl 0 & = m\frac{d^2x(t)}{dt^2}+ kx(t) \nl 0 & = \frac{d^2x(t)}{dt^2}+ \frac{k}{m}x(t). \end{align*} \]
This is called a differential equation. Instead of looking for an unknown number as in normal equations, in differential equations we are looking for an unknown function $x(t)$. We do not know what $x(t)$ is but we do know one of its properties, namely, that its second derivative $x^{\prime\prime}(t)$ is equal to the negative of $x(t)$ multiplied by some constant.
To solve a differential equation, you have to guess which function $x(t)$ satisfies this property. There is an entire course called Differential Equations, in which engineers and physicists learn how to do this guessing thing. Can you think of a function which, when multiplied by $\frac{k}{m}$, is equal to its second derivative?
OK, I thought of one: \[ x_1(t)=A_1 \cos\!\left( \sqrt{ \frac{k}{m}}t \right). \] Come to think of it, there is also a second one which works: \[ x_2(t)=A_2 \sin\!\left( \sqrt{ \frac{k}{m}}t \right). \] You should try this for yourself: verify that $x^{\prime\prime}_1(t) + \frac{k}{m}x_1(t)=0$ and $x^{\prime\prime}_2(t) + \frac{k}{m}x_2(t)=0$, which means that these functions are both solutions to the differential equation $x^{\prime\prime}(t)+\frac{k}{m} x(t)=0$. Since both $x_1(t)$ and $x_2(t)$ are solutions, any combination of them must also be a solution: \[ x(t) = A_1\cos(\omega t) + A_2\sin(\omega t). \] This is kind of the answer we were looking for. I say kind of because the function $x(t)$ is specified in terms of the coefficients $A_1$ and $A_2$ instead of the usual parameters: the amplitude $A$ and a phase $\phi$.
Lo and behold, using the trigonometric identity $\cos(a + b)=\cos(a)\cos(b) - \sin(a)\sin(b)$ we can express the function $x(t)$ as a time-shifted trigonometric function: \[ x(t)=A\cos(\omega t + \phi) = A_1\cos(\omega t) + A_2\sin(\omega t). \] The expression on the left is the preferred way of describing SHM because the parameters $A$ and $\phi$ corresponds to observable aspects of the motion.
Let me go over what just happened here one more time. Our goal was to find the equation of motion which predicts the position of an object as a function of time $x(t)$. To understand what is going on, let us draw an analogy with a situation which we have seen previously. In linear kinematics, uniform accelerated motion with $a(t)=a$ is described by the equation $x(t)=x_i+v_it + \frac{1}{2}at^2$ in terms of parameters $x_i$ and $v_i$. Depending on the initial velocity and the initial position of the object, we obtain different trajectories. Simple harmonic motion with angular frequency $\omega$ is described by the equation $x(t)=A\cos(\omega t + \phi)$ in terms of the parameters $A$ and $\phi$, which are the natural parameters for describing SHM. We obtain different harmonic motion trajectories depending on the values of the parameters $A$ and $\phi$.
Derivation of the pendulum SHM equation
To see how the SHM equation of motion arises in the case of the pendulum, we need to start from the torque equation $\mathcal{T}=I\alpha$.
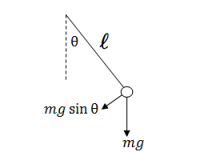 The diagram on the right illustrates how we can calculate the torque on the pendulum
which is caused by the force of gravity as a function of the displacement angle $\theta$.
Recall that the torque calculation only takes into account the $F_{\!\perp}$ component
of any force, since it is the only part which causes rotation:
\[
\mathcal{T}_\theta = F_{\!\perp} \ell = mg\sin\theta \ell.
\]
If we now substitute this into the equation $\mathcal{T}=I\alpha$,
we obtain the following:
\[
\begin{align*}
\mathcal{T} &= I \alpha \nl
mg\sin\theta(t) \ell &= m\ell^2 \frac{d^2\theta(t)}{dt^2} \nl
g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2}
\end{align*}
\]
The diagram on the right illustrates how we can calculate the torque on the pendulum
which is caused by the force of gravity as a function of the displacement angle $\theta$.
Recall that the torque calculation only takes into account the $F_{\!\perp}$ component
of any force, since it is the only part which causes rotation:
\[
\mathcal{T}_\theta = F_{\!\perp} \ell = mg\sin\theta \ell.
\]
If we now substitute this into the equation $\mathcal{T}=I\alpha$,
we obtain the following:
\[
\begin{align*}
\mathcal{T} &= I \alpha \nl
mg\sin\theta(t) \ell &= m\ell^2 \frac{d^2\theta(t)}{dt^2} \nl
g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2}
\end{align*}
\]
What follows is something which is not mathematically rigorous, but will allow us to continue and solve this problem. When $\theta$ is a small angle we can use the following approximation: \[ \sin(\theta)\ \approx \ \theta, \qquad \qquad \text{ for } \theta \ll 1. \] This type of equation is called a small angle approximation. You will see where it comes from later on when you learn about Taylor series approximations to functions. For now, you can convince yourself of the above formula by zooming many times on the graph of the function $\sin$ near the origin to see that $y=\sin(x)$ will look very much like $y=x$. Try this out.
Using the small angle approximation for $\sin\theta$ we can rewrite the equation involving $\theta(t)$ and its second derivative as follows: \[ \begin{align*} g\sin\theta(t) &= \ell \frac{d^2\theta(t)}{dt^2} \nl g\theta(t) &\approx \ell \frac{d^2\theta(t)}{dt^2} \nl 0 &= \frac{d^2\theta(t)}{dt^2}+ \frac{g}{\ell}\theta(t). \end{align*} \]
At this point we recognize that we are dealing with the same differential equation as in the case of the mass-spring system: $\theta^{\prime\prime}(t)+\omega^2 \theta(t)=0$, which has solution: \[ \theta(t) = \theta_{max}\cos(\omega t + \phi), \] where the constant inside the $\cos$ function is $\omega=\sqrt{\frac{g}{\ell}}$.
Examples
When asked to solve word problems, you will usually be told the initial amplitude $x_i=A$ or the initial velocity $v_i=\omega A$ of the SHM and the question will ask you to calculate some other quantity. Answering these problems shouldn't be too difficult provided you write down the general equations for $x(t)$, $v(t)$ and $a(t)$, fill-in the knowns quantities and then solve for the unknowns.
Standard example
You are observing a mass-spring system build from a $1$[kg] mass and a 250[N/m] spring. The amplitude of the oscillation is 10[cm]. Determine (a) the maximum speed of the mass, (b) the maximum acceleration, and (c ) the total mechanical energy of the system.
First we must find the angular frequency for this system $\omega = \sqrt{k/m}=\sqrt{250/1}=15.81$[rad/s]. To find (a) we use the equation $v_{max} = \omega A = 15.81 \times 0.1=1.58$[m/s]. Similarly, we can find the maximum acceleration using $a_{max} = \omega^2 A = 15.81^2 \times 0.1=25$[m$^2$/s]. There are two equivalent ways for solving (c ). We can obtain the total energy of the system by considering the potential energy of the spring when it is maximally extended (compressed) $E_T=U_s(A) = \frac{1}{2}kA^2 = 1.25$[J], or we can obtain the total energy from the maximum kinetic energy $E_T=K=\frac{1}{2}m v_{max}^2 = 1.25$[J].
Discussion
In this section we learned about simple harmonic motion, which is described by the equation $x(t)=A\cos(\omega t + \phi)$. You may be wondering what non-simple harmonic motion is. A simple extension of what we learned would be to study oscillating systems where the energy is slowly dissipating. This is known as damped harmonic motion for which the equation of motion looks like $x(t)=Ae^{-\gamma t}\cos(\omega t + \phi)$, which describes an oscillation whose magnitude slowly decreases. The coefficient $\gamma$ is known as the damping coefficient and indicates how fast the energy of the system is dissipated.
The concept of SHM comes up in many other areas of physics. When you learn about electric circuits, capacitors and inductors, you will run into equations of the form $v^{\prime\prime}(t)+\omega^2 v(t)=0$, which indicates that the voltage in a circuit is undergoing simple harmonic motion. Guess what, the same equation used to describe the mechanical motion of the mass-spring system will be used to describe the voltage in an oscillating circuit!
Links
[ Plot of the simple harmonic motion using a can of spray-paint. ]
http://www.youtube.com/watch?v=p9uhmjbZn-c
NOINDENT
[ 15 pendulums with different lengths. ]
http://www.youtube.com/watch?v=yVkdfJ9PkRQ
