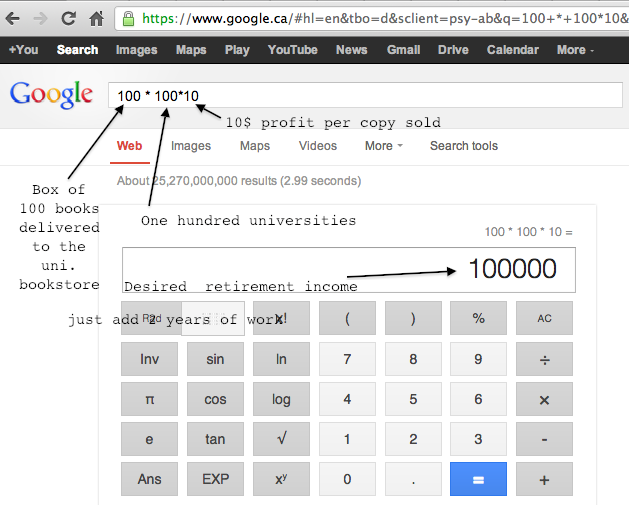
Professor Gilbert Strang’s video lectures on Linear Algebra have been recommended to me several times. I am very impressed with the first lecture. He presents all the important problems and concepts of LA in the first lecture and in a completely as-a-matter-of-fact way.
The lecture presents the problem of solving n equations in n unknowns in three different ways: the row picture, the column picture and the matrix picture.
In the row picture, each equation represents a line in the xy plane. When “solving” these equations simultaneously, we are looking for the point (x,y) which lies on both lines. In the case of the two lines he has on the board (2x-y=0 and -x+2y=3) the solution is the point x=1, y=2.
The second way to look the system of equations is to think of the column of x coefficients as a vector and to think of the column of y coefficients as another vector. In the column picture, solving the system of equations requires us to find the linear combination of the columns (i.e., $x$ times the first column plus $y$ times the second column) gives us the vector on the right hand side.
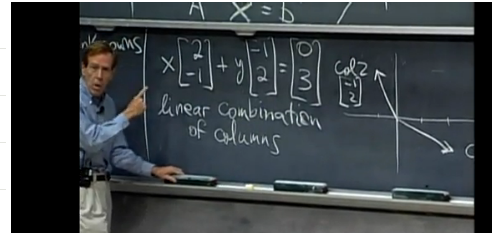
If students start off with this picture, they will be much less mystified (as I was) by the time they start to learn about the column space of matrices.
As a side benefit of this initial brush with linear algebra in the “column picture”, Prof. Strang is also able to present an intuitive picture for the formula for the product between a matrix and a vector. He says “Ax is the combination of the columns of A.” This way of explaining the matrix product is much more intuitive than the standard dot-product-of-row-times-column approach. Who has seen them dot products? What? Why? WTF?
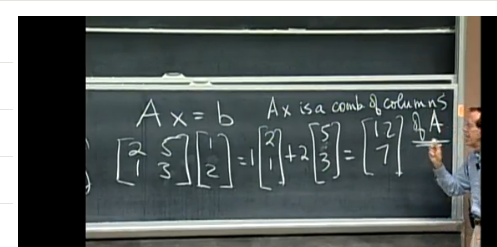
I will definitely include the “column picture” in the introductory chapter on linear algebra in the book. In fact, I have been wondering for some time how I can explain what the matrix product Ax. I want to talk about A as the linear transformation TA so that I can talk about the parallels between $x$, $f:R \to R$, $f^{-1}$ and $\vec{v}$, $A$, $A^{-1}$. Now I know how to fix the intro section!
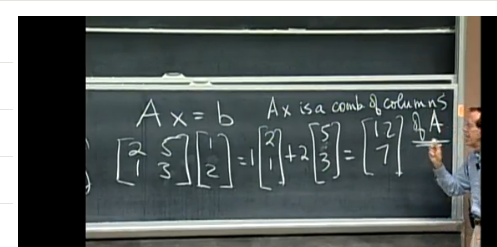
Clearly you are the master of the subject. It is funny that what started as a procrastination activity (watching a youtube video to which I just wanted to link to) led to an elegant solution to an old-standing problem which was blocking my writing. Sometimes watching can be productive 😉 Thank you Prof. Strang!
