I recently compiled a list of linear algebra textbook recommendations for people interested to learn more about linear algebra. These are the books I learned from while working on the No Bullshit Guide to Linear Algebra.
I recently compiled a list of linear algebra textbook recommendations for people interested to learn more about linear algebra. These are the books I learned from while working on the No Bullshit Guide to Linear Algebra.
Learning statistics is greatly facilitated by using a computational platform for doing statistics calculations and visualizations. You can do basic stats calculations using pen-and-paper for small datasets, but you’ll need a computer to help you with larger datasets. Common computational platforms for doing statistics include JASP, jamovi, SPSS, R, and Python, among many others. You can even do statistics calculations using spreadsheet software like Excel, LibreOffice calc, or Google Sheets. I believe using Python is the best computational platform for learning statistics. Specifically, an interactive notebook environment like JupyterLab provides the best-in-class tools for data visualizations and probability calculations.
But what about learners who are not familiar with Python? Should we abandon non-tech learners and say they can’t learn statistics because they don’t know how to use Python? Naaaah, we ain’t having none of that! Instead, my plan is to bring non-technical learners up to speed on Python by teaching them the Python basics that they need to use for statistics. Anyone can learn Python, it’s really not a big deal. I hope to convince you of this fact in this blog post, which is intended as a Python crash-course for the absolute beginner.
If I’ve learned anything about the startup world, it is that you have to listen to your customers, which in my case are the readers of the No Bullshit Guide textbooks. With this principle in mind, I sent out a survey to readers interested in the upcoming statistics requesting feedback on the general direction for the book, based on the stats curriculum and book proposal blog posts, the concept map, and the detailed book outline.
I’ll summarize the results of the survey below (140+ respondents) and comment on some of the readers’ suggestions and advice. The survey is still open in case you want to add your feedback, or feel free to send me an email directly. My email is ivan at this domain.
I was talking with friends recently about an interesting phenomenon that all self-taught programmers have observed, which we ended up calling “learning loops.” A learning loop is a process in which learners are motivated to advance their knowledge thanks to the positive feedback on their performance.
In this blog post, I want to look at the mechanics that make learning loops work and think about ways they could be used by teachers, private tutors, and publishers to build learning experiences in which learners have more agency and control over their learning. We’ll also look at the related phenomenon of game mechanics that exists in certain “addictive” computer games. Figure 1 contains a visual summary of the ideas we’ll discuss in this blog post. The two main questions we’re interested in are: “What can teachers within the formal educational system learn from autodidacts?” and “What can autodidacts learn from the gaming industry about staying motivated?”
In the second part of the blog post we’ll think about the role of teachers and educational resources in supporting and reinforcing learning loops. I’m writing this mostly as a self-reflection and welcome comments by other educators, content creators, and learning experience designers interested in this phenomenon.
Figure 1: The main question I’m interested in thinking about is how to introduce aspects of self-directed learning into the formal educational system, in order to give students more agency over their learning process.
Over the years several readers have suggested (sometimes demanded!) that I write a book on statistics. Indeed, since the company’s mission is to make the most useful parts of math accessible to the people, it makes sense to pursue statistics as the next title. Statistics is some of the most useful math out there! The 21st century is going to be all about data, so it makes sense to learn about the concepts and tools you need to analyze data, discover patterns, and make decisions.
I’ve now been working on the No Bullshit Guide to Statistics for three years so I figured it’s about time for an update to let y’all know how it’s going. My goals with this blog post are to share with you the detailed book outline and chapter previews, and also ask for your help to validate certain assumptions about the readers’ background (math and programming skills) and their motivation to learn statistics. Please jump to the short survey before continuing with the rest of the blog post. It won’t take longer than 2 mins.
Continue reading “No Bullshit Guide to Statistics progress update”
Let’s talk about the problems with the teaching of statistics. Understanding statistics is essential for many fields of academic research, and also useful in industry. Why is it that first-year statistics courses sucks so bad? It seems that conceptual understanding of statistics ideas only marginally improve after taking a STATS 101 course. Is this because statistics is a really difficult subject to teach, or are we teaching it wrong?
I’ve been looking into this question for the last three years and I finally have a plan for how we can improve things. I’ll start wiht a summary of the statistics curriculum—the set of topics students are supposed to learn in STATS 101. I’ll list all the topics of the “classical” curriculum based on analytical approximations like the t-test. This is the approach currently taught in most high schools and universities around the world.
The “classical” curriculum has a number of problems with it. The main problem is that it’s based on difficult to understand concepts, and these concepts are often presented as procedures to follow without understanding the details. The classical curriculum is also very narrow, since it covers a slim subset of all the possible types of statistical analysis that can be described as math formulas that can be used blindly by plugging in the numbers. In the end of the introductory stats course, students know a few “recipes” for statistical analysis they can apply if they ever run into one of the few scenarios where the recipe can be used (comparison of two proportions, comparison of two means, etc.). That’s nice, but in practice this leaves learners totally unprepared to solve all stats problems that don’t fit the memorized templates, which is most of the problems they will need to solve in their day-to-day life. The current statistics curriculum is simply outdated (developed in times when the only computation available was simple algebraic formulas for computing test statistics and lookup tables for finding p-values). The focus on formulas and use of analytical approximations in the classical curriculum limits learners development of adjacent skills like programming and data management. Clearly there is room for improvement here, we can’t let the next generation of scientists, engineers, and business folks grow up without basic data literacy.
Something must be done.
Continue reading “Fixing the introductory statistics curriculum”
I want to tell you about my journey to produce the ePub files for the No Bullshit Guide textbooks. This has been an epic battle with lots of technological obstacles, but I got it working in the end, and the results are beautiful:
In this blog post, I want to share what I’ve learned about generating ePub and Mobi files from LaTeX source files that contain lots of math equations. I feel this ought to be recorded somewhere for the benefit of other STEM authors and publishers who have LaTeX manuscripts and want to convert them to .epub and .mobi formats. Read on to watch the “How it’s made” episode about math eBooks.
The end-to-end book production pipeline looks like this:
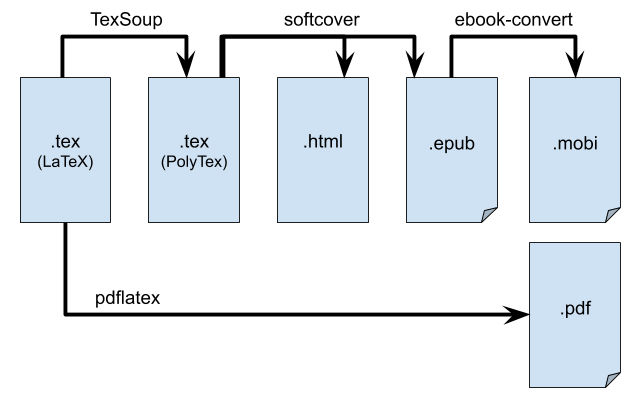
Figure 1: The eBook production pipeline described in this blog post. Each box represents a different markup format and the arrows indicate the software used to convert between formats. The hard step is to produce clean .html+MathJax format from the .tex source. The generation of the other formats is standard.
I’m happy to announce the No Bullshit Guide to Linear Algebra v2.2 is out. This update contains two years’ worth of text improvements based on readers’ feedback.
In this blog post I’ll summarize the changes to the book and provide some more context about why these changes were needed. I’ve included links to PDF excerpts of all the new sections[1,2,3,4] and a detailed red-blue diff that shows all edits.
Continue reading “No Bullshit Guide to Linear Algebra v2.2 update”
I’m happy to announce the No Bullshit Guide to Math & Physics version 5.4 has been released. This update contains two years’ worth of text improvements based on readers’ feedback and suggestions. The main focus of the edits was the math fundamentals chapter, making it easier to follow for beginners. The other big news is that the book is now available in .epub and .mobi formats.
In this blog post I’ll give an overview of the changes to the book with additional comments about the importance of each change. I’ve included links to PDF excerpts of all the new sections[1,2,3,4,5,6] as well as a detailed red-blue diff that shows all edits. All this with the goal to make the PDFs linked to from this blog post to contain a the complete “patch” information for readers who have an older version of the book.
Continue reading “No Bullshit Guide to Math & Physics v5.4 update”
I have been working on a French translation for the math book and in the process I stumbled upon some really powerful “authoring hacks” that I would like to describe here in case they might be useful for other bilingual authors and educators.
Before we begin with the “How it’s made” episode, let me show you some examples of the final product. I have selected the best four “backports” — explanations that now exist in the English version thanks to the additions in the French version.
Contuinuez à lire si ça a l’air intéressant. Read on if you’re interested.